Построение сечений многогранников

А вы знаете, что называется сечением многогранников плоскостью? Если вы пока сомневаетесь в правильности своего ответа на этот вопрос, то можете довольно просто себя проверить. Предлагаем пройти небольшой тест, представленный ниже.

Вопрос. Назовите номер рисунка, на котором изображено сечение параллелепипеда плоскостью?

Итак, правильный ответ – на рисунке 3.

Если вы ответите правильно, это подтверждает то, что вы понимаете, с чем имеете дело. Но, к сожалению, даже правильный ответ на вопрос-тест не гарантирует вам наивысших отметок на уроках по теме «Сечения многогранников». Ведь самым сложным является не распознавание сечений на готовых чертежах, хотя это тоже очень важно, а их построении.

Для начала сформулируем определение сечения многогранника. Итак, сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.

Теперь потренируемся быстро и безошибочно строить точки пересечения данной прямой с заданной плоскостью. Для этого решим следующую задачу.

Построить точки пересечения прямой MN с плоскостями нижнего и верхнего оснований треугольной призмы ABCA₁B₁C₁, при условии, что точка M принадлежит боковому ребру CC₁, а точка N – ребру BB₁.

Начнем с того, что продлим на чертеже прямую MN в обе стороны (рис. 1). Затем, чтобы получить необходимые по уловию задачи точки пересечения, продлеваем и прямые, лежащие в верхнем и нижнем основаниях. И вот наступает  самый сложный момент в решении задачи: какие именно прямые в обоих основаниях необходимо продлить, так как в каждом из них имеется по три прямые.

Чтобы правильно сделать заключительный шаг построения, необходимо определить, какие из прямых оснований находятся в той же плоскости, что и интересующая нас прямая MN. В нашем случае – это прямая CB в нижнем и C

1B₁ в верхнем основаниях. И именно их и продлеваем до пересечения с прямой NM (рис. 2).

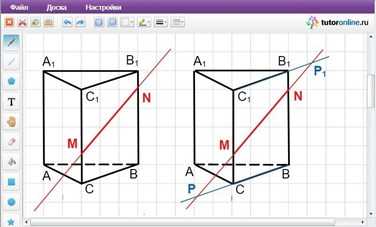
Полученные точки P и P₁ и есть точки пересечения прямой MN с плоскостями верхнего и нижнего оснований треугольной призмы ABCA₁B₁C₁.  

После разбора представленной задачи можно перейти непосредственно к построению сечений многогранников. Ключевым моментом здесь будут рассуждения, которые и помогут прийти к нужному результату. В итоге постараемся в итоге составить шаблон, который будет отражать последовательность действий при решении задач данного типа.   

Итак, рассмотрим следующую задачу. Построить сечение треугольной призмы ABCA₁B₁C₁ плоскостью, проходящей через точки X, Y, Z, принадлежащие ребрам AA₁, AC и BB₁ соответственно.

Решение: Выполним чертеж и определим, какие пары точек лежат в одной плоскости.

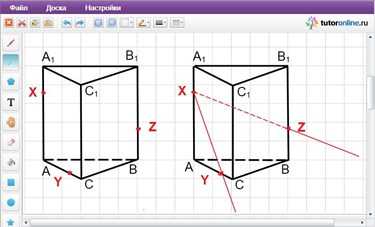Пары точек X и Y, X и Z можно соединить, т.к. они лежат в одной плоскости.

Построим дополнительную точку, которая будет лежать в той же грани, что и точка Z. Для этого продлим прямые XY и СС₁, т.к. они лежат в плоскости грани AA₁C₁C. Назовем полученную точку P.

Точки P и Z лежат в одной плоскости – в плоскости грани CC₁B₁B. Поэтому можем их соединить. Прямая PZ пересекает ребро CB в некоторой точке, назовем ее T. Точки Y и T лежат в нижней плоскости призмы, соединяем их. Таким образом, образовался четырехугольник YXZT, а это и есть искомое сечение.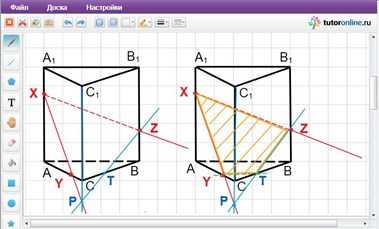 

Подведем итог. Чтобы построить сечение многогранника плоскостью, необходимо:

1) провести прямые через пары точек, лежащих в одной плоскости.

2) найти прямые, по которым пересекаются  плоскости сечения и грани многогранника. Для этого нужно найти точки пересечения прямой, принадлежащей плоскости сечения, с прямой, лежащей в одной из граней.

Процесс построения сечений многогранников сложен тем, что в каждом конкретном случае он различен. И никакая теория не описывает его от начала и до конца. На самом деле есть только один верный способ научиться быстро и безошибочно строить сечения любых многогранников – это постоянная практика. Чем больше сечений вы построите, тем легче в дальнейшем вам будет это делать.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Построение сечений многогранника на примере призмы

Слайд 1

Построение сечений многогранников на примере пр измы ® Создатели : Антон Дмитриев, Киреев Александр. При содействии: Гудковой Ольги Викторовны

Слайд 2

План урока Алгоритмы построения сечений Самопроверка Демонстрационные задачи Задачи для закрепления материала

Слайд 3

Алгоритмы построения сечений следов параллельных прямых параллельного переноса секущей плоскости внутреннего проектирования комбинированный метод дополнения n -угольной призмы до треугольной призмы Построение сечения методом :

Слайд 4

Построение сечения методом следов Основные понятия и умения Построение следа прямой на плоскости Построение следа секущей плоскости Построение сечения

Слайд 5

Алгоритм построения сечения методом следов Выяснить имеются ли в одной грани две точки сечения (если да, то через них можно провести сторону сечения). Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом). Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани. Выполнить п.1.

Слайд 6

Построение сечения призмы Двух точек принадлежащих одной грани нет. Точка R лежит в плоскости основания. Найдем след прямой KQ на плоскости основания: — KQ ∩K1Q1=T1, T1R- след сечения. 3. T1R ∩CD=E. 4. Проведем EQ. EQ∩DD1=N. 5. Проведем NK. NK ∩AA1=M. 6. Соединяем M и R . Построить сечение плоскостью α , проходящей через точки K,Q,R; K є ADD1, Q є CDD1, R є AB.

Слайд 7

Метод параллельных прямых В основу метода положено свойство параллельных плоскостей: «Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Основные умения и понятия Построение плоскости параллельной данной Построение линии пересечения плоскостей Построение сечения

Слайд 8

Алгоритм построения сечения методом параллельных прямых. Строим проекции точек, определяющих сечение. Через две данные точки (например P и Q ) и их проекции проводим плоскость. Через третью точку (например R) строим параллельную ей плоскость α . Находим линии пересечения (например m и n) плоскости α с гранями многогранника содержащими точки P и Q . Через точку R проводим прямую а параллельную PQ . Находим точки пересечения прямой а с прямыми m и n. Находим точки пересечения с ребрами соответствующей грани.

Слайд 9

(ПРИЗМА) Строим проекции точек P и Q на плоскости верхнего и нижнего оснований. Проводим плоскость P1Q1Q2P2. Через ребро, содержащее точку R, проводим плоскость α параллельную P1Q1Q2. Находим линии пересечения плоскостей ABB1 и CDD1 с плоскость α . Через точку R проводим прямую a||PQ . a∩n=X, a∩m=Y. XP∩AA1=K, XP∩BB1=L; YQ∩CC1=M, YQ∩DD1=N. KLMNR – искомое сечение. Построить сечение плоскостью α , проходящей через точки P,Q,R; P є ABB1, Q є CDD1, R є EE1.

Слайд 10

Метод параллельного переноса секущей плоскости Строим вспомогательное сечение данного многогранника, которое удовлетворяет следующим требованиям: оно параллельно секущей плоскости; в пересечении с поверхностью данного многогранника образует треугольник. Соединяем проекцию вершины треугольника с вершинами той грани многогранника, которую пересекает вспомогательное сечение, и находим точки пересечения со стороной треугольника, лежащей в этой грани. Соединяем вершину треугольника с этими точками. Через точку искомого сечения проводим прямые параллельные построенным отрезкам в предыдущем пункте и находим точки пересечения с ребрами многогранника.

Слайд 11

ПРИЗМА R є AA1, P є EDD1, Q є CDD1. Построим вспомогательное сечение AMQ1 ||RPQ. Проведем AM||RP, MQ1||PQ, AMQ1∩ABC=AQ1. P1- проекция точек Р и М на АВС. Проведем Р1В и Р1С. Р1В∩ AQ1=O1, P1C ∩ AQ1=O2. Через точку Р проведем прямые m и n соответственно параллельные МО1 и МО2. m∩BB1=K, n∩CC1=L. LQ∩DD1=T, TP∩EE1=S. RKLTS – искомое сечение Построить сечение призмы плоскостью α , проходящей через точки P,Q,R; P є EDD1, Q є CDD1, R є AA1 .

Слайд 12

Алгоритм построения сечения методом внутреннего проектирования. Построить вспомогательные сечения и найти линию их пересечения. Построить след сечения на ребре многогранника. Если точек сечения не хватает для построения самого сечения повторить пп.1-2.

Слайд 13

Построение вспомогательных сечений. ПРИЗМА Параллельное проектирование .

Слайд 14

Построение следа сечения на ребре

Слайд 15

Комбинированный метод. Через вторую прямую q и какую-нибудь точку W первой прямой р провести плоскость β . В плоскости β через точку W провести прямую q‘ параллельную q . Пересекающимися прямыми p и q‘ определяется плоскость α . Непосредственное построение сечения многогранника плоскостью α Суть метода состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом. Применяется для построения сечения многогранника с условием параллельности. 1. Построение сечения многогранника плоскостью α , проходящей через заданную прямую p параллельно другой заданной прямой q .

Слайд 16

ПРИЗМА Построить сечение призмы плоскостью α , проходящей через прямую PQ параллельно AE1; P є BE, Q є E1C1. 1. Проведем плоскость через прямую AE1 и точку P. 2. В плоскости AE1P через точку P проведем прямую q’ параллельную AE1. q’∩E1S’=K. 3. Пересекающимися прямыми PQ и PK определяется искомая плоскость α. 4. P1 и K1- проекции точек Р и К на А1В1С1. P1K1∩PK=S”. S”Q∩E1D1=N, S”Q∩B1C1=M, NK∩EE1=L; MN∩A1E1=S”’, S”’L∩AE=T, TP∩BC=V. TVMNL-искомое сечение.

Слайд 17

Метод дополнения n -угольной призмы(пирамиды) до треугольной призмы(пирамиды). Данная призма(пирамида) достраивается до треугольной призмы(пирамиды) из тех граней на боковых ребрах или гранях которой лежат точки, определяющие искомое сечение. Строится сечение полученной треугольной призмы(пирамиды). Искомое сечение получается как часть сечения треугольной призмы(пирамиды).

Слайд 18

Основные понятия и умения Построение вспомогатель- ных сечений Построение следа сечения на ребре Построение сечения Центральное проектирование Параллельное проектирование

Слайд 19

ПРИЗМА Q є BB1C1C, P є AA1, R є EDD1E1. Достраиваем призму до треугольной. Для этого продлим стороны нижнего основания: AE, BC, ED и верхнего основания: A 1 E 1 , B 1 C 1 , E 1 D 1. AE ∩BC=K, ED∩BC=L, A1E1∩B1C1=K1, E1D1∩B1C1=L1. Строим сечение полученной призмы KLEK1L1E1 плоскостью PQR , используя метод внутреннего проектирования. Это сечение является частью искомого. Строим искомое сечение.

Слайд 20

Правило для самоконтроля Если многогранник выпуклый, то сечение выпуклый многоугольник. Вершины многоугольника всегда лежат на ребрах многогранника. Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении. Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении. Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника. Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Слайд 21

Базовые задачи на построение сечений многогранников Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей. M є AD, N є DCC1, D1 ; ABCDA1B1C1D1- куб M є ADD1, D1 є ADD1, MD1. D1 є D1DC, N є D1DC, D1N ∩ DC=Q. M є ABC, Q є ABC, MQ. II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. M є CC1, AD1; ABCDA1B1C1D1- куб. MK||AD1, K є BC. M є DCC1, D1 є DCC1, MD1. A є ABC, K є ABC, AK.

Слайд 22

III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер трехгранного угла). M є AB, N є AA1, K є A1D1; ABCDA1B1C1D1- куб. NK∩AD=F1 — вершина трехгранного угла образованного плоскостями α , ABC, ADD1. F1M∩CD=F2 — вершина трехгранного угла образованного плоскостями α , ABC, CDD1. F1M ∩BC=P. NK∩DD1=F3 — вершина трехгранного угла образованного плоскостями α , D1DC, ADD1. F3F2∩D1C1=Q, F3F2∩CC1=L. IV. Если плоскость проходит через прямую, параллельную другой плоскости и пересекает ее, то линия пересечения параллельна данной прямой. A1, C, α ||BC1; ABCA1B1C1- призма. α∩ BCC1=n, n||BC1, n∩BB1=S. SA1∩AB=P. Соединяем A1,P и C.

Слайд 23

V. Если прямая лежит в плоскости сечения, то точка ее пересечения с плоскостью грани многогранника является вершиной трехгранного угла, образованного сечением, гранью и вспомогательной плоскостью, содержащей данную прямую. M є A1B1C1, K є BCC1, N є ABC; ABCDA1B1C1- параллелепипед. 1 . Вспомогательная плоскость MKK1: MKK1∩ABC=M1K1, MK∩M1K1=S, MK∩ABC=S, S- вершина трехгранного угла образованного плоскостями : α , ABC, MKK1. 2. SN∩BC=P, SN∩AD=Q, PK∩B1C1=R, RM∩A1D1=L.

Слайд 24

Задачи . На каком рисунке изображено сечение куба плоскостью ABC ? Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе? Давайте вспомним этапы построения сечений тетраэдра (параллелепипеда, куба). Какие многоугольники могут при этом получиться?

nsportal.ru

Призма и её виды. Сечение призмы плоскостью. Поверхность призмы.

Призма – многогранник, две грани которого в n-угольнике расположены в параллельных плоскостях, а остальные грани параллелограммы.

Основание призмы, боковые ребра, ребра основания-стороны основания, боковые грани, вершины призмы-вершины оснований.

Высота призмы – это расстояние между основаниями.

Виды призм:

1. Прямая призма. Призма прямая, если боковые ребра перпендикулярны основанию.

2. Наклонная призма. Призма наклонная, если боковые ребра не перпендикулярны

3. Правильная призма. Призма правильная если призма прямая и в основании призмы лежит правильный n-угольник.

Диагональ призмы – отрезок, соединяющий две вершины призмы, не принадлежащей ни к одной грани.

Диагональное сечение – это сечение, содержащее диагональ призмы.

Перпендикулярное сечение– это сечение, проходящее перпендикулярно боковым ребрам призмы.

Объем наклонной призмы:

Объем прямой призмы:

 

Параллелепипед. Его виды. Свойства граней и диагоналей. Поверхность параллелепипеда.

Параллелепипед – это призма, в основании которой лежит параллелограмм

Виды параллелепипеда:

1. Наклонный – это наклонная призма, в основании которой лежит параллелограмм

2. Прямой – это прямая призма, в основании которой лежит параллелограмм

3. Прямоугольный– это прямая призма, в основании которого прямоугольник

Свойства граней и диагоналей:

1. В параллелепипеде противоположные грани параллельны и равны

2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам

3. Длины трех непараллельных ребер прямоугольного параллелепипеда называются его

критериями. Сумма квадратов этих измерений равна квадрату диагоналей.

Объем прямоуг. парал-да:

Пирамида. Правильная пирамида. Поверхность пирамиды. Объем пирамиды.

Пирамида – многогранник, у которого одна грань который произвольный n-угольник, а остальные грани – треугольники, имеющие одну вершину

Высота пирамиды – длина перпендикуляра, опущенного из вершины пирамиды на плоскость основания.

Пирамида называется правильной, если в основании пирамиды лежит правильный n-угольник и вершина пирамиды проектируется в центр основания (описанной вписанной окружности). В ней все боковые грани равнобедренные треугольники. Все ребра и грани наклонены под одним углом.

Апофема – это высота боковой грани правильной пирамиды.

Диагональное сечение пирамиды – сечение, проходящее через диагональ, вершину.

Те пирамиды, которые не являются правильными, называются произвольными.

Треугольная призма называется тетраэдром.

Объем пирамиды:

 

Усеченная пирамида. Нахождение полной поверхности и объема.

Усеченная пирамида – это многогранник, расположенный между основанием пирамиды и плоскостью сечения, параллельному основанию.

Теорема: площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему (высоту боковой грани). S_б = 1/2 *P_осн*ha

Чтобы найти площадь полной поверхности пирамиды нужно к площади боковой поверхности прибавит площадь основания S_полн. = S_б+S_осн

Для произвольной пирамиды площадь боковой поверхности равна сумме боковых граней

S_б= S_sac+S_scb+ S_sab. Чтобы найти полную: S_полн. = S_б+S_осн

Объем усеченной пирамиды:

 

Понятие о правильных многогранниках.

Правильный многогранник— это выпуклый многогранник с максимально возможной симметрией.

Многогранник называется правильным, если: Он выпуклый; Все его грани являются равными правильными многоугольниками; В каждой его вершине сходится одинаковое число рёбер.

 

Цилиндр. Его поверхность. Объем.

Состоит из радиуса основания, оси вращения и образующей.

Цилиндр– фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.

S_б=2π*r*h;h-высота цилиндра, hr-радиус основания

S_полн. = Sб+2S

осн ; S_осн= π*r²

Осевое сечение цилиндра– это сечение, проходящее через диаметр основания и ось цилиндра.

 

Рекомендуемые страницы:

lektsia.com

Пошаговое построение сечения шестиугольной призмы

В этой статье приведено несколько примеров пошагового построения сечения правильной шестиугольной призмы методом следов. Иногда к методу следов был взят в помощь аксиоматический метод. Я старалась избегать пользоваться методом внутреннего проецирования намеренно, чтобы показать построение именно методом следов.

Задача 1. Построить методом следов  сечение шестиугольной призмы плоскостью, проходящей через точки .

Задача 1. Дано.

Шаг 1. Проведем прямую , принадлежащую плоскости сечения. Благодаря тому, что точки и лежат в основании призмы, прямая также принадлежит плоскости основания, а значит, будет пересекаться с другими прямыми, также лежащими в этой плоскости. Тогда можно провести прямую , и определить точку пересечения и – . Точка принадлежит плоскости грани , поскольку прямая принадлежит ей.

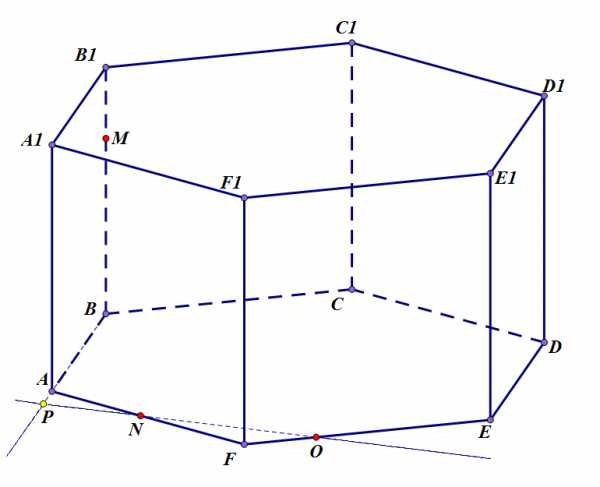
Задача 1. Шаг 1.

Шаг 2. Точки и можно соединить прямой. Прямая пересечет ребро в точке . Проводим прямую в плоскости основания и находим ее пересечение с прямой – точку .

Задача 1. Шаг 2.

Шаг 3. Через точки и проводим прямую. Она принадлежит плоскости грани , поэтому обязательно пересечется с прямой этой плоскости – в точке . Точка лежит “под” призмой, ниже ее основания. Точка , благодаря принадлежности прямой , также принадлежит и плоскости грани , а в этой плоскости у нас имеется точка – точка .

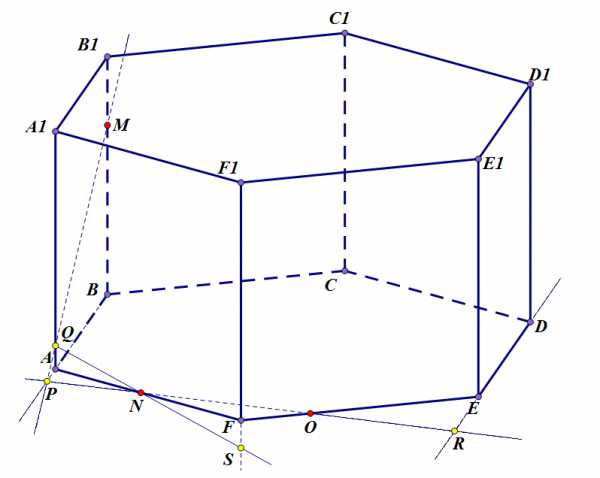
Задача 1. Шаг 3.

Шаг 4. Следовательно, можно соединить точки и прямой. Эта прямая пересечет ребро в точке .

Задача 1. Шаг 4.

Шаг 5. Точка принадлежит прямой , а следовательно, лежит в плоскости грани , таким образом, ее можно соединить с точкой этой же плоскости прямой . Эта прямая пересечет ребро в точке . Для дальнейшего построения нам нужны точки в плоскости верхней грани призмы. Добудем их. Продлим прямую до пересечения с прямой . Отметим точку .

Задача 1. Шаг 5.

Шаг 6. Проведем прямую , принадлежащую грани , и найдем точку ее пересечения с прямой – точку . Тогда точки и принадлежат плоскости верхней грани (за счет принадлежности прямым этой плоскости) и их можно соединять прямой.

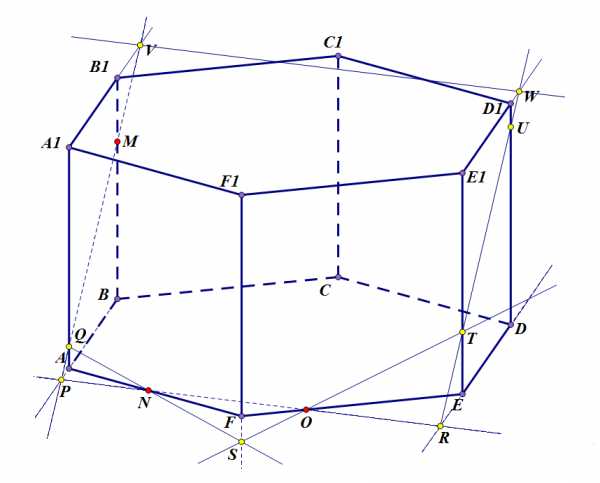
Задача 1. Шаг 6.

Шаг 7. Находим точки пересечения прямой с ребрами и – точки и .

Задача 1. Шаг 7.

Шаг 8. Соединяем все полученные точки отрезками.

Задача 1. Шаг 8.

Окончательный вид сечения:

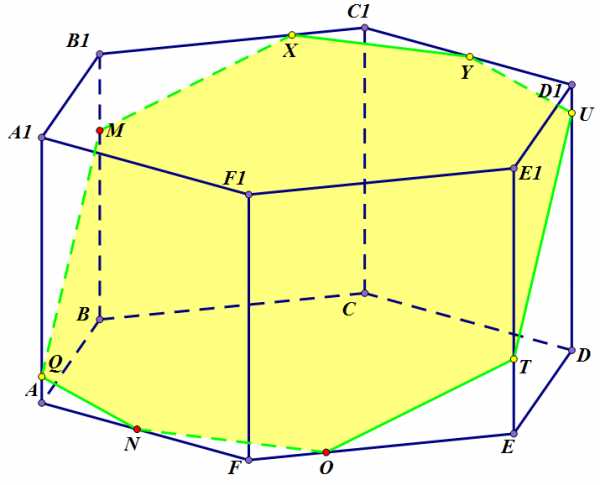
Окончание построения

 

Задача 2. Построить методом следов  сечение шестиугольной призмы плоскостью, проходящей через точки .

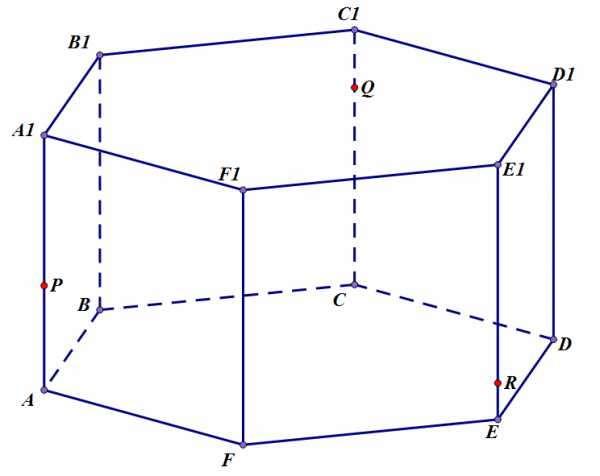
Задача 2. Дано

Шаг 1. Проведем прямую . Она принадлежит секущей плоскости. Также проведем проекцию этой прямой на плоскость нижнего основания призмы – прямую . Точка их пересечения одновременно принадлежит секущей плоскости и плоскости нижнего основания призмы. Обозначим ее .

Задача 2. Шаг 1.

Шаг 2. Аналогично поступим с точками и : проводим прямую и ее проекцию в плоскости нижнего основания. Их пересечение – точка секущей плоскости , одновременно лежащая в нижнем основании.

Задача 2. Шаг 2.

Шаг 3. Имея две точки в плоскости нижнего основания, проведем через них прямую , точки которой принадлежат секущей плоскости.

Проведем прямую . Она лежит в плоскости основания, но одновременно – в плоскости боковой грани, поэтому ее точки принадлежат этой боковой грани. Точка пересечения прямых и , таким образом, принадлежит плоскости боковой грани призмы и плоскости сечения.

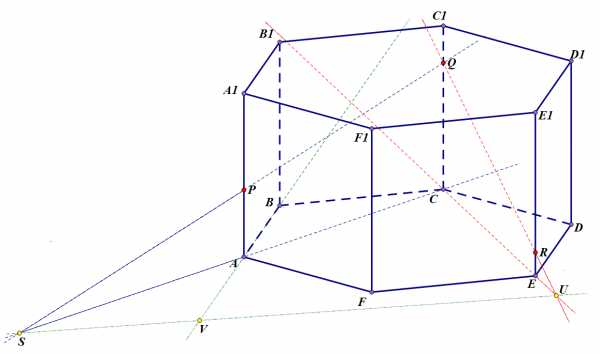
Задача 2. Шаг 3.

Шаг 4. Проводим прямую в плоскости боковой грани и отыскиваем точку пересечения ею ребра – точку .

Осталось немного: найти точку плоскости сечения на ребре , и пару точек в плоскости основания.

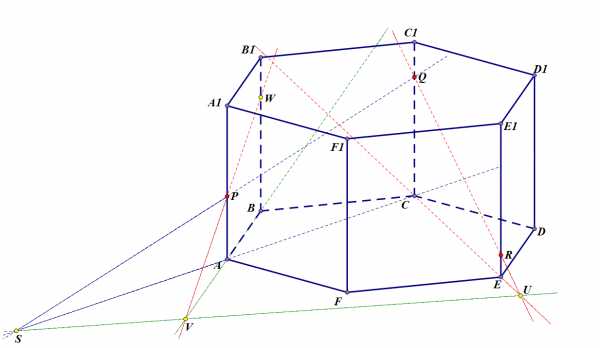
Задача 2. Шаг 4.

Шаг 5. Проведем прямые и в плоскости основания. Они пересекут прямую секущей плоскости в точках и .

Задача 2. Шаг 5.

Шаг 6. Точки и принадлежат плоскости грани , проведем через них прямую. Найдем точку, где эта прямая пересечет ребро – точку . Точки и лежат в плоскости грани . Проводим через них прямую и находим точку пересечения этой прямой с ребром – .

 

Задача 2. Шаг 6.

Шаг 7. Соединяем точки отрезками.

Задача 2. Шаг 7.

Окончательный вид построенного сечения:

Окончательный вид построенного сечения

 

Задача 3. Построить методом следов  сечение шестиугольной призмы плоскостью, проходящей через точки .

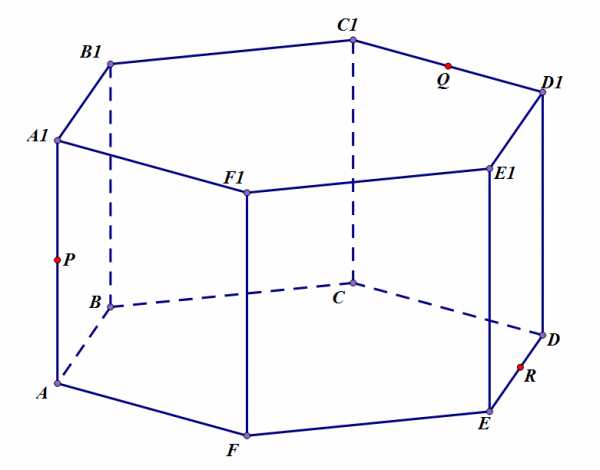
Задача 3. Дано

Шаг 1. Проводим прямую секущей плоскости, а также ее проекцию в плоскости основания . Прямая принадлежит плоскости основания и пересечет прямую в точке . Заметим, что точка не является точкой секущей плоскости.

Задача 3. Шаг 1.

Шаг 2. Из точки проводим перпендикуляр к плоскости основания (к прямой ), его пересечение с прямой – точка – принадлежит секущей плоскости, а также плоскости грани .

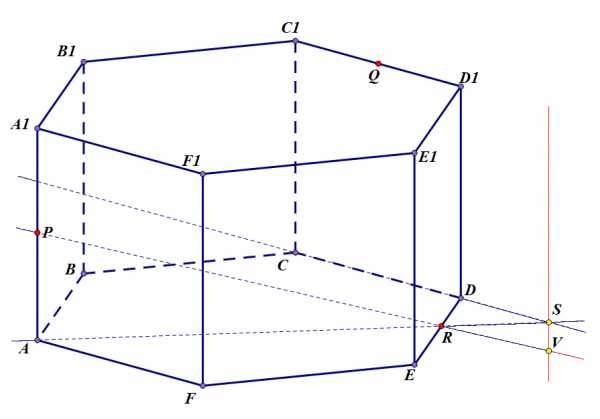
Задача 3. Шаг 2.

Шаг 3. Соединим точки и . Прямая пересечет ребро призмы в точке .

Задача 3. Шаг 3.

Шаг 4. Заполучив точку , можем провести отрезок . Вот тут-то нам и понадобится аксиоматический метод. Так как грань    параллельна грани , то плоскость рассечет ее по прямой, которая будет параллельна . Вот и проведем через такую параллельную прямой прямую. Она пересечет ребро в точке .

Задача 3. Шаг 4.

Шаг 5. Проведем также через точку прямую, параллельную прямой . Это можно сделать, так как грань параллельна грани . Прямая эта пересечет ребро в точке .

Задача 3. Шаг 5.

Шаг 6. Соединяем точки отрезками.

Задача 3. Шаг 6.

Окончательный вид:

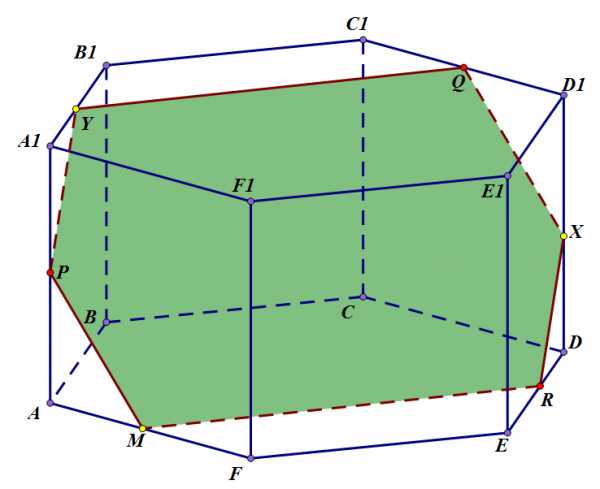
Задача 3. Окончательный вид

 

 

Задача 4. Построить методом следов  сечение шестиугольной призмы плоскостью, проходящей через точки .

Задача 4. Дано

Шаг 1. Через точки и проводим прямую секущей плоскости. Также проведем проекции этой прямой на верхнее и нижнее основание – на верхнее, и – на нижнее. Точки пересечения прямой с проекциями – это точки прокола данной прямой оснований призмы. Верхнее основание прямая прошьет в точке , а нижнее – в точке . Таким образом, мы заполучили точки секущей плоскости в плоскостях верхнего и нижнего оснований.

Задача 4. Шаг 1.

Шаг 2. Точки и принадлежат одной плоскости, проводим через них прямую. Эта прямая даст нам две точки: точку , в которой она пересечет ребро , и точку , в которой она пересечет ребро .

Шаг 3. Приобретя точку в грани , проведем прямую . Она пересечет ребро в точке .

Задача 4. Шаги 2-3.

Шаг 4.  Проведем через точку в плоскости основания призмы прямую, параллельную прямой (или можно провести через точки и ). Эта прямая пересечет ребро в точке .

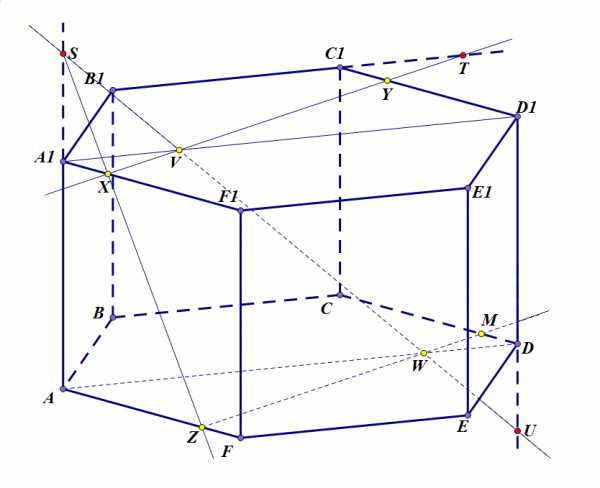
Задача 4. Шаг 4.

Шаг 5.  Соединяем точки  отрезками.

Задача 4. Шаг 5.

Окончательный вид:

Окончательный вид сечения

easy-physic.ru

Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Стереометрия

Сечения призмы

     Определение 1.Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости  α.

      В качестве примера рассмотрим сечение куба куба   ABCDA₁B₁C₁D₁   плоскостью, проходящей через точку   D  и середины ребер   A₁B₁   и   B₁C₁ . Рассмотрим процесс построения сечения подробно.

      Обозначим буквами   E   и   F середины ребер   A₁B₁   и   B₁C₁ (рис. 1).

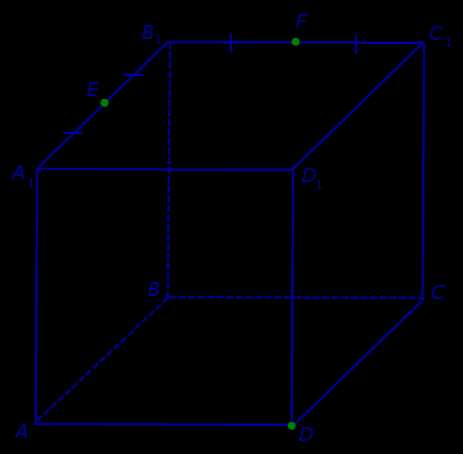
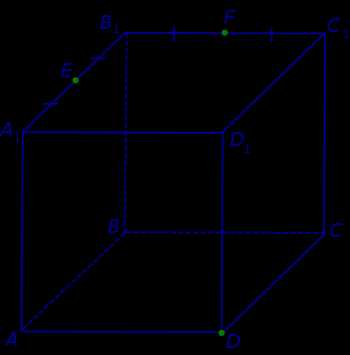
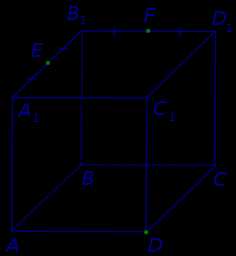
Рис.1

      Поскольку точки   E   и   F   лежат на ребрах одной грани куба   A₁B₁C₁D₁ , то проведем прямую   EF   до пересечения с продолжениями двух других ребер этой грани. Обозначим буквой   G   точку пересечения прямой   EF   с продолжением отрезка   D₁C₁   за точку   C₁,   а буквой   Н   – точку пересечения прямой   EF   с продолжением отрезка   D₁A₁  за точку  A₁ . Эти точки пересечения существуют, поскольку все указанные прямые лежат в одной плоскости   A₁B₁C₁D₁   и не параллельны параллельны попарно (рис. 2).

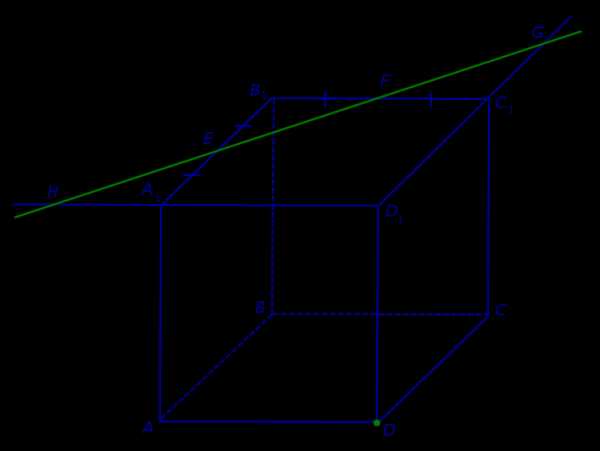
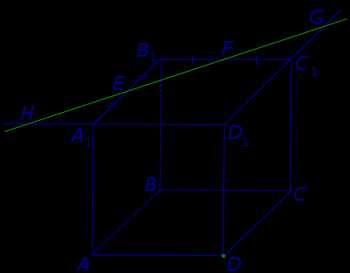
Рис.2

      Точки   G   и   D   принадлежат плоскости сечения, а, значит, и вся прямая   DG   лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба   DD₁C₁C.   Значит, точка пересечения   DG   с ребром куба   C₁C (точка   N ) будет принадлежать сечению. Таким образом, мы получаем еще два отрезка сечения:   FN  и   DN   (рис. 3).

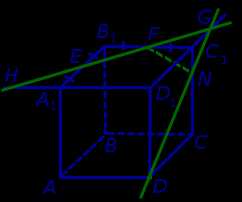
Рис.3

      Теперь, действуя аналогичным образом, проводим прямую   HD,   обозначаем точку перечения этой прямой с ребром   AA₁ буквой   M   и проводим линии сечения   ME   и   MD   в плоскостях граней   AA₁B₁B   и   AA₁D₁D   (рис. 4).

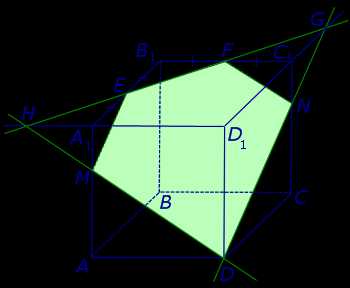
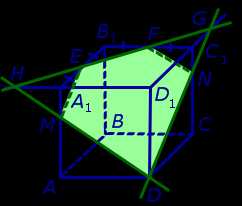
Рис.4

      В результате, как и показано на рисунке 4, получаем, что искомое сечение – пятиугольник   DMEFN.

      Предлагаем посетителю нашего сайта решить в качестве полезного упражнения следующую задачу.

     Задача. Найти площадь сечения   DMEFN, если ребро куба равно 6.

     Указание к решению. Треугольники   HA₁E,   EB₁F и   FC₁G равны.

Перпендикулярные сечения призмы

      Определение 2. Перпендикулярным сечением призмы называют такое сечение, плоскость которого пересекает все боковые ребра призмы и перпендикулярна к ним.

     На рисунке 5 построено перпендикулярное сечение наклонной треугольной призмы – треугольник   KLM.   Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней. Такой способ представления призмы на чертеже часто очень удобен при решении задач.

Рис.5

      Замечание 1. Все перпендикулярные сечения призмы равны между собой.

     Замечание 2. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».

     Замечание 3. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Нахождение площади сечения треугольной призмы — «Шпаргалка ЕГЭ»

Решение задачи

В данном уроке показано решение геометрической задачи, которое можно использовать в качестве примера при решении задач С2 при подготовке к ЕГЭ по математике.

Прежде всего, условие задачи изображается схематически на рисунке. Далее выполняется построение сечения. Боковая грань  — прямая, по которой плоскость пересекает основание призмы . Так как верхнее основание параллельно нижнему основанию, то прямые, по которым плоскость пересекает данные плоскости, будут параллельны. Так как параллельно , то четырехугольник  по определению — трапеция. Площадь трапеции определяется по формуле: . Далее утверждается, что является средней линией и при этом она равна половине стороны . Высота определяется из треугольника . При этом применяется свойство высоты равностороннего треугольника , где — сторона треугольника, а также теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Таким образом, подставив найденные значения в формулу площади трапеции, определяется искомое значение площади сечения.

shpargalkaege.ru

Найти сечение призмы плоскостью

Задача:  Точки А, В, С — точки на разных ребрах четырехугольной призмы. Найдем сечение призмы плоскостью ABC.

Решение:

Построение искомого сечения зависит от того, на каких ребрах призмы лежат точки А, В, С. Наиболее просто строить сечение в том случае, когда точки А, В, С лежат на ребрах, выходящих из одной вершины. Искомое сечение в этом случае — треугольник: АВС.

Если точки А, В, С расположены так, как изображено на рисунке, то строить сечение сложнее. Здесь сначала построим след секущей плоскости АВС на плоскости нижнего основания. Для этого найдем точки М и N пересечения прямых АВ и ВС, которые лежат в секущей плоскости, с плоскостью RSUV: М — точка пересечения прямых АВ и RV, N — точка пересечения прямых ВС и UV. Прямая MN — общая прямая секущей плоскости и плоскости нижнего основания.

Точка Р пересечения прямой RS со следом MN принадлежит и секущей плоскости, и плоскости грани RR₁S₁S. Учитывая, что этим двум плоскостям принадлежит и точка А, получаем, что прямая РА — след секущей плоскости на плоскости RR₁S₁S. Значит, плоскость АBС пересекает грань RR1S1S по отрезку AD, а грань UU₁S₁S — по отрезку CD. Искомым сечением является четырехугольник ABCD.

Видим, что новым элементом в этом решении по сравнению с задачей построить сечение треугольной пирамиды является построение следа секущей плоскости на плоскости основания.

На рисунке показан случай, когда искомым сечением является пятиугольник. Здесь использована точка Сх пересечения ребра UU₁с секущей плоскостью. Следы секущей плоскости на боковых гранях пирамиды строятся таре же, как и в предыдущем случае. 

Рисунок показывает, что искомым сечением четырехугольной призмы может быть и шестиугольник. След АВ секущей плоскости на плоскости основания позволяет последовательно найти точки X и Y его пересечения с гранями SUU₁S₁ и RSS₁R₁, след ХС секущей плоскости на плоскости SUU₁S₁, точку Z пересечения ребра SS₁ с секущей плоскостью и след ZY секущей плоскости на грани RSS₁R₁.

belmathematics.by