С 7 совместные действия с алгебраическими дробями – Решение задач на совместные действия с алгебраическими дробями, часть 1. — Алгебра — 7 класс
Задание №7 Действия с алгебраическими дробями
Задание № 7
Действия с алгебраическими дробями
Сложение и вычитание алгебраических дробей:
С одинаковыми знаменателями выполняется по правилу:
С разными знаменателями: Привести все дроби к общему знаменателю; если они с самого начала имели одинаковые знаменатели, то этот шаг алгоритма опускают. Выполнить сложение (вычитание) полученных дробей с одинаковыми знаменателями.
Алгоритм отыскания общего знаменателя для нескольких алгебраических дробей: Разложить все знаменатели на множители.
Из первого знаменателя выписать произведение всех его
множителей, из остальных знаменателей приписать к этому
произведению недостающие множители. Полученное произведение
Найти дополнительные множители для каждой из дробей.
Записать каждую дробь с новым числителем и общим знаменателем.
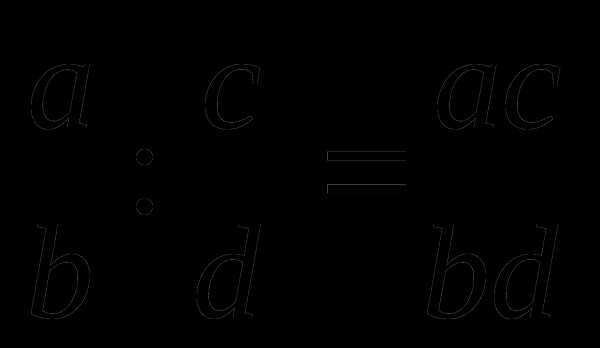
Умножение и деление алгебраических дробей:

 .
.
Пример:
1. ;
2. 3.
Тренировочные упражнения:
Выполни действия:
1) 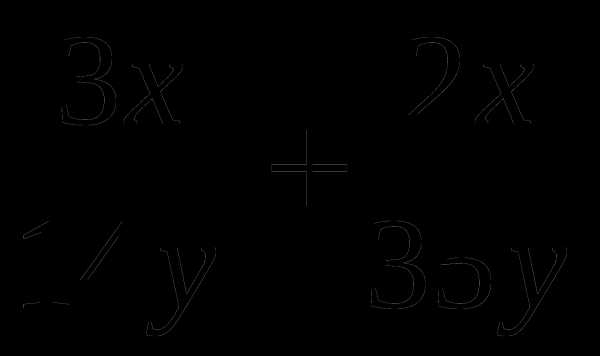 ;
2)
;
2)  ;
3)
;
3)  ;
4)
;
4) 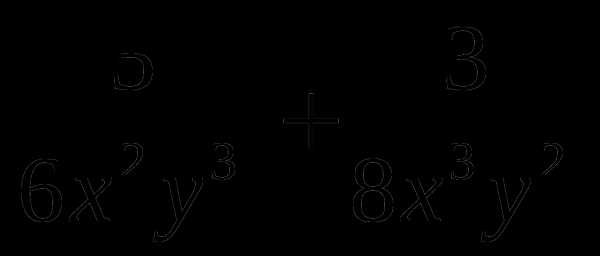
5)  ;
6)
;
6) 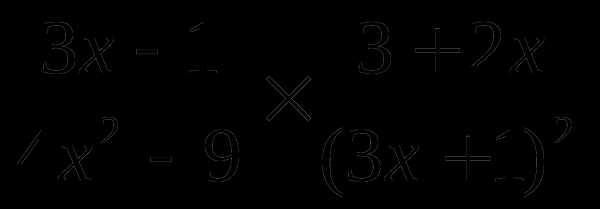 7)
7)  8)
8) 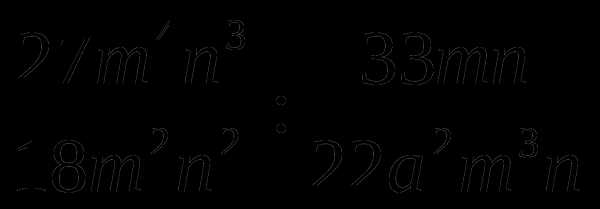 .
.
Контрольные задания:
Выполни действия:
1) 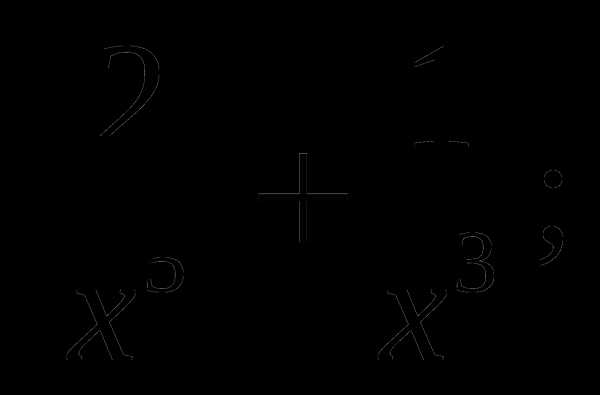
а) 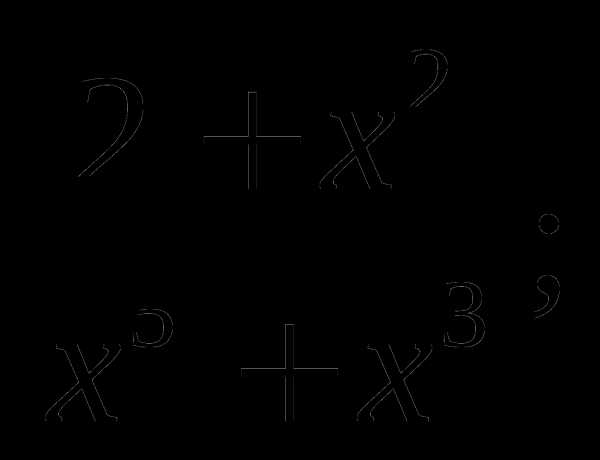 б)
б) 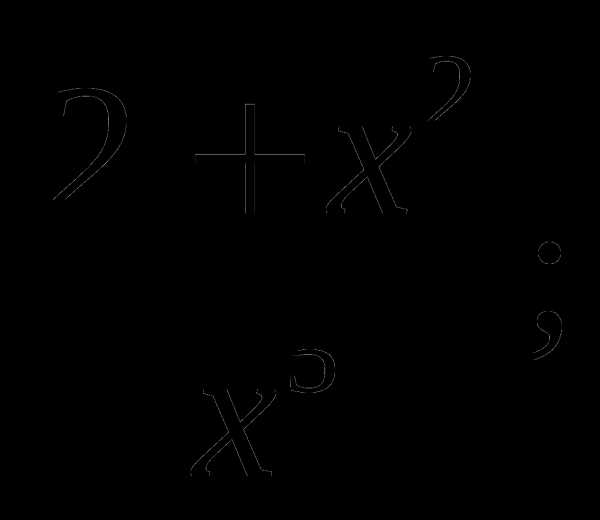 в)
в) 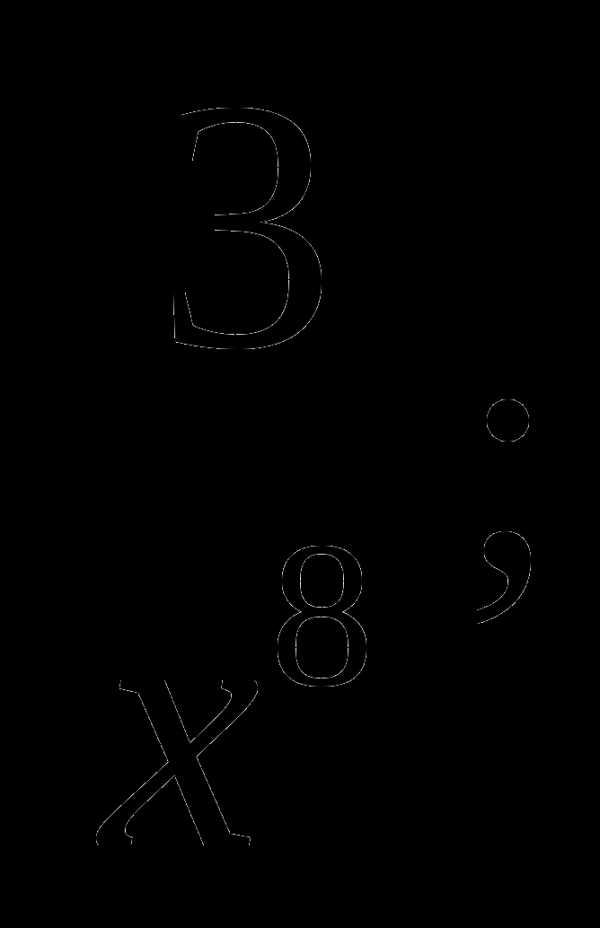 г)
г) 
2) 
a) 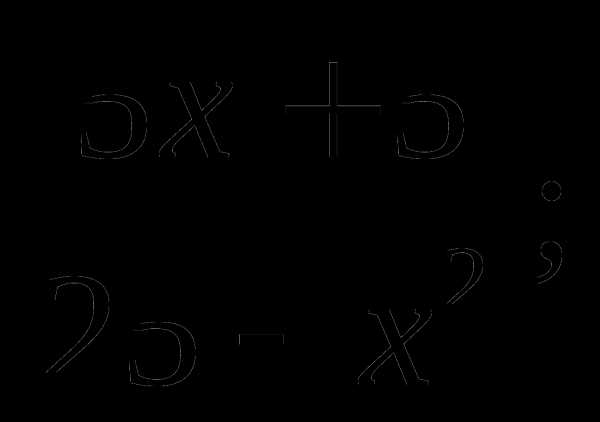 б)
б)  в)
в)  г)
г) 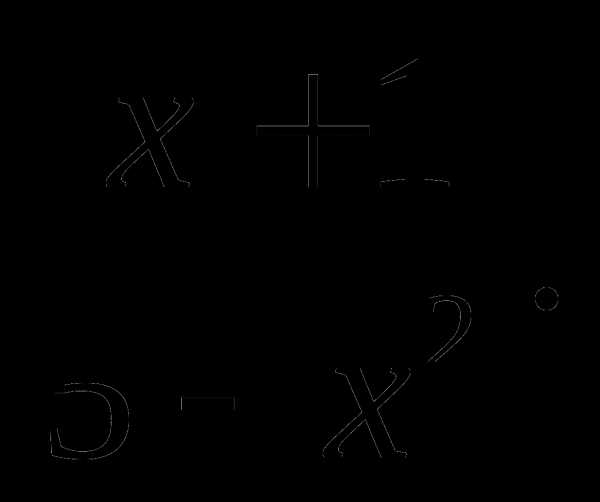
3) 
a)  б)
б) 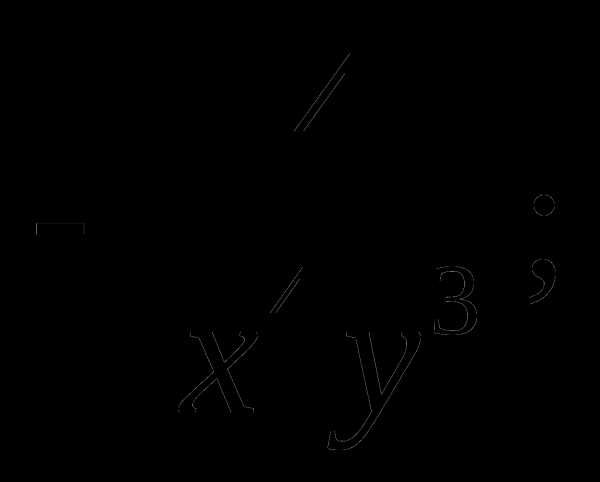 в)
в) 

4) 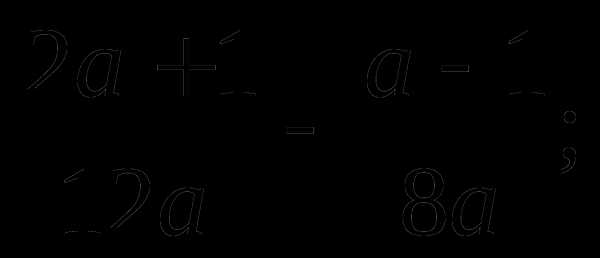
a) 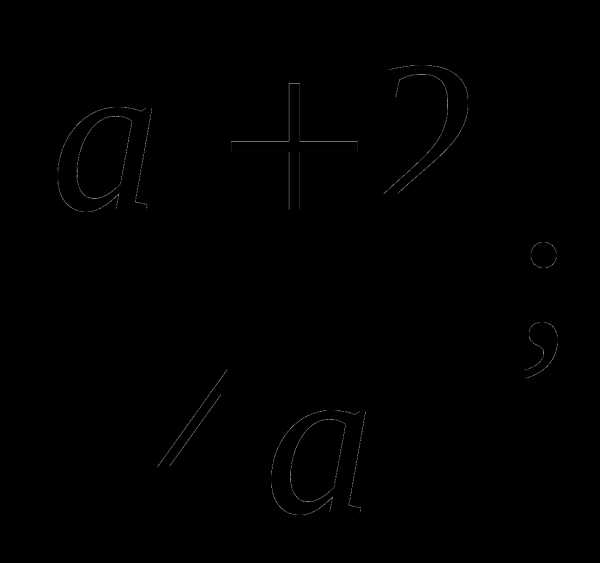 б)
б) 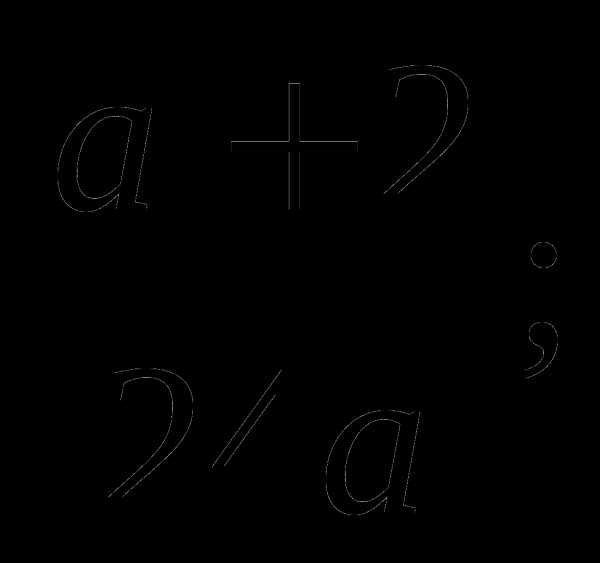 в)
в) 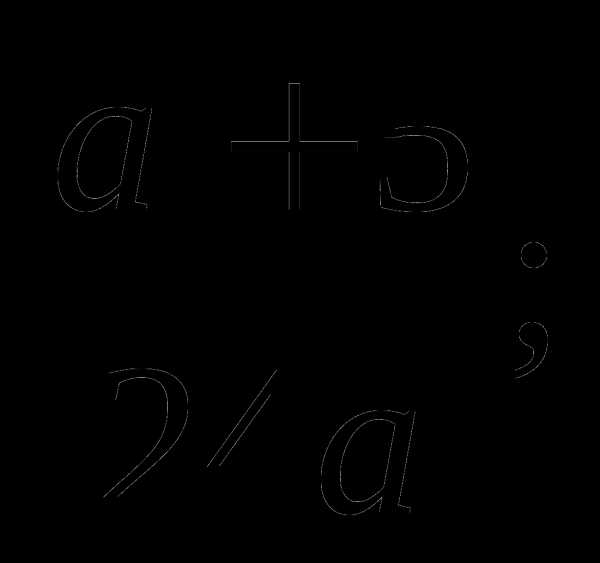 г)
г) 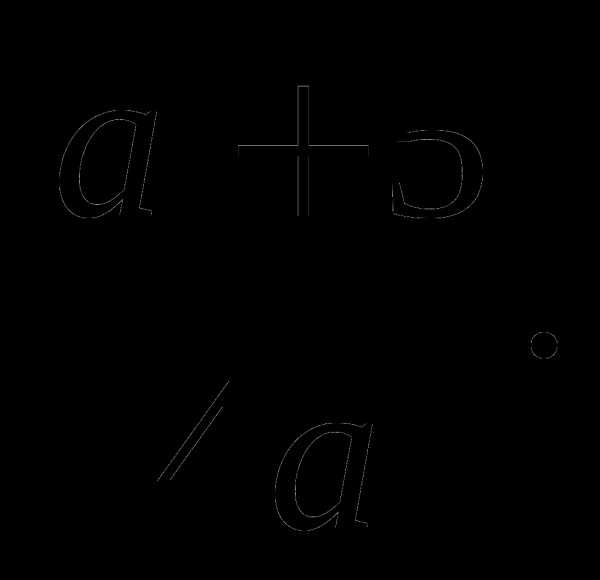
5) 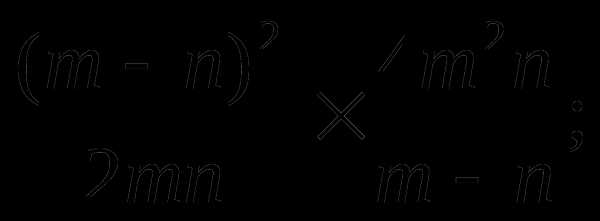
a) 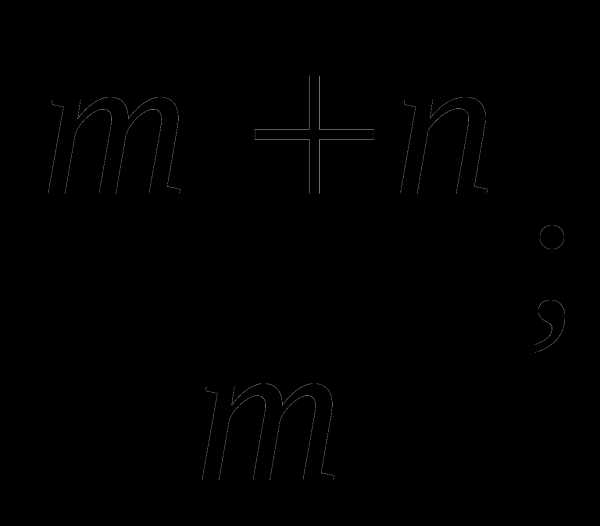 б)
в)
б)
в)  г)
г)
6) 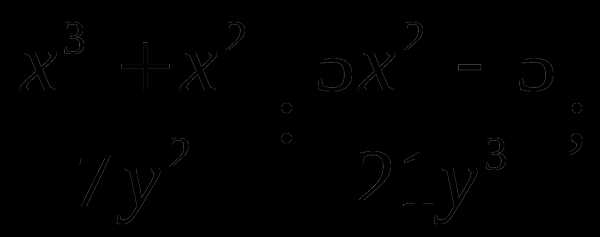
a) 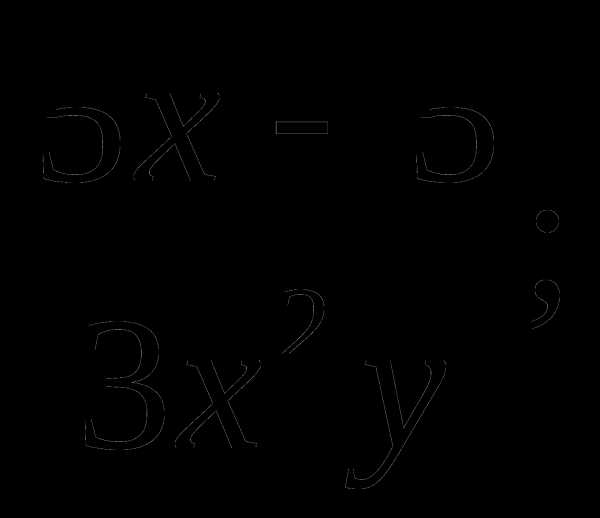 б)
б)  в)
в) 
 г)
г) 
Ответы: 1) б;
2) а;
3) г;
4) в;
5) б;
6) в.
gigabaza.ru
| № этапа. | Кол-во минут. | Задание. | Деятельность учителя. | Деятельность ученика. |
| Организационный момент. Приветствие. | При входе каждому ребенку дается
цветной квадратик. Желтый -«руки за головой» Красный — «руки на поясе», Зеленый — «руки на коленях». Надо поздороваться локтями. |
|||
| Рефлексия: когда удобно было
здороваться? В жизни тоже приходится зачастую подстраиваться под другого, чтобы достигнуть цели и приобрести друга. Ведь недаром говорят, что друг познается в беде. И это качество характера мы сегодня попробуем развить в себе. |
С равным себе. Рассаживаются по местам. |
|||
| 1 | 1 мин | Объявление темы урока, формулировка целей урока. | Сегодня мы отправляемся в путешествие,
связанное с поиском сокровищ затонувшего
корабля. Путешествие это опасно и трудно. Если вы
готовы, то отправляемся в путь! Для этого вы
должны распределиться по группам так, чтобы вам
было комфортно трудиться в команде. Предлагаю выбрать капитана вашей команды, который будет контролировать процесс работы в команде. Помогать, брать ответственность на себя в трудную для команды минуту. Как вы думаете: чему мы должны научиться на уроке, исходя из названия темы? Путешествие будет увлекательнее, если мы вспомним все действия с алгебраическими дробями, и сможем применить, объединив наши знания, умения и навыки, приобретенные на предыдущих уроках. Свои наблюдения записывайте в «Дневнике путешествия», который сдадите в конце урока для «проведения экспертизы путешествия».Итак, ПОДНЯТЬ ПАРУСА! |
Слушают учителя, рассматривают
приготовленный материал, готовят перед собой
«Дневник путешествия» Научиться выполнять все изученные действия в определенном порядке. |
| 2 | 7 мин | Устный счет. (15 заданий с выбором ответа. Приложение 1. В соответствие ставится буква. Получится выражение: «счастливого пути!») Работа в парах. Взаимопроверка. |
Дает задание поменяться работами для проверки. Оценка: «5»-верно 14-15 заданий, «4»-верно 10-13 заданий, «3»-верно 6-9 заданий. |
Решают устно самостоятельно. В
«дневник путешествия» записывают букву,
соответствующую пра-вильному ответу. Меняются работами для проверки |
| Фронтально подводит итог этапа: Что повторили в процессе устного счета? | Отвечают: действия сокращения, сложения, вычитания, умножения и деления. | |||
| На каком уровне понимания вы находитесь? | Показывают номер уровня понимания. | |||
| 3 | 5 мин | Обойди айсберги, ответив на следующие теоретические вопросы. Приложение 2. Тест состоит из 5 заданий с выбором ответа. В соответствие ставится буква. Получится выражение: удачи!) | Показывает задание теста на доске. Показывает правильный выбор ответа. Фронтально подводит итог этапа: Что повторили в этом этапе? Оценка: «5»-верно 5 заданий, «4»-верно 4 заданий, «3»-верно 3 заданий. |
Отвечают на вопросы теста. Ответы
записывают в «Дневник». Самопроверка. Отвечают: правила выполнения арифметических действий |
| На каком уровне понимания вы находитесь? | Показывают номер уровня понимания. | |||
| 4 | 2 мин | Уплыви от пиратов. Приложение
3. Расставить порядок действий в схемах. (4 схемы) Групповая работа. |
На нашем пути появляются пираты!!! Показывает схемы различных выражений. Оценка: «5»-нет ошибок, «4»-одна ошибка, «3»-верны 2 схемы. Показывает правильные ответы. Фронтально подводит итог этапа: Что повторили в этом этапе? Итак, в каком порядке выполняются действия в числовом выражении? |
Расставляют порядок действий в
приготовленных листах. Взаимопроверка. Отвечают: порядок действий в схемах. Ответ: Сначала действия 3 ступени, потом — 2 ступени, а затем — действия 1 ступени. |
| На каком уровне понимания вы находитесь? | Показывают номер уровня понимания. | |||
| 5 | 1 мин | Освободись от щупальцев осьминога. Физминутка. | Совместная деятельность с учащимися. Капитан каждой команды предлагает по очереди одно упражнение (гимна- стика плеч, пальцев, глаз) |
Совместная деятельность с учителем |
| 6 | 3 мин | Не угоди в пасть акулы. | Дается задание: выполнить действия. Отвечающему правильно ученику добавляется 1 балл. | Ученик комментирует решение у доски и показывает образец ведения правильной записи. |
| 7 | 10 мин | Отыщи сокровища на затонувшем корабле.
Обучающая самостоятельная работа уровня А по
вариантам (3 выражения в два действия с выбором
ответа. Приложение 4. В соответствие ставится
буква. Получится выражение: бочонок,) Для тех, кто быстро справится с заданием, приготовлено доп.задание. (Получится: 12) |
Индивидуальная корректирующая работа с
учащимися. (Продумать фамилии учеников) Фронтально подводит итог этапа: Чем мы занимались на этом этапе? Вопрос капитанам: как проявила себя команда? Легко ли было работать в команде? Оказывалась ли кому-то индивидуальная помощь? Кому было трудно? Кто помог? Вопрос: как вы оцениваете свою работу в коллективе? Поставьте себе оценку в виде символа Каков уровень понимания вами сегодняшней темы? |
Самостоятельная работа в группах. Ответ: выполняли совместные действия с алгебраическими дробями Ответ: поднимают номера. |
| Учитель достает бочонок. Приглашает учеников для «добычи клада» из бочонка . | Рассказывают и показывают головоломки. | |||
| 8 | 5 мин | В сундуке сокровища: игры-головоломки народов Севера. | Учитель предлагает рассмотреть и показать умение в использовании игр-головоломок. | Учащиеся показывают умение в использовании игр-головоломок. |
| 9 | 6 мин | Итог урока | Путешествие подошло к концу. И как
принято, после сдачи сокровищ государству,
участники путешествия получают 25% стоимости
находки. Ваша награда в конвертах под названием
«Домой!». Приложение 5. «Дневники» с
записями каждого этапа путешествия нужно сдать
эксперту — своему учителю для назначения
«Премии». Урок хочется закончить словами русского писателя Л. Н.Толстого: «Человек подобен дроби: в знаменателе то, что он о себе думает. В числителе, то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь». А вы — какая дробь? Я желаю вам, чтобы ваша дробь всегда была либо неправильной, либо равной единице! А почему? Подумайте! Об этом вы скажете на следующем уроке: |
Учащиеся разбирают конверты с
названием «Домой!» Учащиеся оставляют на парте символ своего настроения после урока. |
xn--i1abbnckbmcl9fb.xn--p1ai
Урок-игра по алгебре в 7-м классе «Совместные действия над алгебраическими дробями»
Разделы: Математика
Цель урока: систематизировать знания учащихся по теме “Алгебраические дроби”, отработать умения и навыки выполнения совместных действий с алгебраическими дробями.
Только двигаясь вперед можно дойти до поставленной цели, а цель у нас одна – это знания. К нашей цели мы будем добираться по железной дороге. Чтобы прибыть в конечный пункт, нужно выполнить задания. А вы знаете, что работу лучше выполнять командой.
Класс делится на команды по 5 человек. Каждая команда — это бригада работников железной дороги.
“Бригадиры” — капитаны команд получают схему маршрута.
Схема маршрута
- Станция “Эрудитов”.
- Товарная станция.
- Станция “Экономическая”.
- Станция “Любознательных”.
- Семафор.
- Станция “Конкурс мастерства”
- Станция “Знания”.
Учитель сообщает правила игры:
- Время прохождения маршрута 40 минут.
- За каждый верный ответ “бригада” получает “1” балл, та “бригада”, которая в конце пути будет иметь большое количество баллов, получит “премию”.
- Если “бригада” не справляется с заданием, можно проконсультироваться у учителя – “диспетчера”, но за это снимается 0,5 баллов.
- Задания проверяет “диспетчер” и трое учащихся из числа тех, кто хорошо учится.
- На станции “конкурс мастерства” “бригадиры” вызывают любого ученика из другой “бригады” и просят выполнить любое задание из карточек. Если ученик выполняет правильно, то его “бригаде” добавляют еще балл.
- Задача “бригадира” правильно распределить задания между всеми членами “бригады”, т.е. каждый решает задание соответствующее своему уровню подготовки, но после их выполнения решают остальные задания карточки.
- Решение выполняют в рабочих тетрадях, а ответы записывают на карточках, которые сдают в “диспетчерскую”.
Как старт к началу движения звучит песня “Голубой вагон”
I. Станция “Эрудитов”
Собрать формулы сокращенного умножения.
Каждой “бригаде” выдаётся набор “разрезанных” формул, для этого необходимо собрать их так, чтобы получить искомые тождества.
II. Товарная станция
На перроне стоят многочлены, которые нужно погрузить в вагоны, но в вагон можно погрузить только множитель. Для этого надо многочлен разложить на множители.
Карточка № 1
а) 2а2 – 8а;
б) 18ав2 +27а2 в;
в) 3х + ху2 – х2 у – 3у;
г) 9в2 + 18вс + 9с2;
д) 1 – х2 + 2ху – у2.
III. Станция “Экономическая”
В машинах находятся алгебраические выражения, их нужно погрузить в вагоны, но по техники безопасности вагон перегружать нельзя, поэтому грузим только то, что получится после упрощения выражения.
Карточка № 2
IV. Станция “Любознательных”
Заранее подготовленный ученик делает сообщение о жизни и деятельности Франсуа Виете.
V. Семафор
На семафоре красный свет
Значит, хода дальше нет,
А зелёный свет зажжется,
Если слово соберётся.
Решить уравнения и найти букву соответствующую найденному корню. Если уравнения решены, верно, то из букв получится слово.
Карточка № 3
Ключ ответов:
И |
В |
Р |
Г |
А |
О |
— 6 |
_ 11 14 |
5,5 |
5 12 |
-7 |
— 9 |
VI. Станция “конкурс мастерства”
VII. Станция “Знания”
VIII. Подведение итога урока.
Те “бригады”, которые заняли I и II место получают оценки в журнал.
Лист учета результатов (образец)
“Бригады” |
I станция |
II станция |
III станция |
V станция |
VI станция |
ИТОГ |
МЕСТО |
I |
|||||||
II |
|||||||
III |
24.01.2008
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
План-конспект урока по алгебре (7 класс) на тему: Совместные действия с алгебраическими дробями
Совместные действия с алгебраическими дробями.
Цели урока:
Дидактическая
- повторить правила сложения, вычитания, умножения, деления алгебраических дробей;
- уметь выполнять совместные действия с алгебраическими дробями;
- уметь решать уравнения.
Воспитательная
- воспитывать дружеские отношения в классе;
- умение работать в парах, развивать интерес к математике.
- формирование интереса к предмету;
- воспитание чувства коллективизма, ответственности за результаты своей работы и учёбы.
Развивающая
- умение сопоставить и сравнить факты,
- делать самостоятельные выводы;
- развивать творческую самостоятельность учащихся, творческое мышление, умение работать с различными источниками информации.
ХОД УРОКА
1. Организационный момент (2 мин).
Проконтролировать, чтобы за каждой партой сидело по одному сильному ученику. Объявить тему урока и его задачи.
Учитель: Сегодня у нас урок – путешествия в страну алгебраических дробей и мы с вами отправимся в полет, и у нас будет много приключений.
2. Устная работа (8 мин).
Учитель: Сначала проверим готовность к полету. Мы проверим это умение в устном счете. Вам нужно стараться отвечать правильно и быстро, от этого зависит, полетим мы в путешествие или нет.
Вопросы учащимся
1) Сформулируйте правила сложения, умножения, деления алгебраических дробей?
2) Повторить порядок выполнения действий.
3) Повторить формулы сокращённого умножения.
1. Сократите дроби 2. Упрости
Учитель: Теперь мы к полету готовы. Но нам надо узнать, на каком самолете мы должны совершить полет (По таблице нужно ответить на вопросы)
1). Какой порядок действий в выражениях:
2). Выполнить действия:
2,1,4,3 | -3m/5n | 2а | 1,3,2 | 1,2,3 | -1/4х | 3m/5n | -2а | 1/4х | 3,1,4.2 |
У | 4 | 6 | Т | И | 1 | 5 | 3 | 7 | Л |
Правильный ответ: ТУ — 134
Учитель: Теперь мы с вами летим в самолете ТУ-134.
В самолетах обычно слушают музыку, читают газеты, разгадывают кроссворды. Итак, мы будем лететь, играть в “математическое лото”. Кто быстрее решит и зачеркнет все числа в лото тот победит? Можно решать устно.
(1-n)2 | 252-242 | |||
1-2n+n2 | 49 | (х+у)2 | 4+4n+n2 | 625 |
3. Работа в тетрадях (5 мин).
Учитель: Ужасно, но наш самолет терпит крушение. Пилот у нас очень хороший, поэтому он с трудом, но сажает самолет на остров. На этом острове встречаются аборигены и путешественники. Аборигены — это ребята первого варианта, а путешественники – это ребята второго варианта. Внимание кризисная ситуация, аборигены ходят уничтожить наших путешественников. Чтобы этого не произошло, путешественникам надо доказать, что они умеют выполнять действия с дробями.
Работа в парах. Ребята второго варианта контролируют выполнения заданий первого варианта.
Вычислите
4. Самостоятельная работа (10 мин).
Учитель: Аборигенам путешественники понравились. И они не только стали враждовать с ними, но и рассказали о своей цивилизации.
Путешественники и аборигены познакомились, обменялись знаниями и подружились. Для закрепления своего союза они решили сыграть в дружеский футбольный матч. Гол – это правильно выполненное действие.
5. Физминутка(2 мин).
1. В презентации записаны формулы сокращённого умножения, если это формула:
-разности квадратов, то руки вверх;
-квадрата разности — то вперёд;
-квадрата суммы – то в стороны.
2.На доске записаны примеры, а учитель показывает ответ, если ответ верный — учащиеся хлопают в ладоши, а неправильный — топают ногами.
Учитель: На стол накрыли. Хорошо поужинали, при этом никого не обидели. Особо смелые перепрыгивали через костер. Для того, чтобы перепрыгнуть надо решить задание на смекалку.
- Кирпич весит 2 кг и еще полкирпича. Сколько весит кирпич? (3 кг)
- Пара лошадей пробежала 40 км. Сколько километров пробежала каждая лошадь? (40 км)
- У семи братьев по одной сестре. Сколько всего детей? (8)
- К Айболиту на прием пришли звери. Все, кроме 2, собаки. Все, кроме 2, кошки. Все, кроме 2, зайцы. Сколько животных пришло к Айболиту? (3)
- Зайцы пилят бревно. Они сделали 12 распилов. Сколько получилось чурбаков? (13)
- Решение задачи (5 мин).
Учитель:Поели, поплясали, даже через костер попрыгали, пора бы и спать ложиться.
7. Подведение итогов (2 мин).
Учитель: Ну, вот и наступило утро. За путешественниками прилетел вертолёт. Но в аэропорту их ждали журналисты, которые стали спрашивать, что же произошло за время полета и что повторили за время этого путешествия?
8. Рефлексия (2 мин)
Продолжите фразу:
“Сегодня на уроке я узнал…”
“Сегодня на уроке я научился…”
“Сегодня на уроке я познакомился…”
“Сегодня на уроке я повторил…”
“Сегодня на уроке я закрепил…”
Учитель комментирует оценки за урок.
- Домашняя работа. № 498(2,4)
nsportal.ru
Совместные действия над алгебраическими дробями
Елизенцева Ольга Васильевна
Учитель математики
Педагогический стаж — 25 лет
Высшая категория
Целевой компонент урока
Педагогические цели
- Организовать работу учащихся по обобщению и систематизации знаний по теме для обеспечения их использования при выполнении действий с алгебраическими дробями.
- Организовать работу в парах по выполнению учебных заданий.
- Координировать работу учащихся-консультантов при устной работе
Ожидаемые результаты
- Учащиеся умеют сокращать алгебраические дроби.
- Учащиеся владеют приёмами:
- разложения многочлена на множители
- приведение дробей к общему знаменателю
- применения формул сокращенного умножения
- сложения, умножения, вычитания, деления алгебраических дробей.
- Учащиеся умеют решать уравнения с использованием совместных действий над алгебраическими дробями
- Учащиеся умеют взаимодействовать в парах
- Учащиеся, выполняющие обязанности консультантов, демонстрируют регулятивные умения по оцениванию деятельности одноклассников
- Учащиеся уважают одноклассников.
Методы обучения: частично-поисковый, урок личных достижений по данной теме.
Формы работы на уроке: коллективная, индивидуальная, работа в парах, в диалоге.
Оснащение урока: мультимедиа комплекс.
План урока
|
Этапы урока |
Деятельность учителя |
Деятельность ученика |
УУД |
|
|
Создание мотивации для работы на уроке |
Приветствие |
Коммуникативные |
|
Вводно-мотивационный |
Постановка цели урока |
Участие в беседе |
Коммуникативные |
|
|
Актуализация знаний по предыдущим темам |
Выявление связей предыдущего материала и данного |
Регулятивные, Познавательные |
|
|
Организация презентации для учащихся |
Нахождение ответов при работе в парах, запись решений в тетрадь |
Познавательные, Общеучебные, Логические, Коммуникативные |
|
Информационно-групповой
|
Координирование деятельности консультантов |
Запись результатов ответов на устные вопросы учащихся |
Общеучебные, Коммуникативные |
|
|
Таблица перевода полученных баллов в оценку |
Подсчет баллов личных результатов |
Регулятивные |
|
Рефлексивный
|
Подведение итогов |
Самооценка результативной деятельности |
Регулятивные |
Сценарий урока
Вводно-мотивационный этап.
Учитель: Ребята, сегодня на уроке мы повторим большую тему “Алгебраические дроби”, подготовимся к контрольной работе. Наш урок пройдет в виде соревнования за личное первенство. В ходе работы на уроке каждый из вас может “заработать” баллы за правильно выполненные задания, ответы и получить соответствующую оценку.
Информационно-групповой этап
Время работы ограничено. Выбор заданий – по желанию, после предъявления правильных ответов учащиеся делают самопроверку самостоятельной работы.
Давайте попытаемся ответить на вопросы
1. Что такое алгебраическая дробь? 1балл
2. Любое ли значение могут принимать буквы, входящие в алгебраическую дробь? 1балл
3. В чем заключается основное свойство дроби? 1балл
4. Что значит сократить обыкновенную дробь? 1балл
5. Что значит сократить алгебраическую дробь? 1балл
6. Отличаются ли правила сокращения обыкновенных и алгебраических дробей? 3балла
7. Какие способы разложения многочлена на множители вы знаете? 3балла
Дифференцированное выполнение заданий
Сократить дробь
1б) 2б) 3б) 4б) 5б)
Давайте попытаемся ответить на вопросы
1. Назовите правила сложения и вычитания алгебраических дробей 1балл
2.Сравнивните правила сложения обыкновенных и алгебраических дробей? 3балла
1б) 2б) 3б) 4б) 5б)
Давайте попытаемся ответить на вопросы
1.Правило умножения алгебраических дробей? 1 балл
2.Правило деления алгебраических дробей? 1 балл
3. Сравните правила умножения и деления обыкновенных и алгебраических дробей. 3балла
Умножение и деление алгебраических дробей
1б) 1б) 2б) 3б)
4б) 5б)
Давайте попытаемся ответить на вопросы
1.Как определяется порядок действий в числовом выражении? 1 балл
2.Как определяется порядок действий в алгебраическом выражении? 1 балл
3.Какие способы записи решения при выполнении совместных действий над алгебраическими дробями вы знаете? 3 балла
Совместные действия над алгебраическими дробями
3б) 5б)
Давайте попытаемся ответить на вопрос
Что значит решить уравнение? 1 балл
Решить уравнение
Рефлексивно-оценочный этап
Учитель: Какова была цель нашего урока?
Ученики: Вспомнить действия с обыкновенными дробями, все правила с ними связанные.
Учитель: Достигли ли мы поставленной цели? Аргументируйте
Ученики дают развёрнутый ответ на данный вопрос.
Учитель: А теперь каждый подсчитает свои баллы, заработанные на уроке.
Ученики: Каждый самостоятельно подсчитывает число полученных баллов, суммируя их с баллами, полученными за ответы на устные вопросы, ставит себе оценку.
“5” – более 46 баллов
“4” – 30-45 баллов
“3” – 13-29 баллов
Если вы довольны своим результатом, то похлопайте себе в ладошки.
Показатель результативности урока-количество тех, кто захлопал себе в ладоши.
Каждый рисует своё настроение в виде смайлика.
Тетради сдаются на проверку.
Список источников:
1. Алгебра: Учебн. Для 7кл. общеобр. учережд./ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- М.:Просвящение,1999.
2.Л.В. Арьяева. Информационное взаимодействие в современной школе: опыт диалога. Монография. Санкт-Петербург 2012
1. Поурочные планы. Алгебра. 7 кл.IIчасть: Составили Г.И. Григорьева, Н.Н. Морозова- Корифей. Волгоград,2007
Ответы:
I блок ; x-3y; ;
IIблок ; ; ; ;
IIIблок ; ; ; —
IVблок ; 4a+4
Vблок -0,5Урок по математике “ Совместные действия над алгебраическими дробями “. 7 класс
Елизенцева Ольга Васильевна
Учитель математики
Педагогический стаж-25 лет
Высшая категория
Целевой компонент урока
Педагогические цели
1) Организовать работу учащихся по обобщению и систематизации знаний по теме для обеспечения их использования при выполнении действий с алгебраическими дробями.
2) Организовать работу в парах по выполнению учебных заданий.
3) Координировать работу учащихся-консультантов при устной работе
Ожидаемые результаты
1) Учащиеся умеют сокращать алгебраические дроби.
2) Учащиеся владеют приёмами:
-разложения многочлена на множители
-приведение дробей к общему знаменателю
-применения формул сокращенного умножения
-сложения, умножения, вычитания, деления алгебраических дробей.
3) Учащиеся умеют решать уравнения с использованием совместных действий над алгебраическими дробями
4) Учащиеся умеют взаимодействовать в парах
5) Учащиеся, выполняющие обязанности консультантов, демонстрируют регулятивные умения по оцениванию деятельности одноклассников
6) Учащиеся уважают одноклассников.
Методы обучения: частично-поисковый, урок личных достижений по данной теме.
Формы работы на уроке:коллективная, индивидуальная, работа в парах, в диалоге.
Оснащение урока:мультимедиа комплекс.
План урока
|
Этапы урока |
Деятельность учителя |
Деятельность ученика |
УУД |
|
|
Создание мотивации для работы на уроке |
Приветствие |
Коммуникативные |
|
Вводно-мотивационный |
Постановка цели урока |
Участие в беседе |
Коммуникативные |
|
|
Актуализация знаний по предыдущим темам |
Выявление связей предыдущего материала и данного |
Регулятивные, Познавательные |
|
|
Организация презентации для учащихся |
Нахождение ответов при работе в парах, запись решений в тетрадь |
Познавательные, Общеучебные, Логические, Коммуникативные |
|
Информационно-групповой
|
Координирование деятельности консультантов |
Запись результатов ответов на устные вопросы учащихся |
Общеучебные, Коммуникативные |
|
|
Таблица перевода полученных баллов в оценку |
Подсчет баллов личных результатов |
Регулятивные |
|
Рефлексивный
|
Подведение итогов |
Самооценка результативной деятельности |
Регулятивные |
Сценарий урока
Вводно-мотивационный этап.
Учитель: Ребята, сегодня на уроке мы повторим большую тему “Алгебраические дроби”, подготовимся к контрольной работе. Наш урок пройдет в виде соревнования за личное первенство. В ходе работы на уроке каждый из вас может “заработать” баллы за правильно выполненные задания, ответы и получить соответствующую оценку.
Информационно-групповой этап
Время работы ограничено. Выбор заданий – по желанию, после предъявления правильных ответов учащиеся делают самопроверку самостоятельной работы.
Давайте попытаемся ответить на вопросы
1. Что такое алгебраическая дробь? 1балл
2. Любое ли значение могут принимать буквы, входящие в алгебраическую дробь? 1балл
3. В чем заключается основное свойство дроби? 1балл
4. Что значит сократить обыкновенную дробь? 1балл
5. Что значит сократить алгебраическую дробь? 1балл
6. Отличаются ли правила сокращения обыкновенных и алгебраических дробей? 3балла
7. Какие способы разложения многочлена на множители вы знаете? 3балла
Дифференцированное выполнение заданий
Сократить дробь
1б) 2б) 3б) 4б) 5б)
Давайте попытаемся ответить на вопросы
1. Назовите правила сложения и вычитания алгебраических дробей 1балл
2.Сравнивните правила сложения обыкновенных и алгебраических дробей? 3балла
1б) 2б) 3б) 4б) 5б)
Давайте попытаемся ответить на вопросы
1.Правило умножения алгебраических дробей? 1 балл
2.Правило деления алгебраических дробей? 1 балл
3. Сравните правила умножения и деления обыкновенных и алгебраических дробей. 3балла
Умножение и деление алгебраических дробей
1б) 1б) 2б) 3б)
4б) 5б)
Давайте попытаемся ответить на вопросы
1.Как определяется порядок действий в числовом выражении? 1 балл
2.Как определяется порядок действий в алгебраическом выражении? 1 балл
3.Какие способы записи решения при выполнении совместных действий над алгебраическими дробями вы знаете? 3 балла
Совместные действия над алгебраическими дробями
3б) 5б)
Давайте попытаемся ответить на вопрос
Что значит решить уравнение? 1 балл
Решить уравнение
Рефлексивно-оценочный этап
Учитель: Какова была цель нашего урока?
Ученики: Вспомнить действия с обыкновенными дробями, все правила с ними связанные.
Учитель: Достигли ли мы поставленной цели? Аргументируйте
Ученики дают развёрнутый ответ на данный вопрос.
Учитель: А теперь каждый подсчитает свои баллы, заработанные на уроке.
Ученики: Каждый самостоятельно подсчитывает число полученных баллов, суммируя их с баллами, полученными за ответы на устные вопросы, ставит себе оценку.
“5” – более 46 баллов
“4” – 30-45 баллов
“3” – 13-29 баллов
Если вы довольны своим результатом, то похлопайте себе в ладошки.
Показатель результативности урока-количество тех, кто захлопал себе в ладоши.
Каждый рисует своё настроение в виде смайлика.
Тетради сдаются на проверку.
Список источников:
1. Алгебра: Учебн. Для 7кл. общеобр. учережд./ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- М.:Просвящение,1999.
2.Л.В. Арьяева. Информационное взаимодействие в современной школе: опыт диалога. Монография. Санкт-Петербург 2012
1. Поурочные планы. Алгебра. 7 кл.IIчасть: Составили Г.И. Григорьева, Н.Н. Морозова- Корифей. Волгоград,2007
Ответы:
I блок ; x-3y; ;
IIблок ; ; ; ;
IIIблок ; ; ; —
IVблок ; 4a+4
Vблок -0,5
ext.spb.ru
Совместные действия над алгебраическими дробями
495
1) ∣a + a
5;
6a
A2 (a 2 3j a2 a3 + 4 ) ~ ∖2 + O2 J^ ~ ∙ 2a 2
A3 +4
4)
A + b ∣ 5 5 ) (a + b)∙5 ab (1 1 ∣ ab a — b
A — b I b a ) a — b ab
5) 1:|1 — — I= -±-:
A ) a — 1
B2 +1
6) b:’b +bI =b: b
B2 +1
(опечатка в ответе задачника).
496. 1) I 1 + -|:|l -1 a I ∣ a
A +1 a a +1 a a-1 a-1
2) ∣ a+a
A ∣ ab + a ab — a a2 ∙ (b2 -1)
^^ = = b2
A
A I =
B
497. 1) I1-
A-b
A+b
2+
Bb
2b I a + b — a + b 2a — 2b + 2b
A-b
A+b
A-b
4ab
~ TT
A — b
2) I1 +
A+b
A-b
2-
2a
A-b+a+b 2a+2b-2a
498. 1)
A-b a+bI a+11b
(a +11b)∙(a — b)=
A+bI a-b a+b
A — b 6 a + 6b — 5a + 5b a — b
22
A — b
A +11b
(a-b)∙(a+b)∙(a+11b)a+b
( 3 3 I c 3c + 3 d + 3c
2) I — +
4ab
2 t2
A — b
C c + d ) 18 ∙(2c + d) c ∙(c + d) 18 ∙(2c + d)
3 ∙(2c + d) = 1
18 ∙(c + d )(c + d) 6 ∙(c + d)
Y -1:( y2 +1 = y -1: y2 +1 — 2y
Y l, y2 + 2y y + 2) y y∙(y + 2) (y-ι)∙ У(У+2) = У+2
^ У -1
.. m — 2 I m2 + 24 4
4) 😐 -2
M — 5 I m — 25 m — 5 = (m — 2)∙(m — 5)∙(m + 5) = m+5 (m — 5)∙)m — 2)2 m — 2
M — 2 m2 + 24 — 4m — 20 m — 5 (m — 5 )(m + 5 )
499. 1)
A2 + ab
A 2 + b 2
Ab
A-b a+b
2
∙ (a + b) α2 + ab — ab + b2
A2 + b2
2)
(a + b)(a — b)
α ∙(a + b)∙(α2 + b2) a (a2 + b2)(a + b)a — b) a — b
B ∙(a — b) a2 — ab + ab + b2 (a+b)(a-b)
Ab — b2 a2 +b2
Ab
+
A+b a-b
A2 + b2
3)
4)
B ∙(a — b)∙(a2 + b2) b
(a2 + b2)∙(a + b)a — b) a + b
C + d 2c ‘,∣ d — c (c2 — d2 — 2c2)∙ (d — c) c — d _ 1
C — d J c2 + d2 c ∙(c — d)∙(c2 + d2 ) c ∙ (c — d)
D — c 1 c + d
C
2c
(c2 + d2)
2c2 +d2 — c2 c+d
C+d (c2 + d2 )∙(c + d)
∙(c + d )(
C2 + d2
1
C
∙ (c + d)
C2 +d2
500. 1)
2)
A2 + 2a +1 b + 2 a (a +1)2 ∙ (b + 2) a
B2 — 4 a +1 b + 2 (b + 2) ∙ (b — 2)∙(a +1) b + 2
A+1 a ab+b+2a+2-ba+2a 4a+2+b
B-2-b+2
2 2 2
B2 -4
B2 -4
A — 2a +1 a2 -1 2a — b (a -1)2 ∙ (b — 2)(b + 2) 2a — b
B — 2 b2 — 4 a +1 (b — 2) ∙ (a + 1)a -1) a +1
(a -1)(b+ 2) 2a — b ab-b+ 2a -2-2a +b ab -2
A + 1 a + 1
3) m -1 m ∙ (1 — m2 )
M + 1
M -1- m+ m
M+1
(m+1)2 m+1
-1
= m — 1
A + 1
M — 1 m(1 — m)
A+1
2n+ 4 mn+ n2 m+ n
4) : =
2-n 4-4n+n2 4-n2
2n + 4 n(m + n)(2 — n)(2 + n) 2(n + 2) n(2 + n)
2 — n (2 — n)2(m + n) 2 — n 2 — n
= 2n + 4 — 2n — n 2 (2 — n)(2 + n) = 2 + n
2 — n 2 — n
X3-2x2y+xy2 x-2y
X ∙ (x — 2y) ∙ (x + 2y) ∙ (x — y)2
x(x — y )2 ∙ (x — 2 y)
25 + 5 — 2-I — I= 30 +1 = 31
2 2n[44] + 2n + 2 n[45] + n2 + n 3 3(n2 — 2n +1)∙ n(n2 + n +1) 3 3(n — l)∙z
2 2(rc2 + n +1)∙ (n -1) 2 2
3 — 3n2 + 3n 3
∙ (1 — n2 + n)
6a+3b = 3a +3b+3a ∙ (a +b)2
— b b2 — a2 ) a2 + 2ab + b2 (a — b)a + b) 3(a + b)
3(2,a + b) ∙ (a + b)2 a + b
(a — b)(a + b)∙3(2a + b)a — b
2n — 2m ) 2n
= 2mn-mn-n2 ∙ m2 — n2 = n(m-n) = m-n
m = 6-; n = -1,5:
2
6-+1- 8
C-d
D
C(c2 — d2 )
C(c + d) d (d + c)
Cd — d2 — c2 d2 + c2 — cd = (c2 + d2 — cd)’ c(c — d )(c + d)
Cd ∙(c + d) c ∙(c2 — d2) cd ∙( c + d) ∙ (d + c — cd)
C — d d-c
2)
2n 1
+
K + 2n k2 + 4nk + 4n2 Il k2 — 4n2 2n — k
2n
4n2
2n
L k + 2n (k + 2n)2 J v (k — 2n)k + 2n) 2n — k
2nk + 4n 2 — 4n 2 (k — 2n)(k + 2n)
(k + 2n)2 2n — k — 2n
2nk ■ (k — 2n)k + 2n) 2n ■ (2n — k)
(k + 2n)2 ■ k
K+ 2n
3)
B2 b3 I l b b2
B + x b2 + x2 + 2bx) l b + x (b — x)b + x)
B 2 b3 II l b b 2 I
L b + x (b + x)2 ) l b + x (b — x)b + x) )
B3 + b2x — b3: b2 — bx — b2 b2x ∙(b — x)(b + x) b ∙(x — b)
(b + x)2 (b — x)b + x) (b + x)2 ∙(-bx) b + x
4)
2q
4q2
2q
2q+m 4q2+4qm+m2) l4q2-m2 m-2q
2q
4q2
2q
2q + m (2q + m)2 J l(2q — m)(2q + m) m — 2qj
= 4q2 + 2mq — 4q2 2q — 2q — m = 2mq ∙(2q — m)(2q + m) =
(2q + m)2 ‘ (2q — m)(2q + m) (q + m)2 ■ (-m)
2q ■ (m — 2q)
2q+ m
504. Возьмем в куб обе части равенства x + — = а:
1I 3 11 3
X +— I — x + 3x + 3—I—— — а
Xx
3 1 l 1I 3
X3 l x )
X3 + -1∙ = а3 — 3а = а| а -;
А(а2-3)
1- x — 1 2- 4 — 4x
(x[46] [47] — 2x +1- x[48] -2x -1)
X +1 x -1 2 4 4xJ (x +1)( x -1)
2 x — x2 — 1 — 4 x 2 x — x2 — 1 (x — 1)2
4x
X2 -1
4x
X2 -1
Так как при -1<x < 1
(x — 1)2 >0, x2 -1<0, то выражение отрицательное.
peregorodky-msk.ru
Совместные действия с алгебраическими дробями
План открытого урока в 7 классе
Тема урока: Совместные действия с алгебраическими дробями.
Цель урока: Систематизация знаний учащихся по выполнению арифметических действий над алгебраическими дробями и формирование умений в выполнении двух-трех совместных действий с дробями.
Ход урока
І. Работа у доски: а) Решить уравнение: — = 4
б) Преобразовать, используя формулы 1) (х-4)2 2) х2 – 4 3) х2 +10х +25
4) 4x2—5) х2+9 6) (6х-)(6х+) 7)100-4х2 8)х3-8 9)81-18у+у2
10) -(а+в)3
Работа с классом: 1) «Лови ошибку»: на партах задание : «Из приведенных формул выбрать и записать номера правильных формул».
Вариант 1.1) а2 –в2 =(а+в)(а-в) Вариант 2. 1) (а-в)2 =(а-в)(а+в)
2) а3-в3=(а-в)(а2+2ав+в2 ) 2) (а+в)2 = а2+2ав+в2
3) (а+в)3 = а3+3а2в + 3ав2+в3 3) (а-в)3 = а3-3а2в + 3ав2-в3
4) а3+в3=(а+в)(а2-ав+в2 ) 4) а3+в3= а3+3а2в + 3ав2+в3
5) а2 –в2 =(а-в)2 5) а3-в3=(а-в)(а2+ав+в2 )
(проверка выполнения задания, на доске вывешиваются верные ответы)
2) Преобразовать выражения, используя формулы сокращенного умножения. (Письменно , в тетради, с последующей проверкой на доске)
а) -х2-8х-16 б) -х2+6х-9 в)-х2+81
^
Π. Изучение материала
(Перед учащимися раздаточный материал, где приведены указанные примеры)
— на доске числовое выражение -0,02*(6,2:0,31-*7,2) – 1,52. Задание: расставить порядок действий.
Ш.Закрепление нового материала
— Задание. Расставить порядок действий :
—1)(- ) : 2) :
3) (
— Рассмотрим задачу 2 и задачу 3 на стр.116 учебника и определим порядок действий
(У доски и в тетрадях учащиеся решают ПРИМЕР №3, предварительно проговаривая алгоритм сложения, вычитания , умножения и деления алгебраических дробей)
1)===
2)
3) := =
4) +=
Самостоятельная работа Упростите выражение
В1
В2
Задание на дом: § 28, № 495(2,4,6),506 (2)
microbik.ru


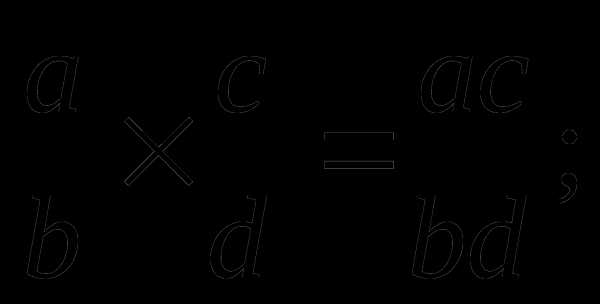
 .
.