Прямоугольная система координат в пространстве презентация савченко – Координаты вектора — 11 класс — — Каталог файлов
Презентация по теме «Прямоугольная система координат в пространстве»
Презентация по теме «Прямоугольная сиситема координат в пространстве» по геометрии для 11 класса. Предназначена для изучения новой темы, ознакомления учащихся с прямоугольной системой координат в пространстве, координатами вектора, правилами вычисления координат векторов, содержит примеры простых действий с координатами векторов. Материал соответствует программе и учебнику Л.C.Атанасяна.
Просмотр содержимого документа
«Презентация по теме «Прямоугольная система координат в пространстве» »

Прямоугольная система координат в пространстве
Геометрия – 11 класс
Белоброва Татьяна Валерьевна
учитель математики высшей категории
МКОУ СОШ №1 г.Сим
Челябинской области
z
1
A
y
1
О
1
x
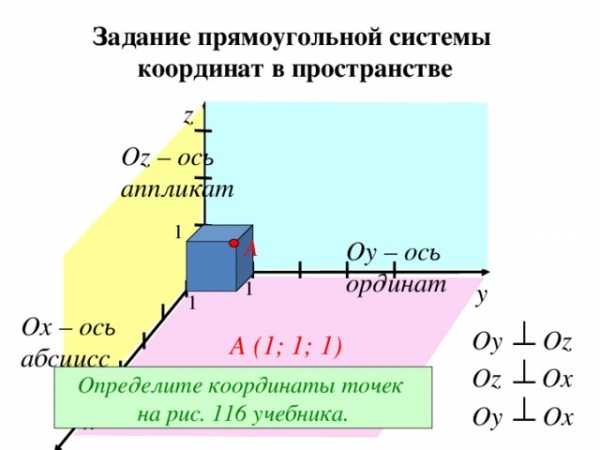
Задание прямоугольной системы координат в пространстве
z
О z – ось аппликат
1
A
Оу – ось ординат
1
y
О
1
Ох – ось абсцисс
О y О z
A (1; 1; 1)
О z О x
Определите координаты точек
на рис. 116 учебника.
О y О x
x
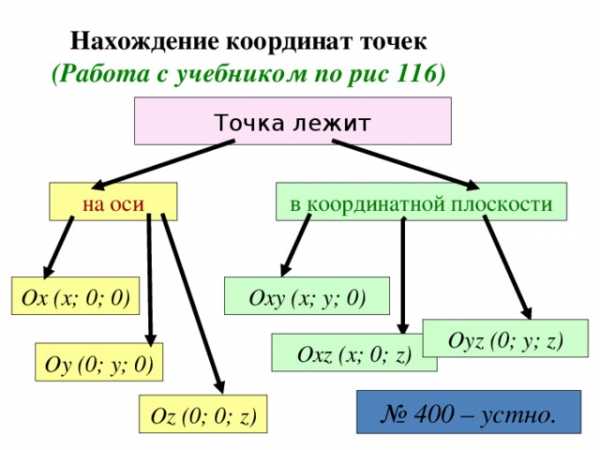
Нахождение координат точек (Работа с учебником по рис 116)
Точка лежит
в координатной плоскости
на оси
Ох (х; 0; 0)
Оху (х; у; 0)
Оу z ( 0 ; у; z )
Ох z (х; 0 ; z )
Оу (0; у; 0)
№ 400 – устно.
О z (0; 0; z)

Даны точки:
Назовите точки, лежащие
в плоскости Оу z
А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
Назовите точки, лежащие
в плоскости Ох z
D ( -4 ; -1; 0)
Е (0; -3; 0)
Назовите точки, лежащие
в плоскости Оху
F ( 1 ; 2 ; 3 )
Р (0; 5; -7)
К (2; 0; -4)
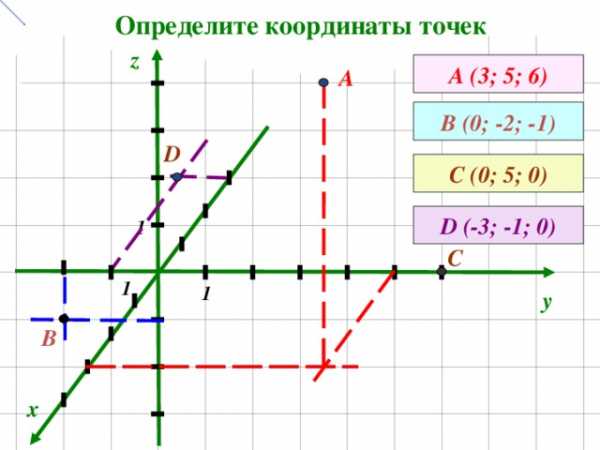
Определите координаты точек
z
А ( 3 ; 5 ; 6 )
А
В (0; -2; -1)
D
С (0; 5; 0)
D (-3; -1; 0)
1
С
1
1
y
В
x
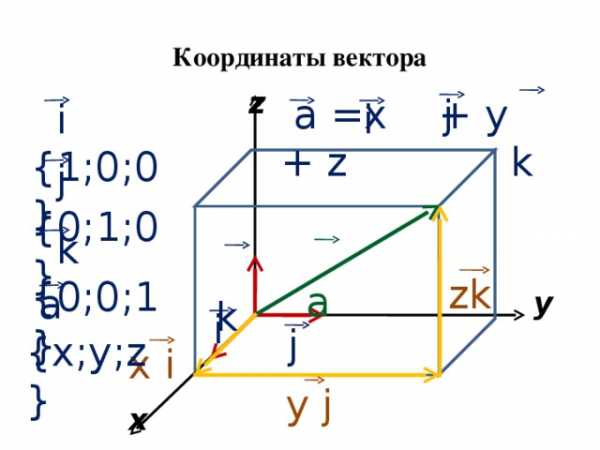
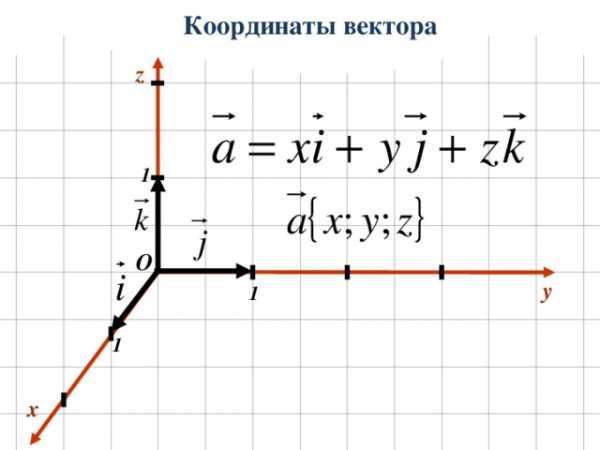
Координаты вектора
z
j
k
а =x + y + z
i { 1 ;0;0}
i
j { 0 ; 1 ;0}
k { 0 ;0; 1 }
а
y
k
zk
a { x ; y ; z }
i
j
x i
x
y j
Координаты вектора
z
1
О
y
1
1
x

Правила действий над векторами с заданными координатами
1. Равные векторы имеют равные координаты
, тогда
Пусть
х

2 . Каждая координата суммы двух (и более) векторов равна сумме соответствующих координат этих векторов
Дано:
Следовательно

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
4. Каждая координата разности двух векторов равна разности соответствующих координат на этих векторов.
Дано:
 Выполнить задание устно:
Выполнить задание устно:- Найти вектор равный:
kopilkaurokov.ru
Презентация на тему «Прямоугольная система координат в пространстве.Координаты вектора.»
Цель урока:
1.Ввести определение прямоугольной системы координат в пространстве.
2.Показать способ построения точки в системе координат.
3.Ввести понятие координатных векторов, координат вектора и правила действий с векторами.
4.Проверка усвоения изученного.
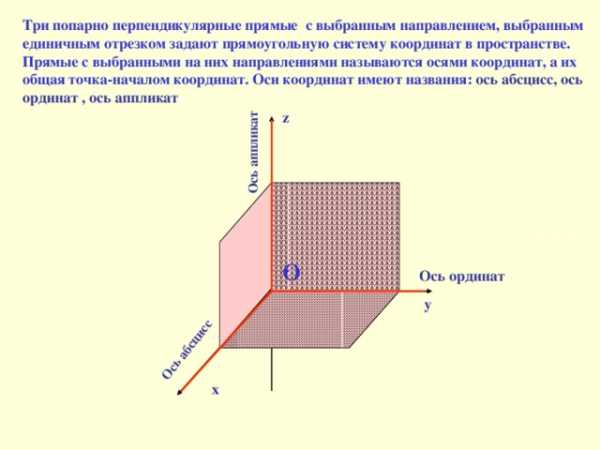
Три попарно перпендикулярные прямые с выбранным направлением, выбранным единичным отрезком задают прямоугольную систему координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка-началом координат. Оси координат имеют названия: ось абсцисс, ось ординат, ось аппликат
Просмотр содержимого документа
«Презентация на тему «Прямоугольная система координат в пространстве.Координаты вектора.» »

ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ. КООРДИНАТЫ ВЕКТОРА.
Цель урока:
1.Ввести определение прямоугольной системы координат в пространстве.
2.Показать способ построения точки в системе координат.
3.Ввести понятие координатных векторов, координат вектора и правила действий с векторами.
4.Проверка усвоения изученного.
 Ось абсцисс
Ось абсциссОсь аппликат
Три попарно перпендикулярные прямые с выбранным направлением, выбранным единичным отрезком задают прямоугольную систему координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка-началом координат. Оси координат имеют названия: ось абсцисс, ось ординат , ось аппликат
z
О
Ось ординат
y
x
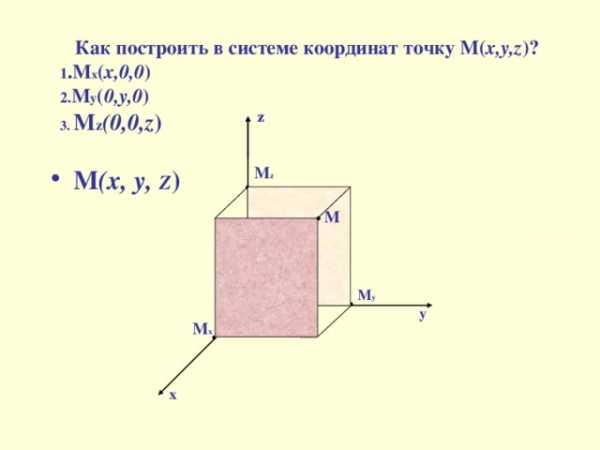
Как построить в системе координат точку М( x,y,z )?
1 .М x ( х,0,0 )
2. М y ( 0,у,0 )
3. М z (0,0,z )
z
z
z
z
М 3
М 3
М 3
•
•
•
•
М
•
•
•
•
М
М
М
О
М 2
О
М 2
М у
М 2
О
О
•
•
•
•
y
y
y
y
М х
М 1
М 1
М 1
•
•
•
•
x
x
x
x
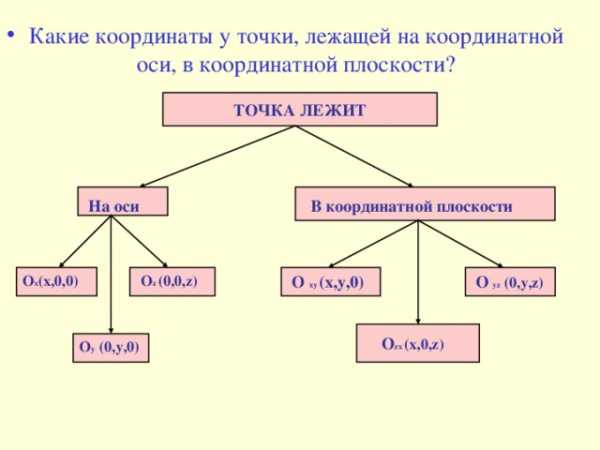
- Какие координаты у точки, лежащей на координатной оси, в координатной плоскости?
ТОЧКА ЛЕЖИТ
На оси
В координатной плоскости
О уz (0,у,z)
О ху (х,у,0)
О х (х,0,0)
О z (0,0,z)
O zx (x,0,z)
О y (0,y,0)

КООРДИНАТЫ ВЕКТОРА
i , j , k-единичные векторы осей х,у,z, координатные векторы.
z
k
o
j
y
i
x
a = x i + y j +z k,
a
x; y; z
i
j
k
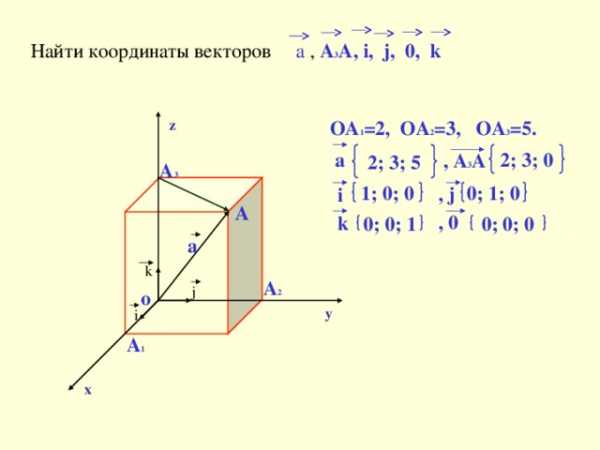
Найти координаты векторов a , A 3 A, i, j, 0, k
z
OA 1 =2, OA 2 =3, OA 3 =5.
a
2; 3; 5
, A
2; 3; 0
A 3
, j
i
0; 1; 0
1; 0; 0
A
, 0
k
0; 0; 1
0; 0; 0
a
k
A 2
j
o
y
i
A 1
x

Правила действий с векторами 1.Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. 2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. 3.Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Самостоятельная работа
1.Записать разложение векторов по координатным векторам
i, j, k:
I в-т II в-т
а)
а а
b b
б) Найти координаты векторов: -а; a+b; b-a; 2а – 3 b.
2. Найти сумму расстояний от точки
А(2;-5;1) до оси Ох и до A(-7;3;-1) до оси Оу и до
плоскости Охz . плоскости Оху.
kopilkaurokov.ru
Презентация. Прямоугольная система координат в пространстве. 11 класс
| |||||
www.openclass.ru
Презентация на тему «Прямоугольная система координат в пространстве»
Презентация на тему «Прямоугольная система координат в пространстве» по алгебре в формате powerpoint. В презентации для школьников дается понятие прямоугольной системы координат в пространстве, а также приведены задачи на нахождение координат точки. Автор презентации: Кошкарева Галина Фёдоровна.
Фрагменты презентации
Цель урока: ввести понятие прямоугольной системы координат в пространстве.
Умения и навыки: выработать умения строить точку по заданным её координатам и находить координаты точки, изображённой в заданной системе координат.
Идея координат зародилась в науке Вавилона и Греции в связи с потребностью географии, астрономии и мореплавания. Во II в. греческий учёный Гиппарх предложил определять положение точки на земной поверхности с помощью географических координат – широты и долготы, выражаемых числами.
В IIV в. француз Оресм перенёс эту идею в математику.В XIX в. французский учёный Рене Декарт перенёс эту идею в математику, предложив покрывать плоскость прямоугольной сеткой. Работа М.Эшера отражает идею введения прямоугольной системы координат в пространстве.
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана система координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.
- Ох – ось абсцисс,
- Оу – ось ординат,
- Оz – ось аппликат.
Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оzх.
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты. М (х,у,z), где х – абсцисса, у – ордината, z — аппликата.
Итог урока
На уроке познакомились с прямоугольной системой координат, научились строить точку по заданным ее координатам и находить координаты точки, изображенной в заданной системе координат. Декартова система координат не единственная. К следующему уроку найти в Интернете другие системы координат.
fevt.ru
Презентация на тему Прямоугольная система координат в пространстве (11 класс)
Презентацию на тему Прямоугольная система координат в пространстве (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет презентации : Математика. Красочные слайды и илюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого презентации воспользуйтесь плеером, или если вы хотите скачать презентацию — нажмите на соответствующий текст под плеером. Презентация содержит 7 слайдов.
Слайд 1МОУ СОШ №16 г. Славянск – на Кубани
презентация по геометрии 11 класс по теме: Прямоугольная система координат в пространстве Учитель математики высшей категории Куижева Людмила Евгеньевна 2011 год
Слайд 2Прямоугольная система координат в пространстве
Проведем через точку пространства три попарно перпендикулярные прямые, на каждой из них выбрано направление(обозначается стрелкой) и выбрана единица измерения отрезка, то говорят,что задана прямоугольная система координат в пространстве.
.O ось ординат y x ось абсцисс ось апликат z
Слайд 3x y
точка О -начало координат, оси координат: ox, oy, oz., координатные плоскости :Оxy, Oyz, Oxz.
О .
т. А( x ,0.0) Є OX т.В ( 0,y,0 ) Є OY т.С( 0,0,z ) Є OZ
А. В С .
Слайд 4т. М Є Оxy т. К Є Оyz т. Д Є Оxz
.М ( x,y,0) .K ( 0,y, z) Д (x,0,z) .
Слайд 5М( x,y,z) . М4( x,y,0) . М2( 0,y,0) М6( x,0,z) . М5( 0,y,z ) . М1( x,0,0) . М3( 0,0,z) .
Слайд 6Координаты вектора
а i k j а =x + y + z x i y j zk i {1;0;0} j {0;1;0} k {0;0;1} a {x;y;z}
Слайд 7А1. С1 . В1 О1 .
prezentacii.org
Презентация по математике «Прямоугольная система координат в пространстве»

Прямоугольная система координат в пространстве

Вопросы:
1. Сколькими координатами может быть задана точка на прямой?
Одной .
2. Сколькими координатами может быть задана точка в координатной плоскости?
Двумя .
Вопрос урока.
3. Сколькими координатами может быть задана точка в пространстве?
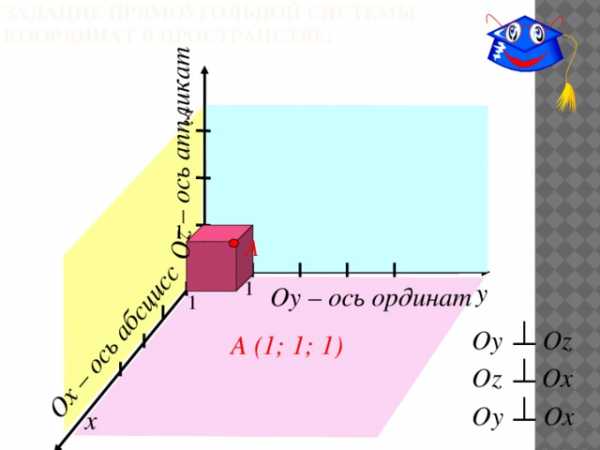
Задание прямоугольной системы координат в пространстве:
Ох – ось абсцисс
Оz – ось аппликат
z
1
A
1
y
О
Оу – ось ординат
1
Оy Оz
A (1; 1; 1)
Оz Оx
Оy Оx
x
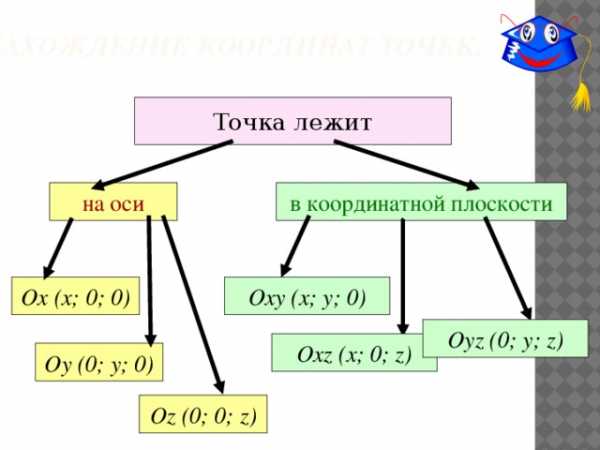
Нахождение координат точек.
Точка лежит
на оси
в координатной плоскости
Оху (х; у; 0)
Ох (х; 0; 0)
Оуz (0; у; z)
Охz (х; 0; z)
Оу (0; у; 0)
Оz (0; 0; z)
z
E
С
5
1
А
O
y
1
2
1
В
3
D
x

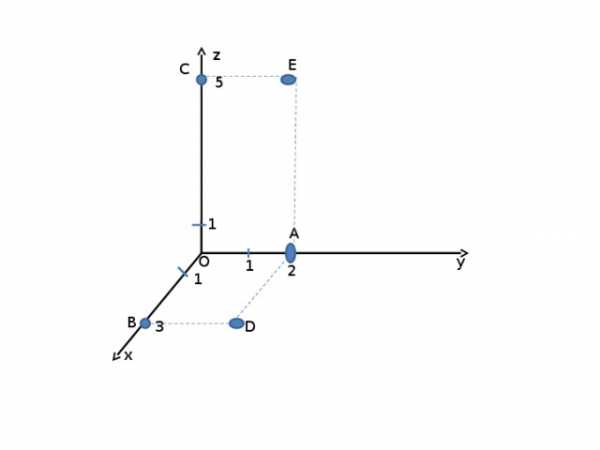
Построить в ПСК
A(1;0;0)
B(0;1;0)
C(0;0;1)
D(2;3;0)
E(1;3;5)

Решение задач.
№ 401 (а) Рассмотрим точку А (2; -3; 5)
A 3
2
z
1) A 1 : Oxy
A 1 (2; -3; 0)
A 2
A
2) A 2 : Oxz
5
A 2 (2; 0; 5)
3) A 3 : Oyz
A 3 (0; -3; 5)
у
0
A 1
Точки В и С рассмотреть самостоятельно.
Проверка – фронтально.
х
-3

Решение задач.
№ 401 (б) Рассмотрим точку А (2; -3; 5)
A 6
2
z
1) A 4 : Ox
A 4 (2; 0; 0)
A
2) A 5 : Oу
5
A 5 (0; -3; 0)
3) A 6 : Oz
A 5
A 6 (0; 0; 5)
у
0
A 4
Точки В и С рассмотреть самостоятельно.
Проверка – фронтально.
х
-3

Решить стр 287
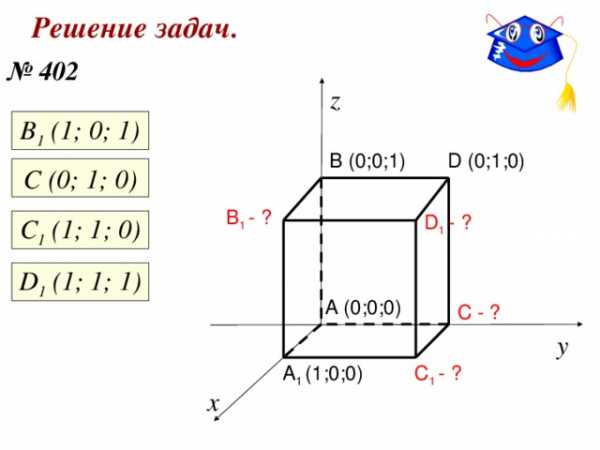
Решение задач.
№ 402
z
В 1 (1; 0; 1)
B (0;0;1)
D (0;1;0)
С (0; 1; 0)
B 1 — ?
D 1 — ?
С 1 (1; 1; 0)
D 1 (1; 1; 1)
A (0;0;0)
C — ?
у
C 1 — ?
A 1 (1;0;0)
х
videouroki.net
презентация «Системы координат» | Социальная сеть работников образования
Слайд 1
СИСТЕМЫ КООРДИНАТ работа команды «Эйнштейны» для 3 этапа проекта : «системы координат : взгляд в прошлое и в настоящее » руководители: Урум Елена николаевна бурцева наталья евгеньевнаСлайд 2
Систе́ма координа́т — комплекс определений, реализующий метод координат , то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Слайд 3
Наиболее употребительные координатные системы – декартовы прямоугольные. Иногда на плоскости применяют полярные системы координат, а в пространстве – цилиндрические или сферические системы координат.
Слайд 4
Обобщением всех перечисленных систем координат являются криволинейные системы координат.
Слайд 5
Криволинейные системы координат. В двухмерном пространстве задаются два семейства линий (координатных линий), зависящих каждое от одного параметра, причем через каждую точку проходит только по одной линии каждого семейства. Значения параметров, соответствующие этим кривым, являются криволинейными координатами этой точки. В трехмерном пространстве задаются три семейства координатных поверхностей , таких, что через каждую точку проходит по одной поверхности каждого семейства. Положение точки в такой системе определяется значениями параметров координатных поверхностей, проходящих через эту точку.
Слайд 6
Декартовы прямоугольные системы координат
Слайд 7
Впервые, такую привычную для нас, прямоугольную систему координат ввел французский ученый Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также – декартова система координат
Слайд 8
Так как Декарт публиковал свои работы под псевдонимом Картезий ( Cartesius ), то в западной научной литературе ее называют Картезианова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии .. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
Слайд 9
Вклад в развитие координатного метода внес еще один французский математик Пьер Ферма , однако его работы были впервые опубликованы уже после его смерти
Слайд 10
Для задания декартовой прямоугольной системы координат нужно выбрать несколько взаимно перпендикулярных прямых, называемых осями. Точка пересечения осей O называется началом координат. На каждой оси нужно задать положительное направление и выбрать единицу масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P. Декартовыми прямоугольными координатами точки P на плоскости называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых — осей координат или, что то же, проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси.
Слайд 11
Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей или, что то же, проекции радиус-вектора r точки P на три взаимно перпендикулярные координатные оси. В зависимости от взаимного расположения положительных направлений координатных осей возможны левая и правая координатные системы. Как правило, пользуются правой координатной системой. Положительные направления выбирают: на оси Ox — на наблюдателя; на оси Oy — вправо; на оси Oz — вверх. Координаты x, y, z называются соответственно абсциссой, ординатой и аппликатой.
Слайд 12
Полярные системы координат
Слайд 13
Основными понятиями этой системы являются точка отсчёта – полюс , и луч, начинающийся в этой точке – полярная ось . О х Полярный радиус ρ – длина отрезка ОА А Полярный угол φ – величина угла между полярной осью и отрезком ОА φ ρ Положительным направлением отсчета углов считается направление «против часовой стрелки»
Слайд 14
x 1 = ρ cos φ , y 1 = ρ sin φ Переход от полярной системы координат к декартовой Если полюс полярной системы координат совместить с началом прямоугольной системы координат, у х 0 О а полярную ось с положительной полуосью Ox , то по известным полярным координатам точки А( ρ ; φ ) А ρ φ её прямоугольные координаты вычисляются по формулам: х 1 у 1
Слайд 15
Переход от декартовой системы координат к полярной
Слайд 16
Применение
Слайд 17
В фотографии Эрмитаж. Полярная проекция Вертикальные линии после того, как к ним применен фильтр (переводящий координаты точек из прямоугольной системы в полярную), стали расходиться из центральной точки. На правой части картинки горизонтальные линии превратились в концентрически расходящиеся из центра круги.
Слайд 18
В военном деле Радиолокационные станции (РЛС ) Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y), геодезической (широта, долгота).
Слайд 19
В медицине Компьютерная томография сердца в системе полярных координат.
Слайд 20
В системах идентификации (подтверждение личности человека) Идентификация по радужной оболочке глаза Результат преобразования кольца радужной оболочки из декартовой системы координат в полярную.
Слайд 21
Позиционирование и навигация Полярную систему координат часто применяют в навигации , поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. В этой системе, обычно используемой для навигации, луч 0° называют направлением 360, а углы отсчитываются в направлении по часовой стрелке. Направление 360 соответствует магнитному северу, а направления 90, 180, и 270 соответствуют магнитным востоку, югу и западу. Так, самолёт , летящий 5 морских миль на восток можно описать как самолёт , летящий 5 единиц в направлении 90 (центр управления полётами назовёт его найн-зиро ).
Слайд 22
Моделирование Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических полярных координатах при шести частотах.
Слайд 23
Цилиндрические системы координат
Слайд 24
ρ и φ — полярные координаты проекции точки P на основную плоскость (обычно xOy ), z — аппликата — расстояние от точки P до основной плоскости. Для цилиндрических координат координатными поверхностями являются плоскости, перпендикулярные к оси Oz (z= const ), полуплоскости, ограниченные осью z (φ= const ) и цилиндрические поверхности, осью которых является ось z (ρ= const ). Координатные линии — линии пересечения этих поверхностей.
Слайд 25
Формулы для перехода от цилиндрических координат к декартовым x=ρ* cos (φ), y=ρ* sin (φ), z=z и обратно: ρ= sqrt ( x 2 + y 2 ), φ= arctg ( y / x )= arcsin ( y /ρ).
Слайд 26
Сферические системы координат
Слайд 27
r — длина радиус-вектора, φ — долгота, θ — полярное расстояние. Положительные направления отсчета показаны на рисунке 6. Если давать сферическим координатам значения в следующих пределах: 0 ≤ r
Слайд 28
Формулы перехода от сферических координат к декартовым x=r*sin( θ )*cos( φ ), y=r*sin( θ )*sin( φ ), z=r*cos( φ ) и обратно r= sqrt (x 2 +y 2 +z 2 ), φ = arctg (y/x), φ = arctg ( sqrt ((x 2 +y 2 )/z)).
Слайд 29
Кардиоида
Слайд 30
Кардиоида – плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Кардиоида (от греческих слов сердце и вид) – получила свое название из-за схожести своих очертаний с изображением сердца.
Слайд 31
Свойства кардиоиды Кардиоида — алгебраическая кривая четвёртого порядка. Кардиоида имеет один касп ( Касп ( англ. cusp — заострение ) — точка, в которой кривая линия разделяется на две (или более) ветви, имеющие в этой точке одинаковый направляющий вектор. То есть, ветви в данной точке имеют общую касательную и движение вдоль них из данной точки изначально происходит в одном и том же направлении) Кардиоида – функция четная
Слайд 32
В декартовых координатах X = 2r cos(t) — r cos( 2 t) Y = 2r sin(t)-r sin(2t)
Слайд 34
В полярных координатах r = a(1 + cos( φ ))
Слайд 38
Выводы : При сравнении прямоугольной и полярной системы координат мы поняли, что прямоугольная система координат является наиболее простой и понятной, в том числе и школьникам, но в полярной системе существует возможность размещения более сложных изображений.
Слайд 39
СПАСИБО ЗА ВНИМАНИЕ
nsportal.ru

