Практическая работа операции над матрицами – Методическая разработка на тему: Практическое работа по математике по теме «Матрицы. Операции над матрицами» для 2 курса в системе СПО
Методическая разработка на тему: Практическое работа по математике по теме «Матрицы. Операции над матрицами» для 2 курса в системе СПО
Практическая работа №1
Тема: Матрицы. Операции над матрицами.
Цель: сформировать умение выполнять основные операции над матрицами.
Теоретические сведения к практической работе
Определение. Матрицей размером n×m называется прямоугольная таблица, составленная из n m чисел и имеющая n строк и m столбцов. Числа αij, составляющие матрицу, называются элементами матрицы
А=(αij)=
Определение. Матрицу Аt называют транспонированной по отношению к матрице А, если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.
.
Пример, , .
Определение. Квадратная матрица называется треугольной, если все ее элементы, размещенные над главной диагональю (под ней), равны нулю, т.е.
— верхняя треугольная матрица,
– нижняя треугольная матрица.
Определение. Матрица, все элементы которой равны нулю, называется нуль-матрицей.
Матрица-строка , матрица-столбец .
Операции над матрицами.
1) Пусть матрицы и одинаковой размерности. Суммой матриц и называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы и .
для всех и .
2) Разностью матриц и одинаковой размерности называется матрица той же размерности, каждый элемент которой рамен разности соответствующих элементов матрицы и .
для всех и .
3) Произведением матриц на число называется матрица , каждый элемент которой равен .
4) Матрицу можно умножить на матрицу () лишь в то случае, когда число столбцов первой матрицы равно число строк второй матрицы , т.е. . При этом каждый элемент матрицы-произведения определяется так:
, для всех и .
Т.е., элемент равен сумме произведений элементов -й строки матрицы на соответствующие элементы -го столбца матрицы .
Найти произведение матрицы-строки и матрицы-столбца:
Пример 1.
1) ,
2) ,
3) ,
4) ,
5) .
Пример 2
Для заданных матриц , , найти матрицы , , , , , , .
, , .
Решение
1.1)
;
1.2) ;
1.3)
;
1.4)
;
1.5)
.
Подчеркнем еще раз, что .
1.6)
;
Содержание практической работы:
Задание 1. Для матриц , , вычислить:
1) , 2) , 3) ,
4) , 5) , 6) , если
, , .
Задание 2. Для матриц , , вычислить:
1) , 2) ,
3) , 4) , если
, , .
Задание 3. Найти произведение матриц:
1) ; 2) ;
3) ; 4) ;
5) ; 6) ;
7) ; 8)
nsportal.ru
Перечень практических работ
№ п/п | № раздела дисциплины | Тематика практических занятий (семинаров) | Трудо-емкость (час.) |
1. | 1 | Линейные операции над матрицами. Произведение матриц. Транспонирование. | 2 |
2. | 1 | Определитель матрицы. Обратная матрица. | 2 |
3. | Решение систем линейных уравнений. | 2 | |
4. | 2 | Решение систем линейных уравнений методом Гаусса. | 2 |
5. | 3 | Линейные операции над векторами. Скалярное произведение векторов. | 2 |
6. | 3 | Векторное и смешанное произведения векторов. | 2 |
7. | 4 | Способы задания прямой на плоскости. | 4 |
8. | 4 | Способы задания плоскости. | 2 |
9. | 4 | Способы задания прямой в пространстве | 2 |
10. | 4 | Взаимная ориентация прямой и плоскости. | 2 |
11. | 5 | Кривые второго порядка. | 2 |
Практическое занятие № 1 Тема: «Линейные операции над матрицами. Произведение матриц. Транспонирование»
Примеры решения задач.
Пример 1.
Найти сумму и разность матриц:;
Решение:
Складывая и вычитая соответствующие элементы матриц, находим:
;
Пример 2.
Вычислить , если.
Решение:
Используя правила вычитания матриц и умножения матрицы на число, имеем:
Пример 3.
Найти произведение матриц:
Решение:
Число столбцов первой матрицы равно числу строк второй матрицы, поэтому произведение этих матриц существует. Используем правило умножения матриц: каждый элемент результирующей матрицы равен сумме произведений элементов соответствующей строки первой матрицы на элементы соответствующего столбца второй матрицы:
Пример 4.
Транспонировать матрицу:
Решение:
По определению операции транспонирования, меняем в исходной матрице строки и столбцы местами:
Пример 5.
Вычислить АВ-ВА, если матрицы А и В заданы:
Решение:
Находим произведения матриц:
Находим разность полученных матриц:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Вычислить если
2. ;
3.
Найти произведение матриц:
1. . 2..
3.. 4..
5. ; 6.
Транспонировать матрицы:
; 2. ; 3..
Вычислить АВ-ВА, если матрицы А и В заданы:
2.
3. 4.
5. 6.
Практическое занятие № 2 Тема: «Определитель матрицы. Обратная матрица»
Примеры решения задач.
Пример 1.
Вычислить определитель матрицы размерности :
Решение:
Определитель второго порядка равен разности произведений элементов главной и побочной диагонали:
Пример 2.
Вычислить определитель матрицы размерности :
Решение:
Определитель третьего порядка находится по правилу треугольников:
Пример 3.
Вычислить определитель матрицы, используя разложение определителя по строке или столбцу:
Решение:
Запишем разложение определителя по первой строке:
, где — алгебраическое дополнение элемента.
Найдем алгебраические дополнения по формуле , где- минор элемента, который получается из исходного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Подставляем полученные значения в разложение определителя:
.
Пример 4.
Для данной матрицы найти обратную матрицу:
Решение:
Используем алгоритм нахождения обратной матрицы:
Матрица квадратная (число строк равно числу столбцов), следовательно обратная к ней матрица существует.
Находим определитель исходной матрицы:
Находим матрицу, состоящую из алгебраических дополнений элементов исходной матрицы:
Таким образом, получаем матрицу:
4. Полученную матрицу транспонируем:
Осуществляем проверку полученного результата. Для этого находим произведение полученной матрицы на исходную:Таким образом, получили в результате единичную матрицу. Следовательно, обратная матрица была найдена верно.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Вычислить определители:
1.2.. 3.; 4.. 5.. 6.;
7.. 8.; 9.
Для данной матрицы найти обратную матрицу:
1. ; 2.; 3.; 4.; 5..
studfiles.net
Образец выполнения практической работы № 1 «Выполнение операций над матрицами. Вычисление определителей»
Образец выполнения практической работы № 1 «Выполнение операций над матрицами. Вычисление определителей»
Задание 1.Пусть .
Найти матрицу .
Решение.
Ответ.
Задание 2.Найти , если
,
Решение.
Ответ
.
Задание 3. Найти матрицу ,
если
Решение.
Ответ.
Задание 4. Вычислить и ,
если
Решение. Так как , а , то произведение возможно и результатом операции умножения будет матрица , а это матрица вида .
Вычислим элементы матрицы :
Итак, .
Выполним произведения в более компактном виде:
Найдем теперь произведение . Так как количество столбцов матрицы (первый сомножитель) не совпадает с количеством строк матрицы (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы не совпадает с количеством строк матрицы .
Задание 5. Найти матрицу , если
Решение.
Ответ.
Задание 6. Найти минор к элементу определителя
.Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда
Ответ.
Задание 7. Найти алгебраическое дополнение к элементу определителя
.
Решение.
= — (1.8-7.2)= — (8-14)=6
Ответ. 6
Задание 8. Вычислить определитель матрицы.
Решение.
Ответ. 54
Задание 9. Найти обратную матрицу к матрице
Решение. Вычисляем определитель матрицы:
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле:
Найдем союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы :
Таким образом,
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
Итак,
Ответ.
Список рекомендуемой литературы
Богомолов Н.В., Математика, Учебник для ССУЗов . – М.: Дрофа. 2010. – 398 с.
Григорьев С.Г.Математика. Учебник для ССУЗов . – М.: Академия. 2010. – 384 с.
Башмаков М.И. Математика. Учебник для учреждений начального и среднего профессионального образования. – М.,: Академия. 2011. – 256 с.
infourok.ru
Практическая работа по теме «Матрицы»
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ по теме
«ДЕЙСТВИЯ НАД МАТРИЦАМИ»
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
1. Найти матрицу, противоположную матрице А =  .
.
Решение. Для нахождения противоположной матрицы умножаем матрицу А на к = -1: — А =  .
.
2. Найти линейную комбинацию 3А — 2В, если
А =  , В =
, В = 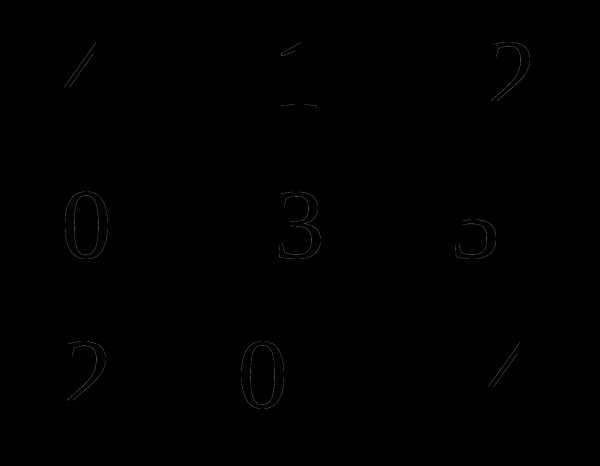 .
.
Решение. Сначала находим произведение А на к1 = 3 и В на к2 = -2:
3А = 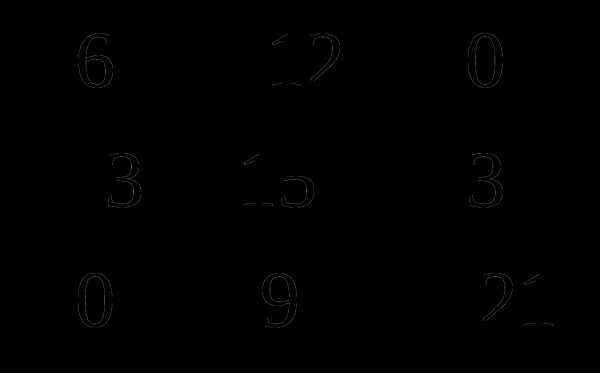 , — 2В =
, — 2В =  .
.
Теперь найдем сумму полученных матриц:
3А — 2В =  =
= 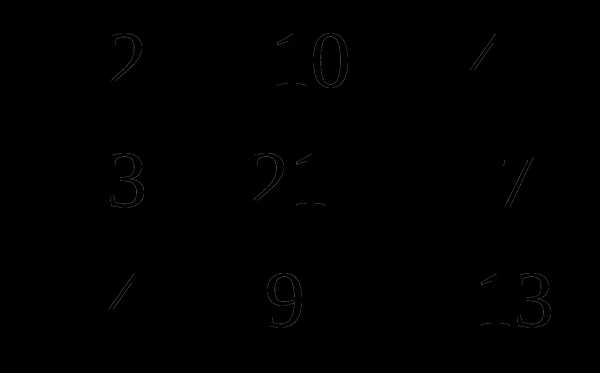 .
.
3. Найти произведение АВ, если А =  , В =
, В =  .
.
Решение. АВ =  =
=  .
.
4. Найти произведение АВ:
а) А =  , В =
, В =  Ответ:
Ответ: 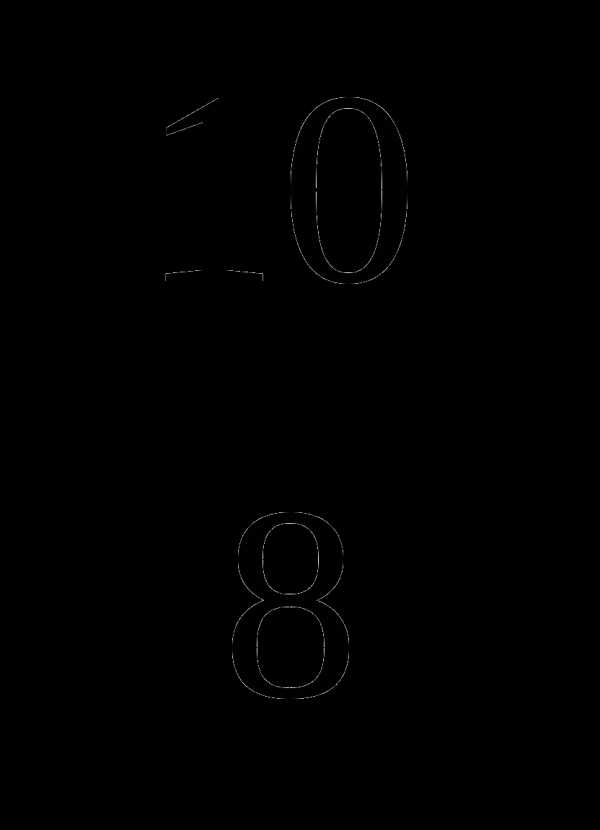 .
.
б) А = 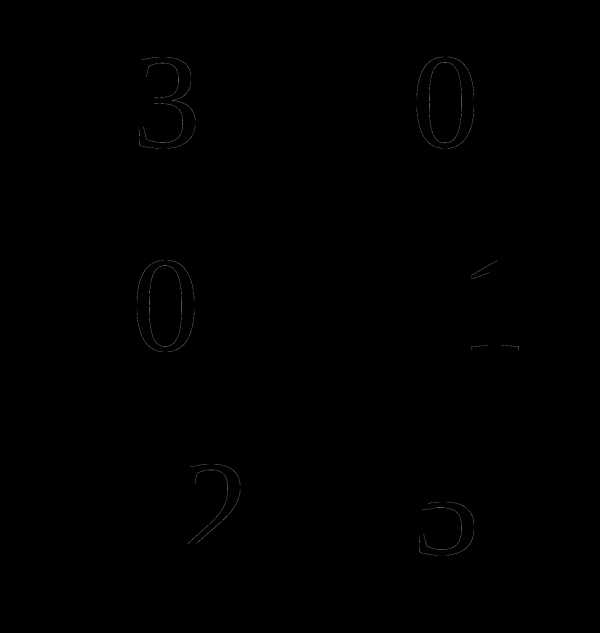 , В =
, В =  Ответ:
Ответ: 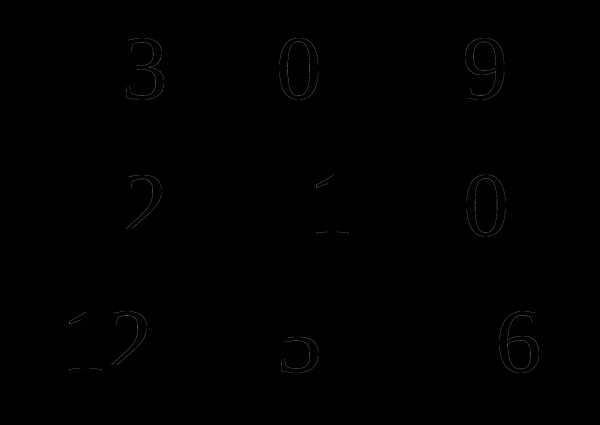 .
.
5. Вычислить С = А2 + 2В, где А =  , В =
, В = 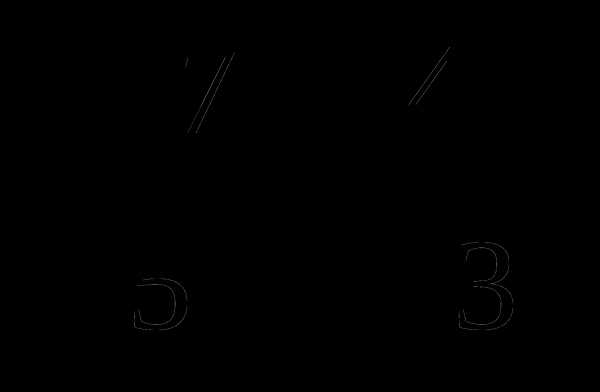 .
.
Ответ: 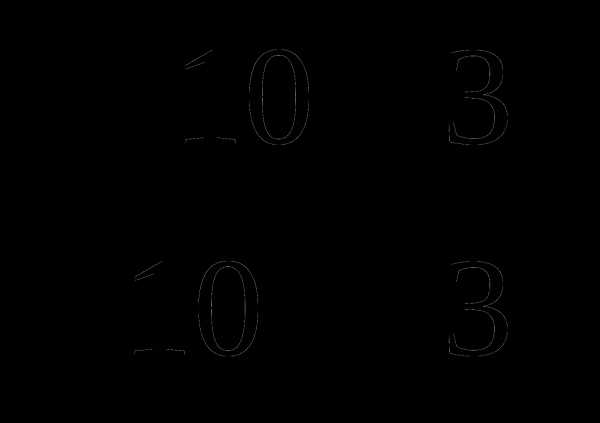 .
.
6. Найти АВ — ВА, где А =  , В =
, В = 
Ответ:  .
.
7. Найти АЕ, если А =  , Е =
, Е = 
Ответ:  .
.
ЗАДАНИЕ
Вычислить линейные комбинации матриц:
а) 2А — В, если А = 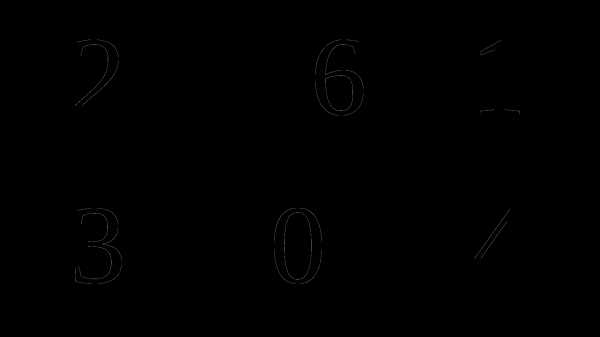 , В =
, В = 
Ответ:  .
.
б) 3А + 2В, если А =  , В =
, В = 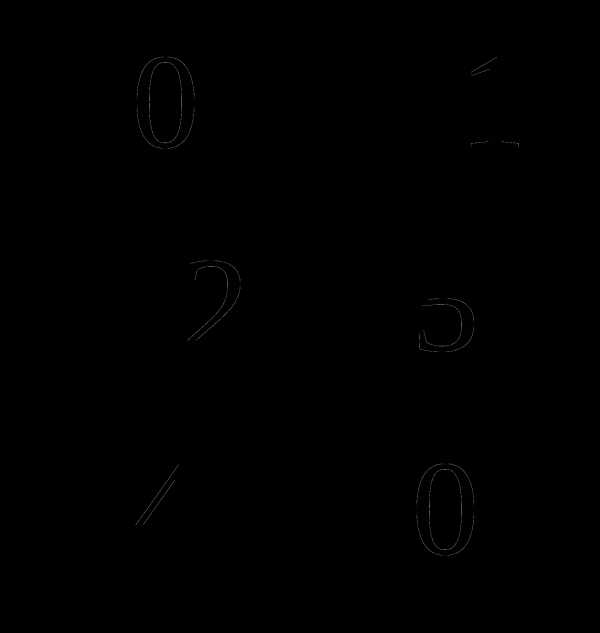
Ответ:  .
.
Найти произведение АВ:
а) А =  , В =
, В =  Ответ:
Ответ: 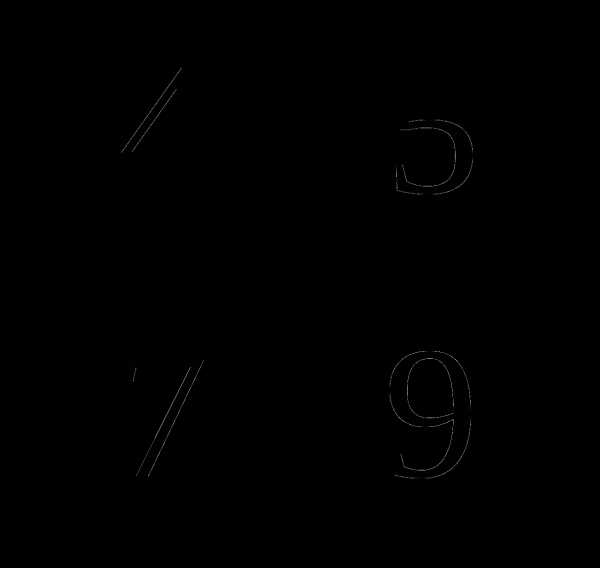 .
.
б) А = 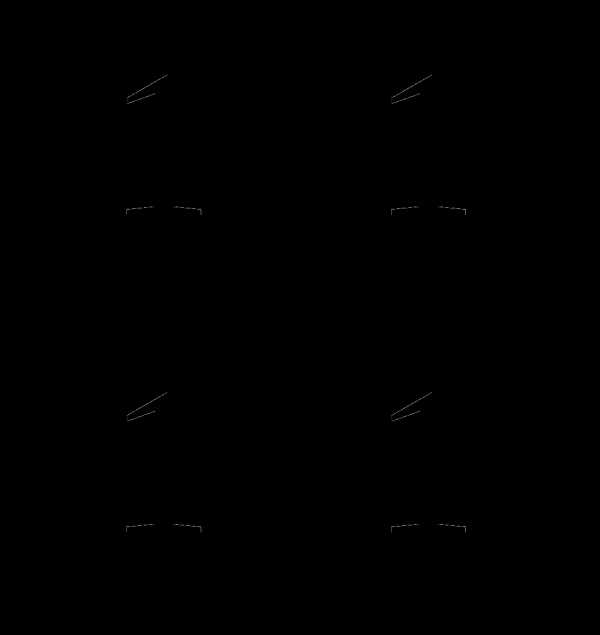 , В =
, В =  Ответ:
Ответ:  .
.
Найти
 , если А =
, если А =  , В =
, В = 
Ответ:  .
.
Найти ЕА, если Е =
 , А =
, А = 
Ответ: 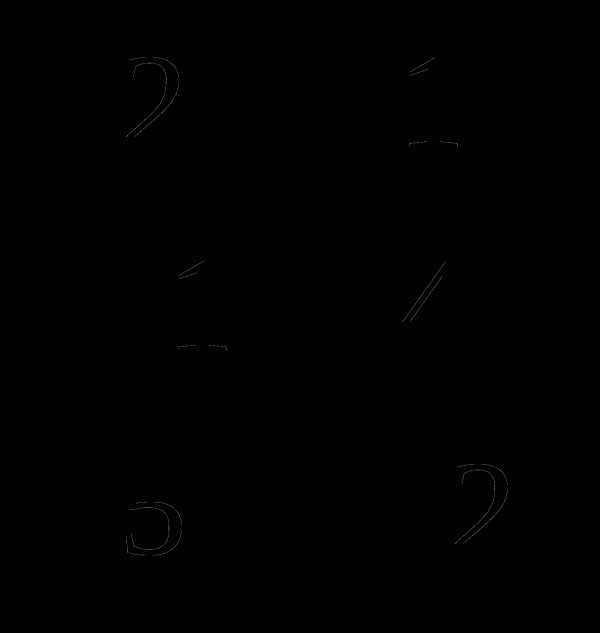 .
.
ВОПРОСЫ ДЛЯ ЗАКРЕПЛЕНИЯ
ВАРИАНТ 1
Определение матрицы и ее обозначение.
Линейные операции над матрицами (сложение матриц и умножение матрицы на число)
Умножение квадратных матриц третьего порядка.
Правила умножения прямоугольных матриц.
ВАРИАНТ 2
Виды матриц.
Равные матрицы. Транспонированная матрица.
Умножение квадратных матриц второго порядка.
Свойства умножения матриц.
infourok.ru
«Матрицы и действия с ними»
Дисциплина – «Математика»
Курс -2
Семестр -3
Практическая работа №1
Тема: «Матрицы и действия с ними»
Цель: сформировать умение выполнять арифметические действия с матрицами.
Методические указания и теоретические сведения к практической работе
Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
.
Для обозначения матрицы используют заглавные латинские буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием номера строки и столбца, на пересечении которых стоит данный элемент. Запись «матрица B имеет размер mxn» означает, что речь идет о матрице, состоящей из m строк и n столбцов.
Например, матрица имеет размер 2x3. Далее, bij — обозначение элемента, стоящего на пересечении i-й строки и j—го столбца данной матрицы (в примере b23=5).
При ссылке на i-ю строку матрицы A используют обозначение Ai, при ссылке на j-й столбец – обозначение Aj.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера nxn называют матрицей n-го порядка. Элементы a11 , a22 ,…, ann квадратной матрицы A (размера nxn) образуют главную диагональ.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
Например, — единичная матрица 4-го порядка.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали треугольной. Например, среди квадратных матриц размера 3x3
, , ,
матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.
Матрицы A, B называются равными (A=B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.
Действия над матрицами.
Сложение
Операция сложения матриц вводится только для матриц одинаковых размеров.
Чтобы найти сумму матриц A, B одной размерности, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):
Пример 1. + =
Умножение на число
Чтобы умножить матрицу A на отличное от нуля действительное число k, необходимо каждый элемент матрицы умножить на это число:
.
Пример 2. Найти 2A—B, если , .
Решение. Сначала умножаем матрицу A на число 2, затем матрицу B на число -1, и, наконец, находим сумму полученных матриц:
Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы Аmxn=(aij) на матрицу Вnxp=(bjk) называется матрица Сmxp=(cik) такая, что элемент i-ой строки и k-ого столбца произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-ого столбца матрицы В.
Если матрицы А и В квадратные одного размера, то произведение АВ и ВА всегда существует.
Пример 3. Найти произведение матриц и .
Решение. Размер матрицы A 3x2, матрицы — В 2х2. Поэтому произведение АВ найти можно, произведение ВА – нет. Действуя по сформулированному выше правилу, получаем:
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается AT .
Так, если , то .
Если , то .
Пример 4. Найти АВ+СТ , если
Решение. Воспользовавшись вычислениями примера 3, также правилами умножения матрицы на число и сложения матриц, получим:
АВ+СТ =.
Практическая работа №1
Тема: «Матрицы и действия с ними»
Содержание практической работы
Вариант 1.
Найти сумму и разность матриц А и В, где
Найти СТ, где
Найти матрицы:
а) 2А;
б) 8ВТ;
в) 2А+5В;
г) -3А-7,5В, где
Найти произведения матриц АВ и ВА, где
Найти А3 , где
Найти значение матричного многочлена 2А2+3А+5Е, где
Доказать равенство (AB)C=A(BC) для матриц:
1) , , ;
2) , , .
Дополнительные задания
8. Выполнить арифметические действия с матрицами:
1) ; 2) ;
3) ; 4) ;
5) ;
6);
7)
9. Доказать равенство для матриц (АВ)С=А(ВС)
, , ;
10. Найти: 1) ; 2) ; 3) .
infourok.ru
«Обратная матрица» для студентов 2 курса СПО
Дисциплина – «Элементы высшей математики»
Курс -2
Практическая работа
Тема: «Обратная матрица»
Цель: формирование умений вычислять обратные матрицы;
закрепление умений вычислять определители второго и третьего порядков, составлять и вычислять алгебраические дополнения к элементам матрицы.
формирование общих компетенций, включающими в себя способность:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях.
ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
Методические указания и теоретические сведения к практической работе
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
А зачем нужно искать обратную матрицу?
Ели обратная матрица известна, то решение системы уравнений сводится к операции простого умножения матриц. При программировании задач 3D-графики и компьютерных игр обратные матрицы также находят широкое применение.
Матрица называется обратной по отношению к квадратной матрице A, если выполнено условие , где E – единичная матрица, порядок которой равен порядку матрицы A.
Невырожденная матрица – матрица, определитель которой не равен нулю. Вырожденная матрица – матрица, определитель которой равен нулю.
Обратная матрица существует тогда и только тогда, когда матрица A – невырожденная. Если обратная матрица существует, то она единственная.
Метод присоединённой (союзной) матрицы
Пусть задана матрица An×n. Для того, чтобы найти обратную матрицу A−1, требуется осуществить три шага:
Найти определитель матрицы A и убедиться, что ΔA≠0, т.е. что матрица А – невырожденная.
Составить алгебраические дополнения каждого элемента матрицы A и записать матрицу из найденных алгебраических дополнений.
Записать обратную матрицу по формуле
Матрица называется присоединённой (взаимной, союзной) к матрице A.
Союзной или присоединенной к матрице A называют матрицу , которая получается из матрицы A, если все ее элементы заменить соответствующими алгебраическими дополнениями и к полученной матрице применить операцию транспонирования. (Присоединенная матрица – это транспонированная матрица, составленная из алгебраических дополнений к элементам данной матрицы)
Пример 1.
Найти обратную матрицу к матрице
Решение. Вычисляем определитель матрицы:
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле:
Найдем (присоединенную) союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы :
Таким образом, – матрица, составленная из алгебраических дополнений к элементам матрицы .
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером), поучим присоединенную (союзную)матрицу :
Итак, ,
Ответ:
Дисциплина – «Элементы высшей математики»
Курс -2
Практическая работа
Тема: «Обратная матрица»
Задание 1.Найти , если: а) ; б) .
Задание 2. Выполните проверку для задания 1.
Указание. Используйте формулу:
Задание 3. Докажите равенство для матриц из задания 1.
Задание 4. Определите, при каких x значениях существует матрица, обратная данной:
а)
; б) .
Задание 5. Показать, что матрица А является обратной для матрицы В, если:
а)
а) , .
б) .
Задание 6. Найти , если: а) ; б) /
Задание 7. Выполните проверку для матриц из задания 6.
Отчет о практической работе
1.Тема практической работы
2.Цель практической работы
3.Умения
В ходе выполнения практической работы я научился (закрепил умения) вычислять…
Я получил (совершенствовал) практические навыки…
4.Знания
5.Выводы
Мне было сложно выполнять…, потому, что…
Мне было несложно выполнять…, потому, что…
Теоретические вопросы
1.Вырожденные и невырожденные матрицы
2.Присоединенная (союзная) матрица
3.Обратная матрица
4.Алгоритм нахождения обратной матрицы
xn--j1ahfl.xn--p1ai
Операции над матрицами. Вычисление определителей
⇐ ПредыдущаяСтр 2 из 12Следующая ⇒
Цель: Формирование навыков выполнения операций над матрицами и вычисления определителей второго, третьего и четвертого порядков.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Прямоугольная матрица размера ( -матрица) имеет вид таблицы, состоящей из строк и столбцов:
.
Элемент матрицы находится на пересечении -ой строки и -го столбца, ; .
У нулевой матрицы 0 все элементы равны нулю:
.
Матрица – столбец ( -матрица) состоит из одного столбца:
,
а матрица – строка ( -матрица) из одной строки:
.
Произведением двух матриц и называется матрица , каждый элемент которой определяется по правилу строка на столбец, то есть элемент стоки матрицы умножается на элемент столбца матрицы стоящие на соответствующих местах.
Из определения произведения матриц следует, что не любые две матрицы можно перемножать. Произведение имеет смысл только тогда, когда число столбцов первой матрицы-сомножителя равно числу строк второй матрицы-сомножителя, что символически записывается так:
.
Транспонирование -матрицы заключается в замене строк столбцами, а столбцов – строками с теми же номерами:
.
Матрица размера называется суммой двух -матриц и , если каждый элемент матрицы равен сумме соответствующих элементов матриц и :
.
Определителем второго порядка называется число, определяемое равенством
. (1)
Числа называются элементами определителя; при этом элементы и образуют главную диагональ, а элементы и — побочную диагональ. Таким образом, определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Определителем третьего порядка называется число, определяемое равенством
(2)
.
Таким образом, каждый член определителя третьего порядка представляет собой произведение трех его элементов, взятых по одному из каждой строки и каждого столбца. Эти произведения берутся с определенными знаками: со знаком «плюс» – члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком «минус» – три члена, расположенные аналогичным образом относительно побочной диагонали.
Указанное правило, называется правилом треугольников.
Минором элемента называется определитель , полученный из вычеркиванием -ой строки и -го столбца.
Алгебраическим дополнением элемента называется его минор, умноженный на :
.
Определитель -го порядка равен сумме произведений элементов какой – либо строки или столбца на их алгебраические дополнения:
(разложение определителя по элементам -ой строки) или
(разложение определителя по элементам -го столбца).
В частности, для определителя третьего порядка имеем
,
что совпадает с результатом, полученным по формуле (2).
Примеры
Задание 1: Найти сумму и разность матриц и .
Решение: Здесь даны матрицы одного размера , следовательно, существуют их сумма и разность. Согласно определению алгебраической суммы матриц имеем
,
.
Задание 2: Вычислить определители: 1) ; 2) .
Решение: 1) По формуле (1) находим .
2) Разлагая данный определитель, например, по элементам первой строки, находим
.
Тот же результат получится, если воспользоваться формулой (2):
.
Задания для самостоятельной работы
1. Найдите сумму матриц и .
2. Транспонируйте матрицу . Укажите размеры данной и транспонированной матриц.
3. Даны матрицы: , . Произведите указанные действия, а в случае, когда это невозможно, указать причину: 1) ;
2) .
4. Даны матрицы и . Найдите матрицу .
5. Вычислите определители второго порядка: а) ;
б) .
6. Вычислите определители третьего порядка: а) ;
б) .
7. Вычислите определитель четвертого порядка .
Вопросы для самоконтроля:
1. Что называется матрицей? Как установить размеры матрицы?
2. Назовите линейные операции над матрицами. Как они производятся?
3. Какие матрицы можно перемножать? Как это делается?
4. Что называется определителем? Как вычисляются определители второго и третьего порядков?
5. Что называется минором и алгебраическим дополнением для произвольного элемента определителя?
Практическое занятие №2
Рекомендуемые страницы:
lektsia.com


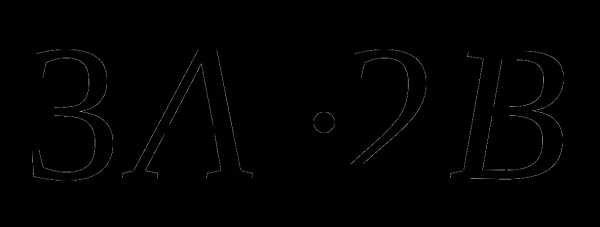 , если А =
, если А =  , В =
, В =