Порядок вычисления примеров – Порядок выполнения действий: правила, примеры.

Содержание

Порядок выполнения действий в выражениях без скобок и со скобками

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Запишем.

8-3+4=5+4=9

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

8-3+4=8-7=1

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя.

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

38-10+6

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

24:3*2

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

18:2-2*3+12:3

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

1 4 2 5 3

18:2-2*3+12:3

Вычислим значение выражения.

1 4 2 5 3

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

3 2 1

30 + 6 * (13 — 9)

Вычислим значение выражения.

3 2 1

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

2 * 9 — 18:3

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

4 3 1 2

37 + 9 — 6 : 2 * 3 =

3 1 2

18 : (11 — 5) + 47=

1 3 2

7 * 3 — (16 + 4)=

Рассуждаем так.

3 4 1 2

37 + 9 — 6 : 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

3 4 1 2

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

3 1 2

18:(11-5)+47=

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

2 1 3

18:(11-5)+47=18:6+47=3+47=50

Рассуждаем далее.

1 3 2

7*3-(16+4)=

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

2 3 1

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.

«Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Festival.1september.ru (Источник).
Sosnovoborsk-soobchestva.ru (Источник).
Openclass.ru (Источник).

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

68+2-50+43

(36-18):(72:8)

35:5+6*2

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

25+30:6-3*5+45

15+6*5-48:6-10

20+8*5-45:9+12

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

interneturok.ru

Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий

Основные операции в математике

Базовыми формами вычисления являются:

Сложение +
Умножение х или ∗
Вычитание —
Деление ÷ или /

К ним также можно отнести возведение в степень, однако с ним действуют те же законы, что и при умножении. Итак, последовательность расчетов регулируется следующими правилами. По умолчанию, при отсутствии дополнительных элементов, они выполняются в порядке написания.

15 — 3 + 7 = 19

При наличии скобок сначала выполняется действие, в них заключенное.

15 — (3 + 7) = 5

При появлении знаков или первыми выполняются они, лишь затем сложение или вычитание.

2 + 2 х 2 = 2 + 4 = 6

2 + 2 ÷ 2 = 2 + 1 = 3

Скобки могут частично ослабить эти правила, так как действие в них заключенное всегда выполняется в первую очередь.

(2 + 2) х 2 = 4 х 2 = 8

(2 + 2) ÷ 2 = 4 ÷ 2 = 2

Если в скобки заключено сложное выражение, внутри них работают стандартные правила.

(4 + 7 — 1) + 5 = (11 — 1) + 5 = 15

(5 + 3 х 2) — 4 = (5 + 6) — 4 = 11 — 4 = 7

При появлении двух и более знаков или нужно учитывать их очередность.

5 х 2 — 8 ÷ 4 = 10 — 2 = 8

Решение примеров с множественными скобками

Вариант 1:

5 + 8 ÷ 2 + 3 х (15 — 6 х 2 + 1) + 3 х (6 — 4) = ?

Распишем все расчеты поэтапно:

6 х 2 = 12
15 — 12 + 1 = 4
6 — 4 = 2

8 ÷ 2=4

Получаем сокращенную версию:

5 + 4 + 3 х 4 + 3 х 2 = ?

Снова расписываем:

3 х 4 = 12
3 х 2 = 6

Еще сократили: 5 + 4 + 12 + 6 = 27 Вариант 2: 3 + 2 х [10 — 3 х (6 ÷ 2)] + 1 = ? Сокращаем:

6 ÷ 2 = 3
10 — 3 х 3 = 10 — 9 = 1

Получили: 3 + 2 х 1 + 1 = 3 + 2 + 1 = 6 Вариант 3: {50 — [11 — (5 + 2)} х 4 = ? Сокращаем:

5 + 2 = 7
11 — 7 = 4
50 — 4 = 46
46 х 4 = 184

Ответ: 184

Законы сложения и умножения Также описывают общие принципы проведения вычислений.

Переместительный:

a + b = a + b

Сочетательный:

(a + b) + c = a + (b + c)

a х (b х c) = (a х b) х c

Распределительный:

a х (b + c)=a х b + a х c

(a + b) х c= a х c + b х c

Законы нуля:

a + 0 = a

a х 0=0

Правило единицы:

a х 1 = a

Знание этих законов поможет проводить необходимые вычисления быстрее.

Важно! В случае замены + и х на — и ÷ соответственно эти правила перестают действовать.

Несмотря на легкость понимания, очередность выполнения операций жизненно важна, так как все сложные формулы (логарифмы, интегралы и так далее) по сути представляют собой сокращенную форму написания длинной цепи простых вычислений. Чтобы закрепить материал статьи, рекомендуем посмотреть видео ниже. Рекомендуем посмотреть видео о порядке дейсивий в математике

nauka.club

Порядок выполнения действий / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Порядок выполнения действий

В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.

1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.

Например,

В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:

Вычисляем:

1) 10 + 15 = 25

2) 25 — 6 = 19

3) 19 — 8 = 11

Полностью пример записываем так:

10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11

Например,

В числовом выражении 3 арифметических действия: деление, умножение и деление.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:

Вычисляем:

1) 15 : 5 = 3

2) 3 • 4 = 12

3) 12 : 6 = 2

Полностью пример записываем так:

15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2

2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.

1)15 : 3 = 5

2) 6 • 8 = 48

3) 10 — 5 = 5

4) 5 + 48 = 53

Полностью пример записываем так:

10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53

3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

1) 25 — 10 = 15

2) 15 : 3 = 5

3) 6 • 8 = 48

4) 5 + 48 = 53

Полностью пример записываем так:

(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53

Например,

В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

1) 12 : 4 = 3

2) 6 + 3 = 9

3) 18 : 9 = 2

4) 42 + 2 = 44

Полностью пример записываем так:

42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44

Вывод:

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Скобки

Правило встречается в следующих упражнениях:

2 класс

Страница 55. Вариант 2. № 2, Моро, Волкова, Проверочные работы

Страница 68. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы

Страница 17, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 31, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 37, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 63, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 65, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 105, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 31, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 37, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 66, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть

5 класс

Задание 30, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 64, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 74, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 86, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 98, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 167, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 191, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 3, Мерзляк, Полонский, Якир, Учебник

Упражнение 13, Мерзляк, Полонский, Якир, Учебник

Упражнение 37, Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 73, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 85, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 92, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 373, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 378, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 400, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 411, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 413, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 417, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 422, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

budu5.com

Порядок арифметических действий, скобки | Формулы и расчеты онлайн

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Например,

\[ 4 — 2 + 1 = 3 \]

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

\[ (4 — 2) + 1 = 3 \]

\[ 4 — (2 + 1) = 1 \]

Пример 1:

\[ (2 + 4) · 5 = 6 · 5 = 30 \]

\[ 2 + (4 · 5) = 2 + 20 = 22 \]

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Пример 2:

\[ 2 · 5 — 3 · 3 \]

Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1

Пример 3:

\[ 9 + 16 : 4 — 2 · (16 — 2 · 7 + 4) + 6 · (2 + 5) \]

Сначала выполняем действия в скобках:
16 — 2 · 7 + 4 = 16 — 14 + 4 = 6
2 + 5 = 7

Теперь выполняем остающиеся действия:
9 + 16 : 4 — 2 · 6 + 6 · 7 =
= 9 + 4 — 12 + 42 =
= 43

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками {}. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.

Пример 4:

\[ 5 + 2 · [14 — 3 · (8 — 6)] + 32 : (10 — 2 · 3) \]

Выполняем действия в круглых скобках, имеем:
8 — 6 = 2
10 — 2 · 3 = 10 — 6 = 4

действия в квадратных скобках дают:
14 — 3 · 2 = 8

выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29

Пример 5:

\[ {100 — [35 — (30 — 20)]}· 2 \]

Порядок действий:
30 — 20 = 10
35 — 10 = 25
100 — 25 = 75
75 · 2 = 150

В помощь студенту

Порядок арифметических действий, скобки	стр. 19

www.fxyz.ru

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения. Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто, как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 10 − 1 = 9

2) 9 + 2 = 11

3) 11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 3 + 5 = 8

2) 2 × 3 = 6

3) 8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1) 5 − 3 = 2

2) 5 × 2 = 10

3) 2 : 2 = 1

4) 10 + 1 = 11

5) 11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1) 3250 − 2905 = 345

2) 345 : 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1) 6 411 × 8 = 51 288

2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934

Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

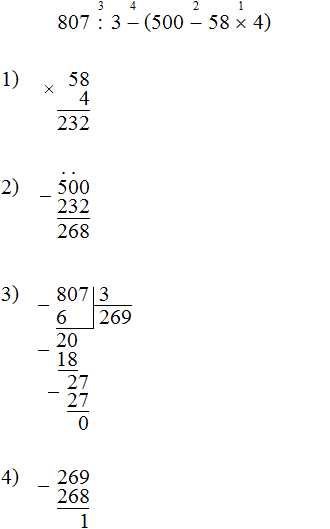
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

Порядок выполнения математических действий | интернет проект BeginnerSchool.ru

Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Итак, вспомним о том, что сначала вычисляются выражения в скобках

38 – (10 + 6) = 22;

1) в скобках: 10 + 6 = 16;

2) вычитание: 38 – 16 = 22.

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20;

Порядок выполнения действий:

1) слева направо, сначала деление: 10 ÷ 2 = 5;

2) умножение: 5 × 4 = 20;

10 + 4 – 3 = 11, т.е.:

1) 10 + 4 = 14;

2) 14 – 3 = 11.

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9;

2) 2 × 3 = 6;

3) 12 ÷ 3 = 4;

4) 9 – 6 = 3; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54, т.е.:

1) выражение в скобках: 13 – 9 = 4;

2) умножение: 6 × 4 = 24;

3) сложение: 30 + 24 = 54;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.

Понравилась статья — поделитесь с друзьями:

Подпишитесь на новости сайта:

Оставляйте пожалуйста комментарии в форме ниже

beginnerschool.ru

Порядок выполнения действий в выражениях без скобок

Порядок действий в выражениях без скобок

Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:

Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.

В качестве примера рассмотрим следующее выражение:

	3	1	5	2	4		6
3	·	4²	—	2³	:	2	+	20

Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):

3 · 16 — 8 : 2 + 20

Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):

48 — 4 + 20

И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):

48 — 4 + 20 = 44 + 20 = 64

Действия первой и второй ступени

Арифметические действия делятся на действия первой и второй ступени. Сложение и вычитание называются действиями первой ступени, умножение и деление – действиями второй ступени.

Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.

Пример 1. Вычислить значение выражения:

15 + 17 — 20 + 8 — 12

Решение. Данное выражение содержит действия только одной ступени – первой (сложение и вычитание). Надо определить порядок действий и выполнить их.

	1		2		3		4
15	+	17	—	20	+	8	—	12

1) 15 + 17 = 32

2) 32 — 20 = 12

3) 12 + 8 = 20

4) 20 — 12 = 8

Ответ: 8.

Пример 2. Вычислить значение выражения:

60 : 15 · 7 : 2 · 3

Решение. Данное выражение содержит действия только одной ступени – второй (умножение и деление). Надо определить порядок действий и выполнить их.

	1		2		3		4
60	:	15	·	7	:	2	·	3

1) 60 : 15 = 4

2) 4 · 7 = 28

3) 28 : 2 = 14

4) 14 · 3 = 42

Ответ: 42.

Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.

Пример. Вычислить значение выражения:

24 : 3 + 5 · 2 — 17

Решение. Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым – умножение, третьим – сложение, а четвёртым – вычитание.

Теперь приступим к вычислению:

1) 24 : 3 = 8

2) 5 · 2 = 10

3) 8 + 10 = 18

4) 18 — 17 = 1

Ответ: 1.

naobumium.info