Первообразная задания – Первообразная функции. Задания ЕГЭ по математике (профильный уровень)
Задачи В9. Первообразная и интеграл
Часть 4.
В данной статье мы разбираем Задачи №7 ЕГЭ по математике, связанные с первообразной.
Здесь смотрите части 1, 2, 3.
Задача 1.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где — одна из первообразных функции .
Решение: + показать
Задача 2.
На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Решение: + показать
Задача 3.
На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Решение: + показать
Задача 4.
На рисунке изображён график функции – одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения на отрезке .
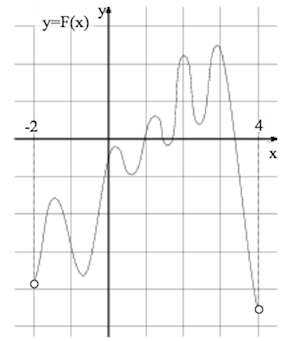
Решение: + показать
Загляните –> + показать
Препод по матану встречает своего студента через лет десять после окончания ВУЗа.
– А скажите, молодой человек, Вам когда-нибудь пригодились знания, полученные на моих лекциях?
– А Вы знаете, профессор, ведь было такое.
– Ах, как интересно! Расскажите!
– У меня один раз шляпу ветром сорвало и в лужу бросило. Так я проволочку подобрал, свернул ее интегралом и шляпу-то из лужи вытянул!

Вы можете пройти тест «Задачи №7. Первообразная».
egemaximum.ru
Индивидуальные задания по теме «Первообразная и интеграл» для 11 класса
Индивидуальная работа №21
Первообразная. Интеграл
сдатьВариант 1, 11
Найдите первообразные следующих функций:
Вычислите
1.  ; 2.
; 2. 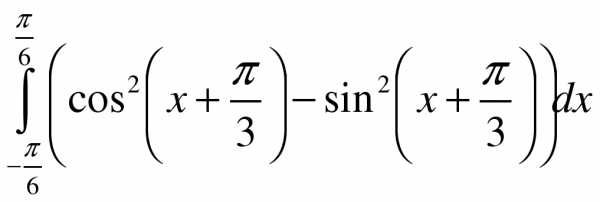
Вариант 2, 5
1. Докажите, что функция Н есть первообразная для функции h на промежутке I:
а)
б)
2. Для функции 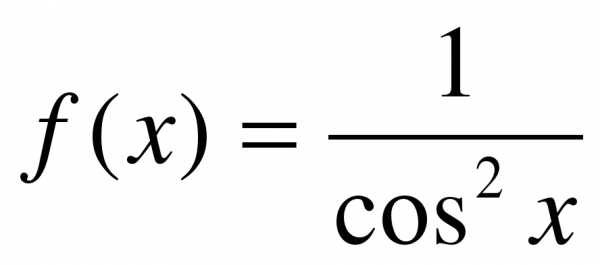 найдите первообразную, график которой проходит через точку
найдите первообразную, график которой проходит через точку  .
.
3. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок):
у = -х2+4х, у = 0.
4. Найдите
Вариант 3, 4, 17
1. Докажите, что функция Н есть первообазная для функции h на промежутке I:
а)
б)
2. Одна из первообразных функции 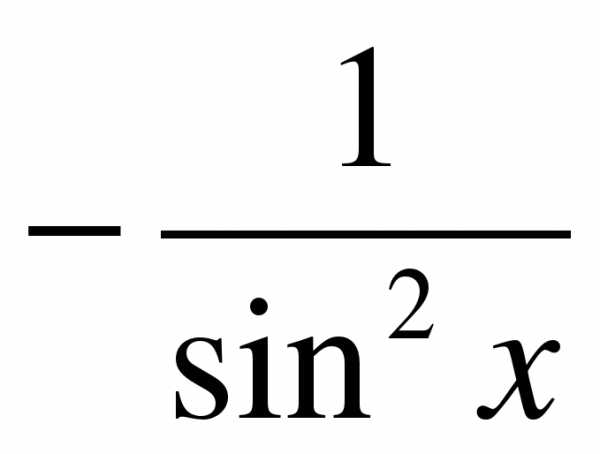 проходит через точку
проходит через точку 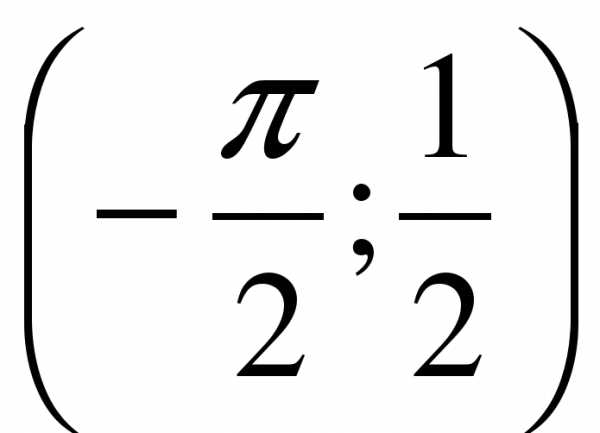 , а вторая – через точку
, а вторая – через точку  . График какой из них расположен выше? Какова разность этих первообразных?
. График какой из них расположен выше? Какова разность этих первообразных?
3. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок):
у = — (х2 – 5х + 4), у = 0.
4. Найдите 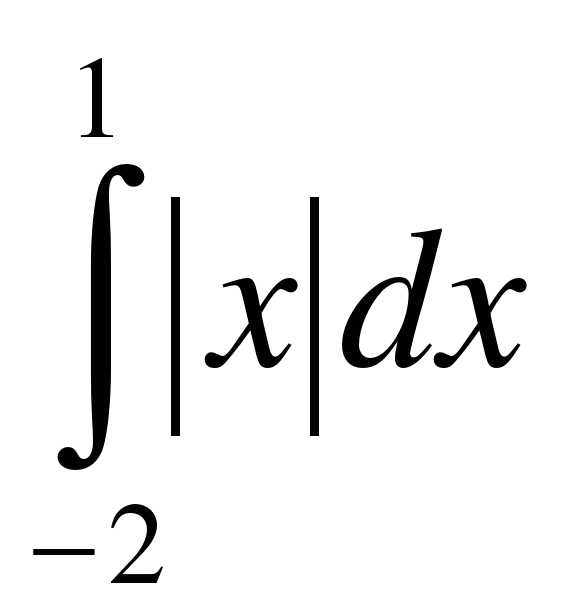
Вариант 6, 22
Найдите первообразные следующих функций:
Вычислите
1.  ; 2.
; 2. 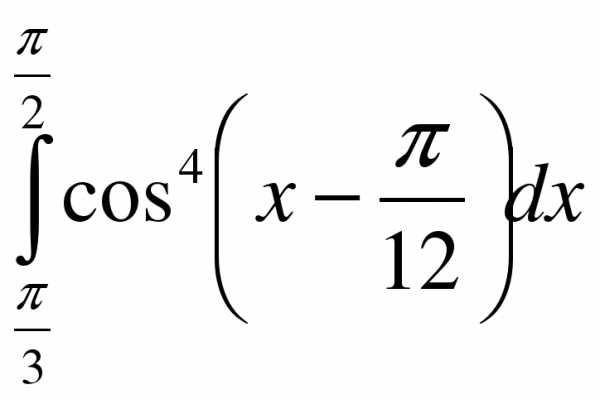
Вариант 7, 14
Найдите первообразные следующих функций:
Вычислите
1. 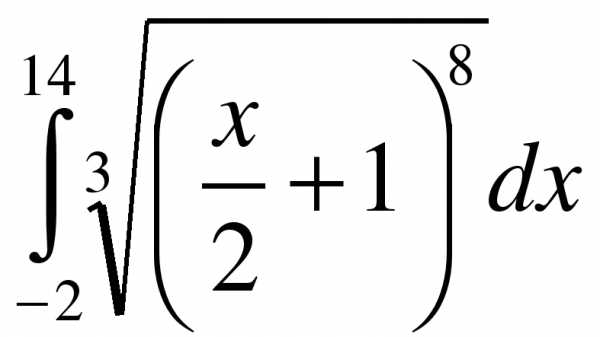 ; 2.
; 2.
Вариант 8, 13
Найдите первообразные следующих функций:
Вычислите
1. 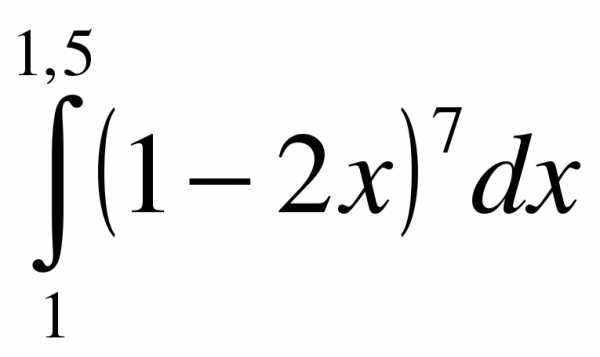 ; 2.
; 2.
Вариант 15, 21
1. Докажите, что функция Н есть первообазная для функции h на промежутке I:
а)
б)
2. Одна из первообразных функции 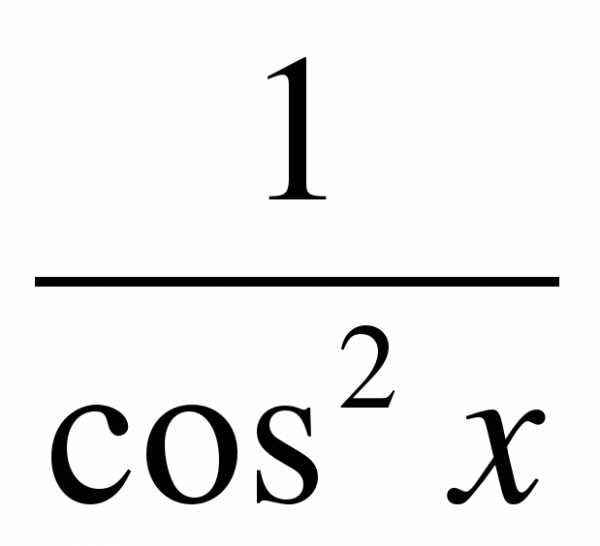
 , а вторая – через точку
, а вторая – через точку  . График какой из них расположен выше? Какова разность этих первообразных?
. График какой из них расположен выше? Какова разность этих первообразных?3. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок):
у = х+1, у = 4 + 3х – х2.
4. Найдите 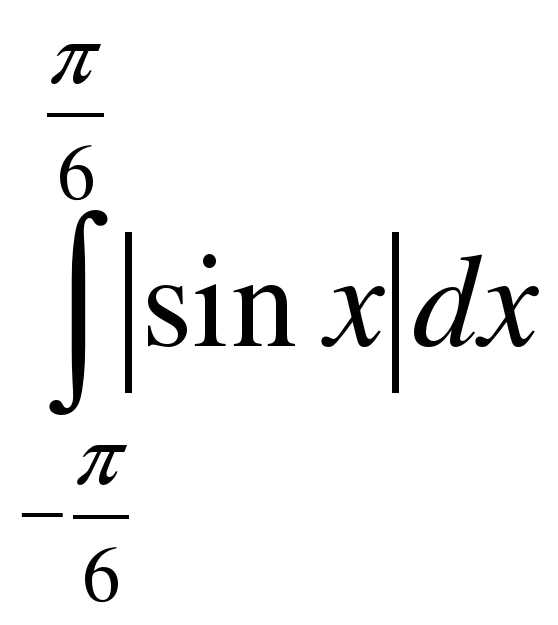
Вариант 9, 25
Найдите первообразные следующих функций:
Вычислите
1.  ; 2.
; 2. 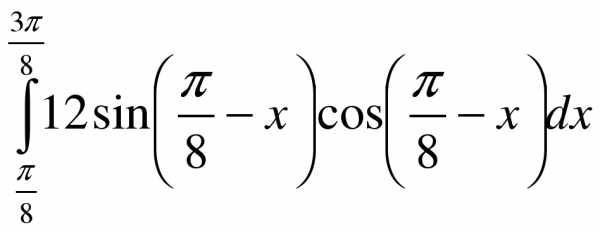
Вариант 16, 24
Найдите первообразные следующих функций:
Вычислите
1. 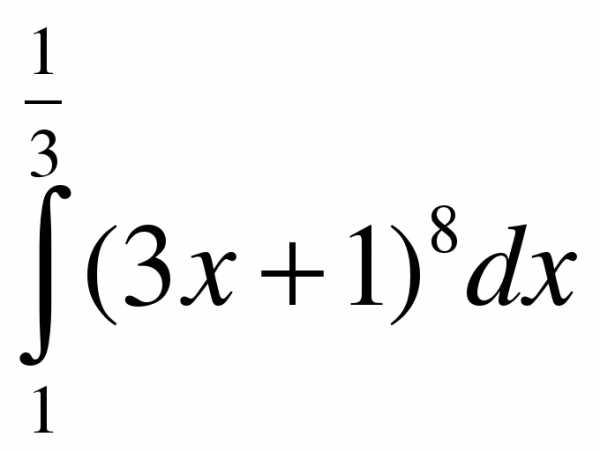 ; 2.
; 2.
Вариант 18, 12
1. Найдите первообразные для функции f:
а)  ; б)
; б)
2. График одной из первообразных функции проходит через точку (-1;2), а график другой – через точку (0;4). Какой из графиков расположен выше? Какова разность этих первообразных?
3. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок):
у = 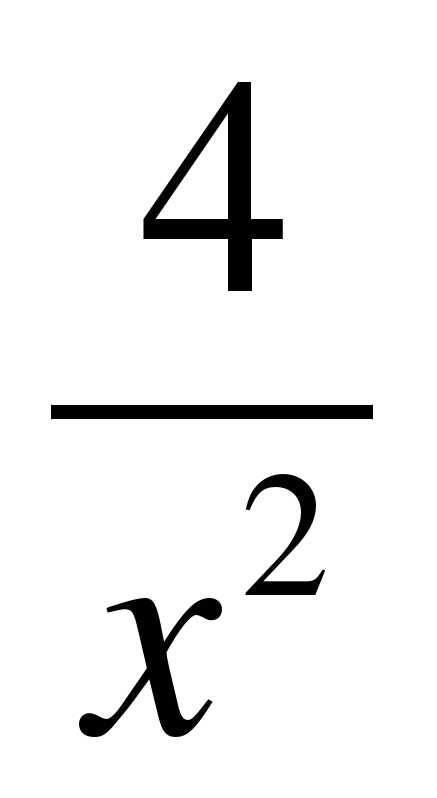 , х = 1, у = х — 1.
, х = 1, у = х — 1.
4. Найдите 
Вариант 19, 23
1. Найдите первообразные для функции f:
а) 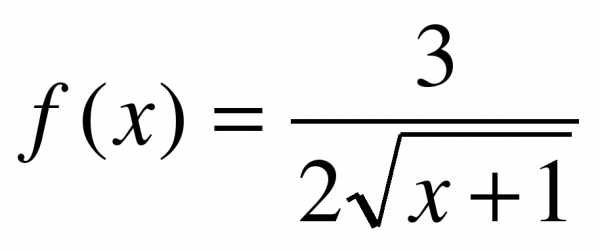 ; б)
; б)
2. График одной из первообразных функции проходит через точку (0;2), а график другой – через точку (1;4). Какой из графиков расположен выше? Какова разность этих первообразных?
3. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок):
у =2cosx, — 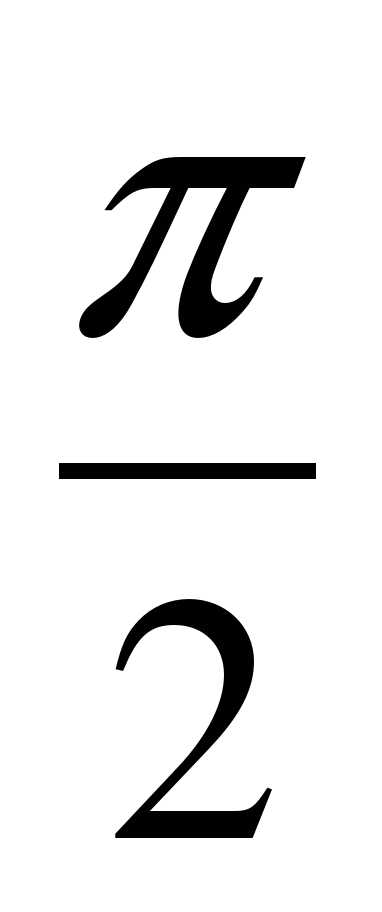 х
х 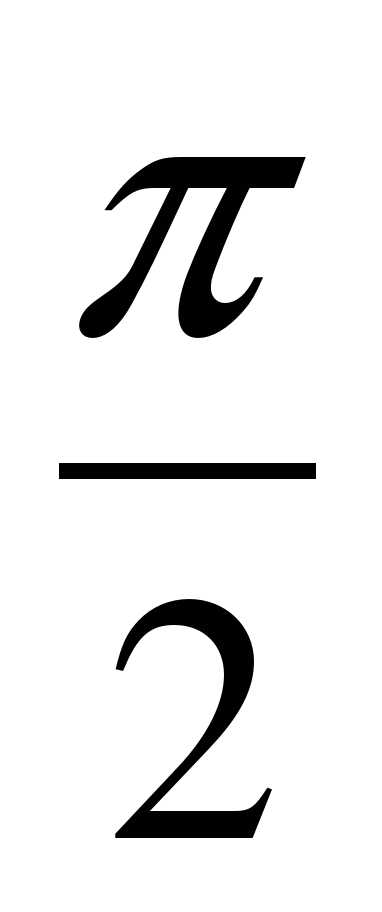 , у = 1.
, у = 1.
4. Найдите 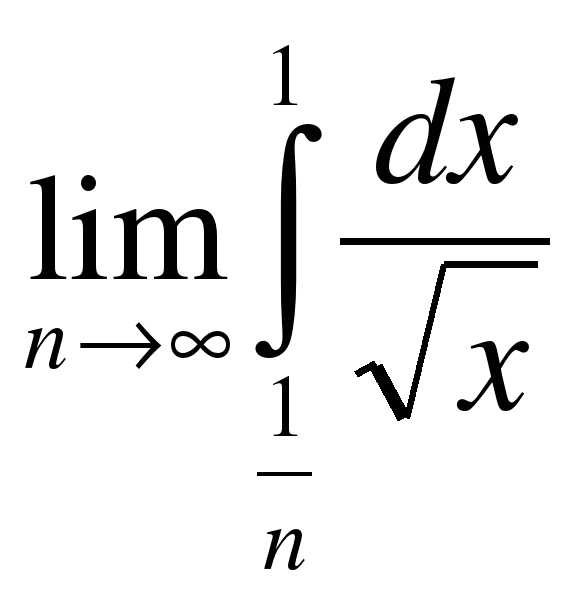
Вариант 24, 10
1. Докажите, что функция Н есть первообразная для функции h на промежутке I:
а)
б) 2. Для функции 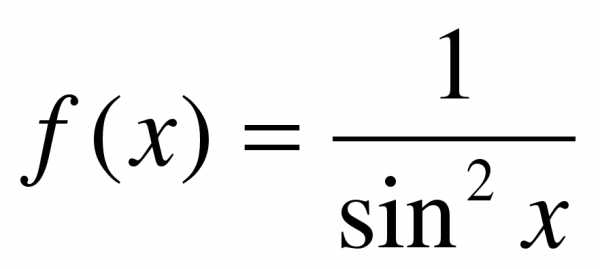 найдите первообразную, график которой проходит через точку
найдите первообразную, график которой проходит через точку  .
.
3. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок):
у = (х+1)2, х = -3, у = 0.
4. Найдите
multiurok.ru
Прототипы задания № 7 ЕГЭ по математике по теме «Первообразная»
ПЕРВООБРАЗНАЯ. ЗАДАНИЕ № 7. ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ
1. На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3; 5). Пользуясь рисунком, определите количество решений уравнения
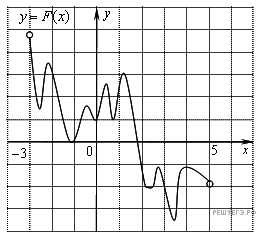
Решение.
По определению первообразной на интервале (−3; 5) справедливо равенство
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение имеет 10 решений.
Ответ: 10.
Ответ: 10
323077
10
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Решение.
3.
На рисунке изображён график функции y = f(x). Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ:7.
Ответ: 7
323078
7
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1.
. Решение.
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках и
Имеем:
Приведем другое решение.
Получим явное выражение для Поскольку
имеем:
Примечание.
Внимательный читатель отметит, что второй подход эквивалентен выделению полного куба:
что позволяет сразу же найти
Еще один способ рассуждений покажем на примере следующей задачи.
Ответ:6.
Ответ: 6
323079
6
4. На рисунке изображён график некоторой функции y = f(x). Функция — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Решение.
Найдем формулу, задающую функцию график которой изображён на рисунке.
Следовательно, график функции получен сдвигом графика функции на единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции и отрезком оси абсцисс. Имеем:
Ответ: 4.
Еще несколько способов рассуждений покажем на примере следующей задачи.
Ответ: 4
323080
4
5. На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл
6.На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
7.На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
8. На рисунке изображён график функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где — одна из первообразных функции .
6.На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
7.На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
.
11.На рисунке изображен график функции , определенной на интервале . Найдите количество решений уравнения на отрезке .
infourok.ru
11 класс. Алгебра. Интеграл. Первообразная. Неопределенный и определенный интеграл. — Первообразная. Правила отыскания первообразных.
Комментарии преподавателя
Пример нахождения первообразной
Математические задачи, операции часто различаются как прямые и обратные. Например: сложение и вычитание, умножение и деление. Мы в последнее время занимались дифференцированием, то есть нахождением производных. На этом уроке мы займемся обратной операцией – интегрированием, или нахождением первообразных.
Прямая задача:
Дано: .
Найти:.
Пример:
Обратная задача:
Дано: .
Найти: .
Пример:
– первообразная для .
Строгое определение первообразной функции
Определение:
Функцию называют первообразной для функции
www.kursoteka.ru
Тренажёр по алгебре (11 класс) по теме: Первообразная
Тест по теме: «Первообразная и интеграл»
1. Определите функцию, для которой F(x) = x2 – sin2x – 1 является первообразной:
1) f(x) = ; 2) f(x) = 2x – 2cos2x; 3) f(x) = 2x +cos2x; 4) f(x) = cos2x + x.
2. Найдите первообразную для функции. F (x) = 4х3 + cos x
1) F(x) = 12×2 – sinx + c; 2) F(x) = 4×3 + sinx + c; 3) F(x) = x4 – sinx + c; 4) F(x) = x4 + sinx + c.
3. Для функции f(x) = х2 найдите первообразную F, принимающую заданное значение в заданной точке F (- 1) = 2
1) F(x) = ; 2) F(x) = 2x + ; 3) F(x) = – ; 4) F(x) = .
4. Точка движется по прямой так, что её скорость в момент времени t равна V (t) = t + t2. Найдите путь, пройденный точкой за время от 1 до 3 сек, если скорость измеряется в м /сек. 1) 18 м; 2) 12м; 3) 17м; 4) 20 м.
5. Вычислите 1) 6; 2) 6; 3) 2; 4) 3.
6. Найдите площадь криволинейной трапеции, ограниченной линиями у = – х2 + 3 и у = 0
1) 4; 2) 6; 3) 9; 4) 8.
7. Найдите площадь фигуры, ограниченной линиями у = и у = х
1) 2; 2) 1; 3) 2; 4) 1.
8. Вычислите площадь фигуры, ограниченной графиком функции у = 2 – х2, касательной к этому графику в его точке с абсциссой х = — 1 и прямой х = 0
1) 1; 2) 2; 3) ; 4) 1.
9. Вычислите
10. Найдите сумму абсцисс точек пересечения графиков функции у = (х – 1)(х + 2) и её первообразной, если одна из этих точек находится на оси ординат.
11. Найдите ту первообразную функции f(x) = 3х – 1 , для которой уравнение F(x) = 5 имеет единственный корень.
nsportal.ru
Первообразная. Интеграл. Формула Ньютона-Лейбница | Подготовка к ЕГЭ по математике
Математики любят всякому действию сопоставить противодействие.
Сложению противодействует вычитание, умножению – деление, возведению в степень – извлечение корня и т.п.
И противодействие дифференцированию (то есть взятию производной) есть! Это интегрирование.
Но давайте по порядку.
Первообразная
Первообразной функцией (также называют антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть .
Вычисление первообразной называется интегрированием.
Пример:
+ показать
Множество первообразных функций для называют неопределенным интегралом функции y = f(x) и обозначают :
Определенный интеграл
Определенный интеграл записывается так:
То есть у нас появляются границы интегрирования. – нижняя граница интегрирования, – верхняя.
Так вот формула Ньютона-Лейбница позволяет вычислять определенный интеграл следующим образом:
При вычислении первообразных вы можете пользоваться таблицей первообразных.
Пример:
+ показать
Вычислить интегралРешение:
Ответ: 0,25.
Геометрический смысл определенного интеграла
Сначала нам придется познакомиться с понятием «криволинейная трапеция».
Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой неотрицательной непрерывной функции , осью и прямыми :

Так вот, с геометрической точки зрения площадь криволинейной трапеции, ограниченной графиком функции , осью и прямыми есть интеграл от на отрезке :
Примеры:
+ показать
1. Найти площадь фигуры, ограниченной графиком функции , осью и прямымиРешение:

В общем-то, перед нами – прямоугольная трапеция с основаниями 3 и 7 и высотой 2.
Мы легко можем посчитать площадь трапеции по формуле :
.
Но, все же, мы посчитаем площадь через интеграл, а затем сверим результаты.
Итак,
Ну вот, все сошлось.
Ответ: 10.
Никто не спорит, здесь можно обойтись и без интеграла, но без него не обойтись в случаях, когда представляет из себя кривую, отличную от прямой линии.
2. Найти площадь фигуры, ограниченной графиком функции , осью и прямыми
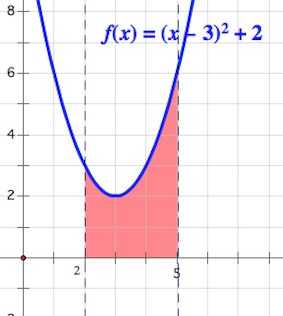
Решение:
Ответ:
egemaximum.ru
Правила отыскания первообразных. Видеоурок. Алгебра 11 Класс
На этом уроке мы вспомним определение первообразной и изучим правила отыскания первообразной.
Определение. Функцию называют первообразной для функции на заданном промежутке , если для всех из выполняется равенство .
Несколько разъясняющих примеров:
– первообразная для
Чтобы это подтвердить, возьмем производную
первообразная для
Итак, мы привели 2 примера, которые подтверждают определение и используют его.
Напомним две задачи:
Прямая задача: Дана функция . Найти . Процесс называется дифференцированием.
Обратная задача: Дана функция – производная неизвестной функции Найти Процесс называется интегрированием.
Какие основные инструменты для нахождения первообразных?
Нахождение
— таблице первообразных, которую мы повторим;
— правилам отыскания первообразных, которые мы изучим.
Таблица
|
Функция |
Первообразная |
|
0 |
1 |
|
1 |
|
interneturok.ru

