Математика вокруг нас картинки – математика картинки, Фотографии и изображения
Картинки про математику (44 фото) ⭐ Забавник
Подборка картинок про математику ➕: доски, исписанные мелом, примеры ➗, цифры и знаки, геометрические фигуры, непонятные иероглифы ➖, циркули, линейки и прочее. Смотрим.

Мальчик пишет на доске мелом.

Математика.
Загрузка…
Загрузка…

Уравнения на доске.
Циркуль и линейка треугольник.

Тетрадь с карандашом.
Доска, исписанная цветными мелками.

Математика.

Цифры.

Осторожно: религия. Осторожно: математика.

Графики.

Школьная доска.

Деление и умножение.

Математика в жизни человека.

Учебные принадлежности.

Веселая математика.
Два плюс два равно четыре.


Цифры.

Уравнения.

Один плюс один равно два.


Примеры.


Окружность.

Четырехугольники.

Уравнения.

Цветные цифры.
Математические действия.
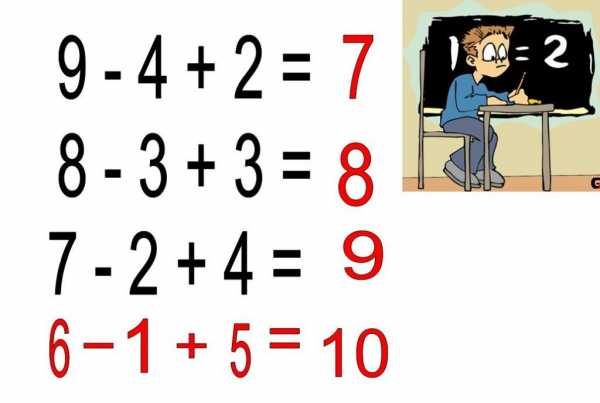
Примеры.



На сколько рыбок больше…

Математический набор.
Обложка учебника по математике.

Разбросанные цифры и мел.

Графики и чертежи.

Тригонометрия.

Прочитай равенства.

Цифры на ниточке.
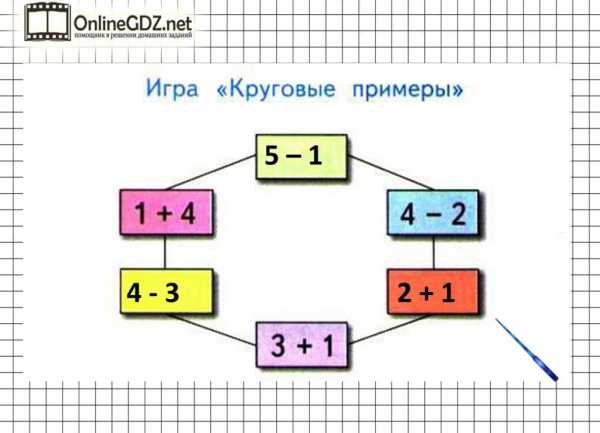
Круговые примеры.

Заточенный карандаш на листе бумаги.


Девочка считает по счетам.
zabavnik.club
Презентация «Математика вокруг нас»

Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа с.Верхние Услы муниципального района Стерлитамакский район Республики Башкортостан
МАТЕМАТИКА ВОКРУГ НАС
Автор презентации: ученица 6 класса
Нигматуллина Гульназ
Консультант: учитель математики и физики
Гималова ВинераТимиршиновна

КАК ВОЗНИКЛА МАТЕМАТИКА
Люди учились считать тогда же, когда они учились говорить, и первые названия чисел – ровесники первых слов. Самые древние дошедшие до нас математические документы – это хозяйственные записи вавилонян. Они сделаны за шесть тысяч лет до нашей эры, то есть восемь тысячелетий назад! Еще через две тысячи лет в вавилонских клинописных таблицах мы встречаем уже не только хозяйственные расчеты, связанные с торговыми сделками или с записями домашних расходов, а и настоящие задачи по математике..
Математика не родилась сразу. В древнем Египте, например, знали только такие дроби, у которых в числителе единица: 1/2, 1/3, 1/17, 1/298. Это очень усложняло вычисления. Не так давно люди не знали ни десятичных дробей, ни действий с ними. Десятичные дроби изобрел самаркандский математик Джемшид ибн-Масуд аль-Каши всего пятьсот лет назад, а в употребление у европейцев их ввел еще на полтораста лет позднее фламандский математик Стевин. В математике делаются открытия и сейчас; она, как и другие науки, все время движется вперед и развивается.

С момента рождения жизнь человека сопровождается цифрами. Первые и самые главные цифры на заветной бирочке, которую мамы сохраняют на всю жизнь, — это вес и рост ребенка, а также время и дата рождения. Вес новорожденного ребенка – главный показатель здоровья малыша.
.

МАТЕМАТИКА И ДЕТИ
Ещё в детстве ребёнок знакомится с простыми геометрическими фигурами: кругом, треугольником, квадратом, шаром, кубом, конусом. Малыш играет с погремушкой, собирает пирамидку, составляет из кубиков рисунки. В начальной школе делает аппликации из геометрических фигур

Великая книга природы написана математическими символами. (Галилео Галилей)
БИОЛОГИЯ широко использует математический аппарат при проведении тех или иных исследований . При изучении генетических законов, решении задач по генетике, биохимии и популяционной генетике математический аппарат необходим как при освоении теоретического материала, так и при решении конкретных задач

ФИЗИКА И ХИМИЯ для описания различных явлений, происходящих в природе используют формулы, таблицы, графики, математические вычисления.

Одной из задач АСТРОНОМИИ является изучение видимых, а затем и действительных положений и движений небесных тел в пространстве, определение их размеров и формы. Помогает ей МАТЕМАТИКА.

МАТЕМАТИКА В АРХИТЕКТУРЕ
. Одним из способов моделирования архитектурных моделей – математическое моделирование

МАТЕМАТИКА И МЕДИЦИНА
В медицине, прежде всего в фармацевтике, особенно важна математика. Ведь нужно точно рассчитать, сколько нужно ввести лекарства человеку, чтобы оно помогло выздороветь.

МАТЕМАТИКА И СЕЛЬСКОЕ ХОЗЯЙСТВО
С древнейших времен человеку приходилось измерять размеры полей, вычислять урожай, считать своих домашних животных, готовить необходимое количество кормов для их содержания.

МАТЕМАТИКА И ПРОМЫШЛЕННОСТЬ
Математические модели и графики часто используются в промышленности. В частности при планировании, составлении отчетов, а также на самом производстве.

МАТЕМАТИКА И ТОРГОВЛЯ
Некоторые историки считают возникновение математики с возникновением торговли. Если даже это не так, никто не усомнится в том, что торговля не могла бы развиваться без математики.

МАТЕМАТИКА И АРМИЯ
Могущество армии измеряется численностью бойцов, количеством и качеством боевой техники. Значит математика служит армии.

МАТЕМАТИКА В БЫТУ
Комнаты, в которых мы живем, наша мебель, кухонная утварь, бытовая техника имеют геометрическую форму

Какую бы область жизни человека мы не взяли, везде присутствует математика, не зря её назвали царицей наук. Изучая математику, мы совершенствуем себя, изменяем свою жизнь в лучшую сторону.

ИСТОЧНИКИ
- Википедия
- http://pedsovet.su » , шаблоны презентаций Хамадиевой Н.А.
- Яндекс картинки
multiurok.ru
Математика вокруг нас — Блог идеальной жены
Вчера, первого апреля, мы праздновали наш профессиональный праздник — День Математика.В преддверии Дня Математика студенты мои замутили флеш-моб, челлендж или как он там называется модным словом.
Короче, организаторы конкурса дают математическое понятие, а участники должны в течении суток сфотографировать это понятие и выложить его в Инстаграм или Вконтакте с тегом #МатематикаВокругНас. Разрешалось использовать старые фотографии. Дополнительное условие: фотография должна быть сделана в публичном, общедоступном месте, а не у себя дома. Т.е. на фотографии должна быть Математика, которая реально просто Вокруг Нас!
Для меня кто-то из студентов предложил дополнительный вызов: искать математические понятия только на кухне (в еде, в напитках, в продуктах…)
Хочу поделиться с вами тем, что получилось. Конкурс мне страшно понравился!
В процессе моя лента насыщалась математическими картинками, я прямо видела, как студентам интересно искать математику в природе, в университете, в магазинах, на улицах. Лично меня это очень вдохновляет и мотивирует )))
1. Параллельные прямые:
2. Ортогональность:
3. Пересекающиеся окружности:
К этой фотографии возникла дискуссия: точно ли тут изображены пересекающиеся окружности? Может, это пересекающиеся круги?
Окружность — это граница круга. Для математика очень естественно: видишь круг, видишь и окружность. Я тут вижу явно пересекающиеся окружности.
И вдогонку к предыдущей фотографии фотография вне конкурса.
Пересекающиеся окружности всегда дают пересекающиеся круги. Обратное — неверно. Вот на этой фотографии пересекающиеся круги, которые не дают пересекающиеся окружности.
4. Симметрия.
Симметрия постоянно нас окружает, так что сфотографировать ее не трудно )
Еще симметрия.
5. Кривые второго порядка. Это уже понятие посложнее. Наверное, не все нематематики знают, что это такое.
Кривые второго порядка — это эллипс, гипербола и парабола (такие слова вам говорили в школе и они примерно значат то, что вы думаете).
Если говорить строго: это кривые, уравнения которых задаются многочленом второй степени.
Где же вы можете увидеть эти кривые в повседневной жизни?
Например, если наклонить бокал, сечение жидкость будет эллипс.
Или если порезать огурец не перпендикулярно его оси, то получатся эллипсы.
6. Касательная к графику функции.
Функция двух переменных — кружка, а ложка — касательная к графику.

На самом деле, практически любая кривая может быть задана как график функции. Здесь — касательные к окружностям. Окружности — тоже график функции.
7. Конус. В еде как раз найти не сложно )

8. Фрактал. Опять сложное понятие. Я пыталась уже как-то в своем блоге его объяснить для нематематиков. ) Примерно, это значит следующее: часть фигуры — это как вся целая фигура, только меньше. Например, из еды отлично подходят брокколи.
9. Матрица. Понятие сложнее тем, что это не геометрическое понятие. Точнее, не только геометрическое.
Грубо говоря, матрица — это таблица с числами. Вот вафли — это точно таблица! )

10. Лемма о двух милиционерах.
Тоже нематематикам надо пояснить, что это такое.
Вот представьте, у вас есть некий процесс во времени. И он дает результат точно меньше какого-то второго процесса, но точно больше третьего. А вот эти второй и третий со временем приводят к одному и тому же результату Р. Тогда и ваш процесс приводит к тому же результату Р.
И вот иллюстрация: если котлета между двумя булочками, а булочки обе стремятся к нулю, то и котлета постепенно исчезнет )
11. Булева алгебра. Самая простая булева алгебра — это 0 (или «ложь») и 1 (в качестве «истины»). И, соответственно, картинка из студенческой столовой.
Все правильно, математические понятия со временем становятся все изощреннее и непонятнее. Это логично. Наверное, только математики способны в окружающей реальности заметить что-то, напоминающее это понятие. Но исключительно потому, что другие с таким понятием не знакомы. )))))
Хотя вот с двенадцатым понятием, в принципе, знакомы все.
12. Многочлен.
А теперь поясняю картинку. Что есть салат, как не сумма кубиков нескольких переменных?
А в математике сумма кубов нескольких переменных — это в точности многочлен.
13. И последнее понятие. Очень сложное. Даже не все люди, у которых в дипломе написано «математик» с ходу скажут вам, что же это такое.
Групповая алгебра.
(Понятие заявлено как специальная тема от меня — это отсылка к вот этому видео, которое я уже показывала).
[нематематики могут скипнуть без потери смысла]
Тут я поясню, но пояснения нематематикам будут вообще непонятны.
Любую ассоциативную алгебру легче всего себе представлять вложенной в пространство преобразований (это называется «представление алгебр» и это отдельная отрасль математики). Групповую алгебру представляют себе, вкладывая группу в алгебру линейных преобразований.
Можно доказать, что если у вас группа вложена в линейные преобразования векторного пространства над полем действительных или комплексных чисел, можно так ввести скалярное произведение, что все преобразования из группы — движения. Таким образом, любая групповая алгебра над полем действительных чисел суть какая-то комбинация движений.
Верно и обратное. Любые движения суть какая-то группа, а ими можно породить всю групповую алгебру.
В частности, движение воды на картинке — тоже намекает нам (нам — это мне) на групповую алгебру )
А нематематикам пусть картинка символизирует математическое понятие бесконечность. Ведь на льющуюся воду можно смотреть бесконечно )
kukina-kat.livejournal.com

