Макет окружности – Числовая окружность, макеты числовой окружности — урок. Алгебра, 10 класс.
Числовая окружность, макеты числовой окружности — урок. Алгебра, 10 класс.
Единичная окружность — это окружность, радиус которой принимается за единицу измерения.
Длина единичной окружности \(l\) равна l=2π⋅R=2π⋅1=2π.Считаем, что R=1.
Если взять π≈3,14, то длина окружности \(l\) может быть выражена числом 2π≈2⋅3,14=6,28.
Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры \(CA\) и \(DB\) (см. рис.)
Принято называть дугу \(AB\) — первой четвертью, дугу \(BC\) — второй четвертью, дугу \(CD\) — третьей четвертью, дугу \(DA\) — четвёртой четвертью, причём это открытые дуги, т. е. дуги без их концов.
Длина каждой четверти единичной окружности равна 14⋅2π=π2.
Принято в обозначении дуги на первом месте писать букву, обозначающую начало дуги, а на втором месте писать букву, обозначающую конец дуги.
Для работы с числовой окружностью часто используются два макета числовой окружности.
Каждая из четырёх четвертей числовой окружности разделена на две равные части, и около каждой из полученных восьми точек записано число, которому она соответствует.Каждая из четырёх четвертей числовой окружности разделена на три равные части, и около каждой из полученных двенадцати точек записано число, которому она соответствует.
Для числовой окружности верно следующее утверждение:
если точка \(M\) числовой окружности соответствует числу \(t\), то она соответствует и числу вида t+2πk,k∈ℤ.
На указанных двух макетах написаны числа, соответствующие точкам при первом обходе числовой окружности в положительном направлении, т. е. на промежутке 0;2π.
Таким образом,единичная окружность с установленным соответствием между действительными числами и точками окружности называется числовой окружностью.
www.yaklass.ru
Числовая окружность, макеты числовой окружности — урок. Алгебра, 10 класс.
Единичная окружность — это окружность, радиус которой принимается за единицу измерения.
Длина единичной окружности \(l\) равна l=2π⋅R=2π⋅1=2π.Считаем, что R=1.
Если взять π≈3,14, то длина окружности \(l\) может быть выражена числом 2π≈2⋅3,14=6,28.
Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры \(CA\) и \(DB\) (см. рис.)
Принято называть дугу \(AB\) — первой четвертью, дугу \(BC\) — второй четвертью, дугу \(CD\) — третьей четвертью, дугу \(DA\) — четвёртой четвертью, причём это открытые дуги, т. е. дуги без их концов.
Длина каждой четверти единичной окружности равна 14⋅2π=π2.
Принято в обозначении дуги на первом месте писать букву, обозначающую начало дуги, а на втором месте писать букву, обозначающую конец дуги.
Для работы с числовой окружностью часто используются два макета числовой окружности.
Каждая из четырёх четвертей числовой окружности разделена на три равные части, и около каждой из полученных двенадцати точек записано число, которому она соответствует.
Для числовой окружности верно следующее утверждение:
если точка \(M\) числовой окружности соответствует числу \(t\), то она соответствует и числу вида t+2πk,k∈ℤ.
На указанных двух макетах написаны числа, соответствующие точкам при первом обходе числовой окружности в положительном направлении, т. е. на промежутке 0;2π.
Таким образом,единичная окружность с установленным соответствием между действительными числами и точками окружности называется числовой окружностью.
www.yaklass.by
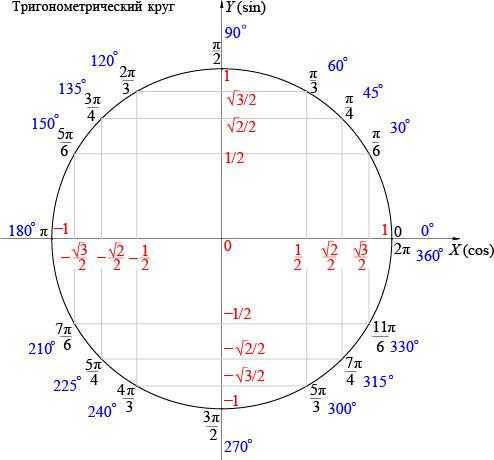
Тригонометрический круг — материалы для подготовки к ЕГЭ по Математике
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
- Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.
- Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .
- И синус, и косинус принимают значения от до .
- Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.
- Знаки синуса, косинуса, тангенса и котангенса.
- Синус — функция нечётная, косинус — чётная.
- Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .
Вот что мы видим на этом рисунке:
Ты нашел то, что искал? Поделись с друзьями!
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Например:
;
;
;
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
,
.
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
,
.
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
,
,
где — целое число. То же самое можно записать в радианах:
,
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
,
.
В результате получим следующую таблицу.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Числовая окружность. 10 класс. — математика, презентации

Долецкая Татьяна Анатольевна МБОУ СОШ № 11 г.Волжского

План занятия:
- Числовая прямая. Числовая окружность.
2. Движение по числовой окружности.
3. «Хорошие» числа на числовой окружности(макет 1 , макет 2).
О
•
1
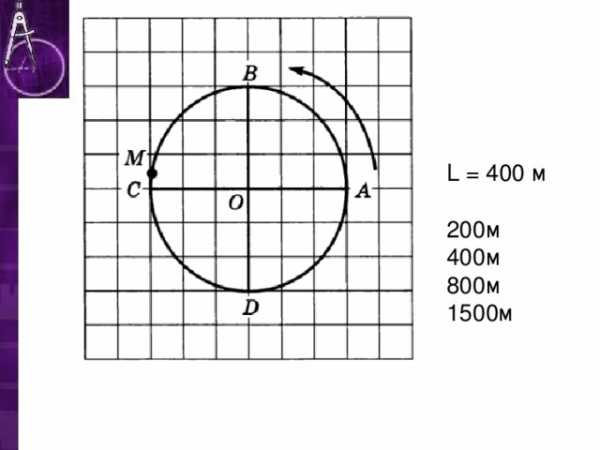
L = 400 м
200м
400м
800м
1500м
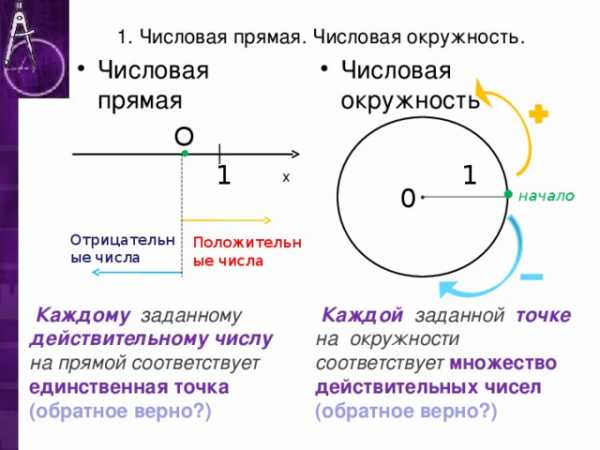
1. Числовая прямая. Числовая окружность.
- Числовая окружность
- Числовая прямая
О
•
•
1
1
х
•
0
начало
Отрицательные числа
Положительные числа
Каждой заданной точке на окружности соответствует множество действительных чисел
Каждому заданному действительному числу
на прямой соответствует единственная точка
(обратное верно?)
(обратное верно?)
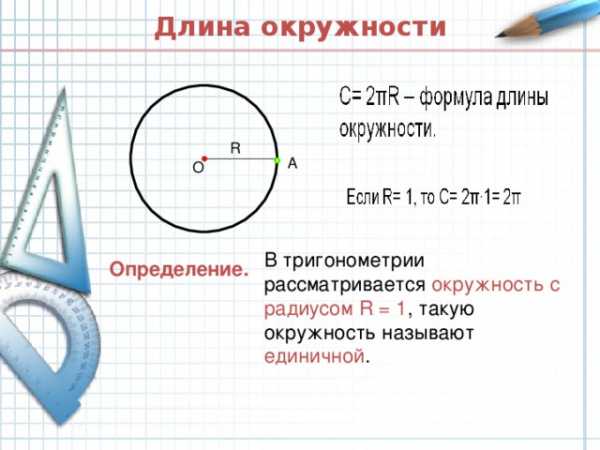
Длина окружности
R
A
О
В тригонометрии рассматривается окружность с радиусом R = 1 , такую окружность называют единичной .
Определение.
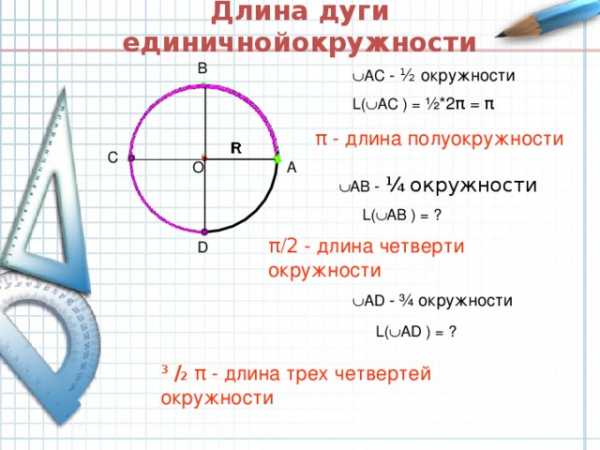
Длина дуги единичнойокружности
B
АС — ½ окружности
L( АС ) = ½*2 π = π
π — длина полуокружности
R
C
О
A
АВ — ¼ окружности
L( АВ ) = ?
π / 2 — длина четверти окружности
D
А D — ¾ окружности
L( А D ) = ?
³ / ₂ π — длина трех четвертей окружности
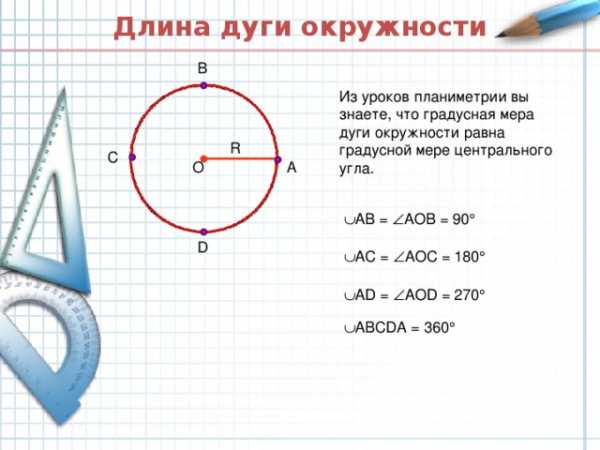
Длина дуги окружности
B
Из уроков планиметрии вы знаете, что градусная мера дуги окружности равна градусной мере центрального угла.
R
C
О
A
АВ = АОВ = 90
D
А C = АО C = 18 0
А D = АО D = 27 0
АВ CD А = 36 0

2. Движение по числовой окружности.
Задание 1
Найдите на числовой окружности точку, которая соответствует заданному числу:
90 0
9090
•
45 0
• 45 0
90 0
•
•
•
О
270 0
•
•
270 0
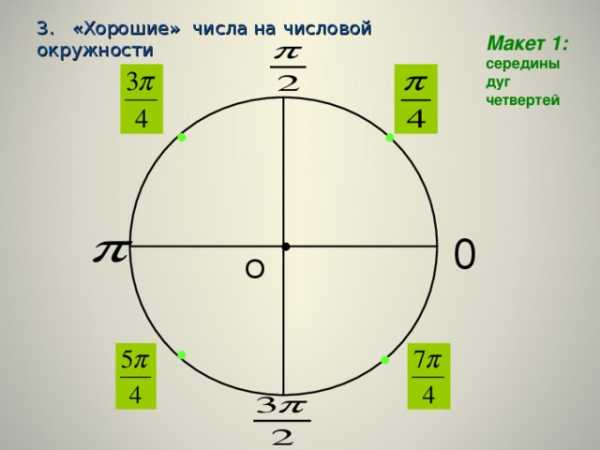
3. «Хорошие» числа на числовой окружности
Макет 1: середины дуг четвертей
•
•
•
0
О
•
•
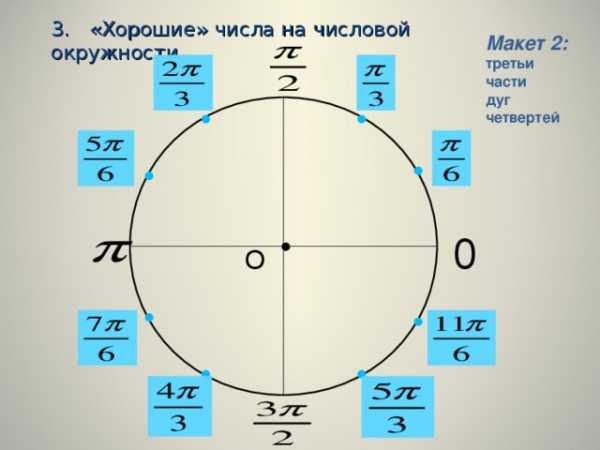
3. «Хорошие» числа на числовой окружности
Макет 2: третьи части
дуг четвертей
•
•
•
•
•
0
О
•
•
•
•
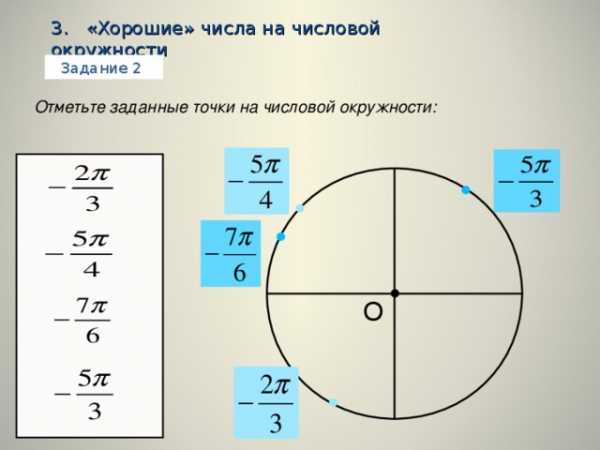
3. «Хорошие» числа на числовой окружности
Задание 2
Отметьте заданные точки на числовой окружности:
•
•
•
•
О
•
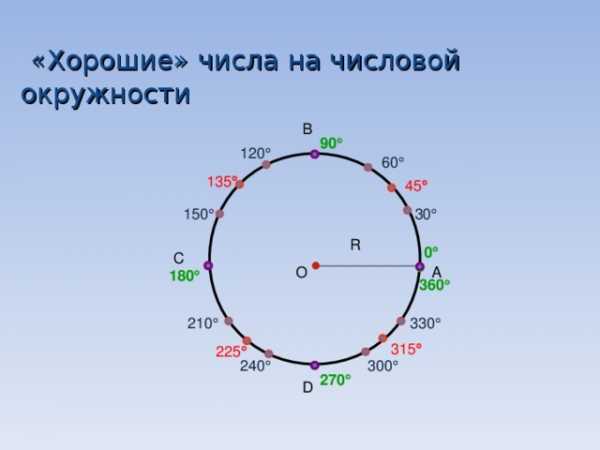
«Хорошие» числа на числовой окружности
B
90
120
60
135
45
30
150
R
0
C
A
О
180
360
330
210
315
225
240
300
270
D
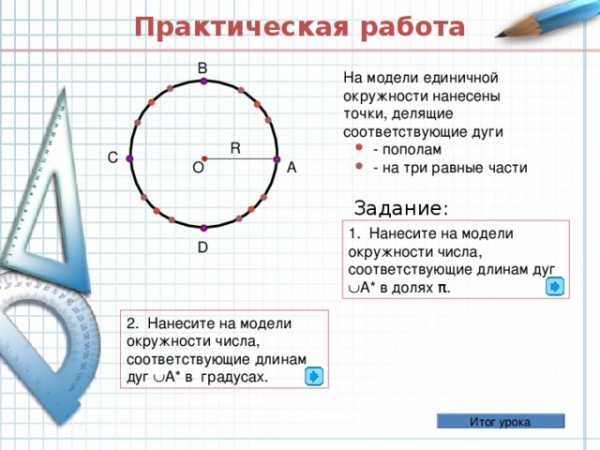
Практическая работа
B
На модели единичной окружности нанесены точки, делящие соответствующие дуги — пополам — на три равные части
R
C
О
A
Задание:
1. Нанесите на модели окружности числа, соответствующие длинам дуг А* в долях π .
D
Учащимся выдается раздаточный материал с тремя окружностями, на которых нанесены точки.
2. Нанесите на модели окружности числа, соответствующие длинам дуг А* в градусах.
Итог урока
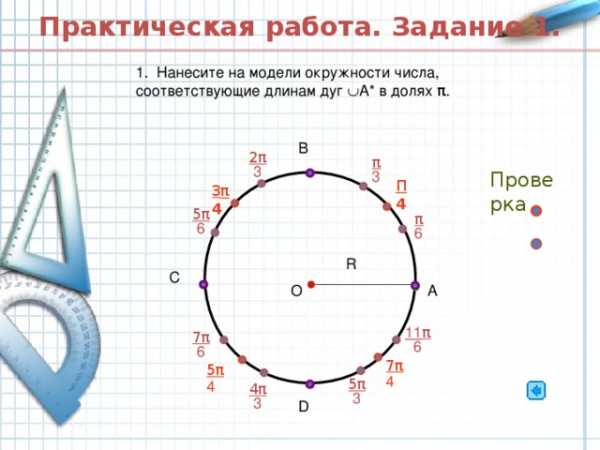
Практическая работа. Задание 1.
1. Нанесите на модели окружности числа, соответствующие длинам дуг А* в долях π .
B
2 π
π
3
Проверка
3
Π 4
3 π 4
5 π
π
6
6
R
C
О
A
11 π
7 π
6
6
7 π
5 π
4
5 π
4
4 π
3
3
D
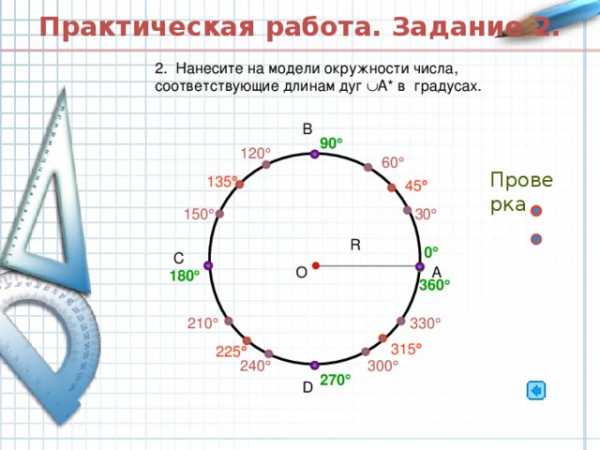
Практическая работа. Задание 2.
2. Нанесите на модели окружности числа, соответствующие длинам дуг А* в градусах.
B
90
120
60
Проверка
135
45
30
150
R
0
C
О
A
180
360
330
210
315
225
300
240
270
D

Итог занятия
- Каким вопросам было посвящено занятие?
- Чему научились на занятии?
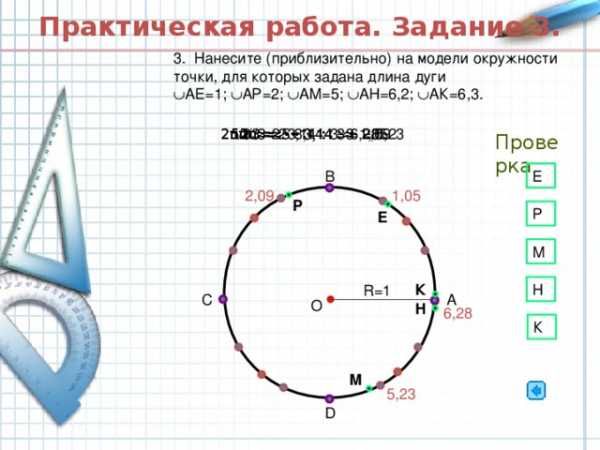
Практическая работа. Задание 3.
3. Нанесите (приблизительно) на модели окружности точки, для которых задана длина дуги АЕ=1; АР=2; АМ=5; АН=6,2; АК=6,3.
5 π /3 ≈ 5 • 3,14 : 3 = 5,23
2 π /3 ≈ 2 • 3,14 : 3 = 2,09
π /3 ≈ 3,14 : 3 ≈ 1,05
2 π ≈ 2 • 3,14 = 6,28
Проверка
B
Е
2,09
1,05
Р
Р
Е
М
Н
К
R =1
C
A
О
Н
6,28
К
М
5,23
D

Домашнее задание

Источники
- В.В. Репьев, «Методика тригонометрии», Государственное учебно-педагогическое издательство, Москва, 1937.
- А.Г. Мордкович, «Алгебра и начала анализа», 10 — 11 классы, часть 1, учебник.
- А.Г. Мордкович, «Алгебра и начала анализа», 10 — 11 классы, часть 2, задачник.
kopilkaurokov.ru
Числовая окружность
Вопросы занятия:
· познакомиться с понятием числовой окружности;
· познакомиться со свойствами точек числовой окружности;
· познакомится с точками первого и второго макетов.
Материал урока
Прежде чем приступить к изучению нового материала, давайте повторим понятие числовая прямая.
Давайте выполним упражнение.
Упражнение.
Давайте решим задачу.
Задача.
Определение.
Числовая окружность ̶ модель числовой прямой, на которой можно отметить точку с самой удалённой координатой.
На числовой прямой каждая точка имеет единственное «имя» ̶ число, а на числовой окружности каждая точка может иметь бесконечное множество «имён» ̶ чисел.
Для дальнейшего изучения темы нам пригодятся два макета окружностей.
Рассмотрим несколько примеров.
Пример.
Пример.
Из всех рассмотренных примеров можно вывести и сформулировать следующее утверждение.
Если точка М числовой окружности соответствует числу t, то она соответствует и числу вида t + 2πk, где k – любое целое число (kϵZ).
M(t) = M(t+2πk), где kϵZ
Вернёмся к нашим макетам и, с учётом выше сформулированного утверждения, запишем все точки, отмеченные на макетах.
videouroki.net
Наглядное пособие по тригонометрии | Социальная сеть работников образования
Слайд 1
Наглядное пособие по тригонометрии и система дидактических задач к нему Автор проекта ученица 10 «Б» класса МБОУ СОШ № 3 г. Вязьмы Алексеева Ольга Руководитель проекта учитель математики МБОУ СОШ № 3 г. Вязьмы Малышева И. Н .Слайд 2
Для успешного изучения материала мы создали наглядное пособие по тригонометрии и разработали систему дидактических задач к нему
Слайд 3
Дидактические задачи к модели «Числовая окружность» №1. Вычисление длин дуг единичной окружности. Учащиеся должны запомнить: длина всей окружности равна 2 π половина окружности – π , четверти окружности — π/2 и т.д .
Слайд 4
Дидактические задачи к модели «Числовая окружность» №2. Отыскание на числовой окружности точек, соответствующих заданным числам, которые выражены в долях числа π : π/2 , π/4, π/6, π/3, Например М(11 π/4), Р(-37 π/6) («хорошие» точки и числа) М(11 π/4) Р(-37 π/6)
Слайд 5
Дидактические задачи к модели «Числовая окружность» №3. Отыскание на числовой окружности точек, соответствующих заданным числам, которые выражены не в долях числа π . Например М(1 ), М(-4 ) («плохие» точки и числа) 1 -4
Слайд 6
Дидактические задачи к модели «Числовая окружность» №4. Запись чисел, соответствующих данной «хорошей» точке числовой окружности Например: «хорошая» точка-середина первой четверти и ей соответствуют все числа вида π/4 +2 π n, n є Z
Слайд 7
Дидактические задачи к модели «Числовая окружность» №5. Составление аналитических записей (двойных неравенств) для дуг числовой окружности. Открытая дуга М Р: π/6 +2 π n
Слайд 8
Дидактические задачи к модели «Числовая окружность на координатной плоскости» №1. Отыскание координат «хороших» точек числовой окружности. Переход от записи М( t) к записи М(х; у). Например, М( π/2 ) =М(0;1) М( π/6 ) =М(√3/2;1/2) М( π/2) М( 0;1) М(√3/2;1/2)
Слайд 9
Дидактические задачи к модели «Числовая окружность на координатной плоскости» №2. Отыскание знаков координат «плохих» точек числовой окружности. Если М(2)= М(х ; у), то х 0. Фактически определяем знаки тригонометрических функций по четвертям числовой окружности, значит s in 2 >0, cos 2 0 х 0
Слайд 10
Дидактические задачи к модели «Числовая окружность на координатной плоскости» №3. Отыскание на числовой окружности точек, координаты которых удовлетворяют заданному уравнению. Например, если у =1/2, то имеем М( π/6 +2 π n ) и Р(5π/6 +2 π n ), n є Z Фактически готовим учащихся к решению простейших тригонометрических уравнений вида s in t= а, cos t= а М( π/6 +2 π n ) Р(5π/6 +2 π n )
Слайд 11
Дидактические задачи к модели «Числовая окружность на координатной плоскости» №4. Отыскание на числовой окружности точек, координаты которых удовлетворяют заданному неравенству. Если у >1/2, то имеем π/6 +2 π n а, cos t > а +
nsportal.ru
Числовая окружность. — Математика — 10 класс
Просмотр содержимого документа
«Числовая окружность.»

Урок 1-2.
ЛЕКЦИЯ с примерами

План лекции:
- Числовая прямая. Числовая окружность.
2. Движение по числовой окружности.
3. «Хорошие» числа на числовой окружности(макет 1 , макет 2).
4. Аналитическая запись дуги числовой окружности.
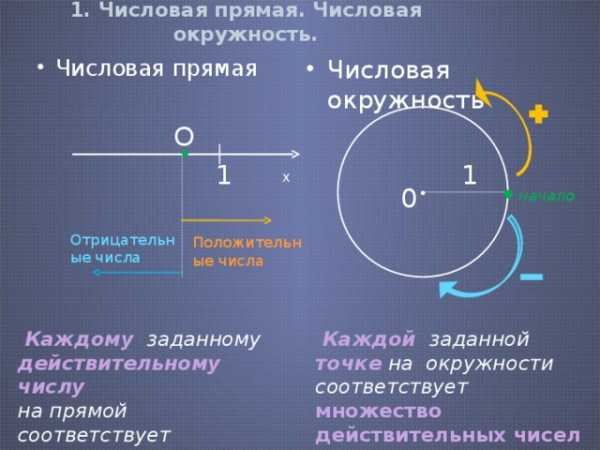
1. Числовая прямая. Числовая окружность.
- Числовая прямая
- Числовая окружность
•
О
•
1
1
х
•
0
начало
Отрицательные числа
Положительные числа
Каждому заданному действительному числу
Каждой заданной точке на окружности соответствует множество действительных чисел
(обратное верно?)
на прямой соответствует единственная точка
(обратное верно?)
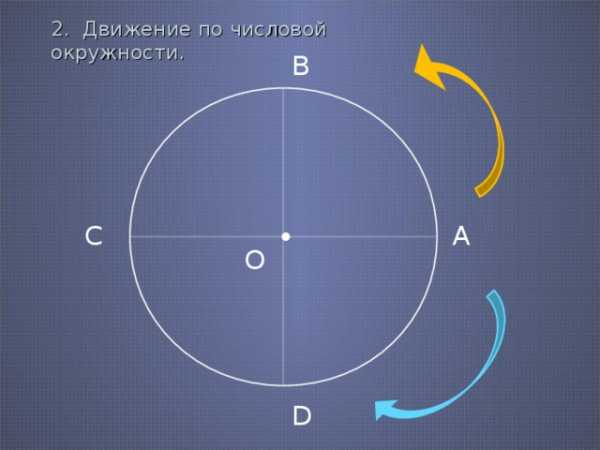
2. Движение по числовой окружности.
В
•
А
С
О
D

2. Движение по числовой окружности.
Задание 1
Найдите на числовой окружности точку, которая соответствует заданному числу:
•
•
•
•
•
О
•
•
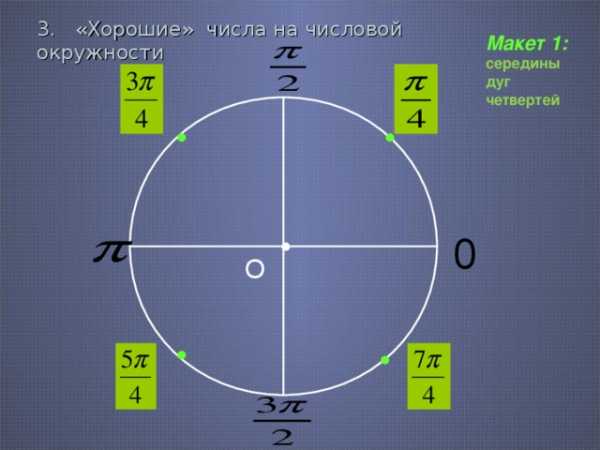
3. «Хорошие» числа на числовой окружности
Макет 1: середины дуг четвертей
•
•
•
0
О
•
•
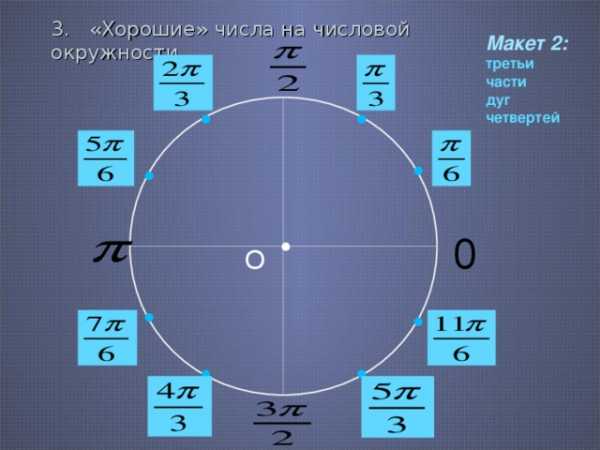
3. «Хорошие» числа на числовой окружности
Макет 2: третьи части
дуг четвертей
•
•
•
•
•
0
О
•
•
•
•
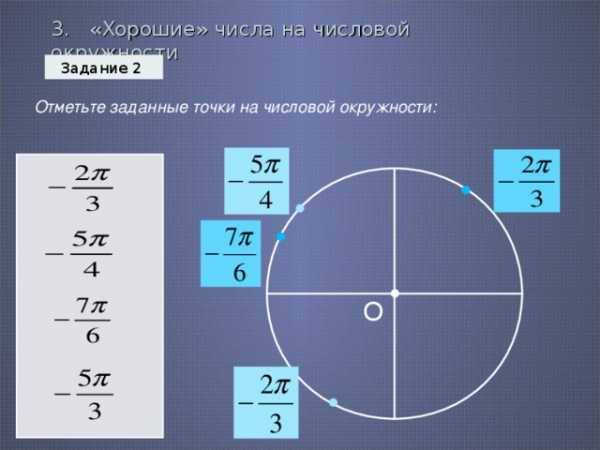
3. «Хорошие» числа на числовой окружности
Задание 2
Отметьте заданные точки на числовой окружности:
•
•
•
•
О
•

3. «Хорошие» числа на числовой окружности
Задание 3
Найдите и запишите все числа, которым соответствуют выделенные на числовой окружности точки:
•
•
•
•
•
О
•
•
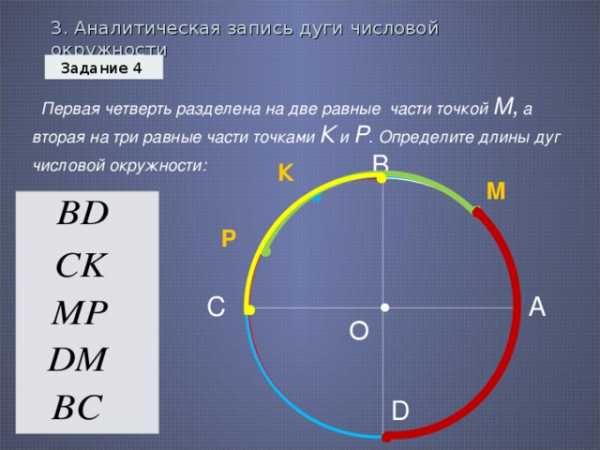
3. Аналитическая запись дуги числовой окружности
Задание 4
Первая четверть разделена на две равные части точкой М, а вторая на три равные части точками К и Р . Определите длины дуг числовой окружности:
В
•
К
•
М
•
•
•
•
•
Р
•
•
•
А
•
С
•
О
D
•
•

3. Аналитическая запись дуги числовой окружности
Задание 5
Найдите все числа t , которым на числовой окружности соответствуют точки принадлежащие указанной открытой дуге, где М – середина первой четверти
В
М
•
А
С
•
О
D

- Числовая прямая. Числовая окружность.
2. Движение по числовой окружности.
3. «Хорошие» числа на числовой окружности(макет 1 , макет 2).
4. Аналитическая запись дуги числовой окружности.

Дома:
Глава 2, параграф 4 (разобрать все примеры).
1) Знать понятие числовой окружности.
2) Выучить расположение и название точек на макетах 1,2
Задачник:
№ 2, 5( а, г), 6( а, г), 8-11 ( а, г), 16
multiurok.ru