Как решать теорию вероятности в огэ – Ключевые задачи по теории вероятностей. Подготовка к ОГЭ по математике (№9)
Разбор и решение задания №9 ОГЭ по математике
Статистика и вероятности
Рассмотрим типовые задания 9 ОГЭ по математике. Тематика 9 задания — статистика и вероятности. Задание не является трудным даже для человека, не знакомого с теорией вероятностей или статистикой.
Обычно нам предлагается набор вещей — яблок, конфет, чашек или чего угодно различающихся цветом или другим качеством. Нам необходимо оценить вероятность попадания одного из класса вещей одному человеку. Задача сводится к вычислению общего количества вещей, а затем делению числа вещей необходимого класса на общее количество.
Итак, перейдем к рассмотрению типовых вариантов.
Разбор типовых вариантов задания №9 ОГЭ по математике
Первый вариант задания
У бабушки 20 чашек: 6 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение:
Как было сказано выше, найдем общее число чашек — в данном случае это известно по условию — 20 чашек. Нам необходимо найти число синих чашек:
20 — 6 = 14
Теперь мы можем найти вероятность:
14 / 20 = 7 / 10 = 0,7
Ответ: 0,7
Второй вариант задания
В магазине канцтоваров продаётся 138 ручек, из них 34 красные, 23 зелёные, 11 фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка.
Решение:
Найдем вначале число черных ручек, для этого из общего числа вычитаем все известные цвета и делим на два, так как синих и чёрных ручек поровну:
(138 — 34 — 23 — 11) / 2 = 35
После этого можем найти вероятность, сложив количество чёрных и красных, разделив на общее количество:
(35 + 34) / 138 = 0,5
Ответ: 0,5
Третий вариант задания
В фирме такси в данный момент свободно 12 машин: 1 чёрная, 3 жёлтых и 8,зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Решение:
Найдем общее число машин:
1 + 3 + 8 = 12
Теперь оценим вероятность, разделив количество желтых на общее число:
3 / 12 = 0,25
Ответ: 0,25
Демонстрационный вариант ОГЭ 2019
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Решение:
Классическая задача по теории вероятностей. В нашем случае удачный исход — это пирожок с яблоком. Пирожков с яблоками 3, а всего пирожков:
4 + 8 + 3 = 15
Вероятность того, что попадется пирожок с яблоками — это количество пирожков с яблоками, деленное на общее количество:
3 / 15 = 0,2 или 20%
Ответ: 0,2
Четвертый вариант задания
Вероятность того, что новый принтер прослужит больше года, равна 0,95. Вероятность того, что он прослужит два года или больше, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но не меньше года.
Решение:
Введем обозначения событий:
X – принтер прослужит «больше 1 года»;
Y – принтер прослужит «2 года или больше»;
Z – принтер прослужит «не менее 1 года, но меньше 2-х лет».
Анализируем. События Y и Z независимы, т.к. исключают друг друга. Событие X произойдет в любом случае, т.е. и при наступлении события Y, и наступлении события Z. Действительно, «больше 1 года» означает и «2 года», и «больше 2-х лет», и «меньше 2-х лет, но не менее 1 года».
Если так, то событие X можно считать суммой событий, и тогда на основании теоремы о сложении вероятностей запишем:
Р(X)=Р(Y)+Р(Z).
По условию вероятность события Х (т.е. «больше года») равно 0,95, события Y (т.е. «2 года и больше») – 0,88.
Подставим в формулу числовые данные:
0,95=0,88+Р(Z)
Получаем:
Р(Z)=0,95–0,88=0,07
Р(Z) – искомое событие.
Ответ: 0,07
Пятый вариант задания
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что девочки окажутся на соседних местах.
Решение:
Для расчета вероятности используем классическую ее формулу:
где m – кол-во благоприятных исходов для искомого события, n – общее кол-во всех возможных исходов.
Одна из девочек (которая села первой) занимает стул произвольно. Значит, для другой имеется 9-1=8 стульев, чтобы сесть. Т.е. кол-во всех возможных вариантов событий равно n=8.
Другая девочка должна занять один из 2-х стульев, соседствующих со стулом первой. Только такая ситуация может считаться благоприятным исходом события. Значит, кол-во благоприятных исходов составляет m=2.
Подставляем данные в формулу для расчета вероятности:
Ответ: 0,25
spadilo.ru
Теория вероятности. Задачи ГИА В15
Прежде, чем мы начнем решать задачи, давайте-ка освежим знания по теории вероятностей.
Для чего же нужна теория вероятностей? Дело в том, что вся наша жизнь состоит из событий, которые случаются с нами или нет. Это хорошие и плохие события – неважно, какие они, важно то, произошли они, или нет, произойдут, или минуют. Поскольку мы не знаем, случится событие или нет – мы называем его случайным. Как оценить шансы события на то, что оно все-таки произойдет – это задача теории вероятности.
События, которые никогда не произойдут – это события невозможные. Например, вероятность того, что Земля без причин изменит направление своего вращения вокруг Солнца – очевидно, равна нулю. Или что число дней в следующем месяце будет равно 32. Или выпадение 7 при бросании игрального кубика.
События, которые точно произойдут, называются достоверными. Их вероятность равна 1 – например, вероятность наступления зимы, по крайней мере, календарной.
Случайное событие, как мы уже сказали, может произойти, а может не произойти. Частотой такого события называется отношение удачных опытов (таких, в которых событие произошло) к числу всех проведенных опытов. Исходы таких опытов называют элементарными исходами, которые могут включать благоприятные исходы – такие, в которых событие произошло. Чем больше проведенных опытов, тем ближе частота к вероятности. То есть, если опыт был проведен достаточно много раз, то можем считать, что вероятность события равна его частоте.
1. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 1 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Всего пирожков 8, то есть Петя может выбрать любой – один из восьми. Тогда элементарных исходов – 8. Благоприятных исходов всего 3 – ведь пирожков с яблоками три на тарелке. Тогда вероятность такого выбора равна 3/8. Задача решена, однако, ответ надо записать в бланк. Для этого его надо представить десятичном виде – в виде дроби с основанием 10, 100, 1000 и т.д. Как это сделать в данном случае? Чтобы получить в основании 100, разделим на 2 всю дробь и умножим на 25:
Ответ: 0,375
2. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Кому-то первым стартовать придется, это может быть любой из спортсменов. То есть всего исходов столько, сколько всего спортсменов – 20. Благоприятны нашему событию такие, когда стартовать первым будет не россиянин – а не россиян всего 7. Иными словами, вероятность, что первым будет не россиянин – 7/20. Представим результат в виде десятичной дроби:
Ответ: 0,35
3. Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Элементарных исходов столько, сколько всего игроков – пять. Из них мальчиков двое, благоприятных исходов – два из пяти. Вероятность равна
Ответ: 0,4
4. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Сначала посчитаем, сколько у нас всего трехзначных чисел: из тысячи отбрасываем 99 первых, и последнее, 1000 – четырехзначное число. Тогда имеем 900 трехзначных чисел. на 5 делится каждое пятое: 900/5= 180. Проверим результат. Имеем алгебраическую прогрессию со знаменателем d=5. Первый член прогрессии – 100. Последний – 995. Определим число членов с помощью формулы n-ного члена:
, откуда , тогда
Считаем: .
Ну и осталось определить вероятность: благоприятных исходов 180, а всего 900:
Ответ: 0,2
5.В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
Данная задача – на противоположные события. Некоторые события могут образовывать пары “случилось – не случилось”. Так как одно событие из пары произойдет обязательно, то вероятность пары событий равна 1. Если событие 1 с вероятностью А – “случилось” – то противоположное ему событие 2 с вероятностью В – “не случилось”. Тогда вероятность события 2 равна 1 – А.
Раз приз в каждой 10-й банке, значит, вероятность выиграть его – 1/10. Тогда вероятность не выиграть:
Ответ: 0,9
6. В среднем на 50 исправных фонариков приходится два неисправных. Найдите вероятность купить работающий фонарик.
Результат округлите до сотых.
Итак, здесь важно не ошибиться. Если на 50 работающих фонариков с одной стороны приходится 2 неработающих, то всего фонариков – 52! Это тонкость этой задачи. Вероятность купить работающий фонарик равна 50/52, и к сожалению, придется считать в столбик, чтобы дать правильный ответ: 0,9615. Округляем до сотых:
Ответ: 0,96
7. В мешке содержатся жетоны с номерами от 2 до 51 включительно. Какова вероятность, того, что номер извлеченного наугад из мешка жетона является однозначным числом?
Всего жетонов в мешке – . Однозначных номеров 8 штук: 2, 3, 4, 5, 6, 7, 8, 9. Значит, благоприятных исходов 8 из 50. Тогда вероятность равна 8/50 или 16/100.
Ответ: 0,16.
8. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда Волга должна сыграть два матча — с командой Енисей и с командой Сургут. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда Волга.
Всего у монетки 2 стороны – то есть имеем два исхода для первого матча, и два исхода для второго. То есть всего четыре исхода. Составим дерево: событие А – выпадает орел, событие В – выпадает решка. Если выпадает орел, мячом владеет Волга.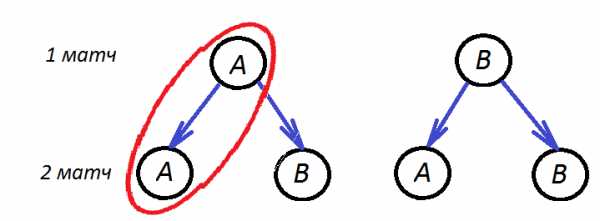
Видим, что изо всех исходов (из 4) нас устраивает единственный. Тогда вероятность равна 1/4, или 0,25.
Ответ: 0,25.
9. Из каждых 1000 электрических лампочек – 5 бракованных. Какова вероятность купить исправную лампочку?
В ответе укажите результат, округленный до тысячных.
Всего лампочек у нас 1000: 995 работают, и 5 – нет. Вероятность купить исправную лампу равна 995/1000. Осталось это записать десятичным числом: 0,995.
Ответ: 0,995.
Задачи для ОГЭ. Теория вероятностей
Задачи для ОГЭ с ответами и решениями
Теория вероятностей

перейти к содержанию задачника
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 50.
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 11.
- На тарелке 10 пирожков: 2 с мясом, 6 с капустой и 2 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Вова наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- В фирме такси в данный момент свободно 30 машин: 7 черных, 6 желтых и 17 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
- В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Петя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Петя не найдет приз в своей банке.
- Игорь с папой решили покататься на колесе обозрения. Всего на колесе двадцать кабинок, из них 3 — синие, 14 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Игорь прокатится в красной кабинке.
- Петя с папой решили покататься на колесе обозрения. Всего на колесе двенадцать кабинок, из них 3 — синие, 6 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке.
- У дедушки 10 чашек: 7 с красными цветами, остальные с синими. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- У бабушки 20 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- На экзамене 50 билетов. Петя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.
- На экзамене 50 билетов. Петя не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет.
- Родительский комитет закупил 10 пазлов для подарков детям на окончание года, из них 2 с машинами и 8 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с машиной.
- Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной.
- В среднем на 100 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем на 75 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем из каждых 100 поступивших в продажу аккумуляторов 91 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- Саша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
- Определите вероятность того, что при бросании кубика выпало нечетное число очков.
- Определите вероятность того, что при бросании кубика выпало 1.
- Одновременно бросают две симметричные монеты. Какова вероятность того, что выпадут орел и решка?
- Одновременно бросают три симметричные монеты. Какова вероятность того, что выпадут два орла и одна решка?
- В классе 21 учащийся, среди них два друга — Петя и Вася. На уроке физкультуры класс случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Петя и Вася попали в одну группу.
- Перед началом футбольного матча судья бросают монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть три матча — с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах владение мячом первыми будет принадлежать команде А.
- В соревнованиях по толканию ядра участвуют 6 спортсменов из Греции, 4 спортсмена из Болгарии, 3 спортсмена из Румынии и 7 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Венгрии.
- В соревнованиях по толканию ядра участвуют 4 спортсмена из Дании, 8 спортсменов из Швеции, 4 спортсмена из Румынии и 9 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
- В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Треугольники», равна 0,5. Вероятность того, что это окажется задача на тему «Окружность» равна 0,25. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Окружность», равна 0,45. Вероятность того, что это окажется задача на тему «Углы» равна 0,5. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
- Стрелок четыре раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- В девятом экономическом классе учатся 24 мальчика и 6 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
- В девятом математическом классе учатся 2 мальчика и 23 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет девочка?
- Вероятность того, что новый компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Вероятность того, что новый сканер прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Какова вероятность того, что случайно выбранное натуральное число от 25 до 39 делится на 5?
- Какова вероятность того, что случайно выбранное натуральное число от 15 до 36 делится на 2?
- На олимпиаде по химии участников рассаживают по трем аудиториям. В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
- На олимпиаде по математике участников рассаживают по трем аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 300 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
- Вероятность того, что на тесте по физике Петя верно решит больше 11 задач, равна 0,65. Вероятность того, что он верно решит больше 10 задач, равна 0,71. Найдите вероятность того, что Петя верно решит ровно 11 задач.
- Вероятность того, что на тесте по математике Вася верно решит больше 12 задач, равна 0,7. Вероятность того, что он верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что Вася верно решит ровно 12 задач.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 22 пассажиров, равна 0,86. Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,96. Вероятность того, что окажется меньше 11 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 11 до 20.
- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
перейти к содержанию задачника
Ответы
- 0,02
- 0,09
- 0,2
- 0,3
- 0,2
- 0,9
- 0,15
- 0,25
- 0,3
- 0,8
- 0,82
- 0,98
- 0,2
- 0,88
- 0,93
- 0,92
- 0,09
- 0,15
- 0,1
- 0,5
- 1/6
- 0,5
- 0,375
- 0,1
- 0,125
- 0,35
- 0,32
- 0,11
- 0,13
- 0,75
- 0,95
- 0,0625
- 0,063
- 0,243
- 0,375
- 0,8
- 0,92
- 0,14
- 0,09
- 0,2
- 0,5
- 0,2
- 0,2
- 0,06
- 0,09
- 0,36
- 0,45
- 0,078
- 0,0776
Метки ОГЭ. Смотреть запись.
www.itmathrepetitor.ru
Теория вероятностей на ОГЭ и ЕГЭ

УМК любой
Теория вероятностей
на ОГЭ и ЕГЭ
Автор: Богданова Ольга Николаевна, учитель математики МКОУ «Овечкинская СОШ Завьяловского района»
Алтайского края

Задачи
на вероятность
с игральным кубиком
(игральная кость)

1. Определите вероятность того, что при бросании игрального кубика (игральной кости) выпадет нечетное число очков.
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Нечетное число – 3 (1; 3; 5)
P = 3:6 = 0,5
Ответ: P=0,5

2. Определите вероятность того, что при бросании игрального кубика (игральной кости) выпадет менее 4 очков.
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Менее 4–х очков – 3 (1; 2; 3)
P = 3:6 = 0,5
Ответ: P=0,5

3 . Определите вероятность того, что при бросании игрального кубика (игральной кости) выпадет более 3 очков.
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Более 3–х очков – 3 (4; 5; 6)
P = 3:6 = 0,5
Ответ: P=0,5

4 . Определите вероятность того, что при бросании игрального кубика (игральной кости) выпадет более 2 очков. Ответ округлите до десятых.
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Более 2–х очков – 2 (3; 4; 5; 6)
P = 4:6 = 0,66…
Ответ: P=0,7

5. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел нечетна.
Решение задачи:
Сумма будет нечетна, когда: 1) в первый раз выпадет нечетное число, а во второй четное . 2) в первый раз — четное , а во второй раз нечетное .
1) 3 : 6 = 0,5 — Вероятность выпадения нечетного числа в первое бросание.
3 : 6 = 0,5 — Вероятность выпадения четного числа во второе бросание.
0,5 · 0,5 = 0,25 – т.к. эти два события должны произойти совместно. 2) 3 : 6 = 0,5 — Вероятность выпадения четного числа в первое бросание.
3 : 6 = 0,5 — Вероятность выпадения нечетного числа во второе бросание.
0,5 · 0,5 = 0,25 – т.к. эти два события должны произойти совместно,.
3) 0,25 + 0,25 = 0,5
Ответ: P=0,5

6. Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до десятых.
Решение задачи:
1) При первом броске выпадет 1, или 2, или 3, или 4, или 5, а при втором броске выпадет 5 2) При первом броске выпадет 5, а при втором броске выпадет 1, или 2, или 3, или 4, или 5
- 5 : 6 = 5/6 – вероятность того, что выпадут 1; 2; 3; 4; 5
1 : 6 = 1/6 — вероятность выпадения 5
5/6 · 1/6 = 5/36 — вероятность, что произойдут оба события
- 1 : 6 = 1/6 — вероятность выпадения 5
5 : 6 = 5/6 — вероятность выпадения 1; 2; 3; 4; 5
1/6 · 5/6 = 5/36 — вероятность, что произойдут оба события
- 5/36 + 5/36 = 10/36 = 5/18 = 0,277…
Ответ: 0,3

7. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.
Решение задачи:
1) При первом броске выпадет 1, или 2, или 3, а при втором броске выпадет 4; или 5 или 6 2) При первом броске выпадет 4; или 5 или 6, а при втором броске выпадет 1, или 2, или 3. 3) При первом броске выпадет 4; или 5 или 6, а при втором броске выпадет 4, или 5, или 6.
- 3 : 6 = 0,5 — вероятность выпадения 1; 2; 3
3 : 6 = 0,5 — вероятность выпадения 4; 5; 6
0,5 · 0,5 = 0,25 — вероятность, что произойдут оба события
2) 3 : 6 = 0,5 — вероятность выпадения 4; 5; 6
3 : 6 = 0,5 — вероятность выпадения 1; 2; 3
0,5 · 0,5 = 0,25 — вероятность, что произойдут оба события
3) 3 : 6 = 0,5 — вероятность выпадения 4; 5; 6
3 : 6 = 0,5 — вероятность выпадения 4; 5; 6
0,5 · 0,5 = 0,25 — вероятность, что произойдут оба события
4) 0,25+ 0,25 + 0,25 = 0,75 Ответ: 0,75

Задачи
на вероятность
с монетами

8. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно 1 раз .
Решение задачи: Найдём число возможных исходов, переберём все варианты бросков. Составим таблицу и покажем все варианты:
2 : 4 = 0,5 — вероятность того, что выпадет орел при броске.
2) Ответ: 0,5

9. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 3 раза .
Решение задачи:
1 бросок
2 бросок
орел
3 бросок
орел
решка
решка
орел
орел
орел
решка
решка
орел
решка
орел
решка
решка
решка
решка
решка
орел
орел
орел
решка
орел
решка
орел
1 : 8 = 0,125 – вероятность того, что выпадет орел при броске.
Ответ: 0,125
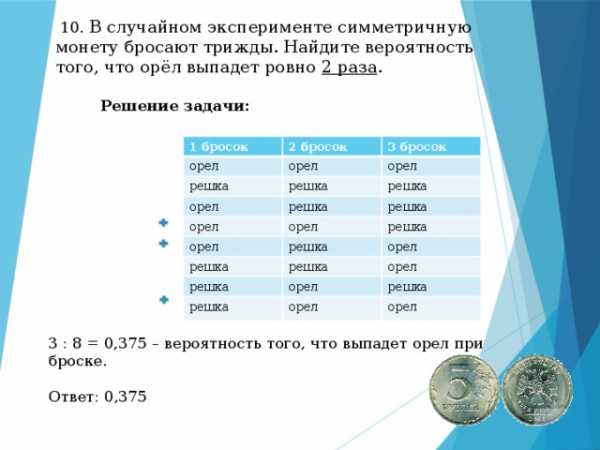
10. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза .
Решение задачи:
1 бросок
2 бросок
орел
орел
решка
3 бросок
решка
орел
орел
решка
решка
орел
орел
орел
решка
решка
решка
решка
решка
орел
решка
орел
орел
решка
орел
решка
орел
3 : 8 = 0,375 – вероятность того, что выпадет орел при броске.
Ответ: 0,375

11 . В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Решение задачи:
1 бросок
2 бросок
орел
решка
3 бросок
орел
решка
орел
орел
решка
решка
орел
орел
решка
орел
решка
решка
решка
решка
орел
решка
орел
орел
решка
орел
решка
орел
1 : 8 = 0,125 — вероятность того, что выпадет орел при броске.
Ответ: 0,125

Задачи
на вероятность
(разные)

12. Известно, что в некотором регионе вероятность того, что родившийся младенец окажется мальчиком, равна 0,512. В 2010 г. в этом регионе на 1000 родившихся младенцев в среднем пришлось 477 девочек. Насколько частота рождения девочки в 2010 г. в этом регионе отличается от вероятности этого события?
Решение задачи:
- 1 — 0,512 = 0,488 – вероятность рождения девочек в регионе
2) 477 : 1000 = 0,477 – вероятность рождения девочек в 2010 г
3) 0,488 — 0,477=0,011
Ответ: 0,011

13. Известно, что в некотором регионе вероятность того, что родившийся младенец окажется мальчиком, равна 0,486. В 2011 г. в этом регионе на 1000 родившихся младенцев в среднем приходилось 522 девочки. На сколько частота рождения девочки в 2011 г. в этом регионе отличается от вероятности этого события?
Решение задачи:
- 1 — 0,486 = 0,514 – вероятность рождения девочек в регионе
2) 522 : 1000 = 0,522 – вероятность рождения девочек в 2011 г
3) 0,522 — 0,514 = 0,008
Ответ: 0,008

14. Стас выбирает трехзначное число. Найдите вероятность того, что оно делится на 48.
Решение задачи:
- 999 — 99 = 900 – всего трехзначных чисел
2) 999 : 48 = 20,8125 — т.е. всего 20 чисел делятся на 48
- Из них два числа двузначные — это 48 и 96, то 20 – 2 = 18
4) 18 : 900 = 0,02
Ответ: 0,02

15 . Андрей выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 33.
Решение задачи:
- 999 — 99 = 900 – всего трехзначных чисел
2) 999 : 33 = 30,29… — т.е. всего 30 чисел делятся на 33
- Из них три числа двузначные — это 33, 66, 99 то 30 – 3 = 27
4) 27 : 900 = 0,03
Ответ: 0,03

16 . В каждой четвёртой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Аля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Аля не найдёт приз в своей банке.
Решение задачи:
1) 1 : 4 = 0,25 — вероятность выпадения приза.
2) 1 – 0,25 = 0,75 – вероятность не выпадения приза
Ответ: 0,75

17. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий: 0,35 + 0,2 = 0,52
Ответ: 0,52

18. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение:
вероятность попадания — 0,8
вероятность промаха – 0,2
События промаха и попадания независимы, значит
Ответ: 0,2

19. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,12 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
Найдем вероятность, что неисправны оба автомата.
Эти события независимы, т.е. 0,12² = 0,0144
Событие, состоящее в том, что исправен хотя бы один
автомат – противоположное, значит 1 – 0,0144 = 0,9856
Ответ: 0,9856

20. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение:
Рассмотрим события:
А – кофе закончится в первом автомате
В – кофе закончится во втором автомате
А·В – кофе закончится в обоих автоматах
А+В — кофе закончится хотя бы в одном автомате
Значит, вероятность противоположного события (кофе останется в обоих автоматах) равна
Ответ: 0,56

21. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло, купленное на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135
Вероятность того, что стекло, купленное на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055
Значит, полная вероятность того, что случайно купленное в магазине стекло окажется бракованным: 0,0135 + 0,0055 = 0,019
Ответ: 0,019

Источники
Задачи открытого банка заданий по математике ФИПИ, 2014-2015 http://www.fipi.ru/
Монета — https :// upload.wikimedia.org/wikipedia/commons/e/e8/Russia-1998-Coin-5.jpg
Игральный кубик — http ://clipstock.ucoz.ru/_ ph/21/365284339.jpg
ЕГЭ 2016 –
http ://cs.ankaraschool.ru/DwABAIQAzQISAc0BSv_D-w8/6yi0I7wdPdUVWti_caKcxg/sv/image/bc/d7/32/186172/228/% D0%95%D0%93%D0%AD.jpg?1445859675
ОГЭ 2016 — http :// www.school25.nichost.ru/images/banners/oge.jpg
multiurok.ru
Подбор заданий для самостоятельной работы в 9 классе по теме «Решение задач по теории вероятностей» (из Открытого банка заданий ОГЭ-9)
Вариант 1
1.В магазине канцтоваров продаётся 120 ручек: 32 красных, 32 зелёных, 46 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
2. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
3. В среднем из 100 карманных фонариков, поступивших в продажу,
четыре неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
4. Родительский комитет закупил 10 пазлов для подарков детям в связи с окончанием учебного года, из них 4 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.
5. На экзамене 50 билетов, Сеня не выучил 5 из них. Найдите вероятность того, что ему попадётся выученный билет.
6. У бабушки 25 чашек: 2 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
7. В фирме такси в данный момент свободно 20 машин: 2 чёрных, 2 жёлтых и 16 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
8. На тарелке лежат одинаковые на вид пирожки: 5 с мясом, 2 с капустой и 3 с вишней. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
9. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,2. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Вариант 2
1.В магазине канцтоваров продаётся 170 ручек: 47 красных, 33 зелёных, 14 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
2. В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен
из Норвегии и 2 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии.
3. В среднем из 150 карманных фонариков, поступивших в продажу,
шесть неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
4. Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 21 с машинами и 4 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Саша. Найдите вероятность того, что Саше достанется пазл с машиной.
5. На экзамене 35 билетов, Стас не выучил 7 из них. Найдите вероятность того, что ему попадётся выученный билет.
6. У бабушки 20 чашек: 15 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
7. В фирме такси в данный момент свободно 12 машин: 3 чёрных, 6 жёлтых и 3 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
8. На тарелке лежат одинаковые на вид пирожки: 3 с мясом, 24 с капустой и 3 с вишней. Лёша наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
9. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,26. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
infourok.ru
Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Подготовка к ОГЭ. Задачи по теории вероятности.
Подготовка к ОГЭ. Задачи по теории вероятности.
- Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
- На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
- В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке?
- Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.
- У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- Коля наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 3.
- На экзамене 50 билетов, Руслан не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет
- Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
- В среднем из каждых 80 поступивших в продажу аккумуляторов 76 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
- Вероятности сдать каждый из трёх экзаменов экзаменационной сессии на “отлично” для студента равны, соответственно, р1=0,7; р2=0,65; р3=0,85. Определите вероятность того, что студент сдаст на “отлично”:
а) все три экзамена;
б) два экзамена;
в)хотя бы один экзамен.
- В реке водятся пескари и караси. Утром после дождя при однократном закидывании удочки с вероятностью 0,2 попадается пескарь, и с вероятностью 0,1 — карась. Какова вероятность, что один раз забросив удочку, рыбак ничего не поймает?
- На соревнованиях по художественной гимнастике участвуют: три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступления определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
- Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе — 0,9, в третье — 0,8. Найти вероятность, что только одно отделение получит газеты вовремя;
- Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
- Саша дважды бросает игральный кубик. В сумме у него выпало 6 очков. Найти вероятность, что при первом броске выпало 3 очка.
- Перед началом волейбольного матча капитаны команд бросают жребий, чтобы определить, какая из команд выиграет право первой подачи. Команда «Изумруд» по очереди играет с командами «Сапфир», «Аметист»,» Алмаз» и «Хризолит». Найти вероятность того, что во всех четырех матчах первым подавать мяч будет команда «Изумруд»
- Перед началом матча по футболу судья бросает монету, чтобы определить. Какая из команд будет первая владеть мячом. Команда «Хуторянка» по очереди играет с командами «Радуга», «Дружба», «Заря» и «Воля». Найти вероятность того. Что команда «Хуторянка» будет первой владеть мячом только в двух первых играх.
- Конкурс исполнителей проводиться в 3 дня. Всего заявлено 60 выступлений – по одному от каждой страны. В первый день 30 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступления определяется жребием. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
nsportal.ru
Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Готовимся к ОГЭ. Презентация «Ключевые задачи по теории вероятности»
Слайд 1
ТЕОРИЯ ВЕРОЯТНОСТЕЙ КЛЮЧЕВЫЕ ЗАДАЧИ Готовимся к ОГЭСлайд 2
БРОСАНИЕ МОНЕТЫ
Слайд 3
1. Монета брошена два раза. Какова вероятность выпадения одного «орла» и одной «решки»? Решение: При бросании одной монеты возможны два исхода – «орёл» или «решка». При бросании двух монет – 4 исхода (2*2=4): «орёл» — «решка» «решка» — «решка» «решка» — «орёл» «орёл» — «орёл» Один «орёл» и одна «решка» выпадут в двух случаях из четырёх. Р(А)=2:4=0,5. Ответ: 0,5.
Слайд 4
2. Монета брошена три раза. Какова вероятность выпадения двух «орлов» и одной «решки»? Решение: При бросании трёх монет возможны 8 исходов (2*2*2=8): «орёл» — «решка» — «решка» «решка» — «решка» — «решка» «решка» — «орёл» — «решка» «орёл» — «орёл» — «решка» «решка» — «решка» -«орёл» «решка» — «орёл» — «орёл» «орёл» — «решка» — «орёл» «орёл» — «орёл» — «орёл» Два «орла» и одна «решка» выпадут в трёх случаях из восьми. Р(А)=3:8=0,375. Ответ: 0,375.
Слайд 5
3. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу. Решение: При бросании четырёх монет возможны 16 исходов: (2*2*2*2=16): Благоприятных исходов – 1 (выпадут четыре решки). Р(А)=1:16=0,0625. Ответ: 0,0625.
Слайд 6
ИГРА В КОСТИ
Слайд 7
4. Определите вероятность того, что при бросании кубика выпало больше трёх очков. Решение: Всего возможных исходов – 6. Числа большие 3 — 4, 5, 6 . Р(А)= 3:6=0,5. Ответ: 0,5.
Слайд 8
5. Брошена игральная кость. Найдите вероятность того, что выпадет чётное число очков. Решение: Всего возможных исходов – 6. 1, 3, 5 — нечётные числа; 2, 4, 6 —чётные числа. Вероятность выпадения чётного числа очков равна 3:6=0,5. Ответ: 0,5.
Слайд 9
6. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение: У данного действия — бросания двух игральных костей всего 36 возможных исходов, так как 6² = 36. Благоприятные исходы: 2 6 3 5 4 4 5 3 6 2 Вероятность выпадения восьми очков равна 5:36 ≈ 0,14. Ответ: 0,14.
Слайд 10
7. Дважды бросают игральный кубик. В сумме выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков. Решение: Всего исходов выпадения 6 очков — 5: 2 и 4; 4 и 2; 3 и 3; 1 и 5; 5 и 1. Благоприятных исходов — 2. Р(А)=2:5=0,4. Ответ: 0,4.
Слайд 11
ЛОТЕРЕЯ
Слайд 12
8. На экзамене 50 билетов, Тимофей не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет. Решение: Тимофей выучил 45 билетов. Р(А)=45:50=0,9. Ответ: 0,9.
Слайд 13
СОРЕВНОВАНИЯ
Слайд 14
9. В чемпионате по гимнастике участвуют 20 спортсменов: 8 из России, 7 из США, остальные из Китая. Порядок выступления определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решение: Всего исходов 20. Благоприятных исходов 20-(8+7)=5. Р(А)=5:20=0,25. Ответ: 0,25.
Слайд 15
10. На соревнования по метанию ядра приехали 4 спортсмена из Франции, 5 из Англии и 3 из Италии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что спортсмен, выступающий пятым, будет из Италии . Решение: Число всех возможных исходов – 12 (4 + 5 + 3 = 12). Число благоприятных исходов – 3. Р(А)=3:12=0,25. Ответ: 0,25.
Слайд 16
11. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 12 участников из России, в том числе Владимир Орлов. Найдите вероятность того, что в первом туре Владимир Орлов будет играть с каким-либо бадминтонистом из России? Решение: Всего исходов – 25 (Владимир Орлов с 25 бадминтонистами). Благоприятных исходов – (12-1)=11. Р(А)=11:25 = 0,44. Ответ: 0,44.
Слайд 17
12. Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Решение: Всего исходов – 75. Исполнители из России выступают на третий день. Благоприятных исходов – (75-27):4=12. Р(А)=12 : 75 = 0,16. Ответ: 0,16 .
Слайд 18
ЧИСЛА
Слайд 19
13. Коля выбирает двузначное число. Найдите вероятность того, что оно делится на 5. Решение: Двузначные числа: 10;11;12;…;99. Всего исходов – 90. Числа, делящиеся на 5: 10; 15; 20; 25; …; 90; 95. Благоприятных исходов – 18. Р(А)=18:90=0,2. Ответ: 0,2.
Слайд 20
РАЗНЫЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Слайд 21
14. Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решение: Всего исходов – 176. Благоприятных исходов – 170. Р(А)=170:176 ≈ 0,97. Ответ: 0,97.
Слайд 22
15. В среднем из каждых 100 поступивших в продажу аккумуляторов 94 аккумулятора заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен. Решение: Всего исходов – 100. Благоприятных исходов – 100-94=6. Р(А)=6:100=0,06. Ответ: 0,06.
Слайд 23
ИСТОЧНИКИ http://mathgia.ru http:// www.schoolmathematics.ru
nsportal.ru

