Исследовательская работа треугольник паскаля – Учебно-исследовательская работа (проект) «Блез Паскаль и его удивительный треугольник»
Научно-исследовательская работа по теме «Треугольник Паскаля»
Муниципальное казенное общеобразовательное учреждение
«Богучарская средняя общеобразовательная школа № 1»
Научно-исследовательская работа
по теме: «Треугольник Паскаля»
Автор: Карпенко Софья Владимировна 8 «А» класс
Руководитель: Алабина Галина Юрьевна
Богучар 2015
ОглавлениеВведение
Основная часть
Теоретическая часть работы
а) Блез Паскаль – французский математик
б) треугольник Паскаля как разновидность треугольника
в) свойства треугольника Паскаля и их применение в решении
задач
Практическая часть работы
а) составление последовательности тренировочных задач
по теме «Треугольник Паскаля»
б) создание презентации «Треугольники вокруг нас»
Заключение
Актуальность проекта
Данный проект предназначен для выявления того, насколько широко треугольники используются в практической жизни.
Новизна проекта
Новизна моего исследования состоит в том, что я попыталась показать связь треугольников с жизнью.
Практическая значимость проекта
Данный проект может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель проекта
— ознакомиться с треугольником Паскаля как разновидностью треугольников;
— рассмотреть применение треугольника Паскаля в различных сферах;
Гипотеза
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать волшебным.
Задачи
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— определить применение свойств чисел треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
Направления работы:
— выбор проблемы, источников литературы, составление плана;
— работа с литературой и другими источниками;
— обработка полученных данных;
— анализ результатов, формулирование вывода;
Основные этапы проекта: подготовительный; деятельностный;
ход исследования; рефлексивный; аналитический; презентационный.
Введение
В прошлом учебном году мы начали изучать новый предмет «геометрия».Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень загадочен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.
Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Теоретическая часть работы
Б лез Паскаль – французский математик
лез Паскаль – французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольника
Изучая разновидности треугольников, я выяснила, чтотреугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.В действительности, треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении задач
Изучая свойства треугольника Паскаля, я рассмотрела одно из свойств биномиальных коэффициентов:
Данное равенство показывает, что биномиальные коэффициенты можно последовательно выписывать в виде треугольной таблицы, которая называется треугольником Паскаля. В n-ой строке треугольника Паскаля стоят коэффициенты разложения , причем каждый коэффициент, кроме крайних двух, которые равны 1, равен сумме соответствующих коэффициентов из предыдущей строки.
Я узнала, что треугольник Паскаля — это бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел. В такой форме треугольник Паскаля появился в сочинении Паскаля «Трактат об арифметическом треугольнике», изданном в 1665 г. уже после смерти автора.

Паскаль подробно исследовал свойства и применения своего «треугольника». Приведу для примера лишь 3 свойства «треугольника», найденные самим Паскалем; при этом буду исходить из того расположения «треугольника» на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах. Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы).
рис.1 рис. 2 рис. 3
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. Рис. 2. Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются). Рис. 3.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность исследования обусловлена ежегодным усложнением заданий ГИА и ЕГЭ, что требует углубленных знаний не только в алгебре, но и в геометрии.
Практическая часть работы
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника. 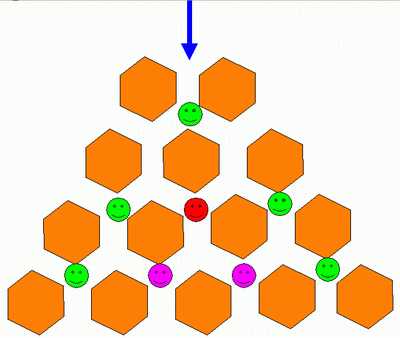
Задача 1.В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Р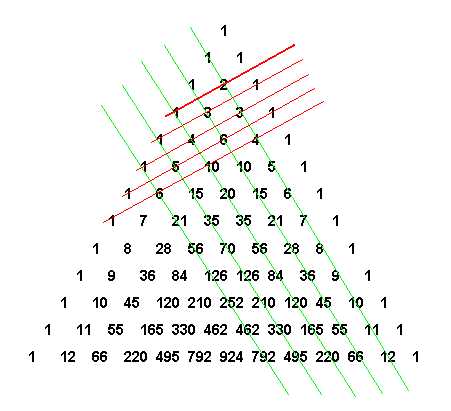 ешение:
ешение:
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56.
Задача 2.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Р ешение:
ешение:
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Р ешение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
ешение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.
По формуле нахождения вероятности получим
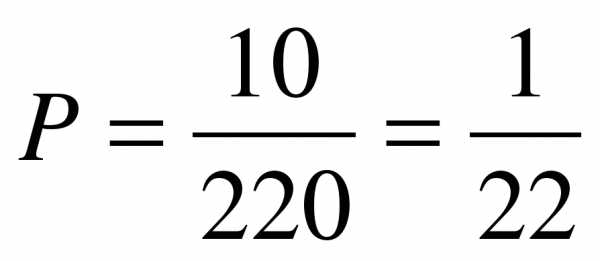
Задача4.На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Р ешение: ответ находится на пересечении -45 точек!
ешение: ответ находится на пересечении -45 точек!
Задача 5.
В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 имеющихся можно 45 способами. Вероятность нашего события 2 из 45.
Заключение
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: объект и предмет исследования, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля — понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Используя треугольник Паскаля, можно решить задачи из теории вероятности.
Практическая значимость данной работы заключается в следующем:
я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке. Работа по данной теме оказалась интересной и полезной.
Список использованных источников и литературы
1. Абачиев С. К. Радужная фрактальность треугольника Паскаля
2. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с. 3. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. – М.: Наука, 1979. – 48с.
4. Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
5. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
7. http://ru.wikipedia.org/wiki/
8. Weisstein, Eric W. Pascal’s Triangle (англ.) насайте Wolfram MathWorld.
kopilkaurokov.ru
Исследовательская работа по математике на тему «Треугольник Паскаля» (7 класс)
Отдел образования, спорта и туризма Борисовского райисполкома
Государственное учреждение образования
«Средняя школа № 16 г. Борисова»
Треугольник Паскаля
Автор:
учащаяся 7 «А» класса
Абоян Елизавета Александровна,
домашний адрес: г. Борисов,
ул Смолевичская, д. 8, 76-51-80
Руководитель:
Ищук Ольга Эдуардовна, учитель математики
Борисов, 2016
Оглавление
В этом учебном году мы начали изучать новый предмет «геометрия».
Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках, об их происхождении и значении в нашей жизни. Ведь мир треугольников очень загадочен и интересен.
Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы.
Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу — Отца, Сына и Святого Духа.
Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Проблема исследования:
Проблема моего исследования состоит в том, что я попыталась выявить и показать то, насколько широко треугольники используются в практической жизни.
Практическая значимость исследования:
Данная исследовательская работа может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель исследования:
— ознакомиться с треугольником Паскаля и его применением как разновидностью треугольников;
Гипотеза:
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать уникальным для решения различных задач
Задачи:
— определить применение свойств чисел треугольника Паскаля;
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
— поиск информации в интернет — ресурсах.
Направления работы:
— выбор проблемы, источников литературы, составление плана;
— работа с литературой и другими источниками;
— обработка полученных данных;
— анализ результатов, формулирование вывода;
— мультимедийная подготовка.
Основные этапы исследования: подготовительный; деятельностный;
Ход исследования: рефлексивный; аналитический; презентационный.
Знакомство с треугольником Паскаля
Моё первое знакомство с треугольником Паскаля произошло во время изучения темы «Возведение двучлена в степень» на уроке алгебры. Мне уже известны формулы квадрата суммы и квадрата разности, куба суммы и куба разности. Я заметила, что получить формулы для возведения двучлена в четвёртую, пятую и т.д. степень возможно, учитывая некоторую закономерность в коэффициентах и степенях каждого слагаемого.
Коэффициенты всех строк можно расположить в виде треугольника:

Таким образом я познакомилась с треугольником Паскаля и решила продолжить изучение арифметического треугольника.
Блез Паскаль – французский математик
Б лез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
лез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольника
Изучая разновидности треугольников, я выяснила, что треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника уже около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Ещё я узнала из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера, что «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
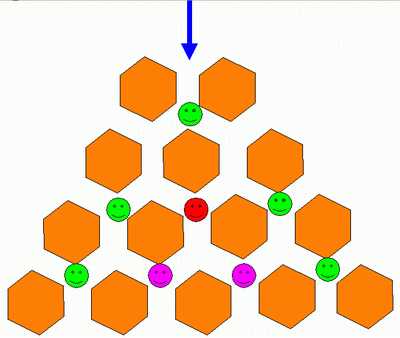
( Рисунок 1)
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел.
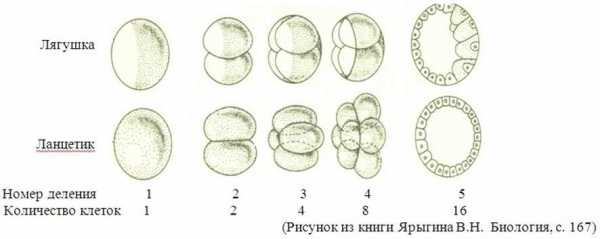
Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей. Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две — итого три — к двум можно приладить еще три — итого шесть.
Получили треугольные числа на рисунке: 3; 6; 10; 15.
Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66…, что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 — совершенные числа, 36 — квадратное число, 8 и 21 — числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдральные числа — один шар мы можем положить на три — итого четыре, под три подложим шесть — итого десять, и так далее.
Чтобы найти сумму чисел, стоящих на любой диагонали от начала до интересующего нас места, достаточно взглянуть на число, расположенное снизу и слева от последнего слагаемого, (слева для правой диагонали, для левой диагонали будет справа, а вообще — ближе к середине треугольника). Пусть, например, мы хотим вычислить сумму чисел натурального ряда от 1 до 9. «Спустившись» по диагонали до числа 9, мы увидим слева снизу от него число 45. Оно то и дает искомую сумму. Чему равна сумма первых восьми треугольных чисел? Отыскиваем восьмое число на второй диагонали и сдвигаемся вниз и влево. Ответ: 120.
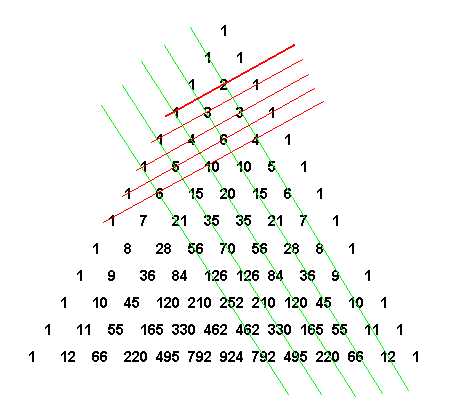
(Рисунок 2)
Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении задач
Паскаль подробно исследовал свойства и применения своего «треугольника». Приведу для примера лишь 3 свойства «треугольника», найденные самим Паскалем; при этом буду исходить из того расположения «треугольника» на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах.
Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы). (Рисунок 4)
(Рисунок 4) (Рисунок 5) (Рисунок 6)
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. (Рисунок 5)
Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются). (Рисунок 6)
Треугольник Паскаля и теория вероятности.
Блез Паскаль и другой великий француз, Пьер Ферма, стали основателями теории вероятностей, когда Паскаль и Ферма независимо друг от друга дали правильное объяснение так называемого парадокса раздела ставки. Два игрока играют в «безобидную» игру (т.е. шансы победить у обоих одинаковы), договорившись, что тот, кто первым выигрывает шесть партий, получит весь приз. Предположим, что игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл пять партий, а второй — три). Как справедливо разделить приз? Так, согласно одному решению следовало разделить приз в отношении 5 : 3, т.е. пропорционально выигранным партиям, согласно другому — в отношении 2 : 1 (здесь рассуждения велись, по всей видимости, следующим образом: поскольку первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы шести партий, то он должен получить одну треть от приза, а оставшуюся часть нужно разделить пополам).
А между тем делить надо в отношении 7:1. И Паскаль, и Ферма рассматривали парадокс раздела ставки как задачу о вероятностях, установив, что справедливым является раздел, пропорциональный шансам первого игрока выиграть приз. Предположим, первому игроку осталось выиграть только одну партию, а второму для победы необходимо выиграть еще три партии, причем игроки продолжают игру и играют все три партии, даже если некоторые из них окажутся лишними для определения победителя. Для такого продолжения все 23 = 8 возможных исходов будут равновероятными. Так как второй игрок получает приз только при одном исходе (если он выиграл все три партии), а в остальных случаях побеждает первый игрок, справедливым является отношение 7 : 1.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач.
Рассмотрим основные формулы комбинаторики:
Размещение

Это любое упорядоченное подмножество m из элементов множества n.
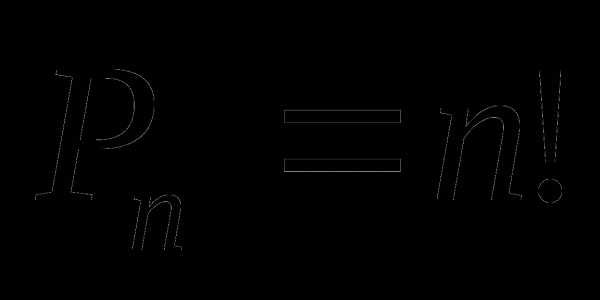
Перестановки (
 ). Если k= n, то эти размещения называются перестановками.
). Если k= n, то эти размещения называются перестановками.
Сочетания (
 ) – это любое подмножество из k – элементов, которые принадлежат множеству, состоящему из n – различных элементов.
) – это любое подмножество из k – элементов, которые принадлежат множеству, состоящему из n – различных элементов.
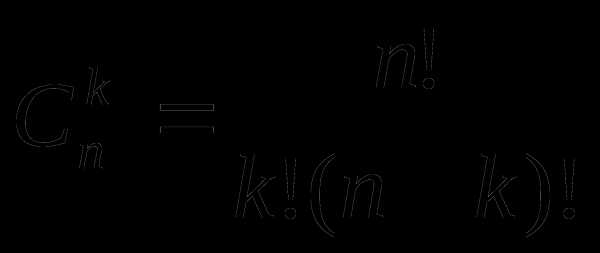 .
.
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки. Чтобы вычислить сочетание , найду диагональ седьмую сверху и отсчитываю три числа по горизонтали. Получу число 35.
Можно использовать треугольник Паскаля и для вычисления размещений. 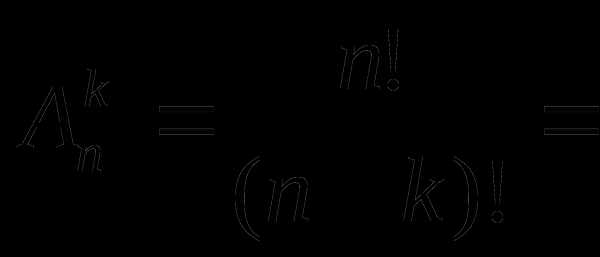
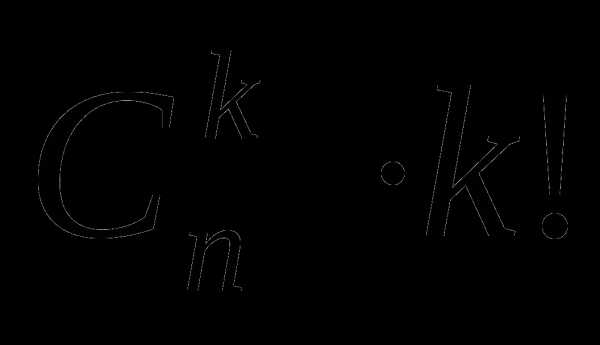 .Если нам нужно посчитать , то зная что , а 3!=6, получим значение данного размещения 210.
.Если нам нужно посчитать , то зная что , а 3!=6, получим значение данного размещения 210.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность исследования обусловлена ежегодным усложнением заданий ЦТ, что требует углубленных знаний не только в алгебре, но и в геометрии.
В своей практической работе я подобрала ряд задач по теме «Треугольник Паскаля»
З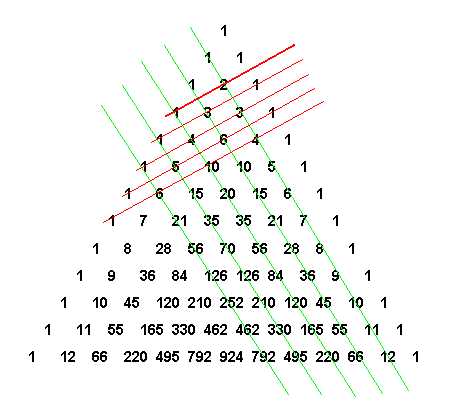 адача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
адача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56. (Рисунок 8)
Задача 2.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Р ешение:
ешение:
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
(Р(Рисунок 9)
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Решение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.
По формуле нахождения вероятности получим
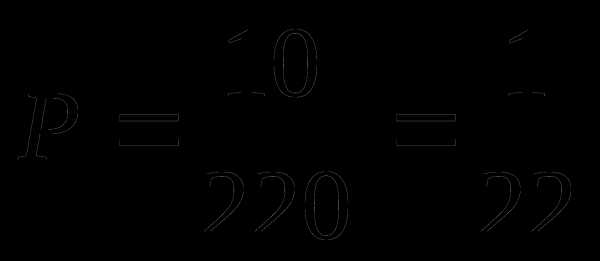
(Рисунок 10)
З адача4. На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
адача4. На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении -45 точек!
Задача 5. В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 имеющихся можно 45 способами. Вероятность нашего события 2 из 45. (Рисунок 11)
В ходе проведения практического исследования я пришла к следующим выводам: при решении комбинаторных задач и задач по теории вероятностей можно пользоваться не только формулами комбинаторики, но и использовать свойства треугольника Паскаля
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: объект и предмет исследования, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля — понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Используя треугольник Паскаля, можно решить задачи из теории вероятности и комбинаторики. С комбинаторными задачами я встречалась на уроках математики в 6 классе и при решении олимпиадных задач
Практическая значимость данной работы заключается в следующем: я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке.
Я узнала, что треугольник Паскаля применяется:
В курсе алгебры
При решении комбинаторных задач
Для решения различных задач в области физики
С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.
Работа по данной теме оказалась интересной и полезной.
1. Абачиев С. К., Радужная фрактальность треугольника Паскаля / С. К. Абачиев, — Минск, 1999.—168с.
2. Галкин Е.В. Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11кл.Москва, «Просвещение», 1996г. – 194 с.
3. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля / Математические новеллы. — Минск: Мир, 1974.— 456 с.
4. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. – Москва: Наука, 1979. – 48с.
5. Фукс Д., Фукс М., Арифметика биномиальных коэффициентов / Квант. — 1970. — № 6. — С.17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
7. http://ru.wikipedia.org/wiki/
8. http://davaiknam.ru/text/volshebnij-treugolenik.
infourok.ru
Исследовательский проект «Треугольник Паскаля»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №3
г. Ногинск Московская область
Выполнили:
ученики 7 класса
МБОУ СОШ №3 г. Ногинск МО
Руководитель проекта:
Кирина О. В. – учитель математики
МБОУ СОШ №3 г. Ногинск МО
2018 год
«Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным»
Б. Паскаль
Цель исследования:
— ознакомиться с треугольником Паскаля и его применением как разновидностью треугольников;
Гипотеза:
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать уникальным для решения различных задач
Задачи:
— определить применение свойств чисел треугольника Паскаля;
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
— поиск информации в интернет — ресурсах.
Всвоейработе я хочу доказатьгипотезу,чточисла треугольника Паскаляобладаютособымисвойствами;приведупримерызадач с ихрешением;построютреугольник Паскаляи расскажу о свойствахчиселвходящихв егосостав.
Блез Паскаль родился 19 июня 1623 г. в г. Клермон-Ферран, Франция — 19 августа 1662, Париж, Франция) — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.
Его отец славился своим интересом к наукам, в том числе и математике, что и сыграло важную роль в жизни мальчика.
Природа наделила Паскаля необычайными способностями, но обделила здоровьем. Заметив сильный интерес сына к геометрии, отец запретил ему заниматься ей, так как мальчик не раз бывал на грани жизни и смерти. Однако, после того, как он сам доказал, что сумма углов треугольника равна двум прямым углам, отец сдался и не стал ему ничего запрещать.
Прогресс человечества во многом связан с открытиями, сделанными гениями. Одним из них является Блез Паскаль. Все научные достижения этого великого ученого трудно перечесть. К их числу относится одно из самых элегантных изобретений в мире математики — треугольник Паскаля.
www.prodlenka.org
Работа на школьную НПК по теме:Треугольник Паскаля
Муниципальное Казённое Общеобразовательное Учреждение
Средняя Общеобразовательная Школа с. Лохово
Школьная НПК
Секция математика
«Треугольник Паскаля»
Выполнил: Абраменко Сергей
7 класс
Проверила: Шаянова С.Б.
Учитель математики
С. Лохово ул. Школьная -25
2015г.
Содержание:
Треугольник Паскаля. Определение — с.2
Задачи Исследования -с.2
Цель исследования -с.3
Гипотеза -с.3
Ход исследования -с.3
Свойства треугольника -с.5-6
Применение треугольника — с.7-8
Список литературы -с.9
ТРЕУГОЛЬНИК ПАСКАЛЯ
—это бесконечная числовая таблица
«треугольной формы», в которой по боковым
сторонам стоят единицы и всякое число,
кроме этих боковых единиц равно
сумме двух вышестоящих чисел.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
. . . . . . . . . . . . . . .
ЗАДАЧИ ИССЛЕДОВАНИЯ
1.Выявить свойства чисел, входящих в состав треугольника Паскаля
2. Определить применение свойств чисел треугольника Паскаля
3. Сформулировать вывод и итоги исследования
ЦЕЛЬ ИССЛЕДОВАНИЯ
Привести достаточное количество
примеров свойств чисел треугольника
Паскаля и примеров применения
треугольника для доказательства
гипотезы.
ГИПОТЕЗА
Если числа
треугольника Паскаля
обладают особыми
свойствами, то его
можно считать
удивительный.
ХОД ИССЛЕДОВАНИЯ
Выяснить, что высказывали о треугольнике Паскаля ученые или математики.
Собрать первоначальные сведения о треугольнике в энциклопедической и учебно-научной литературе.
«Треугольник Паскаля так прост,что выписать его сможет даже
десятилетний ребенок.В тоже время он таит в себенеисчерпаемые сокровища и связывает
воедино различные аспекты математики,не имеющие на первый взгляд между
собой ничего общего.Столь необычные свойства позволяют
считать треугольник Паскаля одной изнаиболее изящных схемво всей математике».
Мартин Гарднер
«Математические новеллы»
1974
ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА
ТРЕУГОЛЬНИК ПАСКАЛЯ
—это бесконечная числовая таблица
«треугольной формы», в которой по боковым
сторонам стоят единицы и всякое число,
кроме этих боковых единиц.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
. . . . . . . . . . . . . . .
ХОД ИССЛЕДОВАНИЯ
Выявить самые «Удивительные» свойства чисел треугольника
Выяснить, какими еще свойствами обладает треугольник Паскаля
САМЫЕ УДИВИТЕЛЬНЫЕ СВОЙСТВА
Каждое число равно сумме двух расположенных
над ним чисел.
Треугольник можно продолжать неограниченно.
ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА
Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А.
Свойство 2: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются).
СВОЙСТВА ТРЕУГОЛЬНИКА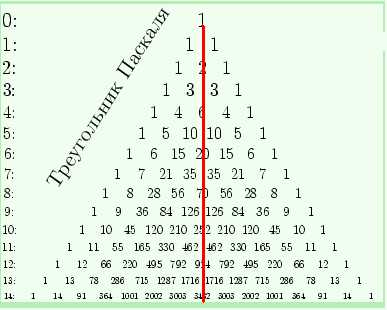
1.Он обладает симметрией
относительно вертикальной
оси, проходящей через его
вершину.
2. Вдоль прямых,
параллельных сторонам 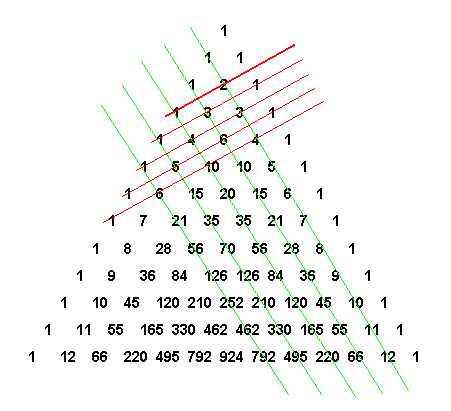
треугольника (на рисунке
отмечены зелеными линиями)
выстроены треугольные
числа и их обобщения на
случай пространств всех
размерностей.
3.Треугольные числа показывают, сколько касающихся кружков можно расположить в виде треугольника
Классический пример начальная расстановка шаров в бильярде.
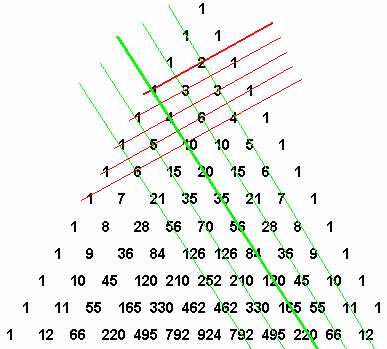
4.Следующая зеленая
линия покажет нам
тетраэдральные числа
— один шар мы можем
положить на три –
итого четыре, под три
подложим шесть
далее.
ЗАМЕЧАНИЕ
В нашем мире такое невозможно, только в
четырехмерном, виртуальном. И тем более
пятимерный тетраэдр, о котором
свидетельствует
следующая зеленая линия, он может существовать только в рассуждениях
топологов… или фантастов.
Хотя… Попробуйте с вишнями или яблоками одинакового размера, только не пытайтесь выйти с ними в четвертое измерение, они могут исчезнуть
НАВЕРНОЕ ВЫ ХОТИТЕ СПРОСИТЬ…
А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда?
Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии — сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц — это тоже треугольные числа в нульмерном пространстве — сколько бы шаров мы не взяли — больше одного расположить не сможем, ибо просто негде — нет ни длины, ни ширины, ни высоты.
4.Удивительное свойство треугольника Паскаля
Заменим каждое число в
треугольнике Паскаля точкой. 
Причем, нечетные точки
выведем контрастным цветом,
а четные — прозрачным, или
цветом фона.
Результат
окажется непредсказуемо-
удивительным: треугольник
Паскаля разобьется на более
мелкие треугольники,
образующие изящный узор.
ХОД ИССЛЕДОВАНИЯ
Изучить возможности применения треугольника Паскаля
Продемонстрировать примеры
ПРИМЕНЕНИЕ
1.Пусть, например, мы хотим 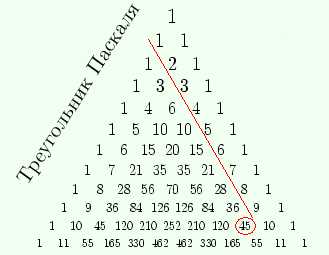
вычислить сумму чисел
натурального ряда от 1 до 9.
«Спустившись» по диагонали
До числа 9, мы увидим слева
снизу от него число 45.
Оно то и дает искомую сумму.
2..Биномиальные коэффициенты естькоэффициэнты разложения многочлена
по степеням x иy

3.Предположим , что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен. Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35.
Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться
5.
6.
Формулируем итоги и выводы
ПОДТВЕРЖДЕНИЕ ГИПОТЕЗЫ
ОБЛАДАЯ ТАКИМИ СВОЙСТВАМИ, ТРЕУГОЛЬНИК МОЖЕТ НАЗЫВАТЬСЯ УДИВИТЕЛЬНЫМ.
Вывод:
Треугольник Паскаля используется во многих науках, помогает решать сложные задачи и расширяет кругозор
числа треугольника Паскаля Имеют особые свойства, значит его можно считать удивительным.
Список Литературы
Интернет ресурсы
Учебник Алгебры
Дополнительная Литература
Задачи по планиметрии. Прасолов В. В.
Планиметрия. Пособие для углублённого изучения математики — Бутузов, Кадомцев. 2005
Я познаю мир. Детская энциклопедия. Математика 2002 изд. «Просвещение»
12
multiurok.ru
Исследовательская работа: Треугольник Паскаля | Образовательный портал EduContest.Net — библиотека учебно-методических материалов
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
Удивительный треугольник великого француза – треугольник Паскаля 1.Выявить свойства чисел, входящих в состав треугольника Паскаля2. Определить применение свойств чисел треугольника Паскаля3. Сформулировать вывод и итоги исследованияЗАДАЧИ ИССЛЕДОВАНИЯ ЦЕЛЬ ИССЛЕДОВАНИЯПривести достаточное количество примеров свойств чисел треугольника Паскаля и примеров применения треугольника для доказательства гипотезы. ГИПОТЕЗАЕсли числа треугольника Паскаляобладают особыми свойствами, то его можно считать удивительным.style.fontSize Мартин Гарднер «Математические новеллы» 1974″Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике». ТРЕУГОЛЬНИК ПАСКАЛЯ — это бесконечная числовая таблица “треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно.ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКАСАМЫЕ УДИВИТЕЛЬНЫЕ СВОЙСТВА Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА Он обладает симметриейотносительно вертикальнойоси, проходящей через его вершину. Вдоль прямых, параллельных сторонам треугольника (на рисунке отмечены зелеными линиями)выстроены треугольные числа и их обобщения на случай пространств всех размерностей. СВОЙСТВА ТРЕУГОЛЬНИКА
СВОЙСТВА ТРЕУГОЛЬНИКАТреугольные числа показывают, сколько касающихся кружков можно расположить в виде треугольника Классический пример начальная расстановка шаров в бильярде. Треугольник Паскаля СВОЙСТВА ТРЕУГОЛЬНИКАСледующая зеленаялиния покажет нам тетраэдральные числа- один шар мы можемположить на три – итого четыре, под три подложим шесть итого десять, и так далее. СВОЙСТВА ТРЕУГОЛЬНИКАСледующая зеленаялиния продемонстрирует попытку выкладывания гипертетраэдра в четырехмерном пространстве — один шар касается четырех, ате, в свою очередь, десяти… Хотя… Попробуйте с вишнями или яблоками одинакового размера, только не пытайтесь выйти с ними в четвертое измерение, они могут ЗАМЕЧАНИЕ АВТОРАВ нашем мире такое невозможно, только в четырехмерном, виртуальном. И тем более пятимерный тетраэдр, о котором свидетельствует следующая зеленая линия, он может существовать только в рассуждениях топологов… или фантастов. исчезнуть.
НАВЕРНОЕ ВЫ ХОТИТЕ СПРОСИТЬ…Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии — сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц — это тоже треугольные числа в нульмерном пространстве — сколько бы шаров мы не взяли — больше одного расположить не сможем, ибо просто негде — нет ни длины, ни ширины, ни высоты. А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда? Удивительное свойство треугольника ПаскаляЗаменим каждое число в треугольнике Паска
educontest.net
«Исследовательская работа по математике на тему «Треугольник Паскаля» (7 класс)»
Отдел образования, спорта и туризма Борисовского райисполкомаГосударственное учреждение образования
«Средняя школа № 16 г. Борисова»
Треугольник Паскаля
Автор:
учащаяся 7 «А» класса
Абоян Елизавета Александровна,
домашний адрес: г. Борисов,
ул Смолевичская, д. 8, 76-51-80
Руководитель:
Ищук Ольга Эдуардовна, учитель математики
Борисов, 2016
Оглавление
13 TOC \o «1-2» \h \z \u 1413 LINK \l «_Toc444105535» 14Введение 13 PAGEREF _Toc444105535 \h 1431515
13 LINK \l «_Toc444105536» 14Теоретическая часть работы 13 PAGEREF _Toc444105536 \h 1451515
13 LINK \l «_Toc444105537» 14Знакомство с треугольником Паскаля 13 PAGEREF _Toc444105537 \h 1451515
13 LINK \l «_Toc444105538» 14Блез Паскаль – французский математик 13 PAGEREF _Toc444105538 \h 1451515
13 LINK \l «_Toc444105539» 14Треугольник Паскаля как разновидность треугольника 13 PAGEREF _Toc444105539 \h 1461515
13 LINK \l «_Toc444105540» 14Свойства треугольника Паскаля и их применение в решении задач 13 PAGEREF _Toc444105540 \h 1481515
13 LINK \l «_Toc444105541» 14Треугольник Паскаля и теория вероятности. 13 PAGEREF _Toc444105541 \h 1491515
13 LINK \l «_Toc444105542» 14Практическая часть работы 13 PAGEREF _Toc444105542 \h 14111515
13 LINK \l «_Toc444105543» 14Заключение 13 PAGEREF _Toc444105543 \h 14131515
13 LINK \l «_Toc444105544» 14Список использованных источников и литературы 13 PAGEREF _Toc444105544 \h 14141515
15
Введение
В этом учебном году мы начали изучать новый предмет «геометрия».
Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках, об их происхождении и значении в нашей жизни. Ведь мир треугольников очень загадочен и интересен.
Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы.
Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу — Отца, Сына и Святого Духа.
Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Проблема исследования:
Проблема моего исследования состоит в том, что я попыталась выявить и показать то, насколько широко треугольники используются в практической жизни.
Практическая значимость исследования:
Данная исследовательская работа может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель исследования:
— ознакомиться с треугольником Паскаля и его применением как разновидностью треугольников;
Гипотеза:
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать уникальным для решения различных задач
Задачи:
— определить применение свойств чисел треугольника Паскаля;
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
— поиск информации в интернет — ресурсах.
Направления работы:
— выбор проблемы, источников литера
schoolfiles.net
Проектная работа в 9 классе по математике «Треугольник Паскаля»

Проект по математике:
«Треугольник Паскаля»
Подготовила ученица 9 в класса Тараканова Елена
Учитель: Чеснокова Ирина Николаевна

Цель и задачи моей работы:
1. Ознакомиться с созданием треугольника Паскаля.
2. Научиться строить треугольник
3. Выявить свойства чисел, входящих в состав треугольника Паскаля.
4. Определить применение свойств треугольника в решение задач.
5. Сформулировать вывод и итоги исследования

История создания
Треугольник Паскаля названа в честь Блеза Паскаля, но оказывается, что его строение было известно задолго до описания его Паскалем. Паскаль описал эту систему расположения чисел в своей работе 1653г и поэтому он был назван треугольником Паскаля.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму
Определение:
Свойства:
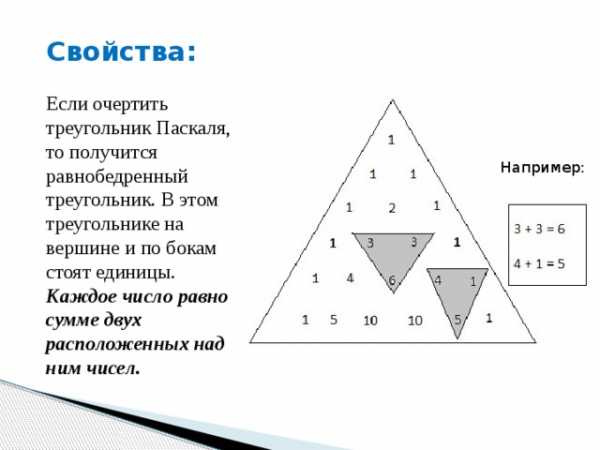
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы.
Каждое число равно сумме двух расположенных над ним чисел.
Например:

Свойство:
Чтобы найти сумму чисел, стоящих на любой диагонали от начала до интересующего места, расположенное снизу или слева от последнего слагаемого.

Свойства :
Строки треугольника симметричны относительно вертикальной оси.

Свойства :
Сумма чисел в строках треугольника Паскаля – ,
где n- номер строки.
1=2 0
1+1=2=2 1
1+2+1=4=2 2
1+3+3+1=8=2 3
1+4+6+4+1=16=2 4
1+5+10+10+5+1=32=2 5
1+6+15+20+15+6+1=64=2 6

Свойства :
Первые диагональ треугольника паскаля- это натуральные числа, идущие по порядку.

Свойства:
В каждой строчке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах.

Биномиальные коэффициенты
Биномиальные коэффициенты есть коэффициенты разложения многочлена по степеням x и y
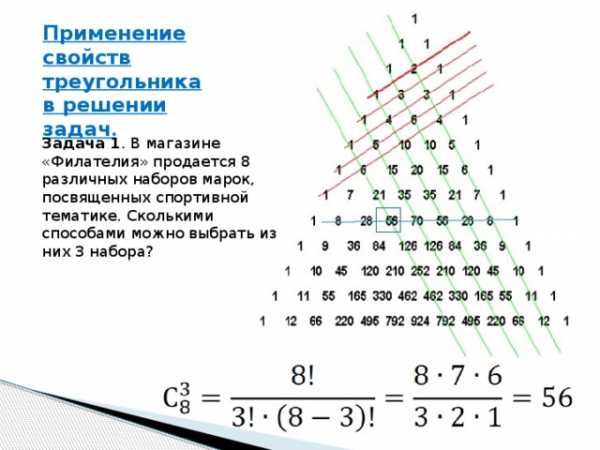
Применение свойств треугольника в решении задач .
Задача 1 . В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

Задача 2 . Из шести врачей поликлиники двух необходимо отправить на курсы по повышения квалификации. Сколькими способами это можно сделать?

Заключение
Закончив свой проект, я могу сказать, что всё из того, что было задумано, получилось.
Я узнала много интересной информации.
Планирую показать этот проект одноклассникам, когда мы будем проходить тему «Элементы комбинаторики».
С помощью Треугольника Паскаля можно легко раскрывать скобки при , где n- натуральное число, и a и b — любые числа.

Список используемой литературы
- Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант . —970. — № 6. — С. 17-25.
- Weisstein, Eric W. Pascal’s Triangle на сайте Wolfram MathWorld .
Категория:
3. Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
4. http://ru.wikipedia.org/wiki/
5. Мордкович А.Г., Семёнов П.В. Алгебра и начала математического анализа.
multiurok.ru


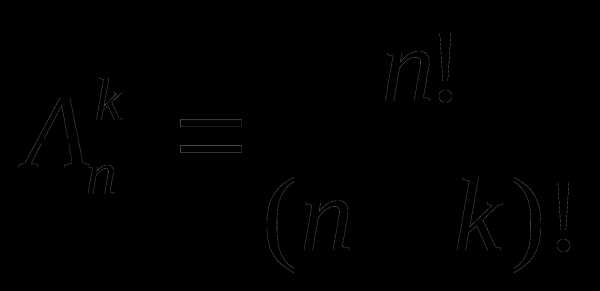
 ). Если k= n, то эти размещения называются перестановками.
). Если k= n, то эти размещения называются перестановками. ) – это любое подмножество из k – элементов, которые принадлежат множеству, состоящему из n – различных элементов.
) – это любое подмножество из k – элементов, которые принадлежат множеству, состоящему из n – различных элементов.