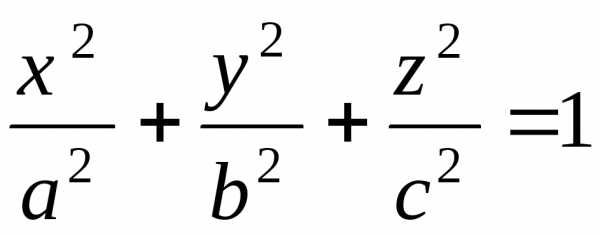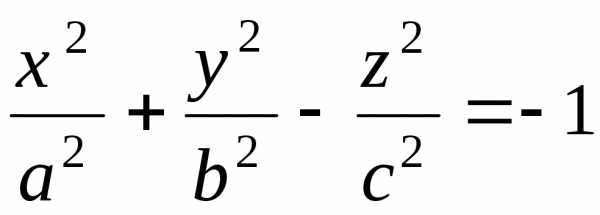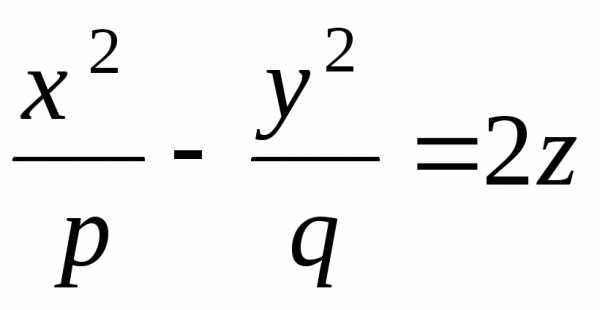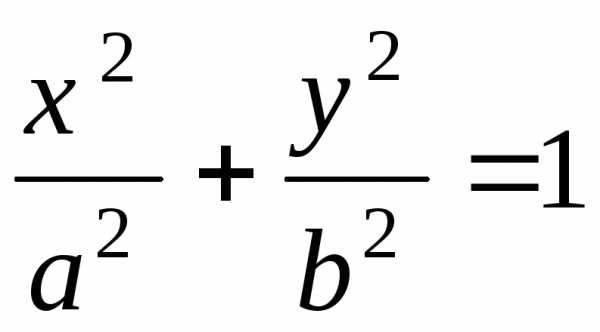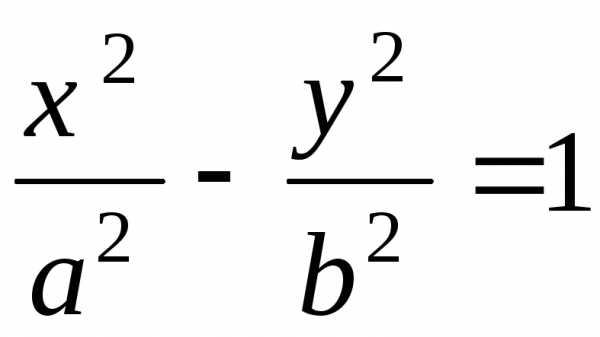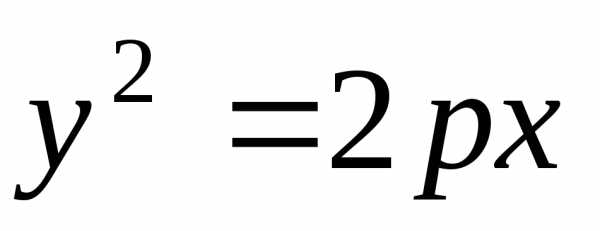Фигуры с кривыми поверхностями – 8.Многогранники и кривые поверхности.
8.Многогранники и кривые поверхности.
Общее понятие о многогранниках и кривых плоскостях
Многогранником называют тело, поверхность которого состоит из взаимно пересекающихся плоскостей.
Основными элементами всякого многогранника являются: грани, ребра и вершины
( рис. 57).
Из многогранников наибольшее распространение получили пирамиды и призмы.
Пирамида – многогранник, боковые грани и ребра которого пересекаются в одной точке, называемой вершиной.
Призма – многогранник, боковые грани и ребра которого перпендикулярны к пл.σ, называемой пл. нормального сечения, или боковые ребра которого параллельны между собой.
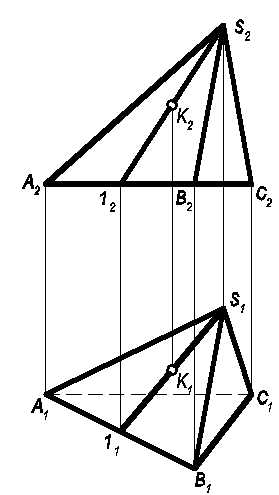
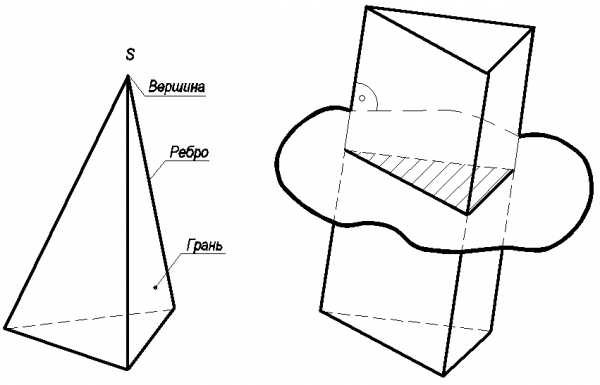
Рис. 57 Рис. 58
Если точка находится на пов. многогранника, то ее проекции следует искать на проекциях прямой, проходящей через эту точку в соответствующей грани многогранника (рис.58).
Кривой поверхностью называется поверхность, образованная при движении прямой или кривой линии в пространстве по определенному закону. (cм. рис. 59).
Линия, производящая поверхность наз. образующей.
Линия, по которой движется образующая называется направляющей.
Рис. 59
Поверхности разделяются на линейчатые – образующая прямая линия и нелинейчатые — образующая кривая линия.
Из линейчатых поверхностей получили наибольшее распространение цилиндрические и конические поверхности, из нелинейчатых поверхности вращения.

Рис. 60
Если точка находится на поверхности тела, то ее проекции следует искать на проекциях линии (образующей), принадлежащей поверхности данного тела.(см. рис. 60).
Особую группу кривых поверхностей составляют поверхности вращения, полученные при вращении образующей вокруг какой – либо оси(рис. 61).
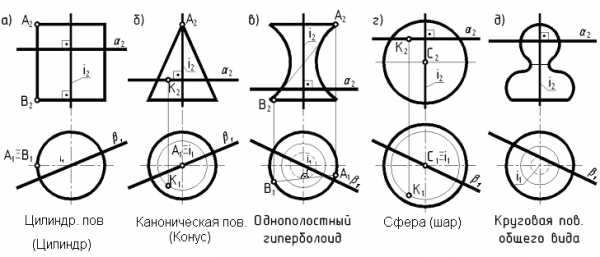
Рис. 61
При сечении пов. вращения плоскостью (α) ┴ оси вращения в сечении получается окружность — параллель. Наименьшая параллель наз. горлом, наибольшая — экватором.
При сечении поверхности вращения плоскостью (β), проходящей через ось i в сечении получается фигура, называемая меридианом. Меридиан, параллельный пл. П2 наз. главным.
9.Кривые линии
Кривые линии широко применяются в машиностроении, архитектуре, в строительстве и других областях науки и техники.
Кривую линию можно рассматривать как непрерывную совокупность последовательных положений движущейся точки , а также как линию пересечения поверхностей или поверхности с плоскостью.
Кривые линии могут быть плоскими, если все точки их лежат в одной плоскости.
Например: окружность, эллипс, парабола, гипербола.
Кривые линии называются пространственными, если они не лежат всеми своими точками в плоскости.
Например: винтовые линии.
Кривые линии — плоские и пространственные (двойной кривизны) – делятся на математические (аналитические или трансцендентные) и графические (определяемые только их изображениями).
Степень уравнения, которое описывает алгебраическую кривую (окружность, эллипс и т.д.) определяет порядок кривой. Геометрический порядок плоской кривой определяется числом точек пересечения с прямой линией. Порядок пространственной кривой определяется числом точек пересечения кривой с плоскостью.
Свойства проекций кривой : 1) в общем случае проекции кривой линии являются так же кривыми линиями; 2) если точка принадлежит кривой линии , то её проекция принадлежит одноимённым проекции этой кривой; 3) касательная к кривой линии проецируется в касательную к проекции этой линии.
Плоские кривые получили широкое распространение. Для исследования локальных
свойств плоской кривой строят в некоторой точке касательную и нормаль.
Касательной к плоской кривой (t) в некоторой точке(А) называется предельное положение секущей, когда две общие точки сечения, стремясь друг к другу совпадают.(рис. 62 а.).
Нормальюназывается прямая лежащая в плоскости кривой и перпендикулярная касательной в точке (А) её касания (рис. 62 а.)
При решении некоторых задач приходится проводить касательную (t) к кривой из некоторой точки (А) с помощью “кривой ошибок” (рис. 62 б.). Применение этого метода основано на том, что в точке касания (М) кривизна равна нулю. Через точку (А) проводят пучок прямых пересекающих кривую. Полученные хорды делят пополам. Плавная кривая, проведённая через средние точки (“кривая ошибок”),пересекает заданную кривую в точке касания (М).
Рис. 62
Свойства точек кривой:
Рис. 63
Т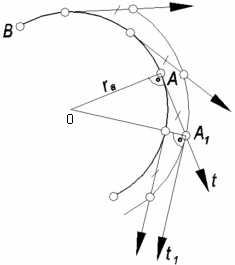 очка
кривой, в которой можно провести
единственную касательную, называетсягладкой.
Кривая состоящая только из таких точек
называется гладкой.
Точка кривой называется обыкновенной,
если при ее движении по кривой направление
её движения и направление поворота
касательной не изменяется. Точки не
удовлетворяющие этим условиям называются особыми.
очка
кривой, в которой можно провести
единственную касательную, называетсягладкой.
Кривая состоящая только из таких точек
называется гладкой.
Точка кривой называется обыкновенной,
если при ее движении по кривой направление
её движения и направление поворота
касательной не изменяется. Точки не
удовлетворяющие этим условиям называются особыми.
На рис. 63 изображены особые точки кривой: точка перегиба А – касательная пересекает кривую; точка возврата В; точка возврата второго рода С; точка излома Д- кривая в этой точке имеет две касательные.
Рис. 64
Понятие о кривизне.
Кривизной (К) плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности (К=1/r).
Например , кривизна прямой линии равна нулю, а кривизна окружности во всех ее точках величина постоянная. Кривизна других кривых в каждой точке различна. Она определяется с помощью окружности соприкасающейся в этой точке.
Соприкасающейся окружностью называется предельное
положение окружности, когда она проходит
через данную точку и две другие бесконечно
близкие к ней точки. На риc.
64 показано построение центра и радиуса
кривизны кривой линии ВС в заданной
точке. На кривой по обе стороны от данной
точки помечают несколько точек и проводят
из них и из точки А полукасательные. На
полукасательных откладывают произвольные,
но равные отрезки и через полученные
точки проводят кривую линию. Точке А заданной кривой соответствует точка A
Проекции плоских кривых.
Важное прикладное значение имеют некоторые кривые второго порядка – эллипс, парабола, гипербола.
а) б) в)
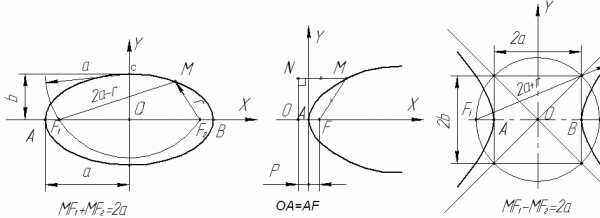 Рис.
65
Рис.
65
Эллипс(замкнутая кривая с двумя осями симметрии и центром) представляет собой геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная, равная большой оси(рис. 65 а.). Эллипс можно построить по точкам исходя из этого описания. Из точки С радиусом а
проводят дугу , которая пересекает большую ось эллипса в точках F1 и F2 . Затем из этих точек проводят дуги окружностей r и 2a—r. Точки пересечения дуг принадлежат кривой эллипса (например точка М) . Уравнение эллипсаПарабола (незамкнутая кривая с одной осью симметрии) представляет собой геометрическое место точек, равноудалённых от заданной точки (фокуса) и прямой (рис. 65 б.). параболу можно построить по точкам исходя из её определения, если задан фокус F и прямая ON— директриса. Вершина А делит пополам расстояние между фокусом и директрисой. Уравнение параболы Y2=2*p*x .
Гипербола (кривая, состоящая из двух ветвей, с
двумя осями симметрии и центром)
представляет собой геометрическое
место точек, разность расстояний от
которых до двух заданных точек (фокусов)
есть величина постоянная(рис. 65 в.). Две
прямые линии, проходящие через центр О
и касающиеся гиперболы в бесконечно
удалённых точках, называются
Уравнение гиперболы
Пространственные кривые линии
Для пространственной кривой судить о характере её точек можно только при наличии двух проекций. Широкое применение в практике получили цилиндрические и конические винтовые линии. Рассмотрим одну из них.
Цилиндрическая винтовая линия представляет собой кривую линию одинакового уклона. Эта траектория описывается в пространстве точкой, равномерно перемещающейся вдоль образующей цилиндра , которая одновременно равномерно вращается вокруг оси цилиндра. (рис. 66).
На рисунке 66 представлена проекция цилиндрической винтовой линии. Окружность основания цилиндра (диаметром d) и шаг n разделены на одинаковое число частей (n=8). Так как ось цилиндра перпендикулярна к плоскости П 1 , то горизонтальная проекция винтовой линии сливается с окружностью представляющую горизонтальную проекцию поверхности цилиндра. Фронтальная проекция винтовой линии ясна из построения, она подобна синусоиде.
Развёртка витка цилиндрической винтовой линии показана на рис. 66. В развёрнутом виде каждый виток представляет собой отрезок прямой с углом падения φ, который можно определить по формуле tg φ = h/πd, где h –шаг винтовой линии , а d– диаметр цилиндра.
Винтовая линия может быть левой или правой. Если на видимой(передней) стороне цилиндра подъём проекции винтовой линии слева направо – это правая винтовая линия; если справа на лево — то левая винтовая линия.
Е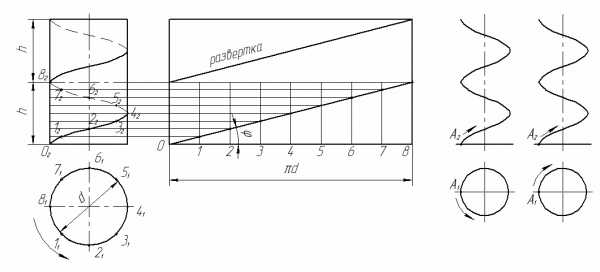 сли
винтовая линия изображена без цилиндра
и без проекции точек, то указание о том,
является ли она правой или левой, надо
делать или надписью или стрелками, как
показано на рис.67а.- для правой и рис.
67б. – для левой.
сли
винтовая линия изображена без цилиндра
и без проекции точек, то указание о том,
является ли она правой или левой, надо
делать или надписью или стрелками, как
показано на рис.67а.- для правой и рис.
67б. – для левой.
а) б)
Рис. 66 Рис. 67
studfiles.net
«Плоская и кривая поверхность». (2 класс)
Урок в рамках внеурочной деятельности «Наглядная геометрия» на тему: «Плоская и кривая поверхность». 2 класс.
О курсе «Наглядная геометрия»
Программа курса «Наглядная геометрия» разработана на основе Концепции стандарта второго поколения с учётом межпредметных и внутрипредметных связей, логики учебного процесса, задачи формирования у младшего школьника умения учиться.
В начальной школе геометрия служит опорным предметом для изучения смежных дисциплин, а в дальнейшем знания и умения, приобретённые при её изучении, станут необходимыми для применения в жизни и фундаментом обучения в старших классах общеобразовательных учреждений.
Целью курса является формирование у младших школьников универсальных интеллектуальных умений (приёмов умственной деятельности: анализа и синтеза, сравнения, классификации, аналогии, обобщения) в процессе усвоения математического содержания.
Изучение курса «Наглядная геометрия» в начальной школе направлено на достижение следующих целей:
— развитие пространственного мышления как вида умственной деятельности и способа её развития в процессе обучения;
— формировать умения решать учебные и практические задачи средствами геометрии;
— проводить простейшие построения, способы измерения;
— воспитывать интерес к умственному труду, стремление использовать знания геометрии в повседневной жизни.
Задачи:
Обучающие:
знакомство детей с понятиями поверхности, плоской поверхности, кривой поверхности,
обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин,
обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе,
сформировать умение учиться.
формирование умения следовать устным инструкциям, читать и зарисовывать схемы изделий,
обучение различным приемам работы с бумагой,
применение знаний, полученных на уроках природоведения, труда, рисования и других, для создания композиций с изделиями, выполненными в технике оригами.
Развивающие:
развитие внимания, памяти, логического и абстрактного мышления, пространственного воображения,
развитие мелкой моторики рук и глазомера,
развитие художественного вкуса, творческих способностей и фантазии детей,
выявить и развить математические и творческие способности.
Воспитательные:
воспитание интереса к предмету «Геометрия»,
расширение коммуникативных способностей детей,
формирование культуры труда и совершенствование трудовых навыков.
Планируемые результаты освоения материала урока
«Плоская и кривая поверхность».
Личностные:
— формирование внутренней позиции школьника;
— адекватная мотивация учебной деятельности, включая познавательные мотивы.
Метапредметные:
Регулятивные УУД:
— способность принимать и сохранять учебную цель и задачу:
— планировать реализацию учебной задачи:
— контролировать и оценивать свои действия, вносить соответствующие коррективы в их выполнение.
Познавательные УУД:
— использование знаково-символических средств;
— овладение действиями моделирования;
— умения использовать логические действия и операции при решении геометрических задач
Личностные, метапредметные и предметные результаты изучения материала урока «Плоская и кривая поверхность».
Личностными результаты
развитие любознательности, сообразительности при выполнении разнообразных заданий проблемного и эвристического характера;
развитие внимательности, настойчивости, целеустремленности, умения
преодолевать трудности – качеств весьма важных в практической деятельности любого человека;
воспитание чувства справедливости, ответственности;
развитие самостоятельности суждений, независимости и нестандартности
мышления.
Метапредметные результаты
Ориентироваться в понятиях «влево», «вправо», «вверх», «вниз».
Ориентироваться на точку начала движения, на числа и стрелки «1→», «1↓» и др., указывающие направление движения.
Проводить линии по заданному маршруту (алгоритму).
Выделять фигуру заданной формы на сложном чертеже.
Анализировать расположение деталей в исходной конструкции.
Составлять фигуры из частей. Определять место заданной детали в конструкции.
Выявлять закономерности в расположении деталей; составлять детали в соответствии с заданным контуром конструкции.
Сопоставлять полученный (промежуточный, итоговый) результат с заданным условием.
Объяснять (доказывать) выбор деталей или способа действия при заданном условии.
Анализировать предложенные возможные варианты верного решения.
Моделировать объёмные фигуры из различных материалов и развёрток.
Осуществлять развернутые действия контроля и самоконтроля: сравнивать построенную конструкцию с образцом.
Предметные результаты
Пространственные представления. Понятия «влево», «вправо», «вверх», «вниз». Маршрут передвижения. Точка начала движения; число, стрелка 1→ 1↓, указывающие направление движения. Проведение линии по заданному маршруту (алгоритму): путешествие точки (на листе в клетку). Построение собственного маршрута (рисунка) и его описание.
Расположение деталей фигуры в исходной конструкции. Части фигуры. Место заданной фигуры в конструкции.
Поиск заданных фигур в фигурах сложной конфигурации.
Решение задач, формирующих геометрическую наблюдательность.
Распознавание (нахождение) окружности на орнаменте. Составление
(вычерчивание) орнамента с использованием циркуля (по образцу, по собственному замыслу).
Объёмные фигуры: цилиндр, конус, пирамида, шар, куб. Моделирование из проволоки. Создание объёмных фигур из разверток: цилиндр, призма шестиугольная, призма треугольная, куб, конус и т.д.
Универсальные учебные действия
Сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания.
Моделировать в процессе совместного обсуждения алгоритм решения числового кроссворда; использовать его в ходе самостоятельной работы.
Применять изученные способы учебной работы и приёмы вычислений для работы с числовыми головоломками.
Анализировать правила игры. Действовать в соответствии с заданными правилами.
Включаться в групповую работу. Участвовать в обсуждении проблемных вопросов, высказывать собственное мнение и аргументировать его.
Выполнять пробное учебное действие, фиксировать индивидуальное затруднение в пробном действии.
Аргументировать свою позицию в коммуникации, учитывать разные мнения,
использовать критерии для обоснования своего суждения.
Сопоставлять полученный (промежуточный, итоговый) результат с заданным условием.
Контролировать свою деятельность: обнаруживать и исправлять ошибки.
план-конспект урока
Плоская и кривая поверхность.
Задачи:
Повторить знания о видах многоугольников, познакомиться с понятием поверхности, научиться различать плоские и кривые поверхности;
Развивать логическое и пространственное мышление, память, внимание, воображение;
Воспитывать трудолюбие, аккуратность.
Класс разбит на три группы («Кружочки», «Треугольнички», «Квадратики»)
I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ
Девиз нашего занятия таков: Чтоб врачом, космонавтом,
Учителем стать,
Нужно прежде всего
Геометрию знать!
II. ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
Ребята, вы любите путешествовать? Сегодня на занятии мы совершим путешествие. Наш маршрут будет проходить по городам и населенным пунктам страны Геометрия.
Проезжая по дорогам этой удивительной страны, мы вместе будем вспоминать изученный материал. А путешествовать мы будем на автомобиле
Чтобы машина завелась и поехала, вам надо назвать и сосчитать геометрические фигуры, из которых она состоит.
СЛАЙД 1
1. Наш волшебный автомобиль быстро катит по дорогам страны Геометрия. Мы подъезжаем к большому городу Многоугольники.
СЛАЙД 2
Логические задания (дети поднимают сигналы: «ложно» — красный, «истинно» — зеленый).
Некоторые фигуры на рисунке — треугольники (истинно, ложно)
Все фигуры на рисунке — треугольники (истинно, ложно)
Все фигуры на рисунке — четырехугольники (истинно, ложно)
На рисунке нет ни одного пятиугольника (истинно, ложно)
Некоторые фигуры на рисунке — четырехугольники (истинно, ложно)
Некоторые фигуры на рисунке квадраты (истинно, ложно)
СЛАЙД 3
Итог:
1. Каких фигур на рисунке больше?
2. Что вы можете рассказать о треугольнике
2. Проехав большой город, мы выбрались на простор. Вокруг зеленеют сады, созревают фрукты. Посмотрите, жители какого населенного пункта так усердно работают на своих приусадебных участках?
СЛАЙД 4
Мы подъехали к поселку Чертежниково
Ребята, готовьте карандаши, поработаем и мы (у каждого листок в клетку).
Графический диктант
Итак, стартовая точка А:
вправо 2 клетки,
вправо вниз по диагонали 1 клетка,
вниз 2 клетки,
вправо вниз по диагонали 3 клетки,
вниз 3 клетки,
влево вниз по диагонали 3 клетки,
влево 4 клетки,
вверх влево по диагонали 3 клетки,
вверх 3 клетки,
вверх вправо по диагонали 3 клетки,
вверх 2 клетки,
вправо вверх по диагонали 1 клетка.
СЛАЙД 5
III. ФИЗМИНУТКА
Цель: снять утомление с плечевого пояса и рук, улучшение кровообращения
1. И. П. – стоя у парты
1-2 – плавно наклонить голову назад.
3-4 – голову наклонить вперёд, плечи не поднимать. (3-4 раза)
2. И. П. – стоя, руки на пояс
1- поворот головы направо
2 — И. П.
3. поворот головы налево
4 — И. П. (4-6 раз)
3. И. П. – стоя, руки на пояс
1- махом левую руку через правое плечо, голову повернуть налево
2 — И. П.
3-4 – тоже правой рукой. (4-6 раз)
4. И. П. – стоя, руки на пояс
1- наклоны вправо, влево. (4-6 раз)
2 — переменить положение рук (вниз – потрясти кистями, голова наклонена вперёд) – 3-4 раза.)
СЛАЙД 6
Новый материал
3.Нам уже скоро нужно возвращаться обратно. Последний город, который мы посетим, это город Строителей.
Ребята, в своем путешествии мы вспомнили разные геометрические фигуры. Из этих фигур можно составлять новые фигуры, соединяя их друг с другом сторонами между собой. Полученные фигуры называются поверхностями. Поверхности бывают плоскими и кривыми. Попробуйте вместе со мной собрать модели поверхностей из заготовленных на ваших партах материалов. В процессе конструирования вам будет легче понять сходства и различия между гладкими и кривыми поверхностями.
СЛАЙД 7
4. Хорошо в гостях, а дома лучше. Отправляемся в обратный путь.
И чтобы быстрее добраться до дома, мы сократим путь. Нам для этого нужно обвести границы кривых поверхностей в синий цвет, а плоских – в красный и произойдет чудо, мы окажемся дома!
СЛАЙД 8
IV. РЕФЛЕКСИЯ
Какие задания вызвали затруднение?
Какие задания, при их выполнении, вы выполнили без особых затруднений?
Какие фигуры (геометрические) вам сегодня понадобились для выполнения заданий?
Для чего нужны занятия по «Наглядной геометрии»?
Литература
Гендентштейн, Л. Э. Геометрические игры для детей 6 – 7 лет [Текст]: серия «Энциклопедия развивающих игр»/ Л. Э. Гендентштейн, Е. Л. Мадышева. – М.: ИЛЕКСА, 2004. – 170 с.
Жильцова, Т. В. Поурочные разработки по наглядной геометрии, 1-4 классы [Текст]: Т. В. Жильцова, Л. А. Обухова. – М.: ВАКО, 2004. – 288 с.
infourok.ru
§10. Кривые на поверхности
Пусть
гладкая поверхность задана уравнением 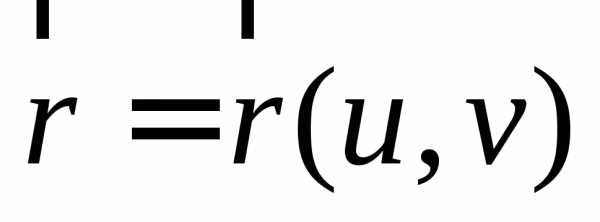 .
Если
.
Если и
и задать как функции от параметра
задать как функции от параметра ,
который пробегает некоторый промежуток
,
который пробегает некоторый промежуток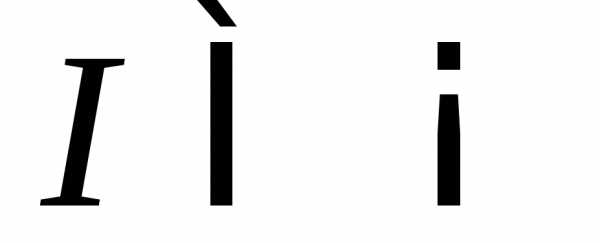 так, что,
функции
так, что,
функции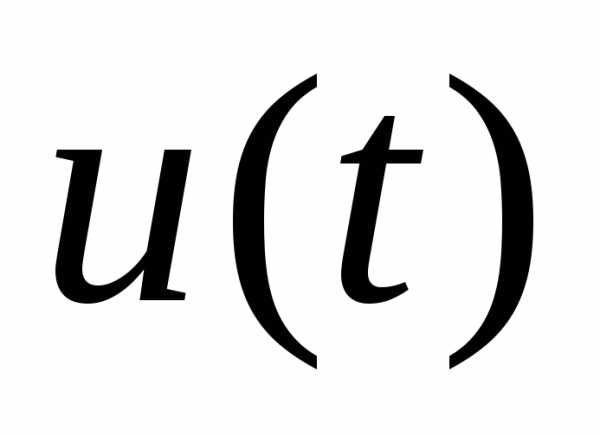 и
и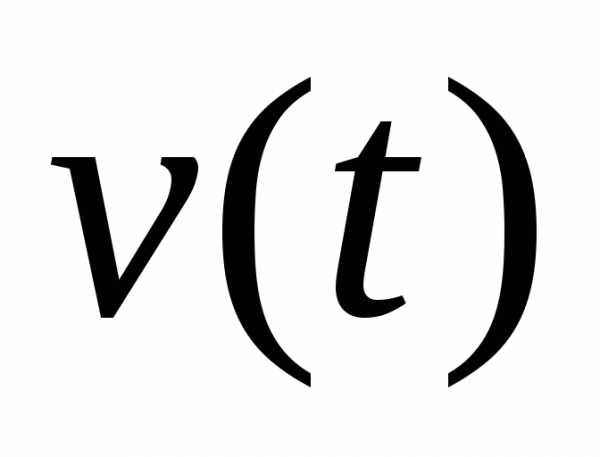 имеют непрерывные производные до порядка
имеют непрерывные производные до порядка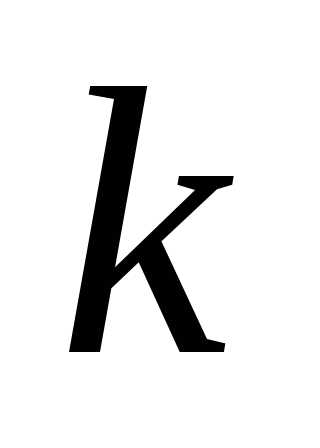 включительно, а производные
включительно, а производные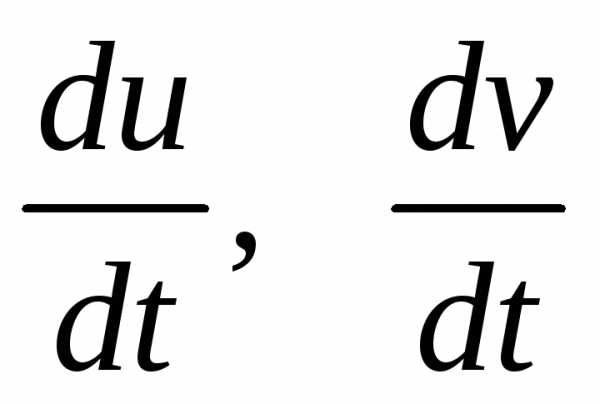 не обращаются в нуль одновременно ни в
одной точке из
не обращаются в нуль одновременно ни в
одной точке из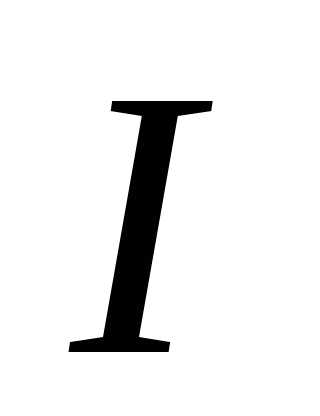 ,
то будем иметь на поверхности гладкую
линию, задаваемую уравнением
,
то будем иметь на поверхности гладкую
линию, задаваемую уравнением
.
Равенства называютсявнутренними уравнениями линии на поверхности.
Касательный
вектор линии на поверхности в точке 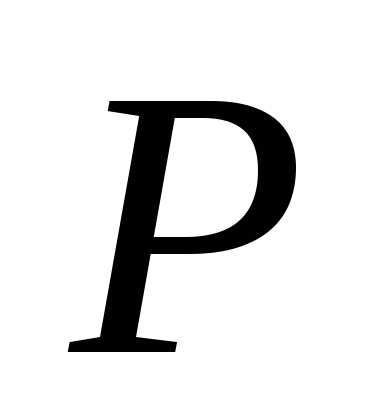 :
:
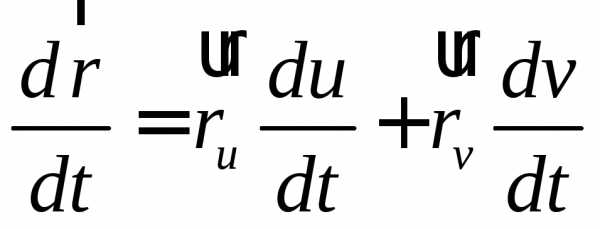 .
.
В
частности, если положить
,
то получим гладкую линию на поверхности,
которая называется  линией. Вектор
линией. Вектор  является касательным к
является касательным к 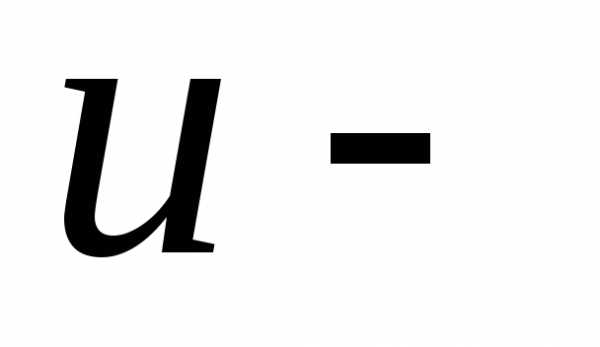 линии
в точке
линии
в точке 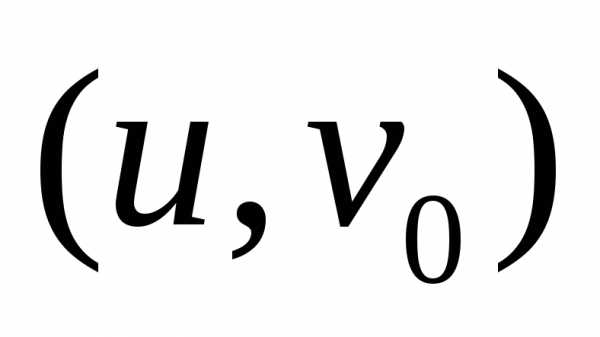 .
.
Аналогично,
при
имеем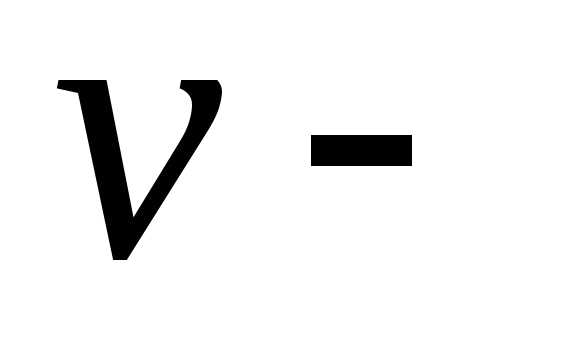 линию,
касательный вектор которой в точке.
линию,
касательный вектор которой в точке.
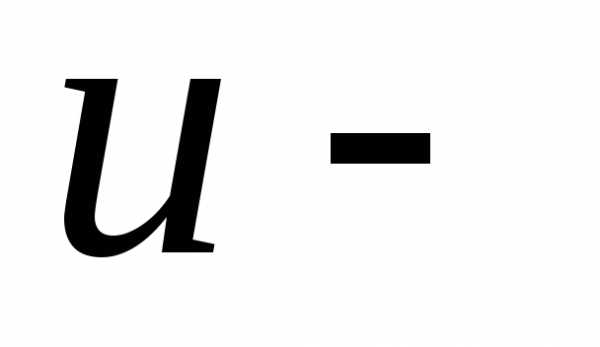 и
и 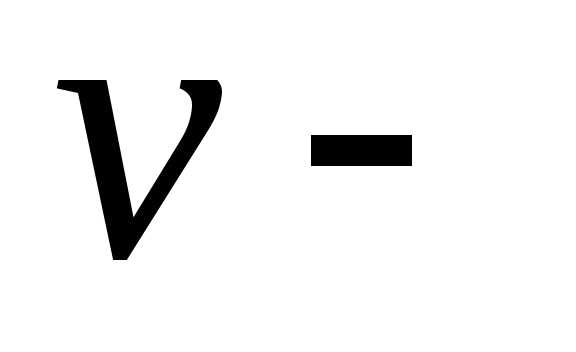 линии
называюткоординатными
линиями.
Через каждую точку гладкой поверхности
проходит в точности по одной линии из
каждого семейства координатных линий.
линии
называюткоординатными
линиями.
Через каждую точку гладкой поверхности
проходит в точности по одной линии из
каждого семейства координатных линий.
§11. Касательная плоскость и нормаль к поверхности
Касательный
вектор 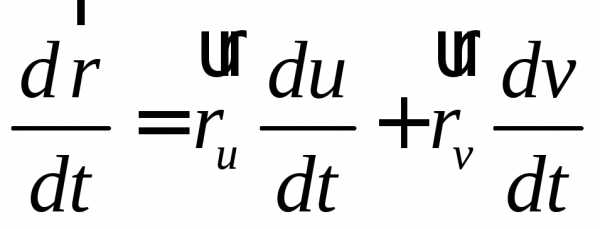 гладкой линии на гладкой поверхности
в точке
гладкой линии на гладкой поверхности
в точке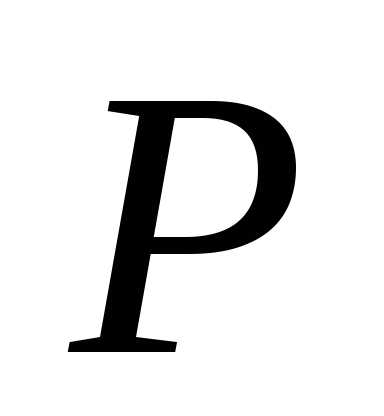 параллелен плоскости
параллелен плоскости ,
а значит, касательная к линии в точке
,
а значит, касательная к линии в точке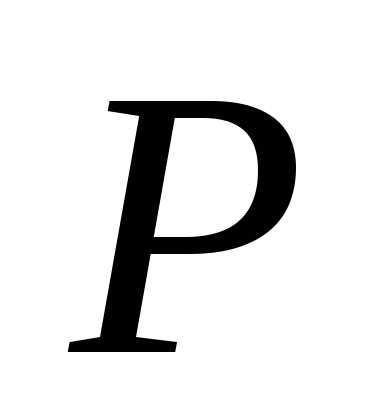 лежит в этой плоскости. Более того, имеет
место
лежит в этой плоскости. Более того, имеет
место
Т
е о р е м а. Любая
прямая 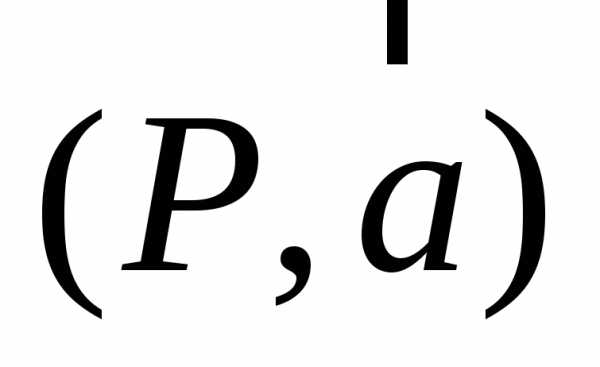 плоскости
плоскости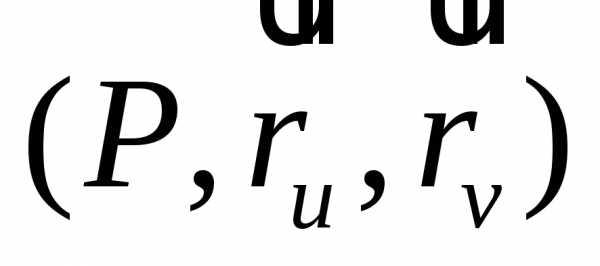 является касательной к некоторой линии
на поверхности в точке
является касательной к некоторой линии
на поверхности в точке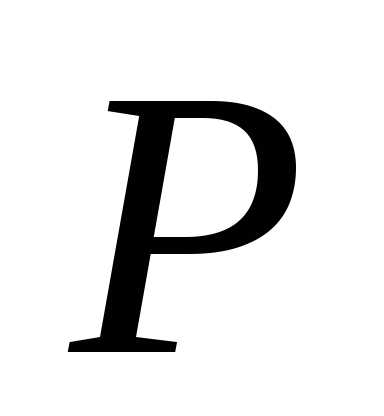 .
.
Плоскость 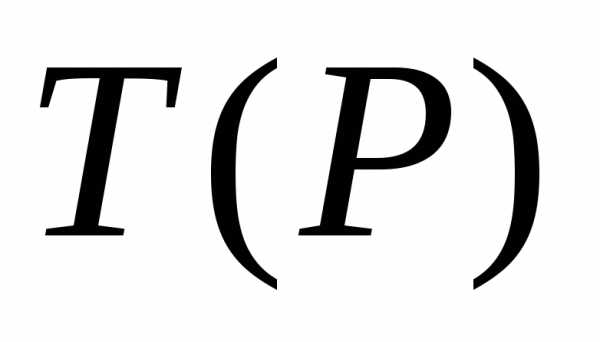 ,
в которой лежат касательные ко всем
гладким линиям на гладкой поверхности,
проходящим через точку
,
в которой лежат касательные ко всем
гладким линиям на гладкой поверхности,
проходящим через точку 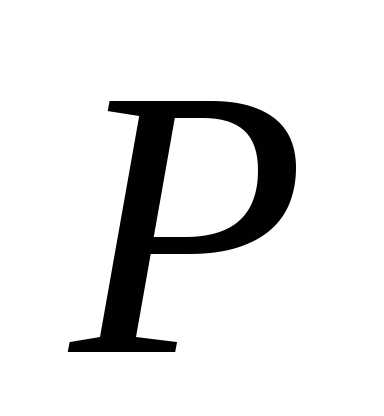 ,
называется касательной
плоскостью к поверхности в точке
,
называется касательной
плоскостью к поверхности в точке 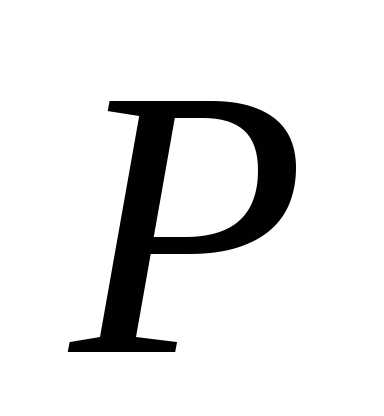 .Эта
плоскость определяется точкой
.Эта
плоскость определяется точкой 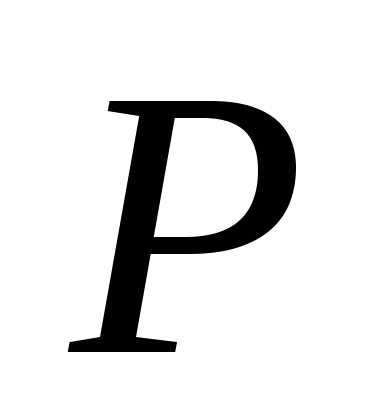 и
векторами
и
векторами 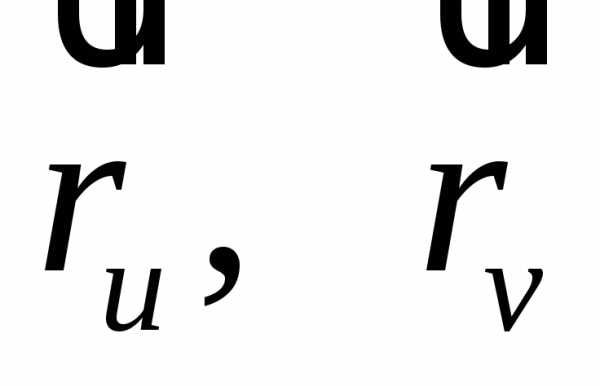 .
.
Нормалью
к гладкой поверхности в точке  называется прямая, проходящая через
точку
называется прямая, проходящая через
точку 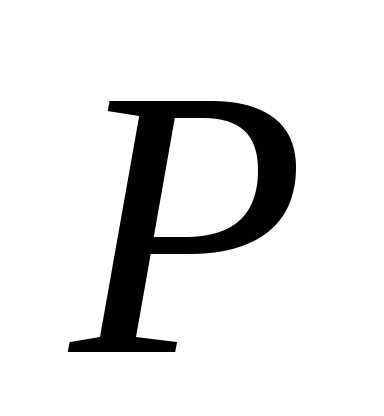 перпендикулярно касательной плоскости.
перпендикулярно касательной плоскости.
Нормаль
к поверхности определяется точкой 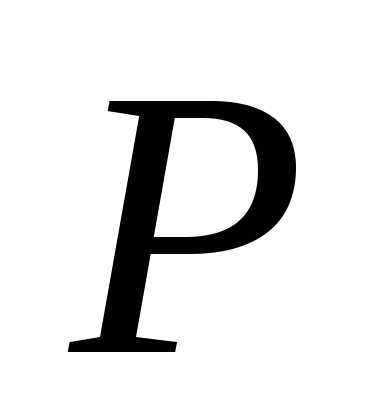 и вектором
и вектором  .
Несложно показать, что при замене
криволинейных координат, получим вектор,
коллинеарный вектору
.
Несложно показать, что при замене
криволинейных координат, получим вектор,
коллинеарный вектору .
Это значит, что направление нормали к
поверхности в точке, а значит, нормаль
и касательная плоскость не зависят от
выбора криволинейных координат,
определяются только геометрической
формой поверхности.
.
Это значит, что направление нормали к
поверхности в точке, а значит, нормаль
и касательная плоскость не зависят от
выбора криволинейных координат,
определяются только геометрической
формой поверхности.
Лекция 4. Первая и вторая квадратичная форма поверхности §12. Первая квадратичная форма поверхности
Смещая
по гладкой поверхности  вдоль какой-либо кривойиз точки
вдоль какой-либо кривойиз точки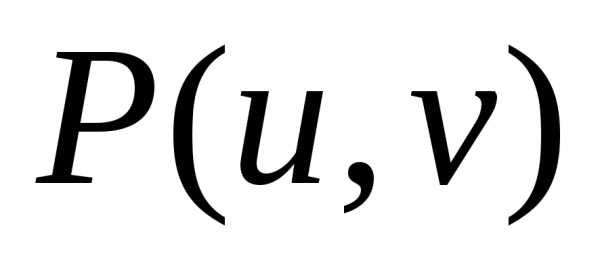 в бесконечно близкую точку
в бесконечно близкую точку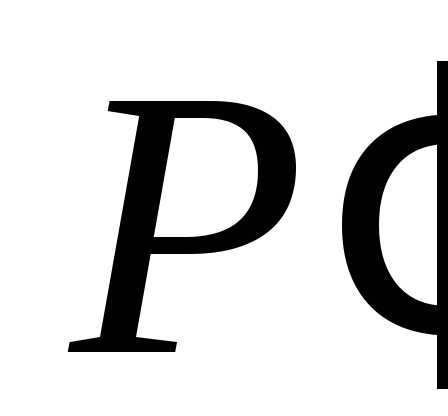 имеем,
где.
имеем,
где.
Тогда .
Векторы 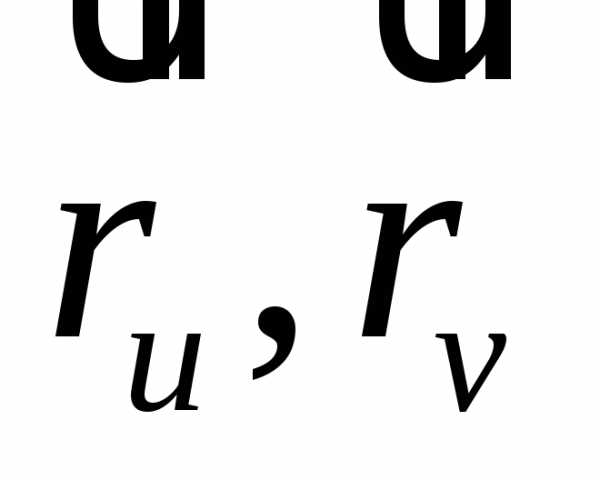 ,
а следовательно, и их скалярные
произведения суть функции от
,
а следовательно, и их скалярные
произведения суть функции от и
и и зависят лишь от выбора точки
и зависят лишь от выбора точки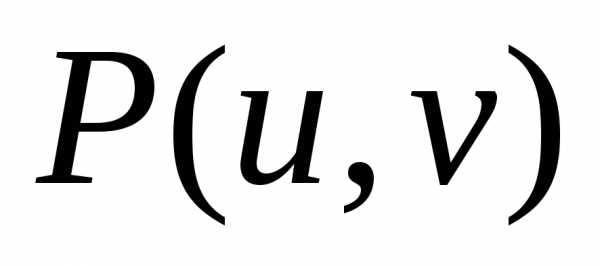 .
Введем для скалярных произведений
обозначения:
.
Введем для скалярных произведений
обозначения:
.
Имеем
.
Правая часть этой формулы является
квадратичной формой по отношению к
дифференциалам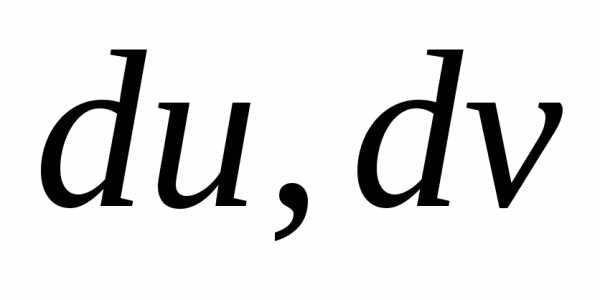 .
.
Квадратичная форма положительно определенная и называетсяпервой квадратичной формой гладкой поверхности или её линейным элементом.
Из принятых обозначений следует, что . Кроме того, применяя тождество Лагранжа, получим, поэтому.
Если задана первая квадратичная форма поверхности, другими словами, заданы функции , то хотя бы мы ничего больше не знали о поверхности (ни её формы, ни её уравнения и др.), мы можем вычислять длины кривых на поверхности, углы между ними и площади областей поверхности.
1. Длина
дуги находится по формуле  .
.
Отсюда 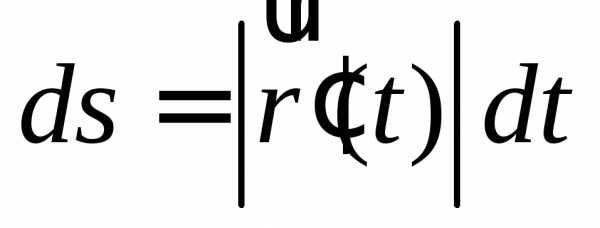 .
Так как,
то получаемформулу
для вычисления длины дуги
.
Так как,
то получаемформулу
для вычисления длины дуги
.
При этом 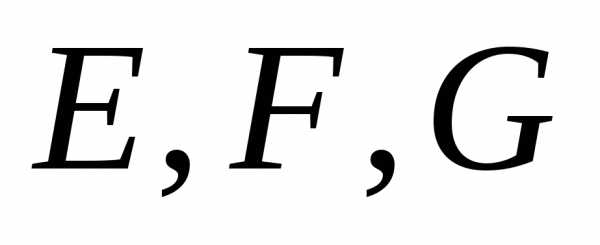 являются функциями от
являются функциями от и
и ,
а те в свою очередь функциями от
,
а те в свою очередь функциями от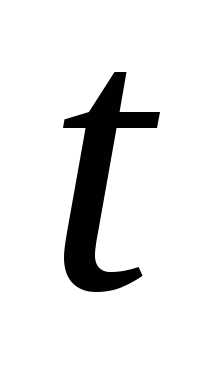 ,
то есть под знаком интеграла стоит
функция от
,
то есть под знаком интеграла стоит
функция от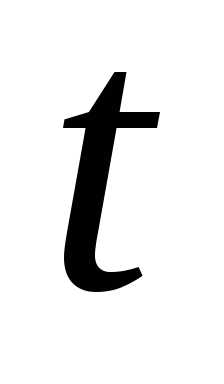 .
.
2. Углом
между пересекающимися кривыми называется угол между их касательными
в точке пересечения. Если
– касательные векторы к линиям в точке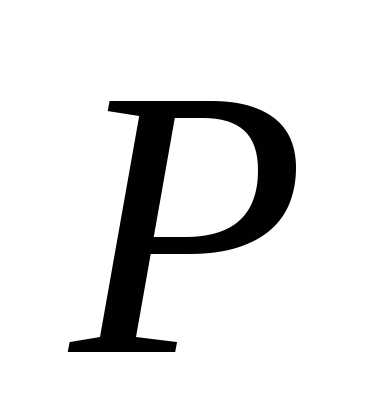 (символы
(символы и
и обозначают дифференцирование вдоль
рассматриваемых линий), то угол
обозначают дифференцирование вдоль
рассматриваемых линий), то угол можно найти из условия
можно найти из условия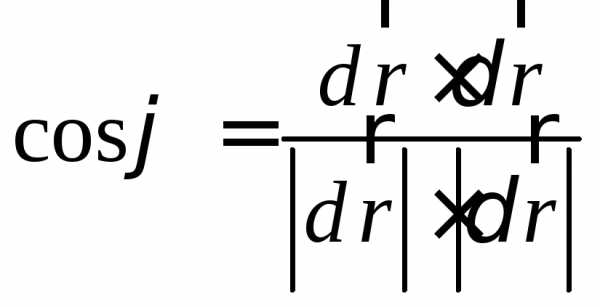 .
Получаем
.
Получаем
,
где 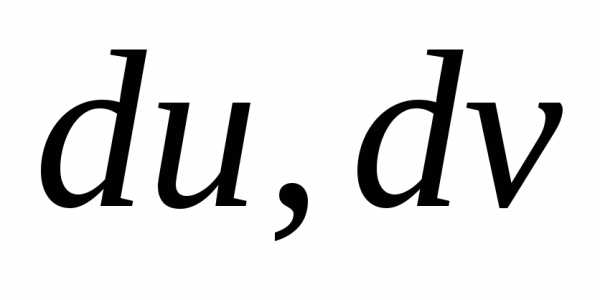 находятся из уравнений
находятся из уравнений ,
,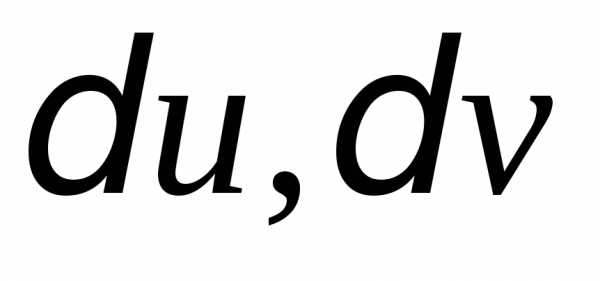 из уравнений
из уравнений ,
значения всех функций вычисляются в
точке
,
значения всех функций вычисляются в
точке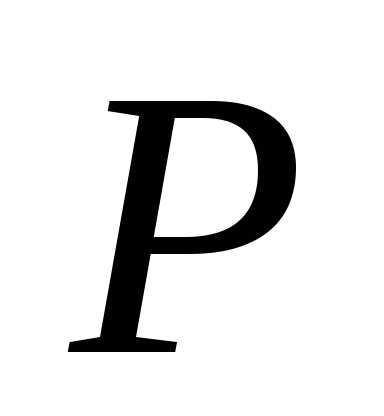 пересечения кривых.
пересечения кривых.
В
частности, для координатных линий
получаем 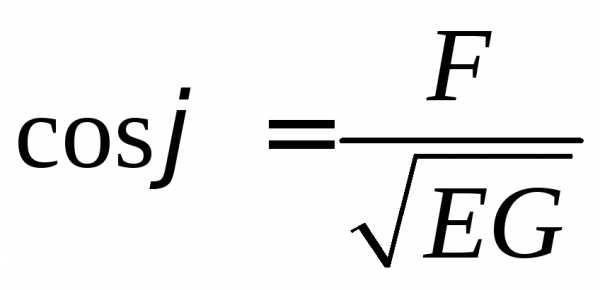 .
Таким образом, координатная сеть является
ортогональной тогда и только тогда,
когда
.
Таким образом, координатная сеть является
ортогональной тогда и только тогда,
когда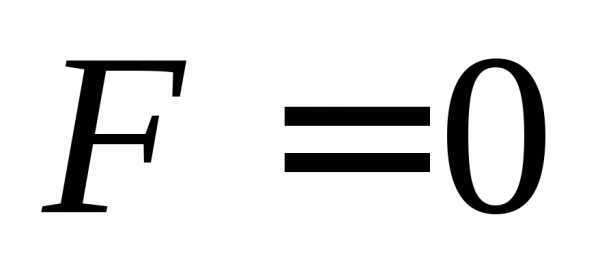 .
.
3. Для
площади элементарной гладкой поверхности,
заданной векторной функцией 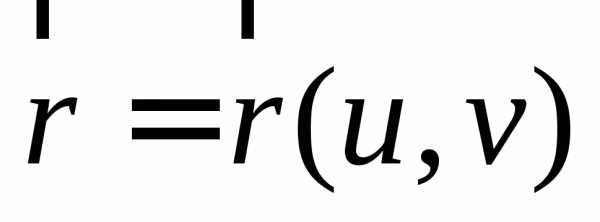 с областью определения
с областью определения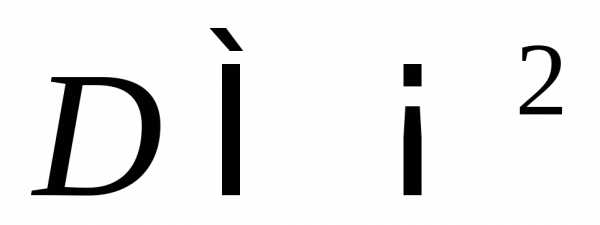 ,
справедлива формула
,
справедлива формула
.
studfiles.net
Кривые поверхности — Справочник химика 21
В более общем случае, когда правые части дифференциальных уравнений содержат несколько параметров, можно говорить о бифуркационных кривых, поверхностях, гиперповерхностях, разделяющих пространство параметров на области, внутри каждой из которых топологическая структура фазового портрета остается неизменной. Определение такого разбиения пространства параметров и характера бифуркаций, происходящих на границах областей, является завершающим этапом качественного исследования динамической системы. [c.137]Рассмотрев потенциальную кривую (поверхность), можно дать еще одно определение молекулы молекула — физически устойчивая система из двух ядер или более и определенного числа электронов, состояние которой описывается потенциальной кривой (поверхностью) с минимумом. Говоря о физической устойчивости, понимают, что соединение атомов в молекулу сопровождается понижением энергии системы. Данным здесь определением охватываются кроме обычных молекул (На, СН4 и др.) также радикалы (СН, ОН, СН3 и др.) и молекулярные ионы (Нг, О2 и др.). Этому отвечает одинаковый подход теории строения к изучению перечисленных типов частиц. [c.46]
Тыловая сторона седла обработана так, что запирающая стальная пластина 4, отгибаясь иод действием газового потока, почти соприкасается с кривой поверхностью седла. [c.369]
Располагая такой треугольник на горизонтальной плоскости и принимая его за основу, восстановим перпендикулярно плоскости его вертикальную ось. Так можно получить пространственную фигуру для выражения зависимости того или другого свойства от состава. Откладывая по вертикальной оси температуры начала кристаллизации, получают трехгранную призму, каждая из граней которой представляет собой диаграмму состояния соответствующей двойной системы, а верхняя поверхность выражает зависимость температур кристаллизации от состава для тройной системы. В то время как в диаграмме двойной системы зависимость температур кристаллизации данного вещества от состава расплава выражается участком какой-то линии (кривой кристаллизации), здесь она будет выражаться участком соответствующей кривой поверхности, называемым полем кристаллизации. [c.115]
Гиббсом получены условия равновесия для, общего случая кривых поверхностей и проникновения компонентов г в объемные фазы по обе стороны от поверхности раздела. Условиями равновесия газа с инертным однородным адсорбентом, имеющим плоскую поверхность, является равенство гидростатических давлений в газе и в адсорбенте, равенство их температур и равенство химических потенциалов каждого компонента г в адсорбированном состоянии ((гг) и в объемном газе (ц1 ) [c.132]
Из курса физики известно, что смачиванием называется явление, проявляющееся в том, что жидкость как бы прилипает к твердому телу. Например, вода смачивает стекло, металлы и другие тела, ртуть смачивает олово, цинк и т. д. В то же время вода не смачивает тела, покрытые жиром, а ртуть не смачивает фарфор, стекло и ряд других тел. Если жидкость смачивает твердое тело, то молекулярное сцепление между твердым телом и жидкостью больше молекулярного сцепления в жидкости, и мениск (кривая поверхности жидкости от греческого слова лунообразный ) смачивающей жидкости вогнутый (вода в стеклянной трубке) в отличие от выпуклого мениска несмачивающей жидкости (например, ртути в стеклянной трубке). Ртуть не смачивает стекло, следовательно, молекулярное сцепление в ртути больше сцепления между молекулами стекла и ртути. Иначе говоря, явление смачивания, возникающее при контакте твердых тел с жидкостями, обусловлено силами молекулярного взаимодействия между ними. [c.174]
Третий параметр, температуру, можно откладывать по оси, перпендикулярной к плоскости треугольника. Для этого из каждой точки треугольника нужно восстановить перпендикулярные отрезки. Высота отрезка должна отвечать температуре насыщения раствора, состав которого определяется точкой основания перпендикуляра. Получается уже не треугольник, а треугольная призма. Кривые поверхности насыщения, которые служат геометрическим местом верхних концов перпендикулярных от- [c.85]
Для практических целей обычно пользуются не проекциями политермы, а ее изотермическими сечениями. При пересечении кривых поверхностей равновесия политермы горизонтальной плоскостью на уровне, соответствующем определенной температуре, получаются кривые линии — изотермы растворимости, которые лежат внутри плоского треугольника. [c.86]
Рассмотренные диаграммы не дают представления о содержании воды в системе. Оно может быть показано с помощью водной диаграммы, которая строится путем восстановления перпендикуляров к плоскости проекции изотермической диаграммы в отдельных ее точках. На перпендикулярах откладывают содержание воды в растворе, выраженное, например, в молях на 100 (или на 1) молей или эквивалентов суммы солей, находящихся в растворе, солевая масса которого изображается точкой основания перпендикуляра . Очевидно, что точки чистой воды, лежащие на всех перпендикулярах, удалены в бесконечность. Точки, дающие содержание воды в насыщенных растворах, можно соединить кривыми поверхностями. Получится пространственная водная диаграмма (рис. 5.54). Для выполнения расчетов строят не пространственную [c.176]
Такое представление называется диабатическим (т.е. не адиабатическим). Оно заметно отличается от адиабатического в тех областях изменения/ , где расстояние между потенциальными кривыми (поверхностями) невелико. В этих областях Су(Я) 6 , и потенциальные кривые диабатического представления уже не соответствуют энергии быстрой подсистемы в поле медленной подсистемы, а сами коэффициенты сильно зависят от К. Тем не менее диабатическое представление полезно, поскольку оно лучше адаптировано к описанию медленной подсистемы, когда она меняется достаточно быстро, например, при описании тех ситуаций, когда реагирующие молекулы сталкиваются достаточно быстро. Не останавливаясь на критериях, при которых слова достаточно быстро приобретают вполне определенный смысл, можно лишь отметить, что такие критерии существуют и что переход к диабатическому представлению при рассмотрении химических реакций проводится во многих случаях. [c.253]
Изделия с кривой поверхностью могут быть отшлифованы путем скобления осколком оконного стекла (рис. 62, А). При за- [c.67]
Нанесение зеркального слоя. Для некоторых приборов по оптике нужны зеркала. Зеркало проще всего приобрести готовым. Такое зеркало можно разрезать на части нужной величины., например на полоски для демонстрации отражения света от кривых поверхностей или для устройства шкал в лабораторных приборах. Резание алмазом или стеклорезом производят с той стороны зеркала, которая свободна от зеркального слоя. [c.331]
Л и в — неправильные и С — правильное положения ножа при обрезании, О— положение ножа при обрезании бумаги, Е— положение ножа и руки при обрезании картона. Р, О, 1 — сгибание бумаги, К и — сгибание картона под углом и оклеивание кантиком, М вид (изнутри) вершины куба, склеенного при помощи полосок, N — соединение двух листов картона под прямым углом, О —соединение плоской и кривой поверхностей, Р — присоединение осно
www.chem21.info
6.2. Принадлежность кривой поверхности её элементов на чертеже
Как и для любой поверхности, для кривой поверхности справедливы рассмотренные выше правила определения принадлежности:
1.Точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности, удобной для изображения её на чертеже (например, прямой линии или окружности).
2.Линия принадлежит поверхности, если она проходит через соответствующие точки этой поверхности. Точек должно быть достаточно для вычерчивания проекций рассматриваемой линии.
Пример (рис. 6.23). Построить недостающие
профильные проекции
линий m и n,
а также точек А и В на сфере 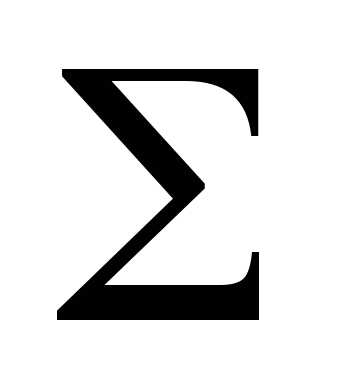 .
.
m

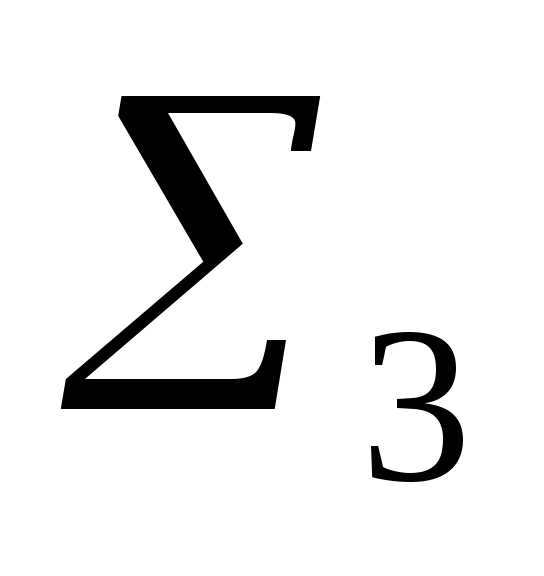 A
A m
m
A
n
B
B n
n
Рис. 6.23
Профильные проекции точек А и В определяем по принадлежности их соответственно: главному фронтальному и главному профильному меридианам.
Так
как проекции m и n
и n выглядят, как отрезки ломаной прямой,
то это значит, что линии m и n представляют собой дуги окружностей,
касательных в точке А.
Плоскости этих дуг окружностей занимают
фронтально проецирующее положение.
Плоскость окружности n параллельна профильной плоскости
проекций, поэтому на ней окружность n изобразится в истинную величину.
Плоскость дуги m не параллельна профильной плоскости
проекций, поэтому проекция m
выглядят, как отрезки ломаной прямой,
то это значит, что линии m и n представляют собой дуги окружностей,
касательных в точке А.
Плоскости этих дуг окружностей занимают
фронтально проецирующее положение.
Плоскость окружности n параллельна профильной плоскости
проекций, поэтому на ней окружность n изобразится в истинную величину.
Плоскость дуги m не параллельна профильной плоскости
проекций, поэтому проекция m представляет собой дугу эллипса. Эту
проекцию строят по точкам, выбранным
на фронтальной проекции m
представляет собой дугу эллипса. Эту
проекцию строят по точкам, выбранным
на фронтальной проекции m ,
привязывая их к параллелям и меридианам
заданной сферы.
,
привязывая их к параллелям и меридианам
заданной сферы.
6.3. Пересечение кривой поверхности с прямой
линией на чертеже (1.ГПЗ)
Определение результатов пересечения геометрических фигур на чертеже связано с решением позиционных задач третьего типа, так называемых главных позиционных задач.
Решение
задач 1.ГПЗ. 1 (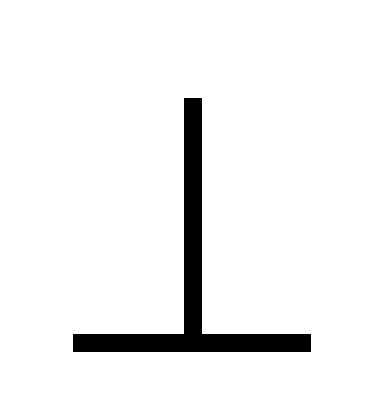 ,
,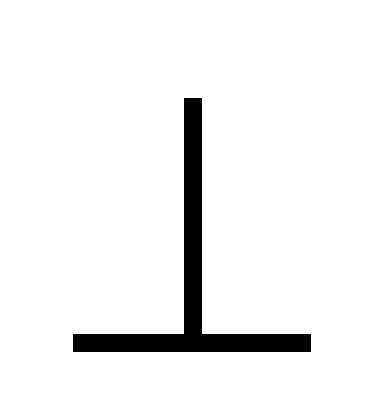 )
)
Алгоритм решения
1.Искомые проекции точек пересечения проецирующих геометрических фигур уже изображены на чертеже по принадлежности их главным проекциям.
2.Определяют видимость элементов геометрических фигур.
Пример (рис. 6.24).
Построить трёх картинный чертёж
пересекающихся прямой линии а и цилиндра
вращения 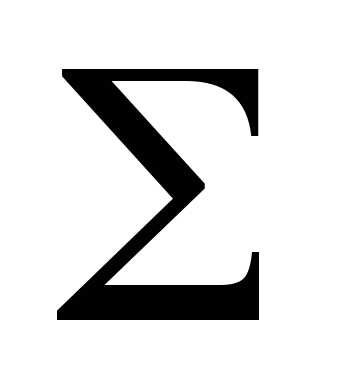 .
.
Алгоритм решения
1. 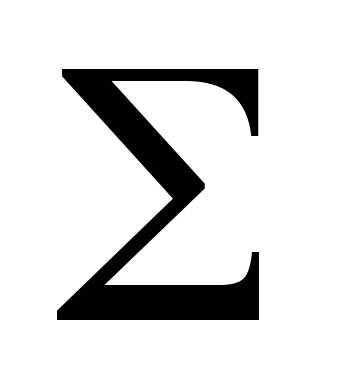
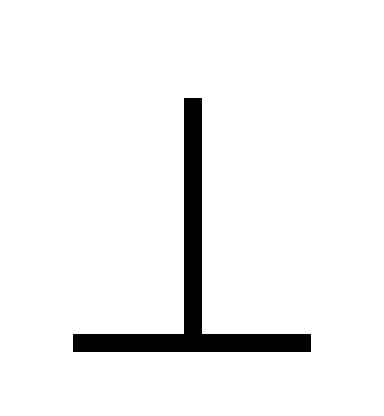
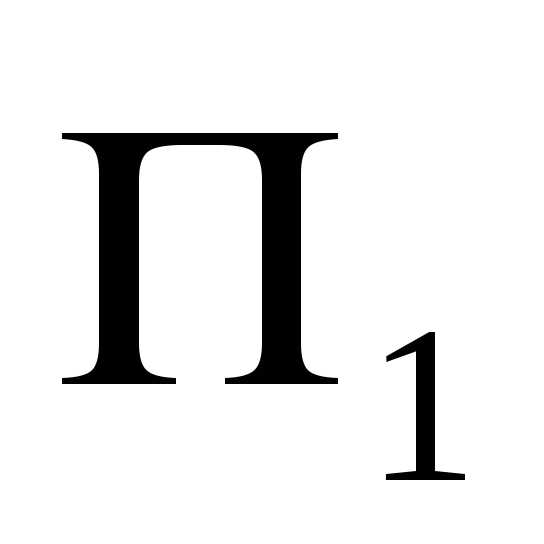
 P
P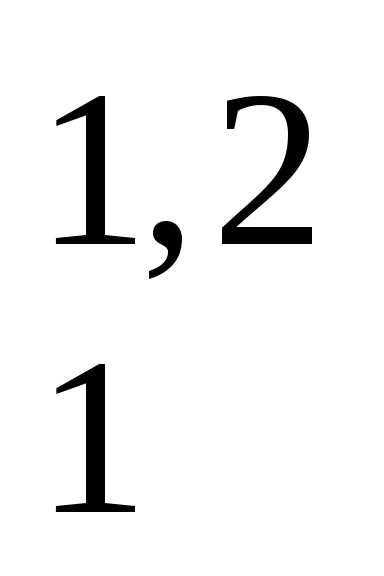 = a
= a 
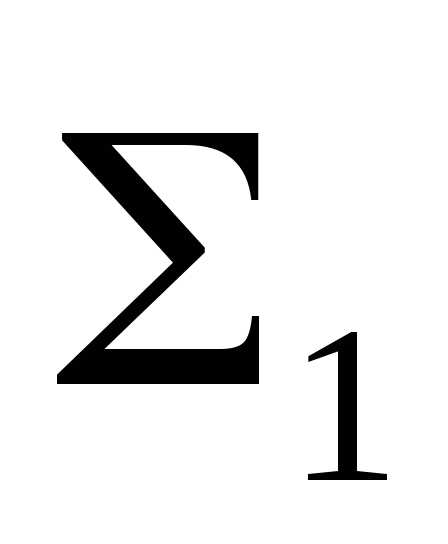 ;
;
2. a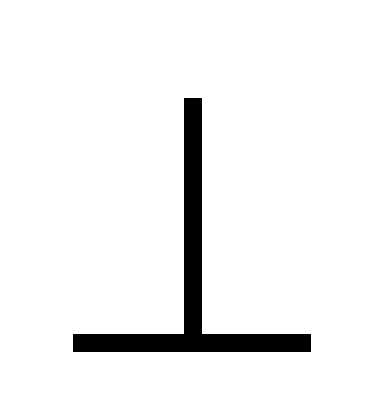
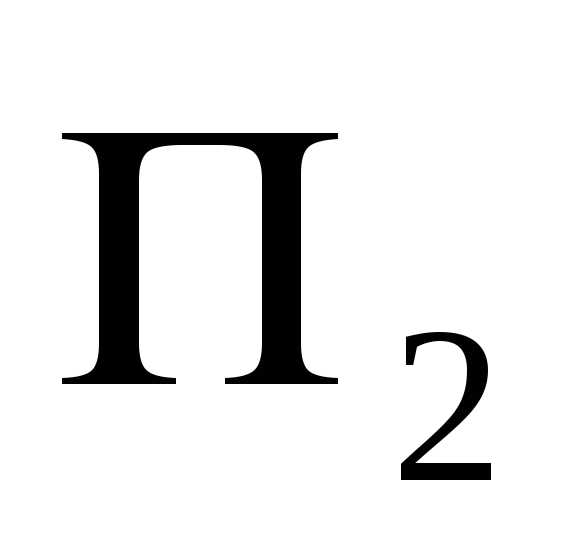
 P
P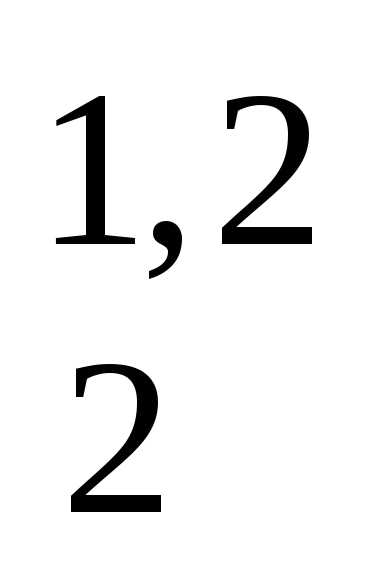 = a
= a ;
;
3. P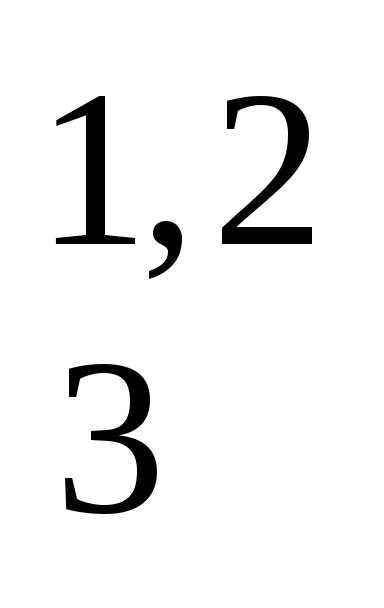 = a
= a .
.
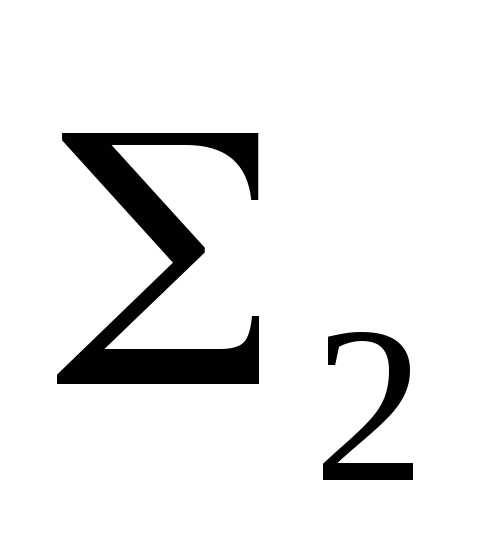
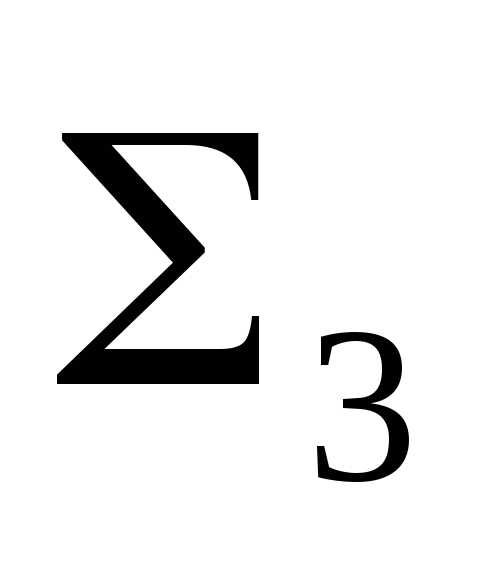
a =
P
=
P
a
P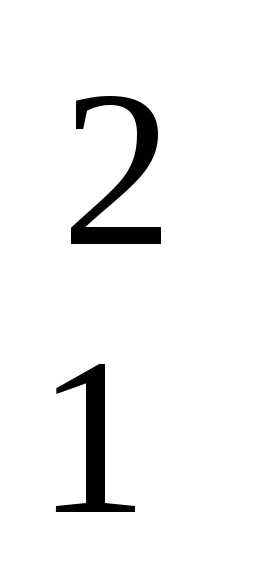
a
P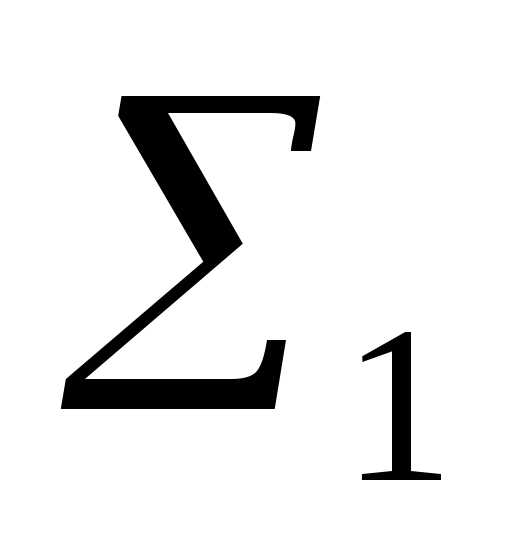
Рис. 6.24
Решение
задач 1.ГПЗ . 2 ( 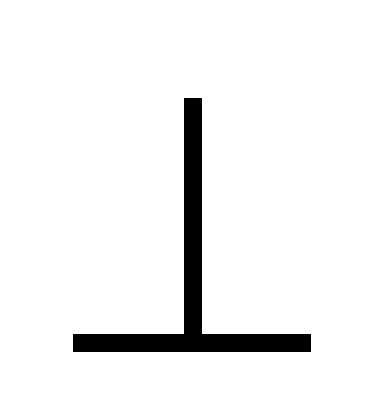 ,
не
,
не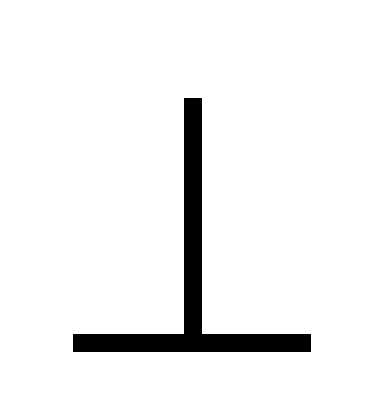 )
)
При пересечении кривой поверхности с прямой линией для нахождения точек их пересечения используется тот же алгоритм решения, что и при пересечении прямой с плоской поверхностью:
1.Одна из искомых проекций точки пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры.
2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения.
3.Определяют видимость элементов заданных фигур.
Пример (рис. 6.25). Определить проекции точек
пересечения прямой линии а с цилиндром
вращения 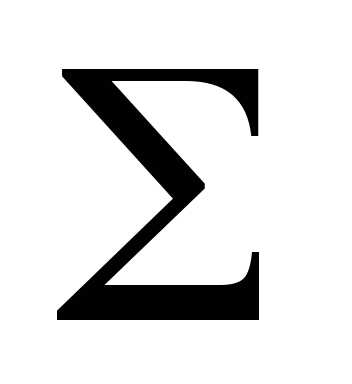 .
.
studfiles.net
Как найти площадь поверхности вращения с помощью интеграла
Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой поверхности вращения. Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).
Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой. Тело, образованное вращением этой трапеции вокруг то же оси Ox, и есть тело вращения. А площадь поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов, образованных вращением вокруг оси прямых x = a и x = b.
Заметим, что тело вращения и соответственно его поверхность могут быть образованы также вращением фигуры не вокруг оси Ox, а вокруг оси Oy.
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая, вращением которой вокруг координатной оси образовано тело вращения.
Формула для вычисления площади поверхности вращения следующая:
(1).
Пример 1. Найти площадь поверхности параболоида, образованную вращением вокруг оси Ox дуги параболы , соответствующей изменению x от x = 0 до x = a.
Решение. Выразим явно функцию, которая задаёт дугу параболы:
Найдём производную этой функции:
Прежде чем воспользоваться формулу для нахождения площади поверхности вращения, напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда найденную только что производную:
Далее по формуле (1) находим:
Ответ: длина дуги кривой равна
.
Пример 2. Найти площадь поверхности, образуемой вращением вокруг оси Ox астроиды .
Решение. Достаточно вычислить площадь поверхности, получающейся от вращения одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности вращения:
.
Производим интегрирование от 0 до a:

Ответ: площадь поверхности вращения равна .
Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими уравнениями
Тогда площадь поверхности вращения вычисляется по формуле
(2).
Пример 3. Найти площадь поверхности вращения, образованной вращением вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a. Циклоида задана параметрическими уравнениями
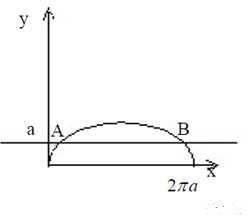
Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды и уравнение прямой y = a, найдём
Из этого следует, что границы интегрирования соответствуют
Теперь можем применить формулу (2). Найдём производные:
Запишем подкоренное выражение в формуле, подставляя найденные производные:
Найдём корень из этого выражения:
.
Подставим найденное в формулу (2):
 .
.
Произведём подстановку:

И, наконец, находим

В преобразовании выражений были использованы тригонометрические формулы
Ответ: площадь поверхности вращения равна .
Пусть кривая, вращением которой образована поверхность, задана в полярных координатах:
Площадь поверхности вращения вычисляется по формуле:
(3).
Пример 4. Найти площадь поверхности, образованной вращением лемнискаты вокруг полярной оси.
Решение. Действительные значения для ρ получаются при , то есть при (правая ветвь лемнискаты) или при (левая ветвь лемнискаты).
Решение. Дифференциал корня из формулы площади поверхности вращения равен:
В свою очередь произведение функции, которой задана лемниската, на синус угла равно
.
Поэтому площадь поверхности вращения найдём следующим образом:
.
Начало темы «Интеграл»
function-x.ru
Поверхности второго порядка
§ 7. Цилиндрические и конические поверхности. Поверхности вращения
Основные теоретические сведения
Цилиндрической поверхностью или просто цилиндром называется всякая поверхность, которую можно получить движением прямой, перемещающийся параллельно некоторому вектору и все время пересекающей данную линию, которая носит название направляющей. Движущаяся прямая называется образующей.
Конической поверхностью или просто конусом называется поверхность, образованная движением прямой, проходящей через данную точку, называемую вершиной конуса, и скользящей по данной кривой. Движущаяся прямая называется образующей конуса, а кривая, по которой скользит образующая, — направляющей.
Вращением фигуры  вокруг данной прямой (оси вращения)называется
такое движение, при котором каждая точка
фигуры
вокруг данной прямой (оси вращения)называется
такое движение, при котором каждая точка
фигуры  описывает
окружность с центром на оси вращения,
лежащую в плоскости, перпендикулярной
к оси вращения.
описывает
окружность с центром на оси вращения,
лежащую в плоскости, перпендикулярной
к оси вращения.
Поверхность, образованная вращением линии вокруг оси, называется поверхностью вращения.
Канонические уравнения поверхностей второго порядка
Поверхность второго порядка задается в прямоугольных координатах уравнением второй степени
(7.1)
Путем преобразования
координат (поворотом осей и параллельным
переносом) уравнение (7.1) приводится к
каноническому виду. В случае, когда в
уравнении (7.1) отсутствуют члены с
произведением координат
,
это уравнение выделением полных квадратов
по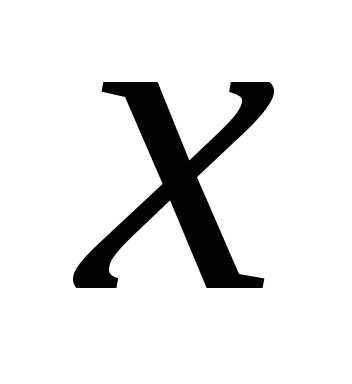 ,
, ,
, и параллельным переносом осей координат
приводится к каноническому виду подобно
тому, как это делалось для линий второго
порядка (см. Исследование общего уравнение
линии второго порядка). Поверхности
второго порядка и их канонические
уравнения представлены в табл. 3.
и параллельным переносом осей координат
приводится к каноническому виду подобно
тому, как это делалось для линий второго
порядка (см. Исследование общего уравнение
линии второго порядка). Поверхности
второго порядка и их канонические
уравнения представлены в табл. 3.
Форму и расположение поверхностей второго порядка обычно изучают методом параллельных сечений. Сущность метода заключается в том, что поверхность пересекается несколькими плоскостями, параллельными координатным плоскостям. Форма и параметры полученных сечений позволяют выяснить форму самой поверхности.
Таблица 3
Поверхность второго порядка, каноническое уравнение | Вид |
1 | 2 |
Эллипсоид
| |
1 | 2 |
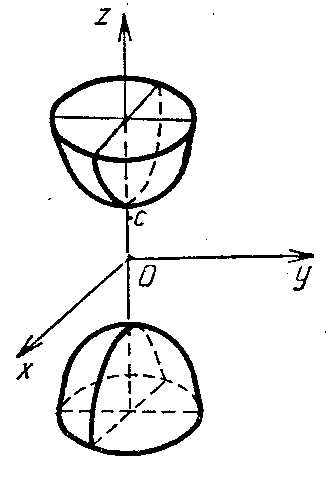
Гиперболоид: однополостный,
двуполостный,
| |
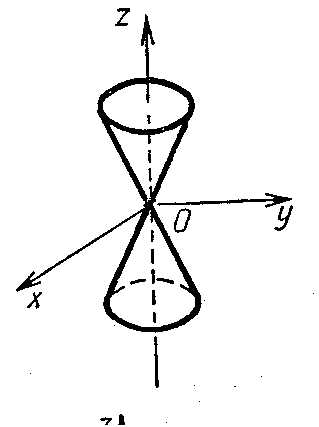
Конус,
| |
Параболоид: эллиптический, гиперболический, | |
1 | 2 |
Цилиндр: эллиптический, гиперболический, параболический, | |
Примеры решения задач
Задача 7.1. Составить
уравнение сферы, радиус которой  ,
а центр находится в точке.
,
а центр находится в точке.
Решение. Сфера – это множество точек, отстоящих
от центра на одном и том же расстоянии.
Следовательно, обозначив через  координаты произвольной точки
координаты произвольной точки сферы и выразив через них равенство
сферы и выразив через них равенство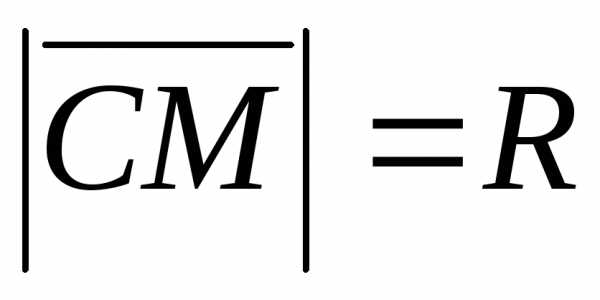 ,
будем иметь
,
будем иметь
.
Возведя обе части равенства в квадрат, получим искомое каноническое уравнение сферы:
.
Если центр сферы поместить в начало координат, то уравнение сферы имеет более простой вид:
.
Ответ. .
Задача 7.2. Составить уравнение конической поверхности с вершиной в начале координат и направляющей
 (7.1)
(7.1)
Решение. Канонические уравнения образующих
через точку 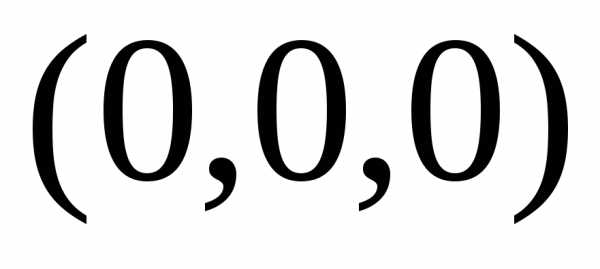 и точку
и точку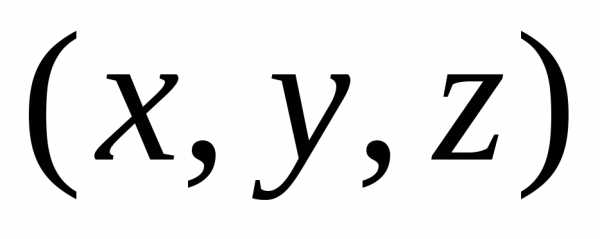 направляющей, имеет вид
направляющей, имеет вид
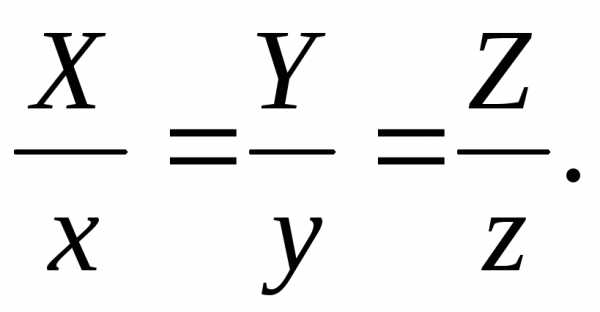 (7.2)
(7.2)
Исключим 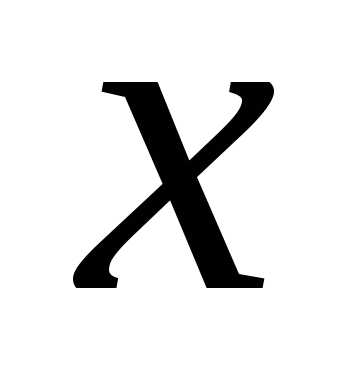 ,
, ,
, из уравнений (7.1) и (7.2). Для этого в
уравнениях (7.2) заменим
из уравнений (7.1) и (7.2). Для этого в
уравнениях (7.2) заменим на
на и определим
и определим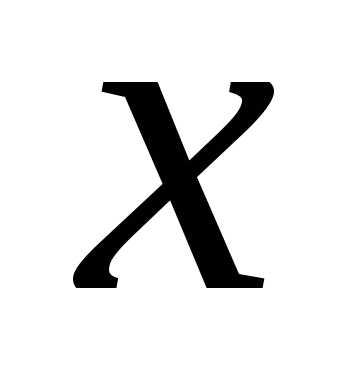 и
и :
:
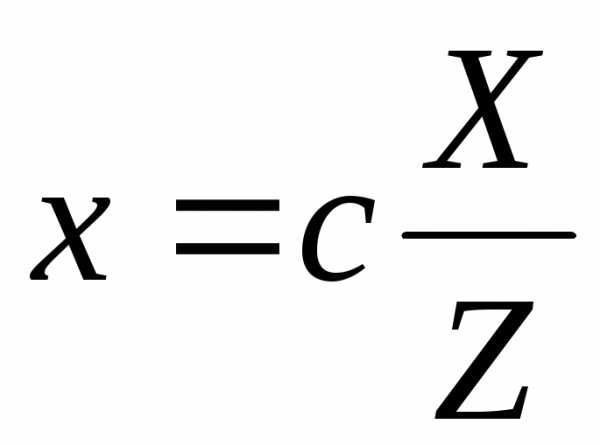 ;
; 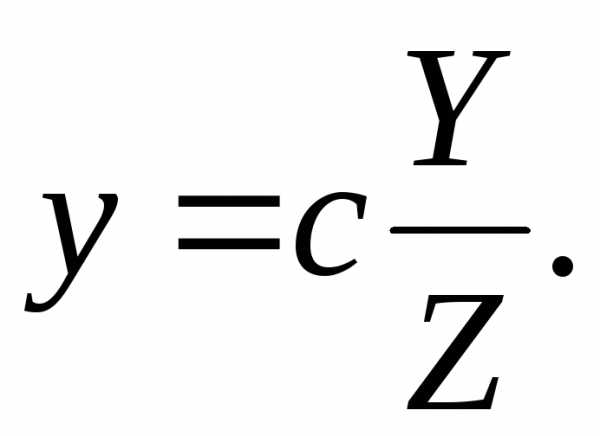
Подставив эти
значения 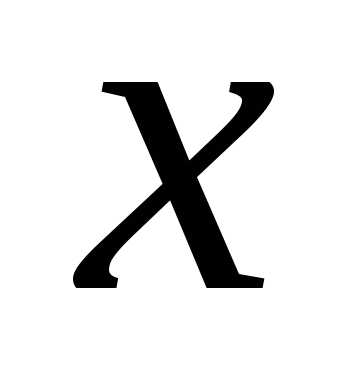 и
и в первое уравнение системы (7.1), будем
иметь:
в первое уравнение системы (7.1), будем
иметь:
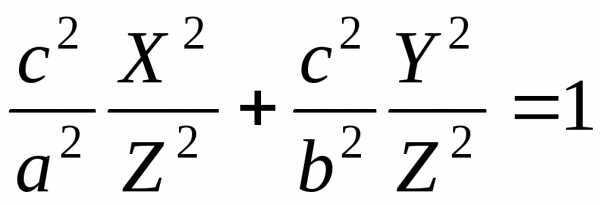 или
или 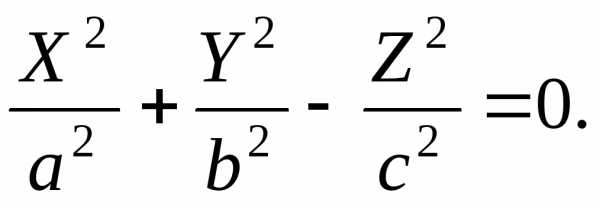
Полученное уравнение определяет конус второго порядка (см. табл. 3)
Задача 7.3. Какую поверхность определяет уравнение
Решение. Эта поверхность есть гиперболический
цилиндр с образующими, параллельными
оси 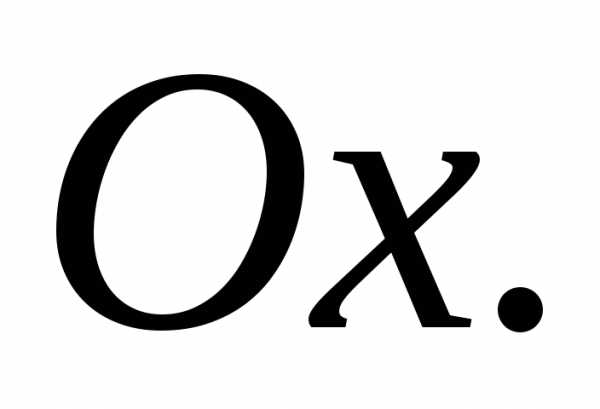 Действительно, данное уравнение не
содержит
Действительно, данное уравнение не
содержит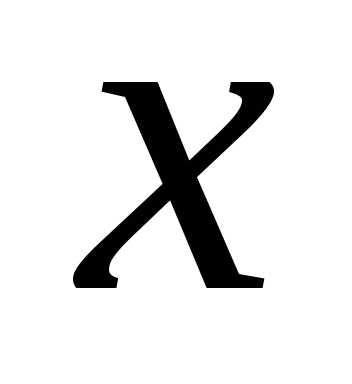 ,
а направляющая цилиндра есть гипербола
,
а направляющая цилиндра есть гипербола
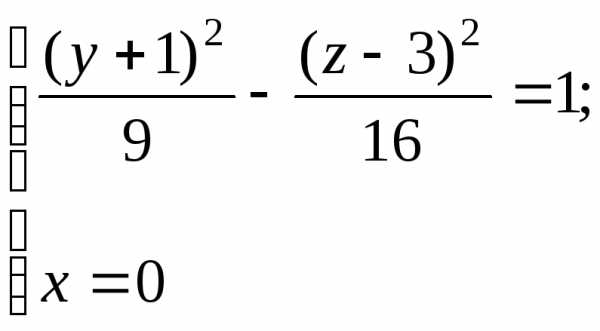
с центром симметрии
в точке 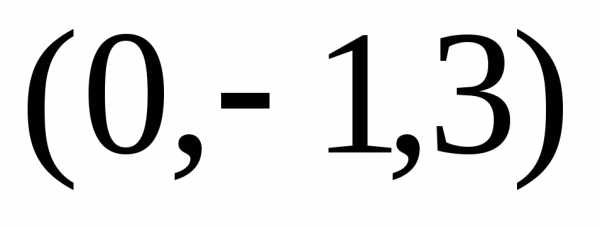 и действительной осью, параллельной
оси
и действительной осью, параллельной
оси .
.
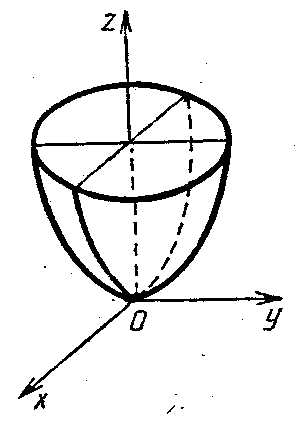
Задача 7.4. Исследовать и построить поверхность, заданную уравнением
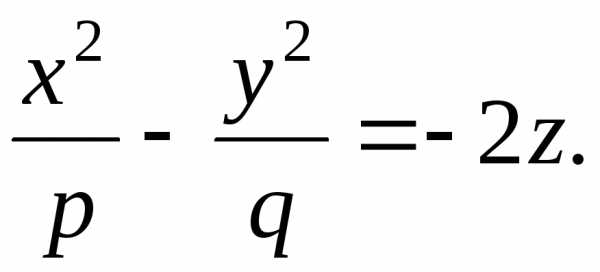
Решение. Пересечем поверхность плоскостью 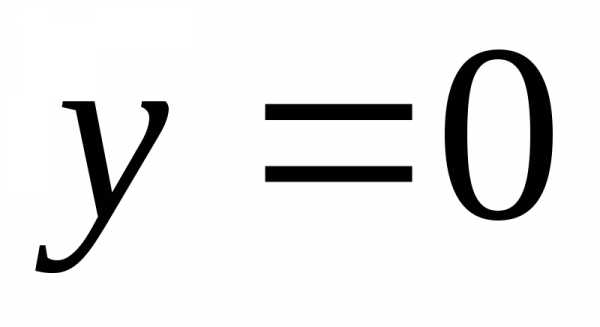 .
В результате имеем
.
В результате имеем

откуда  .
Это уравнение параболы в плоскости
.
Это уравнение параболы в плоскости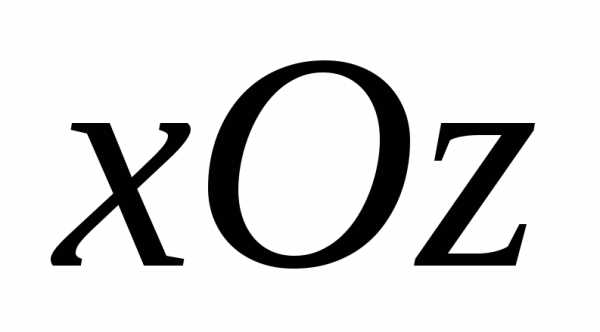
Сечение заданной
поверхности плоскостью 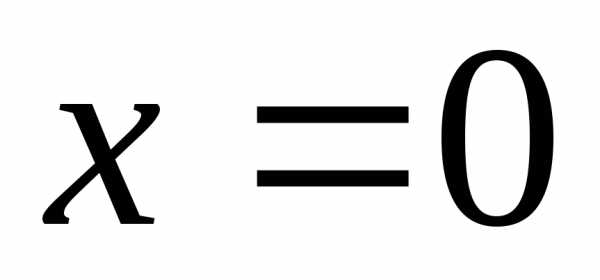 есть парабола
есть парабола
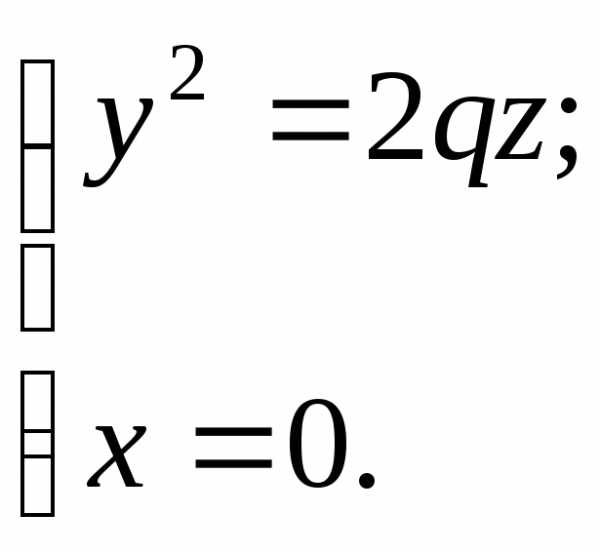
Сечение плоскостью 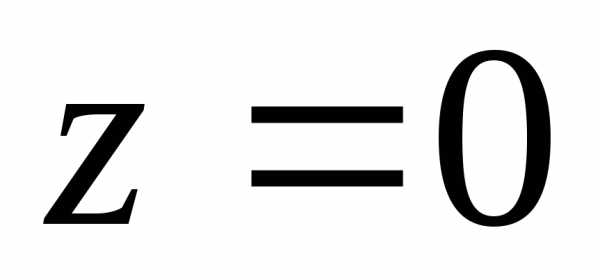 есть пара пересекающихся прямых:
есть пара пересекающихся прямых:
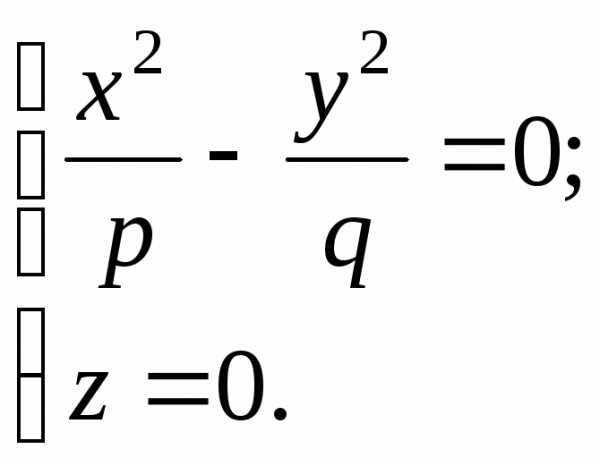
Сечение плоскостями,
параллельными плоскости 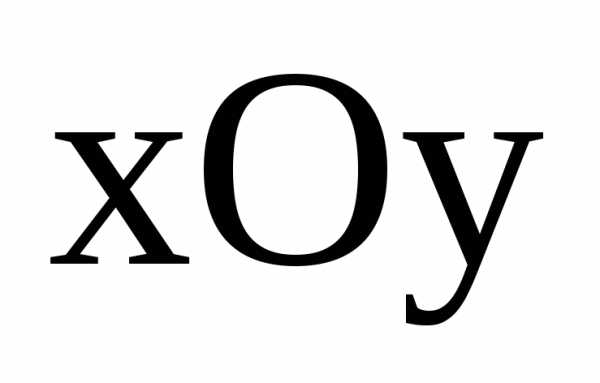 ,
есть гиперболы:
,
есть гиперболы:
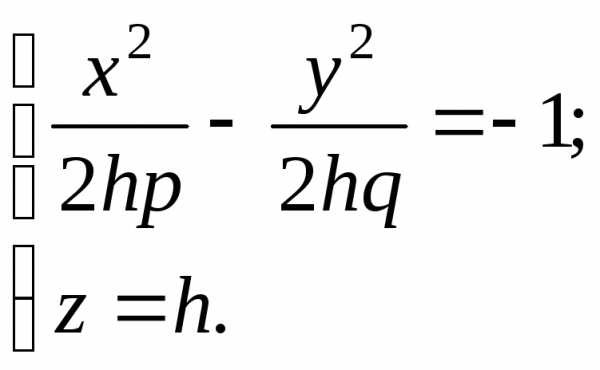
При  действительная ось гиперболы параллельна
оси
действительная ось гиперболы параллельна
оси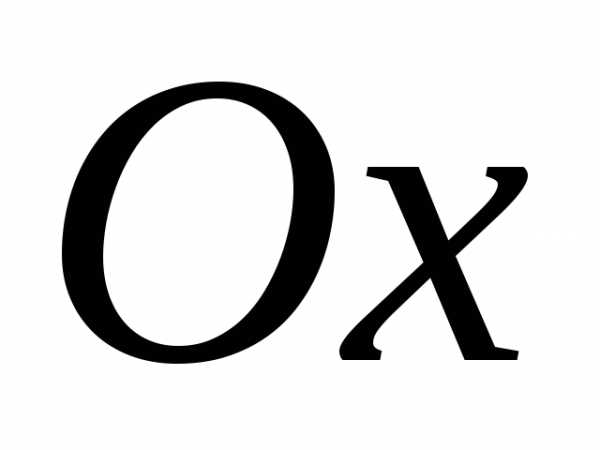 ,
при
,
при оси
оси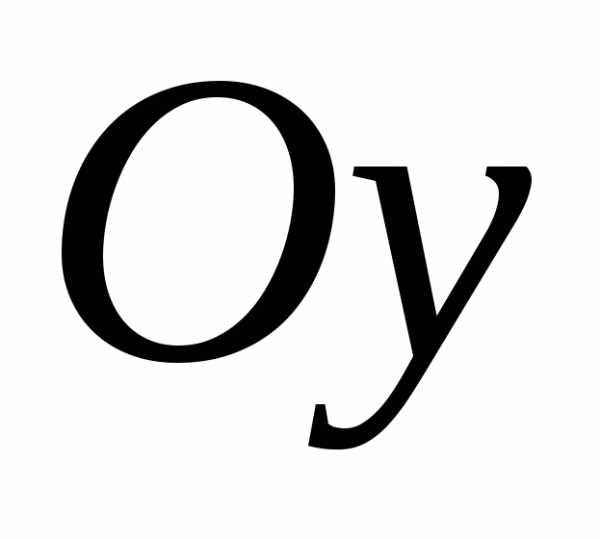 .
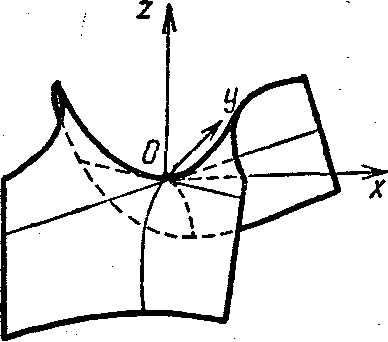
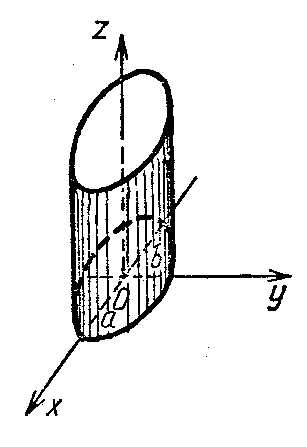
Исследуемая поверхность является
гиперболическим параболоидом (по
ассоциации с формой, поверхность получила
название «седло»).
.
Исследуемая поверхность является
гиперболическим параболоидом (по
ассоциации с формой, поверхность получила
название «седло»).
Замечание. Интересным свойством гиперболического параболоида является наличие прямых линий, лежащих всеми своими точками на его поверхности. Такие прямые называются прямолинейными образующими гиперболического параболоида. Через каждую точку гиперболического параболоида проходят две прямолинейные образующие.
Задача 7.5. Какую поверхность определяет уравнение
Решение. Чтобы привести данное уравнение к
каноническому виду, выделим полные
квадраты переменных 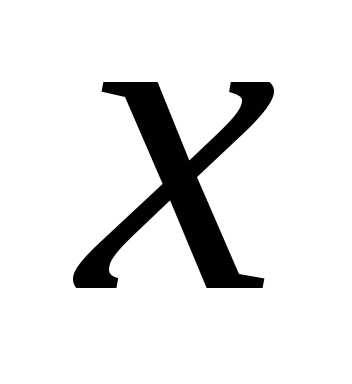 ,
, ,
, :
:
Отсюда
Сравнивая полученное уравнение с табличными (см. табл. 3), видим, что это уравнение однополостного гиперболоида, центр которого смещен в точку Путем параллельного переноса системы координат по формулам
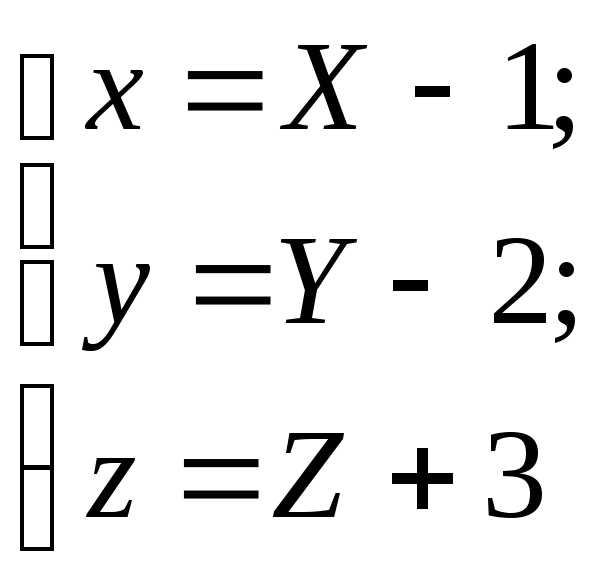
приведем уравнение к каноническому виду:
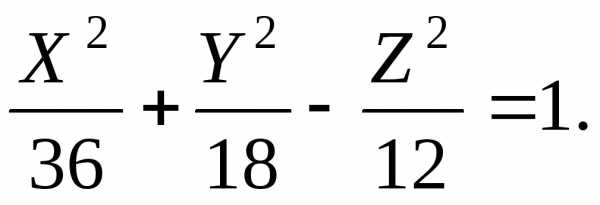
Замечание. Однополостный гиперболоид, как и гиперболический, имеет два семейства прямолинейных образующих.
studfiles.net