Древние системы счисления презентация – «Древние системы счисления. Системы счисления (нумерация) символический метод записи чисел, представление их с помощью письменных знаков.». Скачать бесплатно и без регистрации.
Презентация — Системы счисления
Текст этой презентации
Слайд 1
Тема «Системы счисления»
Слайд 2
Введение
Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами — они с нами везде. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах.
Слайд 3
Система счисления – это определённый способ представления чисел и соответствующие ему правила действия над ними. Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации.
История систем счисления
Системы счисления
Позиционные
Непозиционные
Слайд 4
Древние системы счисления:
Единичная система
Древнегреческая нумерация
Славянская нумерация
Римская нумерация
Слайд 5
Позиционные и непозиционные системы счисления
От положения цифры в записи числа не зависит величина, которую она обозначает. Величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Основание – количество используемых цифр. Позиция – место каждой цифры.
Слайд 6
Запись числа в позиционной системе счисления
Любое целое число в позиционной системе можно записать в форме многочлена: Хs=An · Sn-1 + An-1 · Sn-2 + An-2 · Sn-3 +…+ A2 · S1 + A1 · S0
где S — основание системы счисления, А – цифры числа, записанного в данной системе счисления, n — количество разрядов числа.
Так, например число 629310запишется в форме многочлена следующим образом:
629310=6·103 + 2·102 + 9·101 + 3·100
Слайд 7
Примеры позиционных систем счисления:
Двоичная Система счисления с основанием 2, используются два символа — 0 и 1.
Восьмеричная Система счисления с основанием 8, используются цифры от 0 до 7.
Десятичная Система с основанием 10, наиболее распространённая система счисления в мире.
Шестнадцатеричная С основанием 16, используются цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Шестидесятеричная Система с основанием 60, используется в измерении углов и, в частности, долготы и широты.
Слайд 8
История двоичной системы счисления
Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц. Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл.
В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Слайд 9
Двоичная система счисления
Двоичная система счисления (бинарная система счисления, binary) — позиционная система счисления с основанием 2. Неудобством этой системы счисления является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений.
Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления.
Слайд 10
Сложение, вычитание, умножение и деление в двоичной системе счисления
Сложение Вычитание Умножение Деление
0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10. 0 — 0 = 0;
1 — 0 = 1;
1 — 1 = 0;
10 — 1 = 1. 0 · 1 = 0; 1 · 1 = 1. 0 / 1 = 0; 1 / 1 = 1.
Слайд 11
Двоичное кодирование в компьютере
В конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обраба- тываемая современными ЭВМ, хранится в них в двоичном виде.
В современные компьютеры мы можем вводить текстовую информацию, числовые значения, а также графическую и звуковую информацию. Количество информации, хранящейся в ЭВМ, измеряется ее «длиной» (или «объемом»), которая выражается в битах (от английского binary digit – двоичная цифра).
Слайд 12
Перевод чисел из одной системы счисления в другую
8
16
Слайд 13
Заключение
Высшим достижением древней арифметики является открытие позиционного принципа представления чисел. Нужно признать важность не только самой распространенной системы, которой мы пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами.
Слайд 14
Десятичная Двоичная Восьмеричная Шестнадцатеричная
1 001 1 1
2 010 2 2
3 011 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10
Слайд 15
Перевод двоичного числа в десятичное
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: Х10= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20
Перевод чисел
Слайд 16
Перевод восьмеричного числа в десятичное
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
Х10= Аn·8n-1 + Аn-1·8n-2 + Аn-2·8n-3 +…+А2·81 + А1·80
Перевод чисел
Слайд 17
Перевод шестнадцатеричного числа в десятичное
Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
Х10= Аn·16n-1 + Аn-1·16n-2 + Аn-2·16n-3 +…+А2·161 + А1·160
Слайд 18
Перевод десятичного числа в двоичную систему
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102
Перевод чисел
Слайд 19
Перевод десятичного числа в восьмеричную систему
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 57110 перевести в восьмеричную систему счисления: 57110=10738
Слайд 20
Перевод десятичного числа в шестнадцатеричную систему
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 746710 перевести в шестнадцатеричную систему счисления: 746710=1D2B16
Перевод чисел
Слайд 21
Перевод чисел из двоичной системы в восьмеричную
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоично-восьмеричной таблицей: Пример: Число 10010112 перевести в восьмеричную систему счисления: 001 001 0112=1138
8-ная 0 1 2 3 4 5 6 7
Перевод чисел
Слайд 22
Перевод из двоичной системы в шестнадцатеричную
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр).
Двоично-шестнадцатеричная таблица: Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления:
0010 1110 00112=2E316
2-ная 0000 0001 0010 0011 0100 0101 0110 0111
16-ная 0 1 2 3 4 5 6 7
2-ная 1000 1001 1010 1011 1100 1101 1110 1111
16-ная 8 9 A B C D E F
Перевод чисел
Слайд 23
Перевод восьмеричного числа в двоичное
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример: Число 5318 перевести в двоичную систему счисления:
5318=101 011 0012
2-ная 000 001 010 011 100 101 110 111
Перевод чисел
Слайд 24
Перевод шестнадцатеричного числа в двоичное
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример: Число ЕЕ816 перевести в двоичную систему счисления:
ЕЕ816=1110111010002
2-ная 0000 0001 0010 0011 0100 0101 0110 0111
16-ная 0 1 2 3 4 5 6 7
2-ная 1000 1001 1010 1011 1100 1101 1110 1111
16-ная 8 9 A B C D E F
Перевод чисел
Слайд 25
Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1: Число FEA16 перевести в восьмеричную систему счисления:
FEA16=1111111010102=111 111 101 0102=77528
Пример 2: Число 66358 перевести в шестнадцатеричную систему счисления: 66358=1101100111012=1101 1001 11012=D9D16
Слайд 26
Единичная система
В древние времена, когда появилась потребность в записи чисел, количество предметов, изображалось нанесением черточек или засечек на какой-либо твердой поверхности.
Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.).
В такой системе применялся только один вид знаков – палочка. Каждое число обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу.
Древние системы счисления
Слайд 27
Древнегреческая нумерация
Аттическая нумерация
Ионийская система
В третьем веке до н.э. аттическая нумерация была вытеснена ионийской системой.
В древнейшее время в Греции была распространена аттическая нумерация.
Древние системы счисления
Слайд 28
Славянская нумерация
В России славянская нумерация сохранилась до конца XVII века. Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. Славянская нумерация сохранялась только в богослужебных книгах. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Для обозначения тысяч перед числом (слева внизу) ставился особый знак .
Древние системы счисления
Слайд 29
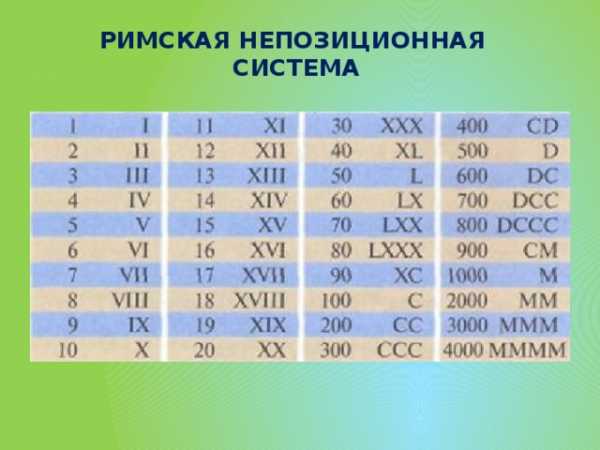
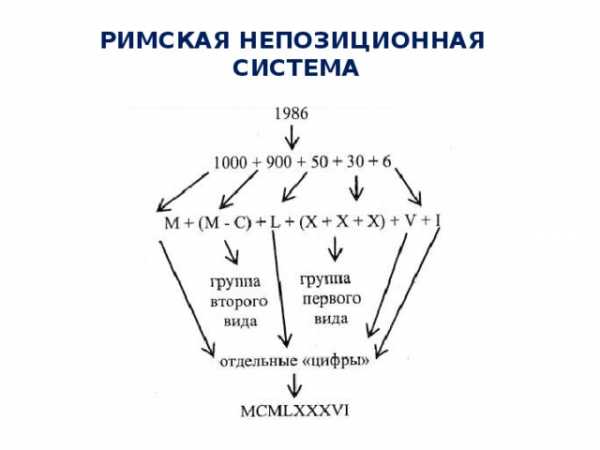
Римская нумерация
Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы пользуемся ей для обозначения веков, юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения.
I — 1 V — 5 X — 10 L — 50 C — 100 D — 500 М — 1000
Запись цифр в римской нумерации:
Древние системы счисления
Слайд 30
Ионийская система
Обозначение чисел в ионийской системе нумерации
Слайд 31
Обозначение чисел в древнеславянской системе нумерации
Славянская нумерация
topslide.ru
Презентация к исследовательской работе по информатике «Системы счисления Древнего мира»
«Все есть число», – говорили пифагорийцы (ученики древнегреческого математика Пифагора). Значит все можно обозначить числом. Так как многие предметы внешнего мира имеет схожую форму, возникла потребность их сосчитать. Например, сколько коров в стаде. Сколько добыто рыб, или зайцев. Т. е. число и арифметика возникли из практической деятельности человека. Так как многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.
Тема нашей исследовательской работы: Системы счисления Древнего мира.
Цели исследования:
Изучение древних систем счисления и выявление применения их в современных сферах деятельности человека.
Для достижения цели были поставлены следующие задачи:
1. Поиск информации о древних системах счисления, как в библиотеке, так и в Интернете.
2. Изучение каждой системы счисления – правил составления чисел в них.
3. Исследование основных сфер деятельности современного человек и выявление связей с древними системами счисления.

Вспомним определение системы счисления. Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.
Ирина, а как ты думаешь для чего нужны были системы счисления?
Система счисления:
даёт возможность представления множества чисел
даёт каждому числу уникальное представление
отражает алгебраическую и арифметическую структуру чисел.
Системы счисления различных народов
1. Древний Египет
Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н. э. ), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. В итоге древние египтяне могли представлять числа до миллиона.
2. Система счисления Вавилона
Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались на солнце или в печи. Эти записи оказались исключительно долговечными, а потому, в отличие от египетских папирусов, дошедших до нас в весьма малом числе экземпляров.
Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта означала единицу; повторенный нужное число раз, этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый коллективный символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку.
3. Система счисления Древней Греции
Аттическая система счисления использовалась греками, по — видимому, уже к 5 в. до н. э. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова «пента” (пять) (буква Г употреблялась для обозначения звука «п”, а не «г”). Дойдя до десяти, они ввели еще один новый символ D, первую букву слова «дека” (десять).
4. Римская система счисления
Легкоузнаваемые, четкие, строгие и ясные обозначения стали весьма удачным изобретением римлян. Бросается в глаза алфавитное обозначение цифр – главная «изюминка» аттической системы. Цифра V (5) – прототип ладони с раскрытыми пятью пальцами. Стало быть, Х (10) – две ладони. Палочками указывали единицы, а для сотен и тысяч предназначены прописные буквы алфавита.
Древнеиндийская система счисления
Сколько бы ни спорили ученые, сколько бы изменений ни претерпевала форма цифр, но возникновение арабских, «наших» цифр приписывают древней Индии. Возможно, арабы позаимствовали древнеиндийскую систему счисления, или изобрели ее сами. Причиной научных мытарств стал фундаментальный математический труд Аль — Хорезми «Об индийском счете». Книга стала своеобразной «рекламой» десятичной позиционной системы. Иначе как объяснить внедрение индийской системы счисления на территории всего Халифата?
Самые распространенные системы счисления
Арабские цифры значительно экономили время и материалы для письма. Один арабский ученый предложил обозначать цифру символом с определенным количеством углов. Количество углов должно равняться значению цифры. Например, «0» — «ничто», углов нет; 1 – 1 угол; 2 – 2 угла и т. д. Слово «цифра» также позаимствовано из арабских языков, где оно звучало как «сыфр», и обозначало «ничто», «пустота». У «сыфр» был синоним – «шунья». На протяжении веков «0» называли именно так. До тех пор, пока не появилось латинское «нуллум» («ничто»), как мы и называем «ноль».
Несмотря на то, что латынь называют «мертвым» языком, ее значимость в научной сфере подтверждена изучением в ВУЗах. Латинские цифры также нашли применение в документоведении, деловодстве, оформлении научных работ. Доступность, понятность и четкость сделали их завсегдатаями учебников и рефератов.
В повседневной жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь одна из многих систем, которая получила свое распространение, вероятно, по той причине, что у человека на руках 10 пальцев. Однако эта система не всегда удобна. Так, в вычислительной технике применяется двоичная система счисления.
В разное время существовали и другие записи цифр, в настоящее время почти забытые. Однако до сих пор мы иногда встречаемся с записью чисел с помощью букв латинского алфавита, например на циферблатах часов, в книгах для обозначения глав или частей, на деловых бумагах для обозначения месяцев и т. д.
В ходе изучения данной темы мы выяснили, что двоичная система счисления намного старше электронных машин. Двоичной системой счисления люди интересуются давно. Особенно сильным это увлечение было с конца 16 до 19 века. Знаменитый Лейбниц считал двоичную систему счисления простой, удобной, красивой. Даже по его просьбе была выбита медаль в честь этой «диадической» системы (так называли тогда двоичную систему счисления). Двоичная система счисления наиболее проста и удобна для автоматизации.
videouroki.net
Презентация по математике на тему «Система счисления древнего мира»
Описание слайда:Рим. Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы. Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Q (или Е, или Д) и f. Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Q и f. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX и XC вместо LXXXX; сравнительно позднее символ IV вместо IIII. Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя еди Интуитивное представление о числе, по-видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только «один», «два» и «много», подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово «три» использовалось только в сочетаниях «три дерева» или «три человека»; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова «один» и «первый», равно как «два» и «второй», во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета «один», «два», «много», слова «три» и «третий», «четыре» и «четвертый» ясно указывают на взаимосвязь между количественными и порядковыми числительными. Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по-видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета. Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово «двадцать три» – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий «два раза по десять и три». Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерения или вычислений использовались основания 12 и 60.
infourok.ru
Презентация на тему: СИСТЕМЫ СЧИСЛЕНИЯ
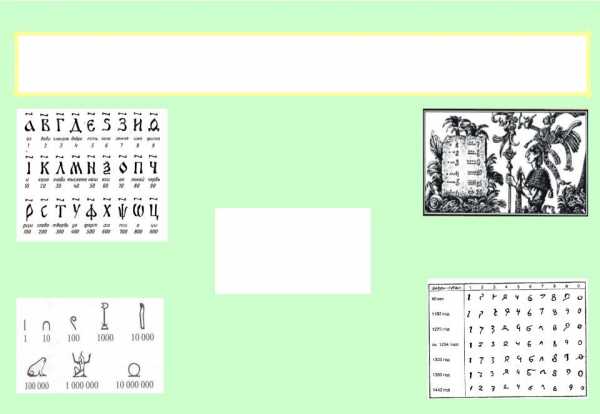
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Древнерусская | Позиционная |
непозиционная | система |
система | счисления |
счисления | Майя |
Все системы счисления делятся на
две группы:
непозиционные и
позиционные
Древнеегипетская | Арабская |
непозиционная | позиционная |
система | система |
счисления | счисления |

ЕДИНИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либозначков (бирок): зарубок, черточек, точек.
Позже значки стали группировать по три или по пять.
Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища).
Отображение количества предметов узелками

ДРЕВНЕЕГИПЕТСКАЯ СИСТЕМА СЧИСЛЕНИЯ
Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.
Все остальные числа составлялись из этих ключевых при помощи операции сложения.
Система счисления Древнего Египта является десятичной, но непозиционной.
Записывались цифры числа начиная с |
|
больших значений и заканчивая | — 1 205 |
меньшими. | |
Если палочек нужно изобразить |
|
несколько, то их изображали в два ряда, |
|
причем в нижнем ряду должно быть | — 1 023 029 |
столько же палочек, сколько и в верхнем, или на одну больше.
Если десятков, единиц, или какого-тодругого разряда не было, то переходили к следующему разряду.

РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
В основе римской системы счисления лежали знаки I (один палец) для числа 1,V (раскрытая ладонь) для числа 5,Х (две сложенные ладони) для 10.
Для обозначения чисел 100, 500 и 1000
применяются первые буквы соответствующих
Календарь на каменной плите, найденный в Риме латинских слов (Centum — сто, Demimille —
половина тысячи, Mille — тысяча).
Число обозначается набором стоящих подряд цифр.
Значение числа определяется как сумма или разность цифр в числе.
Если меньшая цифра стоит слева от большей, то она вычитается, если справа, то прибавляется.
Например, число 1794 будет записано так:MDCCXCIV.

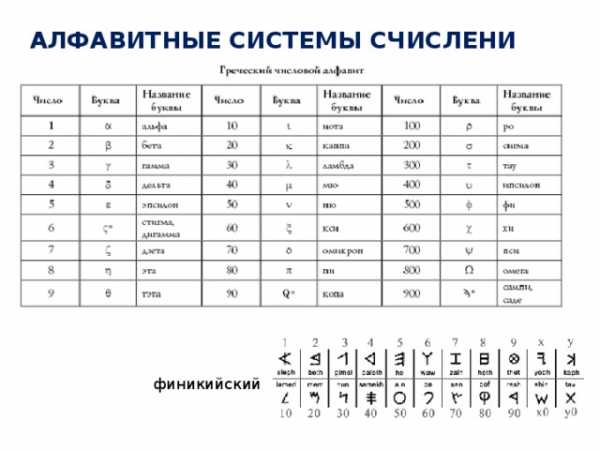
ГРЕЧЕСКАЯ АЛФАВИТНАЯ СИСТЕМА СЧИСЛЕНИЯ
В алфавитной системе счисления Древней Греции числа 1, 2, …, 9 обозначалисьпервыми девятью буквами греческого алфавита (α, β, γ, …).
Для обозначения чисел 10, 20, …, 90 применялись следующие 9 букв(ι, κ, λ,…).
Для обозначения чисел 100, 200, …, 900 – последние 9 букв (ρ, σ, τ,…).
Чтобы не путать числа с буквами, над ними
ставили черточку.
Например, число 141 обозначалосьρμα.
Для обозначения тысяч греки использовали те же буквы, но при их записи слева внизу ставили косую черточку.
Число 10 000 греки называли мириадой.
Таким способом греки могли записать числа до 108. Это число называлось мириада мириад.
Это самое больше число которое называли и записывали греки.

СЛАВЯНСКАЯ АЛФАВИТНАЯ СИСТЕМА СЧИСЛЕНИЯ
Древнерусская алфавитная система счисления, использующая кириллицу
У славянских народов числовые значения букв установились в порядке славянского алфавита, который использовал сначала глаголицу, а затемкириллицу.
Над буквами, обозначающими числа, ставился специальный знак «~» — титло.
Самая высшая из величин называлась «колода» (1050). Считалось, что «боле сего несть человеческому уму разумевати».
В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас.
Славянская нумерация сохранилась только в богослужебных книгах.

НЕДОСТАТКИ НЕПОЗИЦИОННЫХ СИСТЕМ СЧИСЛЕНИЯ
1.Существует постоянная потребность введения новых знаков для записи больших чисел
2.Невозможно представлять дробные и отрицательные числа.
3.Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.

КОМПЬЮТЕРНЫЙ ПРАКТИКУМ
Римская система счисления
studfiles.net
Презентация — Реферат «Системы счисления»
Слайды и текст этой презентации
Слайд 1

Реферат
Тема:«Системы счисления»
Слайд 2
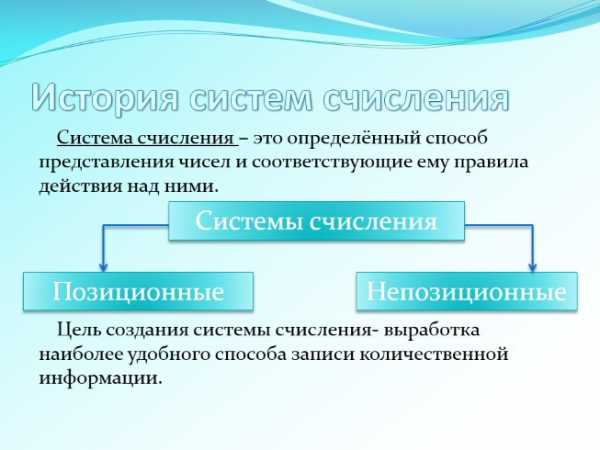
Система счисления – это определённый способ представления чисел и соответствующие ему правила действия над ними.
Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации.
История систем счисления
Системы счисления
Позиционные
Непозиционные
Слайд 3

Древние системы счисления:
Единичная система
Древнегреческая нумерация
Славянская нумерация
Римская нумерация
Слайд 4

Единичная система
В древние времена, когда появилась потребность в записи чисел, количество предметов, изображалось нанесением черточек или засечек на какой-либо твердой поверхности.
Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.).
В такой системе применялся только один вид знаков – палочка. Каждое число обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу.
Древние системы счисления
Слайд 5
 Древнегреческая нумерация
Древнегреческая нумерацияАттическая нумерация
Ионийская система
В третьем веке до н.э. аттическая нумерация была вытеснена
ионийской системой.
В древнейшее время в Греции была распространена аттическая нумерация.
Древние системы счисления
Слайд 6
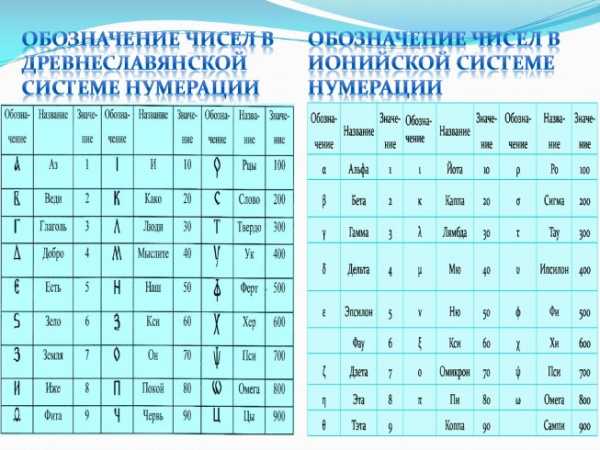
Обозначение чисел в древнеславянской системе нумерации
Обозначение чисел в ионийской системе нумерации
Слайд 7

Славянская нумерация
В России славянская нумерация сохранилась до конца XVII века. Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. Славянская нумерация сохранялась только в богослужебных книгах. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Для обозначения тысяч перед числом (слева внизу) ставился особый знак .
Z
Древние системы счисления
Слайд 8

Римская нумерация
Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы пользуемся ей для обозначения веков, юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения.
I — 1 V — 5 X — 10 L — 50 C — 100 D — 500 М — 1000
Запись цифр в римской нумерации:
Древние системы счисления
Слайд 9

Позиционные и непозиционные системы счисления
Непозиционные системы Позиционные системы
От положения цифры в записи числа не зависит величина, которую она обозначает. Величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Основание – количество используемых цифр.
Позиция – место каждой цифры.
Слайд 10

Запись числа в позиционной системе счисления
Любое целое число в позиционной системе можно записать в форме многочлена:
Хs=An · Sn-1 + An-1 · Sn-2 + An-2 · Sn-3 +…+ A2 · S1 + A1 · S0
где S — основание системы счисления, А – цифры числа, записанного в данной системе счисления, n — количество разрядов числа.
Так, например число 629310запишется в форме многочлена следующим образом:
629310=6·103 + 2·102 + 9·101 + 3·100
Слайд 11

Примеры позиционных систем счисления:
Двоичная Система счисления с основанием 2, используются два символа — 0 и 1.
Восьмеричная Система счисления с основанием 8, используются цифры от 0 до 7.
Десятичная Система с основанием 10, наиболее распространённая система счисления в мире.
Двенадцатеричная Система с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B.
Шестнадцатеричная С основанием 16, используются цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Шестидесятеричная
Система с основанием 60, используется в измерении углов и, в частности, долготы и широты.
Слайд 12

История двоичной системы счисления
Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.).
Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц. Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл.
В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Слайд 13

Двоичная система счисления
Двоичная система счисления (бинарная система счисления, binary) — позиционная система счисления с основанием 2.
Неудобством этой системы счисления является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений.
Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления.
Слайд 14

Сложение, вычитание, умножение и деление в двоичной системе счисления
Сложение Вычитание Умножение Деление
0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10. 0 — 0 = 0;
1 — 0 = 1;
1 — 1 = 0;
10 — 1 = 1. 0 · 1 = 0;
1 · 1 = 1.
0 / 1 = 0;
1 / 1 = 1.
Слайд 15
Перевод чисел из одной системы счисления в другую
8
16
Слайд 16

Перевод двоичного числа в десятичное
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
Х10= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20
Перевод чисел
Слайд 17

Перевод восьмеричного числа в десятичное
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
Х10= Аn·8n-1 + Аn-1·8n-2 + Аn-2·8n-3 +…+А2·81 + А1·80
Перевод чисел
Слайд 18

Перевод шестнадцатеричного числа в десятичное
Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
Х10= Аn·16n-1 + Аn-1·16n-2 + Аn-2·16n-3 +…+А2·161 + А1·160
Перевод чисел
Слайд 19

Перевод десятичного числа в двоичную систему
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102
Перевод чисел
Слайд 20

Перевод десятичного числа в восьмеричную систему
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 57110 перевести в восьмеричную систему счисления: 57110=10738
Перевод чисел
Слайд 21

Перевод десятичного числа в шестнадцатеричную систему
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 746710 перевести в шестнадцатеричную систему счисления: 746710=1D2B16
Перевод чисел
Слайд 22

Перевод чисел из двоичной системы в восьмеричную
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоично-восьмеричной таблицей:
Пример: Число 10010112 перевести в восьмеричную систему счисления:
001 001 0112=1138
2-ная 000 001 010 011 100 101 110 111
8-ная 0 1 2 3 4 5 6 7
Перевод чисел
Слайд 23

Перевод из двоичной системы в шестнадцатеричную
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр).
Двоично-шестнадцатеричная таблица:
Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления:
0010 1110 00112=2E316
2-ная 0000 0001 0010 0011 0100 0101 0110 0111
16-ная 0 1 2 3 4 5 6 7
2-ная 1000 1001 1010 1011 1100 1101 1110 1111
16-ная 8 9 A B C D E F
Перевод чисел
Слайд 24

Перевод восьмеричного числа в двоичное
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример: Число 5318 перевести в двоичную систему счисления:
5318=101 011 0012
2-ная 000 001 010 011 100 101 110 111
8-ная 0 1 2 3 4 5 6 7
Перевод чисел
Слайд 25

Перевод шестнадцатеричного числа в двоичное
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример: Число ЕЕ816 перевести в двоичную систему счисления:
ЕЕ816=1110111010002
2-ная 0000 0001 0010 0011 0100 0101 0110 0111
16-ная 0 1 2 3 4 5 6 7
2-ная 1000 1001 1010 1011 1100 1101 1110 1111
16-ная 8 9 A B C D E F
Перевод чисел
Слайд 26

Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1: Число FEA16 перевести в восьмеричную систему счисления:
FEA16=1111111010102=111 111 101 0102=77528
Пример 2: Число 66358 перевести в шестнадцатеричную систему счисления:
66358=1101100111012=1101 1001 11012=D9D16
Перевод чисел
Слайд 27

Заключение
Высшим достижением древней арифметики является открытие позиционного принципа представления чисел.
Нужно признать важность не только самой распространенной системы, которой мы пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами.
lusana.ru
| Слайд №2 | |
| Содержание Необыкновенная девочка Понятие и история развития систем счисления Позиционные и непозиционные системы счисления 2, 8, 16 системы счисления Перевод чисел в 2, 8, 16 системы счисления Перевод чисел из 2, 8, 16 системы счисления в десятичную Правила преобразования Тест Контрольная работа | |
| Слайд №3 | |
| Необыкновенная девочка Ей было 1100 лет Она в 101 класс ходила В портфеле по 100 книг носила Всё это правда, А не бред Когда пыля 10 ног, Она бежала по дороге За ней всегда бежал щенок С одним хвостом Зато 100 – ногий. И 10 удивлённых глаз Смотрели в этот мир привычно Но станет всё совсем обычно Когда поймете наш рассказ! | |
| Слайд №4 | |
| Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, которые называют цифрами. | |
| Слайд №5 | |
| История развития систем счисления У первобытных народов не существовало развитой системы счисления. Ещё в 19 в. у многих племён Австралии и Полинезии было только два числительных: один и два; сочетания их образовывали числа: 3 — два-один, 4 — два-два, 5 — два-два-один и 6 — два-два-два. О всех числах, больших 6, говорили: “много”, не индивидуализируя их. | |
| Слайд №6 | |
| Египтяне впервые ввели десятичную систему счисления, правда без позиционного обозначения. В развитии математики в государствах ислама получила распространение десятичная позиционная система счисления с применением нуля, ведущая своё происхождение от индийской математики. Возникновение десятичной системы счисления связано со счётом на пальцах. Имелись системы счисления и с другим основанием: 5, 12 (счёт дюжинами), 20 (следы такой системы сохранились во французском языке, например quatre-vingts, то есть буквально четыре-двадцать, означает 80, 40, 60 и др. | |
| Слайд №7 | |
| Вавилонские математики широко пользовались созданной ещё шумерами шестидесятеричной позиционной системой счёта; на основе этой системы были составлены различные вычислительные таблицы: деления и умножения чисел, квадратов и кубов чисел и их корней (квадратных и кубических). | |
| Слайд №8 | |
| Перевод чисел в 2, 8, 16 системы счисления При переводе чисел из десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм: 1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению; 2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P. Перевод чисел из 2, 8, 16 системы счисления. | |
| Слайд №9 | |
| Системы счисления анатомического происхождения Единичная Загнутый палец Десятичная Пальцы обеих рук Пятеричная Пальцы одной руки Двенадцатеричная Фаланги 4 пальцев Двадцатеричная Пальцы рук и ног Алфавитные системы счисления Прочие «Машинные» системы счисления | |
| Слайд №10 | |
| Все системы счисления делятся на две группы Непозиционные Позиционные Единичная Десятичная Алфавитные Двоичная Римская Восьмеричная Древнеегипетская Шестнадцатеричная | |
| Слайд №11 | |
| В непозиционных системах счисления значение (величина) числа определяется как сумма или разность цифр в числе. Недостатки непозиционных систем счисления | |
| Слайд №12 | |
| В позиционных системах счисления значение цифры зависит от ее места (позиции) в числе, а в непозиционных не зависит. В позиционной системе счисления один и тот же числовой символ приобретает различные значения (имеет различный вес) в зависимости от позиции. Каждая позиция соответствует определенной степени основания системы счисления. Основание равно количеству цифр (знаков в алфавите системы счисления) и определяет, во сколько раз отличаются значения одинаковых цифр, стоящих в соседних позициях Достоинства позиционных систем счисления | |
| Слайд №13 | |
| Двоичная система счисления. Двоичная система счисления является основной системой представления информации в памяти компьютера. В этой системе счисления используются цифры: 0, 1. | |
| Слайд №14 | |
| Восьмеричная система счисления. Восьмеричная система счисления является вспомогательной системой представленияинформации в памяти компьютера и используется для компактной записи двоичных чисел и команд. В этой системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7 | |
| Слайд №15 | |
| Шестнадцатиричная система счисления. Шестнадцатеричная система счисления является также как и восьмеричнаявспомогательной системой представления информации в памяти компьютераи используется для компактной записи двоичных чисел и команд. В этой системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Недостающие цифры заменяются буквами: А, В, С, D, E, F. | |
| Слайд №16 | |
| Правила преобразования Для перевода восьмеричного числа в двоичную форму достаточно заменить каждую цифру восьмеричного числа соответствующим трёхразрядным двоичным числом. Таким же образом для перехода от шестнадцатеричной системы к двоичной каждая цифра заменяется соответствующим четырёхразрядным двоичным числом. Для перехода от двоичной системы счисления к восьмеричной (или шестнадцатеричной) системе поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из трёх (четырёх) разрядов заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой. | |
| Слайд №17 | |
| Контрольная работа 1 вариант 1) Что такое система счисления? 2) Чем отличаются позиционные системы счисления от непозиционных, в чем их преимущества? 3) Переведите в десятичную систему счисления: а) 47618; б) A8216; в) 110101002. 4) Переведите число 199810 в системы счисления с основаниями 2, 8, 16. 2вариант 1) Что такое система счисления? 2) Чем отличаются позиционные системы счисления от непозиционных, в чем их преимущества? 3) Переведите в десятичную систему счисления: а) 51428; б) B30516; в) 101101112. 4)Переведите число 156210 в системы счисления с основаниями 2, 8, 16. | |
| Слайд №18 | |
| Спасибо за внимание! Желаю успехов! | |
| Слайд №19 | |
| www//gimn 93.5ballov.ru Н.Угринович Базовый курс.Информатика Н.Угринович Информатика 10 – 11 класс Использованные ресурсы | |
| Слайд №20 | |
| Автор Нигматулина Ирина Юрьевна учитель информатики МОУ СОШ п. Салми | |
volna.org
Презентация по информатике на тему «История систем счисления»

история
(системы счисления)
Плотникова Надежда Михайловна
Плотников Виктор Егорович

Очарование ,
сопровождающее науку,
может победить
свойственное людям
отвращение к
напряжению ума.
Гаспа́р Монж, граф де Пелю́з
(10.5.1746-28.7.1818) —
французский математик,
геометр,
государственный деятель,
морской министр.

наиболее известные нумерации мира
- Древнеегипетская нумерация
- Древнегреческая нумерация
- Вавилонская нумерация
- Нумерация индейцев Майя
- Старо-Китайская нумерация
- Славянская кириллическая нумерация
- Славянская глаголическая нумерация
- Латинская нумерация
- Современная арабская нумерация и др.

- Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, которые называют цифрами.

системы счисления
позиционные
непозиционные

Непозиционные
системы счисления
Непозиционной называют систему счисления, в которой количественное значение цифры не зависит от ее положения в числе.

Позиционные
системы счисления
Позиционной называют систему счисления, в которой количественное значение цифры зависит от ее положения в числе.
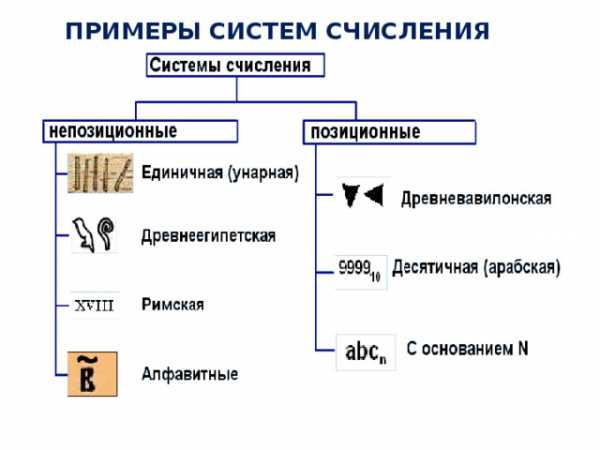
Примеры систем счисления

Примеры систем счисления
- двоичная, восьмеричная, шестнадцатеричная (информатика) двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов) двадцатеричная (1 франк = 20 су) шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
- двоичная, восьмеричная, шестнадцатеричная (информатика)
- двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов)
- двадцатеричная (1 франк = 20 су)
- шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
Единичная непозиционная система счисления
Потребность в записи чисел появилась в очень древние времена, как только люди начали считать. Количество предметов, например овец, изображалось нанесением чёрточек или засечек на какой — либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждой овце в такой записи соответствовала одна чёрточка. Археологами найдены такие «записи» при раскопках культурных слоёв, относящихся к периоду палеолита (10 — 11 тысяч лет до н.э.).
В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки , кружочка , или любой другой фигуры. Числа будут записываться примерно так:
1
2
3
4
5 и т. д.
Такая система счисления использовалась, и до сих пор используется в основном народами, не имеющими письменности.
Учёные назвали этот способ записи чисел единичной («палочной») системой счисления. В ней для записи чисел применялся только один вид знаков — «палочка». Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых и равнялось обозначаемому числу.
Неудобства такой системы записи чисел и ограниченность её применения очевидны: чем большее число надо записать, тем длиннее строка из палочек. Да и при записи большого числа легко ошибиться, нанеся лишнее количество палочек или, наоборот, не дописав их.
Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)

Древнеегипетская десятичная
непозиционная система
Египтяне придумали эту систему около 5 000 лет тому назад. Это одна из древнейших систем записи чисел, известная человеку. В древнеегипетской системе счисления, которая возникла во второй половине третьего тысячелетия до н.э., использовались специальные цифры для обозначения чисел 1, 10, 10 2 , 10 3 , 10 4 , 10 5 , 10 6 , 10 7 . Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз.

Древнеегипетская десятичная
непозиционная система
35 736

Древнеегипетская десятичная
непозиционная система


Вавилонская позиционная
шестидесятеричная система
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр.
Числа составлялись из знаков двух видов:
Единицы – прямой клин
Десятки – лежачий клин
Сотни

Нумерация индейцев Майя
Эта нумерация очень интересна тем, что на ее развитие не повлеяла ни одна из цивилизаций Старого Света. Однако в ней использованы все те же принципы. Сначала эта нумерация обслуживала пятиричную систему счисления, а потом ее приспособили для двадцатиричной.

Нумерация индейцев Майя
Римская непозиционная
система

Римская непозиционная
система
- I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев), X – 10 (две ладони), L – 50, C – 100 ( Centum ), D – 500 ( Demimille ), M – 1000 ( Mille )
Римская непозиционная
система

алфавитные системы счислени
алфавитные системы счислени
финикийский

алфавитные системы счислени


алфавитные системы счислени


Задачи

MDCCLXXXII

MDCCLXXXII =
1000 + 500 + 100 + 100 + 50 + 3*10 + 2 =
1782

На гранитном постаменте памятника Петру I
в Санкт- Петербурге есть римское число:
MDCCLXXXII =
1000 + 500 + 100 + 100 + 50 + 3*10 + 2 =
1782
Это год открытия памятника.

videouroki.net

