Задачи по теме параллельность прямой и плоскости: Решение задач по теме «Параллельность прямых, прямой и плоскости». 10-й класс
Решение задач по теме «Параллельность прямых, прямой и плоскости». 10-й класс
- Степанова Анна Степановна, учитель математики
Разделы: Математика
Класс: 10
Цель урока:
- Знать признак параллельности прямой и плоскости, уметь применять его при решении задач;
- Воспитывать у учащихся точность, аккуратность;
- Развивать логическое мышление учащихся.
Ход урока
1. Организационный момент
2. Актуализация прежних знаний
Один ученик у доски доказывает признак
параллельности прямой и плоскости.
Остальные отвечают на вопросы:
- Какие две прямые в пространстве называются параллельными?
- Сформулируйте теорему о параллельных прямых.
- Какие возможны случаи взаимного расположение прямой и плоскости?
- Какие прямая и плоскость называются параллельными?
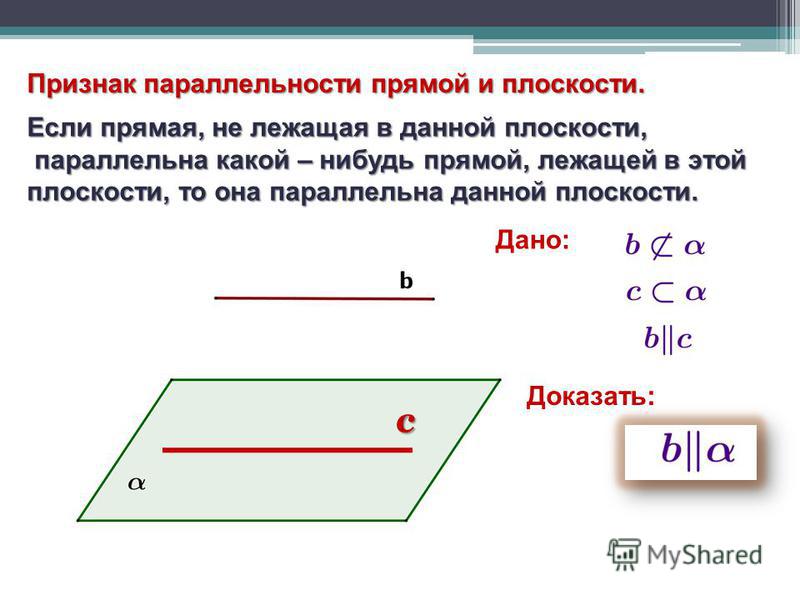
- Сформулируйте признак параллельности прямой и плоскости.
- Дан куб А… D1. Назовите четыре пары параллельных прямых и четыре пары пересекающихся прямых.
Выслушивается доказательство теоремы.
3. Решение задач
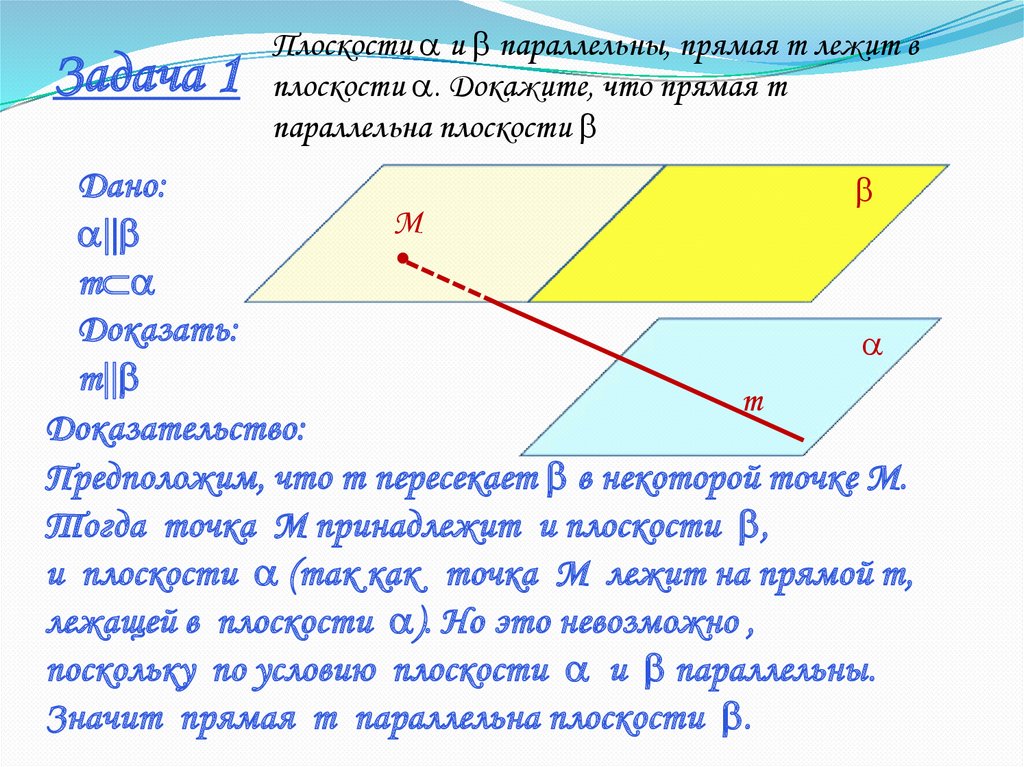
1). Задача 1 (условие и рисунок к задаче записаны на доске или на экране)
Доказательство
МN — средняя линия треугольника АВС, значит МN || АВ, АВ a .
Таким образом, МN || a (по признаку параллельности
прямой и плоскости).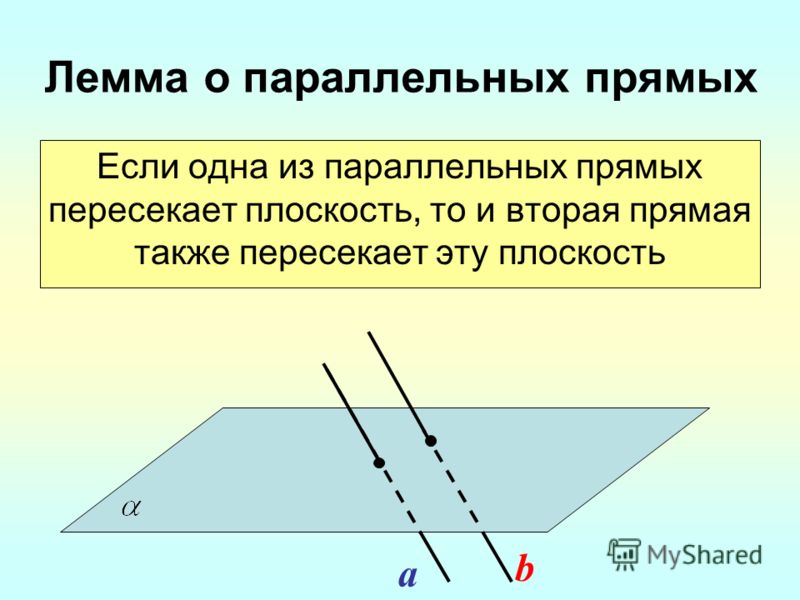
2). Задача 2 (условие и рисунок к задаче записаны на доске или на экране)
Доказательство
МN — средняя линия трапеции АВСD, значит МN || АВ; АВ a (по условию),
Таким образом, МN || a (по признаку параллельности прямой и плоскости).
3). № 26 (Геометрия 10-11, Л.С. Атанасян и др.)
Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны.
Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.
Доказательство
1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).
2. угол В — общий.
З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.
4). № 28 (Геометрия 10-11, Л. С. Атанасян и др.)
С. Атанасян и др.)
На сторонах АВ и АС треугольника АВС взяты соответственно точки D и E так, что ОE = 5 см и ВD = 2/3. Плоскость a проходит через точки B и С и параллельна отрезку ОE. Найдите длину отрезка ВС.
Решение:
Из условия задачи № 26: треугольник АВС подобен треугольнику АDЕ.
Тогда АВ/АD = ВС/DЕ, 5/3 = х/5, х = 25/3, х = 81/3.
Ответ: 81/3.
Подведение итогов урока
Математический диктант
- Какие две прямые в пространстве называются параллельными?
- Cформулируйте теорему о параллельных прямых.
- Какие прямая и плоскость называются параллельными?
- Сформулируйте признак параллельности прямой и плоскости.
- Верно ли утверждение: если одна из двух прямых
параллельна плоскости, а вторая пересекает эту
плоскость, то прямые параллельны.

5. Домашнее задание: №27, № 30, № 31.
Использованная литература
1. Геометрия. 10 класс. Поурочные планы по учебнику Л.С. Атанасян и др. Часть 1 / Сост. Д.Ф. Айвазян — Волгоград: Учитель — АСТ, 2004.
Задачи для урока «Решение задач на параллельность прямых, прямой и плоскости.»(10 класс)
Решение задач на параллельность прямых, прямой и плоскости.
Справедливость утверждений
1. Верно ли, что если две прямые параллельны плоскости, то эти прямые параллельны?
2. Верно ли, что если прямая
3. Верно ли, что если плоскость проходит через прямую,
параллельную другой плоскости, и пересекает эту плоскость, то прямая
пересечения этих плоскостей параллельна данной прямой.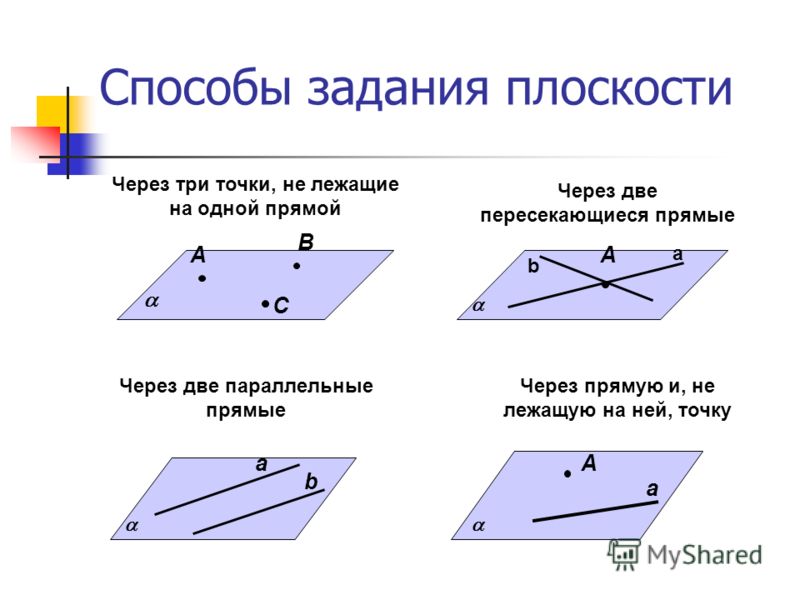
4. Верно ли, что если прямая a перпендикулярна прямой b, перпендикулярной некой плоскости то a параллельна плоскости
Теоремы о параллельности прямой и плоскости
1. Докажите, что если точки A и B лежат в плоскости а точка O — вне ее, то прямая, проходящая через середины отрезков OA и OB, параллельна
2. Докажите, что если плоскость пересекает отрезки и в их серединах, то отрезок параллелен плоскости
3. Докажите, что сечение тетраэдра плоскостью, параллельной ребру и проходящей через середины рёбер и — параллелограмм.
4. Докажите, что плоскость, проходящая через середины рёбер и тетраэдра пересекает его по параллелограмму.
5. Докажите, что если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
6. Докажите, что если из вершин основания тетраэдра в
боковых гранях провести высоты, а затем в каждой из боковых граней основания
двух лежащих в ней высот соединить прямой, то три полученные прямые параллельны
одной плоскости.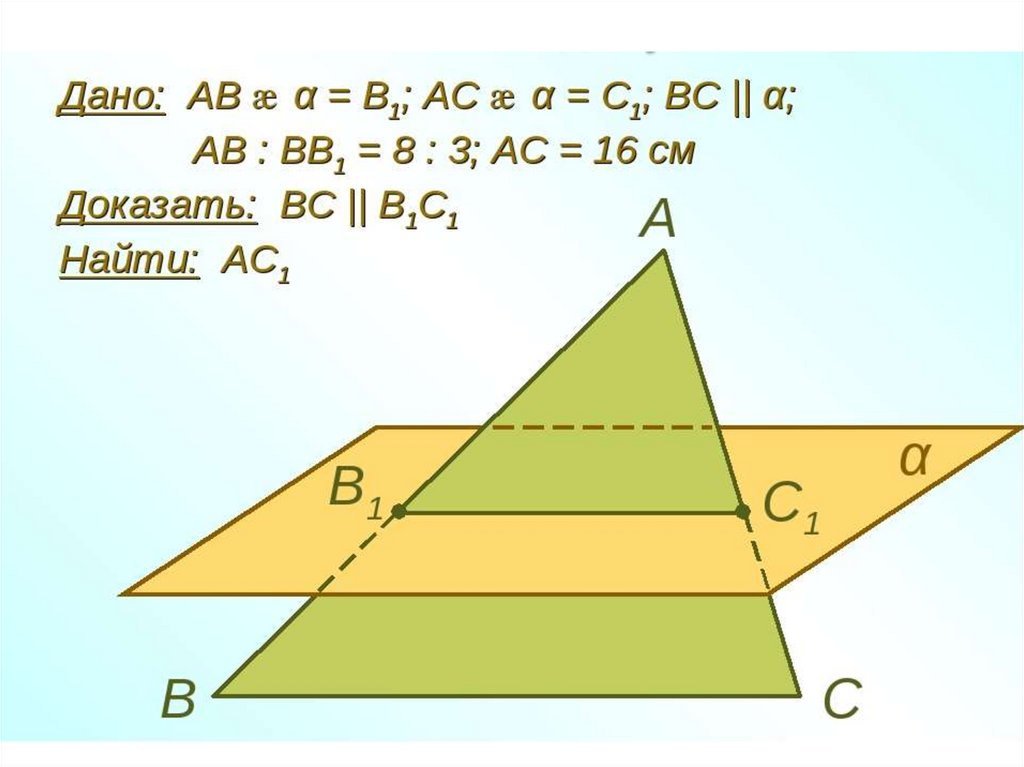
Отрезок и плоскость
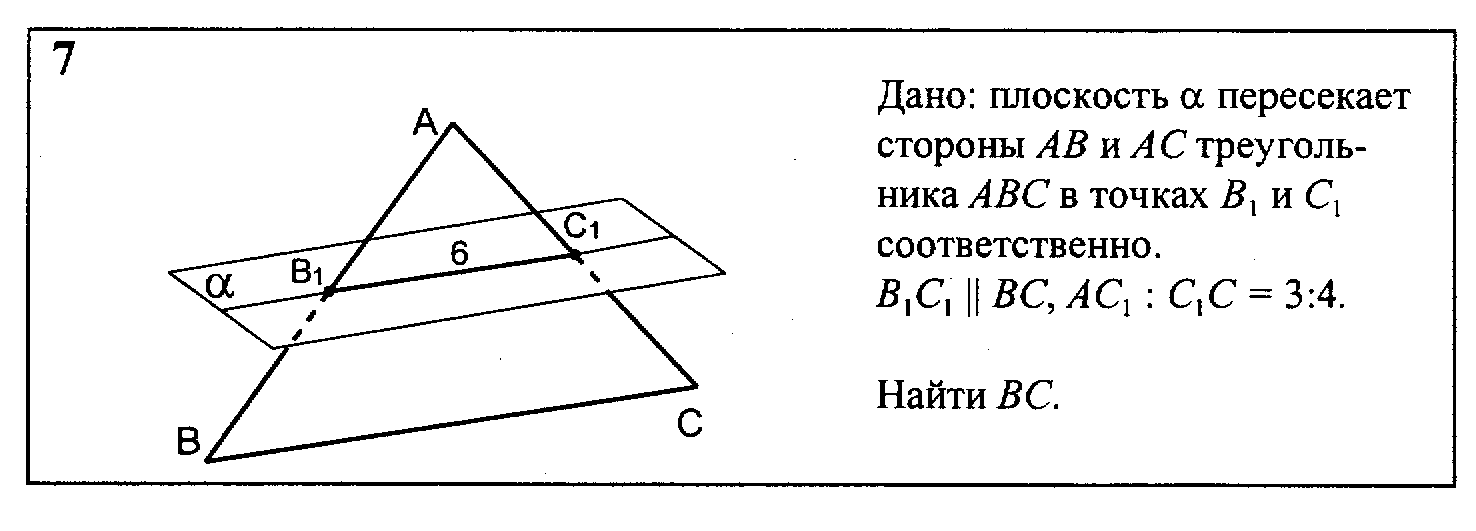
1. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 5, а
2. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 9, а
3. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 6, а
4. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 13, а
5.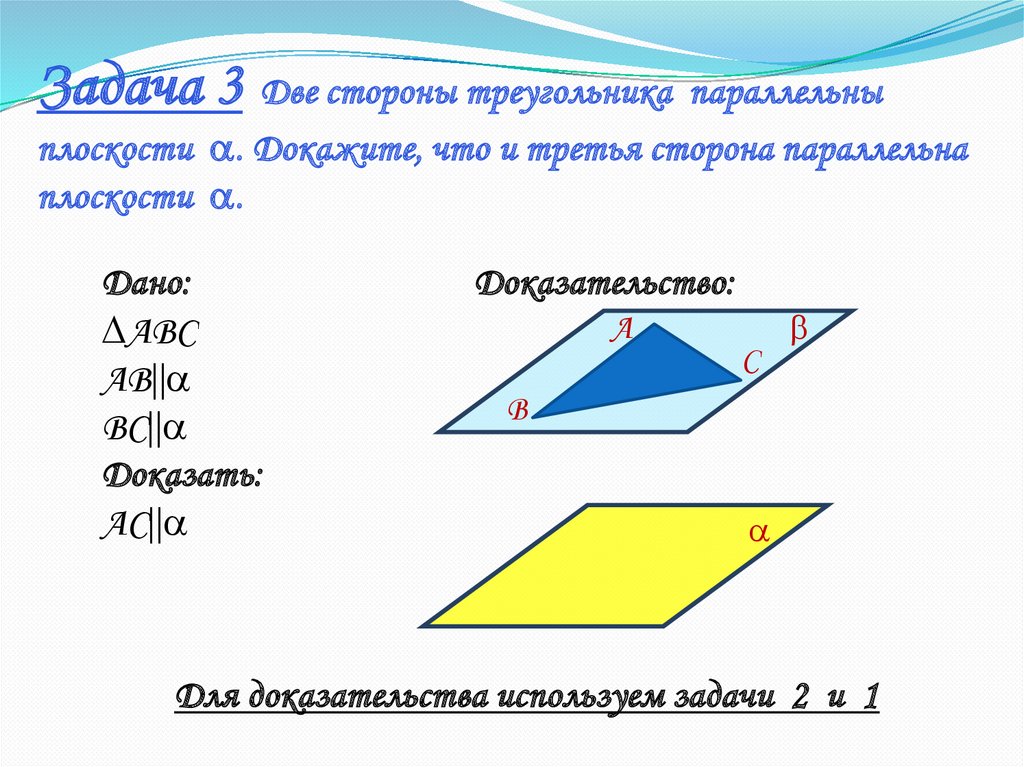 Плоскость проходит
через вершины и треугольника , но
не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты
соответственно точки и так, что
отрезок параллелен плоскости Найдите
отрезок , если = 4, а
Плоскость проходит
через вершины и треугольника , но
не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты
соответственно точки и так, что
отрезок параллелен плоскости Найдите
отрезок , если = 4, а
6. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 7, а
Решение
Справедливость утверждений
1. Верно ли, что если две прямые параллельны плоскости, то эти прямые параллельны?
Решение.
Нет, так как по определению две прямые параллельны, если они лежат в одной плоскости и не пересекаются.
Ответ: Нет.
2. Верно ли, что если прямая а параллельна прямой b, а b параллельна плоскости то a параллельна плоскости
Решение.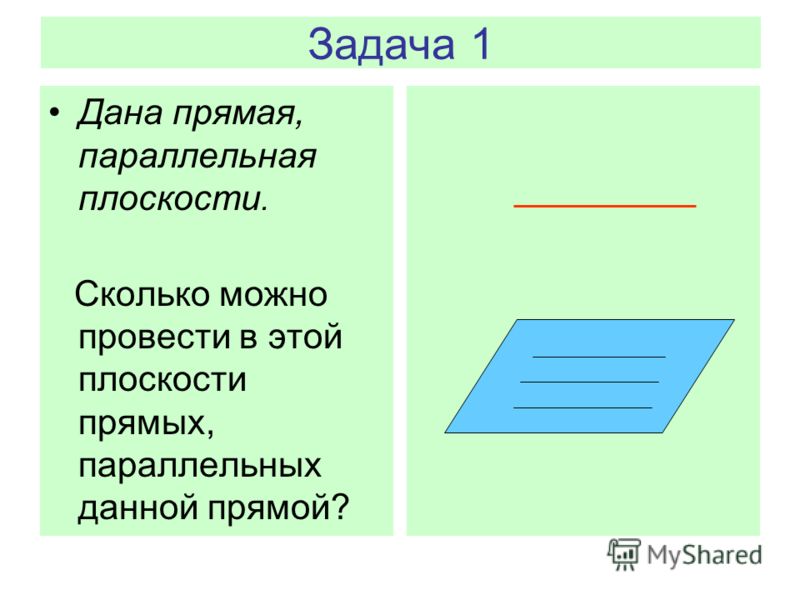
Ответ: Нет.
3. Верно ли, что если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения этих плоскостей параллельна данной прямой.
Решение.
Да, так как по теореме, если плоскость проходит через данную прямую a, параллельную плоскости , и пересекает эту плоскость по прямой b, то .
Ответ: Да.
4. Верно ли, что если прямая a перпендикулярна прямой b, перпендикулярной некой плоскости то a параллельна плоскости
Решение.
Ответ: Нет.
Теоремы о параллельности прямой и плоскости
1. Докажите, что если точки A и B лежат в плоскости а точка O — вне ее, то прямая, проходящая через середины отрезков OA и OB, параллельна
Решение.
Пусть C и D —
середины сторон AO и OB соответственно.
Тогда CD — средняя линия треугольника AOD, откуда
получаем, что CD параллельно AB.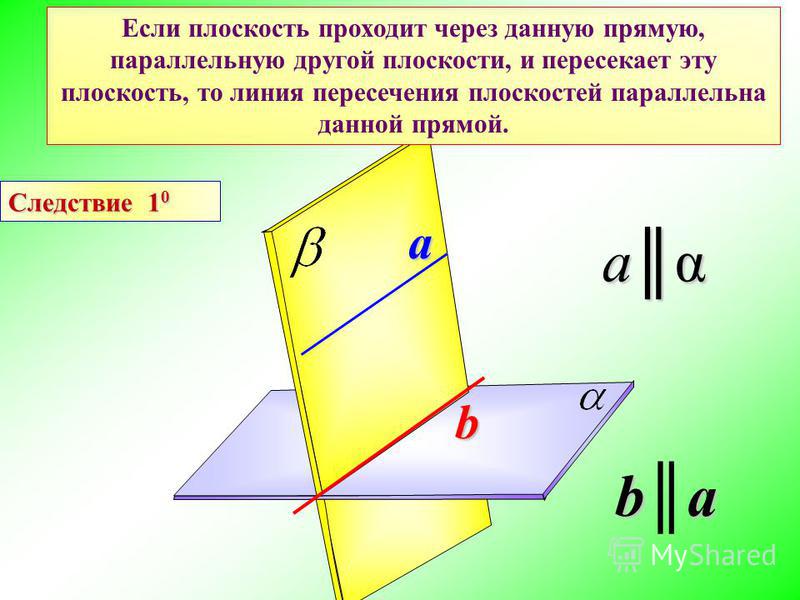 По теореме
прямая CD параллельна плоскости — если
прямая, не лежащая в плоскости, параллельна какой-нибудь прямой. лежащей в
плоскости, то она параллельна всей плоскости.
По теореме
прямая CD параллельна плоскости — если
прямая, не лежащая в плоскости, параллельна какой-нибудь прямой. лежащей в
плоскости, то она параллельна всей плоскости.
2. Докажите, что если плоскость пересекает отрезки и в их серединах, то отрезок параллелен плоскости
3. Докажите, что сечение тетраэдра плоскостью, параллельной ребру и проходящей через середины рёбер и — параллелограмм.
Решение.
Заметим, что G — середина DB по построению. Так как E середина AC по условию, а EF параллельна AD, то F середина DC. Получаем, что EF средняя линия треугольника ADC, EL средняя линия треугольника ABC, LG средняя линия треугольника ABD, EF средняя линия треугольника DCB. Имеем:
Так же FG || CB || EL и LG || AD || EF.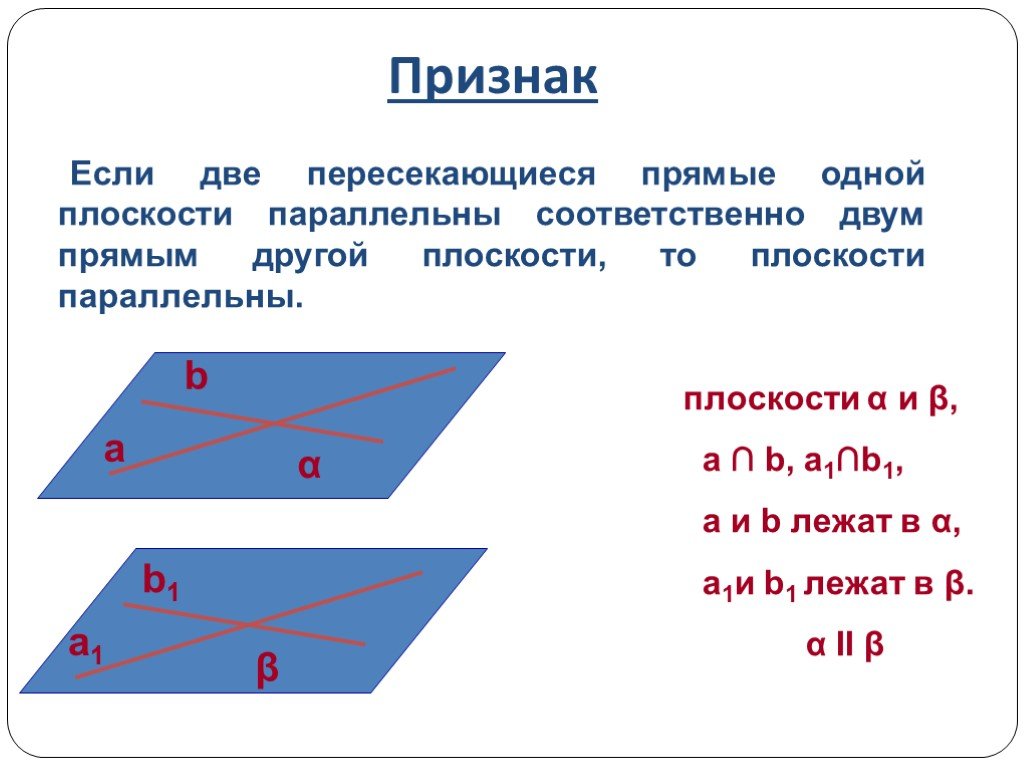 Тогда AFGL — параллелограмм, так как стороны попарно равны и параллельны.
Тогда AFGL — параллелограмм, так как стороны попарно равны и параллельны.
4. Докажите, что плоскость, проходящая через середины рёбер и тетраэдра пересекает его по параллелограмму.
5. Докажите, что если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Решение.
Проведем прямую c, параллельную данной прямой b, которая пересечет плоскость в точке D и прямую в точке C. По теореме прямая DC перпендикулярна плоскости и прямой. Если допустить, что исходная прямая и плоскость не параллельны, то есть имеют хотя бы одну общую точку E, то получим треугольник EDC с двумя прямыми углами при C и D, что невозможно. Тогда прямая a и плоскость параллельны.
6. Докажите,
что если из вершин основания тетраэдра в боковых гранях провести высоты, а
затем в каждой из боковых граней основания двух лежащих в ней высот соединить
прямой, то три полученные прямые параллельны одной плоскости.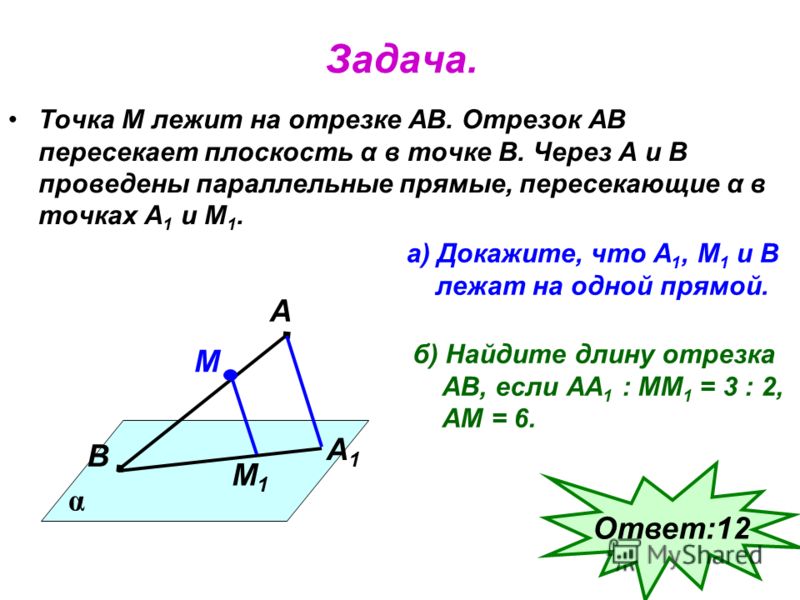
Отрезок и плоскость
1. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 5, а
Решение.
По условию задачи и Так как то
Рассмотрим и
Следовательно, и подобны по двум углам.
Из подобия имеем:
Если то
Подставляем имеющиеся значения:
Ответ: .
2. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 9, а
Решение.
Ответ: .
3. Плоскость проходит через вершины и треугольника ,
но не совпадает с плоскостью этого треугольника.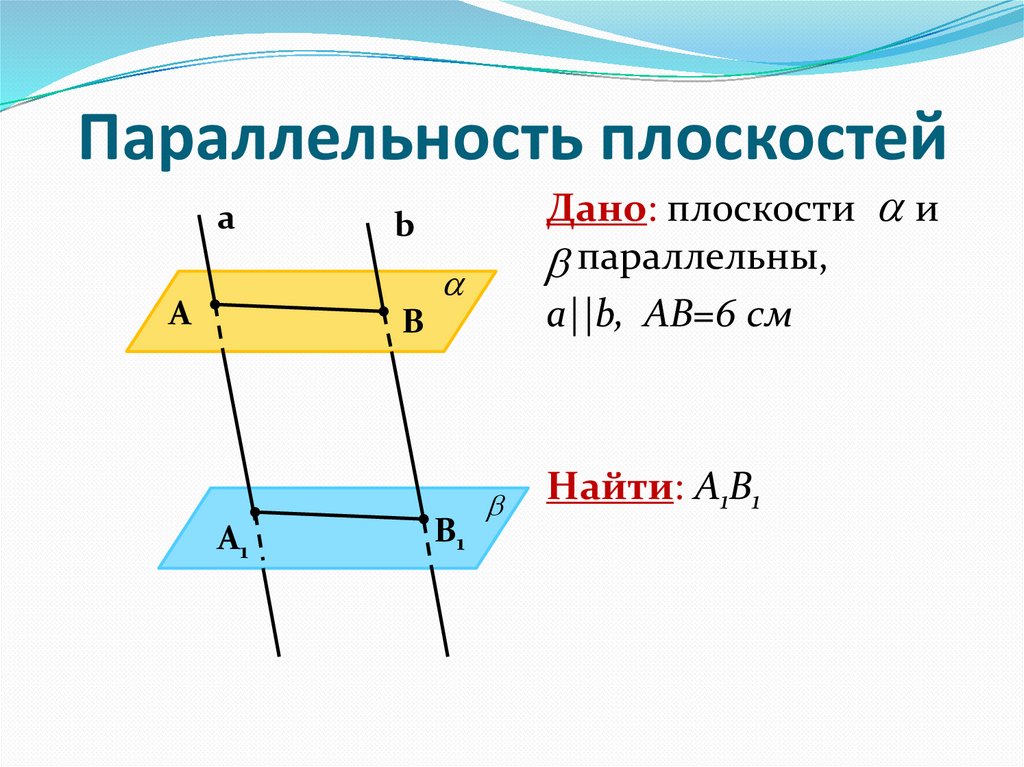 На сторонах треугольника и взяты
соответственно точки и так, что
отрезок параллелен плоскости Найдите отрезок , если =
6, а
На сторонах треугольника и взяты
соответственно точки и так, что
отрезок параллелен плоскости Найдите отрезок , если =
6, а
Решение.
По условию задачи и Так как то
Рассмотрим и
Следовательно, и подобны по двум углам.
Из подобия имеем:
Если то
Подставляем имеющиеся значения:
Ответ: 9.
4. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 13, а
Решение.
Ответ: 60.
5. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 4, а
Решение.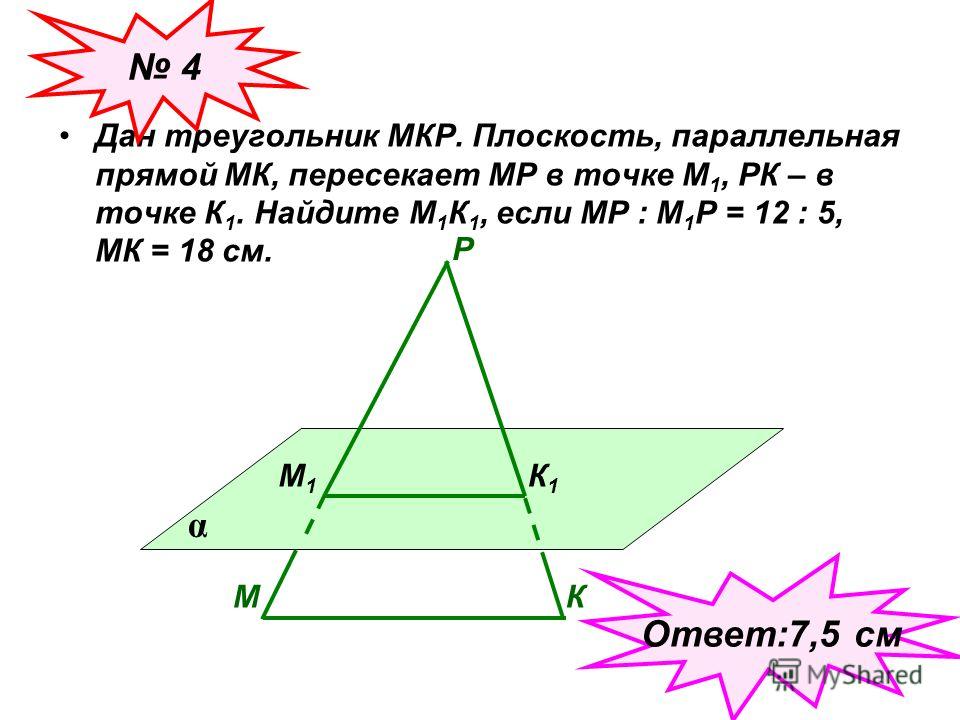
По условию задачи и Так как то
Рассмотрим и
Следовательно, и подобны по двум углам.
Из подобия имеем:
Подставляем имеющиеся значения:
Ответ: 10.
6. Плоскость проходит через вершины и треугольника , но не совпадает с плоскостью этого треугольника. На сторонах треугольника и взяты соответственно точки и так, что отрезок параллелен плоскости Найдите отрезок , если = 7, а
Решение.
Ответ: .
Параллельные и перпендикулярные линии и плоскости
Параллельные и перпендикулярные линии и плоскостиДополнительно
Показать рекламу
Скрыть рекламу
О рекламе
| Это линия: |
Ну, это иллюстрация линии,
, потому что линия не имеет толщины и не имеет концов (продолжается вечно).
| Это самолет: |
Хорошо, иллюстрация плоскости,
потому что плоскость плоская поверхность с без толщины что простирается навсегда .
(Но здесь мы рисуем края только для того, чтобы сделать иллюстрации более четкими.)
Перпендикулярные линии
Две линии перпендикулярны, когда они находятся под прямым углом друг к другу.
Красная линия перпендикулярна синей линии в каждом из следующих примеров:
(Подробнее о перпендикулярных линиях.)
Перпендикулярно плоскости
Линия перпендикулярна плоскости, если она проходит прямо от нее, как карандаш, стоящий на столе.
Если карандаш перпендикулярен линии на столе, то он может быть перпендикулярен столу:
Или может наклоняться над :
две линии (там, где они пересекаются), тогда это перпендикулярно столу:
Он не может указывать ни на что другое, кроме как прямо от стола.
Итак, мы можем сказать так:
Когда прямая перпендикулярна двум прямым на плоскости (в месте их пересечения), она перпендикулярна плоскости . | |
Он также будет перпендикулярен ко всем линиям на плоскости, которые там пересекаются. |
И многое другое, что мы можем сказать:
Через данную точку проходит:
|
| две прямые, перпендикулярные одной плоскости, компланарны (они лежат в одной плоскости — оранжевая) |
| Если это немного сложно понять, представьте себе два карандаша, стоящих на столе: они лежат в одной плоскости (картон): |
Перпендикулярные плоскости
| Плоскость перпендикулярна другой плоскости, если на ней есть линия, перпендикулярная другой плоскости | |
| А когда прямая перпендикулярна плоскости, то каждая плоскость, содержащая эту прямую, перпендикулярна этой плоскости |
Параллельные плоскости
| Когда две плоскости перпендикулярны одной прямой, они являются параллельными плоскостями |
Когда плоскость пересекает две параллельные плоскости , пересечение представляет собой две параллельные линии. |
Copyright © 2017 MathsIsFun.com
уравнений прямых линий: параллельные и перпендикулярные прямые
Slope-Intercept FormPoint-Slope Form
Purplemath
Есть еще одно соображение для уравнений прямых: нахождение параллельных и перпендикулярных линий. Вот общий формат упражнений на эту тему:
Для заданной прямой 2
x − 3 y = 9 и точки (4, −1) найдите прямые в форме пересечения наклона, проходящие через заданную точку, такие, что эти две прямые равны соответственно:
(а) параллельно данной линии, а
(б) перпендикулярно ему.
Мне дали ориентир, а именно 2 x − 3 y = 9; это линия, на наклон которой я буду ссылаться позже в своей работе.
Содержимое продолжается ниже
MathHelp.
 com
comЭта линия имеет некоторое значение наклона (хотя, конечно, не значение «2», потому что это уравнение линии не решено для » y =»).
Сначала мне нужно найти наклон опорной линии. Я мог бы использовать метод двойной подстановки x -значений в опорную линию, находя соответствующие y -значения, а затем подставить две точки, которые я нашел, в формулу наклона, но я бы предпочел просто найти » y =». (Это только мое личное предпочтение. Если ваши предпочтения отличаются, используйте любой метод, который вам больше нравится. .) Итак:
Первым делом я решу «2 x — 3 y = 9″ для » y =», так что я могу найти опорный наклон:
2 x — 3 y = 9
-1 y 9021 2 x + 9
y = ( 2 / 3 ) x − 3
So the reference slope from the reference line is
m = 2 / 3 .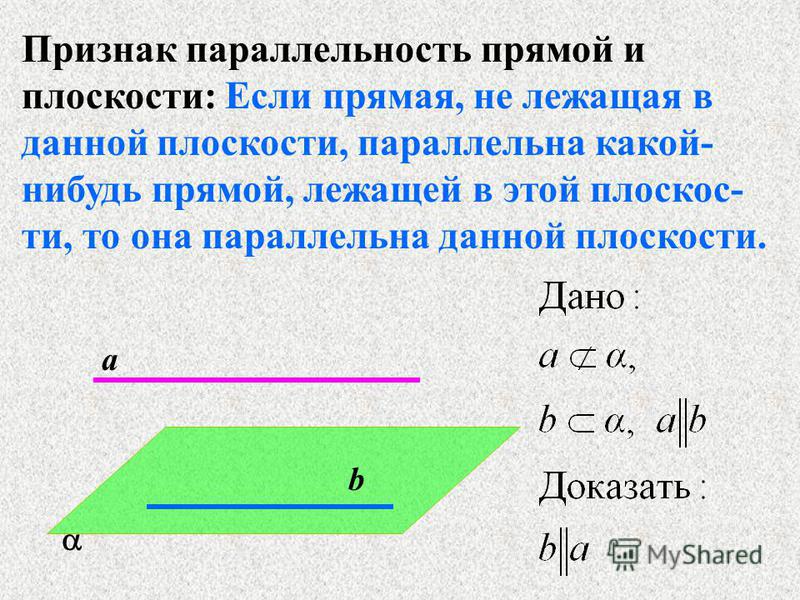
Теперь мне нужно найти два новых склона и использовать их с точкой, которую они мне дали; а именно, с точкой (4, −1). Они хотят, чтобы я нашел прямую через (4, −1), параллельную 2 х — 3 у = 9; то есть через заданную точку они хотят, чтобы я нашел линию, которая имеет тот же наклон, что и исходная линия. Затем они хотят, чтобы я нашел прямую через (4, −1), которая перпендикулярна 2 90 212 x 90 213 − 3 90 212 y 90 213 = 9; то есть через данную точку они хотят, чтобы я нашел линию, имеющую наклон, который является отрицательной обратной величиной наклона базовой линии.
Поскольку параллельная прямая имеет одинаковый наклон, то параллельная прямая, проходящая через (4, −1), будет иметь наклон
м = 2 / 3 . Эй, теперь у меня есть точка и наклон! Поэтому я буду использовать форму точка-наклон, чтобы найти линию:
y — (−1) = ( 2 / 3 ) ( x — 4)
Y + 1 = (9027 270 2
)
)
7)
)
)
7)
)
7)
7)
)
7)
)
7)
7)
7)
7)
)
)
) − 8 / 3
y = ( 2 / 3 ) x − 8 / 3 − 3 / 3
y = ( 2 / 3 ) x − 11 / 3
This is параллельная линия, которую они просили, и она находится в форме пересечения наклона, которую они указали.
Для перпендикулярной линии я должен найти перпендикулярный уклон. Базовый уклон равен
м = 2 / 3 . Для перпендикулярного уклона я переверну эталонный уклон и изменю знак. Тогда перпендикулярный наклон равен м = – 3 / 2 .
Опять же, у меня есть точка и наклон, поэтому я могу использовать форму точка-наклон, чтобы найти свое уравнение. Обратите внимание, что единственное изменение, которое следует из вычислений, которые я только что сделал выше (для параллельной линии), заключается в том, что наклон отличается, теперь он является наклоном перпендикулярной линии.
y − (−1) = ( − 3 / 2 )( x − 4)
Y + 1 = ( — 3 / 2 ) x + 6
y = ( — 3 / 2 ).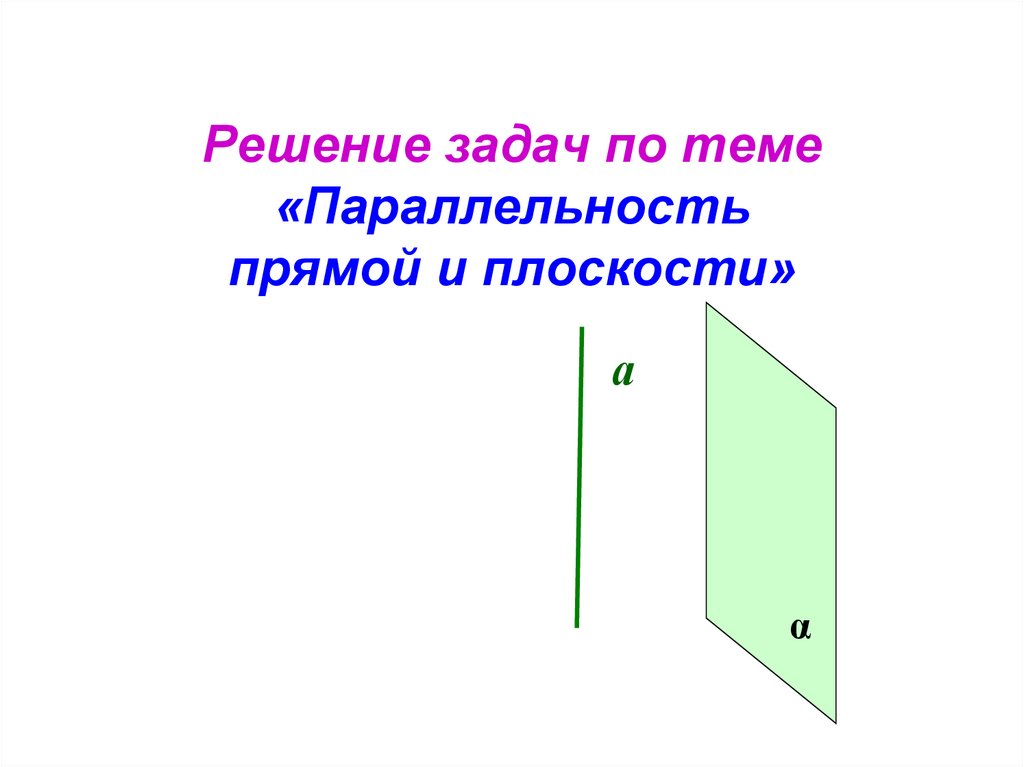 Решение этого упражнения:
Решение этого упражнения:
Параллель:
y = ( 2 / 3 ) x — 11 / 3
. / 2 ) х + 5
Предупреждение: Если вас спросят, являются ли две заданные линии «параллельными, перпендикулярными или ни теми, ни другими», вы должны ответить на этот вопрос, найдя их наклоны, а не рисуя рисунок! Фотографии могут дать вам только приблизительное представление о том, что происходит.
Например, вы бы просто не смогли сказать, просто «взглянув» на картинку, что нарисованные линии с уклонами, скажем, м 1 = 1,00 и м 2 = 0,99 являются НЕ параллельны — и они точно будут черт возьми смотри параллельно на картинке. Но поскольку 1,00 не равно 0,99, прямые не могут быть параллельными.
Другими словами, чтобы ответить на такое упражнение, всегда находите численные наклоны; не пытайтесь просто нарисовать несколько красивых картинок.
Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в поиске параллельной линии, проходящей через заданную точку. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Следующий виджет предназначен для поиска перпендикулярных линий.) Или перейдите к двум сложным примерам, которые следуют ниже.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Щелкнув «Нажмите для просмотра шагов» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.) данная точка. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления. )
)
Почти все упражнения по нахождению уравнений параллельных и перпендикулярных прямых будут аналогичны приведенным ниже. , или точно так же, как тот, что выше. Вот два примера более сложных типов упражнений:
Поскольку наклон представляет собой значение, умноженное на « x », когда уравнение решается для « y =», тогда значение « a » будет значением наклона для перпендикулярной линии. Другими словами, они просят меня указать перпендикулярный наклон, но они немного замаскировали свою цель. Я должен заметить связь.
Первое, что мне нужно сделать, это найти наклон опорной линии. Я решу для « y =»:
(2/3) y − 6 x = 3
2 г − 18 х = 9
г − 9 x = 9/2
y = 9 x + 9/2
. a «, для которого меня попросили) будет отрицательной величиной, обратной эталонному наклону.
a «, для которого меня попросили) будет отрицательной величиной, обратной эталонному наклону.
Я начинаю с преобразования «9» в дробную форму, помещая ее над «1». Затем я переворачиваю и меняю знак. Результат:
a = −1/9
Расстояние между этими двумя линиями может быть только в том случае, если они параллельны. (В противном случае они должны встретиться в какой-то точке, и в этой точке расстояние между прямыми, очевидно, будет равно нулю.) Параллельны ли эти прямые? Я решу каждый за » y =» to be sure:
3 x + 2 y = 15
2 y = −3 x + 15
y 1 = (−3/2) x + 15/2
… и:
4 Y + 6 x = 3
4 Y = –6
4 Y = –621255
4 Y = –6
4 Y = –6
4 Y = –6
4 Y = –60003
4 Y = –60003
4 Y = 3
y = (−6/4) x + 3/4
y 2 = (−3/2) x + 3/4
Линии имеют одинаковый наклон, поэтому они действительно параллельны. И у них разные и -перехваты, так что это не одна и та же линия. Следовательно, между этими двумя линиями действительно есть некоторое расстояние. Но как найти это расстояние? Это будет перпендикулярное расстояние между двумя линиями, но как мне его найти?
И у них разные и -перехваты, так что это не одна и та же линия. Следовательно, между этими двумя линиями действительно есть некоторое расстояние. Но как найти это расстояние? Это будет перпендикулярное расстояние между двумя линиями, но как мне его найти?
Я знаю, что могу найти расстояние между двумя точками; Я подставляю две точки в формулу расстояния. Но у меня нет двух точек. Ах; но я могу выбрать любую точку на одной из прямых, а затем найти перпендикулярную прямую, проходящую через эту точку. Поскольку исходные прямые параллельны, то эта перпендикулярная прямая также перпендикулярна второй из исходных прямых. Тогда я могу найти, где перпендикулярная линия и вторая линия пересекается. Эта точка пересечения будет второй точкой, которая мне понадобится для формулы расстояния.
Я знаю, что эталонный уклон равен
м = −3/2. Тогда мой перпендикулярный уклон будет м = 2/3. Теперь мне нужна точка, через которую я проведу перпендикулярную линию. Я выберу x = 1 и подставлю это в уравнение первой строки, чтобы найти соответствующее значение y :
Я выберу x = 1 и подставлю это в уравнение первой строки, чтобы найти соответствующее значение y :
у = (−3/2)(1) + 15/2
= −3/2 + 15/2
= 12/2 = 6
Итак, моя точка зрения (в первой строке они дал мне) это (1, 6). С помощью этой точки и моего перпендикулярного наклона я могу найти уравнение перпендикулярной линии, которое даст мне расстояние между двумя исходными линиями:
y — 6 = (2/3)( x — 1 )
у — 6 = (2/3) x — 2/3
y = (2/3) x − 2/3 + 18/3
y = (2/3) x + 16/3
3 90; теперь у меня есть уравнение перпендикуляра. Расстоянием будет длина отрезка вдоль этой линии, который пересекает каждую из исходных линий.
Расстоянием будет длина отрезка вдоль этой линии, который пересекает каждую из исходных линий.
Где эта линия пересекает вторую из данных линий? Он будет пересекаться там, где уравнения двух прямых равны, поэтому я приравняю стороны, отличные от y экватора второй исходной линии, и уравнения перпендикулярной линии, и решу:
(-3/2) х + 3/4 = (2/3) х + 16/3
-9 х + 9/2 = 4 х 30 + 16/3
9/2 − 32 = 13 x
(−55/2)/13 = x
x = −55/26
The above more than finishes Линейно-уравнение часть упражнения. Я оставлю остальную часть упражнения для вас, если вам интересно.
(Чтобы закончить, вам нужно подключить последние x -значение в уравнение перпендикулярной линии, чтобы найти соответствующее y -значение.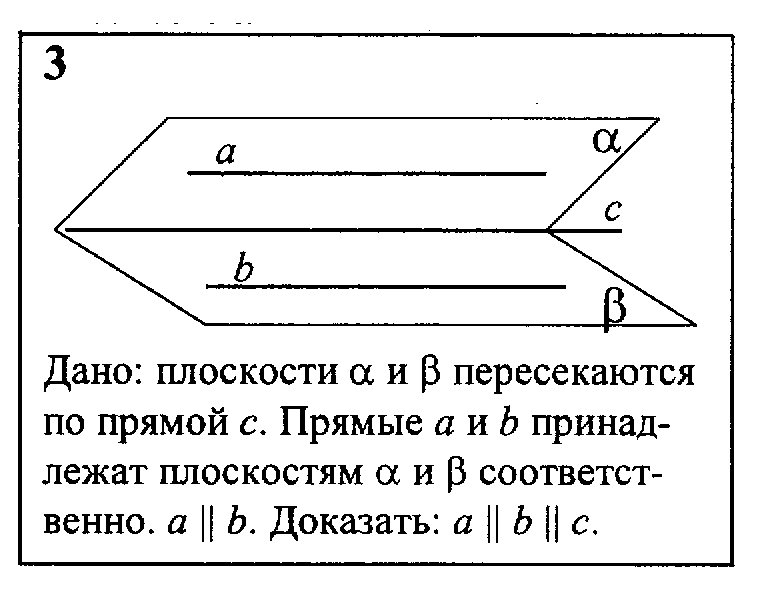 Это даст вам второе очко. [Оказывается,
Это даст вам второе очко. [Оказывается,
(−55/26, 51/13) , если вы посчитаете.] Затем вам нужно будет подставить эту точку вместе с первой (1, 6) в формулу расстояния, чтобы найти расстояние между линиями. [Расстояние оказывается равным (27/26)*кв[13] , или около 3,7442, если разобраться в вычислениях.])
Обратите внимание, что расстояние между линиями , а не совпадает с вертикальным или горизонтальным расстоянием между линиями, поэтому вы можете не использовать точки пересечения x или y в качестве прокси для расстояния.
Что еще более важно, обратите внимание, что в этом упражнении ничего не говорится о параллельных или перпендикулярных прямых и не содержится указания найти какое-либо уравнение прямой. На усмотрение студента оставалось выяснить, какие инструменты могут пригодиться. Не бойтесь таких упражнений.