Имеется 200 грамм сплава содержащего золото и серебро в отношении 2 3: Имеется 200 г сплава содержащего золото и серебро. золото составляет 40 % сплава. сколько г…
Задачи на смеси и сплавы — 4ЕГЭ
26 марта 2022
В закладки
Обсудить
Жалоба
TG 4ЕГЭ
Пробные работы ЕГЭ по математике
Подборка задач для самостоятельной работы.
sm-sp.docx
1. Бронза – сплав меди и олова. В древности из бронзы отливали колокола, если в ней содержалось 75% меди. К куску бронзы 500кг и содержащему 72% добавили некоторое количество бронзы, содержащей 80% меди и получили бронзу, необходимую для изготовления колокола. Определите сколько добавили 80% бронзы.
Ответ: 300кг.
2. В лаборатории изготовили 1кг 16% солевого раствора. Через неделю из этого раствора испарилось 200г воды. Какова стала концентрация соли в растворе?
Ответ: 20%.
3. При выплавке стали из чугуна, выжигается углерод. Содержание углерода в чугуне 4%. Сколько тонн углерода нужно выжечь из 245т чугуна, чтобы получилась сталь с содержанием углерода 2%?
Ответ: 5т.
4. Имеется 600г сплава золота и серебра содержащего золото и серебро в отношении 1:5 соответственно. Сколько грамм золота необходимо добавить к этому сплаву чтобы получить новый сплав содержащий 50% серебра.
Ответ: 400г.
5. Слиток сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди надо добавить к этому куску, чтобы полученный сплав содержал 60% меди?
Ответ: 13,5кг.
6. После смешивания двух растворов, один из которых содержал 48 г, а другой — 20 г безводного йодистого калия, получилось 200 г нового раствора. Найдите концентрацию каждого из первоначальных растворов, если концентрация первого на 15% больше концентрации второго.
Ответ: 40% и 25%.
7. Имелось два слитка меди. Процент содержания меди в первом слитке на 40% меньше, чем во втором. После того как оба слитка сплавили, получился слиток, содержащий 36% меди. Найдите процентное содержание меди в каждом слитке, если в первом было 6 кг меди, а во втором — 12 кг.
Ответ: 20% и 60%.
8. Сколько чистого спирта нужно добавить к 735 г 16%-ного раствора йода и спирта, чтобы получить 10%-ный раствор?
Ответ: 441г.
9. Смешали 30%-ный раствор соляной кислоты с ее 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов 30 % -ного раствора было взято?
Ответ: 150г.
10. В сосуде находится 10%-ный раствор спирта. Из сосуда отлили 1/3 содержимого, а оставшуюся часть долили водой так, что сосуд оказался заполненным на 5/6 первоначального объема. Какое процентное содержание спирта оказалось в сосуде?
Ответ: 8%.
11. Имеются два слитка, состоящие из цинка, меди и олова. Известно, что первый слиток массой 150 кг содержит 40% олова, а второй массой 250 кг — 26% меди. Процентное содержание цинка в обоих слитках одинаково. Сплавив первый и второй слитки, получили сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в полученном сплаве?
Ответ: 170 кг.
12. Имеются два сплава, состоящие из меди, цинка и олова. Известно, что первый сплав содержит 25% цинка, а второй — 50% меди. Процентное содержание олова в первом сплаве в 2 раза меньше, чем во втором. Сплавив 200 кг первого сплава и 300 кг второго, получили новый сплав, в котором оказалось 28% цинка. Определите, сколько килограммов меди содержится в получившемся новом сплаве.
Ответ: 280 кг.
13. Из сосуда, содержащего чистый спирт, отлили 20% содержимого и добавили такое же количество воды. Затем снова отлили 20% содержимого и добавили такое же количество воды. Какое минимальное количество раз надо повторить этот процесс, чтобы содержание спирта в сосуде стало меньше 30%?
Ответ: 6 раз.
14. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра составляет 14 % веса меди. Сколько серебра в данном сплаве?
Ответ: 0,25 кг.
15. Имелись два разных сплава меди, причем процент содержания меди в первом сплаве был на 40% меньше, чем во втором.
После того как их сплавили вместе, получили сплав, содержащий 36% меди. Определите процентное содержание меди в обоих сплавах, если известно, что в первом ее 6 кг, а во втором — вдвое больше.
Ответ: 20% и 60%.
16. Два раствора, первый из которых содержал 800 г, а второй 600 г безводной серной кислоты, смешали и получили 10 кг нового раствора серной кислоты. Определите массу первого и второго растворов, вошедших в смесь, если известно, что процент содержания безводной серной кислоты в первом растворе на 10% больше, чем во втором.
Ответ: 4кг и 6 кг.
17. Морская вода содержит 5% (по весу) соли. Сколько килограммов пресной воды надо прибавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2%?
Ответ: 60 кг.
18. Имеется стальной лом двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 т стали с содержанием 30% никеля?
Ответ: 40т и 100т.
19. Свежие грибы по весу содержат 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 22 кг свежих?
Ответ: 2,5 кг.
20. Имеется сплав серебра с медью. Вычислите вес и пробу этого сплава, если его сплав с 3 кг чистого серебра есть сплав 900-й пробы, а его сплав с 2 кг сплава 900-й пробы есть сплав 840 пробы. (Проба благородного металла, равная например, 760 означает, что масса этого благородного металла в сплаве составляет 0,760 от массы всего сплава.)
Ответ: Вес первоначального сплава 3кг его проба 0,8.
21. Имеются три слитка. Первый весит 5 кг, второй 3 кг и каждый из этих слитков содержит 30% меди. Если первый слиток сплавить с третьим, то получится слиток, содержащий 56% меди, а если второй слиток сплавить с третьим, то получится слиток, содержащий 60% меди. Найдите вес третьего слитка и процент содержания меди в нем.
Ответ: 10кг; 69%
22. Один сплав меди с оловом содержит эти металлы в отношении 2:3, другой — в отношении 3 : 7.
В каком количестве надо взять эти сплавы, чтобы получить 12 кг нового сплава, в котором медь и олово были бы в отношении 3:5?
Ответ: 9кг и 3кг.
23. 40% раствор серной кислоты разбавили 60% раствором, после чего добавили 5кг воды и получили раствор 20% концентрации. Если бы вместо 5кг воды добавили 5 кг 80% раствора серной кислоты, то получился бы 70% раствор. Сколько было 40% и 60% раствора серной кислоты?
Ответ: 1кг 40% и 2кг 60%.
Решение задач на «сплавы», «смеси», «растворы»
Задачи, связанные с понятием “концентрация” и “процентное содержание”,
являются традиционно трудными для обучающихся. В них речь идет о сплавах,
растворах и смесях, которые получаются при сплавлении или смешивании различных
веществ. При решении таких задач принимаются некоторые допущения. Первое: если
смешиваются два раствора, объем которых х и у, то получившаяся
смесь будет иметь объем х +
у. Второе: получившиеся смеси и сплавы имеют однородную консистенцию.
В смесях и растворах содержится некоторый объем чистого вещества. Отношение объема чистого вещества к объему всего раствора называется объемной концентрацией. (Содержание чистого вещества в единице объема).
Концентрация, выраженная в процентах, называется процентным содержанием. При решении таких задач удобно пользоваться таблицей, которая помогает понять задачу и по которой легче составить уравнение или систему. В работе приведены решения нескольких задач, а также предложены задачи для самостоятельного решения. Для удобства к задачам прилагаются ответы.1. Некоторый сплав состоит из двух металлов, входящих в отношении 1 : 2, а другой содержит те же металлы в отношении 2 : 3. Из скольких частей обоих сплавов можно получить третий сплав, содержащий те же металлы в отношении 17 : 27?
Решение: Пусть взято х частей
первого сплава и у частей второго. В х
частях первого сплава содержится
частей первого металла и
частей второго.
В
Составим таблицу:
| В частях | 1 металл | 2 металл | |
| 1 сплав | х частей | частей | частей |
| 2 сплав | у частей | частей | частей |
| 3 сплав | 44 части | 17 частей | 27 частей |
Из таблицы видно, что можно получить три уравнения.
1)
х + у = 44 , 2)
3) . Решив систему из двух уравнений, получим ответ.
Ответ: 9 частей первого сплава и 35 частей второго сплава.
2. Имеется два слитка, представляющие собой сплавы цинка с медью. Масса первого слитка 2 кг, масса второго – 3 кг. Эти два слитка сплавили вместе с 5 кг сплава цинка с медью, в котором цинка было 45 %, и получили сплав цинка с медью, в котором цинка стало 50%. Если бы процентное содержание цинка в первом слитке было бы равно процентному содержанию цинка во втором, а процентное содержание цинка во втором такое же как в первом, то сплавив эти два слитка с 5 кг сплава, в котором содержится 60% цинка, мы бы получили сплав, в котором цинка содержится 55%. Найдите процентное содержание цинка в первом и втором слитках.
Решение: Составим по условию задачи следующую таблицу
| 1 случай | 2 случай | ||||
| масса | Zn (%) | Zn (кг) | Zn (%) | Zn (кг) | |
| 1 сплав | 2кг | х % | 0,02 х кг | у % | 0,02 у кг |
| 2 сплав | 3кг | у % | 0,03 у кг | х % | 0,03 х кг |
| 3 сплав | 5кг | 45% | 2,25 кг | 60% | 3 кг |
| 4 сплав | 10кг | 50% | 5 кг | 55% | 5,5 кг |
По таблице составим систему уравнений
прибавим к первому уравнению второе, получим
Ответ: 40% и 65%.
Имеется два разных сплава меди со свинцом. Если взять 1 кг первого сплава и 1 кг второго сплава и переплавить их, то получится сплав с содержанием 65% меди. Известно, что если взять кусок № 1 и кусок № 2 первого и второго сплавов соответственно, имеющих суммарную массу 7 кг, и переплавить их, то получится сплав с содержанием 60% меди. Какова масса меди, содержащаяся в сплаве, получающемся при совместной переплавке куска первого сплава, равного по массе куску № 2, и куска второго сплава, равного по массе куску № 1?
Решение: Составим по условию задачи следующую таблицу
| 1случай | 2 случай | 3 случай | |||||
| масса | Cu (%) | Cu (кг) | масса | Cu (кг) | масса | Cu (кг) | |
| 1 сплав | 1 кг | n% | 0,01n кг | х кг | 0,01n кг | у кг | 0,01n у кг |
| 2 сплав | 1 кг | m% | 0,01m кг | у кг | 0,01m у кг | х кг | 0,01m х кг |
| 3 сплав | 2 кг | 65% | 1,3 кг | 7 кг | 60% или 4,2 кг | ||
По данным таблицы составим систему уравнений
, найти надо значение выражения 0,01n
у + 0,01m
х.
Представим его в виде 0,01(n у
+ m х).
Решим систему уравнений.
. Умножим первое уравнение на третье и вычтем второе.
Ответ: 4,9 кг.
4. Имеется два слитка сплавов золота и меди. В первом слитке отношение золота к меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с 5/6 второго, то в получившемся слитке окажется столько золота, сколько было бы в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?
Решение: Пусть в первом слитке содержится х кг золота и 2х кг меди. Тогда масса всего слитка 3х кг. Пусть во втором слитке содержится 2у кг золота и 3у кг меди. Тогда масса всего слитка 5у кг. Составим таблицу:
| 1 случай | 2 случай | ||||||
| Масса всего сплава | Масса части сплава | Золото (кг) |
Медь (кг) |
Масса части сплава |
Золото (кг) |
Медь (кг) |
|
| 1 сплав | 3х кг | х кг | 2х кг | ||||
| 2 сплав | 5у кг | 2,5у кг | у кг | 1,5 у кг | |||
| 3 сплав | 2х | (2у + 1) кг | |||||
По данным таблицы составим систему уравнений
Ответ: 1,2 кг и 2,4 кг.
5. Имеется три слитка: первый слиток – сплав меди с никелем, второй – никель с цинком, третий цинка с медью. Если сплавить первый кусок со вторым, то процент меди в получившемся слитке будет в два раза меньше, чем он был в первом слитке. Если сплавить второй слиток с третьим, то процент никеля в получившемся слитке будет в три раза меньше, чем он был во втором слитке. Какой процент цинка будет содержать слиток, получившийся при сплаве всех трех слитков, если во втором слитке было 6% цинка, а в третьем – 11%?
Решение: Заметим, что во втором слитке нет меди, а если его сплавить с первым, в котором есть медь, то процент меди в новом сплаве будет в 2 раза меньше, чем он был в первом слитке, значит масса первого слитка равна массе второго. Пусть их масса будет х.
Если сплавить второй слиток, в котором есть никель, с третьим слитком, в котором
никеля нет, то процент никеля в новом сплаве будет в 3 раза меньше, чем он был
во втором слитке.
Значит второй слиток по массе в 2 раза больше второго. Значит
его масса будет 2х. Занесем данные в
таблицу:
| Масса слитка |
Zn (%) | Zn (масса) | |
| 1 слиток | х | нет | нет |
| 2 слиток | х | 6% | 0,06х |
| 3 слиток | 2х | 11% | 0,22х |
| 4 слиток | 4х | y % | 0,28х |
Ответ: 7%
6. В сосуде находится определенное количество смеси воды с кислотой. Чтобы уменьшить концентрацию кислоты на 34% (было p%, а стало p-34%) в сосуд надо долить 3 л воды, а чтобы уменьшить её на 17%, надо долить 1 л воды. Какова концентрация кислоты в сосуде?
Решение: Составим по условию задачи следующую таблицу:
|
Кол-во смеси |
Кислота в % |
Кислота в литрах |
|
y л |
х% |
0,01xy |
|
(y + 3) л |
(x – 34) % |
0,01(y + 3)(x – 34) |
|
(y +1) л |
(x – 17) % |
0,01(y + 1)(x – 17) |
Если к раствору кислоты добавить чистую воду, то изменится
концентрация кислоты, а количество кислоты не меняется.
На этом основании составим
систему уравнений:
Ответ: 68%.
7. Имеется три слитка золота массой 2 кг, 3 кг и 5 кг с различным процентным содержанием золота. Каждый слиток разделен на три куска и из 9 получившихся кусков получили три слитка массой 2 кг, 3 кг и 5 кг, но уже с равным процентным содержанием золота. На какие части следует разделить каждый слиток, чтобы гарантировать равное процентное содержание золота в получившихся слитках независимо от его содержания в исходных слитках.
Решение: Процентное содержание золота в новых
получившихся слитках 2 кг, 3 кг и 5 кг будет равно процентному содержанию золота в слитке, который
получится если просто сплавить исходные слитки массой 2 кг, 3 кг и 5 кг в
десятикилограммовый кусок. Тогда золото входит в каждый новый слиток в отношении 2 : 3 :
5 . Значит нужно Каждый исходный слиток разделить на части пропорциональные
этим числам. Всего частей 10.
Получим
2 : 10 * 2 = 0,4; 2 : 10 * 3 = 0,6; 2 : 10 * 5 = 1
и т.д. Представим этот результат в виде таблицы.
| Масса слитка | 1часть | 2часть | 3часть | |
| 1 слиток | 2 кг | 0,4 кг | 0,6 кг | 1 кг |
| 2 слиток | 3 кг | 0,6 кг | 0,9 кг | 1,5 кг |
| 3 слиток | 5 кг | 1 кг | 1,5 кг | 2,5 кг |
Задачи для самостоятельного решения
8.
Из трех кусков сплавов меди и никеля с соотношением по массе этих
металлов 2 : 1, 3 : 1, 5 : 1 получили новый сплав. Его масса оказалась равной 12
кг, а соотношение меди и никеля в нем составило 4:1. Найти массу каждого
исходного куска, если первый весил вдвое больше второго.
Ответ: 1,92 кг,
0,96 кг, 9,12 кг.
9. Из трех кусков сплавов серебра и меди с соотношением масс этих металлов 3:2, 2:3, 1:4 получили новый сплав. Его масса оказалась равной 22 кг, а соотношение серебра и меди в нем составило 1:1. Найти массу каждого исходного куска, если второй весил вдвое больше третьего. Ответ: 13,75 кг, 5,5 кг, 2,75 кг.
10. Из трех кусков сплавов олова и свинца с соотношением масс этих металлов
4 : 1, 1 : 1, 1 : 4 получили новый сплав. Его масса оказалась равной 24 кг, а
соотношение олова и свинца в нем составило 2 : 3. Найти массу каждого
исходного куска, если первый весил вдвое больше второго.
Ответ: 6,4 кг, 3,2
кг, 14,4 кг.
11. Из трех кусков сплавов золота и серебра с соотношением масс этих
металлов 1 : 1, 1 : 5, 5 : 1 получили новый сплав. Его масса оказалась равной 24
кг, а соотношение золота и серебра в нем составило 2 : 1. Найти массу каждого
исходного куска, если третий кусок весил втрое больше первого.
12. Имеются два сплава, в одном из которых содержится 20%, в другом 30%
олова. Сколько нужно взять первого и второго сплава, чтобы получить 10 кг
нового сплава, содержащего 27% олова?
Ответ: 3 кг , 7 кг.
13. Имеются два сплава, в одном из которых содержится 40%, а во втором 20%
серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы
получить сплав, содержащий 32% серебра?
14. Имеются два сплава, в одном из которых содержится 10%, а в другом
– 20%
меди. Сколько нужно взять первого и второго сплавов, чтобы получить 15 кг
нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.
15. Имеются два сплава, в одном из которых содержится 30%, а в другом
– 50%
золота. Сколько кг второго сплава нужно добавить к 10 кг первого, чтобы
получить сплав, содержащий 42% золота?
Ответ: 15 кг.
16. Из молока, жирность которого 5%, делают творог, жирностью 0,5%.
Определить, сколько творога получается из 1 тонны молока?
Ответ: 300 кг.
17. При смешивании растворов, содержащих 25% и 60% кислоты, получился
раствор, содержащий 39% кислоты. Определить в какой пропорции были смешаны
растворы?
Ответ: 3 : 2.
18. Добытая руда содержит 21% меди, а обогащенная – 45%. Известно, что в
процессе обогащения 60% добытой руды идет в отходы. Определить процентное
содержание меди в отходах.
Ответ: 5%.
19. В 100 граммов 20%-ного раствора соли добавили 300 граммов ее 10%-ного
раствора. Определить концентрацию полученного раствора.
Ответ: 12,5%.
20. Какое количество воды надо добавить к 100 граммам 70%-ной уксусной
эссенции, чтобы получить 5% раствор уксуса?
Ответ: 1300 гр.
21. Процентное содержание соли в растворе сначала снизилось на 20%, а затем
повысилась на 20%. На сколько процентов изменилось первоначальное содержание
соли?
Ответ: на 4%.
22. Морская вода содержит 5% соли. Сколько килограммов пресной воды надо
добавить к 40 кг морской воды, чтобы содержание соли в последней составляло
2%.
Ответ: 60 кг.
23. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра
составляет
веса меди. Сколько килограммов серебра в данном сплаве?
Ответ: 0,25 кг.
24. Имеется лом стали двух сортов с содержанием никеля 5% и 40% . Сколько
нужно взять каждого из этих сортов металлолома, чтобы получить 140т стали с
содержанием никеля 30%.
Ответ: 40 т и 100 т.
25. Кусок сплава меди с оловом весом 2 кг содержит 45% меди. Сколько чистого
олова надо прибавить к этому куску, чтобы получившийся новый сплав имел 40%
меди?
Ответ: 1,5 кг.
26. Сколько чистого спирта надо прибавить к 735 г 16%-ного раствора йода в
спирте, чтобы получить 10%-ный раствор?
Ответ: 441 г.
27. Сплав из меди и цинка весом в 24 кг при погружении в воду потерял в
своем весе
Определить количество меди и цинка в этом сплаве, если известно, что медь
теряет в воде
своего веса, а цинк
своего веса.
Ответ: 17 кг и 7 кг.
28. Имеются два сплава золота и серебра. В одном количество этих металлов
находится в отношении 2 : 3, а в другом в отношении 3 : 7. Сколько нужно взять
от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и
серебро были бы в отношении 5 : 11?
Ответ: 1 кг, 7 кг.
29. Одна бочка содержит смесь спирта с водой в отношении 2 : 3, а другая в
отношении 3 : 7. По сколько ведер надо взять из каждой бочки, чтобы составить
12 ведер смеси, в которой спирт и вода были бы в отношении 3 : 5?
Ответ: 9
ведер из первой и 3 ведра из второй.
30. Два раствора, из которых первый содержал 800 г безводной серной кислоты,
а второй 600 г безводной серной кислоты, соединили вместе и получили 10 кг
нового раствора серной кислоты. Определить вес первого и второго растворов,
вошедших в смесь, если известно, что процент содержания безводной серной
кислоты в первом растворе на 10% больше, чем процент содержания безводной
серной кислоты во втором.
Ответ: 4 кг и 6 кг.
31. Имелось два разных сплава меди. Процент содержания меди в первом сплаве
был на 40 меньше, чем процент содержания меди во втором сплаве. После того
как их сплавили вместе, получили сплав, содержащий 36% меди. Определить
процентное содержание меди в первом и втором сплавах, если известно,
содержание меди в первом сплаве было 6 кг, а во втором 12 кг.
Ответ: 20% и
60%.
32. 36 г цинка в воде весят 31 г, а 23 г свинца в воде весят 21 г. Сплав
цинка и свинца массой 292 г в воде весит 261 г.
Сколько цинка и сколько
свинца содержится в сплаве?
Ответ: 108 г цинка и 184 г свинца.
33. В двух одинаковых сосудах, объемом по 30 л каждый, содержится всего 30 л
кислоты. Первый сосуд доливают доверху водой и полученной смесью дополняют
второй сосуд, затем из второго сосуда отливают в первый 12 литров смеси.
Сколько кислоты было первоначально в первом сосуде, если во втором сосуде
после переливаний оказалось на 2 л меньше кислоты, чем в первом?
Ответ: 20
литров.
34. Имеется два слитка сплавов золота и меди. В первом слитке отношение
золота к меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с
5/6 второго, то в получившемся слитке окажется столько золота, сколько было
бы в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то
в получившемся слитке окажется меди на 1 кг больше, чем было золота во
втором слитке. Сколько золота в каждом слитке?
Ответ: 1,2 кг и 2,4 кг.
35. Имеется два сосуда. В одном содержится три литра 100%-ной серной
кислоты, а в другом два литра воды. Из первого сосуда во второй перелили
один стакан кислоты, а затем из второго в первый – один стакан смеси. Эту
операцию повторили еще два раза. В результате во втором сосуде образовалась
42%-ная кислота. Сколько серной кислоты в процентах содержится теперь в
первом сосуде?
Ответ: 72%.
36. Имеется два куска металла массой 1 кг и 2 кг. Из этих кусков сделали два
других: первый массой 0,5 кг, содержащий 40% меди, а второй массой 2,5 кг,
содержащий 88% меди. Каково процентное содержание меди в исходных кусках?
Ответ: 40% и 100%.
37. Из колбы в пробирку отлили
раствора соли. Раствор в пробирке выпаривали, пока процентное содержание
соли в нем не увеличилось в два раза. Получившийся раствор вернули в колбу, что
увеличило процентное содержание соли в находившемся в колбе растворе на 2 %.
Какое процентное содержание соли было в растворе первоначально?
Ответ: 10%.
Литература:
- Шарыгин И.Ф. “Математика для поступающих в ВУЗы”. Москва, Дрофа, 2000 г.
- Сканави М.И. “2500 задач по математике для поступающих в ВУЗы”. Москва, Оникс, 2003 г.
- Черкасов О., Якушев А. “Математика”. Москва, Айрис, 2000 г.
- Белоносов В.С., Фокин М.В. “Задачи вступительных экзаменов по математике.” Новосибирск, издательство НГУ, 1995 г.
Коэффициенты пересчета и золотые украшения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50025
- Эд Витц, Джон В.
Мур, Джастин Шорб, Ксавье Прат-Ресина, Тим Вендорф и Адам Хан - Цифровая библиотека химического образования (ChemEd DL)
Мур, Джастин Шорб, Ксавье Прат-Ресина, Тим Вендорф и Адам Хан Ранее мы показали, как использовать коэффициенты единства. можно использовать для выражения величин в разных единицах одного и того же параметра. Например, плотность может быть выражена в г/см 3 или в фунтах/футах 3 . Теперь мы также рассмотрим, как можно использовать коэффициента преобразования , представляющие математические функции, такие как D = m/v, для преобразования величин в различные параметры. Например, что такое том данной массы золота, и какова его стоимость в долларах? Стоимость золота изменчива, а текущая стоимость указана в Интернете. Единичные коэффициенты и коэффициенты преобразования концептуально различны, и мы увидим, что «анализ размерностей», который мы разрабатываем для задач преобразования единиц измерения, должен использоваться с осторожностью в случае функций.
Когда мы говорим об одном и том же объекте или образце материала, часто полезно иметь возможность преобразовать один параметр в другой. Преобразование одного вида величины в другой обычно выполняется с помощью того, что можно назвать коэффициентом преобразования , но коэффициент преобразования основан на математической функции (D = m / V) или математическом уравнении, связывающем параметры. Плотность и стоимость золота зависят от его значения «карат», которое является мерой того, сколько частей в 24 (по массе) составляет чистое золото. 24-каратное золото — это 24/24 (чистое) золото, а 14-каратное золото — это 14/24 (58%) золото.
Ювелиры традиционно выражают массу золота в DWT (пеннивейт), архаичной единице массы, равной 24 гранам, 1/240 тройского фунта, 1/20 тройской унции, примерно 0,055 унции или примерно 1,555 грамма.
Карат не следует путать с каратом (написание различается во всем мире), который является мерой веса ювелиров, первоначально использовавшейся для описания бриллиантов.
Одна каррата составляет 200 миллиграммов, т.е. одну пятую часть грамма.
| Караты | ‰ Содержание золота | Комментарий | Плотность, г/см 3 |
|---|---|---|---|
| 24 | 99,9 | 99,0% Минимум допустимый | 19,3 |
| 22 | 91,6 | Индийский субконтинент | 15,6 |
| 21 | 87,5 | арабских стран | |
| 18 | 75,0 | 75 % Au, 16 % Ag и 9 % Cu [1] | |
| 14 | 58,5 | 58,5 % Au, 4,0 % Ag, 31,2 % Cu и 6,3 % Zn | 12,9 — 14,6 |
| 10 | 41,7 | Минимум в США | |
| 9 | 37,5 | Стандарт Великобритании | |
| 8 | 33,3 |
Поскольку металлы, сплавляемые с золотом для получения, например, 10- или 14-каратного золота, весьма разнообразны, плотность сплава также сильно различается.
Предположим, у нас есть прямоугольный твердый образец золота размером 3,04 см × 8,14 см × 17,3 см. Мы можем легко подсчитать, что его объем составляет 428 см 3 , но сколько это стоит? Цена золота составляет около 5 долларов за грамм, поэтому нам нужно знать массу, а не объем. Маловероятно, что у нас были бы весы или весы, которые могли бы точно взвесить такой большой и тяжелый образец, поэтому нам пришлось бы определять массу золота, эквивалентную объему 428 см 9 .{3}\text{g}=\text{8}\text{0,27 кг}\]
Это более 18 фунтов золота. По цене, указанной выше, это будет стоить более 40 000 долларов!
Формула, определяющая плотность, также может использоваться для преобразования массы образца в соответствующий объем. Если обе части уравнения (1.2) умножаем на 1/ρ, имеем
\[\dfrac{\text{1}}{\rho}\times m=V \rho \times \dfrac{\text{1}}{\rho}=V \]
\[V=m \times \dfrac{\text{1}}{\rho}\label{2}\]
.3)
Обратите внимание, что в этих примерах мы использовали математическую функцию D = m/V для преобразования параметров из массы в объем и наоборот.
Чем это отличается от использования единичных коэффициентов для изменения единиц одного параметра?
Важное предостережение
Ошибка, которую иногда допускают начинающие студенты, состоит в том, что они путают плотность с концентрацией , которая также может иметь единицы измерения г/см 3 . Судя по размерному анализу, это выглядит прекрасно. Чтобы увидеть ошибку, мы должны понять смысл функции 9{3} \]
Объем золота можно рассчитать только в том случае, если известна плотность сплава, чтобы можно было рассчитать объем сплава, представленный 20 г. Этот объем, умноженный на концентрацию, дает массу золота, которую затем можно преобразовать в объем с помощью функции плотности.
Суть в том, что использование простого метода сокращения единиц не всегда приводит к ожидаемым результатам, если только полностью не понята математическая функция, на которой основан коэффициент преобразования. 93\)
, хотя это правильно по размерам.
Обратите внимание, что этот результат требуется, когда использовать функцию C = m/V и когда использовать функцию D=m/V в качестве коэффициентов преобразования. Чисто размерный анализ не мог достоверно дать ответ, так как обе функции имеют одинаковые размерности.
Пример \(\PageIndex{2}\): Объем бензола
Найдите объем, занимаемый образцом бензола массой 4,73 г.
По таблице 1.4 плотность бензола 0,880 г см 9{3}}\) просто переворачивает дробь ― 1 см 3 идет сверху, а 0,880 г идет снизу.)
Два только что выполненных расчета показывают, что плотность — это коэффициент преобразования, который изменяет объем в массу, а величина, обратная плотности, — это коэффициент преобразования, переводящий массу в объем. Это можно сделать из-за математической формулы, уравнение. (1.1), которая связывает плотность, массу и объем. Алгебраические манипуляции с этой формулой дали нам выражения для массы и объема [Ур. (1.2) и (1.3)], и мы использовали их для решения наших задач.
Если мы понимаем, что функция D = m/V, и учтем предостережение, приведенное выше, мы можем разработать соответствующие коэффициенты преобразования путем сокращения единиц, как показано в следующем примере:
Пример \(\PageIndex{3}\): Объем ртути
Учащийся весит 98,0 г ртути. Если плотность ртути 13,6 г/см 3 , какой объем занимает образец?
Мы знаем, что объем связан с массой через плотность.
Следовательно,
\(\text{V} = \text{m} \times \text{коэффициент преобразования}\)
Поскольку масса измеряется в граммах, нам нужно избавиться от этих единиц и заменить их единицами объема. Это можно сделать, если в качестве коэффициента преобразования использовать обратную величину плотности. Это помещает граммы в знаменатель, так что эти единицы сокращаются: 93}\)
(без отмены!)
Понятно, что квадратные граммы на кубический сантиметр — это не те единицы, которые нам нужны.
Использование коэффициента преобразования очень похоже на использование коэффициента единицы — мы знаем, что коэффициент правильный, когда единицы измерения корректно сокращаются.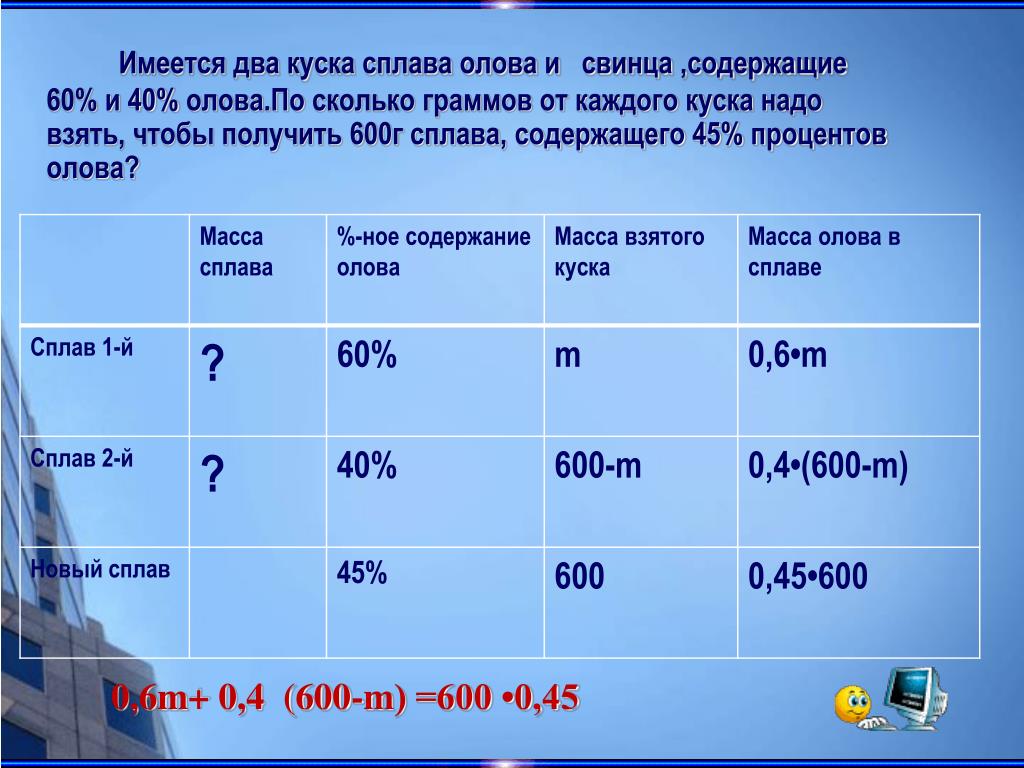
Однако коэффициент преобразования не равен единице. Скорее это физическая величина (или величина, обратная физической величине), которая связана с двумя другими величинами, которые мы преобразуем друг с другом. Коэффициент преобразования работает из-за этого отношения [Eqs. (1.1), (1.2) и (1.3) в случае плотности, массы и объема], , а не , потому что он равен единице. Как только мы установили, что связь существует, больше нет необходимости запоминать математическую формулу. Единицы говорят нам, следует ли использовать коэффициент преобразования или его обратную величину. Однако без такой связи простое аннулирование единиц не гарантирует, что мы поступаем правильно.
Простой способ запомнить отношения между количествами и коэффициентами пересчета — это «дорожная карта» типа, показанного ниже:
\[\text{Масса}\overset{плотность}{\longleftrightarrow}\text{объем или} м\overset{\rho }{\longleftrightarrow}V\text{ }\]
Это указывает на то, что масса конкретного образца вещества связана с его объемом (а объем с его массой) через коэффициент преобразования, плотность.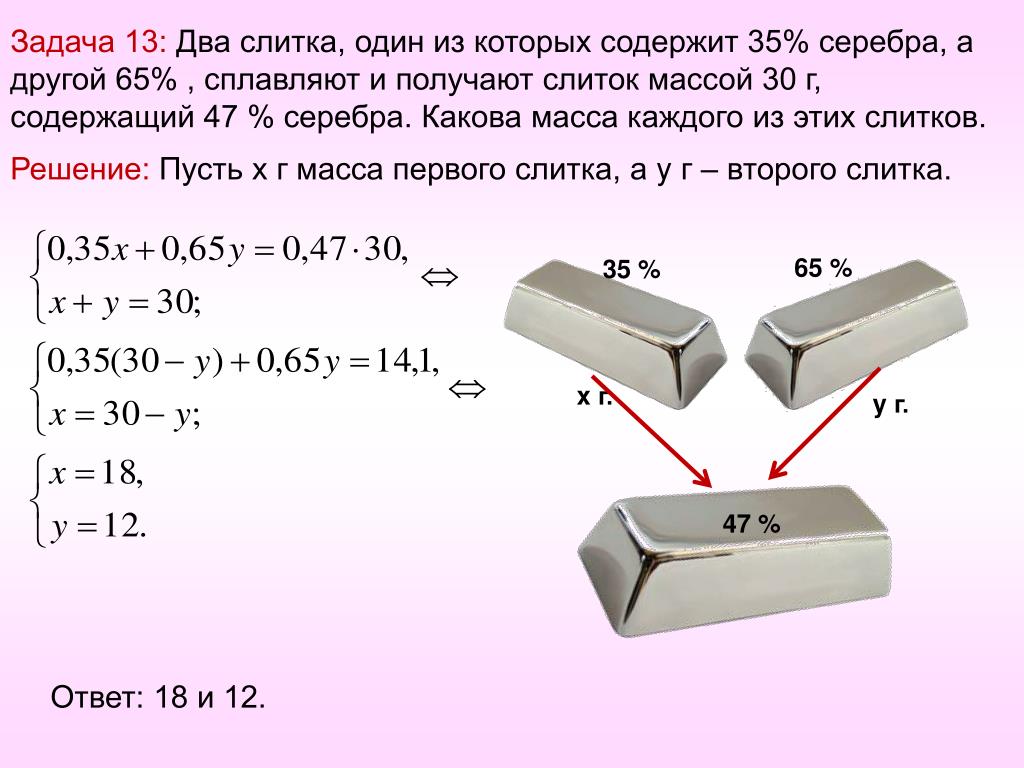
Двойная стрелка указывает на то, что преобразование может производиться в любом направлении при условии, что единицы коэффициента преобразования отменяют единицы количества, которые были известны изначально. Вообще в дорожной карте можно написать
\[\text{Первое количество}\overset{\text{коэффициент преобразования}}{\longleftrightarrow}\text{второе количество}\]
По мере того, как мы подходим к более сложным проблемам, где для получения конечного результата требуется несколько шагов, такие дорожные карты становятся более полезными для определения пути к решению.
Пример \(\PageIndex{4}\): Черное железное дерево
Черное железное дерево имеет плотность 67,24 фунта/фут 3 . Если бы у вас был образец объемом 47,3 мл, сколько бы он весил в граммах? (1 фунт = 454 г; 1 фут = 30,5 см).
Дорожная карта
\[\text{m}\overset{\rho }{\longleftrightarrow}V\text{ }\nonumber\] 93} \times \dfrac{\text{454 г}}{\text{1 фунт}} = \text{50,9 г}\)
В последующих главах мы установим ряд соотношений между физическими величинами.
Будут даны формулы, определяющие эти отношения, но мы не сторонники рабского заучивания и манипулирования этими формулами. Вместо этого мы рекомендуем вам помнить о существовании взаимосвязи, возможно, с точки зрения дорожной карты, а затем корректировать задействованные количества так, чтобы единицы сокращались соответствующим образом. Преимущество такого подхода в том, что вы можете решать самые разные задачи, используя одну и ту же технику.
Веб-источники: http://www.allmeasures.com/Formulae/static/materials/15/density.htm
Из ChemPRIME: 1.9: Коэффициенты преобразования и функции
Эд Витц (Университет Куцтауна), Джон В. Мур (UW-Мэдисон), Джастин Шорб (Колледж Хоуп), Ксавьер Прат-Ресина (Университет Миннесоты в Рочестере), Тим Вендорф и Адам Хан.
Эта страница под названием «Конверсионные коэффициенты и золотые украшения» распространяется по незаявленной лицензии, ее авторами, ремиксами и/или кураторами являются Эд Витц, Джон У.
Мур, Джастин Шорб, Ксавье Прат-Ресина, Тим Вендорф и Адам Хан. .
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ХимПРАЙМ
- Теги
- Образец
Услуги по золочению | ASTM B488, AMS 2422, MIL-G-45204
Advanced Plating Technologies — ведущая в отрасли компания по нанесению золотых покрытий, предоставляющая услуги функционального золочения в соответствии с MIL-G-45204, ASTM B488 или AMS 2422.
Наш шестидесятилетний опыт в этой области Обеспечивая прецизионное покрытие ствола, стойки и вибрационного золочения, в настоящее время используется во многих отраслях, включая медицину, телекоммуникации, аэрокосмическую и электронную промышленность.
APT предлагает полный спектр услуг по нанесению золотых покрытий, включая покрытия типа I, II и III чистоты как в мягком, так и в твердом золоте. Компания Advanced Plating Technologies имеет возможность нанесения нижнего покрытия с помощью наших различных услуг по никелированию, включая блестящее электролитическое никелирование, сульфаматное электролитическое никелирование и осаждение никеля химическим способом, а также меднение или серебрение, если это необходимо.
Недвижимость месторождения золота
Золотое покрытие обладает отличной электро- и теплопроводностью, обеспечивает исключительную способность к пайке и является превосходным отражателем инфракрасного излучения. Кроме того, золото — это благородный металл, который не окисляется и не вступает в химические реакции в обычных условиях.
По этой причине золочение является исключительным выбором для многочисленных технических требований, где электропроводность (особенно при низком напряжении), способность к пайке и коррозионная стойкость являются конструктивными требованиями.
Advanced Plating Technologies, компания из Милуоки, штат Висконсин, предлагает покрытие золотом как в 9Гальванопокрытие «твердое» золото чистотой 9,7% и мягкое золото чистотой 99,9%. Услуги твердого золочения обычно используются в приложениях, где повторяющееся скольжение или износ соединения являются конструктивными соображениями, например, в соединительных штифтах типа «мама-папа» или подпружиненных контактах. Наша компания предлагает гальваническое покрытие твердым золотом, которое легировано небольшим количеством кобальта для достижения необходимых свойств покрытия.
Мягкое золочение обычно используется там, где требуется наивысшая чистота золота для пайки, соединения проводов, применения при высоких температурах или высокой коррозионной стойкости.
Мягкий слой золотого покрытия обеспечивает исключительно чистое золотое покрытие, сохраняющее низкую твердость и высокую коррозионную стойкость золота в соответствии с его элементарной формой. Мягкое золочение предпочтительнее для высокотемпературных применений из-за того, что легирующие элементы твердого золочения могут окисляться при повышенных температурах.
Внешний вид золотого покрытия во многом зависит от подложки, которая наносится перед нанесением последнего слоя золота. Если применяется матовый никель, такой как сульфамат никеля, окончательное покрытие золота будет иметь более матовый вид. Если используется осветленный никель, такой как блестящий электролитический никель, то золотое покрытие будет иметь яркий внешний вид. Как и в случае любого месторождения, блеск основного материала в значительной степени коррелирует с блеском окончательного золотого покрытия.
Gold Lating возможностей
Технические характеристики:
MIL-G-45204
ASTM B488
AMS 2422
Большинство компании по специфике
Purity:
28.
Чистый
Тип покрытия:
Твердый (Код B или C по ASTM B488 или Mil-G-45204)
Мягкий (Код A по ASTM B488 или Mil-G-45204)
Подложки с покрытием:
Черные металлы: Все сплавы черных металлов, включая низкоуглеродистую, нержавеющую, закаленную и инструментальную сталь
Медь: Все медные сплавы, включая чистую медь, медные сплавы, включая теллур и бериллий, латунь, никель-серебро
Алюминий: Все алюминиевые сплавы, включая деформируемые, литые и патентованные сплавы (MIC-6)
Экзотика: , чистый никель (никель 200), кобальт-хром (MP35N), ковар, монель, хасталлой, монель, свинец
Ограничения по размеру детали: 24 дюйма x 22 дюйма x 10 дюймов
Подложки в комплекте:
Ярко -электролитический никель
Электролитический никель сульфамата
Электролетический никель (высокий или средний фосфор)
Медная
Серебро
HEAT .
Выборочное гальваническое покрытие
Листовой продукт (химически фрезерованные/протравленные листы)
Сегментированные полосы (лады)
Цилиндр
Стойка
Проволока
Vibratory
Наши услуги по гальванике золота предназначены для коммерческого применения в больших объемах. В настоящее время мы не предлагаем гальваническое покрытие нестандартных изделий, таких как часы, ювелирные изделия, изделия из серебра и т. д. Пожалуйста, посетите страницу Refinishing & Plating, чтобы получить доступ к специальным наборам для нанесения золотых покрытий.
Спецификации золотого покрытия
Тремя наиболее распространенными услугами по нанесению золотого покрытия, сертифицированными Advanced Plating Technologies, являются MIL-G-45204, ASTM B488 и AMS 2422. Наша компания может предоставить месторождения золота типа I, II и III в соответствии с этими отраслевыми стандартами. . Также могут быть предоставлены услуги по золочению в соответствии с AMS 2425, а также в соответствии с большинством специальных спецификаций компании, как указано в нашей базе данных спецификаций.
Краткое изложение услуг по нанесению золотого покрытия в соответствии со стандартами ASTM B488, MIL-G-45204 и AMS 2422 приведено ниже:
что тип и коды спецификаций ASTM и MIL являются синонимами. Перечисленные ниже типы соответствуют текущей редакции ASTM B488 от 2001 года.
Тип I: Чистое золото 99,7% с твердостью от A (90 HK 25 max) до C (130-200 HK 25 ).
Тип II: Чистое золото 99,0%, часто называемое твердым золотом, с твердостью от B (91-129 KH 25 ) до D (> 200 HK 25 ).
Тип III: Чистое золото 99,9%, часто называемое мягким золотом, с твердостью только A (90 HK 25 Max).
Код A: 90 HK 25 Максимум
Код B: 91-129 HK 25
Код C: 130-200 HK 90 9 012 8 012 8 518 HK
Соотношение между чистотой и твердостью (ASTM B488-01 и новее)
Код типа
904 B и C8 III A Только
Класс Минимальная толщина [мкм/дюйм]
0,25–0,25 мкм (~ 10 мкдюйм)
0,50–0,50 мкм (~ 20 мкдюйм)
0,75–0,75 мкм (~ 30 мкдюйм)
1,0 мкм (4,0 мкдюйм)
1,25–1,25 мкм (~ 50 мкдюйм)
2,5–2,5 мкм (~ 100 мкдюйм)
5,0–5,0 мкм (~ 200 мкдюйм)
6.
5.1 Никелевое покрытие – Для классов толщины, кроме 5.0, перед золотым покрытием должно быть нанесено никелевое покрытие, если изделие изготовлено из меди или медного сплава. Никелевая подложка также применяется по другим причинам (см. Приложение X6).
Приложение X6: Некоторые причины для использования никелевой подложки
X6.1 Диффузионный барьер (например, миграция цинка в золотой слой с латунной подложки)
X6.2 Выравнивающий слой (осветление)
X6.3 Ингибитор коррозии пор
X6.4 Ингибитор потускнения для золота
X6.5 Несущий нижний слой для контактирующих поверхностей
Тип I – минимум 99,7% золота
Тип II – минимальное содержание золота 99,0 %
Тип III – минимальное содержание золота 99,9 %
Класс A – Твердость по Кнупу 90 макс.
Марка С – твердость по Кнупу 130-200, в т.ч.
Класс D – твердость по Кнупу 201 и выше.
Если степень твердости для золотого покрытия не указана, тип I должен иметь степень твердости A (макс. 90 по Кнупу), а тип II должен иметь степень твердости C (от 130 до 200 по Кнупу)
Чистота (тип) соотношение твердости (класса):
Чистота Твердость
Тип I A, B или C
Тип II B, C или D
Тип III A только
Класс 00 – толщина 0,00002 дюйма, минимум
Класс 0 – толщина 0,00003 дюйма, минимум
Класс 1 – толщина 0,00005 дюйма, минимум
Класс 2 – толщина минимум 0,00010 дюйма
Класс 3 – толщина минимум 0,00020 дюйма
Класс 4 – толщина минимум 0,00030 дюйма
Класс 5 – толщина минимум 0,00050 дюйма
Класс 6 – толщина минимум 0,00150 дюйма
При нанесении на поверхность с высоким содержанием меди, такую как латунь, бронза или бериллиевая медь, или на медную пластину или ответную часть, необходимо применять антидиффузионную подложку, такую как никель. Услуги по нанесению золотых покрытий для AMS 2422 