Задачи. Равноускоренное движение — PhysBook

Уровень А

1. Куда направлены ускорения следующих тел:

а) у поезда, который начинает тормозить;

б) у поезда, который отходит от станции?

Решение

2. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?

Рис. 1.

Решение

3. Скорость движения автомобиля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение автомобиля.

Решение

4. С каким ускорением двигался автобус, если, трогаясь с места стоянки, он развил скорость 15 м/с за 50 с?

Решение

5. Двигаясь со скоростью 72 км/ч, мотоциклист притормозил и через 20 с достиг скорости 36 км/ч. С каким ускорением он тормозил?

Решение

6. Поезд подходит к станции со скоростью 21,6 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?

Решение

7. В начале измерения скорость тела равнялась 5 м/с и направлена была на север. Через 50 с измерения показали, что тело двигается со скоростью 15 м/с на юг. Считая движения тела равноускоренным прямолинейным, определите его ускорение.

Решение

8. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с². Через сколько времени он приобретет скорость 54 км/ч?

Решение

9. Через сколько времени останавливается автобус, если его начальная скорость 20 м/с, а ускорение 1,25 м/с²?

Решение

10. Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

Решение

11. Какую скорость приобретает отходящий от станции поезд через 7 с от начала движения, если его ускорение равно 0,9 м/с²?

Решение

12. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с² через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?

Решение

13. Определите скорость тела при торможении с ускорением 0,2 м/с² через 30 с от начала торможения, если начальная скорость его была равна 2 м/с.

Решение

14. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался с ускорением 9,8 м/с²?

Решение

15. Тело движется прямолинейно равнозамедленно с начальной скоростью 10 м/с и ускорением 2 м/с². Определите перемещение тела через 5 с после начала движения.

Решение

16. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с²?

Решение

17. Пассажирский поезд тормозит с ускорением 0,2 м/с². На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 54 км/ч?

Решение

18. Автобус движется со скоростью 36 км/ч. На каком расстоянии от остановки водитель должен начать тормозить, сообщая автобусу ускорение, не превышающее 1,2 м/с²?

Решение

19. Автомобиль движется прямолинейно с постоянным ускорением 2,0 м/с², имея в данный момент скорость 10 м/с. Где он был 4,0 с назад?

Решение

20. Поезд, движущийся после начала торможения с ускорением 0,40 м/с², через 15 с имел скорость 10 м/с. Найдите пройденный путь за это время.

Решение

21. Снаряд, летящий со скоростью 1000 м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200 м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.

Решение

22. После старта гоночный автомобиль достиг скорости 360 км/ч за 25 с. Какое расстояние он прошел за это время?

Решение

23. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь.

Решение

Уровень B

1. Шарик скатывается по желобу длиной 1,25 м с ускорением 1,6 м/с². Какова скорость шарика в конце жалоба?

Решение

2. Хоккейная шайба пересекла ледяное поле длиной 60 м за 3,0 с и остановилась. Какая скорость была сообщена шайбе клюшкой хоккеиста?

Решение

3. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с², пройдет 30 м?

Решение

4. Самолет при отрыве от земли имеет скорость 252 км/ч и пробегает по бетонированной дорожке расстояние 700 м. Сколько времени продолжает разбег самолет? Движение считайте равноускоренным.

Решение

5. Ножной тормоз грузового автомобиля считается исправным если при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее этой норме тормозное ускорение.

Решение

6. При какой начальной скорости поезд пройдет путь 1260 м в течении 60 с, замедляя ход с ускорением 1,5 м/с²?

Решение

7. Электропоезд тормозит с ускорением 0,40 м/с². Определите, за какое время он остановится, если тормозной путь равен 50 м.

Решение

8. Лифт Останкинской телевизионной башни заканчивает свое движение после прохождения 49 м за 14 с. Найдите ускорение и начальную скорость лифта.

Решение

9. Поезд, двигаясь с горы с ускорением 0,2 м/с², прошел путь 340 м и развил скорость 19 м/с. Сколько времени двигался поезд и какой была его скорость в начале отсчета?

Решение

10. Поезд, движущийся после начала торможения с ускорением 0,40 м/с²

, через 25 с остановился. Найдите скорость в момент начала торможения и тормозной путь.

Решение

www.physbook.ru

Задачи ЕГЭ на равноускоренное движение

Задачи для этой статьи взяты из книги “Отличник ЕГЭ. Физика. Решение сложных задач.” Задачи не сложные, но требующие внимательности, и аккуратности при составлении уравнений. И снова тот же совет: решать больше самостоятельно. Но примеры решений всегда полезны.

Задача 1. За время с прямолинейного равноускоренного движения тело прошло путь м, увеличив свою скорость в раза. Определите конечную скорость тела.

Пусть скорость тела была , тогда через 2 с она стала равна .  Зная путь, пройденный телом, можем найти ускорение:

   

   

Тогда можно записать пройденный телом путь как:

   

Получили квадратное уравнение относительно , решим его:

   

   

   

Конечная скорость тогда равна м/с.

Ответ: 15 м/с.

 

Задача 2. Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с. На каком расстоянии от остановки мотоциклист догонит грузовик?

Путь, пройденный мотоциклистом, равен:

   

Путь, пройденный грузовиком до и за время движения мотоцикла:

   

Приравняем и решим квадратное уравнение относительно :

   

   

   

   

Тогда от остановки встреча произошла на расстоянии м.

Ответ: 150 м.

Задача 3. Пассажир, стоящий на перроне, заметил, что первый вагон электропоезда, приближающегося к станции, прошел мимо него в течение с, а второй – в течение с. Определить ускорение поезда , если передний конец поезда остановился на расстоянии м от пассажира? Движение поезда считать равнозамедленным.

Обозначим длину вагона . Поезд  подошел к пассажиру со скоростью . Тогда для первого вагона запишем:

   

Второй вагон подошел к пассажиру уже со скоростью :

   

Тогда для  второго вагона:

   

Так как поезд затем полностью остановился, то

   

   

   

Приравняем выражения, записанные для первого и второго вагонов:

   

   

Подставим :

   

Разделим на обе части:

   

Выразим :

   

   

Чтобы найти ускорение, найдем квадрат скорости:

   

Тогда искомое ускорение:

   

Ответ: м/c.

easy-physic.ru

Равноускоренное движение | Задачи по физике

Определить ускорение автомобиля при торможении и длину пути торможения, если автомобиль за время торможения равное 5 секундам снизил скорость с 10 метров в секунду до 5 метров в секунду.

Дано: v₀=10 м/с; v₁=5 м/с; t=5 с
Найти: a — ?; L — ?

Решение:

Ускорение при торможении определяем по формуле

м/с²

Путь при торможении определяем по формуле

м

Ответ: ускорение автомобиля при торможении составило -1 метр в секунду в квадрате, путь при торможении равен 37,5 метрам

Определить ускорение и путь, пройденный автомобилем за 20 секунд, если его скорость за это время увеличилась с 8 метров в секунду до 16 метров в секунду. Считать движение автомобиля равноускоренным.
Дано: v₁=8 м/с; v₂=16 м/с; t=20 c
Найти: a — ?; L — ?

Решение:

Ускорение определяем по формуле

м/с²

Путь, пройденный автомобилем, определяем по формуле

м.

Ответ: автомобиль за 20 секунд проехал путь равный 240 метрам с ускорением 0,4 метра в секунду в квадрате

zadachi-po-fizike.ru

Прямолинейное равноускоренное движение (продолжение). Примеры решения задач по физике. 9-10 класс

Прямолинейное равноускоренное движение (продолжение). Примеры решения задач по физике. 9-10 класс

Задачи по физике — это просто!

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики по кинематике.

Решение задач на прямолинейное равноускоренное движение. При решении задачи обязательно делаем чертеж, на котором показываем все вектора, о которых идет речь в задаче. В условии задачи, если не оговорено иное, даются модули величин. В ответе задачи также должен стоять модуль найденной величины.

Начало (задачи с 1 по 8) смотри здесь

Задача 9

С какой скоростью надо вести мотоцикл, чтобы перейдя на движение с ускорением 2м/с², можно было пройти 200 метров за 10 секунд? Какая скорость будет у мотоцикла в конце пути?

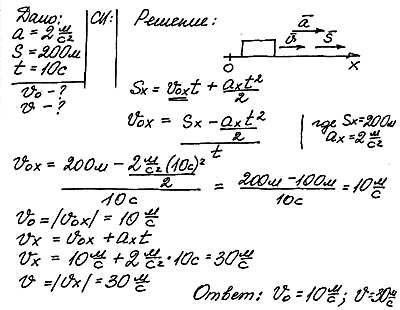
Большинство задач можно решить разными способами. Вполне вероятно, что Ваш способ решения будет лучше.

Задача 10

Поезд двигался прямолинейно с постоянным ускорением 2 м/с², имея в данный момент скорость равную 10 м/с. Какой путь прошел поезд за 2 секунды до этого? Какова была его начальная скорость?

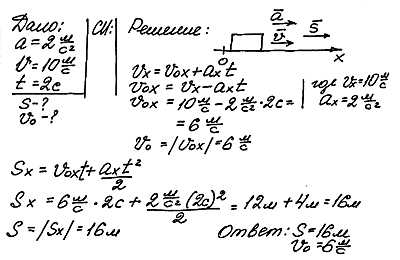
Задача 11

Автобус, двигаясь равномерно,  проходит 10 метров за 4 секунды, после чего он начинает тормозить и останавливается через 5 секунд. Определить тормозной путь и ускорение автобуса.

Задача 12

Пуля пробила стену толщиной 50 см, и ее скорость уменьшилась от 500 до 100 м/с. Определить время движения пули в стене.

Задача 13

В момент падения на сетку акробат имел скорость 6 м/с. C каким ускорением происходило торможение, если до полной остановки акробата сетка прогнулась на 1,2 метра?

 Задача 14

Тело, имея начальную скорость 10 м/с, стало разгоняться с ускорением 1 м/с². За какое время он пройдет  100 метров?

Задача 15

Велосипедист, имея начальную скорость 3 м/с,  стал двигаться с ускорением 1 м/с². За какое время он пройдет путь 50 метров и какую скорость приобретет в конце пути?

Задача 16

Автомобиль увеличил свою скорость с 15 до 19 м/с, пройдя за это время 340 метров. Определить ускорение и время движения.

class-fizika.ru

Равноускоренное движение. Задачи и формулы :: SYL.ru

Важнейшей характеристикой при движении тела является его скорость. Зная ее, а также некоторые другие параметры, мы всегда можем определить время движения, пройденное расстояние, начальную, конечную скорость и ускорение. Равноускоренное движение же является только одним из типов движения. Обычно оно встречается в задачах по физике из раздела кинематики. В подобных задачах тело принимают за материальную точку, что существенно упрощает все расчеты.

Скорость. Ускорение

Прежде всего, хотелось бы обратить внимание читателя на то, что эти две физических величины являются не скалярными, а векторными. А это значит, что при решении определенного рода задач необходимо обращать внимание на то, какое ускорение имеет тело в плане знака, а также каков вектор самой скорости тела. Вообще в задачах исключительно математического плана подобные моменты опускают, но в задачах по физике это достаточно важно, поскольку в кинематике из-за одного неверно поставленного знака ответ может получиться ошибочным.

Примеры

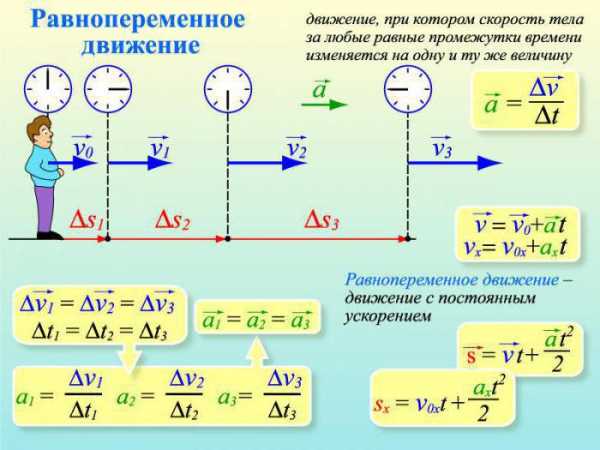
В качестве примера можно привести равноускоренное и равнозамедленное движение. Равноускоренное движение характеризуется, как известно, разгоном тела. Ускорение остается постоянным, но скорость непрерывно увеличивается в каждый отдельный момент времени. А при равнозамедленном движении ускорение имеет отрицательное значение, скорость тела непрерывно снижается. Эти два вида ускорения заложены в основу многих физических задач и достаточно часто встречаются в задачах первой части тестов по физике.

Пример равноускоренного движения

Равноускоренное движение мы встречаем ежедневно повсеместно. Ни один автомобиль не движется в реальной жизни равномерно. Даже если стрелка спидометра показывает ровно 6 километров в час, следует понимать, что это на самом деле не совсем так. Во-первых, если разбирать данный вопрос с технической точки зрения, то первым параметром, который будет давать неточность, станет прибор. Вернее, его погрешность.

Их мы встречаем во всех контрольно-измерительных приборах. Те же самые линейки. Возьмите штук десять хоть одинаковых (по 15 сантиметров, например) линеек, хоть разных (15, 30, 45, 50 сантиметров). Приложите их друг к другу, и вы заметите, что есть небольшие неточности, а их шкалы не совсем совпадают. Это и есть погрешность. В данном случае она будет равна половине цены деления, как и у других приборов, выдающих определенные значения.

Вторым фактором, который будет давать неточность, является масштаб прибора. Спидометр не учитывает такие величины, как половина километра, одна вторая километра и так далее. Заметить на приборе это глазом достаточно тяжело. Практически невозможно. Но ведь изменение скорости есть. Пускай на такую маленькую величину, но все же. Таким образом, это будет равноускоренное движение, а не равномерное. То же самое можно сказать и про обычный шаг. Идем, допустим, мы пешком, и кто-то говорит: наша скорость — 5 километров в час. Но это не совсем так, а почему, было рассказано немного выше.

Ускорение тела

Ускорение может быть положительным и отрицательным. Об этом говорилось ранее. Добавим, что ускорение — это векторная величина, которая числено равна изменению скорости за определенный промежуток времени. То есть через формулу его можно обозначить следующим образом: a = dV/dt, где dV – изменение скорости, dt – промежуток времени (изменение времени).

Нюансы

Сразу может возникнуть вопрос о том, как ускорение при таком раскладе может быть отрицательным. Те люди, которые задают подобный вопрос, мотивируют это тем, что даже скорость не может быть отрицательной, не то что время. На самом деле время отрицательным быть действительно не может. Но очень часто забывают о том, что скорость принимать отрицательные значения вполне может. Это же векторная величина, не следует забывать об этом! Все дело, наверное, в стереотипах и некорректном мышлении.

Так вот, для решения задач достаточно уяснить одну вещь: ускорение будет положительным в том случае, если тело разгоняется. И оно будет отрицательным в том случае, если тело тормозит. Вот и все, достаточно просто. Простейшее логическое мышление или способность видеть между строк уже будет, по сути дела, частью решения физической задачи, связанной со скоростью и ускорением. Частный случай — это ускорение свободного падения, и оно не может быть отрицательным.

Формулы. Решение задач

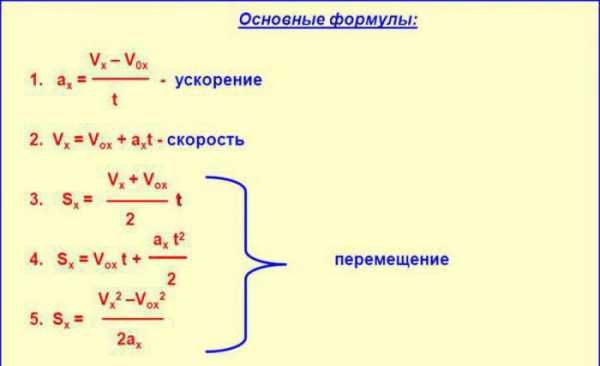
Следует понимать, что задачи, связанные со скоростью и ускорением, бывают не только практического, но и теоретического характера. Поэтому мы будем разбирать их и по возможности постараемся объяснить, почему тот или иной ответ правильный или, наоборот, неправильный.

Теоретическая задача

Очень часто на экзаменах по физике в 9 и 11 классах можно встретить подобные вопросы: «Как будет вести себя тело, если сумма всех действующих на него сил равна нулю?». На самом деле формулировка вопроса может быть самой разной, но ответ все равно один. Здесь первым делом в ход нужно пускать поверхностные здания и обыкновенное логическое мышление.

На выбор ученика предоставляется 4 ответа. Первый: “скорость будет равна нулю”. Второй: “скорость тела убывает в течение некоторого периода времени”. Третий: “скорость тела постоянна, но она точно не равна нулю”. Четвертый: “скорость может иметь любое значение, но в каждый момент времени она будет постоянной”.

Правильным ответом здесь будет, конечно же, четвертый. Сейчас разберемся, почему именно так. Давайте попробуем рассмотреть все варианты по очереди. Как известно, сумма всех сил, действующих на тело, есть произведение массы на ускорение. Но масса у нас остается величиной постоянной, ее мы отбросим. То есть если сумма всех сил равна нулю, ускорение тоже будет равно нулю.

Итак, предположим, что скорость будет равна нулю. Но этого не может быть, поскольку нулю у нас равно ускорение. Чисто физически это допустимо, но только не в данном случае, поскольку сейчас речь идет о другом. Пускай скорость тела убывает в течение некоторого периода времени. Но как она может убывать, если ускорение постоянно, и оно равно нулю? Никаких причин и предпосылок для убывания или возрастания скорости нет. Поэтому второй вариант мы отметаем.

Предположим, что скорость тела постоянна, но она точно не равна нулю. Она действительно будет постоянной в силу того, что ускорение просто-напросто отсутствует. Но нельзя однозначно сказать, что скорость будет отлична от нулевой. А вот четвертый вариант – прямо в яблочко. Скорость может быть любой, но, поскольку ускорение отсутствует, она будет постоянной во времени.

Практическая задача

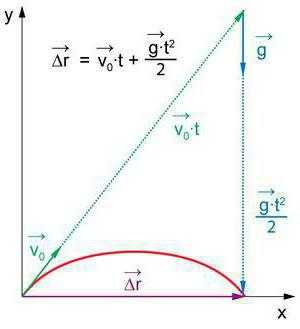
Определите, какой путь был пройден телом в определенный период времени t1-t2 (t1 = 0 секунд, t2 = 2 секунды), если имеются следующие данные. Начальная скорость тела на отрезке от 0 до 1 секунды равна 0 метров в секунду, конечная – 2 метра в секунду. Скорость тела по состоянию на время 2 секунды равна также 2 метрам в секунду.

Решить подобную задачу достаточно просто, нужно лишь уловить ее суть. Итак, требуется найти путь. Ну что же, начнем искать его, предварительно выделив два участка. Как легко заметить, первый участок пути (от 0 до 1 секунды) тело проходит равноускоренно, о чем свидетельствует увеличение его скорости. Тогда найдем это ускорение. Его можно выразить как разность скоростей, разделенную на время движения. Ускорение будет равно (2-0)/1 = 2 метра на секунду в квадрате.

Соответственно, расстояние, пройденное на первом участке пути S будет равно: S = V0t + at^2/2 = 0*1 + 2*1^2/2 = 0 + 1 = 1 метр. На втором же участке пути в период от 1 секунды до 2 секунд тело движется равномерно. Значит, расстояние будет равно V*t = 2*1 = 2 метра. Теперь суммируем расстояния, получаем 3 метра. Это и есть ответ.

www.syl.ru

Решение задач на определение ускорения, мгновенной скорости и перемещения при равноускоренном прямолинейном движении

Задача 1 посвящена исследованию пути и перемещения.

Условие: тело движется по окружности, проходя ее половину. Необходимо определить отношение пройденного пути к модулю перемещения (рис. 1).

Обратите внимание: дано условие задачи, но нет ни одного числа. Такие задачи будут встречаться в курсе физики довольно часто.

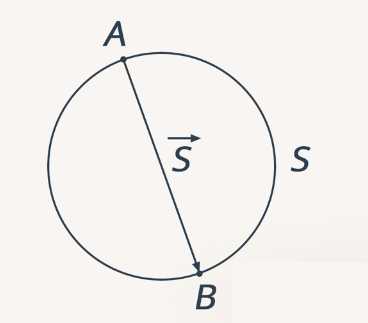
Рис. 1. Путь и перемещение тела

Решение

Введем обозначения. Радиус окружности, по которой движется тело, обозначим . При решении задачи удобно сделать рисунок, на котором изобразим окружность. Произвольную точку, из которой движется тело, обозначим ; точку, в которую переместилось тело, – .  – это дуга половина окружности,  – это перемещение, соединяющее начальную точку движения с конечной.

Найдем половину длины окружности:

С другой стороны модуль перемещения равен диаметру окружности (). Найдем отношение этих величин:

Ответ:.

Несмотря на то что в задаче ни одного числа нет, тем не менее в ответе мы получаем вполне определенное число.

Ветка. Задача на нахождения средней скорости

Задача.Автомобиль первую половину времени двигался со скорость , а вторую – со скоростью  (рис. 2). Определите среднюю скорость автомобиля.

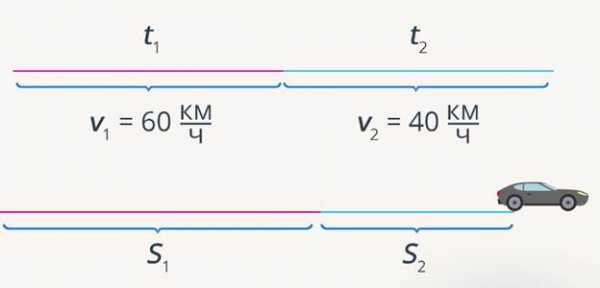
Рис. 2. Рисунок к задаче

Решение

Средняя скорость равна отношению пройденного пути ко времени, за которое произошло движение:

Полное перемещение состоит из двух частей: . Аналогично и время состоит из двух частей: . Промежутки времени у нас одинаковы: .

Перемещение при равномерном движении равно произведению скорости на время. Следовательно:

Ответ: .

Задача 2 будет посвящена графикам скорости.

Условие: Два поезда движутся навстречу друг другу по параллельным путям, скорость первого поезда – , скорость второго – (рис. 3). Ниже представлены 4 графика (рис. 4), и нужно выбрать те, на которых правильно изображены графики проекции скорости движения этих поездов.

Рис. 3. Рисунок к задаче 2

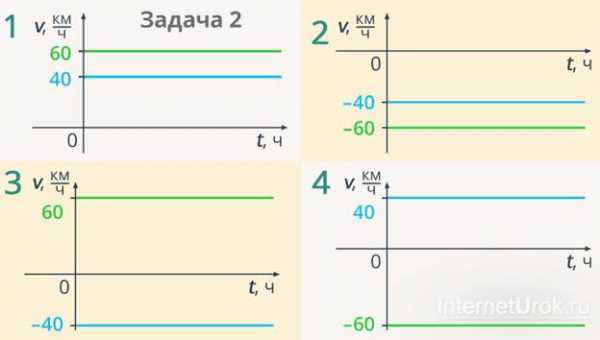
Рис. 4. Графики к задаче 2

Решение

Ось скорости – вертикальная (км/ч), а ось времени – горизонтальная (время в часах).

На 1-м графике две параллельные прямые, это модули скорости движения тела –  и . Если вы посмотрите на график, под номером 2, то увидите то же самое, только в отрицательной области:  и . На двух других графиках  сверху и  снизу. На 4-м графике  в верхней части, а  внизу. Что же можно сказать об этих графиках?

Согласно условию задачи два поезда едут навстречу друг другу, по параллельным путям, поэтому если мы выберем ось, связанную с направлением скорости одного из поездов, то проекция скорости одного тела будет положительной, а проекция скорости другого – отрицательной (поскольку сама скорость направлена против выбранной оси). Поэтому ни первый график, ни второй к ответу не подходят. Когда проекция скорости имеет одинаковый знак, нужно говорить о том, что два поезда движутся в одну сторону. Если мы выбираем систему отсчета, связанную с первым поездом, то тогда проекция скорости первого поезда  будет положительной, а второго – отрицательной, поезд едет навстречу. Или наоборот, если мы связываем систему отчета со вторым поездом, то у одного из них проекция скорости , а у другого , отрицательная. Таким образом, подходят оба графика (3 и 4).

Ответ: 3-й и 4-й графики.

Ветка. Задача на нахождения средней скорости (продолжение)

Поменяем в предыдущей задаче всего одно слово.

 

Задача:

Автомобиль первую половину пути двигался со скоростью , а вторую – со скоростью  (рис. 5). Определите среднюю скорость автомобиля.

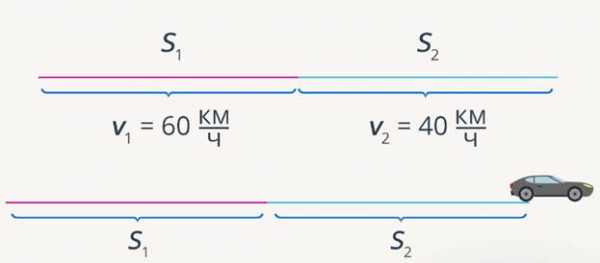
Рис. 5. Рисунок к задаче

Решение

По аналогии с предыдущей задачей запишем выражение для средней скорости:

Полное перемещение состоит из двух частей: , причем . Аналогично и время состоит из двух частей: .

Вспомним, что для равномерного движения время равно отношению перемещения ко времени. Тогда:

Ответ: .

Задача 3.

Условие: автомобиль движется со скоростью  и в течение  тормозит с ускорением . Необходимо определить его скорость в конце торможения.

Решение

В данном случае удобнее выбрать ось  и направить начальную скорость вдоль этой оси, т. е. вектор начальной скорости будет направлен в ту же сторону, что и ось. Ускорение будет направлено в противоположную сторону, ведь автомобиль замедляет свое движение. Проекция ускорения на ось  будет со знаком минус (рис. 6).

Рис. 6. Рисунок к задаче 3

Для нахождения мгновенной конечной скорости воспользуемся уравнением проекции скорости: . Время и ускорение заданы в СИ, поэтому начальную скорость также переведем в СИ: . Подставляя значения, получаем конечную скорость:

Значит, через  после торможения скорость будет .

Ответ: .

Задача 4.

Условие: на графике (рис. 7) представлены 4 зависимости скорости от времени. Необходимо определить, у какого из этих тел максимальный, а у какого минимальный модуль ускорения.

Рис. 7. Графики к задаче 4

Решение

Для решения необходимо рассмотреть все 4 графика поочередно.

Для сравнения ускорений нужно определить их значения. Для каждого тела ускорение будет определяться как отношение изменения скорости ко времени, в течение которого это изменение произошло.

Ниже проведены расчеты ускорения для всех четырех тел:

Как видим, у второго тела модуль ускорения минимальный, а у третьего тела – максимальный.

Ответ: .

 

Список литературы

1. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

interneturok.ru

2.1 Равноускоренное движение: задачи с ответами

(Все задачи по кинематике и ответы к ним находятся также в zip-архиве (332 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить все задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)

2.1.   Скорость автомобиля за 20 с уменьшилась с 20 м/с до 10 м/с. С каким средним ускорением двигался автомобиль?   [−0,5 м/с²]

2.2.   Тело, свободно падающее из состояния покоя, в конце первой половины пути достигло скорости 20 м/с. С какой высоты падало тело?   [40 м]

2.3.   Определить начальную скорость и ускорение автомобиля, если, двигаясь равноускоренно, за первые 3 с он прошел путь 18 м, а за первые 5 с — 40 м.   [3 м/с; 2 м/с²]

2.4.   Во сколько раз необходимо увеличить начальную скорость вертикально вверх брошенного тела, чтобы высота подъема увеличилась вдвое?   [в √2 раз]

2.5.   Тело свободно падает с высоты 540 м. Разделите эту высоту на три части, на прохождение которых тело затрачивает одинаковое время.   [60 м; 180 м; 300 м]

2.6.   От движущегося поезда отцепился последний вагон. Поезд продолжает двигаться с той же скоростью. Найти отношение расстояний, пройденных поездом и вагоном к моменту остановки вагона. Движение вагона равнозамедленное.   [2]

2.7.   Тело, двигаясь равноускоренно, проходит последовательно два одинаковых отрезка пути длиной 10 м за времена 1,06 с и 2,2 с. Найти начальную скорость и ускорение тела.   [−3 м/с²; 11 м/с]

2.8.   Двигаясь равноускоренно, тело проходит некоторое расстояние. Скорость тела в начале пути v₁, а в конце v₂. Определить среднюю скорость V движения тела.   [ V = (v₁ + v₂)/2 ]

2.9.   Бросив камень в колодец, наблюдатель через время t услышал всплеск воды. Определить глубину колодца. Скорость звука в воздухе равна c.

Ответ к задаче 2.9:     h =	с	(gt + с − √(с(с + 2gt))).
	g

2.10.   Двигаясь равноускоренно из состояния покоя, тело проходит некоторое расстояние. Найти отношение средней скорости тела на второй половине пути к средней скорости на первой половине пути.   [ v₂/v₁ = √2 + 1 ]

2.11.   Тело движется равноускоренно из состояния покоя в течение некоторого времени. Найти отношение средних скоростей движения тела за вторую и за первую половины времени движения.   [ v₂/v₁ = 3 ]

2.12.   Двигаясь равноускоренно, тело прошло за первую секунду движения расстояние 1 м, за вторую — 2 м, за третью — 3 м и т. д. Определить начальную скорость и ускорение тела.   [0,5 м/с; 1 м/с²]. Эта задача имеет решение.

2.13.   На рисунке слева приведена зависимость скорости тела от координаты. Где ускорение тела больше: в точке 1 или в точке 2?   [2]

2.14.   Тело, пущенное вверх вдоль наклонной плоскости со скоростью 1,5 м/с, вернулось обратно со скоростью 1 м/с. Найти среднюю скорость тела на всем пути. Вверх и вниз тело двигалось с постоянным ускорением.   [0,6 м/с]

2.15.   Два тела одновременно брошены с одинаковыми скоростями v_o: одно вниз с высоты H, другое — вверх. На какой высоте тела встретятся?

Ответ к задаче 2.15:     h =	H	(1 −	gH	).
	2		4vo2

2.16.   Тело движется равноускоренно из состояния покоя. Найти отношение скоростей тела в конце четвертого и в конце первого метров пути.   [ v₄/v₁ = 2 ]

2.17.   Тело начинает двигаться равноускоренно из состояния покоя. Спустя время t_o ускорение тела меняет знак на противоположный, оставаясь прежним по модулю. Через какое время после начала движения тело пройдет через исходную точку?   [t = t_o(2 + √2) ]

2.18.   Тело, движущееся с ускорением 1 м/с², в некоторый момент времени проходит через точку A, имея скорость 10 м/с. На каком расстоянии от точки A находилось тело секунду назад?   [на расстоянии 9,5 м от точки A]

2.19.   Отходящий от станции поезд на первом километре пути увеличил свою скорость на 10 м/с, а на втором — на 5 м/с. На каком километре среднее ускорение поезда было больше?   [на втором]

2.20.   Тело совершает колебательное движение, в течение времени t ускорение тела равно а, затем в течение того же времени t ускорение равно −a, затем опять a и т. д. Найти расстояние между крайними положениями тела.   [ at²/4 ]

2.21.   Тело движется равноускоренно из состояния покоя с ускорением a. Через время t ускорение тела становится отрицательным. При какой величине нового ускорения тело через время t пройдет через исходную точку?   [ a₁ = −3a ]

2.22. Если мимо стоящего на перроне пассажира первый вагон тронувшегося поезда проходит за 10 с, то за какое время мимо него пройдет весь поезд, состоящий из 16-ти вагонов? Поезд движется равноускоренно.   [40 c]

2.23.   Поезд трогается с места и равноускоренно проходит мимо неподвижного пассажира. При этом первый вагон прошел мимо него за время t₁, а последний — за время t₂. За какое время мимо пассажира прошел весь поезд, если первоначально пассажир стоял у головы поезда?

Ответ к задаче 2.23:	t =	t12 + t22	.
		2t2

2.24.   Тело движется из состояния покоя равноускоренно. Во сколько раз путь, пройденный телом за восьмую секунду движения, больше пути, пройденного за третью секунду?   [ S₈/S₃ = 3 ]

2.25.   Торможение поезда началось на расстоянии 200 м от станции. На каком расстоянии от станции окажется поезд, идущий со скоростью 30 м/с, через 7 с после начала торможения с ускорением −5 м/с²?   [110 м]

2.26.   Расстояние между двумя свободно падающими каплями через время 2 с после начала падения второй капли было 25 м. На сколько позднее первой начала падать вторая капля?   [1 c]

2.27.   Равнозамедленно движущееся тело проходит два последовательных одинаковых участка длиной L за времена t и 2t. Найти скорость тела в начале первого участка и ускорение.   [ v_o = 7L/6t;   a = −L/3t² ]

Далее: следующие 27 задач по равноускоренному движению.   |   Вернуться к списку разделов КИНЕМАТИКИ.

www.afportal.ru