Задача о капусте козе и волке: Задача «Волк, коза и капуста»
Задача «Волк, коза и капуста»
Удивительные находки и неразгаданные загадки
И.Г. СУХИН, Институт теории образования и педагогики РАО
Во многих математических монографиях есть страницы, посвященные истории возникновения знаменитых задач, доступных учащимся старших классов (например, Чистяков В.Д. Старинные задачи по элементарной математике — Минск, 1978). Однако практически нет работ, из которых учитель начальной школы мог бы получить исчерпывающую информацию о не менее известных старинных головоломках, представляющих интерес для учеников I–IV классов. Нам хотелось бы поделиться с читателями журнала результатами своих поисков и начать разговор о поразительной судьбе некоторых из таких задач.
В “Книге 1” труда Е.И. Игнатьева “В царстве смекалки, или Арифметика для всех: Опыт математической хрестоматии: Книга для семьи и школы” (СПб.: Тип. А.С. Суворина, 1911.
“Крестьянину нужно перевезти через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться только крестьянин, а с ним или один волк, или одна коза, или одна капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевез свой груз крестьянин?”
Даже если приводимая задача вам знакома, не спешите читать решение, попробуйте словно впервые поискать оптимальный маршрут и только затем ознакомьтесь с ходом решения, предлагаемым Е.И. Игнатьевым:
“Решение: Ясно, что приходится начать с козы. Крестьянин, перевезши козу, возвращается и берет волка, которого перевозит на другой берег, где его и оставляет, но зато берет и везет обратно на первый берег козу. Здесь он оставляет ее и перевозит к волку капусту.
Данная задача бессчетное число раз публиковалась в самых различных отечественных газетах, журналах и сборниках. При этом почти во всех работах упоминается только одно решение. А ведь есть и альтернативный путь!
Вначале крестьянин опять-таки перевозит козу. Но вторым он не обязательно должен забирать волка! Можно взять капусту, отвезти ее на другой берег, оставить там и вернуть на первый берег козу. Затем перевезти на другой берег волка, вернуться за козой и снова отвести ее на другой берег. В этом случае количество рейсов (7) точно такое же, как и в опубликованном выше варианте.
Существование двух решений не отмечено ни в многократных переизданиях книги Е.И. Игнатьева, ни в других самых авторитетных источниках. В их числе: Э. Люкас “Математические развлечения: Приложение арифметики, геометрии и алгебры к различного рода запутанным вопросам, забавам и играм” (СПб.
Это тем более удивительно, что наличие двух решений было указано, к примеру, еще в начале 20-х годов ХХ века в книге В. Литцмана “Веселое и занимательное в фигурах и числах: Математические развлечения” (М. — Пт.: Изд. Л.Д. Френкель, 1923. — С. 128–129), причем довольно подробное. Видимо, многие издатели сочли необязательным приводить оба варианта, ведь они схожи и являются по сути “зеркальными”. Но в книге для детей, особенно младшего возраста, это необходимо, иначе существенно снижается педагогическая ценность задачи!
Любопытно, что Б.
А. Кордемский в решении отмечает только второй вариант и по какой-то причине не упоминает первый. Загадка? Загадка.
Очень интересен вопрос о времени возникновения данной головоломки и ее первоисточнике. Б.А. Кордемский в книге “Математическая смекалка” говорит вскользь: “Это… старинная задача; встречается в сочинениях VIII века”.
Вначале может показаться, что мы имеем дело с опечаткой, ведь первая или одна из первых отечественных публикаций задачи “Волк, коза и капуста” датирована концом ХVIII века. В фондах Российской Исторической библиотеки сохранилась книга “Гадательная арифметика для забавы и удовольствия” (СПб., 1789). На титульном листе значится: “На ижд. изд. И. Краснопольского”, что означает “на иждивении издателя И. Краснопольского”. В раритете на 62 страницах сорок одна занимательная задача. На с. 42–43 читаем: “Некоторый мужик везши с собою волка, козу и капусту приехал к реке, у берегу коей нашел столь малую лодку, что она кроме его и одного чего-нибудь из везомых им, поднимать не могла.
Интересно, что в пособии болгарских авторов “Математический фольклор” (М.: Знание, 1987. — С. 180) задача о волке, козе и капусте помещена в раздел “Из математического фольклора других стран” с пометкой в скобках “Россия”.
Вернемся к истории задачи и вопросу: прав ли Б.А. Кордемский, датировав задачу восьмым веком.
По мнению ряда историков, задача имеет западные корни. В. Аренс указывает, что авторство хрестоматийной задачи приписывается Алкуину (Аренс В. Математические игры и развлечения. — СПб.: Физика, 1911. — С. 20).
В. Литцман, предлагая читателям познакомиться с задачей о переправе в книге “Веселое и занимательное о числах и фигурах” (М.: Государственное издательство физико-математической литературы, 1963. — С. 189), вскользь пишет: “У Алкуина мы находим следующий рассказ”.
Что же в наши дни известно об этой незаурядной личности? Алкуин (735–804) был ученым монахом и математиком из Ирландии, автором ряда учебников по математике. Король Карл Великий благоволил к ученым и всячески поощрял развитие наук. За королевским круглым столом нередко проводились состязания в решении хитроумных головоломок, в которых Алкуин имел возможность проявить свои незаурядные способности.
Алкуин основал Палатинскую школу в Туре (созданную для детей Карла V), принимал участие в основании университета в Париже. Добавим, что Алкуин был другом и учителем Карла Великого, его ученым советником.
Из других головоломок Алкуина наибольшую известность получили задачи 1) о гончей и зайце, 2) о покупке свиней, 3) о трех наследниках и 21 бочке, 4) о ста мерах пшеницы, 5) о быке. Но только головоломка о волке, козе и капусте до сих пор поражает воображение и детей, и взрослых. Эту и некоторые другие задачи Алкуин поместил в свой трактат “Задачи для оттачивания ума юношей”, написанный, как было принято в то время, латиницей.
Перед публикацией данной статьи очень хотелось подержать в руках текст первоисточника. А вдруг там приведены оба решения? И вот копия латинского манускрипта передо мной. Под №ХVIII легендарная задача. Сразу бросается в глаза, что решение одно — то самое, которое приводится в большинстве пособий. Но сама головоломка имеет иное название: “Задача о человеке, козе и волке”! А ее условие (если переводить близко к оригиналу) таково:
“Один человек должен был перевезти через реку волка, козу и кочан капусты. И не удалось ему найти другого судна, кроме как такого, которое могло выдержать только двоих из них. Задача, таким образом, заключалась в том, как всех перевезти на другой берег целыми и невредимыми. Скажите, кто способен: каким путем они могут перебраться на другой берег невредимыми” (перевод с латинского выполнен Е.И. Сухиной).
Так что же, все загадки разгаданы? Нет, последнее десятилетие преподносит новые сюрпризы.
Вот уже в нескольких изданиях при объяснении решения данной головоломки авторы делают одну и ту же забавную ошибку. Раскроем на с. 244 пособие Е.А. Латия “365 развивающих игр и затей для маленьких детей” (М.: Эксмо-Пресс, 2001), где предлагаемое решение столь фантастично, что его следует воспроизвести дословно: “Разгадка: сперва везут волка и капусту, оставляют капусту на противоположном берегу; везут волка обратно и оставляют на берегу; забирают козу, переправляют на другой берег; там забирают капусту, везут обратно к волку и уже вместе их окончательно перевозят на другой берег”.
Если бы волка и капусту можно было везти в лодке одновременно, то переправа завершилась бы гораздо быстрее, чем указано Е.А. Латием (но по условию задачи их нельзя переправлять вместе!) В вышедшей ранее раскраске “Угадайка: Выпуск 4” (М.: Крона, 1996) волка заменили на крокодила, козу — на пирата Крюка, а капусту — на Питера Пэна, но решение аналогично предыдущему: “Сначала надо перевезти Питера и крокодила.
А вдруг это Алкуин через века задумал подшутить над нами? Ничем другим я не могу объяснить то обстоятельство, что и сам первоначально при объяснении второго варианта решения указал не 7 рейсов, а 11, причем заметил свою оплошность в самый последний момент.
Да, еще не все тайны замечательной задачи разгаданы, и не исключено, что лукавая улыбка Алкуина будет преследовать не одно поколение авторов, составителей и читателей.
Баврин И.И., Фрибус Е.А. Занимательные задачи по математике — М.: ВЛАДОС, 1999.
Баврин И.И., Фрибус Е.А. Старинные задачи — М.: Просвещение, 1994.
Белов В.Н. Головоломки из близкой дали // Компьютерра. — 2000. — № 1.
Депман И.Я. История арифметики — М.: Просвещение, 1965.
Леман И. Увлекательная математика — М.: Знание, 1985.
Попов Г.Н. Сборник исторических задач по элементарной математике — М. — Л.: Главная редакция научно-популярной и юношеской литературы, 1938.
НАЧАЛЬНАЯ ШКОЛА №7-2002, c. 69-70.
15 интересных логических задачек для детей и взрослых
Логические игры и головоломки — это отличное развлечение как для детей, так и для взрослых. Они вырабатывают привычку думать, рассуждать, делать выводы и всегда стараться найти решение проблемы.
Задачка про волка, козу и капусту
Помните старинную задачу про волка, козу и капусту? Кто не решал ее в детстве! Предложите задачу своему ребенку! Мужику нужно перевезти через реку волка, козу и капусту. Но в лодке может поместиться только он сам, а с ним или только волк, или только коза, или только капуста.
Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как мужику перевезти свой груз?
Решение:
Нужно начать с козы. Перевезя ее, мужик возвращается на другой берег и берет волка. Переправив волка, он оставляет его на другом берегу, но зато берет козу и везет ее обратно на первый берег. Здесь он оставляет ее и перевозит к волку капусту. Затем, вернувшись, берет козу — переправа благополучно заканчивается.
Детективная задачка
На лугу лежат пять кусочков угля, одна морковь и шарф. Никто не клал их туда. Почему они там лежат?
Решение:
Дети использовали эти предметы, когда лепили снеговика зимой. С приходом весны снеговик растаял, и пять кусочков угля, морковка и шарф остались лежать уже на лугу.
Летная задачка
Мужчина выпрыгивает без парашюта из самолета. Высадка небезопасная, но мужчина остается целым и невредимым. Почему?
Решение:
Самолет находится ещё на взлётно-посадочной полосе.
Задачка про ноги
Ваня идет к лесному озеру. Ему навстречу движется класс из 25 учеников и двух преподавателей. Родители 10 детей также принимают участие в прогулке. Пять матерей еще везут своих детей на колясках. Преподаватель ведет с собой собаку. Сколько ног идут по дороге к лесному озеру?
Решение:
По дороге к лесному озеру идут только две ноги — Ванины. Все, кого он встретил, возвращаются с озера.
Сколько ворон?
Вишня у Маши плодоносит в большом количестве. К сожалению, на дерево садятся вороны и безжалостно клюют плоды. Вечером Маша считает ворон. Их 38! Это настолько выводит ее из себя, что она ловит одну ворону сачком. Сколько ворон осталось на дереве?
Решение:
Осталась только одна ворона, пойманная Машей. Остальные вороны испугались и улетели.
Задачка на внимательность
Молодая девушка заказывает в кафе яблочный сок, рулет и шоколадное мороженое.
Официант, который принимает заказ, приносит ей вскоре все желаемое. После того как девушка оплатила заказ, официант спросил: «Трудно работать в полиции?» Как он догадался, что девушка — полицейский?
Решение:
Девушка была в полицейской форме.
День рождения князя
Когда князь празднует день рождения, его подданные должны принести ему достойный подарок: самую сочную ветчину, самый пряный сыр, самую упитанную курицу, искусно выделанные шкурки, плетеные корзинки, глиняные кувшины и резные изделия. Крестьянин сделал князю необычный подарок: бутылку с яблочным соком. Отличие этого подарка — яблоко находится в бутылке. Князь поражен: каким образом тот смог засунуть яблоко в бутылку? «Как ты сделал это? При помощи колдовства?» — спрашивает князь. Крестьянин отвечает: «Догадайтесь сами, но я вовсе не чародей!» Как яблоко попадает в бутылку?
Решение:
Крестьянин надевает бутылку на яблоневую ветку вскоре после цветения.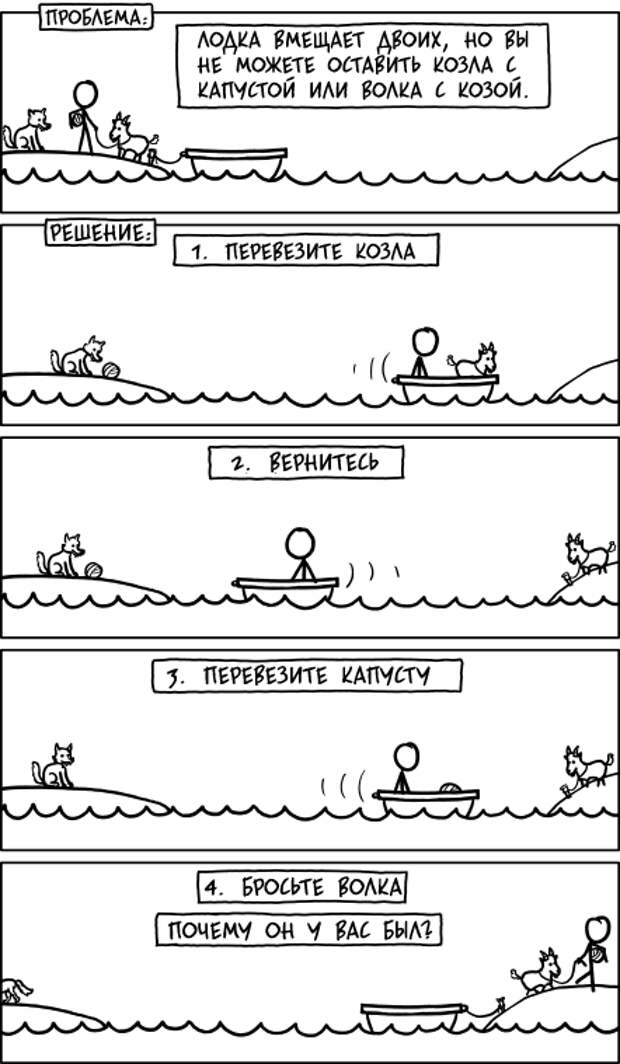
Таким образом, плод развивается в бутылке.
Еще один вид логических игр придется всем по вкусу — это игры с палочками. Для игры понадобится набор счетных палочек или любые палочки одинаковой длины и толщины (например, спички, с которых предварительно счистили серу), подойдут и полоски картона. Если вы играете вместе с детьми, то можно давать устные задания. Если ребенок играет один, подготовьте карточки с рисунком и условием игровой задачи.
Задание № 1
Переложи одну палочку так, чтобы дом смотрел в другую сторону.
Задание № 2
Переложи 3 палочки так, чтобы корова оглянулась и подняла хвост.
Еще несколько заданий с палочками из пособия С. И. Волковой «Математика и конструирование» (1−4 классы):
А в завершении мы хотим предложить вам самостоятельно изготовить знаменитую китайскую головоломку «Танграм». И в этом нам опять поможет пособие С. И. Волковой «Математика и конструирование».
Из деталей этой головоломки можно складывать разные фигуры.
Сложите для начала 1 и 2 фигуры. Рисунок вам поможет. Теперь попробуйте сложить фигуры 3, 4, 5, 6. И с этим справились? Поздравляем!
Надеемся, что выполняя предложенные задания, вы и ваш ребенок не раз испытали радость от приложенных интеллектуальных усилий, а главное — от самостоятельно найденного решения.
Фото: NadyaEugene/masterone/Shutterstock.com, архив пресс-службы,
образованиеполезные советышколаобществоразвитие
Волк, коза и капуста
FutureLearn использует куки-файлы для повышения удобства пользования веб-сайтом. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера. Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.
Йосси Эльран рассказывает нам о волке, козе и капусте пазл
© Институт научного образования Дэвидсона, Институт науки Вейцмана
Головоломки уходят в прошлое.
Одной из самых известных головоломок является головоломка «Волк, коза и капуста», которая восходит как минимум к 9 веку. Известная также как «головоломка с лисой, курицей и зерном», «головоломка с лисой, гусем и мешком с фасолью», «головоломка с пантерой, свиньей и кашей» и многими другими версиями, ее можно найти во многих фольклорах от Африки до Азии, в Европу, Америку и Австралию.
Загадка следующая. Фермер идет на рынок и покупает волка, овцу и капусту. По пути домой он должен пересечь реку на лодке с одного берега на другой. Лодка может перевозить только фермера и еще одну вещь — волка, козу или капусту, поэтому фермеру нужно будет совершить несколько поездок, чтобы переправить всех троих на другой берег. Во время катания на лодке ему всегда придется оставлять две вещи сами по себе на берегу реки. По понятным причинам волка нельзя оставлять наедине с козой — он ее сожрет. Козу нельзя оставлять с капустой, потому что она ее съест. Как же тогда фермер может перевезти всех троих на другой берег реки, оставив их нетронутыми?
Подождите! Попробуйте решить эту головоломку, прежде чем читать дальше.
Волк, овца и капуста – решение
Очевидно, фермер должен сначала забрать козу, оставив волка с капустой. Затем он возвращается один, чтобы плыть через капусту или волка. На самом деле неважно какой. Предположим, что он берет волка. Он не может оставить волка с козой, пока он возвращается за капустой, поэтому он оставляет волка и несет с собой козу на исходный берег. Он оставляет козу и берет капусту, переправляет ее на лодке и оставляет на дальнем берегу с лисой. Наконец, он возвращается один, чтобы перевезти козу на другой берег.
Эта так называемая головоломка «пересечение реки» представляет собой алгоритмическую головоломку. Он просит нас найти алгоритм, который решает данную проблему.
Есть много вариантов головоломки с волком, козой и капустой. Вот одна вариация. Можете ли вы решить это? Пишите свои решения в комментариях! Вам также предлагается опубликовать свои собственные варианты этой головоломки, чтобы все мы могли попытаться решить.
Крестьянин должен переправить через реку лису, курицу, гусеницу и капусту.
Лодка может вместить фермера и две дополнительные вещи. Лису нельзя оставить с курицей, курицу нельзя оставить с гусеницей, а гусеницу нельзя оставить с капустой. Как он может перевезти все на другой берег, оставив все в целости?
© Институт научного образования Дэвидсона, Институт науки Вейцмана
Эта статья взята из бесплатного онлайн-ресурса
Введение в рекреационную математику: развлечения, игры и головоломки
Создано
Присоединяйся сейчас
Достигните своих личных и профессиональных целей
Разблокируйте доступ к сотням экспертных онлайн-курсов и степеней от лучших университетов и преподавателей, чтобы получить аккредитованные квалификации и профессиональные сертификаты для составления резюме.
Присоединяйтесь к более чем 18 миллионам учащихся, чтобы начать, сменить или развить свою карьеру в удобном для вас темпе в самых разных областях.
Начать обучение
Головоломка | Фермер, Коза, Волк и Капуста
Фермер хочет пересечь реку, но он не один.
У него также есть коза, волк и капуста вместе с ним. Доступна только одна лодка, которая может поддерживать фермера, а также козла, волка или капусту. Таким образом, одновременно в лодке может быть только два объекта (фермер и еще один).
Но проблема в том, что если козу и волка оставить наедине (либо в лодке, либо на берегу), волк съест козу. Точно так же, если Козу и капусту оставить в покое, то коза съест капусту. Фермер хочет пересечь реку со всеми тремя своими пожитками: козой, волком и капустой.
Какую стратегию он должен использовать для этого?
Решение 1: Если взять волка на другую сторону, козел и капуста останутся вместе. Также удаление капусты оставит волка и козу наедине. Следовательно, фермер сначала возьмет козу с другой стороны и вернется один. У нас есть фермер, волк и капуста с одной стороны и коза с другой стороны.
Теперь он возьмет с собой волка, бросит волка на другую сторону и вернется с козой. Итак, теперь с одной стороны у нас есть фермер, капуста и коза, а с другой стороны — волк.
Теперь он берет с собой капусту и возвращается один. Итак, теперь сценарий: фермер, коза с одной стороны и волк, капуста с другой стороны.
Теперь, наконец, он переходит реку с козой и, таким образом, ему удается забрать с собой все свое имущество.
Ссылка: https://www.bhavinionline.com/2013/10/river-crossing-puzzle-farmer-wants-to-cross-with-wolf-goat-and-cabbage/
Решение 2: Эту задачу можно решить с помощью теории графов.
Рассмотрим 2 состояния: начальное (A) и конечное (B).
Изначально на правом берегу реки ничего нет, а на левом — коза, капуста и волк. И в конечном состоянии все трое (коза, капуста и волк) будут с правой стороны. Как мы можем перейти в состояние B из состояния A? На правом берегу могут быть такие комбинации козы (G), капусты (C), волка (W).
-> 0, G, W, C, GW , GC , WC, GWC
0 представляет начальное состояние (A), а GWC представляет конечное состояние (B). Мы можем смоделировать эту проблему как неориентированный взвешенный граф.
Где каждое ребро в графе имеет вес 1 или бесконечность.
Этот график можно использовать для представления нашей задачи.
Теперь все пути с бесконечным весом нельзя пройти, иначе ограничения задачи будут нарушены. Итак, мы должны двигаться от A к B, используя пути с весом 1, и мы можем найти допустимый путь, используя алгоритм кратчайшего пути Дейкстры.
Объяснение :
Понятно, что вначале лодочник может взять с собой только козу. Итак, от вершины 0 до вершины G мы устанавливаем вес равным 1. В других случаях (от 0 до W, от 0 до C) кого-то съедят. Следовательно, мы устанавливаем эти веса бесконечными.
Используя подобную интуицию, легко найти решение.
Эта статья предоставлена Arushi Dhamija. . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.