Теорема о соотношении сторон и углов треугольника: Соотношение между углами и сторонами треугольника — урок. Геометрия, 7 класс.
Теорема о соотношениях между сторонами и углами треугольника / Соотношения между сторонами и углами треугольника / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Теорема о соотношениях между сторонами и углами треугольника
Теорема:
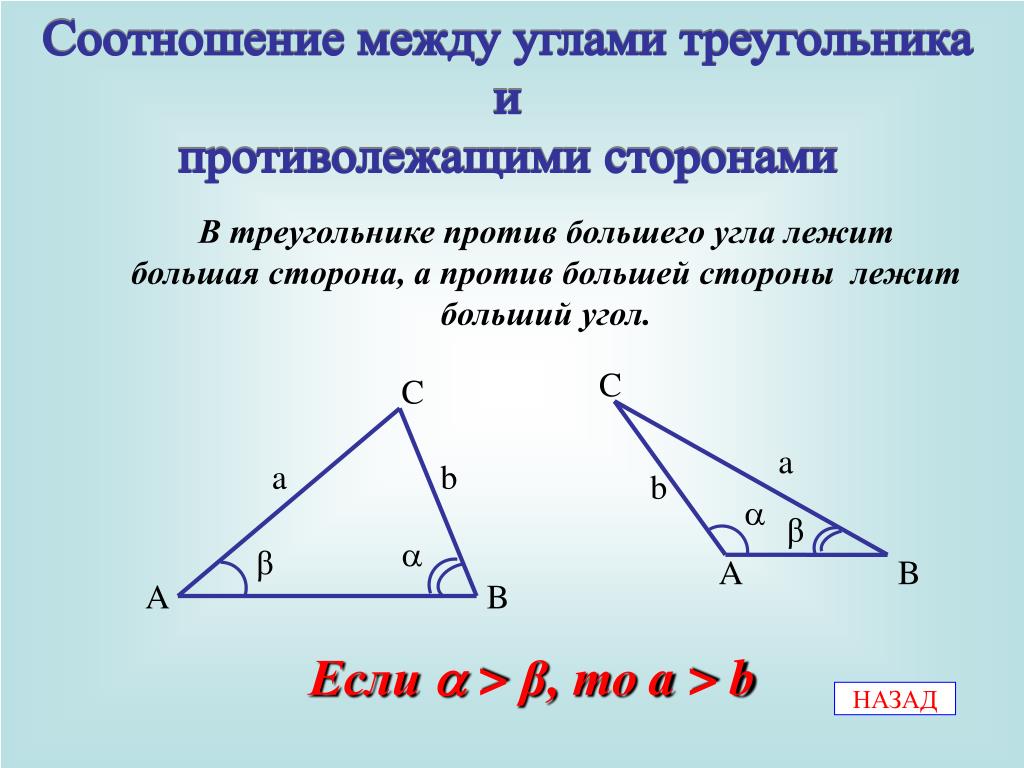
| В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона. |
Доказательство:
1) Дано: АВС, АВАС.
Доказать: СВ.
Доказательство:
Отложим на стороне АВ отрезок АD, равный стороне АС.
Итак, С1, 1 =2, значит, С2, при этом 2В, следовательно, СВ.
2) Дано: АВС, СВ.
Доказать: АВАС.
Доказательство:
Предположим, что это не так. Тогда возможны два варианта:
- либо АВ = АС, тогда АВС — равнобедренный с основанием ВС, значит, С =В (как углы при основании), что противоречит условию: С
- либо АВАС, тогда СВ, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: СВ.

Значит, наше предположение неверно, следовательно, АВАС. Что и требовалось доказать.
Следствие 1
| В прямоугольном треугольнике гипотенуза больше катета. |
Доказательство:
Дано: АВС, ВС — гипотенуза, А — прямой.
Доказать: ВСАС, ВС АВ.
Доказательство:
АВС — прямоугольный, А — прямой, следовательно, углы В и С острые, тогда АВ и АС, значит, ВСАС, ВСАВ (в треугольнике против большего угла лежит большая сторона).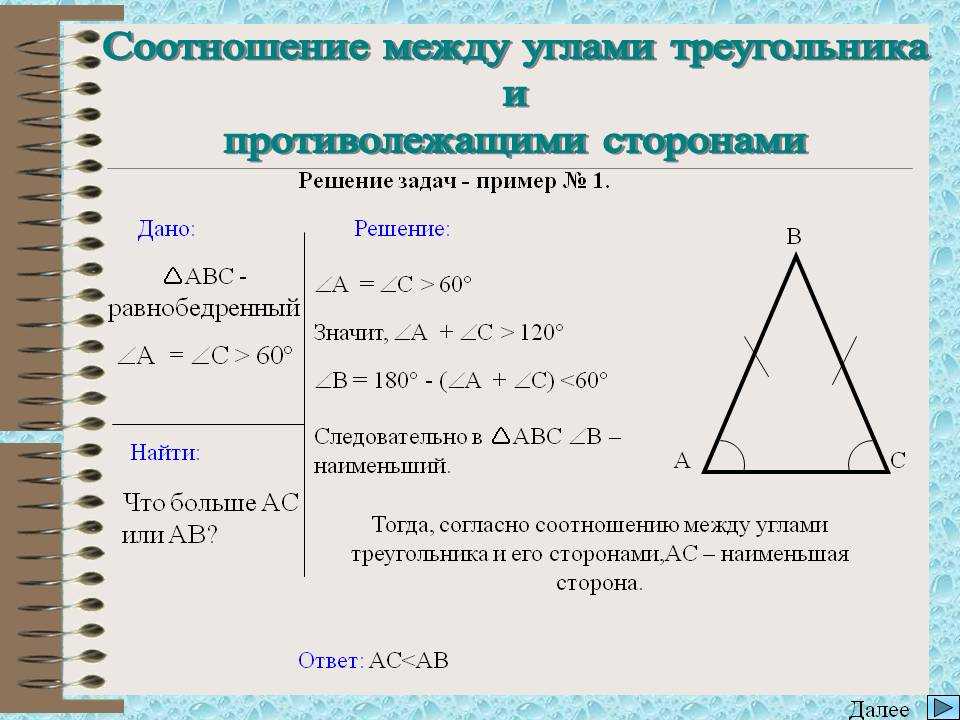 Что и требовалось доказать.
Что и требовалось доказать.
Следствие 2
| Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника). |
Доказательство:
Дано:
Доказать: АС = АВ.
Доказательство:
Предположим, что одна из сторон будет больше, т.е. АСАВ, тогда и угол лежащий против этой стороны будет больше, т.е. ВС (в треугольнике против большей стороны лежит больший угол), а это противоречит условию: В =С, следовательно, наше предположение неверно, значит АС = АВ.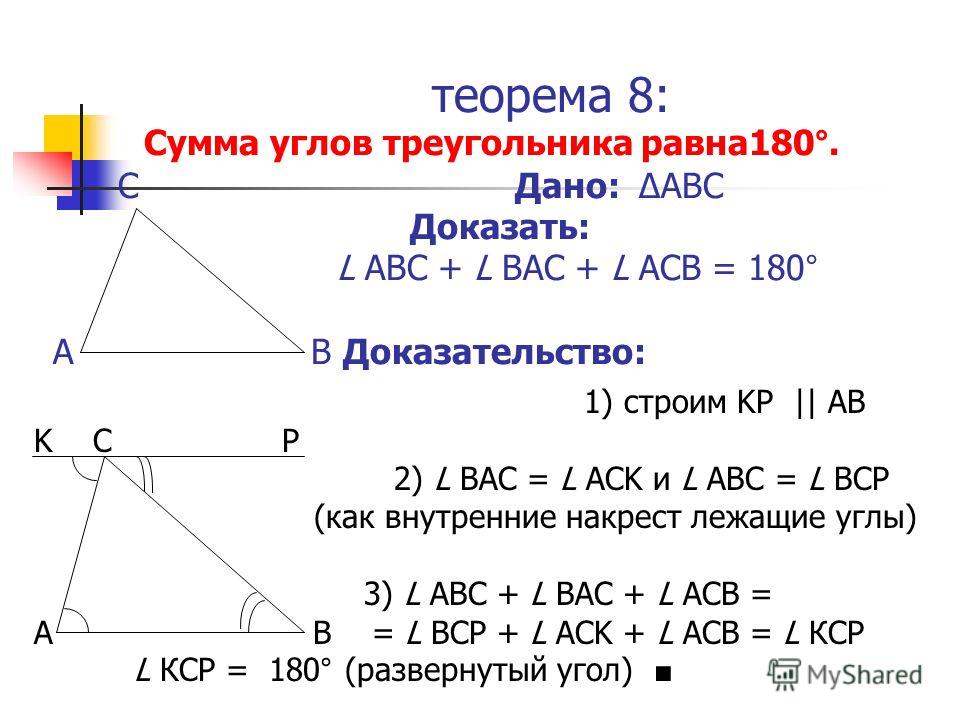
Итак, в АВС равны две стороны (АС = АВ), следовательно, данный треугольник — равнобедренный. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
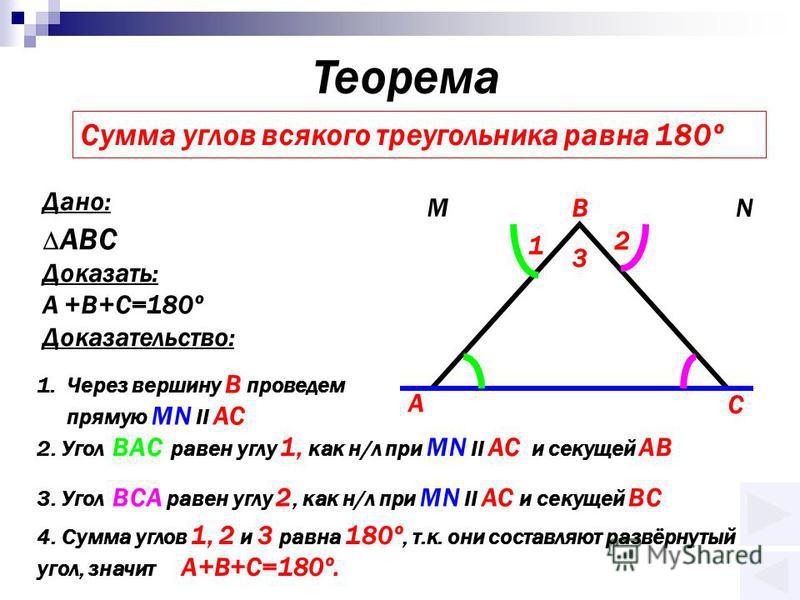
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 236, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 240, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 242, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 243, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 301, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 336, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1036, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1168, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Соотношение между сторонами и углами треугольника 7 класс онлайн-подготовка на Ростелеком Лицей
Тема 3: Параллельные прямые. Сумма углов треугольника
Сумма углов треугольника
- Видео
- Тренажер
- Теория
Заметили ошибку?
109. Теорема о соотношении между сторонами и углами треугольника
Теорема. В треугольнике
- Против большей стороны лежит больший угол;
- Обратно, против большего угла лежит большая сторона.
Докажем каждое утверждение отдельно.
-
Дано: АВ>АС.
Доказать: ∠С>∠В.
Доказательство:
На стороне АВ отложим отрезок AD так, что AD = AC. Так как по условию AB>AC, то точка D будет лежать на стороне AB. Проведем отрезок CD и получим равнобедренный треугольник ACD. В равнобедренном треугольнике ∠1=∠2.
∠B
∠ACB>∠1, так как ∠ACD = ∠1+∠3.

Значит, ∠ACD > ∠1 = ∠2 > ∠B. Следовательно, ∠ACD>∠B, что и требовалось доказать.
-
Дано: ∠С>∠В
Доказать: АВ>AC
Доказательство:
Докажем методом от противного.
Если AB = AC, то ∠С = ∠В по свойству равнобедренного треугольника, что противоречит условию.
Если AB 335320AC, то ∠С
Остаётся только случай АВ>АС, другие случаи невозможны. Что и требовалось доказать.
Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.
Доказательство:
Самый большой угол в прямоугольном треугольнике – прямой, так как сумма всех углов равна 180° и в треугольнике не может быть двух углов ≥ 90°.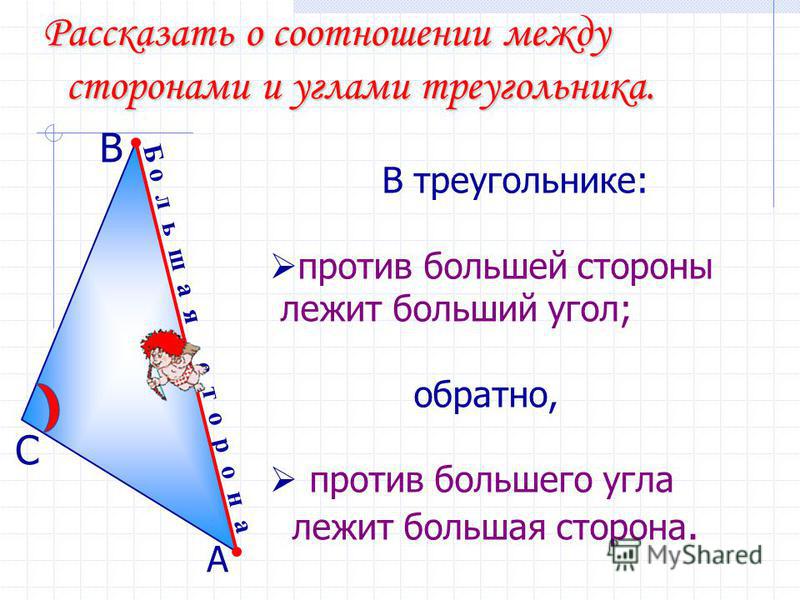 Значит, напротив большего угла лежит большая сторона – это гипотенуза.
Значит, напротив большего угла лежит большая сторона – это гипотенуза.
Следствие 2. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Дано: ∠В = ∠С
Доказать: АС = АВ
Доказательство:
Докажем методом от противного. Если стороны имеют разные длины, например АВ>АС, то по теореме ∠С>∠В, что противоречит условию. Значит, предположение неверно, AB = AC, что и требовалось доказать.
Теорема о неравенстве треугольника. Каждая сторона треугольника меньше суммы двух других сторон.
Дано: ΔАВС.
Доказать: АВ
Доказательство:
Продолжим сторону AC на отрезок CD, выбрав точку D так, что CD = BC. Получим равнобедренный треугольник BCD, в котором ∠1=∠2.
В треугольнике ABD напротив большего угла лежит большая сторона. ∠ABD>∠ADB, следовательно, AD>AB. Так как AD = AC+CD, получаем AC+CD>AB, что и требовалось доказать.
∠ABD>∠ADB, следовательно, AD>AB. Так как AD = AC+CD, получаем AC+CD>AB, что и требовалось доказать.
Запишем эту теорему для всех сторон треугольника.
АВ
BC
CA
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Теоремы о подобных треугольниках
1. Теорема о делителях сторон
Если треугольник ADE и BC параллельны DE, то AB BD = AC CE
Чтобы показать, что это так, проведите прямую BF параллельно AE, чтобы составить параллелограмм BCEF:
Треугольники ABC и BDF имеют одинаковые углы и поэтому подобны (Почему? См. раздел под названием AA на странице Как Чтобы определить, подобны ли треугольники.)
- Сторона AB соответствует стороне BD, а сторона AC соответствует стороне BF.

- Итак, AB/BD = AC/BF
- Но BF = CE
- Итак, AB/BD = AC/CE
Теорема о биссектрисе угла
Если треугольник ABC делит (делит пополам) угол BAC, то AB BD = AC DC
Чтобы показать, что это правда, мы можем обозначить треугольник следующим образом:
- Угол BAD = Угол DAC = x°
- Угол ADB = y°
- Угол ADC = (180−y)°
По закону синусов в треугольнике ABD: sin(x) BD = sin(y) AB
Умножить обе стороны на AB: sin(x)AB1 BD
9 sin (y)
1
Разделите обе стороны на грех (x): AB BD = SIN (Y) SIN (x)
по закону сини в треугольник ACD: sin(x) DC = sin(180−y) AC
Умножить обе стороны на AC: sin(x)AC DC = 1 sin(1800−y)
Разделите обе части на sin(x): AC DC = sin(180−y) sin(x)
Но sin(180−y) = sin(y) : 900 AC DC = sin(y) sin(x)
Оба AB BD и AC DC равны SIN (Y) SIN (x) , так:
AB BD = AC DC
В частности, если Triangle Abc Abc Isosceles, затем треугольники ABD и ACD являются конгруэнтными треугольниками
, и тот же результат верен:
AB BD = AC DC
3.
 Область и сходство
Область и сходство. сторон в отношении x:y,
, то их площади относятся друг к другу x 2 :y 2
Пример:
Эти два треугольника подобны, стороны которых относятся как 2:1 (сторона одного вдвое длиннее другого) :
Что можно сказать об их районах?
Ответ прост, если мы нарисуем еще три линии:
Мы видим, что маленький треугольник вписывается в большой треугольник четыре раза .
Итак, когда длины равны вдвое больше , площадь в четыре раза больше
Таким образом, отношение их площадей равно 4:1
Мы также можем записать 4:1 как 2 2 :1
Общий случай:
Треугольники ABC и PQR подобны и имеют отношение сторон x:y
Площади можно найти по этой формуле из площади треугольника:
Площадь ABC = 1 2 bc sin (A)
Площадь PQR = 1 2 qr sin(P)
И мы знаем, что длины треугольников находятся в соотношении x:y
q/b = y/x, поэтому: q = by/x
и r /c = y/x, поэтому r = cy/x
Кроме того, поскольку треугольники подобны, углы A и P одинаковы:
A = P
Теперь мы можем сделать некоторые вычисления :
Площадь треугольника PQR : 1 2 qr sin(P)
Введите «q = by/x», «r = cy/x» и «P=A»: 1 2 (by)(cy) sin(A) (x)(x)
Упрощение: 1 2 BCY 2 SIN (A) x 2
. bc sin(A)
bc sin(A)
Что равно: y 2 x 2 × Площадь треугольника ABC
Таким образом, мы получаем следующее соотношение:
Площадь треугольника ABC : Площадь треугольника PQR = x 2 : y 2
Простое руководство по треугольнику 30-60-000
Острые, тупые, равнобедренные, равнобедренные… Когда дело доходит до треугольников, существует множество их разновидностей, но лишь немногие являются «особенными». Эти специальные треугольники имеют стороны и углы, которые постоянны и предсказуемы, и их можно использовать для быстрого решения задач по геометрии или тригонометрии. И 30-60-90-треугольник — произносится как «тридцать шестьдесят девяносто» — действительно является особым типом треугольника.
В этом руководстве мы расскажем вам, что такое треугольник 30-60-90, почему он работает и когда (и как) использовать ваши знания о нем. Итак, приступим!
Что такое треугольник 30-60-90?
Треугольник 30-60-90 — это особый прямоугольный треугольник (прямоугольный треугольник — это любой треугольник, содержащий угол в 90 градусов), который всегда имеет углы в 30, 60 и 9 градусов.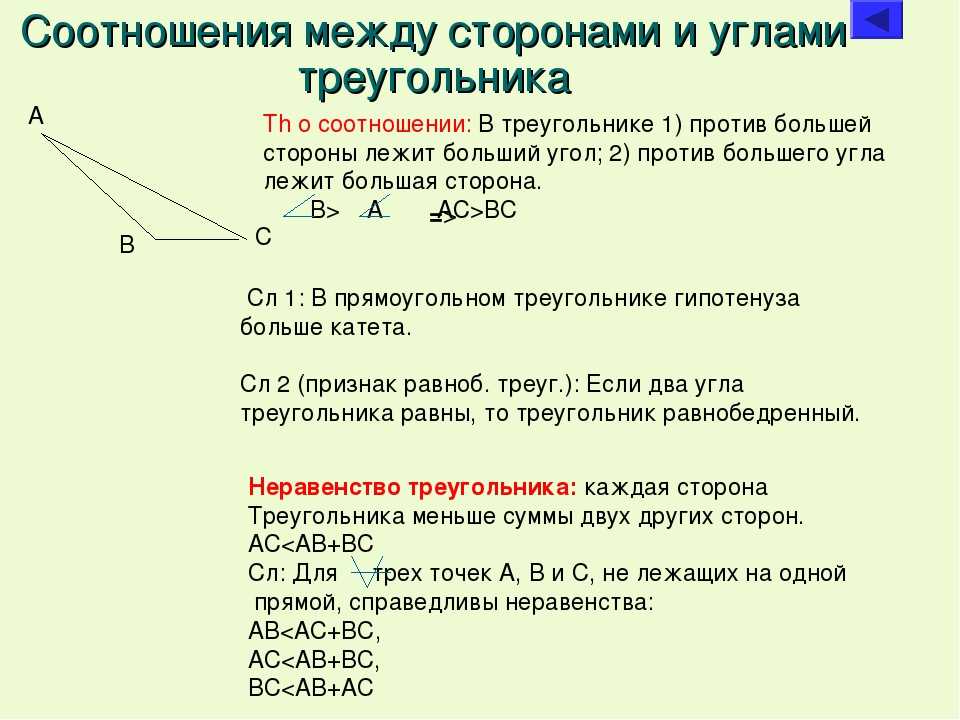 0 градусов. Поскольку это особый треугольник, у него также есть значения длин сторон, которые всегда находятся в постоянном соотношении друг с другом.
0 градусов. Поскольку это особый треугольник, у него также есть значения длин сторон, которые всегда находятся в постоянном соотношении друг с другом.
Основное соотношение треугольника 30-60-90:
Сторона, противоположная углу 30°: $x$
Сторона, противоположная углу 60°: $x * √3$
Сторона, противоположная углу 90°: $2 x$
Например, треугольник 30-60-90 градусов может иметь длины сторон:
2, 2√3, 4
7, 7√3, 14
√3, 3, 2√3
(Почему длиннее катет 3? В этом треугольнике кратчайший катет ($x$) равен $√3 $, поэтому для более длинного катета $x√3 = √3 * √3 = √9 = 3$, а гипотенуза в 2 раза больше самого короткого катета, или $2√3$)
И так далее.
Сторона, противоположная углу 30°, всегда является наименьшим , потому что 30 градусов — это наименьший угол. Сторона, противоположная углу 60°, будет средней длиной , потому что 60 градусов — средний угол в градусах этого треугольника. И, наконец, сторона, противоположная углу 90°, всегда будет наибольшей стороной (гипотенуза) , потому что 90 градусов — это наибольший угол.
И, наконец, сторона, противоположная углу 90°, всегда будет наибольшей стороной (гипотенуза) , потому что 90 градусов — это наибольший угол.
Хотя он может выглядеть похожим на другие типы прямоугольных треугольников, причина, по которой треугольник 30-60-90 настолько особенный, заключается в том, что вам нужно всего три элемента информации, чтобы найти все остальные измерения. Пока вы знаете значение двух углов и длины одной стороны (неважно, какой стороны), вы знаете все, что вам нужно знать о своем треугольнике.
Например, мы можем использовать формулу треугольника 30-60-90, чтобы заполнить все оставшиеся информационные пробелы треугольников ниже.
Пример 1
Мы видим, что это прямоугольный треугольник, в котором гипотенуза вдвое больше длины одного из катетов. Это означает, что это должен быть треугольник 30-60-90 и меньшая заданная сторона противоположна 30°.
Следовательно, более длинная сторона должна располагаться напротив угла 60° и иметь размеры $6 * √3$, или $6√3$.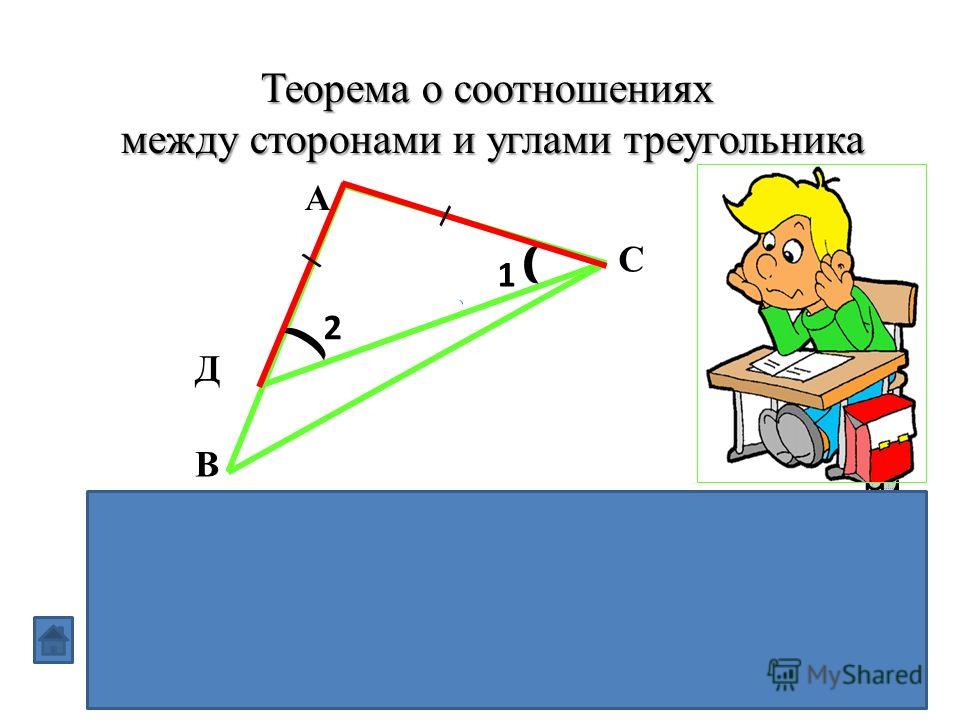
Пример 2
Мы видим, что это должен быть треугольник 30-60-90, потому что мы видим, что это прямоугольный треугольник с одним заданным измерением, 30°. Тогда немаркированный угол должен быть равен 60°.
Так как 18 — это мера, противоположная углу в 60°, она должна быть равна $x√3$. Тогда самая короткая нога должна быть равна $18/√3$.
(Обратите внимание, что длина ноги на самом деле будет $18/{√3} * {√3}/{√3} = {18√3}/3 = 6√3$, потому что знаменатель не может содержать радикальный/квадратный корень ).
А гипотенуза будет равна $2(18/√3)$
(Обратите внимание, что в знаменателе снова не может быть радикала, поэтому окончательный ответ действительно будет в 2 раза больше длины катета $6√3$ = > $12√3$).
Пример 3
Опять же, нам даны два измерения угла (90° и 60°), поэтому третье измерение будет равно 30°. Поскольку это треугольник 30-60-90, а гипотенуза равна 30, самый короткий катет будет равен 15, а более длинный катет будет равен 15√3.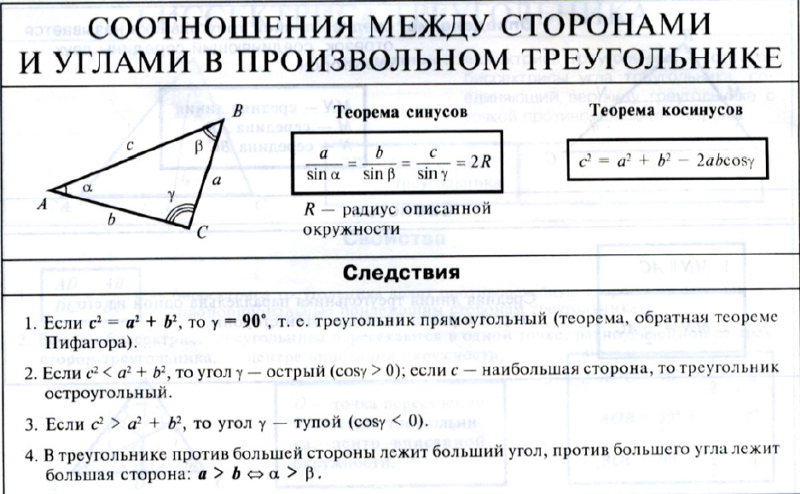
Не нужно обращаться к волшебному шару-восьмерке — эти правила работают всегда.
Почему это работает: 30-60-90 Доказательство теоремы о треугольнике
Но почему этот особый треугольник работает именно так? Откуда мы знаем, что эти правила законны? Давайте рассмотрим, как именно работает теорема о треугольнике 30-60-90, и докажем, почему эти длины сторон всегда будут постоянными.
Во-первых, давайте на секунду забудем о прямоугольных треугольниках и посмотрим на число 9.0009 равносторонний треугольник.
Равносторонний треугольник — это треугольник, у которого все стороны равны и все углы равны. Поскольку сумма внутренних углов треугольника всегда равна 180°, а $180/3 = 60$, равносторонний треугольник всегда будет иметь три угла по 60°.
Теперь опустим высоту от самого верхнего угла к основанию треугольника.
Теперь мы создали два прямых угла и два конгруэнтных (равных) треугольника.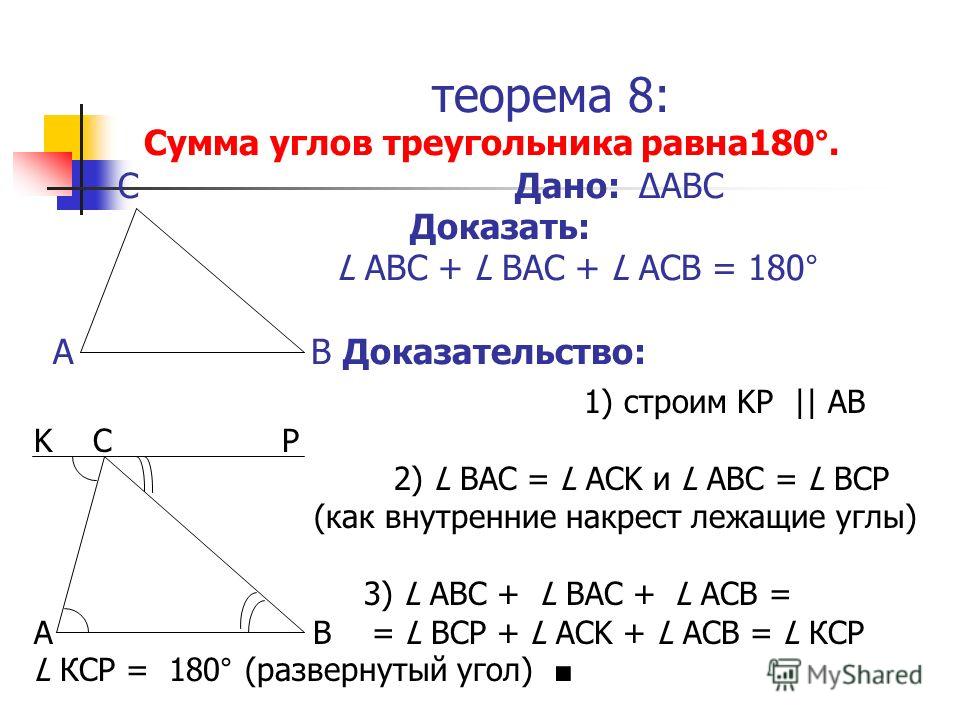
Откуда мы знаем, что это равные треугольники? Поскольку мы отбросили высоту от равностороннего треугольника , мы разделили основание ровно пополам. Новые треугольники также имеют одну общую длину стороны (высоту), и каждый из них имеет одинаковую длину гипотенузы. Поскольку они имеют три общие длины сторон (SSS), это означает, что треугольников конгруэнтны.
Примечание: два треугольника конгруэнтны не только на основе принципов длины стороны-стороны-стороны, или SSS, но и на основе мер сторона-угол-сторона (SAS), угол-угол-сторона (AAS ) и угол-сторона-угол (ASA). В основном? Они определенно конгруэнтны.
Теперь, когда мы доказали конгруэнтность двух новых треугольников, мы можем видеть, что каждый из верхних углов должен быть равен 30 градусам (поскольку каждый треугольник уже имеет углы 90° и 60° и должен составлять 180°). ). Это означает, что мы сделали два треугольника 30-60-90.
А поскольку мы знаем, что мы разрезаем основание равностороннего треугольника пополам, мы можем видеть, что сторона, противоположная углу в 30° (самая короткая сторона) каждого из наших 30-60-90 треугольников, равна половине длины гипотенузы. 92}/4$
92}/4$
$b = {√3x}/2$
Итак, у нас осталось: $x/2, {x√3}/2, x$
Теперь давайте умножим каждую меру на 2. , просто чтобы облегчить жизнь и избежать всех дробей. Таким образом, у нас остается:
$x$, $x√3$, $2x$
Таким образом, мы можем видеть, что треугольник 30-60-90 будет всегда иметь постоянную длину стороны $ x$, $x√3$ и $2x$ (или $x/2$, ${√3x}/2$ и $x$).
К счастью для нас, мы можем доказать 30-60-90 правил треугольника истинны без всего… этого.
Когда использовать правила треугольника 30-60-90
Знание правил треугольника 30-60-90 поможет вам сэкономить время и энергию при решении множества различных математических задач, а именно самых разнообразных геометрических и задачи по тригонометрии.
Геометрия
Правильное понимание треугольников 30-60-90 позволит вам решать вопросы геометрии, которые либо невозможно решить без знания этих правил соотношения, либо, по крайней мере, потребовали бы значительного времени и усилий для решения. решить «длинный путь».
решить «длинный путь».
С помощью специальных соотношений треугольников вы можете вычислить отсутствующие высоты треугольников или длины катетов (без использования теоремы Пифагора), найти площадь треугольника, используя недостающую информацию о высоте или длине основания, и быстро вычислить периметры.
Каждый раз, когда вам нужно быстро ответить на вопрос, вам пригодятся такие сокращения, как ваши правила 30-60-90.
Тригонометрия
Запоминание и понимание соотношения треугольников 30-60-90 также позволит вам решать многие задачи по тригонометрии без использования калькулятора или необходимости аппроксимировать ответы в десятичной форме.
Треугольник 30-60-90 имеет довольно простые синусы, косинусы и тангенсы для каждого угла (и эти измерения всегда будут согласованы).
Синус 30° всегда будет $1/2$.
Косинус 60° всегда равен $1/2$.
Хотя другие синусы, косинусы и тангенсы довольно просты, эти два проще всего запомнить, и они, скорее всего, появятся на тестах. Так что знание этих правил позволит вам найти эти тригонометрические измерения как можно быстрее.
Так что знание этих правил позволит вам найти эти тригонометрические измерения как можно быстрее.
Советы по запоминанию правил 30-60-90
Вы знаете, что эти правила соотношения 30-60-90 полезны, но как удержать информацию в голове? Чтобы запомнить правила треугольника 30-60-90, нужно помнить соотношение 1: √3 : 2 и знать, что самая короткая сторона всегда находится напротив самого короткого угла (30°), а самая длинная сторона всегда находится напротив угла. наибольший угол (90°).
Некоторые люди запоминают соотношение, думая: « $\bi x$, $\bo 2 \bi x$, $\bi x \bo √ \bo3$, «, потому что последовательность «1, 2, 3», как правило, легко запомнить. Единственная мера предосторожности при использовании этого метода состоит в том, чтобы помнить, что самая длинная сторона на самом деле равна $2x$, , а не $x$, умноженному на $√ 3$
Еще один способ запомнить ваши пропорции — это использовать мнемоническую игру слов с соотношением 1: корень 3: 2 в правильном порядке.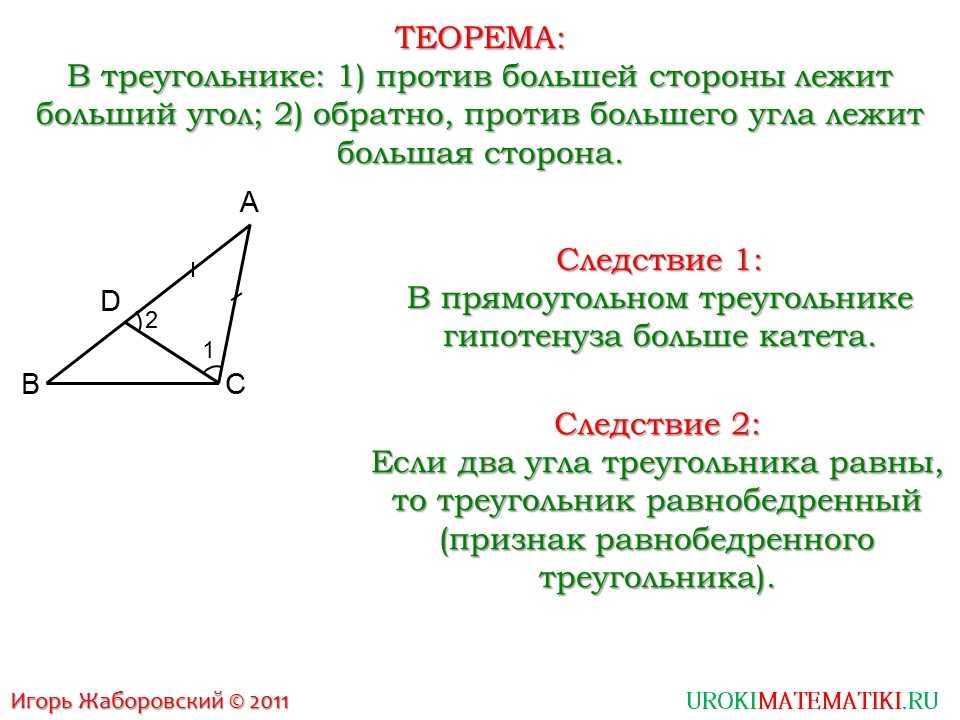 «: один, корень три, два. (И это настоящий факт из истории бейсбола!)
«: один, корень три, два. (И это настоящий факт из истории бейсбола!)
Поэкспериментируйте со своими мнемоническими приемами, если они вас не устраивают, — спойте отношение к песне, найдите свои собственные фразы «один, корень три, два» или придумайте стихотворение с отношением. Вы даже можете просто вспомнить, что треугольник 30-60-90 — это половина равностороннего треугольника, и вычислить измерения оттуда, если вам не нравится их запоминать.
Однако вам имеет смысл запомнить эти правила 30-60-90, держите эти отношения в голове для будущих вопросов по геометрии и тригонометрии.
Запоминание — ваш друг, но вы можете его заставить.
Пример 30-60-90 Вопросы
Теперь, когда мы рассмотрели как и почему треугольники 30-60-90, давайте поработаем над некоторыми практическими задачами.
Геометрия
Строитель прислоняет 40-футовую лестницу к стене здания под углом 30 градусов к земле. Земля ровная, а сторона здания перпендикулярна земле. Как далеко вверх по зданию доходит лестница с точностью до ближайшего фута?
Земля ровная, а сторона здания перпендикулярна земле. Как далеко вверх по зданию доходит лестница с точностью до ближайшего фута?
Не зная наших специальных правил треугольника 30-60-90, нам пришлось бы использовать тригонометрию и калькулятор, чтобы найти решение этой задачи, поскольку у нас есть только одна сторона треугольника. Но поскольку мы знаем, что это особый треугольник из числа , мы можем найти ответ за считанные секунды.
Если здание и земля перпендикулярны друг другу, это должно означать, что здание и земля образуют прямой угол (90°). Также известно, что лестница касается земли под углом 30°. Таким образом, мы видим, что оставшийся угол должен быть равен 60°, что делает его равным 30-60-9.0 треугольник.
Теперь мы знаем, что гипотенуза (самая длинная сторона) этого числа 30-60-90 равна 40 футам, а это значит, что самая короткая сторона будет вдвое меньше. (Помните, что самая длинная сторона всегда в два раза — $2x$ — длиннее самой короткой стороны. ) Поскольку самая короткая сторона находится напротив угла в 30°, а этот угол — градусная мера лестницы от земли, это означает, что верхняя часть лестницы ударяется о здание в 20 футах от земли.
) Поскольку самая короткая сторона находится напротив угла в 30°, а этот угол — градусная мера лестницы от земли, это означает, что верхняя часть лестницы ударяется о здание в 20 футах от земли.
Наш окончательный ответ: 20 футов.
Тригонометрия
Если в прямоугольном треугольнике sin Θ = $1/2$ и длина кратчайшего катета равна 8. Какова длина недостающей стороны, которая НЕ является гипотенузой?
Поскольку вы знаете правила 30-60-90, вы можете решить эту задачу, не прибегая ни к теореме Пифагора, ни к калькулятору.
Нам сказали, что это прямоугольный треугольник, а из наших специальных правил прямоугольного треугольника мы знаем, что синус 30° = $1/2$. Таким образом, недостающий угол должен составлять 60 градусов, что делает это 30-60-9.0 треугольник.
И поскольку это треугольник 30-60-90, и нам сказали, что самая короткая сторона равна 8, гипотенуза должна быть равна 16, а недостающая сторона должна быть равна $8 * √3$, или $8√3$.
Наш окончательный ответ 8√3.
Выводы
Запоминание правил для треугольников 30-60-90 поможет вам быстрее решать различные математические задачи . Но имейте в виду, что хотя знание этих правил и является удобным инструментом, который можно всегда носить на поясе, вы все же можете решить большинство проблем без них.
Следите за правилами $x$, $x√3$, $2x$ и 30-60-90 любым удобным для вас способом и старайтесь соблюдать их, если можете, но не паникуйте, если ваш разум отключается, когда наступает решающий момент. В любом случае, у вас есть это.
А если вам нужно больше практики, пройдите тест на треугольник 30-60-90. Удачной сдачи теста!
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша база проверенных преподавателей включает в себя ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления.