Понятие логарифма. Свойства логарифмов. | Презентация к уроку по алгебре (11 класс) на тему:

Опубликовано 30.11.2017 — 18:25 — Кудейкина Татьяна Юрьевна

Краткое содержание.
 

1. Определение логарифмов. Основное логарифмическое тождество.
2. Свойства логарифмов:

• логарифм произведения, частного и степени,
• формула перехода от одного основания логарифма к другому.

3. Десятичные и натуральные логарифмы, число .
4. Типичные ошибки при решении задач с логарифмами.
5. Тождественные преобразования логарифмических выражений.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Понятие логарифма. Свойства логарифмов.

Слайд 2

Определение логарифма. Логарифмом положительного числа b по положительному и отличному от 1 основанию а называется показатель степени, в которую надо возвести число а , чтобы получить число b .

Слайд 5

Вычислите:

Слайд 6

Виды логарифмов Обыкновенные Десятичные Натуральные

Слайд 7

Обыкновенные логарифмы : Читается: «логарифм 7 по основанию 2»

Слайд 8

Натуральные логарифмы : Читается: «натуральный логарифм 5»

Слайд 9

Десятичные логарифмы : Читается: «десятичный логарифм 3»

Слайд 10

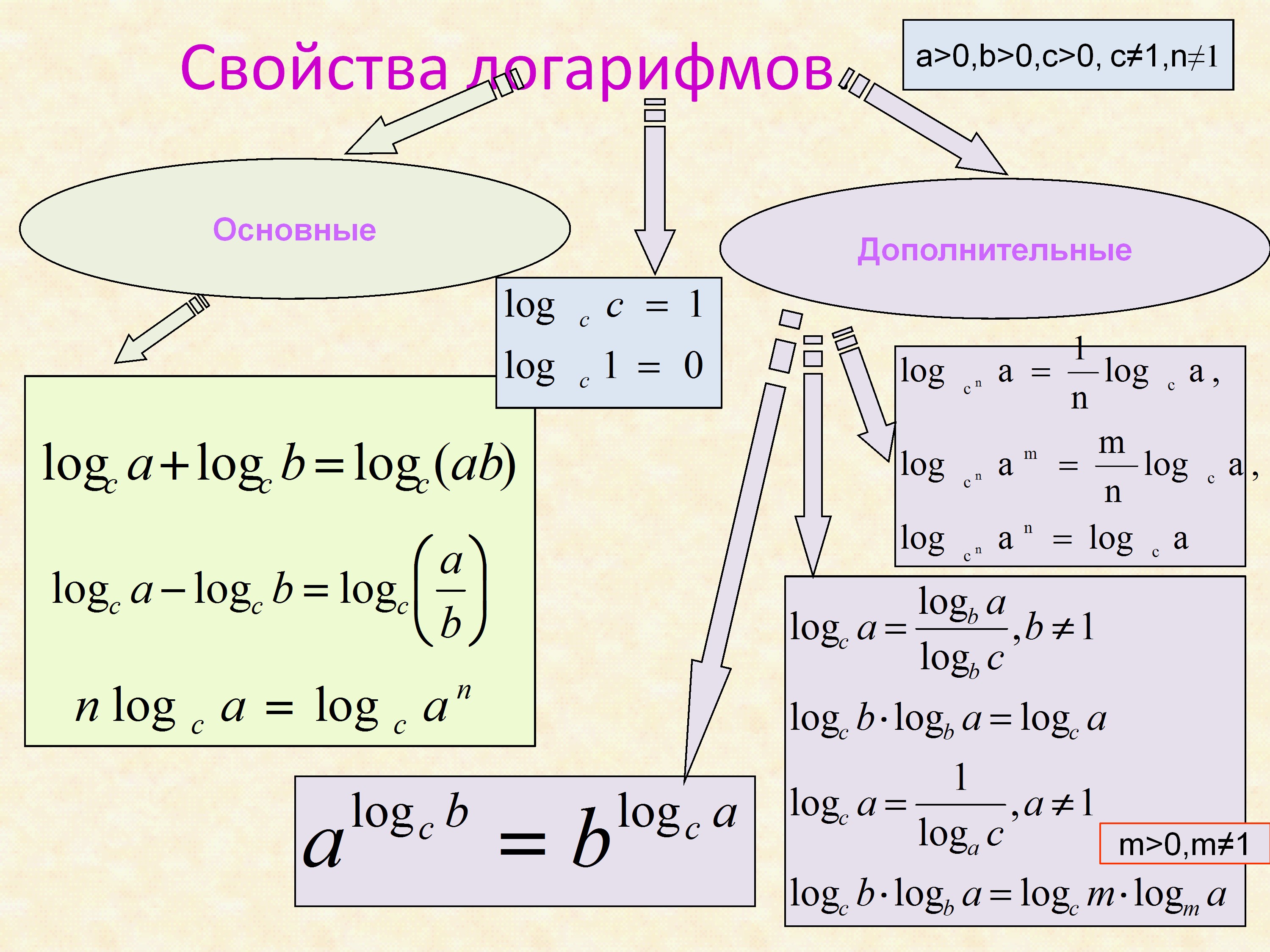
Свойства логарифмов

Слайд 11

Свойства логарифмов

Слайд 12

Свойства логарифмов т. е. логарифм произведения равен сумме логарифмов сомножителей (взятых по тому же основанию). log 6 2 + log 6 3= log 6 ( 2 ∙ 3 ) = log 6 6=1

Слайд 14

Вычислите: log 18 2 + log 18 9 log 4 8 + log 4 32 log 32 2 + log 32 2 lg 40 + lg 25 1 4 0, 2 3

Слайд 15

Свойства логарифмов

Слайд 16

Свойства логарифмов

Слайд 18

Вычислите: log 6 2 16 — log 6 3 6 log 3 243 – log 3 27 l og 0,2 40 — log 0,2 8 log 2 64 – log 2 4 1 2 -1 4

Слайд 19

Свойства логарифмов

Слайд 21

Вычислите: 3 4 16 0,01

Слайд 22

Примеры

Слайд 23

Вычислите: 1 2 3 2 0,5

Слайд 24

Справочная информация.

По теме: методические разработки, презентации и конспекты

конспект урока по теме: «Логарифм. Свойства логарифмов»

Урок обобщения и систематизации знаний. Основной целью является: повторить определение логарифма, свойства логарифмов и применять их при решении заданий. В данной разработке представлены материалы для. ..

Логарифмы. Свойства логарифмов.

Повторить, закрепить знания теоретического материала по теме. Продолжить формирование практических умений при решении задач. Проверить  знания учащихся по данной теме….

Тема «Определение логарифма. Свойства логарифмов»

Задания с подробным образцом решения.Этот материал может использоваться при работе со слабоуспевающими учащимися, для самостоятельного изучения темы часто болеющими учащимися….

Урок по теме «Логарифмы. Свойства логарифмов»

Урок обобщения и закрепления знаний….

Определение логарифма. Свойства логарифма.

1) понятие логарифма2) отрабатывается определения логарифма…

Тренировочные упражнения по теме:»Логарифмы. Свойства логарифмов»

Даны тренировочные упражнения на вычисление логарифмов и применение свойств логарифмов. Приведены ответы к заданиям….

Урок по теме «Логарифм. Свойства логарифмов.»

Технологическая карта урока…

Поделиться:

 

Основные свойства логарифмов

Тип урока: комбинированный.

Вид урока: урок совершенствования знаний, умений и навыков.

Методы и приёмы: информационный, частично-поисковый, словесный, наглядный.

Формы работы: индивидуальная, групповая, коллективная, устная, письменная.

Цели урока:

Образовательные:

• повторить определение логарифма;
• познакомиться с основными свойствами логарифмов;
• научиться применять свойства логарифмов при решении упражнений.

Развивающие:

• Развивать способности к самостоятельному планированию и организации работы;
• Развивать мыслительную деятельность обучающихся, формировать умения чётко и ясно излагать свои мысли.

Воспитательные:

• Воспитывать умение работать с имеющейся информацией.
• Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность.
• Воспитывать интерес к предмету и потребности в приобретении знаний.

Используемое оборудование: компьютер, мультимедийная установка, Мультимедийная презентация «Логарифмы и их свойства», тесты, карточки для индивидуальной работы.

Ход урока

Эпиграф к уроку:

Три пути ведут к знанию:

путь размышления — это путь самый благородный,

путь подражания — это путь самый легкий и
путь опыта — это путь самый горький.
Конфуций

1. Организационный момент

— Значит, на уроке мы будем размышлять, подражать, т.е. делать по образцу и набираться опыта.

Начнём его с разминки.

Разминка. На экране помещается слайд с кроссвордом из 8 математических вопросов.

Вопросы:

1. Граница отрицательных и положительных чисел. (ноль)
2. Решение уравнения? (корень)
3. Часть математики, которую изучаем в настоящее время? (алгебра)
4. Равенство, содержащее переменное?. (уравнение)
5. Равенство двух отношений. (пропорция)
6. Выражение Д=в2-4ас при решении квадратного уравнения? (дискриминант)
7. Как называется функция вида? (подскажу сама — логарифмическая)),
8. Как называется независимая переменная? (аргумент)

Преподаватель задаёт вопросы, при правильном ответе на которые кроссворд на слайде заполняется и даёт ключевое слово «Логарифм».
Какое ключевое слово у нас получилось, что выучили дома на сегодня? — спрашивает преподаватель.

Студенты отвечают: — Логарифм.

2. Проверка домашнего задания

Вычислим устно: На экране появились вопросы, на которые студенты должны были ответить дома. Появляются на экране правильные ответы. Студенты проверяют свои ответы, если что-то не правильно, то исправляют. Преподаватель проверяет у студентов домашнее задание, проходя между рядами.

Повторение теории.

На экране по одному появляются теоретические вопросы, на которые обучающиеся отвечают устно.

— Что называется логарифмом числа в по основанию а?

— Какими могут быть числа а, в?

— Какую формулу называют основным логарифмическим тождеством?

После ответов обучающихся, на экране появляется правильный ответ.

3. Изучение нового материала

— Сегодня на уроке мы повторили определение логарифма, основное логарифмическое тождество, дальше мы научимся определять свойства логарифмов( цели урока), которые значительно упрощают нахождение значений выражений, содержащих логарифмы, а в дальнейшем с их помощью мы будем решать логарифмические уравнения и неравенства.

Итак:

— Тема урока «Логарифмы и их основные свойства».

— Открываем тетради и записываем число и тему урока.

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день.

Итак, приступим.

Перечислим основные свойства логарифмов:

В заключение скажу про два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» обучающихся.

1. log_a a
   = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
2. log_a 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому, что a⁰ = 1 — это прямое следствие из определения.

4. Проверка знаний: тренировочные упражнения-закрепления

— Мы изучили свойства логарифмов, теперь проверим, как вы ими можете пользоваться (работа у доски).

№495 (а, в), №496(в,г).

1.Вычислите:

1. log₃6 + log₃18 — log₃4

2. log

124 + log₁₂36

3. log₂11- log₂44

4. log_0,39 — 2log_0,310

Тест по теме

log3135 — log35;	А) 130; Б) 3; В) 27; Г) 15.
log171	А) 17; Б)0; В) 117; Г) 1.
log375 — log325;	А) log350; Б) 3; В) 1; Г)15.
log0,416 — 2 log0,410;	А) 12; Б) 2; В) — 12; Г) 0,16.

— Вы демонстрировали свои умения в решении упражнений по теме «Логарифмы и их основные свойства» — вы размышляли, подражали и набирались опытом.

— Закончить урок хочется словами известного математика Мориса Клайна:

«Музыка может возвышать или умиротворять душу,
Живопись — радовать глаз,
Поэзия — пробуждать чувства,
Философия — удовлетворять потребности разума,
Инженерное дело — совершенствовать материальную сторону жизни людей, а Математика способна достичь всех этих целей.

Группе студентов было дано задание на сегодняшний урок: подготовить сообщение — презентация, в виде нескольких слайдов: «Из истории возникновения логарифмов», даем одному из них слово.

5. История возникновения логарифмов

Домашнее задание

1. Выучить свойства логарифмов
2. Учебник: § 10, П37 стр. 232-233;

Используемая литература

1. Алгебра и начала математического анализа : учеб. для 10-11 кл. общеобразоват. учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.] ; под ред. А.Н.Колмогорова. — 17-е изд. — М.: Просвещение, 2013.

Литература

1. А. Н. Колмогоров и др «Алгебра и начала анализа» 10 — 11 класс.
2. С.М. Никольский и др. «Алгебра и начала анализа» 11 класс.
3. М.И. Сканави «Сборник задач по математике».
4. Н. В. Богомолов «Практические занятия по математике»
5. Журнал «Математика в школе».

6. Рефлексия

В конце урока мне бы хотелось вам сказать: Спасибо за урок!

Свойства логарифмов

Свойства логарифмов

Реклама

1 из 29

Верхний вырезанный слайд

Скачать для чтения офлайн 2 Объявление

Объявление

Свойства логарифмов

1. Свойства логарифмов
2. Поскольку логарифмы и экспоненты одного основания являются обратными функциями друг друга, они «отменяют» друг друга. Помните, что: Это означает, что: инверсии «отменяют» друг друга = 5 = 7
3. CONDENSED EXPANDED Свойства логарифмов = = = = (эти свойства основаны на правилах экспонент, поскольку логарифмы = экспоненты) 3. 2. 1.
4. Используя свойства логарифма, запишите выражение в виде суммы и/или разности логарифмов (расширять). используя второе свойство: при работе с журналами перепишите любые радикалы как рациональные показатели степени. используя первое свойство: используя третье свойство:
5. Используя свойства журнала, запишите выражение в виде одинарного логарифма (уплотнить). используя третье свойство: используя второе свойство: в этом направлении в этом направлении
11. Запишите следующее выражение в виде единичного логарифма.
13. Дополнительные свойства логарифмов Здесь говорится, что если у вас есть уравнение, вы можете взять логарифм обеих сторон, и равенство все равно будет выполнено. Здесь говорится, что если у вас есть уравнение, и каждая его сторона имеет логарифм одного и того же основания, вы знаете, что такое «материал». вы берете журналы равны.
14. (2 к чему равно 8?) (2 к чему равно 16?) (2 к чему равно 10?) На это есть ответ, и он должен быть больше 3, но меньше 4, но мы можем не делайте этого в нашей голове. Положим его равным х и будем решать за х. Переход к экспоненциальной форме. использовать свойство журнала и взять журнал с обеих сторон (мы будем использовать общий журнал) использовать 3-е свойство журнала решить для x путем деления на журнал 2 использовать калькулятор для приблизительной проверки, подставив 2 3,32 в свой калькулятор (мы округлили, чтобы это не было точно)
15. Двойной и натуральный логарифмы
20. Используйте формулу изменения основания и калькулятор для аппроксимации логарифма. Округлите ответ до трех знаков после запятой. Поскольку 3 2 = 9 и 3 3 = 27, наш ответ о том, какой экспонент положил 3, чтобы довести его до 16, будет чем -то между 2 и 3. Поместите в калькулятор
26. Решение
27. Решение
28. Благодарность Я хочу поблагодарить Шону Хейдер из Общественного колледжа Солт-Лейк-Сити, штат Юта, США, за ее усердную работу по созданию этой PowerPoint. www.slcc.edu Шона любезно разрешила загрузить этот ресурс с сайта www.mathxtc.com и изменить его в соответствии с учебным планом по математике Западной Австралии. Стивен Коркоран Глава школы математики Святого Стефана в Каррамаре www.ststephens.wa.edu.au
29. Формула смены базы Основой, на которую вы меняете, может быть любая база, поэтому, как правило, мы хотим перейти на базу, чтобы использовать наш калькулятор. Это будет либо основание 10, либо основание e . «обычная» логарифмическая база 10 «естественная» логарифмическая база e Пример для TI-83 Если мы обобщим процесс, который мы только что сделали, мы получим: LOG LN

Реклама

Логарифмические свойства

Логарифмические свойства Вернуться к оглавлению

Числа и их применение — Урок 17

Обзор урока

• Определение логарифма
• Четыре основных свойства журналов
• Логарифмическая линейка
• Применение логарифмов
• Домашнее задание

Логарифм является показателем степени.

Обратите внимание, вышеприведенное не является определением , а просто содержательным описанием.

Так как вычитание является обратной операцией сложения, а извлечение квадратного корня — это операция, обратная возведению в квадрат, возведение в степень и логарифмирование являются обратными операциями. В поисках

антилог это обратная операция поиска лога, так это другое название возведения в степень. Однако исторически это делалось как поиск по таблице. Некоторая история была дана ранее и формальное определение повторяется ниже, на этот раз с ограничениями.

y = log b x тогда и только тогда, когда b y = x , где x > 0, б > 0 и б 1.

Как отмечалось выше, основанием может быть любое положительное число (кроме 1). Однако чаще всего используются два варианта: 10 и е = 2,718281828. … Журналы с основанием 10 часто называют общими логами , тогда как бревна по базе e часто называют натуральными бревнами . Логи к базам 10 и и теперь оба довольно стандартны для большинства калькуляторов. Часто при взятии лога база произвольная и не нужна уточнять. Однако в другое время необходимо и должно быть принятым или заданным.

Только на уровне средней школы, log x последовательно означает log 10 x . В колледже, особенно по математике и физике, log x последовательно означает log e x . Популярное обозначение (которое презирают): ln x означает log e x .

Для расчета логов на другие базы, следует использовать изменение базового правила, приведенное ниже (#4). Это всего лишь умножение на константу (1/log _а б ).

log b ( xy ) = log b x + log b и . log b ( x/y ) = log b x — log b 9010 2 и . бревно б ( х н ) = н бревно б х . бревно б x = бревно a x / бревно a 901 06 б .

Все эти четыре основных свойства вытекают непосредственно из того факта, что журналы являются показателями степени. На словах первые три можно запомнить как: Лог произведения равен сумме логов факторов. Лог частного равен разнице между логами числителя и демонинатора. Журнал мощности равен произведению мощности на логарифм основания.

Перечислены дополнительные свойства, некоторые очевидные, некоторые не столь очевидные ниже для справки. Число 6 называется взаимным свойством .

log b 1 = 0.           log b b = 1.           90 022 бревно б б 2 = 2.          бревно б б х = х . б журнал б х = х . log a b = 1/log b a .

Изобретение бревен быстро последовало изобретение логарифмической линейки. Логарифмические правила упрощают умножение и деление путем преобразования этих операций в сложение и вычитание. Это делается путем размещения чисел на шкале, которая является логарифмической. Ниже приведены журналы некоторых небольших целых чисел.

n	бревно 10 n	бревно e n 9 0102
1	0,000	0,000
2	0,301	0,693
3	0,477	1,099
4	0,602	1,386
5	0,699	1,609
6	0,778	1,792
7	0,845	1,946
8	0,903	2,079
9	0,954	2,197
10	1,000	2,303

Отсюда легко проверить такие свойства, как: log 10 = log 2 + log 5 и log 4 = 2 log 2. Это верно для любого основания. На самом деле полезный результат 10 ³ = 1000 1024 = 2 ¹⁰ легко увидеть как 10 журнал ₁₀  2 3.

Логарифмическая линейка ниже представлена ​​в разобранном состоянии для облегчения резки. (Кроме того, поместив его ниже, он будет внизу страницы 3 и будет пустым бумага за ним.) Верхняя часть скользит по центру нижней части и должна распечатать, а затем вырезать для демонстрационных целей следующим образом.

1. Совместите левую 1 на шкале D с 2 на шкале C. Соблюдайте число выше 4 по шкале D по шкале C. Так как эти числа разложены в логарифмическом масштабе, вы показали, что log 2 + log 4 = log (2×4) = log 8. Обведите цифру 8.
2. Совместите правую 1 на шкале D с 4 на шкале C. Соблюдайте число ниже левой 1 по шкале C. Вы только что показали, что log 10 — log 4 = log 2,5. Обведите 2,5.
3. Совместите шкалу D и шкалу A. Шкала A выложена аналогично, за исключением присутствуют два цикла. Обратите внимание на число чуть выше 9 по шкале D. Вы только что показали, что 2 log 9 = log 9 ² = log 81. Обведите 81.
4. Посмотрите, как шкалу К можно использовать для кубирования вещей.
5. Обратите внимание, что шкалу CI также можно использовать для деления.

Обычно там курсор (исходное значение, а не мерцание на экране компьютера) присутствует, что позволяет получить около трех знаков после запятой, отсюда термин точность логарифмической линейки . Журналы используются в различных приложениях в науке, некоторые из наиболее распространены: измерение громкости (децибелы), измерение интенсивности землетрясений (Шкала Рихтера), радиоактивный распад и кислотность (pH= -log ₁₀ [H ⁺ ]). Они необходимы в математике для решения некоторых задач экспоненциального типа.

Ниже приводится интересная задача, которая связывает квадратичную формулу: логарифмы и экспоненты вместе очень аккуратно.

log(2 x +2) + log x — log(12) = 0 Упростите логарифмы, объединив их.
log(2 x ² + 2 x ) — log(12) = 0
лог(( 2x ² + 2x )/12) = 0
После деления на 2 возведите в степень обе части (основание b произвольное, так как это не было указано выше)!
( х ² + х )/6 = б ⁰
( х ² + х )/6 = 1
х ² + х = 6
х 901 10 2 + х — 6 = 0
( х + 3)( х — 2) = 0 x {-3, 2}

 

 

Пустое место, поэтому при печати с помощью Mozilla (упс, без полей) оно находится позади логарифмической линейки.

 

 

Однако х -3 поскольку домен журнала — это только положительные реалы. ( b ^x никогда не может быть отрицательным числом с b > 0).

В следующем примере (6.11#51) логарифмы сочетаются с одновременными уравнениями. Это также очень удобно ввести понятие подстановки, столь полезное в исчислении.

log ₉ x + log _y 8 = 2.   
логарифм _x 9 + логарифм ₈ у = 8/3.

Пусть u = log ₉ x и v = log ₈ y . По взаимному свойству выше, 1/u = log _x 9 и 1/v = log _y 8.

Теперь мы можем переписать наши уравнения как:

u + 1/ v = 2   
1/ u + v = 8/3 Решение подстановкой, u = 2 — 1/ v , таким образом: 1/(2 — 1/ v ) + v = 8/3.
3(1 + 2 v — 1) = 8(2 — 1/ v )
6 v ² = 16 v — 8.
6 v ² — 16 v + 8 = 0.
3 v ² — 8 v + 4 = 0.
Применим к этому квадратичную формулу и найдем, что
v = (8 ± (64 — 48))/6.
= (8 ± 4)/6 или 2, 2/3.
Таким образом, u = 3/2 или 1/2 или ( и , v )={(3/2, 2), (1/2, 2/3)}
Таким образом ( x , y ) = {(27, 64), (3, 4)}

ЗАДНЯЯ ЧАСТЬ	ДОМАШНЕЕ ЗАДАНИЕ	ДЕЯТЕЛЬНОСТЬ	ПРОДОЛЖИТЬ

---

• электронная почта: [email protected]
• голос/почта: 269 471-6629; BCM&S Smith Hall 105; Университет Эндрюса;
• факс/аудитория: 269 471-6646; Смит Холл 100; Берриен Спрингс, Мичиган, 49104-0140
• домашний: 269 473-2572; 610 Н. Главная улица; Берриен Спрингс, Мичиган 49103-1013
• URL-адрес: http://www.