Решение систем неравенств с одной переменной

Вы можете изучить и скачать доклад-презентацию на тему Решение систем неравенств с одной переменной. Презентация на заданную тему содержит 12 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Презентации» Образование» Решение систем неравенств с одной переменной

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Решение систем неравенств с одной переменной

---

---

Слайд 2

Описание слайда:

Математика учит преодолевать трудности и исправлять собственные ошибки

---

Слайд 3

Описание слайда:

---

Слайд 4

Описание слайда:

---

Слайд 5

Описание слайда:

---

Слайд 6

Описание слайда:

---

Слайд 7

Описание слайда:

---

Слайд 8

Описание слайда:

Алгоритм решения систем неравенств 1) решить каждое неравенство системы 2)изобразить решение каждого неравенства данной системы на одной числовой прямой 3) записать решение системы, используя скобки 4) записать ответ

---

Слайд 9

Описание слайда:

Найти все решения системы неравенств и записать ответ с помощью числового промежутка: х>5 х<8 Ответ: (5;8)

---

Слайд 10

Описание слайда:

Решите систему неравенств 3х-5>1 2х-1<11 3х> 1+5 2х<11+1 3х > 6 2х<12

---

Слайд 11

Описание слайда:

х>6 :3 Х<12 :2 х>2 х<6 Ответ: 2; 6)

---

Слайд 12

Описание слайда:

Желаю вам цвести, расти, Копить, крепить здоровье, Оно для дальнего пути – Главнейшее условие.

Пусть каждый день и каждый час Вам новое добудет, Пусть добрым будет ум у вас И сердце умным будет

---

Tags Решение систем неравенств с одной переменной

Похожие презентации

Презентация успешно отправлена!

Ошибка! Введите корректный Email!

Email

Презентация по математике «Решение систем неравенств с одной переменной»; 9 класс — Презентации — Математика, алгебра, геометрия

Егорова Елена 5.0

Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям

Хочу выразить большую благодарность от лица педагогов начальных классов гимназии «Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу.

С начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у нас пока нет, одни благодарности. Очень простая и понятная инструкция, что немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда коллеги понимают, как можно «упростить» работу учителя.

Наговицина Ольга Витальевна 5.0

учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ

Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология. Очень облегчило аналитическую работу, выявляются узкие места в подготовке к экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.

Чазова Александра 5. 0

Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ

Очень хороший шаблон, удобен в использовании, анализ пробного тестирования занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз разобраться. Большое спасибо за качественный анализатор.

Лосеева Татьяна Борисовна 5.0

учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса

Большое спасибо за оперативное изготовление сертификатов! Все очень красиво. Мой ученик доволен, свой сертификат он вложил в портфолио. Обязательно продолжим с Вами сотрудничество!

Язенина Ольга Анатольевна 4.0

учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы

Я посмотрела вебинар! Осталась очень довольна полученной информацией.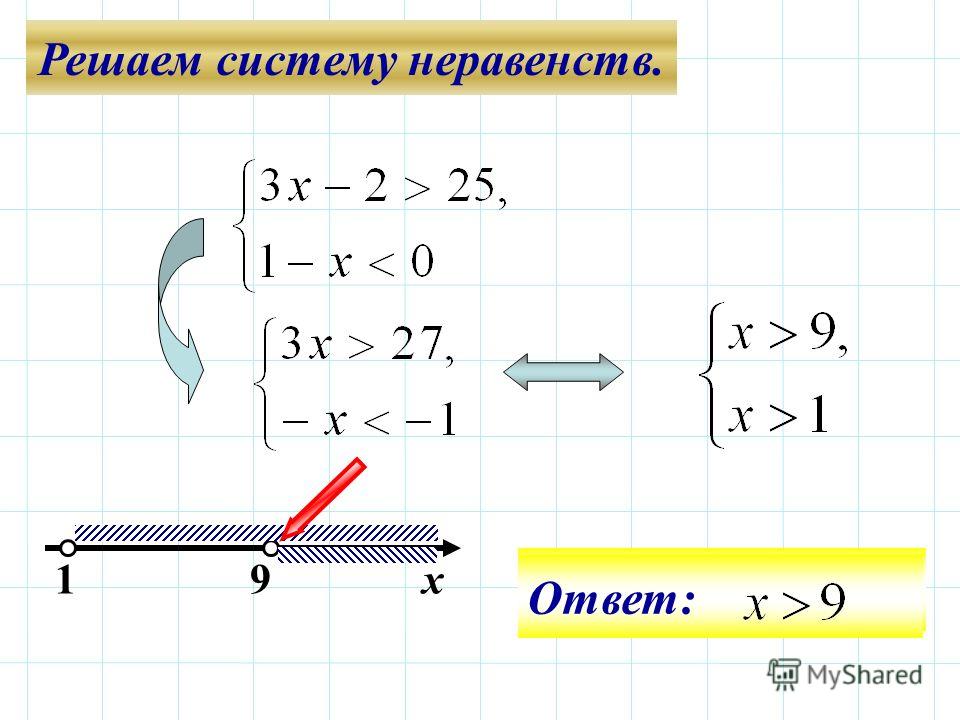 Всё очень чётко, без «воды». Всё, что сказано, показано, очень пригодится в практике любого педагога. И я тоже обязательно воспользуюсь полезными материалами вебинара. Спасибо большое лектору за то, что она поделилась своим опытом!

Арапханова Ашат 5.0

ША Табель посещаемости + Сводная для ДОУ ОКУД

Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень аккуратно и оперативно. Нет ни одного недостатка.

Я не пожалела, что доверилась и приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же составляю табель для работников. Удачи и успехов Вам в дальнейшем!

Дамбаа Айсуу 5.0

Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ

Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и особенно радует, что есть варианты с сочинением, без сочинения, только анализ сочинения! Превосходно!

Графики и решения систем линейных уравнений

Результаты обучения

• Графические системы уравнений
  • График системы двух линейных уравнений
  • Нарисуйте график системы двух линейных неравенств
• Оцените упорядоченные пары как решения для систем
  • Определить, является ли упорядоченная пара решением системы линейных уравнений
  • Определить, является ли упорядоченная пара решением системы линейных неравенств
• Классифицировать решения для систем
  • Определить тип решения системы на основе ее графа

 

То, как течет река, зависит от многих переменных, в том числе от того, насколько велика река, сколько в ней воды, какие предметы плавают в реке, идет ли дождь и так далее. Если вы хотите лучше всего описать его поток, вы должны принять во внимание эти другие переменные. В этом может помочь система линейных уравнений.

Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Вы найдете системы уравнений в каждом приложении математики. Они являются полезным инструментом для обнаружения и описания того, как поведение или процессы взаимосвязаны. Например, редко можно найти модель транспортного потока, на которую влияет только погода. Аварии, время суток и крупные спортивные мероприятия — это лишь некоторые из других переменных, которые могут повлиять на транспортный поток в городе. В этом разделе мы рассмотрим некоторые основные принципы построения графика и описания пересечения двух линий, составляющих систему уравнений.

Нарисуйте график системы линейных уравнений

В этом разделе мы рассмотрим системы линейных уравнений и неравенства с двумя переменными. Сначала мы попрактикуемся в построении графиков двух уравнений на одной и той же системе осей, а затем рассмотрим различные соображения, которые необходимо учитывать при построении графиков двух линейных неравенств на одной и той же системе осей. Для построения графика системы линейных уравнений используются те же методы, что и для построения отдельных линейных уравнений. Мы можем использовать таблицы значений, наклона и y — точка пересечения, или x — и y — точки пересечения для построения обеих линий на одном наборе осей.

Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс]\begin{array}{r}2x+y=-8\\ x-y=-1\end{array}[/latex]

Давайте нарисуем их, используя форму пересечения наклона на том же наборе осей. . Помните, что форма пересечения наклона выглядит как [latex]y=mx+b[/latex], поэтому нам нужно решить оба уравнения для [latex]y[/latex].

Сначала найдите y в [латекс]2x+y=-8[/латекс]

[латекс]\begin{array}{c}2x+y=-8\\ y=-2x — 8\end {array}[/latex]

Во-вторых, найдите y в [latex]x-y=-1[/latex]

[latex]\begin{array}{r}x-y=-1\,\,\,\ ,\,\\ y=x+1\end{array}[/latex]

Теперь система записывается как

[latex]\begin{array}{c}y=-2x — 8\\y= x+1\end{array}[/latex]

Теперь вы можете построить графики обоих уравнений, используя их наклоны и точки пересечения на одном и том же наборе осей, как показано на рисунке ниже. Обратите внимание, что графики имеют одну общую точку. Это их точка пересечения, точка, которая лежит на обеих линиях. В следующем разделе мы проверим, что эта точка является решением системы.

 В следующем примере вам будет предложена система для построения графика, состоящего из двух параллельных линий.

Пример

Постройте график системы [латекс]\begin{array}{c}y=2x+1\\y=2x-3\end{массив}[/latex], используя наклоны и точки пересечения y линий .

Показать раствор

В следующем примере вам будет дана система, уравнения которой выглядят по-разному, но после построения графика оказываются одной и той же линией.

Пример

Постройте график системы [latex]\begin{array}{c}y=\frac{1}{2}x+2\\2y-x=4\end{array}[/latex], используя x — и y-перехваты.

Показать раствор

Построение графика системы линейных уравнений состоит из выбора метода построения графика, который вы хотите использовать, и построения графиков обоих уравнений на одном и том же наборе осей. Когда вы рисуете систему линейных неравенств на одном и том же наборе осей, вам нужно учитывать еще несколько моментов.

Нарисуйте график системы двух неравенств

Помните из модуля по построению графиков, что график одного линейного неравенства расщепляет координатную плоскость на две области. На одной стороне лежат все решения неравенства. С другой стороны решений нет. Рассмотрим график неравенства [latex]y<2x+5[/latex].

Пунктирная линия: [латекс]у=2х+5[/латекс]. Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте подставить в неравенство x и y координаты точек A и B — вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.

Линия границы делит координатную плоскость пополам. В данном случае она показана пунктирной линией, так как точки на прямой не удовлетворяют неравенству. Если бы неравенство было [латекс]y\leq2x+5[/латекс], то граница была бы сплошной.

Нарисуем другое неравенство: [латекс]у>-х[/латекс]. Вы можете проверить пару точек, чтобы определить, какую сторону линии границы следует заштриховать. Проверка точек M и N дает верные утверждения. Итак, заштриховываем область над линией. Линия пунктирная, так как точки на прямой не соответствуют действительности.

Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств. Давайте использовать [латекс]y<2x+5[/латекс] и [латекс]у>-х[/латекс], так как мы уже построили график каждого из них.

Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [латекс]у>-х[/латекс], так и для [латекс]у<2x+5[/латекс].

В следующем примере вам дана система двух неравенств, граничные линии которых параллельны друг другу.

Примеры

График системы [латекс]\начало{массив}{с}у\ге2х+1\\у\lt2x-3\конец{массив}[/латекс]

Показать решение

В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.

Определите, является ли упорядоченная пара решением системы линейных уравнений

Линии на приведенном выше графике определены как

[латекс]\начало{массив}{r}2x+y=-8\\ x-y=-1\конец{массив}[/латекс].

Они пересекаются в месте, похожем на [латекс]\влево(-3,-2\вправо)[/латекс].

Используя алгебру, мы можем проверить, что эта общая точка на самом деле [латекс]\влево(-3,-2\вправо)[/латекс], а не [латекс]\влево(-2,999,-1,999\вправо)[/ латекс]. Подставляя значения x и y упорядоченной пары в уравнение каждой линии, вы можете проверить, находится ли точка на обеих линиях. Если подстановка дает верное утверждение, значит, вы нашли решение системы уравнений!

Поскольку решение системы должно быть решением всех уравнений в системе, вам нужно будет проверить точку в каждом уравнении. В следующем примере мы заменим -3 на x и -2 на y в каждом уравнении, чтобы проверить, действительно ли это решение.

Подумай об этом

Является ли [латекс](−2,4)[/латекс] решением для системы

[латекс]\begin{array}{r}y=2x\\3x+2y=1\ end{array}[/latex]

Прежде чем делать какие-либо вычисления, посмотрите на заданную точку и первое уравнение в системе. Можете ли вы предсказать ответ на вопрос, не занимаясь алгеброй?

Показать раствор

Помните, что для решения системы уравнений значения точки должны быть решением обоих уравнений. Как только вы найдете одно уравнение, для которого точка неверна, вы определили, что оно не является решением системы.

Мы можем использовать тот же метод, чтобы определить, является ли точка решением системы линейных неравенств.

Определить, является ли упорядоченная пара решением системы линейных неравенств

На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, поскольку их координаты делают оба утверждения неравенства верными.

Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [латекс]y>−x[/латекс], а точка А является решением неравенства [латекс]у<2x+5[/латекс], ни одна из точек не является решением система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.

Вот график системы в приведенном выше примере. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия двух неравенств.

Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).

Как показано выше, найти решения системы неравенств можно путем построения графика каждого неравенства и определения области, которую они разделяют. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графе для системы двух линейных неравенств. Общие шаги описаны ниже:

• Изобразите каждое неравенство в виде линии и определите, будет ли она сплошной или пунктирной
• Определите, какая сторона каждой граничной линии представляет решения неравенства, проверив точку на каждой стороне
• Закрасьте область, представляющую решения для обоих неравенств

В этом разделе мы видели, что решения систем линейных уравнений и неравенств могут быть упорядочены попарно. В следующем разделе мы будем работать с системами, которые не имеют решений или имеют бесконечно много решений.

Используйте график для классификации решений систем.

Вспомните, что график линейного уравнения представляет собой линию, которая указывает на то, что все точки на линии являются решениями этого линейного уравнения. Существует бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, которые пересекаются в одной точке, эта точка является решением системы. Что произойдет, если прямые никогда не пересекутся, как в случае с параллельными прямыми? Как бы вы описали решения для такой системы? В этом разделе мы рассмотрим три возможных результата решения системы линейных уравнений.

Три возможных результата для решений систем уравнений

Напомним, что решением системы уравнений является значение или значения, которые верны для всех уравнений в системе. Есть три возможных результата для решений систем линейных уравнений. Графики уравнений в системе могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждом изображены две линии, составляющие систему уравнений.

Одно решение	Нет решений	Бесконечные решения
Если графики уравнений пересекаются, то существует одно решение, верное для обоих уравнений.	Если графики уравнений не пересекаются (например, если они параллельны), то нет решений, верных для обоих уравнений.	Если графики уравнений одинаковы, то существует бесконечное число решений, верных для обоих уравнений.

• Одно решение:  Когда система уравнений пересекается по упорядоченной паре, система имеет одно решение.
• Бесконечное количество решений: Иногда два уравнения представляют собой одну линию, и в этом случае у нас есть бесконечное количество решений.
• Нет решения: Когда линии, составляющие систему, параллельны, решений нет, потому что две линии не имеют общих точек.

В следующем разделе мы познакомимся с некоторыми алгебраическими методами поиска решений систем уравнений. Напомним, что линейные уравнения с одной переменной могут иметь одно решение, не иметь решения или иметь много решений, и мы можем проверить это алгебраически. Мы будем использовать те же идеи для алгебраической классификации решений систем с двумя переменными.

PPT – Решение линейных неравенств Презентация PowerPoint | скачать бесплатно

Об этой презентации

Стенограмма и примечания докладчика

Title: Solving Linear Inequalities

1
6-5
Solving Linear Inequalities
Warm Up
Lesson Presentation
Lesson Quiz
Holt Algebra 1
2
Warm Up Graph each inequality. 1. x gt 5 2. y
0 3. Запишите 6x 2y 4 в форме
наклон-пересечение и постройте график.
y 3x 2
3
Задача
Построить график и решить линейные неравенства с двумя переменными
.
4
Словарь
линейное неравенство решение линейного неравенства
5
Линейное неравенство похоже на линейное уравнение
, но знак равенства заменен символом неравенства
. Решением линейного неравенства
является любая упорядоченная пара, которая делает неравенство
верным.
6
Пример 1A Определение решения неравенства
Скажите, является ли упорядоченная пара решением
неравенства.
(2, 4) л 2x 1
Замените (2, 4) на (x, y).
(2, 4) не является решением.
7
Пример 1B Определение решений неравенств
Скажите, является ли упорядоченная пара решением
неравенства.
(3, 1) y gt x 4
Замените (3, 1) на (x, y).

?
(3, 1) — это решение.
8
Проверьте это! Пример 1
Скажите, является ли упорядоченная пара решением
неравенства.
а. (4, 5) у л х 1
б. (1, 1) у gt x 7
y lt x 1
Замените (4, 5) на (x, y).
Замените (1, 1) на (x, y).
г х 7
?
?
(1, 1) — это решение.
(4, 5) не является решением.
9
Линейное неравенство описывает область координатной плоскости
, называемую полуплоскостью. Все точки
в области являются решениями линейного неравенства
. Границей области является
график связанного уравнения.
10
(без стенограммы)
11

Графики линейных неравенств

12
Пример 2A Графики линейных неравенств с двумя переменными

Нарисуйте решения линейного неравенства.
г ? 2x 3
Шаг 1 Неравенство уже решено для y.
Шаг 2 Нарисуйте линию границы y 2x 3.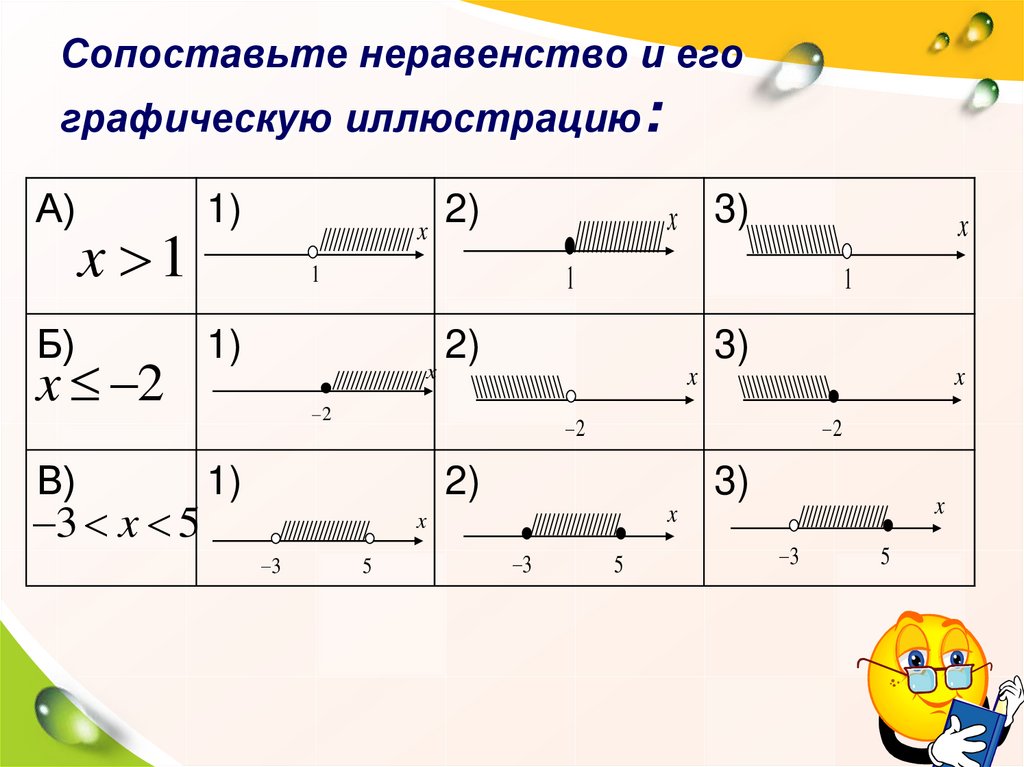 Используйте сплошную линию
для ?.
Шаг 3 Неравенство равно ?, поэтому заштрихуйте линию ниже
.
13
Пример 2A Продолжение
Нарисуйте графики решений линейного неравенства.
г ? 2x 3
Замените (0, 0) на (x, y), потому что это не
граничная линия.
Неверное утверждение означает, что полуплоскость
, содержащая (0, 0), НЕ ДОЛЖНА быть заштрихована. (0, 0)
не является одним из решений, поэтому график заштрихован
правильно.
14
(без расшифровки)
15
Пример 2B. Построение графика линейных неравенств с двумя переменными

Нарисуйте решения линейного неравенства.
5x 2y gt 8
Шаг 1 Решите неравенство для y.
16
Пример 2B Продолжение
Изобразите решения линейного неравенства.
5x 2y gt 8
Шаг 3 Неравенство равно gt, поэтому заштрихуйте выше линии
.
17
Пример 2B Продолжение
Изобразите решения линейного неравенства.
5x 2y gt 8
Подставьте ( 0, 0) вместо (x, y), потому что это не
на граничной линии.
Точка (0, 0) удовлетворяет неравенству, поэтому график
закрашен правильно.
18
Пример 2C. Построение графика линейных неравенств с двумя переменными

Нарисуйте решения линейного неравенства.
4x y 2 0
Шаг 1 Решите неравенство для y.
4x y 2 0
y 4x 2
1
1
y 4x 2
Шаг 2 Нарисуйте линию границы y 4x 2. Используйте сплошную линию
для .
19
Пример 2C Продолжение
Изобразите решения линейного неравенства.
4x y 2 0
Шаг 3 Неравенство равно , поэтому заштрихуйте
строка.
20
Пример 2C Продолжение
Замените ( 3, 3) на (x, y), потому что это не
на граничной линии.
Точка (3, 3) удовлетворяет неравенству, поэтому
график закрашен правильно.
21
Проверьте это! Пример 2a
Нарисуйте графически решения линейного неравенства.
4x 3y gt 12
Шаг 1 Решите неравенство для y.
3 года GT 4x 12
22
Проверьте это! Пример 2а Продолжение
Нарисуйте графики решений линейного неравенства.
4x 3y gt 12
Шаг 3. Неравенство меньше, поэтому закрасьте его ниже линии
.
23
Проверьте это! Пример 2а Продолжение
Нарисуйте графики решений линейного неравенства.
4x 3y gt 12
Точка (1, 6) удовлетворяет неравенству, поэтому
график закрашен правильно.
Подставьте ( 1, 6) вместо (x, y), потому что это не
на граничной линии.
24
Проверьте это! Пример 2b
Нарисуйте графически решения линейного неравенства.
2x y 4 gt 0
Шаг 1 Решите неравенство для y.
2x y 4 gt 0
y gt 2x 4
y lt 2x 4
Шаг 2 Нарисуйте линию границы 2x 4. Используйте пунктирную линию
для lt.
25
Проверьте это! Пример 2б (продолжение)
Нарисуйте графики решений линейного неравенства.
2x y 4 gt 0
Шаг 3 Неравенство равно lt, поэтому заштрихуйте линию ниже
.
26
Проверьте это! Пример 2б (продолжение)
Нарисуйте графики решений линейного неравенства.
2x y 4 gt 0
Точка (3, 3) удовлетворяет неравенству, поэтому
график закрашен правильно.
Замените (3, 3) на (x, y), потому что это не
на граничной линии.
27
Проверьте это! Пример 2c
Постройте график решения линейного неравенства.
Шаг 1 Неравенство для y уже решено.
Шаг 3 Неравенство равно , поэтому заштрихуйте выше линии
.
28
Проверьте это! Пример 2c Продолжение
Нарисуйте графики решений линейного неравенства.
Замените (0, 0) на (x, y), потому что это не
граница.
Неверное утверждение означает, что полуплоскость
, содержащая (0, 0), НЕ ДОЛЖНА быть заштрихована. (0, 0)
не является одним из решений, поэтому график заштрихован
правильно.
29
Пример 3a Применение
У Ады есть не более 285 бусин для изготовления украшений. Для ожерелья
требуется 40 бусин, а для браслета
— 15 бусин.
Напишите линейное неравенство, описывающее ситуацию
.
Пусть x обозначает количество ожерелий, а y — количество браслетов.
Запишите неравенство. Используйте не более.
30
Пример 3a Продолжение
Решите неравенство для y.
Вычтите 40x с обеих сторон.
Разделите обе стороны на 15.
31
Пример 3b
b. Нарисуйте решения.
32
Пример 3b Продолжение
b. Нарисуйте решения.
Шаг 2 Заштрихуйте ниже линии. Ада может сделать только
целых чисел украшений. Все баллы на или ниже
строка с целым числом координат — это
различных комбинаций браслетов и ожерелий
, которые может сделать Ада.
33
Пример 3c
c. Назовите две комбинации ожерелий и 90 255 браслетов, которые могла бы сделать Ада.
Две разные комбинации украшений, которые Ада
может сделать из 285 бусин, могут быть 2 ожерелья
и 8 браслетов или 5 ожерелий и 3 браслета.

34
Проверьте это! Пример 3
Что если? Дирк собирается принести два типа
оливок для вступления в Общество чести и
могут потратить не более 6. Зеленые оливки стоят 2 за
фунтов, а черные оливки стоят 2,50 за фунт. а.
Напишите линейное неравенство, описывающее ситуацию
. б. Нарисуйте решения. в. Назовите два 90 255 комбинаций оливок, которые мог бы купить Дирк.
35
Проверьте это! Пример 3 (продолжение)
Пусть x представляет количество фунтов
зеленых оливок, а y представляет количество фунтов черных оливок
.
Запишите неравенство. Использовать не более.
Решите неравенство для y.
2x 2,50y 6
Вычесть 2x с обеих сторон.
2,50y 2x 6
Разделите обе стороны на 2,50.
36
Проверьте это! Пример 3 Продолжение
y 0,80x 2,4
b. Нарисуйте решения.
Шаг 1 Поскольку Дирк не может купить отрицательное количество оливок
, система построена на графике только в квадранте I.
Нарисуйте граничную линию для y 0,80x 2,4. Используйте
сплошную линию для.
37
Проверьте это! Пример 3, продолжение
c. Назовите две комбинации оливок, которые мог бы купить Дирк
.
Две разные комбинации оливок, которые Дирк
может купить за 6, могут быть 1 фунт зеленых оливок
и 1 фунт черных оливок или 0,5 фунта
зеленых оливок и 2 фунта черных оливок.
Черные оливки
Зеленые оливки
38
Пример 4A Запись неравенства на основе графика
Напишите неравенство для представления графика.
Напишите уравнение в форме пересечения наклона.
График затенен над пунктирной линией границы.

39
Пример 4B. Запись неравенства на основе графика
Напишите неравенство для представления графика.
Напишите уравнение в форме пересечения наклона.
График заштрихован ниже сплошной граничной линии.
40
Проверьте это! Пример 4a
Напишите неравенство для представления графика.
y-пересечение 0 наклон 1
Напишите уравнение в форме наклона-пересечения.
График заштрихован ниже пунктирной граничной линии.

Замените на lt, чтобы записать неравенство y lt x.
41
Проверьте это! Пример 4b
Напишите неравенство для представления графика.
Пересечение по оси y 3, наклон 2
Запишите уравнение в форме пересечения с наклоном.
График затенен над сплошной граничной линией.
Замените на , чтобы записать неравенство y 2x
3.
42
Контрольная работа, часть I
1. Вы можете потратить максимум 12.00 на напитки в 902:55 пикник. Чай со льдом стоит 1,50 галлона, а лимонад
стоит 2,00 галлона. Напишите неравенство
, чтобы описать ситуацию.