Плоские и объемные геометрические фигуры: Плоскость. Плоские и объёмные геометрические фигуры
учим плоские и объемные геометрические фигуры
Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.
Конечно, нам может казаться, что ребенок слишком мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.
Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно. Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Зачем ребенку учить геометрические фигуры?
Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений.
Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Знание геометрических фигур помогает:
- развивать пространственное мышление, ориентацию в пространстве;
- расширять кругозор;
- развивать способность сравнивать, анализировать, обобщать и выделять главное, классифицировать;
- пополнять словарный запас.
И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.
Как учить геометрические фигуры с дошкольником?
- Обучение для дошкольников должно строиться в виде увлекательной игры.
- Не нужно ругать ребенка, если он не запомнил названия фигур с 1 раза, даже если с 31 – не стоит.
- Не забывайте органично вплетать геометрические познания в жизнь: «подай квадратную коробочку», «возьми яблоко с круглой тарелки».
- По дороге в сад ищите предметы прямоугольной или круглой формы, соревнуйтесь, кто больше найдет и назовет.
- В игровом арсенале у вас должны быть игрушки правильной геометрической формы — мячи, кубики, детали конструктора.
- Обычно малыши любят помогать маме на кухне. Приобретите круглые, квадратные, прямоугольные формочки и испеките съедобные геометрические фигуры.
- Важно при изучении фигур задействовать и тактильную память. Ребенку гораздо интереснее будет не только увидеть, но и пощупать, погладить, а может еще и лизнуть объект изучения.
- Нагружайте мозг ребёнка дозировано, постепенно дополняя информацией. Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».
Основные техники и методики запоминания фигур
Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.
- До достижения 1,5 лет проговариваем вслух окружающие предметы, снабжая свой рассказ информацией о форме (давай возьмем круглое яблоко).
- В возрасте 1,5 — 2 лет пользуемся картинками, раскрашиваем фигуры, используем сортеры для изучения фигур. Начинаем с самого простого — круга. Остальные фигуры будем подключать только после того, как ребенок усвоил понятие «круг».
- С 2 лет до достижения школьного возраста можем применять все существующие методики, следуя от простого к сложному.
При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал. Знания этих фигур доступны для детей 2-3 лет.
Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.
Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.
Разберем некоторые варианты техник по изучению геометрических фигур:
1.
Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.
3. Объемные наклейки и магниты
, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.
6. Обводить пунктирные геометрические фигуры.
7. Раскрасить или заштриховать предложенные вами геометрические фигуры.
7. Дорисовать фигуру по образцу.
8. Рисовать фигуры при помощи трафаретов.
9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.
10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.
11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру. Задача ребенка обнаружить и назвать, какой фигуры нет.
12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.
13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.
14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.
16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.
17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.
Учим объемные геометрические фигуры
Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:
- Найти объемную фигуру по плоскому образцу — отличное упражнение на развитие пространственного мышления.
- «Сыщик». Детям раздают «ориентировку» – плоский рисунок искомой фигуры со всех сторон. Детям необходимо сопоставить картинки и найти нужную фигуру.
- Создать трехмерную модель самому. Взрослый может распечатать трафареты с интернета. Ребенку остается согнуть по линиям и склеить, чтобы получилась фигура.
- Макеты, оригами – можно попробовать с вместе с ребенком создать свою объемную игрушку из бумаги.
- Конструктор. Постройте при помощи деталей башню или замок для принцессы. Эта игра будет способствовать развитию мелкой моторики, воображению, пониманию свойств объемных фигур.
Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Геометрические фигуры плоские и объёмные
Цели урока:
- Познавательная: создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
- Коммуникативная: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
- Регулятивная: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.
предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные:
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные:
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока: изучение нового материала.
Методы: словесные, исследовательские, наглядные, практические.
Формы работы: фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий.
И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
— Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
— Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
— По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
— Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
— Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
— Чем они похожи?
— Можно ли сказать, что это одно и тоже?
— Чем же отличается куб от квадрата?
— Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
— Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
— Можно ли куб полностью (весь) прижать к парте? Проверим.
— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
ПЛОСКИЕ
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
— Какую форму имеют основания этих фигур?
— Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
— Предложите свои названия.
— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
+ Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.
Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1. (Для изучения параллелепипеда)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 2. (Для изучения пирамиды)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 3. (Для изучения куба)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . 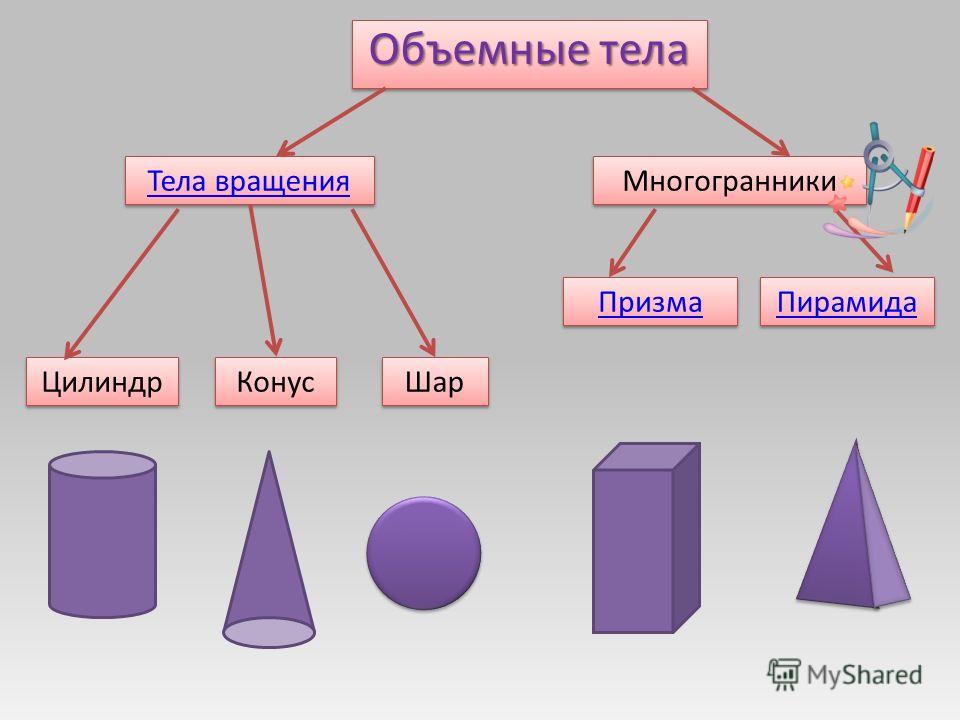 Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Далее каждая группа выступает, представляя свою объемную фигуру другим.
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
— Что нового вы для себя сегодня открыли?
+ Все геометрические фигуры можно разделить на объёмные и плоские.
+ А я узнал названия объёмных фигур
Volumes of Solid Shapes – Formulas, Examples
В геометрии трехмерные фигуры называются трехмерными фигурами или телами. Они занимают пространство и имеют 3 измерения. Обычно 3D-формы получаются путем вращения 2D-форм. Грани сплошных фигур представляют собой только 2D-формы. Некоторыми примерами трехмерных форм являются куб, прямоугольный параллелепипед, конус, цилиндр, сфера, призма и так далее. Количество любого вещества, которое могут удерживать эти формы, называется его объемом.
| 1. | Введение в объем трехмерных фигур |
| 2. | Объем формул 3D-фигур |
| 3. | Решенные примеры объемных 3D-фигур |
| 4. | Практические вопросы по объему трехмерных фигур |
| 5. | Часто задаваемые вопросы по объему 3D-фигур |
Введение в объем 3D-фигур
Лучший способ визуализировать объем — представить его в терминах пространства, заключенного/занятого любым трехмерным объектом или твердой формой.
Выполните простое упражнение:
- Возьмите прямоугольный лист бумаги длиной l см и шириной h см.
- Соедините противоположные стороны листа бумаги, не сгибая и не сгибая лист.
- Смотрите! Вы сделали трехмерный объект (цилиндр), который заключает в себе пространство, из двухмерного листа (прямоугольника).
Объем трехмерной фигуры определяется как общее пространство, заключенное/занятое любым трехмерным объектом или твердой формой.
Его также можно определить как количество единичных кубов, которые можно поместить в фигуру. Единицей объема в системе СИ являются кубические метры. Другими единицами измерения являются унция жидкости, галлон, кварта, пинта, чайная ложка, драм жидкости, кубический ярд, баррель и т. д.
Объем формул 3D-фигур
Объем различных трехмерных фигур можно рассчитать, используя разные формулы для каждой формы. Некоторые важные из них вместе с их реальными примерами перечислены в разделе ниже:
Объем цилиндра
Чтобы сравнить количество жидкости, содержащейся в цилиндрических банках для напитков разного размера, нам нужно вычислить объем консервной бутылки. Цилиндр представляет собой трубчатую структуру с круглыми гранями одинакового радиуса на каждом конце, соединенными плоской круговой поверхностью. Думайте об этом как о площади круга, умноженной на новое измерение, высоту. Если рассматривать r как радиус круглого основания (и вершины), а h как высоту цилиндра, объем цилиндра = πr 2 h
Объем конуса
Предположим, вы и ваш друг наслаждаетесь охлажденными летними напитками в разных стаканах конической формы.
Как вы узнаете, сколько напитка нужно налить в каждый стакан?
Конус представляет собой трехмерную форму, которая имеет плоскую поверхность на одном конце и криволинейную поверхность, направленную наружу к точке на другом конце (которая называется вершиной). Формула объема конуса определяется как объем конуса = (1/3) πr 2 h кубических единиц, где
- ‘r’ — радиус основания конуса
- ‘l’ – наклонная высота конуса
- ‘h’ высота конуса
Как видно из приведенной выше формулы конуса, вместимость конуса составляет одну треть вместимости цилиндра. Это означает, что если мы возьмем 1/3 объема цилиндра, мы получим формулу объема конуса. Объем конуса = (1/3) πr 2 h
Объем куба
Объем куба можно легко узнать, зная только длину ребра куба. Если длина куба равна s, то формула для расчета объема куба будет следующей: Объем куба = s 3 , где s — длина стороны куба.
Объем прямоугольного параллелепипеда
Что произойдет, если сложить стопку из большого количества листов бумаги? Как это выглядит? Он составляет кубоид.
Пусть площадь прямоугольного листа бумаги равна A, высота, до которой они сложены, равна h, а объем прямоугольного параллелепипеда равен V. Тогда объем прямоугольного параллелепипеда определяется путем умножения площади основания и высоты. Таким образом, объем прямоугольного параллелепипеда = площадь основания × высота = объем прямоугольного параллелепипеда = lbh
Объем сферы
Объем здесь зависит от диаметра или радиуса сферы, так как если взять поперечное сечение сферы, то это круг. Площадь поверхности сферы – это площадь или область ее внешней поверхности. Чтобы рассчитать объем сферы, радиус которой равен r, у нас есть следующая формула: Объем сферы = 4/3 πr 3
шарик мороженого на вафлях? Так как ковш имеет полусферическую форму, мы будем использовать
объем полушария формула для расчета этого. Если разрезать сферу пополам, получится полусфера. Следовательно, объем полусферы того же радиуса равен половине объема сферы того же радиуса.
3D-объект с плоскими гранями, где грани параллельны друг другу. Он имеет одинаковое поперечное сечение по всей длине. Математически объем призмы равен произведению площади основания и высоты.
Следовательно, объем призмы = площадь основания × высота
Объем пирамиды
Пирамиды можно разделить на разные типы в зависимости от их оснований. К ним относятся треугольная пирамида, четырехугольная пирамида, пятиугольная пирамида и т. Д. Объем пирамиды относится к пространству, заключенному между ее гранями. Объем любой пирамиды всегда составляет одну треть объема призмы, где основания призмы и пирамиды равны, а высоты пирамиды и призмы также одинаковы. Таким образом, объем пирамиды = (1/3) (Bh), где
- B = Площадь основания пирамиды
- h = Высота пирамиды (которую также называют «высотой»)
Важные примечания
- Фоторецептор, расположенный в сетчатке глаза, который способствует лучшему зрению, имеет форму конуса.
- Конус имеет только одну вершину или точку вершины.
- Призма — это трехмерный объект с плоскими гранями и одинаковым поперечным сечением по всей длине.
Существует 3 различных типа единиц объема, которые описаны в таблице ниже:
1. Объем емкости:
| Измерение | Эквивалентное значение |
|---|---|
| 1 куб. дюйм (в 3 ) | 16 мл |
| 1 кубический фут (фут 3 ) | 1728 у.е. в |
| 1 кубический ярд (ярд 3 ) | 27 куб. футов |
| 1 акр-фут | 1613,333 куб. ярда |
2. Объем жидкости:
| Мера | Эквивалентное значение |
|---|---|
| 1 минимум | 1 капля |
| 1 жидкий драм США | 60 минимум |
| 1 чайная ложка | 80 минимум |
| 1 столовая ложка | 3 ч. л. |
| 1 жидкая унция США | 2 столовые ложки |
| 1 выстрел США | 3 столовые ложки |
| 1 жабра США | 4 жидких унции |
| 1 чашка США | 2 ги |
| 1 (жидкость) Пинта США | 2 шт. |
| 1 (жидкость) кварта США | 2 балла |
| 1 (жидкость) галлон США | 4 кварты |
| 1 (жидкость) бочка | 31,5 галлона |
| 1 баррель нефти | 42 галлона |
| 1 бочка | 63 галлона |
3. Сухой объем:
| Мера | Эквивалентное значение |
|---|---|
| (сухая) пинта (pt) | 0,6 л |
| 1 (сухая) кварта (кварт) | 2 балла |
| 1 (сухой) галлон (галлон) | 4 кварты |
1 шт. (уп.) | 2 галлона |
| 1 бушель (бушель) | 4 шт. |
| 1 (сухой) баррель (баррель) | 3.281 бу |
Сложный вопрос
Мариам настоящая сладкоежка. У нее есть банка, наполненная сладостями. В каждом кусочке содержится сахарный сироп, который составляет 30% от объема кусочка. Если каждый кусочек имеет форму сферы диаметром 1 дюйм, сколько сиропа потребуется для 45 конфет?
Связанные темы
Ознакомьтесь с этими интересными статьями о трехмерных фигурах. Нажмите, чтобы узнать больше!
- Калькулятор объема
- Калькулятор объема цилиндра
- Калькулятор объема полушария
- Объем сферы a Калькулятор
- Калькулятор объема куба
- Калькулятор объема прямоугольного параллелепипеда
- Калькулятор объема конуса
Часто задаваемые вопросы по объему 3D-фигур
Как найти объем трехмерной фигуры?
Объем трехмерной фигуры — это количество места, которое она занимает.
Обычно измеряется в кубических единицах. Можно легко найти объем любой трехмерной фигуры, используя простые формулы объема.
Что такое объем трехмерной фигуры?
Объем любой трехмерной формы относится к объему занимаемого ею пространства. Объем обычно выражается в кубических единицах.
Как найти объем неправильной трехмерной фигуры?
Мы можем найти объем неправильной трехмерной формы точно так же, как мы находим площадь неправильной двумерной формы, то есть разбив ее на правильные формы.
- Шаг 1: Разделите тело на более мелкие части, пока не получите формы, с которыми вам будет легко работать.
- Шаг 2: Определите все эти фигуры.
- Шаг 3: Найдите их объем.
- Шаг 4: Добавьте свои тома.
- Шаг 5: Запишите эту сумму в подходящей единице измерения.
Какие единицы измерения используются для объема трехмерных фигур?
Объем любого объекта в трехмерном пространстве измеряется в кубических единицах, таких как кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т.
д.
Как измерить объем трехмерных фигур?
Объем различных трехмерных фигур можно рассчитать, используя разные формулы для каждой формы. В случае, если любая фигура состоит из кубических блоков, можно посчитать кубы, чтобы найти объем фигуры.
Какая общая формула для нахождения объема трехмерных фигур?
Объем трехмерных геометрических фигур, таких как куб, прямоугольный параллелепипед, цилиндр, призма, конус и т. д., можно легко рассчитать с помощью простых арифметических формул, например, объем куба равен s 3 , где s — ребро куба, а объем прямоугольного параллелепипеда равен lwh, где l — длина, w — ширина, а h — высота прямоугольного параллелепипеда.
Объем 3D-формы такой же, как и ее емкость?
Мы знаем, что объем и вместимость являются свойствами трехмерных объектов. С одной стороны, объем изображает меру пространства, которое занимает трехмерный объект. С другой стороны, вместимость описывает, сколько чего-либо может вместить контейнер.
Геометрический абстракционизм – плоские и объемные фигуры в живописи
Пожалуй, нет более противоречивого направления в искусстве, чем геометрическое абстракционизм. Она настолько отличается от обычной живописи прежних веков, что производит такое же сильное впечатление, как и в первые годы своего развития. В этой статье мы познакомимся поближе с философией этого направления и рассмотрим известные картины в стиле авангард.
Геометрия в живописи
С самого зарождения искусства в нем присутствовала геометрия. Хотя и в разных формах, он оставил свой след в архитектуре, скульптуре и даже в живописи. Но если сначала нужно было в основном для построения перспективы делать на холсте объемные объекты, то сегодня полноценные картины с геометрическими фигурами в качестве основных элементов.
Без преувеличения геометрия обогатила живопись. На его основе возникло много перспективных направлений, и вполне вероятно, что смогут появиться и новые. Сначала человечество решило изобразить окружающий мир плоским и узнаваемым.
И только потом художники стали воспроизводить то, что мы видим на самом деле, со всей его глубиной и ощущением пространства. А через некоторое время абстракции известных художников стали нести нам определенные обещания, даже не воплощая реальную картину мира. Значит, смысл геометрии в человеке, а не в окружающей природе.
Абстракция называется геометрической, если она состоит из четких линий и геометрических фигур. Многие думают, что оно появилось в начале ХХ века, когда на арену вышел авангард, но это не так. На самом деле подобные произведения встречаются в искусстве с незапамятных времен, просто раньше они не были поняты и приняты обществом.
Еще в 700 г. до н.э. пришелся расцвет протогеометрического стиля в декоративно-прикладном искусстве. Но только сто лет назад геометрические картины наконец были представлены современной публике. Не говорить о них больше было невозможно.
Принципы геометрического абстракционизма
Геометрическое искусство характеризуется не только картинами из геометрических фигур: их отличает субъективное расположение в композициях и совершенно иррациональное пространство.
Но как к этому пришли художники? Вот так просто, из прямого протеста против общепринятого, чересчур эмоционального творчества и даже против трехмерного изображения действительности.
Геометрические фигуры заняли прочные позиции в искусстве по одной причине: они показали публике, что живопись может вызывать яркие эмоции, представлять идеи, облекать слова в форму, даже не используя узнаваемые образы. В этом необыкновенном свойстве они нашли сходство роли музыки и геометрии в искусстве. Теперь это не просто инструмент художника, а иногда даже сама суть работы. Оно будоражит души зрителей и по сей день, раскрывая грани нашей реальности каждый раз по-новому.
Художники и картины направления геометрического абстракционизма
Геометрические формы в искусстве не только положили начало новой творческой эпохе, они стали причиной рождения множества различных направлений: футуризма, супрематизма, кубизма, прецизионизма, конструктивизма и других. Произведения в этих стилях и сегодня вдохновляют молодых творцов и вызывают бурные дискуссии.
Фамилии Пикассо, Дали, Кандинский и Малевич известны даже тем, кто совершенно далек от живописи. А все потому, что они дали миру нечто большее, чем точная передача реальности: сильные и ясные идеи, мысли, чувства.
Казимир Малевич
Нельзя не сказать о великом мастере. Основоположник супрематизма видел в нем самую сущность искусства, его начало и конец. Сначала он стремился изобразить сущность абсолютной беспредметности. Примером тому могут служить картины «Белое на белом» и знаменитый «Черный квадрат». Но через некоторое время творец стал изображать некоторые сюжеты. Картина «Спортсмены» — это та же геометрия, абсолютная горизонтальная симметрия, строгие линии и яркие цветные блоки. Но теперь за ними стоят конкретные персонажи и даже подобие пейзажа.
Эль Лисицкий
В годы Гражданской войны, когда ни конструктивизма, ни супрематизма еще почти не было слышно, Лисицкий занимался коммунистической пропагандой и поддерживал Красную Армию. Один из его плакатов получил громкое название «Бей белых красным клином» и нес не менее сильный посыл.
Используя минимум элементов, он построил мощный эмоциональный посыл. Этот прием, как и само художественное произведение, и по сей день берется за основу логотипов и элементов изображения, как пример лаконичности и ясности самовыражения.
Пит Мондриан
Цвет как эмоция был основным элементом творчества Модриана. Он закрашивал большие площади холста одним чистым тоном, активно использовал горизонтальные и вертикальные линии, в которых находил вибрации и ритм самой жизни. Явный контраст на полотне передает чувство гармонии, присущее автору. «Композиция с красным, синим и желтым» в полной мере раскрывает художественный стиль Модриана. Он утверждал, что «нет ничего конкретнее линии, цвета, плоскости», и умело подтверждал эти слова своими геометрическими картинами.
Кстати, во время тяжелых душевных мук, когда он не смог вернуться в родную Францию из-за Первой мировой войны, родилась картина под названием «Композиция №10 (Причал и океан)». Отсутствие ярких красок обнажало его пустоту и меланхолию.