cart-icon Товаров: 0 Сумма: 0 руб.
г. Нижний Тагил
ул. Карла Маркса, 44
8 (902) 500-55-04

Контрольная работа номер 1 основы кинематики 9 класс: Контрольная работа №1 по физике «Основы кинематики» 9 класс

    Содержание

    Контрольная работа по физике Кинематика 9 класс

    Контрольная работа по физике Кинематика Законы взаимодействия и движения тел 9 класс с ответами. Работа состоит из 4 вариантов в каждом варианте по 9 заданий.

    1 вариант

    1. Исследуется перемещение слона и мухи. Модель мате­риальной точки может использоваться для описания движения

    1) только слона
    2) только мухи
    3) и слона, и мухи в разных исследованиях
    4) ни слона, ни мухи, поскольку это живые существа

    2. Вертолёт Ми-8 достигает скорости 250 км/ч. Какое время он затратит на перелёт между двумя населённы­ми пунктами, расположенными на расстоянии 100 км?

    1) 0,25 с
    2) 0,4 с
    3) 2,5 с
    4) 1440 с

    3. На рисунках представлены графики зависимости коор­динаты от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с наибольшей по моду­лю скоростью?

    4. Велосипедист съезжает с горки, двигаясь прямоли­нейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение ве­лосипедиста 0,5 м/с2. Сколько времени длится спуск?

    1) 0,05 с
    2) 2 с
    3) 5 с
    4) 20 с

    5. Лыжник съехал с горки за 6 с, двигаясь с постоянным ускорением 0,5 м/с2. Определите длину горки, если из­вестно, что в начале спуска скорость лыжника была равна 18 км/ч.

    1) 39 м
    2) 108 м
    3) 117 м
    4) 300 м

    6. Моторная лодка движется по течению реки со скоро­стью 5 м/с относительно берега, а в стоячей воде — со скоростью 3 м/с. Чему равна скорость течения реки?

    1) 1 м/с
    2) 1,5 м/с
    3) 2 м/с
    4) 3,5 м/с

    7. Установите соответствие между физическими величи­нами и формулами, по которым эти величины опреде­ляются.

    Физические величины

    А) Ускорение
    Б) Скорость при равномер­ном прямолинейном движении
    В) Проекция перемещения при равноускоренном прямолинейном движе­нии

    Формулы

    8. На пути 60 м скорость тела уменьшилась в 3 раза за 20 с. Определите скорость тела в конце пути, считая ус­корение постоянным.

    9. Из населённых пунктов А и В, расположенных вдоль шоссе на расстоянии 3 км друг от друга, в одном на­правлении одновременно начали движение велосипедист и пешеход. Велосипедист движется из пункта А со ско­ростью 15 км/ч, а пешеход со скоростью 5 км/ч. Опре­делите, на каком расстоянии от пункта А велосипедист догонит пешехода.

    2 вариант

    1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Пути, пройденные этими телами, отличаются на

    1) 5 м
    2) 20 м
    3) 10м
    4) 30 м

    2. За 6 минут равномерного движения мотоциклист про­ехал 3,6 км. Скорость мотоциклиста равна

    1) 0,6 м/с
    2) 10 м/с
    3) 15 м/с
    4) 600 м/с

    3. На рисунках представлены графики зависимости про­екции перемещения от времени для четырёх тел. Какое из тел движется с наибольшей по модулю скоростью?

    4. Во время подъёма в гору скорость велосипедиста, дви­гающегося прямолинейно и равноускоренно, изменилась за 8 с от 18 км/ч до 10,8 км/ч. При этом ускорение ве­лосипедиста было равно

    1) -0,25 м/с2
    2) 0,25 м/с2
    3) -0,9 м/с

    2
    4) 0,9 м/с2

    5. Аварийное торможение автомобиля происходило в тече­ние 4 с. Определите, каким был тормозной путь, если начальная скорость автомобиля 90 км/ч.

    1) 22,5 м
    2) 45 м
    3) 50 м
    4) 360 м

    6. Пловец плывёт по течению реки. Определите скорость пловца относительно берега, если скорость пловца от­носительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.

    1) 0,5 м/с
    2) 0,1 м/с
    3) 0,5 м/с
    4) 0,7 м/с

    7. Установите соответствие между физическими величи­нами и их единицами измерения в СИ.

    Физические величины

    А) скорость
    Б) ускорение
    В) время

    Единицы измерения СИ

    1) мин
    2) км/ч
    3) м/с
    4) с
    5) м/с2

    8. Поезд начинает равноускоренное движение из состоя­ния покоя и проходит за четвёртую секунду 7 м. Какой путь пройдёт тело за первые 10 с?

    9. Катер, переправляясь через реку шириной 800 м, дви­гался перпендикулярно течению реки со скоростью 4 м/с в системе отсчёта, связанной с водой. На сколько будет снесён катер течением, если скорость течения реки 1,5 м/с?

    3 вариант

    1. Решаются две задачи:

    А: рассчитывается маневр стыковки двух космических кораблей;
    Б: рассчитываются периоды обращения космических кораблей вокруг Земли.

    В каком случае космические корабли можно рассмат­ривать как материальные точки?

    1) Только А
    2) Только Б
    3) И А, и Б
    4) Ни А, ни Б

    2. Средняя скорость поезда метрополитена 40 м/ с. Время движения между двумя станциями 4 минуты. Опреде­лите, на каком расстоянии находятся эти станции.

    1) 160 м
    2) 1000 м
    3) 1600 м
    4) 9600 м

    3. На рисунках представлены графики зависимости про­екции скорости от времени для четырёх тел, движу­щихся вдоль оси ОХ. Какое из тел движется с постоян­ной скоростью?

    4. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с2 На этом спуске его скорость увеличилась на 18 м/с. Велосипедист спускается с горки за

    1) 0,07 с
    2) 7,5 с
    3) 15 с
    4) 21,6 с

    5. Какое расстояние пройдёт автомобиль до полной останов­ки, если шофёр резко тормозит при скорости 72 км/ч, а от начала торможения до остановки проходит 6 с?

    1) 36 м
    2) 60 м
    3) 216 м
    4) 432 м

    6. Катер движется по течению реки со скоростью 11 м/с относительно берега, а в стоячей воде — со скоростью 8 м/с. Чему равна скорость течения реки?

    1) 1 м/с
    2) 1,5 м/с
    3) 3 м/с
    4) 13 м/с

    7. Установите соответствие между физическими величи­нами и формулами, по которым эти величины определяются.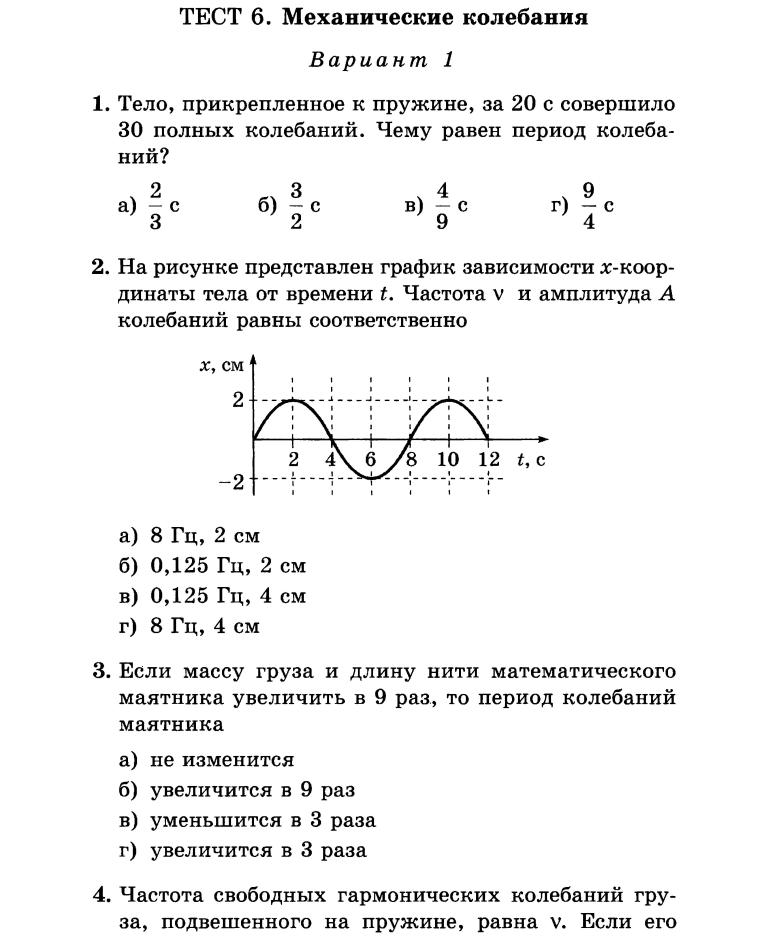

    Физические величины

    А) Проекция ускорения
    Б) Проекция перемещения при равномерном прямолинейном движении
    В) Проекция скорости при равноускоренном прямолинейном движении

    Формулы

    8. Скорость материальной точки на пути 60 м увеличи­лась в 5 раз за 10 с. Определить ускорение, считая его постоянным.

    9. Товарный поезд едет со скоростью 36 км/ч. Спустя 30 минут с той же станции по тому же направлению выходит экспресс со скоростью 144 км/ч. На каком рас­стоянии от станции экспресс догонит товарный поезд?

    4 вариант

    1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Перемещения этих тел соответственно равны

    1) 10 м, 20 м
    2) 20 м, 40 м
    3) Ом, Ом
    4) Ом, 20 м

    2. Велосипедист, двигаясь равномерно по шоссе, проехал 1800 м за 3 минуты. Скорость велосипедиста равна

    1) 12 км/ч
    2) 24 км/ч
    3) 36 км/ч
    4) 60 км/ч

    3.

    На рисунках представлены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?

    4. Санки съехали с одной горки и въехали на другую. Во время подъёма на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с, при этом модуль ускорения был равен

    1) -2,5 м/с2
    2) 2,5 м/с2
    3) -3,5 м/с2
    4) 3,5 м/с2

    5. При равноускоренном прямолинейном движении ско­рость катера увеличилась за 10 с от 5 м/с до 9 м/с. Ка­кой путь пройден катером за это время?

    1) 50 м
    2) 70 м
    3) 80 м
    4) 90 м

    6. Пловец плывёт против течения реки. Определите скорость пловца относительно берега, если скорость пловца относи­тельно воды 0,4 м/с, а скорость течения реки 0,3 м/с.

    1) 0,1 м/с
    2) 0,2 м/с
    3) 0,5 м/с
    4) 0,7 м/с

    7.

    Установите соответствие между физическими величи­нами и их единицами измерения в СИ.

    Физические величины

    А) перемещение
    Б) скорость
    В) время

    Единицы измерения СИ

    1) мин
    2) км/ч
    3) м/с
    4) с
    5) м

    8. Тело, двигаясь равноускоренно, в течение пятой секун­ды от начала движения прошло путь 45 м. Какой путь оно пройдёт за 8 с от начала движения?

    9. Пловец пересекает реку шириной 240 м. Скорость тече­ния реки 1,2 м/с. Скорость пловца относительно воды 1,5 м/с и направлена перпендикулярно к вектору тече­ния. На сколько метров пловец будет снесён течением к тому моменту, когда он достигнет противоположного берега?

    Ответы на контрольную работу по физике Кинематика
    1 вариант
    1-3, 2-4, 3-4, 4-4, 5-1, 6-3, 7-425, 8-1,5 м/с, 9-4,5 км

    2 вариант
    1-2, 2-2, 3-3, 4-1, 5-3, 6-4, 7-354, 8-100 м, 9-300 м
    3 вариант
    1-2, 2-4, 3-1, 4-3, 5-2, 6-3, 7-431, 8-0,8 м/с2, 9-24 км
    4 вариант
    1-3, 2-3, 3-4, 4-2, 5-2, 6-1, 7-534, 8-320 м, 9-192 м

    PDF-версия
    Контрольная работа Кинематика(134 Кб, pdf)

    Контрольная Работа Основы Кинематики Физика 9 Класс – Telegraph



    >>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

    Контрольная Работа Основы Кинематики Физика 9 Класс

    Войдите или зарегистрируйтесь , чтобы отправлять комментарии

    Контрольные работы по физике 9 класс

    Войдите или зарегистрируйтесь , чтобы отправлять комментарии

      bovaliservice      +375 29 6226637
    Контрольные по физике №1-4 6 вариантов
    Кинематика. Основы динамики.Законы сохранения в механике. Равномерное и неравномерное движение. Закон сложения скоростей.
    РАВНОМЕРНОЕ И НЕРАВНОМЕРНОЕ ДВИЖЕНИЯ.
    ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ
    а)    перемещение тела за промежуток времени At;
    б)    среднюю скорость перемещения за промежуток времени At;
    в)    мгновенную скорость произвольного движения;
    г)     среднюю путевую скорость за промежуток времени At
    Автомобиль проходит путь s = 108 км за промежуток времени At — 1,5 ч. Чему равна средняя путевая скорость движения автомобиля?
    На рисунке 1 приведен график зависимости мгновенной скорости материальной точки от времени. Определите по графику среднюю скорость движения точки за промежуток времени At — 8,0 с.
    Из одного пункта одновременно в противоположных направлениях отправляются с постоянной скоростью два автомобиля.
    Модули скоростей движения автомобилей            = 54 и v2 — 90
    соответственно. Через какой промежуток времени расстояние между ними будет / = 12 км?
    „                                                                                                               км
    Автомобиль, модуль скорости движения которого и, = /о —,
    обгоняет мотоциклиста, движущегося со скоростью, модуль которой v2 = 50 ™. ОТМ = V2 ~ Vv
    б)         =vt-v2;                          г) vmi =\vy-v2\.
    Какой путь прошел пешеход, двигавшийся со средней путевой
    скоростью (г>) = 4,8               за промежуток времени At — 0,5 ч?
    На рисунке 1 приведен график зависимости модуля мгновенной скорости материальной точки от времени. Определите по графику среднюю скорость движения точки за промежуток времени A t = 8,0 с.
    Автомобиль, двигаясь по прямолинейному участку шоссе со скоростью, модуль которой vt = 82                                      , обгоняет мотоциклиста.
    Чему равен модуль скорости движения мотоциклиста, если через
    промежуток времени At = 2,8 мин от момента обгона расстояние между автомобилем и мотоциклистом стало / = 1,4 км?
    5. На рисунке 2 приведены графики зависимостей координат двух тел, движущихся вдоль оси Ох, от времени. Определите по графикам модуль относительной скорости движения этих тел.
    Если два тела движутся вдоль одной прямой в противоположных направлениях со скоростями, модули которых г/, и v2, то модуль относительной скорости движения тел всегда равен:
    а) 0(т1 =0(+02;                                    в) vmi = v2 -Г),;
    б) ч„„ = 0i -02;                          О vmn =|о, -о2|.
    Двигаясь равномерно вдоль оси Ох, материальная точка за промежуток времени At = 3,0 с совершила перемещение, проекция на ось Ох которого Агх = -6,0 м. Чему равна проекция скорости материальной точки на ось Ох1
    На рисунке 1 приведен график зависимости модуля мгновенной скорости движения материальной точки от времени. Определите по графику среднюю скорость движения точки за промежуток времени At = 8,0 с.
    Два автомобиля движутся по прямолинейному участку шоссе навстречу друг другу со скоростями, модули которых = 58
    и v2 = 62 “• соответственно. Через какой промежуток времени
    произойдет встреча автомобилей, если в момент начала отсчета времени расстояние между ними 1 = 2,0 км?
    На рисунке 2 приведены графики зависимостей координат двух тел, движущихся вдоль оси Ох, от времени. Определите по графикам модуль относительной скорости движения этих тел.
    Если Ъ — скорость движения тела в неподвижной системе отсчета, Z)’ — скорость движения тела в движущейся системе отсчета, а й — скорость движущейся системы отсчета относительно неподвижной системы отсчета, то между скоростями существует связь (закон сложения скоростей):
    а) v = v’+ й;                              в) v = и — v’\
    б) V = д’ — и;                             г) V = -v’ — й. -7
    На рисунке 1 приведен график зависимости модуля мгновенной скорости материальной точки от времени. Определите по графику путь, пройденный точкой за промежуток времени At = 8,0 с.
    Два автомобиля на прямолинейном участке шоссе удаляются
    друг от друга со скоростями, модули которых — /и
    и vn = 62 “ соответственно. В начальный момент време-
    ни расстояние между автомобилями /, = 600 м. Чему будет равно расстояние между ними через промежуток времени At — 2,0 мин?
    На рисунке 2 приведены графики зависимостей координат двух тел, движущихся вдоль оси Ох, от времени. Определите по графикам модуль относительной скорости движения этих тел.
    Если Аг — перемещение тела в неподвижной системе отсчета, Дг’г — перемещение тела в движущейся системе отсчета, а Дг0 — перемещение движущейся системы отсчета относительно неподвижной системы отсчета, то между ними существует связь (закон сложения перемещений):
    а) Дг = Дг0 — Дг’;                                 в) Дг = -Агт — Дг0;
    б) Дг — Дг0 + Дг’;                                 г) Аг = Аг’ — Аг0.
    Чему равен модуль перемещения материальной точки, если его проекции на оси декартовой прямоугольной системы координат Агх = 2,8 м и Агу = -2,1 м?
    На рисунке 1 приведен график зависимости модуля мгновенной скорости материальной точки от времени. Определите по графику путь 5 точки за промежуток времени At = 8,0 с.
    Модуль скорости движения первого автомобиля п, = 85
    второго — v2 = 65 Автомобили движутся навстречу друг
    другу. Какой путь пройдет первый автомобиль до встречи, если в начальный момент времени расстояние между ними I — 3,0 км?
    На рисунке 2 приведены графики зависимостей координат двух тел, движущихся вдоль оси Ох, от времени. Определите по графикам модуль относительной скорости движения этих тел.
    …..  ■■■(——————————
    б ……………………………………………………………………
    Угловая скорость движения материальной точки по окружности определяется по формуле:
    Двигаясь равноускоренно из состояния покоя, автомобиль прошел путь s = 28 м за промежуток времени At = 4,0 с. Чему равен модуль ускорения автомобиля?
    При равномерном вращении барабана точка на его поверхности прошла путь s = 32 см за промежуток времени At = 0,40 с, при этом радиус, соединяющий ось барабана с данной точкой, повернулся на угол ф = 2,0 рад. Чему равен модуль центростремительного ускорения точки?
    Уравнение движения материальной точки вдоль оси Ох имеет
    вид: x-A + Bt+ Ct2, где Л = -3 м, В = 47-, С = -\Ц-. Определите
    модуль скорости точки через промежуток времени At = 6c после начала отсчета времени.
    Проходя путь s = 6,0 км между двумя станциями, поезд потратил At = 6,0 мин на разгон в начале движения и торможение в конце, а остальное время двигался с постоянной путевой скоростью
    v = 80 Чему равна средняя путевая скорость поезда за все
    Линейная скорость движения материальной точки по окружности связана с угловой скоростью соотношением:
    Тело, двигаясь вдоль оси Ох с ускорением, проекция которого на эту ось а. — 2,0 за промежуток времени At — 2,5 с совершило
    перемещение, проекция которого Агх = 30 м. Чему равна проекция начальной скорости движения тела?
    При равномерном вращении диска его радиус за промежуток времени At- 0,60 с совершил поворот на угол <р = 4,0 рад. Определите путь, пройденный точкой, лежащей на краю диска, если
    модуль ее центростремительного ускорения а = 3,0 —
    Уравнение движения материальной точки вдоль оси Ох имеет вид: л: = А + Bt + Ci\ где А = 1 м, 5 = 3 С = -0,5
    Чему равен модуль мгновенной скорости движения точки через промежуток времени At = 5 с после начала отсчета времени?
    Поезд прошел путь 5 = 6,0 км между двумя станциями со средней
    путевой скоростью (v) = 60 При этом на разгон в начале
    движения и торможение в конце он затратил At = 4,0 мин, а остальное время двигался с постоянной скоростью. Чему равна эта скорость?
    Угловая скорость движения материальной точки по окружности связана с периодом вращения соотношением:
    а) Ш = |;                                                          =
    б)    со = 27tv;                                    г) со —
    Двигаясь равноускоренно вдоль оси Ох в течение промежутка времени At = 3,5 с с начальной скоростью, проекция которой на
    эту ось viU = 4,0 —, тело совершило перемещение, проекция
    которого Arv = 63 м. ;
    б) со = 2irv;                                       г) со =
    Начиная движение, автомобиль за промежуток времени At — 3,5 с набрал скорость, модуль которой v = 28 Чему равен модуль ускорения автомобиля?
    Тело движется равноускоренно вдоль оси Ох. Проекция на ось Ох начальной скорости движения тела v0x = -2,5 проекция его ускорения ах = 2,0 Ц-. Чему равен модуль конечной
    скорости движения тела, если проекция его перемещения Агх = -1,0 м?
    При равномерном вращении тела точка на его поверхности прошла путь 5 = 40 см за промежуток времени At = 0,157 с. Найдите модуль центростремительного ускорения точки, если частота
    Уравнение движения материальной точки имеет вид: x=A + Bt+ Ct,
    где Л = 1м, jB = 3—, С = -0,5 -Ц-. Какой путь прошла точка за
    Модуль центростремительного ускорения материальной точки
    при движении по окружности может быть вычислен по формуле:
    Тело, двигаясь с ускорением, модуль которого а = 1,5 за промежуток времени At — 4,0 с совершило перемещение, модуль которого А г = 24 м. . Чему равна проекция начальной скорости тела?
    Модуль центростремительного ускорения материальной точки при движении по окружности может быть вычислен по формуле:
    Трогаясь с места, автомобиль, двигаясь равноускоренно, проехал путь 5 — 4,5 м за промежуток времени At = 3,0 с. Определите модуль ускорения автомобиля.
    При прямолинейном движении с постоянным ускорением модуль
    При этом тело прошло путь s = 21 м. За какой промежуток времени это произошло?
    Тело движется равноускоренно из состояния покоя. Во сколько раз путь ss, пройденный телом за восьмую секунду, больше пути s:i, пройденного телом за третью секунду движения?
    Тело движется вдоль оси Ох с постоянным ускорением. Проекция
    начальной скорости движения тела v0y — 5,0 проекция ускорения ал = -3,0 Чему равна проекция скорости движения
    •                                  С
    тела к тому моменту, когда проекция перемещения тела составила А гх = -24 м?
    скорости движения тела уменьшился от = 8,0 —■ до v = 4,0
    ”=вт .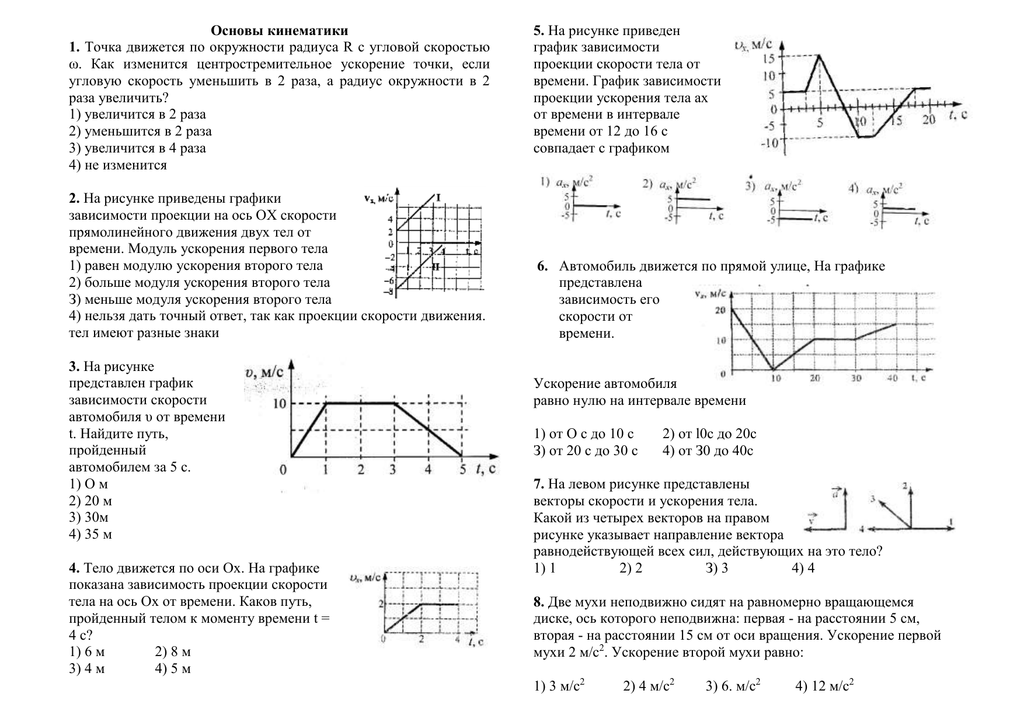
    At с2 ——————————- ———————-
    5= 17 м ——————————- «
    а ■ * ———————————— — ‘ «
    °° = Аг~~2~ = 3’° <■——- !——— :————
    Тело брошено под углом к горизонту. Направление ускорения тела в точке А траектории совпадает с направлением стрелки (рис. 1):
    а) 1;                     в) 3;                      д) 5.
    Тело массой т = 200 г движется с ускорением, модуль которого
    а — 4,0          . Определите модуль равнодействующей сил, действу-
    Проезжая по выпуклому мосту, радиус кривизны которого R = 128 м, автомобиль в верхней точке давит на мост с силой, модуль которой на 20 % меньше модуля силы тяжести, действующей на автомобиль. Определите модуль скорости автомобиля.
    На нити, которая разрывается, если модуль силы упругости превысит F= 20 Н, поднимают груз массой т = 1,0 кг из состояния покоя вертикально вверх. Движение груза равноускоренное. На какую максимальную высоту можно поднять груз за промежуток времени At = 2,0 с?
    Два тела, связанные невесомой нерас-
    тяжимой нитью, перекинутой через
    невесомый неподвижный блок
    (рис.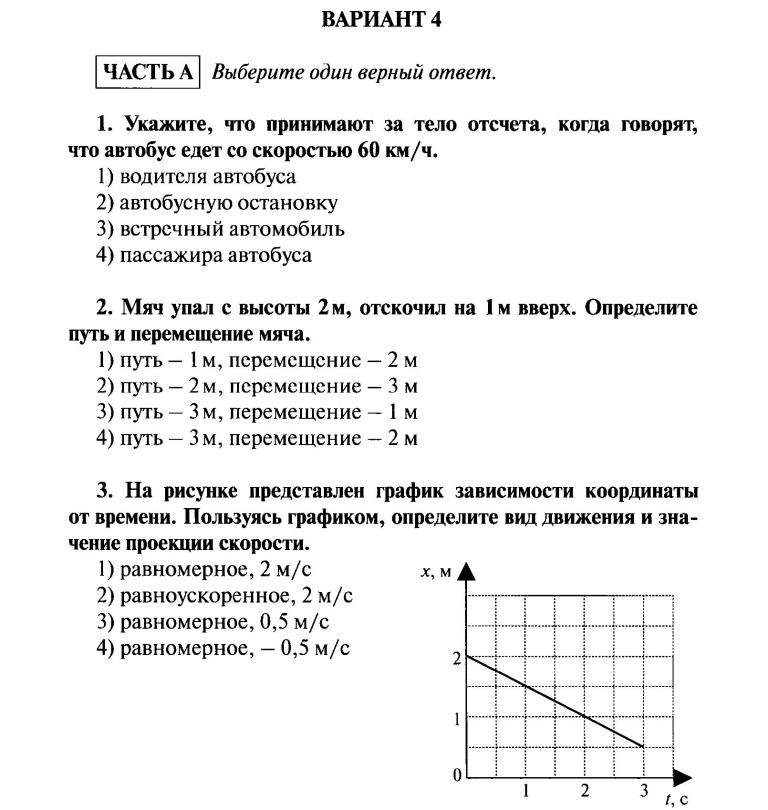 2), движутся с ускорениями,
    модули которых а = 4,5 Коэф-
    фициент трения между телом мас-
    сой тх и горизонтальной поверхно-
    стью ц = 0,65. Определите массу т{
    тела, если масса т2 = 360 г.
    Тело брошено под углом к горизонту. Направление силы, действующей на тело в точке А траектории, совпадает с направлением стрелки (рис. 1):
    а) 1;                     в) 3;                       д) 5.
    Тело движется с ускорением, модуль которого а = 4,0 —j, под
    действием сил, модуль равнодействующей которых F = 1,2 Н. Определите массу тела.
    Проезжая по выпуклому мосту со скоростью, модуль которой
    v = 18 —, автомобиль в верхней точке давит на мост с силой, С
    модуль которой на 20 % меньше модуля силы тяжести, действу ющей на автомобиль. Определите радиус кривизны моста.
    Веревка выдерживает груз массой т1= 150 кг при вертикальном
    подъеме его с некоторым ускорением и груз массой т2 = 750 кг
    при опускании его с таким же по модулю ускорением. Груз ка-
    кой массы можно поднимать с помощью этой веревки равно-
    Два тела массами ш1 = 250гит2 = 400 г
    связаны невесомой нерастяжимой ни-
    тью, перекинутой через невесомый
    неподвижный блок (рис. и F2 — две силы, которые действуют на тело, то согласно второму закону Ньютона:
    а) Ё, = Ё2;                                       в) F{- Р2 = та;
    б) Рх = -Ё2;                                      г) Fj + Ё2 = та.
    Под действием груза, подвешенного на пружине жесткостью
    k = 150 —, пружина растянулась на Д/ = 0,080 м. Определите м
    модуль силы упругости, действующей на груз.
    Вагонетка массой т = 340 кг движется по горизонтальным рельсам с ускорением, модуль которого а = 0,15 Модуль силы
    сопротивления движению вагонетки Fc = 13 Н. Определите модуль силы, под действием которой движется вагонетка.
    Мотоциклист массой т = 52,0 кг, двигаясь по горизонтальной дороге, выполняет поворот по окружности радиусом R = 76,8 м. Чему равен модуль скорости мотоцикла, если модуль силы давления мотоциклиста на сиденье мотоцикла Р = 650 Н?
    Два тела расположены вплотную друг к другу на гладкой горизонтальной поверхности. Массы тел т] = 8,1 кг и т2 = 5,4 кг соответственно. На второе тело действует внешняя горизонтальная сила, модуль которой F> = 25 Н (см. рис.). Модуль силы давления второго тела на первое Р\ = 29 Н. Чему равен модуль внешней горизонтальной силы F{, действующей на первое тело?
    Если и Ё2 — две силы, под действием которых тело покоится, то:
    a )Д=Д;                  в )Д-Д=та;
    б) Д = -Д;                               г) Д + Д = та.
    Тело весом Р= 20 Н подвешено на пружине жесткостью k = 500 —. Чему равно удлинение пружины?
    Вагонетка массой т = 340 кг движется по горизонтальным
    рельсам с ускорением, модуль которого а — 0,15 Модуль
    силы, под действием которой движется вагонетка, F = 65 Н. Определите модуль силы сопротивления движению вагонетки.
    Мотоциклист массой т — 60,0 кг, двигаясь по горизонтальной дороге со скоростью, модуль которой v = 18,0 выполняет поворот по окружности радиусом R — 43,2 м. Чему равен модуль силы давления мотоциклиста на сиденье мотоцикла?
    Два тела, связанные невесомой нерастяжимой нитью, находятся на гладкой горизонтальной поверхности. Массы тел тх = 6,0 кг и т2 = 9,0 кг. На второе тело действует внешняя горизонтальная
    сила, модуль которой F2 = 48 Н (см. рис.). Модуль силы натяжения нити Т= 54 Н. Чему равен модуль внешней горизонтальной силы Fu действующей на первое тело?

    Контрольные работы по физике 9 класс | Контрольные …
    Контрольная работа по физике Кинематика 9 класс
    Конторольная работа по кинематике 9 класс . 12 вариантов.
    Контрольная работа № 1 по теме: « Основы кинематики »…
    Контрольная работа по физике по теме » Кинематика » 9 класс
    Основы Психологии Темы Рефератов
    Сочинение По Рассказу Свет В Окне
    Бозин Дмитрий Александрович Диссертация Рукопись
    Харизма И Ее Роль В Политике Реферат
    Аргументы К Сочинению Какова Роль Исторических Памятников

    Кинематические уравнения: Примеры задач и решений

    Ранее в Уроке 6 были представлены и обсуждены четыре кинематических уравнения. Для использования с этими уравнениями была представлена ​​полезная стратегия решения проблем, и были приведены два примера, иллюстрирующие использование этой стратегии. Затем было обсуждено и проиллюстрировано применение кинематических уравнений и стратегии решения задач к свободному падению. В этой части Урока 6 будет представлено несколько примеров задач. Эти задачи позволяют любому изучающему физику проверить свое понимание использования четырех кинематических уравнений для решения задач, связанных с одномерным движением объектов. Вам предлагается прочитать каждую задачу и попрактиковаться в использовании стратегии при решении задачи. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой для просмотра решения.

    Проверьте свое понимание

    1. Самолет разгоняется по взлетно-посадочной полосе со скоростью 3,20 м/с 2 в течение 32,8 с, пока, наконец, не оторвется от земли. Определить расстояние, пройденное до взлета.
    2. Автомобиль трогается с места и равномерно ускоряется за время 5,21 секунды на расстояние 110 м. Определить ускорение автомобиля.
    3. Аптон Чак едет на Гигантской капле в Большой Америке. Если Аптон будет свободно падать в течение 2,60 с, какова будет его конечная скорость и как далеко он упадет?
    4. Гоночный автомобиль равномерно ускоряется с 18,5 м/с до 46,1 м/с за 2,47 секунды. Определить ускорение автомобиля и пройденный путь.
    5. Перо падает на Луну с высоты 1,40 метра. Ускорение свободного падения на Луне равно 1,67 м/с 2 . Определите время падения пера на поверхность Луны.

      См. решение ниже.


    6. Сани с реактивным двигателем используются для проверки реакции человека на ускорение. Если сани с ракетным двигателем разгоняются до скорости 444 м/с за 1,83 секунды, то каково ускорение и какое расстояние проходят сани?
    7. Велосипед равномерно ускоряется из состояния покоя до скорости 7,10 м/с на пути 35,4 м. Определить ускорение велосипеда.
    8. Инженер проектирует взлетно-посадочную полосу для аэропорта. Из самолетов, которые будут использовать аэропорт, наименьшая скорость ускорения, вероятно, составит 3 м/с 2 . Взлетная скорость этого самолета составит 65 м/с. Предполагая это минимальное ускорение, какова минимальная допустимая длина взлетно-посадочной полосы?
    9. Автомобиль, движущийся со скоростью 22,4 м/с, останавливается за 2,55 с. Определить расстояние заноса автомобиля (считая ускорение равномерным).
    10. Кенгуру способен прыгать на высоту 2,62 м. Определить скорость взлета кенгуру.
    11. Если у Майкла Джордана вертикальный прыжок 1,29 м, то какова его скорость взлета и время зависания (общее время, чтобы подняться вверх до пика и затем вернуться на землю)?
    12. Пуля вылетает из винтовки с начальной скоростью 521 м/с. Разгоняясь через ствол винтовки, пуля проходит расстояние 0,840 м. Определить ускорение пули (ускорение считать равномерным).
    13. Бейсбольный мяч подбрасывается прямо в воздух и имеет время зависания 6,25 с. Определите высоту, на которую поднимается мяч, прежде чем он достигнет своей вершины. (Подсказка: время подъема на пик составляет половину общего времени зависания.
      )
    14. Смотровая площадка высотного небоскреба на высоте 370 м над ул. Определите время, за которое монета свободно упадет с палубы на улицу.

      См. решение ниже.


    15. Пуля, летящая со скоростью 367 м/с, застревает в комке влажной глины. Пуля проникает на расстояние 0,0621 м. Определить ускорение пули при движении в глину. (Предположим, что ускорение равномерное.)
    16. Камень брошен в глубокий колодец, и слышно, как он ударяется о воду через 3,41 с после падения. Определить глубину скважины.
    17. Однажды было зафиксировано, что Jaguar оставил следы заноса длиной 290 метров. Предполагая, что Ягуар занесло до остановки с постоянным ускорением -3,90 м/с 2 , определите скорость Ягуара до начала заноса.
    18. Самолет имеет скорость взлета 88,3 м/с, и для достижения этой скорости требуется 1365 м. Определить ускорение самолета и время, необходимое для достижения этой скорости.
    19. Драгстер разгоняется до скорости 112 м/с на расстоянии 398 м. Определить ускорение (предположим равномерным) драгстера.
    20. С какой скоростью в милях/ч (1 м/с = 2,23 мили/ч) должен быть брошен предмет, чтобы он достиг высоты 91,5 м (эквивалентно одному футбольному полю)? Примите пренебрежимо малое сопротивление воздуха.

    Решения вышеуказанных проблем

    1. Дано:

      а = +3,2 м/с 2

      т = 32,8 с

      v i = 0 м/с

      Найти:

      д = ??
      d = v i *t + 0,5*a*t
      2

      d = (0 м/с)*(32,8 с)+ 0,5*(3,20 м/с 2 )*(32,8 с) 2

      д = 1720 м

      Вернуться к проблеме 1

       

    2. Дано:

      д = 110 м

      т = 5,21 с

      v i = 0 м/с

      Найти:

      а = ??
      d = v i *t + 0,5*a*t 2

      110 м = (0 м/с)*(5,21 с)+ 0,5*(а)*(5,21 с) 2

      110 м = (13,57 с 2 )*a

      а = (110 м)/(13,57 с 2 )

      а = 8,10 м/с 2

      Вернуться к задаче 2

       

    3. Дано:

      а = -9,8 м

      т = 2,6 с

      v i = 0 м/с

      Найти:

      д = ??

      v f = ??

      d = v i *t + 0,5*a*t 2

      d = (0 м/с)*(2,60 с)+ 0,5*(-9,8 м/с 2 )*(2,60 с) 2

      d = -33,1 м (- указывает направление)

      v f = v i + a*t

      v f = 0 + (-9,8 м/с 2 )*(2,60 с)

      v f = -25,5 м/с (- указывает направление)

      Вернуться к проблеме 3

       

    4. Дано:

      v i = 18,5 м/с

      v f = 46,1 м/с

      т = 2,47 с

      Найти:

      д = ??

      а = ??

      а = (Дельта v)/t

      а = (46,1 м/с — 18,5 м/с)/(2,47 с)

      а = 11,2 м/с 2

      д = v i *t + 0,5*a*t 2

      d = (18,5 м/с)*(2,47 с)+ 0,5*(11,2 м/с 2 )*(2,47 с) 2

      d = 45,7 м + 34,1 м

      д = 79,8 м

      (Примечание: d также можно рассчитать с помощью уравнения v f 2 = v i 2 + 2*a*d)

      Вернуться к задаче 4

       

    5. Дано:

      v i = 0 м/с

      d = -1,40 м

      а = -1,67 м/с 2

      Найти:

      т = ??
      d = v i *t + 0,5*a*t 2

      -1,40 м = (0 м/с)*(t)+ 0,5*(-1,67 м/с 2 )*(t) 2

      -1,40 м = 0+ (-0,835 м/с 2 )*(t) 2

      (-1,40 м)/(-0,835 м/с 2 ) = t 2

      1,68 с 2 = т 2

      т = 1,29 с

      Вернуться к проблеме 5

       

    6. Дано:

      v i = 0 м/с

      v f = 444 м/с

      т = 1,83 с

      Найти:

      а = ??

      д = ??

      а = (Дельта v)/t

      а = (444 м/с — 0 м/с)/(1,83 с)

      а = 243 м/с 2

      d = v i *t + 0,5*a*t 2

      d = (0 м/с)*(1,83 с)+ 0,5*(243 м/с 2 )*(1,83 с) 2

      d = 0 м + 406 м

      д = 406 м

      (Примечание: d также можно рассчитать с помощью уравнения v f 2 = v i 2 + 2*a*d)

      Вернуться к задаче 6

       


       

    7. Дано:

      v i = 0 м/с

      v f = 7,10 м/с

      д = 35,4 м

      Найти:

      а = ??
      v f 2 = v i 2 + 2*a*d

      (7,10 м/с) 2 = (0 м/с) 2 + 2*(а)*(35,4 м)

      50,4 м 2 /с 2 = (0 м/с) 2 + (70,8 м)*a

      (50,4 м 2 /с 2 )/(70,8 м) = а

      а = 0,712 м/с 2

      Вернуться к задаче 7

       

    8. Дано:

      v i = 0 м/с

      v f = 65 м/с

      а = 3 м/с 2

      Найти:

      д = ??
      v f 2 = v i 2 + 2*a*d

      (65 м/с) 2 = (0 м/с) 2 + 2*(3 м/с 2 )*d

      4225 м 2 /с 2 = (0 м/с) 2 + (6 м/с 2 )*d

      (4225 м 2 /с 2 )/(6 м/с 2 ) = d

      д = 704 м

      Вернуться к задаче 8

       

    9. Дано:

      v i = 22,4 м/с

      v f = 0 м/с

      т = 2,55 с

      Найти:

      д = ??
      d = (v i + v f )/2 *t

      d = (22,4 м/с + 0 м/с)/2 * 2,55 с

      d = (11,2 м/с)*2,55 с

      д = 28,6 м

      Вернуться к задаче 9

       

    10. Дано:

      а = -9,8 м/с 2

      v f = 0 м/с

      д = 2,62 м

      Найти:

      v i = ??
      v f 2 = v i 2 + 2*a*d

      (0 м/с) 2 = v i 2 + 2*(-9,8 м/с 2 )*(2,62 м)

      0 м 2 /с 2 = v i 2 — 51,35 м 2 /с 2

      51,35 м 2 /с 2 = v i 2

      v i = 7,17 м/с

      Вернуться к проблеме 10

       

    11. Дано:

      а = -9,8 м/с 2

      v f = 0 м/с

      д = 1,29 м

      Найти:

      v i = ??

      т = ??

      v f 2 = v i 2 + 2*a*d

      (0 м/с) 2 = v i 2 + 2*(-9,8 м/с 2 )*(1,29 м)

      0 м 2 /с 2 = v i 2 — 25,28 м 2 /с 2

      25,28 м 2 /с 2 = v i 2

      v i = 5,03 м/с

      Чтобы найти время зависания, найдите время до пика и удвойте его.

      v f = v i + a*t

      0 м/с = 5,03 м/с + (-9,8 м/с 2 )*t до

      -5,03 м/с = (-9,8 м/с 2 )*t до

      (-5,03 м/с)/(-9,8 м/с 2 ) = t up

      t до = 0,513 с

      время зависания = 1,03 с

      Вернуться к задаче 11

       

    12. Дано:

      v i = 0 м/с

      v f = 521 м/с

      d = 0,840 м

      Найти:

      а = ??
      против f 2 = v i 2 + 2*a*d

      (521 м/с) 2 = (0 м/с) 2 + 2*(а)*(0,840 м)

      271441 м 2 /с 2 = (0 м/с) 2 + (1,68 м)*a

      (271441 м 2 /с 2 )/(1,68 м) = a

      а = 1,62*10 5 м/с 2

      Вернуться к задаче 12

       

    13. Дано:

      а = -9,8 м/с 2

      v f = 0 м/с

      т = 3,13 с

      Найти:

      д = ??
      1. (ПРИМЕЧАНИЕ: время выхода на пик траектории составляет половину общего времени зависания — 3,125 с. )

      Первое использование: v f  = v i  + a*t

      0 м/с = v i  + (-9,8 м/с 2 )*(3,13 с)

      0 м/с = v i  — 30,7 м/с

      v i = 30,7 м/с (30,674 м/с)

      Теперь используйте: v f 2  = v i 2  + 2*a*d

      (0 м/с) 2  = (30,7 м/с) 2  + 2*(-9,8 м/с 2 )*(d)

      0 м 2 /с 2 = (940 м 2 /с 2 ) + (-19,6 м/с 2 )*d

      -940 м 2 /с 2  = (-19,6 м/с 2 )*d

      (-940 м 2 /с 2 )/(-19,6 м/с 2 ) = d

      д = 48,0 м

      Вернуться к задаче 13

       

    14. Дано:

      v i = 0 м/с

      d = -370 м

      а = -90,8 м/с 2

      Найти:

      т = ??
      d = v i *t + 0,5*a*t 2

      -370 м = (0 м/с)*(t)+ 0,5*(-9,8 м/с 2 )*(t) 2

      -370 м = 0+ (-4,9 м/с 2 )*(t) 2

      (-370 м)/(-4,9 м/с 2 ) = t 2

      75,5 с 2 = т 2

      т = 8,69 с

      Вернуться к задаче 14

       

       

    15. Дано:

      v i = 367 м/с

      против f = 0 м/с

      d = 0,0621 м

      Найти:

      а = ??
      v f 2 = v i 2 + 2*a*d

      (0 м/с) 2 = (367 м/с) 2 + 2*(а)*(0,0621 м)

      0 м 2 /с 2 = (134689 м 2 /с 2 ) + (0,1242 м)*a

      -134689 м 2 /с 2 = (0,1242 м)*a

      (-134689 м 2 /с 2 )/(0,1242 м) = а

      а = -1,08*10 6 м/с 2

      (Знак — означает, что пуля замедлилась. )

      Вернуться к задаче 15

       

    16. Дано:

      а = -9,8 м/с 2

      т = 3,41 с

      v i = 0 м/с

      Найти:

      д = ??
      d = v i *t + 0,5*a*t 2

      d = (0 м/с)*(3,41 с)+ 0,5*(-9,8 м/с 2 )*(3,41 с) 2

      d = 0 м+ 0,5*(-9,8 м/с 2 )*(11,63 с 2 )

      d = -57,0 м

      (ПРИМЕЧАНИЕ: знак — указывает направление)

      Вернуться к задаче 16

       

    17. Дано:

      а = -3,90 м/с 2

      v f = 0 м/с

      д = 290 м

      Найти:

      в и = ??
      v f 2 = v i 2 + 2*a*d

      (0 м/с) 2 = v i 2 + 2*(-3,90 м/с 2 )*(290 м)

      0 м 2 /с 2 = v i 2 — 2262 м 2 /с 2

      2262 м 2 /с 2 = v i 2

      v i = 47,6 м/с

      Вернуться к задаче 17

       

    18. Дано:

      v i = 0 м/с

      v f = 88,3 м/с

      д = 1365 м

      Найти:

      а = ??

      т = ??

      v f 2 = v i 2 + 2*a*d

      (88,3 м/с) 2 = (0 м/с) 2 + 2*(а)*(1365 м)

      7797 м 2 /с 2 = (0 м 2 /с 2 ) + (2730 м)*a

      7797 м 2 /с 2 = (2730 м)*a

      (7797 м 2 /с 2 )/(2730 м) = а

      а = 2,86 м/с 2

      v f = v i + a*t

      88,3 м/с = 0 м/с + (2,86 м/с 2 )*t

      (88,3 м/с)/(2,86 м/с 2 ) = t

      t = 30,8 с

      Вернуться к задаче 18

       

    19. Дано:

      v i = 0 м/с

      v f = 112 м/с

      д = 398 м

      Найти:

      а = ??
      v f 2 = v i 2 + 2*a*d

      (112 м/с) 2 = (0 м/с) 2 + 2*(а)*(398 м)

      12544 м 2 /с 2 = 0 м 2 /с 2 + (796 м)*a

      12544 м 2 /с 2 = (796 м)*a

      (12544 м 2 /с 2 )/(796 м) = а

      а = 15,8 м/с 2

      Вернуться к проблеме 19

       

    20. Дано:

      а = -9,8 м/с 2

      v f = 0 м/с

      д = 91,5 м

      Найти:

      v i = ??

      т = ??

      Сначала найдите скорость в м/с:

      v f 2 = v и 2 + 2*а*д

      (0 м/с) 2 = v i 2 + 2*(-9,8 м/с 2 )*(91,5 м)

      0 м 2 /с 2 = v i 2 — 1793 м 2 /с 2

      1793 м 2 /с 2 = v i 2

      v i = 42,3 м/с

      Теперь конвертируем из м/с в мили/ч:

      v i = 42,3 м/с * (2,23 мили/ч)/(1 м/с)

      v i = 94,4 миль/ч

      Вернуться к задаче 20

     

    Следующий раздел:

    Обзор кинематики: тест кинематики с множественным выбором

    Для этой страницы требуется JavaScript , который вы кажется, нет. Пожалуйста, попробуйте другой браузер.

    1. Две птицы летят навстречу друг другу с одинаковой скоростью. первая птица летит со скоростью

    против , какова скорость вторая птица?
    • против
    • — против
    • 2 против
    • Невозможно определить

    2. Самолет United Airlines летит со скоростью 300 км/ч, а самолет Air France Concord со скоростью 1200 км/ч Оба самолета летят с одинаковой скоростью. высота Если у каждого самолета возникают проблемы с недисциплинированным пассажиром, и они оба одновременно решают вытолкнуть пассажира за дверь, кто из неуправляемых пассажиров первым упадет на землю? (игнорировать воздух сопротивление)

    • Пассажир Air France
    • Пассажир United Airlines
    • Они оба не упадут на землю одновременно.
    • Невозможно определить Ответ зависит от того, какой пассажир тяжелее

    3. Предполагая, что самолеты в предыдущей задаче продолжают двигаться на той же скорости после катапультирования своих пассажиров, где будет пассажиры приземляются относительно траектории своего самолета?

    • Когда они упадут на землю, они окажутся прямо под самолетом. упал с
    • Когда они упадут на землю, они окажутся прямо под тем местом, где самолет выбросил их
    • Они будут перед самолетом, с которого упали.
    • Это зависит от того, с какого самолета упал пассажир

    4. Функция скорости представляет собой все следующие, КРОМЕ

    • Функция времени
    • Производная функции положения
    • Функция, определяющая скорость объекта в любой момент времени.
    • Ни один из вышеперечисленных

    5. Полицейский, живущий на планете без сопротивления воздуха, сбрасывает пару наручники и носовой платок с одной высоты одновременно Который кто первым достигнет земли?

    • Платок
    • Наручники
    • Они оба упадут на землю одновременно
    • Ответ зависит от того, насколько высоко над землей они находились, когда он упал. их

    6. Какой функцией является функция ускорения, описывающая одномерную движение?

    • Скалярнозначная функция
    • Вектор-функция
    • Нет такой вещи, как ускорение в одном измерении
    • Постоянная функция

    7.

    В общем, ускорение объектов из-за земного притяжения тянуть
    • постоянный
    • 98 м/с 2
    • меньше, если объект находится дальше
    • больше, если объект находится дальше

    8. Кинематика занимается

    • понимание почему объекты движутся именно так
    • описание движения предметов
    • действие на расстоянии
    • Ни один из вышеперечисленных

    9. Капля дождя в дождливый день проходит через одну минуту после того, как она покидает облака, пока оно не коснется вашего зонта, на 3 мили ниже средней скорости капля дождя в своем путешествии

    • 3 мили/час
    • 60 миль/час
    • 180 миль/час
    • Невозможно определить, потому что капля дождя ускоряется под действием силы тяжести.

    10. Средняя скорость и мгновенная скорость тела будут то же самое, если

    • скорость объекта постоянна
    • ускорение объекта равно нулю
    • скорость объекта всегда положительна
    • Они никогда не бывают одинаковыми

    11.

    Автомобиль, движущийся с постоянной скоростью v , внезапно затормозил, пытаясь избегайте столкновения с кроликом, находящимся на расстоянии 8 футов. Если торможение вызывает постоянное замедление a , сколько времени требуется машине, чтобы прийти в полная остановка?
    • т = ва
    • т = 8 a / v
    • т = 8 a
    • т = v / a

    12. В предыдущем вопросе, какое расстояние проехал автомобиль во время торможения?

    • 8 ав
    • а 2

    13. Если машина из двух последних вопросов изначально ехала со скоростью скорость 10 фут/с и испытанное (из-за торможения) замедление 5 ft/s

    2 , попал бы он в кролика, который находился на расстоянии 8 футов? (Предположим кролик был ошеломлен и вообще не шевелился)
    • да
    • нет
    • Невозможно определить, не зная веса автомобиля
    • Невозможно определить, потому что автомобиль никогда не может полностью остановиться.

    14. Найдите производную от 2

    x 5 + x 3 + + 5
    • 10 x 5 + x 2 + 5
    • 10 x 4 + x 2 —
    • 10 x 4 + x 2 + + 5
    • Ни один из вышеперечисленных

    15. Вычислите производную от

    x 3 + x 2 + 5 x при x = — 2
    • -3
    • -14
    • -2
    • Ни один из вышеперечисленных

    16. Найдите скорость объекта, описываемого функцией положения

    x ( t ) = 3 x 2 + в момент времени t = — 1
    • -2
    • 5
    • 2
    • -5

    17. Найдите ускорение объекта, описываемого функцией положения

    x ( t ) = 3 x 2 + в момент времени t = — 1
    • -8
    • 5
    • 18
    • Ни один из вышеперечисленных
      • x ( t ) = (0, 0, — г ) t 2 + (2, 3, 4) t + (5, 0, 1)

    18.

    Какова величина начального (т.е. при t = 0) вектора скорости?
    • 5
    • — г /2

    19. Каково положение объекта в момент времени

    t = — 2?
    • (1, — 6, — 2 г — 7)
    • -12
    • (1, — 6, — 7)
    • (0, 0, 0)

    20. Объект движется

    • в одном измерении
    • в двух измерениях
    • в трех измерениях
    • Ни один из вышеперечисленных

    21. Каково ускорение этого тела в момент времени

    t = 25?
    • — г
    • 25(0, 0, — г )
    • г
    • — (0, 0, г )

    22. Это уравнение может описывать объект

    • в свободном падении
    • движется как снаряд
    • подпрыгивая вверх и вниз
    • с изменением ускорения

    23. В стране существ мера хардкорности напрямую коррелирует насколько высоко можно прыгать К сожалению, существа не могут прыгать прямо вверх, но должен разбежаться Если существо А прыгает с начальной скоростью вектор (2, 2, 5), а существо B прыгает с начальным вектором скорости (5, 4, 2) (где

    z -направление указывает вверх), какое существо больше хардкор?
    • существо А
    • существо Б
    • Оба существа одинаково хардкорны
    • Невозможно определить, не зная ускорения свободного падения в земля существ

    24.

    Согласно предыдущему вопросу, какое существо перемещается дальше всего за время его прыжок?
    • существо А
    • существо Б
    • Оба существа приземляются на одинаковом расстоянии от начальной точки.
    • Невозможно определить, не зная ускорения свободного падения в земля существ

    25. Какая функция может описывать скорость брошенного мяча горизонтально от пожарной лестницы?

    • v ( t ) = — (0, 0, g ) t 2 + (0, v , 0) t + (0, 01, 91)
    • v ( t ) = — (0, 0, g ) t + ( v , 0, 0) т
    • v ( t ) = — gt + vt
    • v ( t ) = — (0, 0, g ) t + (0, 0, v ) t

    26. Фин и Витгенштейн тусуются на Луне, когда решают устроить соревнуйтесь, кто дальше пустит пулю Оба используют одинаковое оружие Фин решает выстрелить под углом 60 градусов, пока Витгенштейн держит пистолет.

    под углом 45 градусов при стрельбе Чья пуля попадает дальше всех?
    • Фин
    • Витгенштейна
    • Обе пули приземляются на одинаковом расстоянии
    • Невозможно определить, не зная ускорения свободного падения на Луна

    27. Офис Harvard Review of Philosophy находится примерно в 10 футов ниже поверхности земли Ускорение силы тяжести, испытываемое членами, работающими в этом офисе,

    • значительно больше, чем у людей на земной поверхности
    • значительно меньше, чем у людей на земной поверхности
    • примерно равно количеству людей на земной поверхности
    • ровно столько же, сколько у людей на земной поверхности

    28. Пара студентов в Путни однажды решает покататься на велосипеде, Саймон. едет со скоростью 10 миль в час, в то время как средняя скорость Лиз составляет 20 миль в час После нескольких часов езды на велосипеде Саймон и Лиз возвращаются домой. и припарковать свои велосипеды именно там, где они начали среднюю скорость на всем пути равна

    • ниже средней скорости Лиз
    • выше, чем средняя скорость Лиз
    • нуль
    • невозможно определить, не зная действительных направлений, в которых он на велосипеде

    29.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *