№ Этапы урока Деятельность учителя Деятельность учащихся Комментарии
1 Организационный этап Приветствие учащихся, проверка готовности учащихся к уроку. Приветствуют учителя, достают тетрадь, учебник Учитель приветствует учащихся, отмечает отсутствующих

schoolfiles.net

Урок по информатике 9 класс «Кодирование числовой информации»

Цели: дать представление о способах кодирования числовой информации; научить переводить числа, представленные в различных системах счисления, в десятичную систему счисления; развитие познавательного интереса к предмету;

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.

Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.

Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.

В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.

Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:

XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).

При записи чисел в римской системе счисления применяется правило: каждый меньший знак, поставленный слева от большего, вычитается из него, в остальных случаях знаки складываются. Например, римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1). Число 99 имеет следующее представление в римской системе счисления: XCIX = -10 + 100 — 1 + 10.

Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.

Выше десятичное число 555 было записано в привычной для нас свернутой форме. В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. 555₁₀ = 5 × 10² + 5 × 10¹ + 5 × 10⁰.

Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:

555,55₁₀ = 5 × 10² + 5 × 10¹ + 5 × 10⁰ + 5 × 10^-1 + 5 × 10^-2.

Число в позиционной системе счисления записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа.

Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:

555,55₁₀ × 10 = 5555,5₁₀,

555,55₁₀ : 10 = 55,555₁₀.

Двоичная система счисления. Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.

Например, развернутая запись двоичного числа выглядит следующим образом:

А₂ = 1 × 2² + 0 × 2¹ + 1 × 2⁰ + 0 × 2^-1 + 1 × 2^-2.

Это же число в свернутой форме:

А₂ = 101,01₂.

Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:

101,01₂ × 2 = 1010,1₂,

101,01₂ : 2 = 10,101₂.

В информатике широко используются восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр {0, 1, 2, 3, 4, 5, 6, 7}. Запишем восьмеричное число 77 в свернутой и развернутой формах и переведем его в десятичную систему счисления:

77₈ = 7 × 8¹ + 7 × 8⁰ = 63₁₀.

В шестнадцатеричной системе основание равно 16 и алфавит состоит из шестнадцати цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F}, причем первые десять цифр имеют общепринятое обозначение, а для записи остальных цифр {10, 11, 12, 13, 14, 15} используются первые шесть букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и развернутой формах и переведем его в десятичную систему счисления:

ABCDEF₁₆ = А × 16⁵ + В × 16⁴ + C × 16³ + D × 16² + Е × 16¹ + F × 16⁰ = 10 × 16⁵ + 11 × 16⁴ + 12 × 16³ + 13 × 16² + 14 × 16¹ + 15 × 16⁰ = 11259375₁₀.

Контрольные вопросы

1. Чем отличаются позиционные системы счисления от непозиционных?

2. Каково основание десятичной системы счисления? Двоичной системы счисления?

3. Какие цифры входят в алфавит десятичной системы счисления? Двоичной системы счисления?

4. На какую величину в позиционных системах счисления различаются одинаковые цифры, стоящие в соседних разрядах числа?

5. Может ли в качестве цифры использоваться символ буквы?

Задания для самостоятельного выполнения

4.1. Задание с кратким ответом. Запишите числа 3,14₁₀ и 10,1₂ в развернутой форме.

4.2. Задание с кратким ответом. Во сколько раз увеличатся числа 10,1₁₀ и 10,1₂ при переносе запятой на один знак вправо?

4.3. Задание с кратким ответом. При переносе запятой на два знака вправо число 11,11_x увеличилось в 4 раза. Чему равно основание системы счисления x?

4.4. Задание с кратким ответом. Какое минимальное основание может иметь система счисления, если в ней записано число 11? Число 99?

4.5. Задание с кратким ответом. Запишите год, месяц и число своего рождения с помощью римских цифр.

3. Д/з 3.1.1

Перевод чисел в позиционных системах счисления

Человек использует десятичную систему счисления, а компьютер — двоичную систему счисления. Поэтому часто возникает необходимость перевода чисел из десятичной системы в двоичную и наоборот.

Перевод чисел из двоичной системы счисления в десятичную систему счисления. Преобразование чисел из двоичной системы счисления в десятичную выполнить довольно легко. Для этого необходимо записать двоичное число в развернутой форме и вычислить его значение.

Возьмем любое двоичное число, например 10,11₂. Запишем его в развернутой форме и произведем вычисления:

10,11₂ = 1  2¹ + 0  2⁰ + 1  2^-1 + 1  2^-2 = 1  2 + 0  1 + 1  1/2 + 1  1/4 = 2,75₁₀.

Перевод целых чисел из десятичной системы счисления в двоичную систему счисления. Алгоритм перевода целого десятичного числа в двоичное следующий:

1) последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы счисления (на 2) до тех пор, пока частное от деления не окажется равным нулю;

2) получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.

В качестве примера рассмотрим перевод десятичного числа 19₁₀ в двоичную систему счисления, записывая результаты в таблицу (табл. 4.2).

В результате получаем двоичное число:

А₂ = 10011₂.

Перевод десятичных дробей в двоичную систему счисления. Алгоритм перевода десятичной дроби в двоичную следующий:

1) последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений;

2) получить искомую двоичную дробь, записав полученные целые части произведений в прямой последовательности.

В качестве примера рассмотрим перевод десятичной дроби 0,75₁₀ в двоичную систему, записывая результаты в таблицу (табл. 4.3).

В результате получаем двоичную дробь:

А₂ = 0,11₂.

Перевод чисел, содержащих и целую, и дробную часть, производится в два этапа. Отдельно переводится по соответствующему алгоритму целая часть и отдельно — дробная. В итоговой записи полученного числа целая часть от дробной отделяется запятой.

Задания для самостоятельного выполнения

4.6. Задание с развернутым ответом. Переведите в десятичную систему двоичные числа: 101₂, 110₂, 111₂

4.7. Задание с развернутым ответом. Переведите целое десятичное число 10₂ в двоичную систему счисления.

4.8. Задание с развернутым ответом. Переведите десятичную дробь 0,25₂ в двоичную систему счисления.

4.9. Задание с развернутым ответом. Переведите десятичное число 10,25₂ в двоичную систему счисления.

Арифметические операции в позиционных системах счисления

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0 + 0 = 0

0 + 1 = 1,

1 + 0 = 1,

1 + 1 = 10.

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления, для двоичной системы счисления — большей или равной 2.

Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 110₂ и 11₂.

Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим.

110₂ = 1  2² + 1  2¹ + 0  2⁰ = 6₁₀

11₂ = 1  2¹ + 1  2⁰ = 3₁₀

6₁₀ + 3₁₀ = 9₁₀

Теперь переведем результат двоичного сложения в десятичное число.

1001₂ = 1  2³ + 0  2² + 0  2¹ + 1  2⁰ = 9₁₀

Сравнение результатов показывает, что сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой.

Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве примера произведем вычитание двоичных чисел 110₂ и 11₂.

Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя. В качестве примера произведем умножение двоичных чисел 110₂ и 11₂.

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 110₂ на 11₂.

Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.

Задания для самостоятельного выполнения

4.10. Задание с развернутым ответом. Выполните сложение, вычитание, умножение и деление двоичных чисел 1010₂ и 10₂.

Двоичное кодирование чисел в компьютере

Числа в компьютере хранятся и обрабатываются в двоичной системе счисления. Оперативная память компьютера состоит из ячеек, в каждой из которых может храниться 8 битов информации, т. е. 8 разрядов двоичного числа.

Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т. е. вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А₂ = 11110000₂ будет храниться в ячейке памяти следующим образом:

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целого неотрицательного числа. Минимальное число записывается в восьми разрядах памяти восемью нулями и равно 0. Максимальное число записывается восемью единицами и равно:

А = 1  2⁷ +1  2⁶ +1  2⁵ + 1  2⁴ + 1  2³ + 1  2² + 1  2¹ + 1  2⁰ = 1  2⁸ — 1 = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное, записывается 1).

Например, отрицательное число -2002₁₀ = 11111010010₂ будет представлено в 16-разрядном представлении следующим образом:

Максимальное положительное число (с учетом выделения одного разряда на знак) для данного формата представления равно:

А = 2¹⁵ — 1 = 32 767₁₀.

Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые дробные, так и очень большие числа.

Для представления чисел в диапазоне от очень маленьких дробей до очень больших чисел с высокой точностью используется формат с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. Число в форме с плавающей запятой занимает в памяти компьютера 4 байта (число обычной точности) или 8 байтов (число двойной точности).

infourok.ru

Разработка урока по информатике для 9 класса на тему «Позиционные системы счисления»

Автор: Бугаева Вера Михайловна,

учитель информатики МАОУ СОШ № 8» с. Кашино

Урок № 2 по информатике для 9 класса

«Позиционные системы счисления»

Методические рекомендации: Данная методическая разработка удобна для проведения второго урока по теме «Системы счисления». Для закрепления понятия «позиционная система счисления» рассматриваются понятия алфавита, основания, базиса системы счисления, изучаются алгоритмы выстраивания натурального ряда чисел в системах счисления и записи развёрнутой формы числа.

Проверку домашнего задания можно организовать в виде взаимопроверки, когда соседи по парте меняются тетрадями, проверяют работы друг друга, выставляют отметку.

Для изучения нового материала используется наглядно-иллюстративный метод. При этом с методической точки зрения бывает очень эффективным прием, когда учитель приводит учеников к самостоятельному, пусть даже маленькому, открытию. В данном случае желательно, чтобы ученики сами подошли к формулировке понятия или алгоритма действий. Сделать это можно, отталкиваясь от конкретных примеров.

Для закрепления понятия «позиционная система счисления» необходимо показать, что позиционных систем счисления существует множество и отличаются они друг от друга алфавитом. Следует показать алфавиты различных позиционных систем счисления. Для наглядного представления взаимосвязи между основанием, названием и алфавитом системы счисления рекомендуется заполнить таблицу 1

Таблица 1

Основание

Название

Алфавит

10

2

8

16

Далее нужно научить учеников записывать натуральный ряд чисел в различных позиционных системах. Объяснение следует проводить на примере десятичной системы, для которой вид натурального ряда чисел им хорошо известен. Принцип построения ряда можно зафиксировать в виде алгоритма. При этом следует обратить внимание учеников на быстрый рост числа цифр в числах двоичного ряда.

Необходимо обратить внимание учеников на то, что ни в коем случае нельзя называть недесятичные числа так же, как десятичные.

Так как на следующем уроке планируется изучение перевода целых чисел в десятичную систему счисления и наоборот целесообразно уже на этом уроке сформулировать алгоритм записи числа в развернутой форме. Для этого снова для объяснения привлекаем десятичную систему, известную учащимся из курса математики.

Для более сильного класса можно организовать самостоятельное изучение материала с помощью различных средств ИКТ (электронное учебное пособие, облачные технологии). Учащиеся делятся на группы, каждая группа в течение отведённого промежутка времени изучает самостоятельно свой блок материала, выполняет задания. В итоге группа выступает в роли учителя, объясняя материал остальным учащимся.

C целью закрепления понятия «позиционная система счисления» учащимся могут быть предложены следующие задания:

• нахождение минимального основания системы счисления для некоторого набора чисел;

• нахождение чисел, записанных с ошибками;

• продолжение записи ряда натуральных чисел для систем счисления с различным основанием;

• выписывание последовательности целых чисел, принадлежащих определенному числовому промежутку;

• определение следующего или предшествующего числа;

• определение большего или меньшего числа из двух чисел;

Закрепление изученного материала можно провести с помощью теста – компьютерного или бланкового. Во втором случае организуется взаимопроверка. Так же для закрепления можно организовать игру «Информбой».

Конспект урока

Тема урока: Позиционные системы счисления.

Класс: 9 класс

Цель урока:

• сформировать понятия алфавита, основания, базиса системы счисления;

• научить выстраивать натуральный ряд чисел позиционных систем счисления;

• научить записывать числа в развёрнутой форме.

Задачи:

Обучающие

• создать условия для овладения учащимися алгоритмами выстраивания натурального ряда чисел позиционных систем счисления и записи развёрнутой формы чисел посредством использования элементов занимательности.

Развивающие

Воспитательные

• обеспечить воспитание норм и правил общения, толерантности по отношению к другим посредством работы в малых группах.

Тип урока: урок изучения и первичного закрепления нового материала

Основные понятия (дидактические единицы):

• алфавит системы счисления

• основание системы счисления

• базис системы счисления

• алгоритм выстраивания натурального ряда чисел позиционных СС

• развёрнутая форма записи числа

Уровень предварительной подготовки учащихся: учащиеся из предыдущего урока знакомы с определением системы счисления, видами систем счисления.

Литература: Информатика. Базовый курс. Учебник для 9 класса / И.Г. Семакин. Л.А. Залогова. С.В. Русаков. Л.В. Шестакова. – 2-е изд., испр. и доп. – М.: БИНОМ. Лаборатория знаний, 2006. – 359 с.

Обеспечение урока: компьютеры учителя и учеников, проектор, интерактивная доска, мультимедийная презентация, рабочая тетрадь по теме, карточки с заданиями, две коробки «ЗНАЮ», «НЕ ЗНАЮ».

Методы и формы обучения: объяснительно-иллюстративный метод, развития критического мышления (кластер), приём «корзина понятий»

Формы работы учащихся: индивидуальная работа.

План и сценарий урока представлены в таблицах 2 и 3 соответственно

Таблица 2

План урока

№

Этап урока

Время (мин)

Организационный момент

2 минуты

Мотивация учебной деятельности

2 минуты

Проверка домашнего задания

5 минут

Актуализация знаний

3 минуты

Изучение нового материала

25 минут

Закрепление изученного материала

5 минут

Рефлексия. Итоги урока.

3 минуты

Инструктаж, домашнее задание

2 минуты

Таблица 3

Сценарий урока

Этап урока

Действия учителя

Действия учащихся

Орг.

момент

Учитель проверяет рабочие места и готовность учащихся к уроку, приветствует их. На входе в класс учащимся раздаются карточки с понятиями относящимися к системам счисления.

Приветствуют учителя

Мотивация учебной

деятельности

Мы с вами продолжаем изучение темы Системы счисления. У каждого из вас есть карточка. Необходимо разложить карточки по двум корзинам «ЗНАЮ» и «НЕ ЗНАЮ» (приём «корзина понятий»)

На прошлом уроке мы познакомились с историей систем счисления и больше внимания уделили непозиционным системам счисления.

Все карточки, которые вы положили в корзину «НЕ ЗНАЮ» тесно связаны с позиционными системами счисления. Как вы думаете, чем же мы займёмся сегодня на уроке?

СЛАЙД 1.

Ученик встаёт, озвучивает карточку. Если понятие уже изучено – даёт определение и кладёт в корзину «ЗНАЮ» (за правильный ответ получает жетон). Если понятие не знакомо – кладёт в корзину «НЕ ЗНАЮ» (на столе стоят две коробки с надписями «ЗНАЮ», «НЕ ЗНАЮ»)

Формулируют тему и цели урока, записывают тему урока в рабочей тетради

Проверка

домашнего задания

Прежде, чем приступить к изучению новой темы, давайте проверим, как вы справились с домашним заданием.

5 учащихся записывают ответы домашнего задания у доски (1 учащийся по 1 заданию). Отгадывают даты рождения одноклассников записанные в различных системах счисления.

Первому кто называет правильный ответ – вручается жетон.

Актуализация знаний

Как вы думаете: почему арабская система называется десятичной системой счисления?

Делаем вывод: в арабской системы счисления используется десять цифр, поэтому она называется десятичной.

Является ли десятичная система счисление единственной, используемой в наше время?

Какая система счисления используется в компьютере?

— Потому что в ней используется 10 цифр

Высказывают предположения. Называют системы счисления

— Двоичная

Изучение

нового

материала

Вы правы, на самом деле позиционных систем очень много. Система счисления является языком представления чисел и как любой язык она имеет свой алфавит. Как вы думаете, из чего состоит алфавит системы счисления?

А размер алфавита (число цифр) называется основанием системы счисления.

За основание системы счисления можно принять любое число не меньшее 2. Системы с основанием не больше 10 используют только арабские цифры. Если основание больше 10, то в роли цифр выступают

латинские буквы в алфавитном порядке. В рабочей тетради заполните таблицу №1 (стр. 11)

Для того чтобы не путать числа, записанные в разных системах счисления мы будем ставить у каждого числа индекс – основание системы счисления.

СЛАЙД 4. Например, 36₈ указывает на то, что это число в восьмеричной системе счисления. В какой системе счисления записаны числа 1А6₁₆, 1011₂, 34₅?

Индекс всегда записывается десятичным числом.

Еще одно важное замечание: ни в коем случае нельзя называть недесятичные числа так же, как десятичные. Например, нельзя называть восьмеричное

число 36₈ как тридцать шесть! Надо говорить: «Три – шесть». Прочитайте числа 101₂ , 1А6₁₆

А теперь попрошу вас рассчитаться по порядку.

А сможете ли вы рассчитаться по порядку используя двоичную систему счисления?

Для того чтобы выполнить это задание нужно знать алгоритм выстраивания натурального ряда чисел позиционной системе. Происходит это по тому же принципу, что и в десятичной системе. СЛАЙД 5. Сначала идут однозначные числа, потом двузначные, затем трехзначные и т. д. Какое самое большое однозначное число в десятичной системе?

первое двузначное число – всегда

10. Далее следуют все двузначные сочетания единицы с другими цифрами; затем – двузначные числа, начинающиеся с 2, затем – с 3, и т. д. Какое самое большое двузначное число?

Затем идут трехзначные числа,

начиная от 100 до 999, и т. д.

СЛАЙД 6. Показать на примере 4ричной СС.

Ну а теперь вы готовы рассчитаться по порядку в двоичной СС?

Следует обратить внимание учащихся на быстрый рост числа в двоичной СС

Игровая разминка «Встать по пальцам» (ПРИЛОЖЕНИЕ 4)

СЛАЙД 7. Предлагает назвать число, записанное на доске (36)

Когда мы читаем число в десятичной системе счисления, мы не просто произносим некий термин, а говорим о вполне определенных свойствах этого числа; «тридцать шесть» — это термин составной, означающий «три раза по десять и шесть».

Действительно, в десятичной системе счисления люди привыкли считать десятками, сотнями, тысячами и т.д., формируя тем самым разряд числа. Каждый разряд в десятичной системе счисления – это число 10 с целым показателем: 10⁰ — разряд единиц,10¹ – разряд десятков, 10² – разряд сотен и т.д. Это означает, что в записи числа каждая последующая цифра «весит» больше предыдущей в 10 раз.

Заменив число 10 другим основанием позиционной системы получим базис любой позиционной системы счисления. Разряды в любой позиционной системе счисления будут называться по показателю степени: n-ый, третий, второй, первый, нулевой, минус первый, минус второй и т.д. Таким образом, базис позиционной системы счисления – это последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.

Более наглядно это проявляется в так называемой развернутой форме записи числа.

Например, в числе 159₁₀, которое записано в свернутой форме, цифра 1 означает одну сотню, цифра 5 — пять десятков и цифра 9 — девять единиц.

Активизировав знания учащихся по возведению в степень числа 10, представим запись десятичного числа 159 в развернутой форме:

159₁₀ = 100 + 50 + 9 =

= 1 · 100 + 5 · 10 + 9 · 1 =

= 1 · 10² + 5 · 10¹ + 9 · 10⁰.

Обратить внимание учащихся, что в свернутой форме записи цифра 9 находится в нулевой позиции, цифра

5 — в первой позиции, цифра 1 — во второй позиции числа.

СЛАЙД 8. Предлагает учащимся составить алгоритм записи числа в развёрнутой форме на примере любого многозначного числа.

СЛАЙД 2.

Формулируют определение алфавита системы счисления, заполняют кластер в рабочей тетради (стр. 9)

Заполняют в рабочей тетради таблицу

СЛАЙД 3. Сверяют со слайдом (без ошибок – жетон), обсуждают и исправляют ошибки

Называют системы счисления

Читают хором числа

Рассчитываются

Затрудняются

— 9

-99

Пробуют рассчитаться

Выполняют разминку

Называют число

Заполняют кластер

Учащийся по желанию работает у интерактивной доски

Обсуждают, записывают алгоритм в тетради

Закрепление изученного материала

СЛАЙД 9-15. Возвращаемся к нашей

«Корзине понятий»

По-очереди вытаскивают из коробки «НЕ ЗНАЮ» карточки (ПРИЛОЖЕНИЕ 5). Называют определение, выполняют задание с обратной стороны карточки. За правильный ответ – жетон.

Рефлексия. Итоги урока.

СЛАЙД 16. Лестница «Успеха»

СЛАЙД 17. Итак, подведём итоги: ученики заработавшие:

• от 4 и более жетонов получают «5»

• 3 жетона — получают «4»

• 1-2 жетона – получают «3»

Кто не согласен с оценкой?

Учащиеся подписывают имя на соответствующие ступени лестницы

Аргументируют своё мнение

Инструктаж, домашнее

задание

Домашнее задание: выучить определения, выполнить задания в рабочей тетради.

Творческое задание (по желанию)

Составить кроссворд на тему «Системы счисления»

Спасибо за урок!

Записывают домашнее задание в дневник, сдают дневники для выставления оценок

В таблице 4 указано, какие универсальные учебные действия формируются на каждом этапе урока.

Таблица 4

Этап урока

УУД

Организационный момент

Личностные: мотивация к учению, развитие интереса к информатике, положительно отношение к процессу познания

Регулятивные:

• целеполагание, как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно;

• планирование, определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий

Познавательные: самостоятельное выделение и формулирование познавательной цели; умение осознанно и произвольно строить речевое высказывание в устной форме; постановка и формулирование проблемы

Коммуникативные:

• планирование учебного сотрудничества с учителем и сверстниками, определение цели, функций участников, способов взаимодействия;

• постановка вопросов – инициативное сотрудничество в поиске и сборе информации;

• уважительное отношение к партнёрам, внимание к личности другого.

Мотивация

учебной

деятельности

Проверка

домашнего задания

Актуализация

знаний

Изучение

нового материала

Личностные: мотивация к учению, развитие интереса к информатике, положительно отношение к процессу познания

Регулятивные:

• прогнозирование – предвосхищение результата и уровня усвоения, его временных характеристик;

• контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;

• коррекция – внесение необходимых дополнений и корректив в план, и способ действия в случае расхождения эталона, реального действия и его продукта;

Познавательные:

• Общеучебные УУД: умение структурировать знания; рефлексия способов и условий действия; извлечение необходимой информации из прослушанного сообщения; определение основной и второстепенной информации;.

• Универсальные логические действия: анализ – выделение элементов и «единиц» из целого; расчленение целого на части; обобщение – генерализация и выведение общности для целого ряда или класса единичных объектов на основе выделения сущностной связи; подведение под понятие – распознавание объектов, выделение существенных признаков и их синтез; установление аналогий.

• Действия постановки и решения проблем: самостоятельное создание алгоритмов деятельности при решении проблем.

Коммуникативные:

• организация и планирование учебного сотрудничества с учителем и сверстниками;

• умение общаться и взаимодействовать с партнёрами по совместной деятельности или обмену информацией;

• речевые действия как средства регуляции собственной деятельности.

Закрепление

изученного

материала

Личностные: формирование ценностных ориентиров и смыслов учебной деятельности на основе развития познавательных интересов, учебных мотивов, формирования мотивов достижения и социального признания, мотива, реализующего потребность в социально значимой деятельности.

Регулятивные:

Познавательные:

Коммуникативные: спрашивать, интересоваться чужим мнением и высказывать своё; умение аргументировать свою точку зрения; уважительное отношение к партнёрам, внимание к личности другого.

Рефлексия.

Итоги урока

Инструктаж,

домашнее задание

infourok.ru

«Обобщающий урок по теме «Системы счисления» Класс: 9

Конспект «открытого» урока информатики в 9 классе

Тема: «Обобщающий урок по теме «Системы счисления»

Класс: 9 А

Дидактическая цель урока: создать условия для повторения и осмоления системы знаний по теме «Системы счисления»

Задачи урока:

I. Формирование предметной компетенции:

Познавательные — повторить понятия «система счисления», определение «позиционные и непозиционные СС»; повторить правила перевода чисел из одной СС в другую и наоборот.

Практические — учить детей работать с инженерным калькулятором

II. Формирование метапредметных компетенций:

Регулятивные компетенции — определять отличие схемы от рисунка — развивать внимание, логическое мышление, умение сопоставлять и делать вывод, творческие умения;

Коммуникативные компетенции — работать в коллективе, слушать и слышать учителя, адекватно реагировать на ошибки, принимать решения.

III. Воспитательные задачи:

Вызвать интерес к изучению информатики как науке, изучающей хранение, передачу и обработку информации.

Тип урока: Обобщение и систематизация знаний и способов действий

Методы обучения: проблемное обучение, проектный метод, здоровьесберегающая технология, ИКТ-технология

Формы работы: фронтальная, индивидуальная, групповая

Дидактический материал: карточки с заданиями, текст стихотворения

Оборудование: раздаточный материал, АРМ учителя, проектор, ноутбуки, телефоны

Перечень используемых ЭОР

1

Понятие о системах счисления

информационный

видеофрагмент

http://www.fcior.edu.ru/card/1610/ponyatie-o-sistemah-schisleniya.html

2

Системы счисления (N 170369)

Информационный, анимация

Интерактивный мультфильм

http://school-collection.edu.ru/catalog/res/15925a41-8dd5-48c5-9187-31628f22b89a/?

ХОД УРОКА:

1. Организационный момент

Учитель: Приветствует учащихся, про­веряет готовность рабочего места школьников к учебному занятию

— Здравствуйте, ребята. Сегодня нам понадобятся рабочие тетради, ручки, ноутбуки и сотовые телефоны.

Учащиеся: Приветствуют учителя, прове­ряют наличие дидактических материалов для работы на за­нятии, слушают учителя

2. Актуализация знаний

Учитель:

— Урок мы начнем с небольшого стихотворения (Приложение 1, Рисунок 1):

  Читает стихотворение:

СКОЛЬКО ЛЕТ ДЕВОЧКЕ

(А. Стариков)

Ей было тысяча сто лет,

Она в сто первый класс ходила,

В портфеле по сто книг носила —

Все это правда, а не бред.

Когда, пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

Она ловила каждый звук

Своими десятью ушами,

И десять загорелых рук

Портфель и поводок держали.

И десять темно-синих глаз

Рассматривали мир привычно,

Но станет все совсем обычным,

Когда поймете наш рассказ

Учитель: задает вопросы по стихотворению, актуализирует внимание учащихся

— Скажите, пожалуйста, что в этом стихотворении необычного?

-Что необходимо сделать, чтобы стихотворение стало понятным?

Учащиеся: слушают учителя, отвечают на вопросы

— Перевести числа из двоичной системы счисления в десятичную.

Учитель: 

— Давайте вспомним определение системы счисления.

— Назовите основные системы счисления?

Ученик:  Двоичная, десятичная, восьмеричная, шестнадцатеричная (Рисунок 3).

Учитель:

— Чтобы стихотворение стало понятным, переведем числа из двоичной системы счисления в десятичную

(Рисунок 1). Читаем первую строчку: Ей было тысяча сто лет. Как мы переведем число из двоичной СС в

десятичную. Вспомним правила перевода вместе. Вы работаете в тетрадях, а я у доски.

(Учитель на доске переводит первое число из двоичной системы счисления в десятичную).

— Итак, девочке было 12 лет (Рисунок 4). 

А теперь каждый из вас самостоятельно переведет все остальные числа в десятичную систему счисления (у вас есть ровно 3 минуты).

(ученики работают в тетрадях)

Учитель:

Итак, проверяем:

— В какой класс ходила девочка?

Ученик: в 5 класс (Рисунок 5)

Учитель: 

— Сколько книг она носила?

Ученик: 4 книги (Рисунок 6)

Учитель: 

— Сколько было ног, рук, ушей и глаз у девочки?

Ученик: конечно по 2 (Рисунок 7).

Учитель:  Показывает интерактивный мультфильм (ЭОР № 2), предлагает выписать в тетрадь пример перевода чисел из десятичной системы счисления в другую.

III. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Учитель:  Сообщает тему урока, предлагает сформулировать учебную задачу

— Мы с вами вспомнили правила перевода из двоичной СС и десятичную.

— А как перевести числа из 8 и 16 сс в десятичную? Точно также.

— Итак, вы уже, наверное догадались чем мы сегодня на уроке будем заниматься.

Учащиеся: Слушают учителя, формулируют учебную задачу урока

— На уроке мы будем повторять тему «системы счисления»

Учитель: Разъясняет условия и последовательность работы школьников

— Сегодня мы проведем урок – обобщение и систематизация знаний по теме «системы счисления». Мы повторим привила перевода из одной СС в другую и наоборот, научимся переводить числа с помощью инженерного калькулятора.

Итак, открываем тетради и записываем дату и тему урока «Системы счисления».

III. Закрепление, систематизация и контроль знаний и способов действий.

Учитель: актуализирует внимание учащихся на экран, задает вопросы (ЭОР № 1)

— Посмотрите на экран и скажите, в какой системе счисления могут быть записаны числа?

2007, 10101, 343434, F12A ?

— Вы знаете, что все СС делятся на 2 большие группы. Какие?

— К какой группе систем счисления относятся эти числа?

Учащиеся: слушают, отвечают на вопросы о непозиционных систем счисления, позиционной системы счисления, формулы перевода чисел из любой системы счисления в десятичную.

— Позиционные и непозиционные. К позиционной.

Учитель: актуализирует внимание учащихся на экран, задает вопросы (Презентация)

— Что вы можешь сказать о числах 333 и ХХХ ?

— Чему в десятичной системе счисления равны следующие числа, записанные римскими цифрами:

а) XI; б) LX; в) MXD?

— По каким правилам вы перевели числа из римской СС в десятичную.

— А эти числа к какой системе счисления относятся?

Учащиеся: К непозиционной.

Учитель: организует самостоятельную работу перевода числа в десятичную СС

— Переведите самостояельно римское число в десятичную СС

MCMXLVI (1946)

Учащиеся: работают самостоятельно, выполняют задания в рабочей тетради

Учитель:

— Это число вам о чем-нибудь говорит? Это год появления первого компьютера в США (Эниак)

-Итак, мы с вами вспомнили, что системы счисления делятся на позиционные и непозиционные СС и вспомнили правила перевода римских чисел.

— Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления.

— Вспомним правила перевода чисел из 10-ичной СС в любую другую. Разберем вместе с вами первый пример, я у доски, а вы в тетрадях. У вас есть одна минута.

Учащиеся: работают самостоятельно, выполняют задания в рабочей тетради

Учитель: организует фронтальную работу проверки задания

— Итак, что у вас получилось?

— Хорошо, мы повторили перевод чисел из 10-ой СС в любую другую СС. Молодцы

Физкультминутка

Учитель организует небольшой перерыв, просит учащихся выполнить упражнения для глаз (Презентация)

Учитель: организует работу в парах.

— Сейчас мы еще раз убедились, на сколько это трудоемкий процесс с использованием только математических навыков. Для перевода чисел из одной системы счисления в другую и проведения вычислений в различных системах счисления можно использовать приложения, которые обычно называются научными или инженерными калькуляторами. Какое стандартное приложение входит в состав операционной системы Windows? (Калькулятор)

Воспользуемся этим приложением для вычислений. Используя инженерный калькулятор выполним задания по карточкам

Задания для парной работы

Учащиеся: выполняют работу в парах, организуют взаимопроверку, взаимооценку

1) Переведите числа из одной системы счисления в другую:

12816  — Х2    Ответ:1001010002

 6418—   Х16   Ответ:1A116

2) Какое из чисел  1100112,  1118,  1В16   является наибольшим, наименьшим?

Ответ: 1В16 < 1100112 < 1118.

— Чтобы проверить правильность выполнения заданий обменяйтесь с соседями карточками и проверьте друг у друга ответы. И поставьте оценки за работу.

IV. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.

Учитель: контроль усвоения знаний и умений через работу по карточкам.

Работа с карточками (Приложение 3)

— У вас у каждого на столе лежат карточки с зашифрованными словами. Но каждая буква представлена в какой-то СС. Вам нужно перевести каждую цифру.

Учащиеся: выполняют задания в тетради, отвечают устно

Учитель: корректирует деятельность учащихся, разбирает допущенные ошибки

V. Подведение итогов. Рефлексия.

Учитель: организует беседу по вопросам

— Какие цели, задачи стояли перед нами в начале урока?

— Смогли ли вы их достичь?

— Какой материал был трудным, непонятным?

— А что воспринималось легко?

— Попробуйте дать оценку уроку

Учащиеся: отвечают на вопросы, анализирую свою деятельность на уроке

Учитель: оценивает работу учащихся, выставляет оценки за урок

— Вы сегодня хорошо поработали на уроке. Особенно активными были…

VI. Информация о домашнем задании

Учитель: формулирует домашнее задание

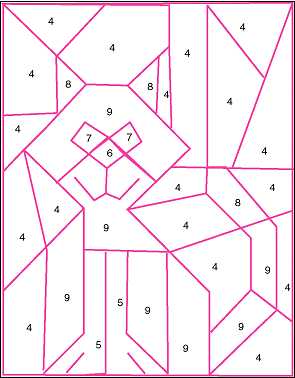
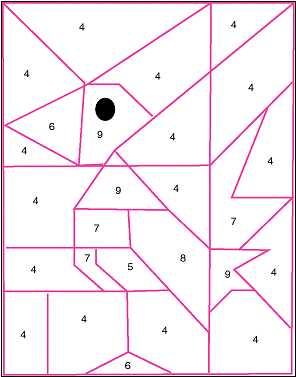
— Выполните творческое задание (Приложение 4) – раскрасьте рисунок, определив его цвета, с помощью перевода чисел в десятичную систему счисления.

Учащиеся: записывают домашнее задание.

Приложение № 1

Приложение № 2

1) Переведите числа из одной системы счисления в другую:

12816 — Х2 Ответ: 1001010002

6418— Х16 Ответ: 1A116

2) Какое из чисел 1100112, 1118, 1В16 является наибольшим, наименьшим?

Ответ: 1В16 < 1100112 < 1118.

Приложение № 3

КАРТОЧКА № 1

1. Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 1101₂ 0100₂ 1010₂ 1011₂

Ответ: _____________

КАРТОЧКА № 2

1. Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 1011₂ 1100₂ 0100₂ 1000₂ 1110₂

Ответ: ___________

КАРТОЧКА № 3

1. Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 1100₂ 0100₂ 0101₂ 1011₂

Ответ: ____________

КАРТОЧКА № 4

1. Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 0010₂ 1011₂ 1000₂ 1110₂ 0010₂ 1011₂

Ответ: ______________

КАРТОЧКА № 5

1. Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 0011₂ 0110₂ 1011₂ 1101₂

Ответ: ______________

Приложение № 4

Творческое домашнее задание

Возьмите цветные карандаши (6 цветов) с номерами в десятичной системе счисления. Задание: раскрасить рисунок соответствующим цветом.

100 – ЗЕЛЕНЫЙ

101 – ГОЛУБОЙ

110 — КРАСНЫЙ

111 – ЖЕЛТЫЙ

1000 – КОРИЧНЕВЫЙ

1001 – ЧЕРНЫЙ

infourok.ru

Конспект Урока по информатике учебник Семакина 9 класс «Арифметика системы счисления»

Конспект урока на тему: «Арифметика системы счисления»

По учебнику Семакина 9 класс

Вид урока: изучение-повторение раннее изученного материала

Цель: научить учащихся выполнять арифметические действиями в двоичной системе счисления.
Задачи:
образовательные: 
— повторение и закрепление знаний учащихся о системах счисления;
— формировать у школьников умение выполнять правильно арифметические действия в двоичной системе счисления;
развивающие: 
— развивать логическое мышление учащихся;
— развивать познавательный интерес учеников.

Ход урока:

— Здраствуйте ребята! Садитесь (проверка наличия домашнего задания, вызываем к доске несколько детей для проверки домашнего задания)

— На этом уроке мы с вами вспомним арифметические действия систем счисления. Для этого давайте попробуем решить задачу. В саду 100 фруктовых деревьев 14 яблонь и 42 груши. В какой системе счисления подсчитаны деревья? Может кто то уже знает ответ?(6) Чтобы научиться решать такие задачи нам необходимо научиться складывать и вычитать в разных системах счисления. Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел.

0+0=0 
0+1=1 
1+0=1 
1+1=10
Обратить внимание учащихся на то, что при сложении двух единиц в двоичной системе счисления в записи получается 0, а единица переносится в следующий разряд. При сложении трех единиц получается в записи 1, и единица переносится в следующий разряд.

 При сложении чисел надо обязательно проговаривать алгоритм сложения. Следует учитывать, что сложение, как обычно, нужно начинать с младшего разряда. Если сумма единиц разряда окажется равной или большей основания системы счисления, то возникает перенос единицы в старший разряд. После сложения, cледует обязательно сделать обратный перевод и убедиться, что число 101 — действительно число 5 в десятичной системе счисления.

Примеры:  Выполните сложение чисел в двоичной системе счисления:

10011+11=1110

Решение:

58(9)+57(9)=126(9)

543₇+355₇ = 1231(7)

Учащиеся самостоятельно решают следующие примеры:
110+110=1100

37(8)+25(8)=64(8)

2103(4)+1312(4)=10021(4)

Правила вычитания:
0-0=0
1-0=1
1-1=0
0-1=-1
Обратить внимание учащихся на то, что «минус» в последнем правиле обозначает – «занять разряд (1)».

Примеры
10110-111=1111

Решение:

Объяснение:
Вычитание выполняется так же, как в математике. Если цифра в уменьшаемом меньше цифры вычитаемого, то для данного вычитания необходимо занять разряд (1), т.к. 10-1=1. Если слева от такого вычитания стоит 0, то мы не можем занять разряд. В этом случае разряд занимаем в уменьшаемом у близстоящей слева от данного вычитания единицы. При этом все нули, у которых мы не могли занять разряд, необходимо поменять на единицу, т.к. 0-1=-1. Желательно все изменения в цифрах записывать сверху данного вычитания. Дальнейшее вычитание выполнять с получившимися сверху цифрами.

100000-11=11101

Решение:

2311(4)-1223(4)=1022(4)

1. В первом разряде от 1 нельзя отнять 3, «занимаем» единицу второго разряда, она содержит четыре единицы первого разряда. К ним добавляем имеющуюся единицу первого разряда, всего получим пять единиц в первом разряде — в четверичной системе они записываются как 11.

2. Вычитаем в первом разряде из пяти единиц три единицы: 11-3=2.

3. Во втором разряде единиц не осталось, занимаем в третьем (в третьем останется 2 единицы). Единица третьего разряда содержит 4 единицы второго. Вычитаем во втором разряде: 4-2 = 2.

4. В третьем разряде: 2-2=0.

5. В четвертом разряде: 2-1=1.

Учащиеся самостоятельно решают следующие примеры:

654₈ — 477_{8 = 155}

3743(8)-247(8)=3474(8)

9С(16)-78(16)=24(16)

Теперь я раздам вам карточки с заданиями и каждый по очереди будет выходить и решать

2)-

3) AFF1₁₆ — 19D₁₆

4) 121211₃ + 221₃

5) +

6) 5В4₁₆ + С52₁₆

1206₁₆

7) 234₅ + 312₅

8)-

9)  5731₈ + 1376₈

7327₈

10) 100001₂ — 1001₂

 11000₂

11) F0B₁₆ + 1DA₁₆

 10E5₁₆

12) 7135₈ — 756₈

 6157₈

13)+

14) —

15) EA35₁₆ — FC8₁₆

DA6D₁₆

16) F1C5₁₆ — DEB₁₆

E3DA₁₆

17) 120₃+100₃-021₃

122₃

18) 256₈-140₈+673₈

1011₈

19) 656₈+523₈-420₈+362₈

1343₈

20) 756₈+307₈+2456₈+24₈

3767₈

21) 156₈+234₈-350₈+362₈-107₈

545₈

22) 2С₁₆+852₁₆-5А₁₆

552₁₆

23) 9F31₁₆-5B51₁₆+BC6₁₆

4FA6₁₆

24) 24E₁₆+F6₁₆-9A3₁₆-69₁₆

F938₁₆

25) 965₁₆-5B5₁₆+B63₁₆-39₁₆

EDA₁₆

26) 5C9₁₆-2B3₁₆+26A6₁₆-1E₁₆+11₁₆

29AF₁₆

Домашняя работа.

Произведите сложение чисел:

1. 0010001₂+1011101₂ (1101110₂ )

2. 211₃+102₃ (1020₃ )

3. 4716₈+866₈ (5804₈ )

4. FD99₁₆+2A88₁₆ (12821₁₆ )

Выполните вычитание чисел:

1. 10101010₂-01010101₂ (1010101₂ )

2. 2000₃-100₃ (1200₃ )

3. 7569₈-2180₈ ( 5369₈ )

4. 34DC₁₆-9EF9₁₆ (F95E3₁₆ )

infourok.ru

Методическая разработка урока «Общие сведения о системах счисления»

Урок информатики на тему: 

«Общие сведения о системах счисления»

Величие человека — в его способности мыслить.
Б. Паскаль

Цель  урока: Познакомить учащихся с понятием система счисления, развитием систем счисления от буквенных до позиционных.

Задачи:

— обучающие 

• познакомить учащихся с историей возникновения и развития систем счисления, дать классификацию систем счисления.
• ввести новые понятия по теме урока,
• дать представление о позиционной и непозиционной системах счисления, указать на основные преимущества и недостатки этих систем счисления.

-развивающие  

• развивать познавательный интерес учащихся,
• развивать умения анализировать, сравнивать, выделять главное, приводить примеры, 
• развитие внимания, восприятия, познавательного интереса у учащихся, умения обобщать и сравнивать;
• формирование ключевых компетенций, а также активизация творческой деятельности учащихся.

-воспитательные

• научить воспринимать компьютер как инструмент информационной деятельности человека,
• воспитывать самостоятельность, аккуратность, трудолюбие,
• научить отстаивать свою точку зрения

Тип урока:  Урок формирования новых знаний.

Формы работы учащихся:    фронтальная, индивидуальная, самостоятельная.

Необходимое техническое оборудование:

• компьютерный класс,
• 8 ученических персональных компьютеров,
• компьютер учителя,
• колонки,
• мультимедийный проектор,
• интерактивная доска.

Новые понятия и термины: система счисления, позиционные и непозиционные системы счисления, число, цифра.

Ход  урока

Этапы урока

Действия учителя

Действия ученика

1

Организационный момент урока

Учитель приветствует учащихся, объявляет тему, цель и задачи урока.

2

Актуализация знаний учащихся

Пифагорийцы говорили: “Всё есть число”. Вы согласны с этим утверждением?

Почему люди разных стран говорят на разных языках, а считают одинаково? Это связано с торговыми расчётами. Еще в древности при покупке и продаже разных товаров люди пришли к выводу, что считать и записывать Количество товаров удобней одинаково, так как это значительно облегчает вычисления, поэтому сегодня мы должны узнать, а как же люди считали в древности?

Учащиеся слушают, анализирую информацию.

Изучение нового материала

Числа были всегда и 4 и 5 тыс. лет назад, только правила изображения их были другими. Сегодня мы с вами рассмотрим  историю создания и развития чисел в разных странах.

Учитель демонстрирует флэш-фильм  (http://files.school-collection.edu.ru/dlrstore/402b749c-240b-4e16-9e4d-bea3fc4fa8fa/9_139.swf):

рассматривается слайд 1 (определение системы счисления), далее слайды 2-7 ресурса с пояснениями учителя.

Далее учитель демонстрирует и комментирует модуль «Понятие о системах счисления»  (http://fcior.edu.ru/card/1610/ponyatie-o-sistemah-schisleniya.html). Рассматриваются позиционные и непозиционные системы счисления. Приводятся примеры.

Позиционные – количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.

Непозиционные – количественное значение  цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.

Учащиеся на своих компьютерах открывают ресурс и слушают объяснения учителя,  анализируют информацию.

Физкульминутка

Учитель руководит действиями учащихся

Для физкультминутки используется презентация  http://www.pedsovet.org/component/

option,com_mtree/task,listcats/cat_id,1277

Выполняют упражнения

4

Закрепление материала

Теперь выполним задание «Проверь себя» в ресурсе http://fcior.edu.ru/card/1610/ponyatie-o-sistemah-schisleniya.html.

Учитель контролирует выполнение заданий, оказывает помощь при затруднении.

Учитель еще раз открывает слайд 1 ресурса http://files.school-collection.edu.ru/dlrstore/402b749c-240b-4e16-9e4d-bea3fc4fa8fa/9_139.swf (схема) и повторяет с учащимися: какие системы счисления являются позиционными и непозиционными.

Вопрос: Какие  недостатки непозиционной системы счисления вы можете отметить?

Учащиеся на компьютерах выполняют работу.

Учащиеся называют позиционные и непозиционные системы счисления.

Недостатки:

1. сложность при выполнении арифметических действий;
2. Для записи больших чисел приходится вводить новые цифры;
3. Невозможно записывать дробные и отрицательные числа.

5

Самостоятельная работа

Теперь запускаем тестовые задания, ресурс http://fcior.edu.ru/card/2770/ponyatie-o-sistemah-schisleniya.html (вопросы 1, 2, 4, 5, 7, 8) и ответим на вопросы.

Учитель контролирует выполнение заданий учащимися.

Учащиеся запускают на своих компьютерах ресурс и выполняют тестовые задания.

6

Обобщение урока

Вопросы:

1. Какие системы счисления называют позиционными? Приведите примеры.
2. Какие системы счисления называют непозиционными? Приведите примеры.
3. В какой системе счисления (позиционной или непозиционной) легче производить вычисления?

Учащиеся отвечают на вопросы.

7

Подведение итогов урока

Учитель предлагает учащимся оценить себя и свою работу на уроке (смайликами). Далее учитель анализирует работу учащихся на уроке и выставляет оценки.

8

Задание на дом

Учебник стр. 38-42

Учащиеся записывают домашнее задание.

Просмотр содержимого документа
«Методическая разработка урока «Общие сведения о системах счисления» »

kopilkaurokov.ru

Урок+презентация на тему «Двоичная система счисления» 9 класс

План-конспект урока по информатике в 9 классе на тему «Двоичная система счисления» (Слайд 1)

Цель: сформировать понятия «двоичная система счисления» и основ арифметических вычислений в двоичной системе. (Слайд 2)

Требования к знаниям и умениям (Слайд 3)

Учащиеся должны знать:

• десятичную и двоичную системы счисления;

• развернутую форму записи числа;

• правила перевода из двоичной системы счисления в десятичную и наоборот;

• правила сложения и умножения двоичных чисел.

Учащиеся должны уметь:

• переводить двоичные числа в десятичную систему;

• переводить десятичные числа в двоичную систему;

• складывать и умножать двоичные числа.

Программно-дидактическое оснащение: Сем., § 16, с. 96; демонстрация «Двоичная система счисления»; проектор. (Слайд 4)

Ход урока

1. Организационный момент

2. Постановка целей урока

-С какими числами работает компьютер? Почему?

-Как ими оперировать?

3. Работа по теме урока

(С помощью демонстрации «Двоичная система счисления» показать развернутую форму числа, перевод из двоичной системы счисления в десятичную и наоборот, арифметику двоичных чисел.)

Двоичная система счисления является основной системой представления информации в памяти компьютера. Эта идея принадлежит Джону фон Нейману (Слайд 5), сформулировавшему в 1946 г. принципы устройства и работы ЭВМ. Но, вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами электронных вычислительных машин, а математиками и философами, задолго до появления компьютеров, еще в XVII—XIX вв. Великий немецкий ученый Лейбниц (Слайд 6) считал: «Вычисление с помощью двоек <…> является для науки основным и порождает новые открытия… При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок». Позже двоичная система была забыта, и только в 1936—1938гг американский инженер и математик Клод Шеннон (Слайд 7) нашел замечательные применения двоичной системы при конструировании электронных схем.

А что же такое система счисления? Это правила записи чисел и связанные с ними способы выполнения вычислений.

Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются десять цифр: 0, 1,2, 3,4, 5, 6, 7, 8,9. (Слайд 8) Число цифр определяет основание системы счисления. Если число цифр — десять, то основание системы счисления равно десяти. В двоичной же системе существует всего две цифры: 0 и 1. Основание равно двум. Возникает вопрос, можно ли с помощью всего двух цифр представить любую величину. Оказывается, можно!

Развернутая форма записи числа(Слайд 9)

Вспомним принцип записи чисел в десятичной системе счисления. Значение цифры в записи числа зависит не только от самой цифры, но и от места расположения этой цифры в числе (говорят: от позиции цифры). Например, в числе 555 первая справа цифра обозначает: три единицы, следующая — три десятка, следующая — три сотни. Этот факт можно выразить как сумму разрядных слагаемых:

555₁₀ = 5 х 10² + 5 х 10¹ + 5 х 10° = 500 + 50 + 5.

Таким образом, с продвижением от цифры к цифре справа налево «вес» каждой цифры увеличивается в 10 раз. Это связано с тем, что основание системы счисления равно десяти.

Перевод двоичных чисел в десятичную систему

А вот пример многозначного двоичного числа: 111011₂. Двойка внизу справа указывает на основание системы счисления. Это нужно для того, чтобы не перепутать двоичное число с десятичным. Ведь существует же десятичное число 111011! Вес каждой следующей цифры в двоичном числе при продвижении справа налево возрастает в 2 раза. Развернутая форма записи данного двоичного числа выглядит так:

111011₂ = 1 х 2⁵+ 1 х 2⁴+ 1 х 2³ + 0х 2²+ 1 х 2¹ + 1 х 2° = 67₁₀.

Таким способом мы перевели двоичное число в десятичную систему.

Переведем в десятичную систему еще несколько двоичных чисел (Слайд 10).

10₂ = 2¹ =2; 100₂= 2² = 4; 1000₂ = 2³ = 8;

10000₂ = 2⁴ = 16; 100000₂ = 2⁵ = 32 и т. д.

Таким образом, получилось, что двузначному десятичному числу соответствует шестизначное двоичное! И это характерно для двоичной системы: быстрый рост количества цифр с увеличением значения числа.

Задание 1. (Слайд 11)Запишите начало натурального ряда чисел в десятичной (А₁₀) и двоичной (А₂) системах счисления.

Задание 2. Переведите в десятичную систему следующие двоичные числа.

101; 11101; 101010; 100011;10110111011.

Ответ: 5; 29; 42; 35; 1467.

Перевод десятичных чисел в двоичную систему (Слайд 12)

Как перевести двоичное число в равное ему десятичное, вам должно быть понятно из рассмотренных выше примеров. А как осуществить обратный перевод: из десятичной системы в двоичную? Для этого нужно суметь разложить десятичное число на слагаемые, представляющие собой степени двойки. Например:

15₁₀ = 8 + 4 + 2 + 1 = 1 х 2³ + 1 х 2² + 1 х 2¹ + 1 х 2° = 1111₂. Это сложно. Есть другой способ, с которым мы сейчас и познакомимся.

Пусть нужно перевести в двоичную систему счисления число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая и про нулевые:

234 = 2 х 117 + 0 14 = 2 х 7 + 0

Выписав все остатки, начиная с последнего, получим двоичное разложение числа: 234₁₀ = 11101010₂.

Задание 3. (Слайд 13) Какие двоичные числа соответствуют следующим десятичным числам?

2; 7; 17; 68; 315; 765; 2047.

Ответ: 10₂; 111₂; 10001₂; 1000100₂; 100111011₂; 1011111101₂; 11111111111₂.

Арифметика двоичных чисел (Слайд 14)

Правила двоичной арифметики гораздо проще правил десятичной арифметики. Вот все возможные варианты сложения и умножения однозначных двоичных чисел:

0+0=0

0+1=1

1+0=1

1+1=10

0*0=0

0*1=0

1*0=0

1*1=1

Своей простотой и согласованностью с битовой структурой компьютерной памяти двоичная система счисления и привлекла изобретателей компьютера. Ее гораздо проще реализовать техническими средствами, чем десятичную систему.

Вот пример сложения столбиком двух многозначных двоичных чисел (Слайд 15):

₊1011011101

111010110

10010110011

А теперь посмотрите внимательно на следующий пример умножения многозначных двоичных чисел:

_х1101101

101

1101101

1101101

1000100001

Задание 4. (Слайд 16)Выполните сложение в двоичной системе счисления. 11 + 1; 111 + 1; 1111 + 1; 11111 + 1.

Ответ: 100; 1000; 10000; 100000.

Задание 5. Выполните умножение в двоичной системе счисления.

111 х 10; 111 х 11; 1101 х 101; 1101 х 1000.

Ответ: 1110; 10101; 1000001; 1101000.

4. Подведение итогов урока (Слайд 17)

Система счисления — это определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений. Основание системы счисления равно количеству используемых в ней цифр.

Двоичные числа — это числа в двоичной системе счисления. В их записи используются две цифры: 0 и 1.

Развернутая форма записи двоичного числа — это его представление в виде суммы степеней двойки, умноженных на 0 или на 1.

Использование двоичных чисел в компьютере связано с битовой структурой компьютерной памяти и с простотой двоичной арифметики

Домашнее задание (Слайд 18)

1. Заданы двоичные числа Х и Y. Вычислить X + Y и X— Y, если Х= 1000111, Y= 11010.

2. Заданы двоичные числа X и У. Вычислить X + Y— 1001101, если X = 1010100, Y= 110101.

3. Выполнить умножение: 100110 х 11001.

Ответы: 1.1100001 и 101101; 2. 111100; 3. 1110110110.

infourok.ru