Рациональные числа — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тема учебного проекта «Рациональные числа» Предмет: математика

Автор: Толстых Лидия Ивановна

2. Творческое название проекта

Погружение в мир чисел

3. Проект охватывает следующие учебные темы:

— Целые числа
— Дробные числа
— Положительные и отрицательные числа

4. Аннотация проекта

Данная проектная работа способствует:
— организации адаптационно-развивающего общения;
— обеспечению актуализации необходимых знаний ;
— умению применять полученную информацию на
практике;
— введению новых понятий;
— формированию и дальнейшему развитию
мыслительных операций, освоению учениками
методов исследования; навыков работы в группе;
— развитию творческого и логического мышления,
качеств творческой личности;
— воспитанию интереса к предмету и деятельности
учащихся;
— расширению кругозора.

5. Дидактические цели

Формирование и дальнейшее развитие
мыслительных операций: анализа, сравнения,
обобщения и т. д.
Формирование навыков работы в группе.
Развитие логического и творческого мышления.
Воспитание интереса к предмету.
Развитие качеств творческой личности, таких,
как познавательная активность, упорство в
достижении цели, самостоятельность.

6. Методические задачи

Расширение множества чисел. Освоение понятий
«положительное число», «отрицательное число»,
«модуль числа», «множество целых чисел»,
«множество рациональных чисел», «противоположные
числа», «неположительные числа» и «неотрицательные
числа»».
Сформировать и развить вычислительные навыки при
выполнении арифметических действий.
Научить применять полученную информацию на
практике при выполнении контролирующих работ и
исследований.

7. Участники проекта

Учащиеся 5-7 классов

8. Этапы работы над проектом

Выбор творческого названия проекта и темы
индивидуальных исследований
Формулирование дидактических целей и
методических задач проекта.
Формирование групп для проведения исследований и
определения формы представления результатов
Выдвижение гипотез решения проблем

9. Этапы работы над проектом

Обсуждение плана работы групп
Самостоятельная работа учащихся в
группах
Подготовка учащимися отчета о
проделанной работе (презентаций,
докладов, сообщений, кроссвордов)
Защита полученных результатов и выводов
Оценивание результатов проекта.
Рефлексия

10. Дидактический материал

Контрольные работы.
Самостоятельные работы.
Тесты.
Карточки.
Устные упражнения.
Математические диктанты
Интернет ресурсы

11. Темы для самостоятельных исследований

Удивительная история нуля.
История возникновения дробей.
Экскурс в страну чисел.
Десятичные дроби.
Ложные числа.

12. Информационные ресурсы

Глейзер Г.И, История математики в школе, М., «Просвещение», 1981 г.
Зубарева И.И., Мордкович А.Г., Математика – 6, М., «Мнемозина», 2005г.
Зубарева И.И., Мордкович А.Г., Математика 5-6 классы, методическое
пособие для учителя, М., «Мнемозина», 2005 г.
Минаева С.С., 20 тестов по математике 5-6 классы, М, «Экзамен», 2007 г.
Шейнина О.С, Соловьева Г.М, Математика. Занятия математического
кружка, 5 – 6 классы, М., Издательство НЦ ЭНАНС,2003 г.
Мордкович А.Г. Беседы с учителем математики.- М.: «Школа-Пресс», 1995 г.
Энциклопедия для детей, том 11, Математика, гл. редактор Аксенова М.Д. –
М., «Аванта +», 2002 г.
Серия «Школьная Энциклопедия» Математика. Гл. редактор Никольский
С.М. – М., «ДРОФА», 1992 г.
Перельман Я.И, Живая математика, М, «Наука», 1994 г.
Депман И.Я, За страницами учебника математики, М., «Просвещение», 1989
г.
Гнеденко Б.В., Энциклопедический словарь юного математика, М.,
«Педагогика – Пресс», 1999 г.
Интернет ресурсы
«Положительные и
отрицательные
числа»

14. Творческое название проекта

Ложные
—
—
—
числа
—

15.

Цели и задачи:-изучить новое математическое понятие
отрицательные числа;
-рассмотреть область применения
отрицательных чисел;
-выяснить их значимость;
-расширение математического и общего
кругозора;
-формирование дружеских отношений в
классе.

16. Аннотация проекта

— Данная проектная работа способствует лучшему
усвоению понятия отрицательные числа;
-Формированию навыков самостоятельной
деятельности;
-Воспитанию интереса к математике;
-Созданию комфортных условий для осознания и
осмысления блока новой учебной информации,
используя приемы проектного обучения.

17. Гипотеза

Отрицательные числа –
«лишние» числа.

18. Проблемные вопросы

1. Как возникли отрицательные числа?
2. Зачем нужны отрицательные числа?
3. Числа разных знаков не в
математической сфере.

19. 1. Исторический экскурс в страну отрицательных чисел

Отрицательные числа появились значительно
позже натуральных чисел и обыкновенных дробей.
Первые
сведения об отрицательных числах
встречаются у китайских математиков во 2 веке до
нашей эры.
Положительные числа тогда толковались
как « имущество», «прибыль»,
Отрицательные числа –как «долг» , «недостача».

20. Ложные числа

История говорит о том, что люди долго не могли
привыкнуть к отрицательным числам. Отрицательные
числа казались им непонятными, ими не пользовались,
просто не видели в них особого смысла.
Лишь в 7 веке индийские математики начали широко
использовать отрицательные числа, но относились к ним
с некоторым недоверием.
В Европе отрицательными числами начали пользоваться
с12-13 века, но до 16 века ,как и в древности, они
понимались как долги, большинство ученых считали их
«ложными»,в отличии от положительных чисел«истинных».

21. Геометрическое истолкование положительных и отрицательных чисел

Признанию отрицательных чисел способствовали работы
французского математика РЕНЕ-ДЕКАРТА. Он предложил
геометрическое истолкование положительных и
отрицательных чисел- ввел координатную прямую.

22. Действительно существующие

Окончательное и всеобщее признание как
действительно существующие отрицательные
числа получили лишь в первой половине 18 века.
Тогда же утвердилось и современное
обозначение для отрицательных чисел.
-5
-7
-3
-8
-1
-2
-15
-11
-29

23. Век Интернета и современных технологий. Отрицательные числа? Зачем???

Чтобы быть умными и шагать в ногу со
временем.

24. Для измерения температуры

25. Для измерения глубин морей и океанов.

26. Отрицательные числа нужны для поддержания равновесия в мире.

27. А еще они нужны для вычислительных действий и решения уравнений .

3+х=0
-(-21)=?
7-y=-15
3+(24 -154)=?

28. 3. Числа разных знаков в различных сферах деятельности

29. математика

противоположные числа
—
—

30.

Историялиния времени
Каким математическим знаком можно
заменить слова: «до нашей эры», «нашей
эры»?
До нашей эры
наша эра

31. География

горы и моря

32. Физика

сила упругости, тяжести;
манометры

33. Погода

дождь
снег

34. Русский язык

антонимы
легкий
Густой
редкий
жидкий
(туман)
(лес)
(суп)

35. Окружающий мир

зима
лето

36. Политика

за
против

English     Русский Правила

Презентация к уроку алгебры по теме «Рациональные числа»

Государственная образовательная организация Тульской области «Первомайская кадетская школа» Урок алгебры в 8 классе

Игнатьева Наталья Викторовна,

учитель математики первой

квалификационной категории

р.п. Первомайский, Щекинский район

Цели урока

• Ввести понятие

— «рациональные числа»;

— определение рациональных чисел;

— обозначение множества рациональных чисел.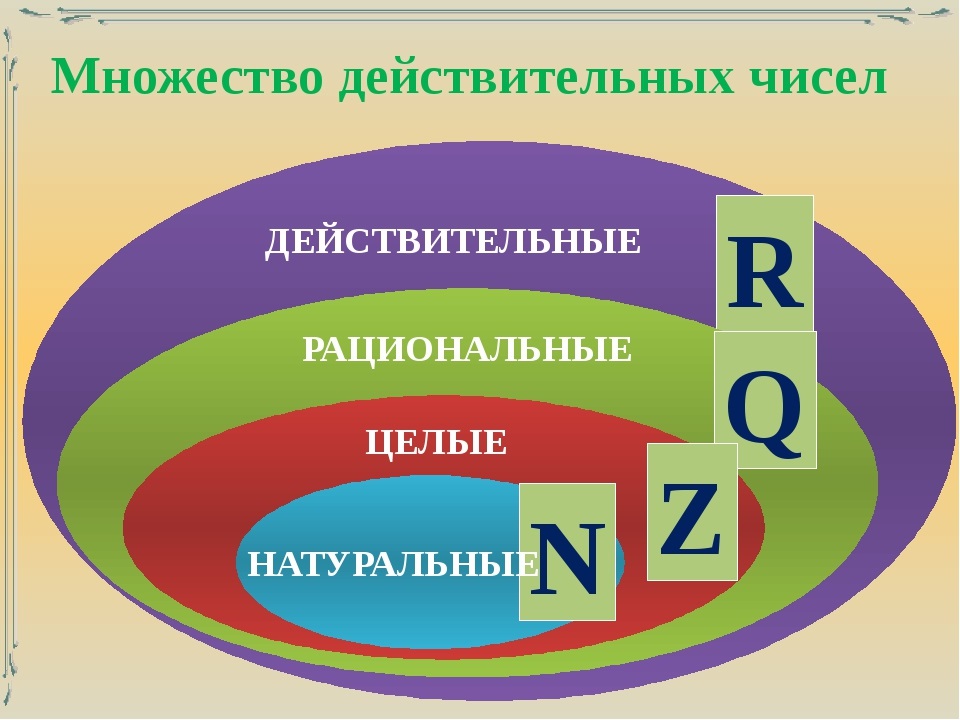

Задачи урока

Образовательные:

• Расширить и обобщить понятие числа; Познакомить с понятием «рациональные числа»; Научить представлять рациональные числа в виде десятичной дроби; Научить записывать любое рациональное число в виде m/n , где m – целое, n — натуральное число.
• Расширить и обобщить понятие числа;
• Познакомить с понятием «рациональные числа»;
• Научить представлять рациональные числа в виде десятичной дроби;
• Научить записывать любое рациональное число в виде m/n , где m – целое, n — натуральное число.

Развивающие:

• Развивающие:

• Развитие логического мышления учащихся, памяти, внимания; Развитие умения самостоятельно мыслить; Развитие грамотной письменной и устной математической речи .
• Развитие логического мышления учащихся, памяти, внимания;
• Развитие умения самостоятельно мыслить;
• Развитие грамотной письменной и устной математической речи .

Воспитывающие:

• Воспитывающие:

• Воспитывать сознательное отношение к учению, познавательную активность, культуру умственного труда.
• Воспитывать сознательное отношение к учению, познавательную активность, культуру умственного труда.

Тема урока: «Рациональные числа» «Если бы ни число и его природа, ничто существующее нельзя было бы постичь им само по себе, ни в его отношениях к другим вещам. Мощь чисел проявляется во всех деяниях и помыслах людей, во всех ремеслах и в музыке» Пифагореец Филолай, 5 в. до н. э.

Число является одним из основных понятий математики. Существует большое количество определений понятия «число».

Евклид

«Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц».

«Начала» 355 г. до н.э.

Русский математик, педагог, помощником учителя математики в школе математических и навигацких наук Магницкий Леонтий Филиппович

в своей

«Арифметике» в 1703 г. писал: «Арифметика — есть наука числительная .

« Число есть бесконечно,

Умом нам недотечно

Никто не знает конца,

Кроме всех, Бога творца».

Еще раньше Евклида Аристотель дал такое определение:

« Число есть множество, которое измеряется с помощью единиц».

Аристотель

Фалес Милетский – родоначальник греческой стихийно-материалистической философии – учил, что « Число — есть система единиц».

Исаак Ньютон – великий английский физик, механик, астроном и математик в своей «Общей арифметике» (1707 г. ) пишет: «Под числом мы подразумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу.

Число бывает трех видов: целое, дробное и иррациональное.

Целое число есть то, что измеряется единицей; дробное – кратной частью единицы; иррациональное – число, не соизмеримое с единицей».

Натуральные числа

Материалом, служащим для записи чисел стали:

Папирус из «Начал» Евклида

Глиняные таблички

Натуральные числа

• Боэций – римский государственный деятель, философ, автор трудов по математике и теории музыки, — впервые применил термин «натуральное число».
• Отрицательные и нецелые числа НАТУРАЛЬНЫМИ не являются.

Натуральные числа

• Множество натуральных чисел обозначают

N

• Например,

При сложении натуральных чисел получается натуральное число , а вот при вычитании… Решим уравнения:

Х + 10 = 4

Х + 10 = 10

Отрицательные числа

В Европе отрицательные числа появились благодаря Леонардо Пизанскому. В 1202 г. он впервые использовал отрицательные числа для подсчета своих убытков. Широко использовать отрицательные числа, выполнять действия с ними, строить координатную прямую стали благодаря работам французского математика Рене Декарта.

Диофант ( III в.)

Рене Декарт

Леонардо Пизанский

Целые числа ( Z )

• Натуральные числа ( N ), противоположные

им (отрицательные) числа и ноль

называются ЦЕЛЫМИ ( Z ) числами.

Дробные числа

• Дроби в древней Руси называли долями, позднее ломаными числами. Так у дробей с числителем 1 были свои названия.

½ — половина, полтина;

1/3 — треть;

¼ — четь;

1/6 – полтреть;

1/8 – полчеть;

1/12 – полполтреть.

Целые и дробные числа составляют множество

РАЦИОНАЛЬНЫХ ЧИСЕЛ

( Q)

Рациональные числа ( Q)

• Числа целые, дробные (положительные и отрицательные) и нуль получили общее название РАЦИОНАЛЬНЫХ чисел ( Q ).

Совокупность рациональных чисел оказыва-ется достаточной для удовлетворения многих практических потребностей, но оказалась недостаточной для изучения непрерывно изменя-ющихся переменных величин.

Рациональные числа (Q )

• — Всякое рациональное число, как целое, так и дробное можно представить в виде дроби m/n , где m — целое, n – натуральное число.
• — Одно и то же рациональное число в таком виде можно представить разными способами:

Самостоятельная работа

• Представьте число и — 5 разными способами.

Проверка самостоятельной работы

Рациональные числа (Q )

• — Среди дробей, с помощью которых записывается данное рациональное число, всегда можно указать дробь с наименьшим знаменателем. Эта дробь несократима. Для целых чисел такая дробь имеет знаменатель, равный 1.

• — Термин «рациональное число» произошел от латинского слова « ratio », что в переводе означает – «отношение» (частное).

Рациональные числа (Q )

Конечная десятичная дробь

Рациональные числа (Q )

Периодическая дробь

Рациональные числа (Q )

• Первичное закрепление (у доски).

Представим в виде десятичной

дроби число .

Рациональные числа (Q )

Дроби с периодом 9

НЕ БЫВАЕТ!!!

Рациональные числа (Q )

Их записывают так:

0,(9)=0,999…=1,000…=1

16,1(9)=16,1999…=16,2000…=16,2

Круги Эйлера

— Все числа, о которых мы сегодня говорили, изобра-жаются на схеме, которая называется Круги Эйлера.

Z

Q

N

Леонард Эйлер

Закрепление изученного

1. Работа по учебнику.

— У доски письменно выполнить

упражнение № 263, стр. 61

2. Устно: Упражнение № 264, стр. 61

3. Самостоятельная работа.

Упражнение № 267 (верхняя строчка),

стр. 62.

Проверка самостоятельной работы

• Игра «Найди ошибку».

Итог урока. Рефлексия.

• Что нового и интересного вы узнали на уроке?
• Какие трудности возникли при изучении нового материала?
• Какое настроение осталось у вас после нашего урока? (С помощью смайликов определите свое настроение).

Домашнее задание

• Пункт 10(правила),

упражнение № 267(вторая строчка),

№ 268 (1 столбик), страница 62.

Тема урока — функция y, корень x. Функция y = квадратный корень из x, ее свойства и график

Республика Татарстан, Черемшанский район, с. Черемшан

МБОУ «Черемшанский лицей»

Тема урока: «Функция y=√x, ее свойства и график»

Сахабиева Эльвира Маратовна

Учитель математики

2 МБОУ «Черемшан»,

02 МБОУ «Черемшан». Черемшан

2015-2016

Функция y = √x, ее свойства и график

Тип урока: Урок по ознакомлению с новым материалом.

Тип занятия: комбинированное.

Класс: 8

Цель урока:

Задачи:

Образовательные

• Закрепить умение находить значения выражений, содержащих квадратный корень.
• Научитесь анализировать и находить правильное решение проблемной ситуации.

Образовательная

• Воспитывать познавательную активность, чувство ответственности, культуру математической речи, изобразительную культуру, осознанное отношение к учебе.

Образовательная

• Развивать логическое мышление, наблюдательность, графические способности.

Оборудование для занятия: Презентация Power Point

УМК: Алгебра 8 класс, Ю.Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2-е изд.-М.: Просвещение, 2014.-287с.

Во время занятий

1. Организационное время

слайд 1 . Приветствие учащимся, Девиз урока… Математику уж тогда надо учить, что она ум приводит в порядок… М.В. Ломоносова

1. Обновление базовых знаний.

Фронтальная работа с классом:

Слайд 2. раз). Ребята, давайте вспомним определение арифметического корня квадратного (Арифм. Квадратный корень из числа а — это неотрицательное число, квадрат которого равен а)

Итак, важное условие здесь а>0

2) Устная работа

Слайд 3. а) Верно ли, что: = 0,3; (Ответы учащихся: да) = 0,5; (Ответы учащихся: нет) = 4?

(Ответы учащихся: нет), (Ответы учащихся: да)

слайд 4. б) Выберите среди чисел иррациональное число ; (=0,8 рациональное число и т.д.)

(Решить за доской)

Слайд 5. в) Вычислить:

7; нет решения. =

3. Обобщение и систематизация знаний. (с места по запросу)

слайд 6 . А теперь посчитаем площадь квадрата со стороной равной

Помните, что такое площадь квадрата?, S= . =18)

Здесь вычислите площадь прямоугольника со сторонами и

Вспомнить площадь прямоугольника (S=a*b, S= .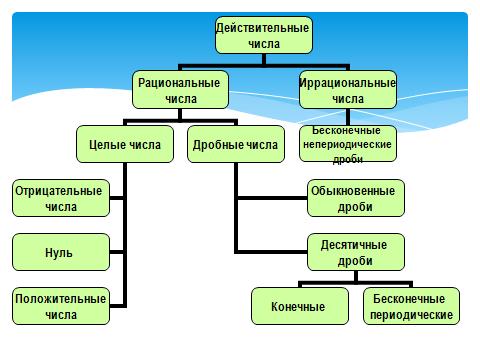 =14*5=70)

Вычислить площадь прямоугольного треугольника, стороны которого

4. Проверка знаний и умений учащихся для подготовки к новой теме.

Слайд 7. Ребята, посмотрите пожалуйста на формулы.

Кто помнит название этой функции. (линейная, квадратичная).

Вспомните, каков график этой функции? (прямая и парабола)

Назовите независимые переменные (они внутри формулы) и зависимые переменные (они отдельные)?

слайд 8. — Сегодня мы рассмотрим новый признак y=

(Давайте определим независимую переменную и зависимую переменную и какие значения они принимают?)

Слайд 9.- Тема урока: Функция у = , ее свойства и график.

Слайд 10. Цель урока:- Мы должны изучить свойства и график функции y=.

Слайд 11. Для этого определим несколько значений этой функции и построим таблицу.

Соедините точки плавной линией (рука движется слева направо)

слайд 12. Посмотрите, через какие точки проходит график?

В каких четвертях будет располагаться график функции у=??

График нужно смотреть слева направо, график идет вверх, значит функция возрастает.

5. Закрепление знаний

слайд 13.

Устно найти значение признаков на слайде

№ 355 (Пользуясь графиком в учебнике на стр. 85, рис. 17, найти значение и составить таблицу

Цели урока:

Оборудование:

Компьютер, интерактивная доска, раздаточный материал.

Презентация к уроку.

ВО ВРЕМЯ ЗАНЯТИЙ

План урока.

Вступительное слово учителя.

Повторение ранее изученного материала.

Изучение нового материала (групповая работа).

Исследование функций. Свойства диаграммы.

Обсуждение графика (фронтальная работа).

Игра в математические карты.

Результаты урока.

I. Актуализация базовых знаний.

Приветствие учителя.

Учитель :

Зависимость одной переменной от другой называется функцией. До сих пор вы изучали функции y = kx + b; у = к/х, у = х 2. Сегодня мы продолжим изучение функций. На сегодняшнем уроке вы узнаете, как выглядит график функции квадратного корня, научитесь строить графики функции квадратного корня самостоятельно.

Запишите тему урока ( слайд1).

2. Повторение пройденного материала.

1. Как называются функции, определяемые формулами:

а) у=2х+3; б) у=5/х; в) у = -1/2х+4; г) у=2х; д) у = -6/х д) у = х 2?

2. Каков их график? Как он расположен? Укажите объем и объем каждой из этих функций (на рис. показаны графики функций, заданных этими формулами, для каждой функции укажите ее тип) ( слайд2).

3. Что представляет собой график каждой функции, как строятся эти графики?

(слайд3, схематически построены графики функций).

3. Изучение нового материала.

Учитель :

Итак, сегодня мы изучаем функцию
и ее расписание.

Мы знаем, что график функции y = x 2 является параболой.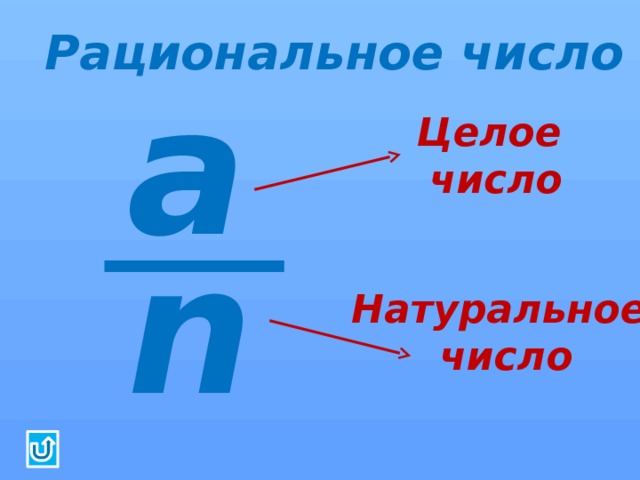 Каким будет график функции у = х 2 если взять только х ≥ 0? Это часть параболы — ее правая ветвь. Теперь построим график функции
.

Повторим алгоритм построения графиков функций (слайд 4, с алгоритмом)

Вопрос : Как вы думаете, глядя на аналитическую запись функции, можно сказать, какие значения допускает X ? (да, х≥0 ). Поскольку выражение
имеет смысл для всех x больше или равно 0,

Учитель: В явлениях природы, в деятельности человека часто существуют отношения между двумя величинами. Каким графиком можно изобразить эту зависимость? (групповая работа)

Класс делится на группы. Каждая группа получает задание: построить график функции
на миллиметровой бумаге, соблюдая все пункты алгоритма. Затем выходит представитель от каждой группы и показывает работу группы. ( склад 5 открывается, идет проверка, далее график строится в блокнотах)

4. Изучение функции. (Групповая работа продолжается)

Учитель:

найти область действия функции;

найти область действия функции;

определяют интервалы убывания (возрастания) функции;

у>0, у

Запишите результаты (слайд 6).

Учитель: Давайте проанализируем схему. График функции является ветвью параболы.

Вопрос : Скажите, вы где-нибудь уже видели эту схему?

Посмотрите на график и скажите, пересекается ли он с линией OX? (Нет) ОУ? (Нет) . Посмотрите на график и скажите, есть ли у графика центр симметрии? Ось симметрии?

Подведем итоги:

Теперь поверим, как мы выучили новую тему и повторили пройденный материал. Игра в математические карты. (Правила игры: каждой группе из 5 человек предлагается набор карточек (25 карточек). Каждый игрок получает по 5 карточек, на которых написаны вопросы. Первый ученик отдает одну из карточек второму ученику, который должен ответить на вопрос из карта Если ученик отвечает на вопрос, то карта бьется, если нет, то ученик забирает карту себе и выдает ход и т. д. всего 5 ходов. Если у ученика не осталось карточек, то счет -5, есть 1 карта — оценка 4, 2 карты — оценка 3, 3 карты — оценка — 2)

5. Итоги урока. (учащиеся оцениваются по контрольным спискам)

Домашнее задание.

Элемент исследования 8.

Решите #172, #179, #183.

Подготовить сообщения на тему «Применение функции в различных областях науки и в литературе».

Отражение.

Покажите свое настроение с помощью картинок на столе.

Сегодняшний урок

Мне нравится.

Мне не понравилось.

Материал урока я понял, не понял).

Основные цели:

1) сформировать представление о целесообразности обобщенного исследования зависимостей реальных величин на примере величин, связанных соотношением у =

2) сформировать умение график y= и его свойства;

3) повторить и закрепить приемы устных и письменных вычислений, возведения в квадрат, извлечения квадратного корня.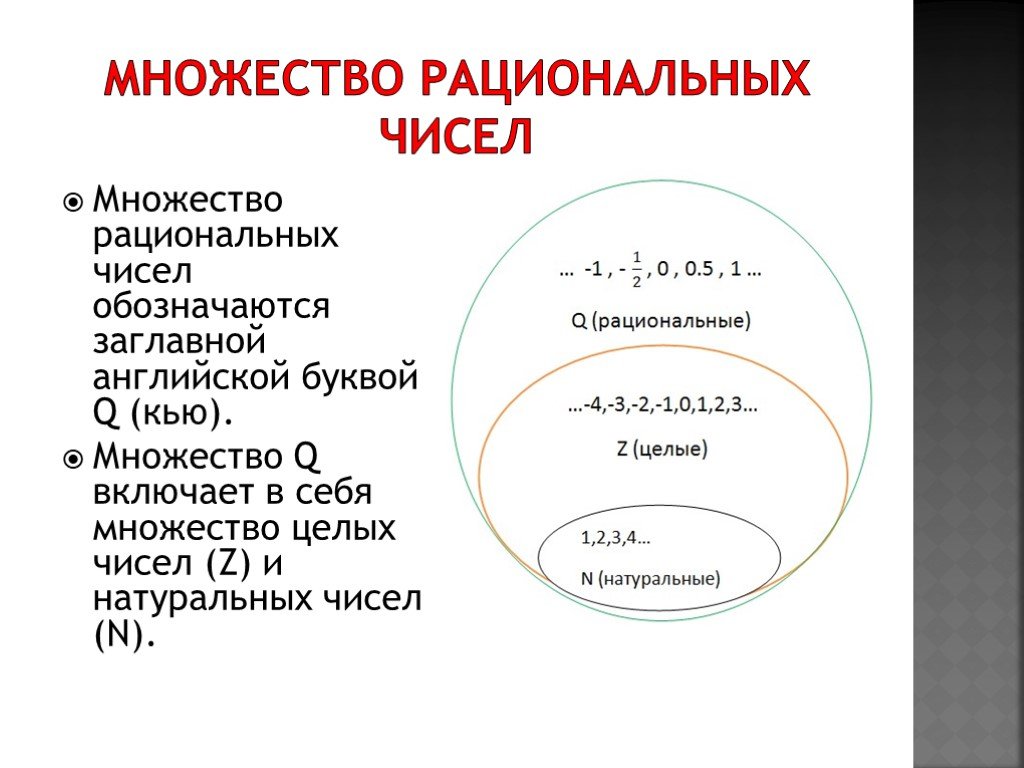

Оборудование, демонстрационный материал: раздаточный материал.

1. Алгоритм:

2. Образец для выполнения задания в группах:

3. Образец для самопроверки самостоятельной работы:

4. Карточка для этапа рефлексии:

) Я понял, как построить график функции y=.

2) Могу перечислить его свойства по графику.

3) В самостоятельной работе ошибок не делал.

4) Я допустил ошибки в самостоятельной работе (перечислите эти ошибки и укажите их причину).

На занятиях

1. Самоопределение к учебной деятельности

Цель этапа:

1) вовлечение обучающихся в учебную деятельность;

2) определить содержание урока: продолжаем работать с действительными числами.

Организация учебного процесса на 1 этапе:

Что мы изучали на прошлом занятии? (Мы изучили множество действительных чисел, действия с ними, построили алгоритм описания свойств функции, повторили функции, изученные в 7 классе).

— Сегодня мы продолжим работу с набором действительных чисел, функцией.

2. Актуализация знаний и устранение трудностей в деятельности

Цель этапа:

1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменная, графики

y = kx + m, y = kx, y\ u003d c, y = x 2, y = — x 2,

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяющиеся понятия и алгоритмы в виде схем и символов;

4) фиксировать индивидуальное затруднение в деятельности, демонстрируя недостаточность имеющихся знаний на личностно значимом уровне.

Организация учебного процесса на 2 этапе:

1. Вспомним, как можно установить зависимости между величинами? (через текст, формулу, таблицу, график)

2. Что называют функцией? (Отношение между двумя величинами, при котором каждому значению одной переменной соответствует одно значение другой переменной y = f(x)).

Как называется x? (Независимая переменная — аргумент)

Как тебя зовут? (Зависимая переменная).

3. Изучали ли мы функции в 7 классе? (y = kx + m, y = kx, y = c, y = x 2 , y = — x 2 , ).

Индивидуальное задание:

Что представляет собой график функций y = kx + m, y =x 2 , y = ?

3. Выявление причин затруднений и постановка цели деятельности

Назначение этапа:

1) организует коммуникативное взаимодействие, в ходе которого выявляется и закрепляется отличительное свойство задания, вызвавшее затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на 3 этапе:

В чем особенность этой задачи? (Зависимость дается формулой y = которую мы еще не встречали).

— Какова цель урока? (Ознакомиться с функцией у =, ее свойствами и графиком. Функция в таблице определяет вид зависимости, построить формулу и график.)

— Угадаете тему урока? (Функция y=, ее свойства и график).

— Запишите тему в блокнот.

4. Создание проекта выхода из затруднения

Цель этапа:

1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленной трудности;

2) зафиксировать новый способ действия в знаковой, словесной форме и с помощью эталона.

Организация учебного процесса на 4 этапе:

Работу на этапе можно организовать в группы, предложив группам построить график y = , затем проанализировать результаты. Также можно предложить группы для описания свойств этой функции по алгоритму.

5. Первичное закрепление во внешней речи

Цель этапа: закрепить изученное учебное содержание во внешней речи.

Организация учебного процесса на 5 ступени:

Построить граф y= — и описать его свойства.

Свойства y= — .

1. Область определения функции.

2.Область значений функции.

3. у=0, у>0, у

у=0, если х=0.

г

4. Функция увеличения, уменьшения.

Функция убывает в точке x.

Построим график y=.

Выделим его часть на отрезке . Отметим, что в Naim. = 1 для x = 1 и y макс. = 3 для х = 9.

Ответ: наим. = 1, при макс. =3

6. Самостоятельная работа с самопроверкой по стандарту

Цель этапа: проверить вашу способность применять новый учебный контент в типовых условиях на основе сравнения вашего решения с эталоном для самопроверки.

Организация учебного процесса на 6 этапе:

Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.

Построим график y=.

Используя график, найдите наименьшее и наибольшее значение функции на отрезке.

7. Включение в систему знаний и повторение

Цель этапа: отработать навыки использования нового содержания в совокупности с ранее изученным: 2) повторить содержание обучения, которое потребуется на следующих уроках.

Организация учебного процесса на 7 ступени:

Решить графически уравнение: = х — 6.

Один ученик у доски, остальные в тетрадях.

8. Отражение деятельности

Цель этапа:

1) закрепить новое содержание, изученное на уроке;

2) оценивать собственную деятельность на уроке;

3) поблагодарить одноклассников, которые помогли получить результат урока;

4) фиксирует нерешенные трудности как направление будущей учебной деятельности;

5) Обсудите и запишите домашнее задание.

Организация учебного процесса на 8 этапе:

— Ребята, какая у нас сегодня была цель? (Изучить функцию у =, ее свойства и график).

— Какие знания помогли нам достичь цели? (Умение искать закономерности, умение читать графики.)

— Проанализируйте свою деятельность в классе. (карточки для рефлексии)

Домашнее задание

п.13 (до примера 2) № 13.3, 13.4

Решите графически уравнение:

Нарисуйте график функции и опишите ее свойства.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, предложения. Все материалы проверяются антивирусной программой.

Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Электронный учебник к учебнику Мордкович А.Г.
Электронная рабочая тетрадь по алгебре за 8 класс

График функции квадратного корня

Ребята, мы уже встречались с построением графиков функций, и не раз. Мы построили наборы линейных функций и парабол. Вообще любую функцию удобно записывать в виде $y=f(x)$. Это уравнение с двумя переменными — для каждого значения x мы получаем y. После выполнения некоторой заданной операции f мы отображаем множество всех возможных x в множество y. В качестве функции f мы можем записать почти любую математическую операцию.

92$ удобно воспользоваться следующей таблицей: Отметьте полученные точки в декартовой системе координат и аккуратно соедините их плавной кривой. Наша функция не ограничена. Только этими точками мы можем подставить абсолютно любые значения х из данной области определения, т. е. те х, для которых выражение имеет смысл.

На одном из предыдущих уроков мы узнали новую операцию извлечения квадратного корня. Возникает вопрос, можем ли мы с помощью этой операции задать какую-то функцию и построить ее график? Воспользуемся общей формой функции $y=f(x)$. Мы оставляем y и x на своих местах, а вместо f вводим операцию извлечения квадратного корня: $y=\sqrt(x)$.
Зная математическую операцию, мы смогли определить функцию.

Построение графика функции извлечения квадратного корня

Построим график этой функции. Исходя из определения квадратного корня, мы можем вычислить его только из неотрицательных чисел, то есть $x≥0$.
Составим таблицу:
Отметим наши точки на координатной плоскости.

Нам осталось аккуратно соединить полученные точки.

Ребята, обратите внимание: если график нашей функции перевернуть набок, то мы получим левую ветвь параболы. На самом деле, если строки в таблице значений поменять местами (верхняя строка с нижней), то мы получим значения как раз для параболы.

Функциональная область $y=\sqrt(x)$

Используя график функции, свойства довольно легко описать.
1. Домен определения: $$.
б) $$.

Раствор.
Мы можем решить наш пример двумя способами. Каждая буква описывает свой путь.

А) Вернемся к построенному выше графику функции и отметим нужные точки отрезка. Хорошо видно, что при $x=9$ функция больше всех остальных значений. Следовательно, в этот момент она достигает своего максимального значения. При $х=4$ значение функции ниже всех остальных точек, а значит, здесь наименьшее значение.

$y_(наиболее)=\sqrt(9)=3$, $y_(наиболее)=\sqrt(4)=2$.

B) Мы знаем, что наша функция увеличивается. Это означает, что каждому большему значению аргумента соответствует большее значение функции. Наибольшее и наименьшее значения достигаются на концах отрезка:

$y_(naib)=\sqrt(11)$, $y_(naim)=\sqrt(2)$.

Пример 2
Решите уравнение:

$\sqrt(x)=12-x$.

Раствор.
Самый простой способ — построить два графика функций и найти их точку пересечения.
На графике четко видна точка пересечения с координатами $(9;3)$. Итак, $x=9$ — это решение нашего уравнения.
Ответ: $x=9$.

Ребята, можем ли мы быть уверены, что у этого примера больше нет решений? Одна из функций возрастающая, другая убывающая. В общем случае они либо не имеют общих точек, либо пересекаются только в одной.

Пример 3

Постройте и прочитайте график функции:

$\begin (cases) -x, x 9. \end (cases)$

Нам нужно построить три частичных графика функции, каждый на своем интервале.

Опишем свойства нашей функции:
1. Область определения: $(-∞;+∞)$.
2. $y=0$ для $x=0$ и $x=12$; $y>0$ для $хϵ(-∞;12)$; $y 3. Функция убывает на отрезках $(-∞;0)U(9;+∞)$. Функция возрастает на отрезке $(0;9)$.
4. Функция непрерывна во всей области определения.
5. Максимальное или минимальное значение отсутствует.
6. Диапазон значений: $(-∞;+∞)$.

Задания для самостоятельного решения

1. Найдите наибольшее и наименьшее значение функции квадратного корня на отрезке:
а) $$;
б) $$.
2. Решите уравнение: $\sqrt(x)=30-x$.
3. Построить и прочитать график функции: $\begin (cases) 2-x, x 4. \end (cases)$
4. Построить и прочитать график функции: $y=\sqrt(- х)$.

Муниципальное учреждение образования

СОШ №1

Арт. Брюховецкая

муниципальное образование Брюховецкий район

Учитель математики

Гученко Анжела Викторовна

Год 2014

Функция у =
, его свойства и график

Тип урока: изучение нового материала

Цели урока:

Задачи, решенные на уроке:

научить студентов работать самостоятельно;

делать предположения и предположения;

уметь обобщать изучаемые факторы.

Оборудование: доска, мел, мультимедийный проектор, раздаточный материал

Время урока.

Определение темы урока совместно с учащимися — 1 минута.

Определение цели и задач урока совместно с учащимися — 1 минута.

Актуализация знаний (фронтальный опрос) — 3 мин.

Устная работа — 3 мин.

Объяснение нового материала, построенное на создании проблемных ситуаций — 7мин

Физминутка — 2 мин.

Построение графика совместно с классом с оформлением конструкции в тетрадях и определением свойств функции, работа с учебником — 10 мин.

Закрепление полученных знаний и развитие навыков преобразования графов — 9 мин .

Подведение итогов урока, установление обратной связи — 3 мин.

Домашнее задание — 1 минута.

Всего 40 минут.

Во время занятий.

Определение темы урока совместно с учащимися (1 мин).

Тема урока определяется учащимися с помощью наводящих вопросов:

функция — работа, выполняемая телом, организмом в целом.

функция — возможность, вариант, способность программы или устройства.

функция — дежурная, круг деятельности.

функция персонаж в литературном произведении.

функция — вид подпрограммы в информатике

функция в математике закон зависимости одной величины от другой.

Определение цели и задач урока совместно с учащимися (1 мин).

Учитель с помощью учащихся формулирует и проговаривает цели и задачи данного занятия.

Актуализация знаний (фронтальный осмотр — 3 мин).

Устная работа — 3 мин.

Фасадная работа.

(A и B принадлежат, C нет)

Объяснение нового материала (на основе создания проблемных ситуаций — 7 мин).

Проблемная ситуация: описывают свойства неизвестной функции.

Разделить класс на команды по 4-5 человек, раздать бланки для ответов на вопросы

Форма №1

у=0, при х=?

Объем функций.

Набор значений функции.

На каждый вопрос отвечает один из представителей команд, остальные команды голосуют «за» или «против» сигнальными карточками и при необходимости дополняют ответы одноклассников.

Вместе с классом сделать вывод об области определения, множестве значений, нулях функции y=.

Проблемная ситуация : попытаться построить график неизвестной функции (идет обсуждение в командах, поиск решения).

С учителем вспоминается алгоритм построения графиков функций. Учащиеся в командах пытаются нарисовать график функции у = на бланках, затем обмениваются бланками друг с другом для само- и взаимной проверки.

Физминутка (Клоунада)

Построение графика совместно с классом с оформлением конструкции в тетрадях — 10 мин.

После общего обсуждения задание на построение графика функции у = выполняется каждым учеником индивидуально в тетради. Преподаватель в это время оказывает дифференцированную помощь учащимся. После выполнения задания учащимся показывается график функции на доске и учащимся предлагается ответить на следующие вопросы:

Заключение: вместе с учащимися еще раз сделать вывод о свойствах функции и прочитать их из учебника:

Закрепление полученных знаний и развитие навыков преобразования графика — 9 мин.

Учащиеся работают по своей карточке (по вариантам), затем меняются и проверяют друг друга. Затем на доске отображаются графики, и учащиеся оценивают свою работу, сравнивая ее с доской.

Карта №1

Карта №2

Заключение: о преобразованиях диаграммы

1) параллельный перенос по оси ОС

2) сдвиг по оси ОХ.

9. Подведение итогов урока, установление обратной связи — 3 мин.

СЛАЙДЫ – вставить пропущенные слова

Область действия этой функции, все числа, кроме … (отрицательные).

График функции расположен в … (I) кварталах.

При значении аргумента x = 0 значение … (функции) y = … (0).

Наибольшее значение функции … (не существует), наименьшее значение — …(равно 0)

10. Домашнее задание (с комментариями — 1 мин).

По учебнику — §13

По задачнику — №13.3, №74 (повторение неполных квадратных уравнений)

Найдите значение выражения алгебраической дроби. Видеоурок «Алгебраические дроби. Основные понятия. Разные задачи и выводы

В этом уроке рассматривается понятие алгебраической дроби. С дробями человек сталкивается в простейших жизненных ситуациях: когда необходимо разделить предмет на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, каждый получит кусок пирога. В данном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда предмет делится на неизвестное количество частей, например, х. В этом случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деления на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее рассмотрим понятие рациональной дроби, а также допустимые значения переменных.

Рациональные выражения делятся на целых и дробных выражений .

Определение Рациональная дробь   представляет собой дробное выражение вида, где — многочлены. — знаменатель числителя.

Примеры рациональные выражения:   — дробные выражения; — целые выражения. В первом выражении, например, он выступает и числителем, и знаменателем.

Значение алгебраическая дробь , как и любое алгебраическое выражение , зависит от числового значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной.

Рассмотрим первую типовую задачу: вычисление значения рациональной дроби для различных значений входящих в него переменных.

Пример 1 Рассчитайте значение дроби для a), b), c)

Решение. Подставляем значения переменных в указанную дробь: а), б), в) — не существует (так как на ноль делить нельзя).

Ответ:   а) 3; б) 1; в) не существует.

Как видите, для любой дроби есть две типичных проблемы: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений литеральных переменных.

Определение Допустимые значения переменных — значения переменных, для которых выражение имеет смысл. Набор всех допустимых значений переменных называется DLD или домен .

Значение литеральных переменных может быть недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значения переменных действительны, потому что дробь может быть вычислена.

Пример 2

Решение.   Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недействительными будут только те значения переменных, у которых знаменатель равен нулю. Знаменатель дроби, следовательно, решаем линейное уравнение:

Следовательно, при значении переменной дробь не имеет смысла.

Ответ: -5.

Из решения примера следует правило нахождения недопустимых значений переменных — знаменатель дроби равен нулю и находятся корни соответствующего уравнения.

Рассмотрим несколько подобных примеров.

Пример 3 Устанавливать при каких значениях переменной дробь не имеет смысла .

Решение. .

Ответ. .

Пример 4 Устанавливать при каких значениях переменной дробь не имеет смысла.

Решение. .

Существуют и другие постановки этой задачи — найти домен или диапазон допустимых значений выражения (ОДЗ) . Это означает нахождение всех допустимых значений для переменных. В нашем примере это все значения, кроме . Область определения удобно представлена ​​на числовой оси.

Для этого выпячиваем на ней точку, как указано на рисунке:

Рис. 1

Таким образом, область определения дроби   будут все цифры, кроме 3.

Ответ. .

Пример 5 Устанавливать при каких значениях переменной дробь не имеет смысла.

Решение. .

Отобразим полученное решение на числовой оси:

Рис. 2

Ответ. .

Пример 6

Решение. . Получили равенство двух переменных, приводим численные примеры: или и т.д.

Изобразим это решение на графике в декартовой системе координат:

Рис. 3. График функции

Координаты любой точки, лежащие на этом графике, не попадают в диапазон допустимых дробей.

Ответ. .

В рассмотренных примерах мы столкнулись с ситуацией, когда произошло деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типов.

Пример 7 Устанавливать при каких значениях переменных дробь не имеет смысла.

Решение. .

Получается, что дробь не имеет смысла. Но можно возразить, что это не так, потому что: .

Может показаться, что если конечное выражение равно 8 for, то исходное тоже можно вычислить, а значит, имеет смысл for. Однако если мы подставим его в исходное выражение, то получим — смысла нет.

Ответ. .

Чтобы подробнее разобраться в этом примере, решим следующую задачу: при каких значениях указанная дробь равна нулю?

Но тогда мы его сформулировали в «упрощенном» виде, удобном и достаточном для работы с обыкновенными дробями. В этой статье мы рассмотрим основное свойство дроби применительно к алгебраическим дробям (то есть к дробям, у которых числитель и знаменатель многочлены, в некоторых учебниках по алгебре такие дроби называются не алгебраическими, а рациональными дробями). Сначала мы констатируем основное свойство алгебраической дроби , обоснуем его, а после этого перечислим основные области его применения.

Навигация по страницам.

Формулировка и обоснование

Для начала вспомним, как было сформулировано основное свойство дроби для обыкновенных дробей: если и числитель, и знаменатель обыкновенной дроби умножить или разделить на некоторое натуральное число, то значение дробь не изменится. Этому утверждению соответствуют равенства и (справедливые и с переставленными частями в форме и), где a, b и m — некоторые.

На самом деле нельзя сказать о делении числителя и знаменателя на число — этот случай покрывается равенством вида. Например, равенство можно обосновать через деление с использованием равенства как , а можно обосновать и с помощью равенства как . Поэтому в дальнейшем основное свойство дроби мы будем связывать с равенством (ями), а на равенстве (ях) останавливаться не будем.

Теперь покажем, что основное свойство дроби распространяется на дроби, числитель и знаменатель которых равны. Для этого докажем, что записанное равенство справедливо не только для натуральных чисел, но и для любых действительных чисел. Другими словами, мы доказываем, что равенство справедливо для любых действительных чисел a, b и m, причем b и m отличны от нуля (иначе мы столкнемся с делением на ноль).

Пусть дробь a/b будет записью числа z, т.е. Докажем, что дробь также соответствует числу z, то есть докажем это. Это докажет равенство.

Стоит отметить, что если алгебраическая дробь имеет дробные коэффициенты, то умножение ее числителя и знаменателя не на определенное число позволяет перейти к целым коэффициентам, и тем самым упростить ее вид. Например, . А на умножении числителя и знаменателя на минус единицу основаны правила смены знаков членов алгебраической дроби.

Второй по значимости областью применения основного свойства дроби является приведение алгебраических дробей. Приведение в общем случае проводится в два этапа: сначала факторизуются числитель и знаменатель, что позволяет найти общий множитель m, а затем на основании равенства переходят к дроби вида а/ b без этого общего множителя. Например, алгебраическая дробь после разложения и знаменателя на множители принимает вид www.сайт, включая внутренние материалы и внешнее оформление, не может быть воспроизведена в какой-либо форме или использована без предварительного письменного разрешения правообладателя.

В § 42 было сказано, что если деление многочленов невозможно провести целиком, то частное записывается в виде дробного выражения, в котором делимое является числителем, а делитель — знаменателем.

Примеры дробных выражений:

Числитель и знаменатель дробного выражения сами могут быть дробными выражениями, например:

Из дробных алгебраических выражений чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются полиномами (в частности, мономами). Каждое такое выражение называется алгебраической дробью.

Определение Алгебраическая дробь, представляющая собой дробь, числитель и знаменатель которой являются полиномами, называется алгебраической дробью.

Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.

Далее, изучив действия над алгебраическими дробями, мы можем любое дробное выражение с помощью идентичных преобразований преобразовать в алгебраическую дробь.

Примеры алгебраических дробей:

Обратите внимание, что все выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно в числителе этого выражения написать, а в знаменателе 1. Например:

2. Действительная буква ценности.

Буквы, входящие только в числитель, могут принимать любые значения (если никакие дополнительные ограничения не наложены условием задачи).

Для букв, входящих в знаменатель, допустимы только те значения, у которых знаменатель не равен нулю. Поэтому в дальнейшем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.

Когда ученик идет в среднюю школу, математика делится на 2 предмета: алгебра и геометрия. Понятий становится все больше, задач все больше и больше. Некоторые с трудом воспринимают дроби. Мы пропустили первый урок по этой теме, и вуаля. дроби? Вопрос, который будет мучить всю школьную жизнь.

Понятие алгебраической дроби

Начнем с определения. Под алгебраической дробью мы подразумеваем выражения P/Q, где P — числитель, а Q — знаменатель. Под буквенной записью может быть скрыто число, числовое выражение, цифро-буквенное выражение.

Прежде чем задаться вопросом, как решать алгебраические дроби, сначала нужно понять, что такое выражение является частью целого.

Как правило, целое число равно 1. Число в знаменателе показывает, на сколько частей была разделена единица. Числитель нужен для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в виде математической операции «Деление». В этом случае числитель — делимое, знаменатель — делитель.

Основное правило обыкновенных дробей

Когда учащиеся проходят эту тему в школе, им даются примеры подкрепления. Чтобы правильно их решать и находить разные выходы из сложных ситуаций, нужно применять основное свойство дробей.

Звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличное от нуля), то значение обыкновенной дроби не изменится. Частным случаем этого правила является разделение обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.

Ниже мы рассмотрим, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.

Математические действия с дробями

Рассмотрим, как решить основное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, всегда нужно придерживаться правил.

Итак, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то этот пункт следует опустить. Когда общий знаменатель найден, как решать алгебраические дроби? Вам нужно добавить или вычесть числители. Но! Необходимо помнить, что если перед дробью стоит знак «-», все знаки в числителе меняются местами. Иногда не следует производить никаких подстановок и математических операций. Достаточно поменять знак перед дробью.

Часто используется такое понятие, как сокращение дроби . Это означает следующее: если числитель и знаменатель разделить на выражение, отличное от единицы (одинаковое для обеих частей), получится новая дробь. Делимое и делитель меньше предыдущих, но по основному правилу дробей остаются равными исходному примеру.

Целью этой операции является получение нового неприводимого выражения. Эту задачу можно решить, сократив числитель и знаменатель на наибольший общий множитель. Алгоритм работы состоит из двух пунктов:

1. Нахождение НОД обеих частей дроби.
2. Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предыдущей.

В таблице ниже показаны формулы. Для удобства его можно распечатать и носить с собой в блокноте. Однако, чтобы в дальнейшем при решении контрольной или экзамена не возникало затруднений в вопросе, как решать алгебраические дроби, эти формулы необходимо выучить наизусть.

Некоторые примеры решений

С теоретической точки зрения рассматривается вопрос о том, как решать алгебраические дроби. Примеры в этой статье помогут вам лучше понять материал.

1. Преобразовать дроби и привести их к общему знаменателю.

2. Преобразовать дроби и привести их к общему знаменателю.

После изучения теоретической части и изучения практической части вопросов больше возникнуть не должно.

§ 1 Понятие алгебраической дроби

Алгебраическая дробь — это выражение

где P и Q — многочлены; P — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.

Вот примеры алгебраических дробей:

Любой многочлен является частным случаем алгебраической дроби, потому что любой многочлен можно записать как

Например:

Значение алгебраической дроби зависит от значения переменные.

Например, вычисляем значение дроби

1)

2)

В первом случае получаем:

Обратите внимание, что эту дробь можно уменьшить: алгебраической дроби упрощается. Воспользуйтесь этим.

Во втором случае получаем:

Как видите, при изменении значений переменных значение алгебраической дроби изменилось.

§ 2 Допустимые значения переменных алгебраической дроби

Рассмотрим алгебраическую дробь

Значение х = -1 недопустимо для этой дроби, так как знаменатель дроби при таком значении х обращается в нуль. При таком значении переменной алгебраическая дробь не имеет смысла.

Таким образом, допустимыми значениями переменных алгебраической дроби являются такие значения переменных, при которых знаменатель дроби не обращается в нуль.

Давайте решим несколько примеров.

При каких значениях переменной алгебраическая дробь не имеет смысла:

Для нахождения недопустимых значений переменных знаменатель дроби равен нулю, и находятся корни соответствующего уравнения.

При каких значениях переменной алгебраическая дробь равна нулю:

Дробь равна нулю, если числитель равен нулю. Приравниваем числитель нашей дроби к нулю и находим корни полученного уравнения:

Таким образом, при х = 0 и х = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.