Проверочная работа сложение и вычитание дробей с разными знаменателями 8 класс: Самостоятельная работа Сложение и вычитание рациональных дробей с рациональными знаменателями, 8 класс
Самостоятельная работа по алгебре 8 класс. Сложение и вычитание дробей с разными знаменателями.
Главная / Старшие классы / Алгебра
Скачать
812.38 КБ, 1342111.docx Автор: Миронова Юлия Валерьевна, 15 Дек 2015
Самостоятельная работа по алгебре 8 класс. Сложение и вычитание дробей с разными знаменателями.
Автор: Миронова Юлия Валерьевна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Самостоятельная работа по алгебре 8 класс. Сложение и вычитание дробей с разными знаменателями. | Миронова Юлия Валерьевна | 15 Дек 2015 |
Тестовые задания по алгебре для 8 класса «Сложение и вычитание дробей с разными знаменателями» (УМК Макарычев Ю. Н.) Н.) | Шапошникова Светлана Ивановна | 14 Ноя 2016 | |
| документ | Конспект урока по теме: «Сложение и вычитание алгебраических дробей с разными знаменателями» (Учебник Мордкович А.Г. 8 класс) | Фридяник Надежда Ивановна | 16 Ноя 2015 |
| презентация | Сравнение, сложение и вычитание дробей с разными знаменателями | Глауберман Олеся Владимировна | 8 Дек 2015 |
| документ | План-конспект урока по алгебре 8классе «Сложение и вычитание дробей с разными знаменателями» | Радюшкина Людмила Николаевна | 16 Ноя 2015 |
| презентация | «Сложение и вычитание дробей с разными знаменателями», 8 класс | Аксенова Надежда Васильевна | 5 Ноя 2015 |
| документ | Конспект урока 8 класс » Сложение и вычитание дробей с разными знаменателями» | Куликова Елена Георгиевна | 3 Мая 2015 |
| документ | Урок алгебры в 8 классе по теме:»Сложение и вычитание дробей с разными знаменателями» | Аникеева Валентина Ивановна МОУ-СОШ с. Калининское Калининское | 1 Апр 2015 |
| документ | План — конспект урока по теме «Сложение и вычитание дробей с разными знаменателями» в 8 классе. | Горская Ольга Анатольевна | 31 Мар 2015 |
| документ | План конспект урока № 10 по алгебре 8 класс. «Сложение дробей с разными знаменателями» УМК Мордкович А.Г. | Губина Клара Владимировна | 21 Дек 2015 |
| документ | План конспект урока № 9 по алгебре 8 класс. «Сложение дробей с разными знаменателями» | Губина Клара Владимировна | 21 Дек 2015 |
| документ | План конспект урока по алгебре 8 класс. «Сложение дробей с разными знаменателями» «Сложение дробей с разными знаменателями» | Губина Клара Владимировна | 21 Дек 2015 |
| документ | План конспект урока № 11 по алгебре 8 класс. «Сложение дробей с разными знаменателями» УМК Мордкович А.Г. | Губина Клара Владимировна | 21 Дек 2015 |
| документ | Тест по математике на тему «Сравнение, сложение и вычитание дробей с разными знаменателями» (6 класс) | Баринова Елена Валерьевна | 31 Мар 2015 |
| презентация, документ | Урок математики по теме «Сложение и вычитание дробей с разными знаменателями» 6 класс | Соловьева Ольга Владимировна | 1 Апр 2015 |
| презентация, документ | Урок математики по теме»Сложение и вычитание дробей с разными знаменателями», 6 класс | Лактионова Марина Петровна | 24 Дек 2015 |
| документ | Самостоятельная работа по теме «Сложение и вычитание дробей с одинаковыми знаменателями» | Акинфиева Наталия Петровна | 1 Апр 2015 |
Тестовые задания по алгебре для 8 класса «Сложение и вычитание дробей с одинаковыми знаменателями» (УМК Макарычев Ю. Н.) Н.) | Шапошникова Светлана Ивановна | 14 Ноя 2016 | |
| документ | Рабочая программа учебного предмета «АЛГЕБРА» 8 класс (3 часа) 2. Основное свойство алгебраической дроби 3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями 4. Сложение и вычитание алгебраических дробей с разными зна | Лукашева Алла Михайловна | 5 Апр 2015 |
| документ | Рабочая программа учебного предмета «АЛГЕБРА» 8 класс 2. Основное свойство алгебраической дроби 3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями 4. Сложение и вычитание алгебраических дробей с разными знаменателя | Лукашева Алла Михайловна | 5 Апр 2015 |
| документ | Сложение и вычитание дробей с разными знаменателями | Попова Любовь Дмитриевна | 21 Мар 2015 |
| документ | Сложение и вычитание дробей с разными знаменателями | Косухина Елена Сергеевна | 21 Мар 2015 |
| презентация | Сравнение, сложение и вычитание дробей с разными знаменателями | Кузьменюк Наталья Сергеевна | 21 Мар 2015 |
| документ | «Сложение и вычитание дробей с разными знаменателями» | Турсукова Татьяна Александровна | 21 Мар 2015 |
| документ | Сложение и вычитание дробей с разными знаменателями | Бабенко Жанна Владимировна | 20 Мар 2015 |
| документ | «Сложение и вычитание дробей с разными знаменателями» | Козырева Людмила Анатольевна | 31 Мар 2015 |
| документ | Сравнение,сложение и вычитание дробей с разными знаменателями | Горлова Надежда Сергеевна | 1 Апр 2015 |
| документ | сравнение, сложение и вычитание дробей с разными знаменателями | Кириллина Людмила Михайловна | 1 Апр 2015 |
| презентация | Сложение и вычитание дробей с разными знаменателями | Большакова Елена Константиновна | 1 Апр 2015 |
| разное | Сложение и вычитание дробей с разными знаменателями | Неворотова Ольга Васильевна | 1 Апр 2015 |
| разное | Сложение и вычитание дробей с разными знаменателями. | Ильин Альберт Геннадиевич | 1 Апр 2015 |
| презентация, документ | Сравнение, сложение и вычитание дробей с разными знаменателями | Топчиёва Анна Михайловна | 1 Апр 2015 |
| документ | Сложение и вычитание дробей с разными знаменателями | Солдатова Ирина Валерьевна | 4 Ноя 2015 |
| документ | Сравнение, сложение и вычитание дробей с разными знаменателями | Рахманкулова Екатерина Равиловна | 9 Авг 2015 |
| презентация | Сложение и вычитание дробей с разными знаменателями. Смешанные числа. Смешанные числа. | Лёгенькая Ирина Анaтольевна | 2 Окт 2015 |
| презентация | Сложение и вычитание алгебраических дробей с разными знаменателями | Кузьминых Надежда Васильевна | 29 Янв 2016 |
| документ | Сложение и вычитание дробей с разными знаменателями. | Буторова Ольга Викторовна | 6 Дек 2015 |
| документ | Сравнение ,сложение и вычитание дробей с разными знаменателями | Павлова Наталия Николаевна | 25 Мар 2016 |
| документ | конспект урока обобщения 8 класс МКСКОУ СКОШИ VIII вида Тема «ДРОБИ, СЛОЖЕНИЕ ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ» | mosina52 | 20 Мар 2015 |
| разное | Урок алгебры в 8 классе на тему:»Сложение и вычитание дробей с разными знаменателями» | аникеева валентина ивановна | 1 Апр 2015 |
Контрольная работа по теме «Сложение и вычитание дробей»
Контрольные работы по математике 8 класс.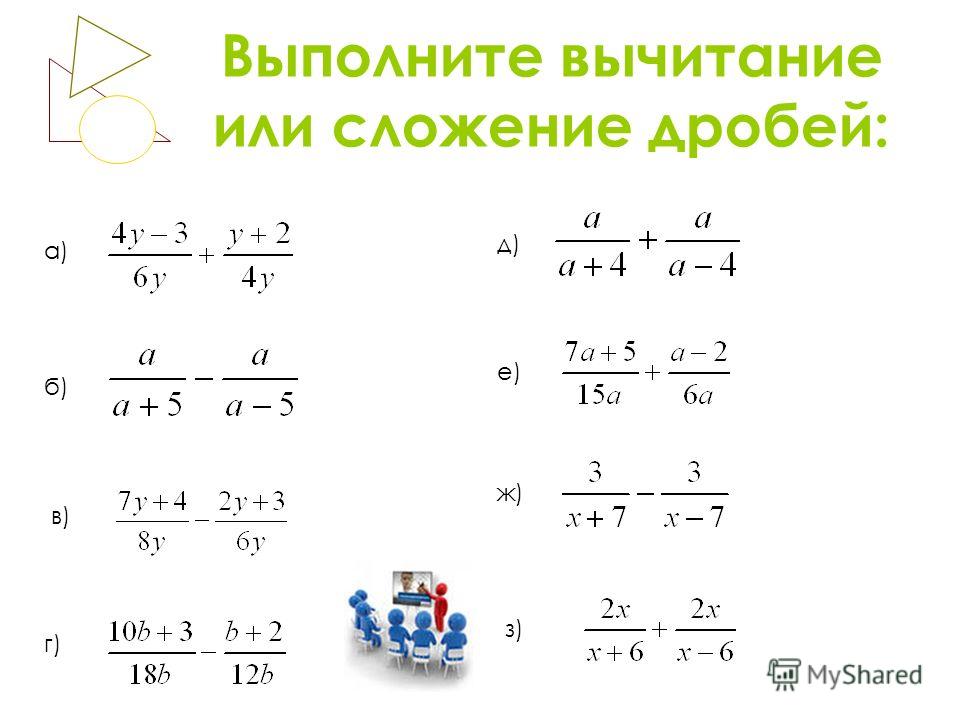
Учитель математики: Кулинич Владимир Григорьевич
Школа: МОУ Негинская СОШ Брянской области Суземского района
Пояснительная записка.
Данные контрольные работы разработаны на основе рабочей программы 8 класса учебного курса составленной на основе примерной программы основного общего образования по математике в соответствии с федеральным компонентом государственного стандарта и с учетом рекомендаций авторских программ Ю.Н.Макарычева по алгебре и Л.С. Атанасяна по геометрии. Всего 14 контрольных: 5 по геометрии и 9 по алгебре. Список источников информации: Ю.Н.Макарычев учебник по алгебре 8 класс и Л.С. Атанасян учебник геометрии 7-9 класс. Все иллюстрации авторские.
Контрольная работа №1 по теме «Сложение и вычитание дробей»
Контрольная работа №1 по теме «Сложение и вычитание дробей»
I-вариант.
Сократите дробь:
а) б)
Ответ:_____________ Ответ:___________
Упростите выражение:
—
Ответ:_____________
Выполните сложение или вычитание:
а) + б) –
Ответ:_____________ Ответ:___________
Преобразуйте в дробь выражение:
— —
Ответ:________________
Туристы прошли s км по шоссе со скоростью v км/ч и вдвое больший путь по проселочной дороге.
 Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скоростью, на 2 км/ч меньшей, чем по шоссе? Найдите t при s=10, v=6.
Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скоростью, на 2 км/ч меньшей, чем по шоссе? Найдите t при s=10, v=6.
Контрольная работа №1 по теме «Сложение и вычитание дробей»
II-вариант.
Сократите дробь:
а) б)
Ответ:_____________ Ответ:___________
Упростите выражение:
—
Ответ:_____________
Выполните сложение или вычитание:
а) + б) –
Ответ:_____________ Ответ:___________
Преобразуйте в дробь выражение:
— —
Ответ:________________
Туристы прошли s км по шоссе со скоростью v км/ч и вдвое больший путь по проселочной дороге. Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скоростью, на 3 км/ч меньшей, чем по шоссе? Найдите t при s=20, v=5.

Контрольная работа №2 по теме «Рациональные дроби»
I-вариант.
Выполните умножение:
а) * б) *
Ответ:_____________ Ответ:___________
Выполните деление:
а) : б) :
Ответ:_____________ Ответ:___________
Возведите в степень:
а) 2 б) 3
Ответ:_____________ Ответ:___________
Выполните действия:
*
Ответ:________________________
На рисунке построен график функции, заданной формулой у=. Найдите по графику значение х, которому соответствует у, равное 4; 2; 1
Контрольная работа №2 по теме «Рациональные дроби»
II-вариант.
Выполните умножение:
а) * б) *
Ответ:_____________ Ответ:___________
Выполните деление:
а) : б) :
Ответ:_____________ Ответ:___________
Возведите в степень:
а) 2 б) 3
Ответ:_____________ Ответ:___________
Выполните действия:
*
Ответ:________________________
На рисунке построен график функции, заданной формулой у=. Найдите по графику значение х, которому соответствует у, равное 2; 1; -2
Контрольная работа №3 по теме «Четырехугольники»
I-вариант.
Периметр параллелограмма ABCD равен 50 см, сторона AB равна 10 см. Найдите стороны параллелограмма.

Найдите углы B и D трапеции ABCD с основаниями AD и ВС, если ∠А=360, ∠С=1170.
Найдите периметр квадрата АСВД, если сторона АВ=4 см.
Найдите периметр ромба АВСД, в котором ∠В=600, АС=10,5 см.
Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.
Контрольная работа №3 по теме «Четырехугольники»
II-вариант.
Периметр параллелограмма ABCD равен 60 см, сторона AB равна 20 см. Найдите стороны параллелограмма.
Найдите углы B и D трапеции ABCD с основаниями AD и ВС, если ∠D=400, ∠B=1000.
Найдите периметр квадрата АСВД, если сторона АВ=7 см.
Найдите периметр ромба АВСД, в котором ∠В=300, АС=15 см.

Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии
Контрольная работа 4 по теме «Арифметический квадратный корень»
I-вариант.
Найдите значение корня:
а) б)
Ответ:_____________ Ответ:___________
Найдите значение выражения:
а)5 б)-2,5
Ответ:_____________ Ответ:___________
Решите уравнение:
а) х2-5=20. б) 80+у2=81
Ответ:__________ Ответ:__________
Найдите значение выражения:
Ответ:___________________
Основанием прямоугольного параллелепипеда является квадрат со стороной а см, высота параллелепипеда равна b см, а его объем равен V см3 Выразите переменную а через b и V.
Контрольная работа 4 по теме «Арифметический квадратный корень»
II-вариант.
Найдите значение корня:
а) б)
Ответ:_____________ Ответ:___________
Найдите значение выражения:
а)7 б)-3,5
Ответ:_____________ Ответ:___________
Решите уравнение:
а) х2-10=71. б) 5+у2=86
Ответ:__________ Ответ:__________
Найдите значение выражения:
Ответ:___________________
Основанием прямоугольного параллелепипеда является квадрат со стороной а см, высота параллелепипеда равна b см, а его объем равен V см3 Выразите переменную b через a и V.
Контрольная работа №5 по теме «Квадратные корни»
I-вариант.
Вынесите множитель из-под знака корня:
а) б)
Ответ:_____________ Ответ:___________
Внесите множитель под знак корня:
а)7 б)12
Ответ:_____________ Ответ:___________
Выполните действие:
*(— 2 )
Ответ:__________
Сравните числа:
0,2 и 10
Ответ:___________________
Освободитесь от иррациональности в знаменатели дроби:
Ответ:________________
Контрольная работа №5 по теме «Квадратные корни»
II-вариант.
Вынесите множитель из-под знака корня:
а) б)
Ответ:_____________ Ответ:___________
Внесите множитель под знак корня:
а)6 б)16
Ответ:_____________ Ответ:___________
Выполните действие:
*(— )
Ответ:__________
Сравните числа:
0,8 и 5
Ответ:___________________
Освободитесь от иррациональности в знаменатели дроби:
Ответ:________________
Контрольная работа №6 по теме «Площадь»
I-вариант.
Найти площадь параллелограмма АВСД, если ВС=12 см, а ВH=6 см.
Найти площадь прямоугольного треугольника ВДК, если ВК=3 дм, а ВД=20см.
Найдите сторону АС прямоугольного треугольника АВС, если ВС=13 см, а АВ=12 см
Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 см.
 Найдите высоту, проведенную к основанию.
Найдите высоту, проведенную к основанию.
Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Контрольная работа №6 по теме «Площадь»
II-вариант.
Найти площадь параллелограмма АВСД, если ВС=2 дм, а ВH=5 см.
Найти площадь прямоугольного треугольника ВДК, если ВК=5 дм, а ВД=2см.
Найдите сторону АС прямоугольного треугольника АВС, если ВС=9 см, а АВ=7 см
Найдите высоты треугольника со сторонами 10 см, 10 см и 12 см.
Найдите сторону и площадь ромба, если его диагонали равны 5 см и 12 см.
Контрольная работа №7 по теме «Формула корней квадратного уравнения»
I-вариант.
Решите уравнение:
а)3х2-7х+4=0 б) х2+5х-6=0
Ответ:_____________ Ответ:___________
Найдите корни уравнения:
а) 4х2-9=0 б)3х2-4х=0
Ответ:_____________ Ответ:___________
Решите уравнение:
5х2=9х+2
Ответ:__________
Сократите дробь:
=
Ответ:___________________
Найдите стороны прямоугольника, если известно, что одна из них на 14 см больше другой, а диагональ прямоугольника равна 34 см.

Контрольная работа №7 по теме «Формула корней квадратного уравнения»
II-вариант.
Решите уравнение:
а)5х2-8х+3=0 б) х2-10х-24=0
Ответ:_____________ Ответ:___________
Найдите корни уравнения:
а) х2-9=0 б)4х2-3х=0
Ответ:_____________ Ответ:___________
Решите уравнение:
25=26х-х2
Ответ:__________
Сократите дробь:
=
Ответ:___________________
В прямоугольном треугольнике один из катетов на 3 см меньше гипотенузы, а другой на 6 см меньше гипотенузы. Найдите гипотенузу.
Контрольная работа №8 по теме «Квадратные уравнения».
I-вариант.
Решите уравнение:
-4=0
Ответ:___________________
При каком значении х значение функции у= равно 5
Ответ:_________________
Найдите корни уравнения:
=
Ответ:___________________
Знаменатель обыкновенной дроби больше её числителя на 3.
 Если к числителю этой дроби прибавить 7, а к знаменателю 5, то она увеличится на . Найдите эту дробь.
Если к числителю этой дроби прибавить 7, а к знаменателю 5, то она увеличится на . Найдите эту дробь.
Катер, развивающий в стоячей воде скорость 20 км/ч, прошел 36 км против течения и 22 км по течению, затратив на весь путь 3ч. Найдите скорость течения реки.
Контрольная работа №8 по теме «Квадратные уравнения».
II-вариант.
Решите уравнение:
=х
Ответ:___________________
При каком значении х значение функции у= равно 2
Ответ:_________________
Найдите корни уравнения:
=
Ответ:___________________
Числитель несократимой обыкновенной дроби на 5 меньше её знаменателя. Если числитель этой дроби уменьшить на 2, а знаменатель увеличить на 16, то дробь уменьшится на . Найдите эту дробь
Турист проплыл на лодке против течения реки 6 км и по озеру 15 км, затратив на путь по озеру на 1 ч больше, чем на путь по реке.
 Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.
Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.
Контрольная работа №9 по теме «Подобные треугольники»
I-вариант.
∠АСВ=∠СКМ. Найти х
Найти FK.
Найти у.
Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АВ, если ОВ=4 см, ОД=10 см, ДС=25 см.
Докажите, что два равносторонних треугольника подобны.
Контрольная работа №9 по теме «Подобные треугольники»
II-вариант.
∠DAN=∠ARW. Найти RW
Найти у.
Найти FK.
Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АО, если АВ=9,6 дм, ДС=24 см, АС=15 см.

Докажите, что два равносторонних треугольника подобны.
Контрольная работа №10 по теме «Применение подобия к решению задач»
I-вариант.
Найти среднюю линий NM треугольника АВС.
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.
Длина тени дерева равна 10 м, а длина тени человека, рост которого 1,8 м равна 3 м. Найти высоту дерева.
Постройте треугольник АВС по двум углам и высоте, проведенной из вершины третьего угла.
Постройте прямоугольный треугольник по гипотенузе и отношению катетов.
Контрольная работа №10 по теме «Применение подобия к решению задач»
II-вариант.
Найти среднюю линий NM треугольника АВС.
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.

Длина тени дерева равна 12 м, а длина тени человека, рост которого 1,6 м равна 2,5 м. Найти высоту дерева.
Постройте треугольник АВС по двум углам и высоте, проведенной из вершины третьего угла.
Постройте прямоугольный треугольник по гипотенузе и отношению катетов.
Контрольная работа №11 по теме «Сложение и умножение числовых неравенств»
I-вариант.
Сравните числа х и у если разность х-у=4.
Докажите неравенство:
х(х+7)>7х-1
Сложите почленно неравенства: 12>-6 и 9>7
Оцените значение выражения , если: 5x
Лист железа имеет форму квадрата. После того как от него отрезали полосу шириной 5 дм, площадь оставшейся части листа стала 6 дм2. Каковы размеры первоначального листа железа?
Контрольная работа №11 по теме «Сложение и умножение числовых неравенств»
II-вариант.
Сравните числа х и у если разность х-у=8.
Докажите неравенство:
(2х+3)(2х+1)>4х(х+2)
Сложите почленно неравенства: 20>-10 и 11>5
Оцените значение выражения , если: 0,125x
Лист железа имеет форму квадрата. После того как от него отрезали полосу шириной 9 дм, площадь оставшейся части листа стала 8 дм2. Каковы размеры первоначального листа железа?
Контрольная работа №12 по теме «Неравенства».
I-вариант.
Изобразите на координатной прямой промежуток (1;4)
Какие из чисел -2;- 3;6; 3,4;5 принадлежат промежутку [-2;4].
Решите неравенство и изобразите множество его решений на координатной прямой: 2х
Решите неравенство: 0,2х2-0,2(х-6)(х+6)>3,6х.
Длина стороны прямоугольника 6 см. Какой должна быть длина другой стороны, чтобы периметр прямоугольника был меньше периметра квадрата со стороной 4 см?
Контрольная работа №12 по теме «Неравенства».
II-вариант.
Изобразите на координатной прямой промежуток (-2;8)
Какие из чисел -4;- 3;0; 2;5 принадлежат промежутку [-3;4].
Решите неравенство и изобразите множество его решений на координатной прямой: 7х
Решите неравенство: (2х-5)2-0,5х
Длина стороны прямоугольника 10 см. Какой должна быть длина другой стороны, чтобы периметр прямоугольника был меньше периметра квадрата со стороной 8 см?
Контрольная работа №13 по теме «Окружность»
I-вариант.
Радиус окружности равен 10 см, а расстояние от одного конца диаметра до точки окружности равно 16 см. Найдите расстояние от другого конца диаметра до этой точки.
Из точки А к окружности с центром О проведены касательные АВ и АС (В и С — точки касания). Найдите периметр треугольника АВС, если ОА=12 см, а угол ВОС=600.

Из точки А к окружности с центром О проведена касательная АВ. Найдите АО, если радиус окружности 12, а угол АОВ=450.
Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см. Найти площадь этого треугольника.
Контрольная работа №13 по теме «Окружность»
II-вариант.
Радиус окружности равен 5 см, а расстояние от одного конца диаметра до точки окружности равно 10 см. Найдите расстояние от другого конца диаметра до этой точки.
Из точки А к окружности с центром О проведены касательные АВ и АС (В и С — точки касания). Найдите периметр треугольника АВС, если ОА=10 см, а угол ВОС=600.

Из точки А к окружности с центром О проведена касательная АВ. Найдите АО, если радиус окружности 12, а угол АОВ=450.
Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Основание равнобедренного треугольника равно 18см, а боковая сторона равна 15см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
.
Итоговая контрольная работа по математике
8 класс.
I-вариант.
Найдите значение дроби:
при х=3
Представьте в виде дроби:
+
Упростите выражение:
1,5ав-3*6а-2в
Решите уравнение:
3х2-7х+4=0
Решите неравенство:
7х-2,4
Итоговая контрольная работа по математике
8 класс.
II-вариант.
Найдите значение дроби:
при х=1
Представьте в виде дроби:
+
Упростите выражение:
3,2х-1у-5*5ху
Решите уравнение:
5х2-8х+3=0
Решите неравенство:
17-х
Сложение и вычитание дробей
Во время сложения и вычитания дробей нам нужно проверить, имеют ли дроби одинаковые знаменатели или разные знаменатели, после чего начинается вычисление. Давайте узнаем больше о сложении и вычитании дробей в этой статье.
| 1. | Как складывать и вычитать дроби? |
| 2. | Сложение и вычитание дробей с одинаковыми знаменателями |
3. | Сложение и вычитание дробей с разными знаменателями |
| 3. | Сложение и вычитание смешанных дробей |
| 4. | Сложение и вычитание дробей с целыми числами |
| 5. | Часто задаваемые вопросы о сложении и вычитании дробей |
Как складывать и вычитать дроби?
Сложение и вычитание дробей производится по аналогичным правилам, в которых перед началом сложения или вычитания проверяются знаменатели. После проверки знаменателей мы можем соответственно складывать или вычитать заданные дроби. Знаменатели проверяются следующим образом.
- Если знаменатели данных дробей совпадают, мы складываем или вычитаем только числители, а знаменатель сохраняем.
- Если знаменатели разные, мы преобразуем дроби в подобные дроби, чтобы знаменатели стали одинаковыми, а затем прибавляем или вычитаем то, что требуется.
Давайте узнаем об этом в следующих разделах.
Сложение и вычитание дробей с одинаковыми знаменателями
Процесс сложения и вычитания дробей с одинаковыми знаменателями довольно прост, потому что нам нужно только работать с числителями.
Сложение дробей с одинаковыми знаменателями
Сложим дроби 1/5 и 2/5, используя прямоугольные модели. В этом случае обе дроби имеют одинаковые знаменатели. Эти дроби называются подобные дроби . На следующем рисунке представлены обе фракции в одной и той же модели.
- 1/5 означает, что 1 из 5 частей окрашены в желтый цвет.
- 2/5 означает, что 2 из 5 частей окрашены в синий цвет.
Из 5 частей 3 части заштрихованы. В дробной форме это можно представить как 3/5.
Теперь давайте сложим дроби с одинаковыми знаменателями в числовом выражении. В этом случае нам нужно добавить 1/5 + 2/5. Давайте используем следующие шаги, чтобы понять дополнение.
- Шаг 1: Сложите числители данных дробей.
 Здесь числители 1 и 2, поэтому будет 1 + 2 = 3 .
Здесь числители 1 и 2, поэтому будет 1 + 2 = 3 . - Шаг 2: Сохраните тот же знаменатель. Здесь знаменатель равен 5, .
- Шаг 3: Следовательно, сумма 1/5 + 2/5 = (1 + 2)/5 = 3/5
Следует отметить, что мы используем тот же метод для вычитания дробей.
Вычитание дробей с одинаковыми знаменателями
Вычтем дроби 2/5 и 1/5, используя прямоугольные модели. Мы представим 2/5 в этой модели, заштриховав 2 из 5 частей. Далее мы заштрихуем 1 часть из заштрихованных частей модели, что будет означать удаление 1/5.
Теперь у нас осталась 1 деталь в заштрихованных частях модели.
Теперь давайте вычтем дроби с одинаковыми знаменателями в числовом выражении. В этом случае нам нужно вычесть 2/5 — 1/5. Давайте разберемся с процедурой, выполнив следующие шаги.
- Шаг 1: Вычтем числители данных дробей. Здесь числители 2 и 1, значит будет 2 — 1 = 1
- Шаг 2: Сохраните тот же знаменатель.
 Здесь знаменатель равен 5,9.0056
Здесь знаменатель равен 5,9.0056 - Шаг 3: Следовательно, разница 2/5 — 1/5 = (2 — 1)/5 = 1/5
Сложение и вычитание дробей с разными знаменателями
Для сложения и вычитания дробей с разными знаменателями нам нужно преобразовать разные дроби в одинаковые, записав их эквивалентные дроби таким образом, чтобы их знаменатели стали одинаковыми. Давайте разберемся в этом с помощью примера.
Пример: Добавить 1/5 + 1/3
Решение: Для сложения разных дробей нам нужно использовать следующие шаги
- Шаг 1: Найдите наименьшее общее кратное (НОК) знаменателей. Здесь LCM 5 и 3 равно 15.
- Шаг 2: Преобразуйте заданные дроби в подобные дроби, написав эквивалентные дроби для соответствующих дробей так, чтобы их знаменатели остались прежними. Здесь это будет \(\frac {1}{5}\)×\(\frac {3}{3}\)=\(\frac {3}{15}\)
- Шаг 3: Аналогично эквивалентная дробь 1/3 со знаменателем 15 равна \(\frac {1}{3}\)×\(\frac {5}{5}\)=\(\frac { 5}{15}\)
- Шаг 4: Теперь, когда мы преобразовали данные дроби в подобные дроби, мы можем сложить числители и сохранить тот же знаменатель.
 Это будет 3/15 + 5/15 = 8/15
Это будет 3/15 + 5/15 = 8/15
Вычитание дробей с разными знаменателями
Для вычитания разнородных дробей мы выполняем те же действия, что и при сложении разнородных дробей. Давайте разберемся в этом с помощью примера.
Пример: Вычесть 5/6 — 1/3
Решение: Для вычитания разных дробей необходимо выполнить следующие шаги.
- Шаг 1: Найдите наименьшее общее кратное (НОК) знаменателей. Здесь LCM 6 и 3 равно 6.
- Шаг 2: Преобразуйте заданные дроби в подобные дроби, написав эквивалентные дроби для соответствующих дробей так, чтобы их знаменатели остались прежними. Здесь это будет \(\frac {5}{6}\)×\(\frac {1}{1}\)=\(\frac {5}{6}\)
- Шаг 3: Аналогично эквивалентная дробь 1/3 со знаменателем 6 равна \(\frac {1}{3}\)×\(\frac {2}{2}\)=\(\frac { 2}{6}\)
- Шаг 4: Теперь, когда мы преобразовали данные дроби в подобные дроби, мы можем вычесть числители и сохранить тот же знаменатель.
 Это будет 5/6 — 2/6 = 3/6. Это может быть дополнительно уменьшено до 1/2
Это будет 5/6 — 2/6 = 3/6. Это может быть дополнительно уменьшено до 1/2
Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей осуществляется путем преобразования смешанных дробей в неправильные дроби, а затем сложение или вычитание выполняется в соответствии с требованием. Давайте разберемся в этом с помощью следующих примеров.
Пример: Складываем смешанные дроби: \(2\dfrac{1}{4}\) + \(1\dfrac{3}{4}\)
Решение: Сначала преобразуем смешанные дроби дроби в неправильные дроби.
- Шаг 1: Преобразуйте данные смешанные дроби в неправильные дроби. Итак, \(2\dfrac{1}{4}\) станет 9/4; и \(1\dfrac{3}{4}\) станет 7/4
- Шаг 2 : Сложите дроби, добавив числители, потому что знаменатели одинаковы. это будет 9/4 + 7/4= 16/4.
- Шаг 3: При необходимости уменьшите дробь. Это станет 16/4 = 4. Следовательно, \(2\dfrac{1}{4}\) + \(1\dfrac{3}{4}\) = 4,
Теперь давайте разберемся с вычитанием смешанных дробей, используя тот же метод.
Пример: Вычесть смешанные дроби: \(5\dfrac{1}{3}\) — \(2\dfrac{1}{3}\)
Решение: Сначала преобразуем смешанные дроби дроби в неправильные дроби.
- Шаг 1: Преобразуйте заданные смешанные дроби в неправильные дроби. Итак, \(5\dfrac{1}{3}\) станет 16/3; и \(2\dfrac{1}{3}\) станет 7/3
- Шаг 2 : Вычтите дроби, вычитая числители, потому что знаменатели одинаковы. Это будет 16/3 — 7/3 = 9/3
- Шаг 3: При необходимости уменьшите дробь. Это станет 9/3 = 3. Следовательно, \(5\dfrac{1}{3}\) — \(2\dfrac{1}{3}\) = 3
Сложение и вычитание дробей с целыми числами
Сложение и вычитание дробей с целыми числами можно выполнить следующим способом. Давайте разберемся в этом на примере.
Пример: Складываем 7/4 + 5
Решение: Складываем 7/4 + 5, используя следующие шаги.
- Шаг 1: Запишите целое число в виде дроби.
 В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 7/4 + 5/1
В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 7/4 + 5/1 - Шаг 2: Теперь найдите НОК знаменателей и преобразуйте данные дроби в подобные дроби. Здесь НОК 4 и 1 равен 4. И после преобразования их в одинаковые дроби мы получаем (7 × 1)/(4 × 1) + (5 × 4)/(1 × 4) = 7/4 + 20/ 4
- Шаг 3: Сложите числители, не изменяя знаменатель. Здесь 7/4 + 20/4 = 27/4 = \(6\dfrac{3}{4}\)
Теперь давайте разберемся с вычитанием дроби из целого числа с помощью следующего примера.
Пример: Вычесть 6 — 3/5
Решение: Давайте вычтем 6 — 3/5, используя следующие шаги.
- Шаг 1: Запишите целое число в виде дроби. В этом случае целое число равно 6, что можно записать как 6/1. Итак, теперь нам нужно вычесть 6/1 — 3/5
- Шаг 2: Теперь найдите НОК знаменателей и преобразуйте данные дроби в подобные дроби.
 Здесь НОК 1 и 5 равен 5. И после преобразования их в одинаковые дроби мы получаем (6 × 5)/(1 × 5) — (3 × 1)/(5 × 1) = 30/5 — 3/ 5
Здесь НОК 1 и 5 равен 5. И после преобразования их в одинаковые дроби мы получаем (6 × 5)/(1 × 5) — (3 × 1)/(5 × 1) = 30/5 — 3/ 5 - Шаг 3: Вычтите числители, пока знаменатель не изменится. Здесь 30/5 — 3/5 = 27/5 = \(5\dfrac{2}{5}\)
Важные замечания по сложению и вычитанию дробей
- Для сложения и вычитания одинаковых дробей мы можем напрямую работать с числителями, в то время как знаменатели остаются прежними.
- Для сложения и вычитания разных дробей никогда не складывать и не вычитать напрямую числители и знаменатели. Преобразуйте их в похожие дроби, а затем сложите или вычтите.
☛ Похожие темы
- Добавление дробей
- Вычитание дробей
- Умножение дробей
- Деление дробей
- Сложение дробей с разными знаменателями
- Вычитание дробей с разными знаменателями
- Как калькулятор дробей
- Калькулятор дробей
Часто задаваемые вопросы о сложении и вычитании дробей
Как складывать и вычитать дроби?
Для сложения и вычитания дробей сначала нужно проверить знаменатели. Если знаменатели совпадают, мы просто добавляем или вычитаем числители и сохраняем тот же знаменатель. В случае неодинаковых дробей, когда знаменатели не совпадают, мы преобразуем неодинаковые дроби в одинаковые, находя НОК знаменателей. Это помогает в написании их соответствующих эквивалентных дробей, а затем они добавляются или вычитаются по мере необходимости.
Если знаменатели совпадают, мы просто добавляем или вычитаем числители и сохраняем тот же знаменатель. В случае неодинаковых дробей, когда знаменатели не совпадают, мы преобразуем неодинаковые дроби в одинаковые, находя НОК знаменателей. Это помогает в написании их соответствующих эквивалентных дробей, а затем они добавляются или вычитаются по мере необходимости.
Как складывать и вычитать дроби с разными знаменателями?
Чтобы складывать и вычитать дроби с разными знаменателями, нам нужно преобразовать дроби в подобные дроби, чтобы знаменатели стали одинаковыми. Когда знаменатели совпадают, мы можем складывать или вычитать числители. Чтобы преобразовать данные дроби в подобные дроби, нам нужно найти НОК знаменателей, а затем записать их соответствующие эквивалентные дроби. Затем можно складывать или вычитать эквивалентные дроби с одинаковыми знаменателями, в зависимости от обстоятельств.
Как складывать и вычитать дроби с целыми числами?
Для сложения и вычитания дробей с целыми числами мы используем следующий метод.
- Запишите целое число в виде дроби, написав 1 в знаменателе. Например, если нам нужно сложить 8/7 + 5, мы запишем целое число в виде дроби. В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 8/7 + 5/1. Найдем НОК знаменателей и преобразуем данные дроби в подобные дроби. Здесь НОК 7 и 1 равен 7. И после преобразования их в одинаковые дроби мы получаем (8 × 1)/(7 × 1) + (5 × 7)/(1 × 7) = 8/7 + 35/ 7 = 43/7 = \(6\dfrac{1}{7}\)
- Тот же метод будет использоваться для вычитания, например, если нам нужно вычесть 7 — 2/5, мы запишем целое число 7 как 7/1, а затем вычтем. Это сделает его 7/1 — 2/5. Найдем НОК знаменателей и преобразуем данные дроби в подобные дроби. Здесь НОК 5 и 1 равен 5. И после преобразования их в одинаковые дроби мы получаем (7 × 5)/(1 × 5) — (2 × 1)/(5 × 1) = 35/5 — 2/ 5 = 33/5 = \(6\dfrac{3}{5}\)
Как складывать и вычитать дроби со смешанными числами?
Чтобы складывать и вычитать дроби со смешанными числами, мы преобразуем смешанные числа в неправильные дроби.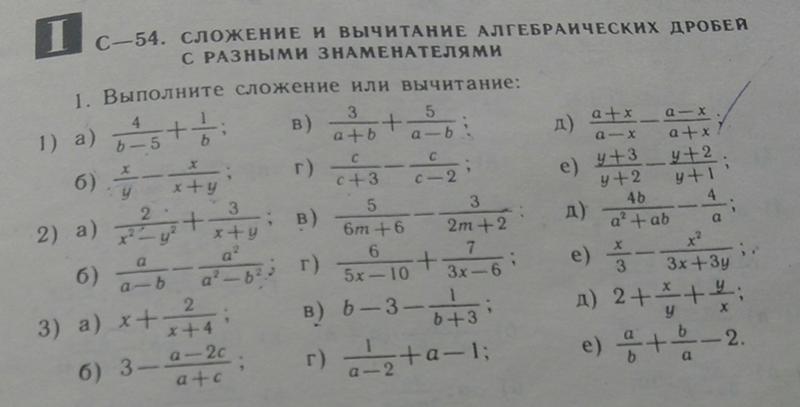 Теперь, если они похожи на дроби, мы можем просто сложить или вычесть числители и сохранить тот же знаменатель. Чтобы сложить или вычесть разные дроби, мы преобразуем их в одинаковые дроби. Находим НОК знаменателей, преобразуем слагаемые в их эквивалентные дроби и складываем их так же, как складываем одинаковые дроби.
Теперь, если они похожи на дроби, мы можем просто сложить или вычесть числители и сохранить тот же знаменатель. Чтобы сложить или вычесть разные дроби, мы преобразуем их в одинаковые дроби. Находим НОК знаменателей, преобразуем слагаемые в их эквивалентные дроби и складываем их так же, как складываем одинаковые дроби.
Каковы правила сложения и вычитания дробей?
Основные правила сложения и вычитания дробей приведены ниже:
- Нам нужно проверить, одинаковы ли знаменатели дробей или разные.
- Если знаменатели совпадают, мы можем просто сложить или вычесть числители.
- Если знаменатели не совпадают, нам нужно преобразовать их в одинаковые дроби, а затем сложить или вычесть.
Сложение и вычитание дробей – Математика для торговли: Том 1
Дроби
Эбигейл, Ханна и Наоми готовятся к промежуточному экзамену. Материал, который они должны изучить, состоит из 16 глав для чтения. Все трое понимают, что 16 глав — это много для каждого из них, поэтому они решают учиться более эффективно. Они составляют план, в котором каждый из них читает определенное количество глав, а затем резюмирует его для двух других. Они будут делиться заметками, и каждый найдет онлайн-видео, соответствующее их конкретному набору глав.
Все трое понимают, что 16 глав — это много для каждого из них, поэтому они решают учиться более эффективно. Они составляют план, в котором каждый из них читает определенное количество глав, а затем резюмирует его для двух других. Они будут делиться заметками, и каждый найдет онлайн-видео, соответствующее их конкретному набору глав.
Теперь главы не создаются одинаково. Некоторые из них довольно легкие, а другие намного сложнее. Их цель — равномерно распределить нагрузку между тремя из них. Помните, что есть 16 глав.
У Эбигейл самое большое количество глав, которые нужно пройти — 6. У Ханны — 5, а у Наоми — только 4. Если бы вы сложили их, вы бы заметили, что получается только 15 глав. Последняя глава книги посвящена устранению неполадок в электрических системах, и ученики решают, что они пройдут ее вместе.
Мы можем представить каждую из их рабочих нагрузок в виде части целого:
[латекс]\БОЛЬШОЙ\текст{У Эбигейл}\dfrac{6}{16}[/латекс]
[латекс]\БОЛЬШОЙ\текст{У Ханны}\dfrac{5}{16}[/латекс]
[латекс]\БОЛЬШОЙ\текст{У Наоми}\dfrac{4}{16}[/латекс]
Что, если сложить эти дроби? Это будет выглядеть примерно так:
[латекс]\БОЛЬШОЙ\dfrac{6}{16}+\dfrac{5}{16}+\dfrac{4}{16}=?[/latex]
Вы заметите, что все числители разные, а знаменатели одинаковые (16). При сложении или вычитании дробей знаменатели должны совпадать. Мы называем это наличием общего знаменателя.
При сложении или вычитании дробей знаменатели должны совпадать. Мы называем это наличием общего знаменателя.
Итак, чтобы получить ответ на поставленный выше вопрос, нужно просто сложить все числители. Сложение дробей в этом отношении очень просто.
Обратите внимание, что знаменатель в окончательном ответе такой же, как и в складываемых дробях. К концу ученики пройдут 15 из 16 глав по отдельности, а последнюю главу они пройдут вместе.
Концепция сложения дробей с общими знаменателями достаточно проста, и мы сделали достаточно, чтобы складывать целые числа, поэтому рассматривать примеры на этом этапе, возможно, не стоит (но если вам нужен обзор, см. Сложение целых чисел). Вместо этого мы запишем несколько примеров сложения дробей, чтобы вы могли понять идею.
[латекс]\БОЛЬШОЙ\dfrac{1}{8}+\dfrac{2}{8}=\dfrac{3}{8}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{5}{16}+\dfrac{6}{16}=\dfrac{11}{16}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{13}{32}+\dfrac{11}{32}=\dfrac{24}{32}[/latex]
Вы ничего не заметили в ответе на последний вопрос? Его можно уменьшить.
[латекс]\БОЛЬШОЙ\dfrac{24}{32}\longrightarrow\dfrac{3}{4}[/латекс]
Прежде чем мы продолжим работу с дробями, самое время сказать, что при работе с дробями мы обычно хотим дать ответ в самом низком выражении.
Как насчет вычитания дробей? Ну, по тому же принципу: у вас должен быть общий знаменатель, а затем вы вычитаете числители. Вот несколько примеров вычитания дробей:
[латекс]\БОЛЬШОЙ\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{9}{16}-\dfrac{5}{16}=\dfrac{4}{16}\longrightarrow\dfrac{1}{4}[/latex]
[латекс]\БОЛЬШОЙ\dfrac{27}{32}-\dfrac{14}{32}=\dfrac{13}{32}[/latex]
Сейчас мы немного усложним задачу. Наши примеры сложения и вычитания дробей довольно просты из-за того, что знаменатели одинаковы. Более сложная ситуация связана с добавлением или вычитанием дробей, имеющих разные знаменатели. Взгляните на следующий пример:
[латекс]\БОЛЬШОЙ\dfrac{1}{2}+\dfrac{3}{8}=?[/latex]
Мы не можем просто сложить числители и знаменатели, так как это просто не сработает. Взгляните на два круга, нарисованные ниже. Один разделен на 2 части, а другой на 8 частей. Вы заметили что-нибудь о размерах деталей?
Взгляните на два круга, нарисованные ниже. Один разделен на 2 части, а другой на 8 частей. Вы заметили что-нибудь о размерах деталей?
Вы заметите, что части в круге из 2 частей намного больше, чем в круге из 8 частей. Если бы мы сложили части в каждом из кругов, это было бы похоже на сложение яблок и апельсинов.
Идея состоит в том, чтобы сделать так, чтобы добавляемые детали были одинакового размера. Если мы каким-то образом доберемся до этой точки, тогда все готово, и мы можем сложить две дроби. Это называется поиском общего знаменателя, и чаще всего мы пытаемся найти наименьший общий знаменатель .
Наименьший общий знаменатель : Наименьшее число, в которое могут входить два знаменателя.
Взгляните на приведенное ниже уравнение. Один из знаменателей равен 2, а другой равен 8,9.0005
[латекс]\БОЛЬШОЙ\dfrac{1}{2}+\dfrac{3}{8}=?[/latex]
Процесс здесь аналогичен тому, как мы приводили дроби к их наименьшему члену в предыдущем разделе, только на этот раз мы будем увеличивать по крайней мере один из знаменателей, а иногда мы будем увеличивать оба, пока не найдем тот, который общий. Мы ищем число, в которое оба знаменателя могут входить поровну. В этом примере мы видим, что 2 может перейти в 8, а 8 может перейти в 8. Это оставляет нас с общим знаменателем 8.
Мы ищем число, в которое оба знаменателя могут входить поровну. В этом примере мы видим, что 2 может перейти в 8, а 8 может перейти в 8. Это оставляет нас с общим знаменателем 8.
Мы определили, что 8 будет нашим общим знаменателем, а это значит, что одна из дробей уже готова.
А как насчет 1 на 2 или наполовину? Мы должны превратить половину в дробь с 8 в знаменателе.
Как мы подсчитали выше, 2 входит в число 8 четыре раза.
[латекс]\БОЛЬШОЙ2\times4=8[/латекс]
Это хорошо для знаменателя, но как насчет числителя? Итак, что бы мы ни сделали с одной частью дроби, мы должны сделать то же самое с другой частью. Это оставляет дробь с тем же значением. Затем мы также должны умножить 1 на 4.
[латекс]\БОЛЬШОЙ1\times4=4[/латекс]
Если бы мы хотели сделать все за один шаг, это выглядело бы примерно так:
Теперь у нас есть кое-что, с чем мы можем работать. Вернитесь к исходному уравнению и замените [latex]\dfrac{1}{2}[/latex] на [latex]\dfrac{4}{8}[/latex].
[латекс]\БОЛЬШОЙ\dfrac{4}{8}+\dfrac{3}{8}=\dfrac{7}{8}[/latex]
Хорошо, это работает для сложения дробей, но как насчет вычитания дробей? Ну, вычитание дробей происходит по тому же принципу: если знаменатели не совпадают, то мы должны сначала найти общий знаменатель, прежде чем вычитать две дроби.
Вычислите следующее:
[латекс]\НАИБОЛЬШИЙ\dfrac{7}{8}-\dfrac{13}{16}=[/latex]
Шаг 1 : Найдите общий знаменатель. Это может стать немного сложнее, когда числа начинают расти. По мере того, как вы лучше знакомитесь с закономерностями в числах, ответы будут даваться легче. Вопрос, который мы задаем прямо сейчас, звучит так: «В какое число могут входить и 8, и 16 без остатка?»
Мы могли бы даже начать с проверки того, может ли меньший знаменатель войти в больший знаменатель. В данном случае так и есть.
Дробь с общим знаменателем 16 уже готова, но нам нужно работать с дробью со знаменателем 8.
Шаг 2 : Умножьте числитель и знаменатель ⅞ на 2, чтобы получить дробь общий знаменатель 16.
Шаг 3 : Вычтите новые версии дробей.
[латекс]\БОЛЬШОЙ\dfrac{14}{16}-\dfrac{13}{16}=\dfrac{1}{16}[/latex]
Ответьте на следующие практические вопросы и посмотрите видеоответы. Не забудьте поставить каждый ответ в самом низком выражении или в смешанном числе, если это необходимо.
[латекс]\БОЛЬШОЙ\dfrac{3}{16}+\dfrac{5}{8}=[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{5}{8}-\dfrac{5}{16}=[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{1}{2}+\dfrac{7}{8}=[/латекс]
[латекс]\БОЛЬШОЙ2\dfrac{1}{2}+1\dfrac{7}{8}=[/латекс]
Минуточку! Этот последний вопрос поднял его на ступеньку выше, добавив смешанные числа. Я знаю, что вы уже посмотрели видеоответ, но давайте сделаем шаг назад и пройдемся по сложению и вычитанию смешанных чисел. Мы начнем с краткого объяснения.
Проблема, с которой мы сталкиваемся при сложении или вычитании смешанных чисел, заключается в том, что смешанное число состоит из двух отдельных частей: есть целое число, а есть дробь. При добавлении чисел это может быть просто, например:
При добавлении чисел это может быть просто, например:
[латекс]\БОЛЬШОЙ4\dfrac{3}{8}+3\dfrac{2}{8}=7\dfrac{5}{8}[/latex]
Довольно просто, не так ли? Вы просто складываете два целых числа, а затем складываете дроби. Это работает довольно хорошо. Но как насчет ситуации, подобной следующему примеру?
[латекс]\БОЛЬШОЙ4\dfrac{5}{8}+3\dfrac{4}{8}=?[/latex]
Вы видите проблему?
Проблема (на самом деле это не проблема) в том, что когда мы складываем дроби, мы получаем большее число в числителе, чем в знаменателе.
[латекс]\БОЛЬШОЙ4\dfrac{5}{8}+3\dfrac{4}{8}=7\dfrac{9}{8}[/latex]
Решение состоит в том, чтобы заменить часть ответа на неправильную дробь смешанным числом, а затем добавить его к целой части ответа.
[латекс]\БОЛЬШОЙ\dfrac{9}{8}\longrightarrow1\dfrac{1}{8}[/латекс]
Возьмите 7 и прибавьте к смешанному числу, чтобы получить окончательный ответ.
[латекс]\БОЛЬШОЙ7+1\dfrac{1}{8}=8\dfrac{1}{8}[/латекс]
Хорошо, это кажется довольно простым, но как насчет вычитания? Что ж, мы следуем тем же правилам. Взгляните на следующий пример:
Взгляните на следующий пример:
[latex]\LARGE8\dfrac{7}{8}-6\dfrac{3}{8}=?[/latex]
Процедура похожа на сложение дробей, но вместо сложения мы вычитаем . Мы можем разбить его на две части. Начнем с вычитания целых чисел, а затем вычтем часть дробей.
Шаг 1 : Вычтите целые числа.
[латекс]\НАИБОЛЬШИЙ8-6=2[/латекс]
Шаг 2 : Вычтите дробную часть уравнения.
[латекс]\БОЛЬШОЙ\dfrac{7}{8}-\dfrac{3}{8}=\dfrac{4}{8}\стрелка вправо\dfrac{1}{2}[/latex]
Шаг 3 : Соберите все вместе.
[латекс]\БОЛЬШОЙ8\dfrac{7}{8}-6\dfrac{3}{8}=2\dfrac{4}{8}\rightarrow2\dfrac{1}{2}[/latex]
Хорошо, не слишком сложно, правда? Но взгляните на следующий пример и посмотрите, сможете ли вы понять проблему, с которой мы столкнемся, когда будем ее решать.
[latex]\LARGE5\dfrac{2}{8}-3\dfrac{7}{8}=?[/latex]
Проблема возникает не тогда, когда вы вычитаете целые числа, а когда вы вычитаете дроби.
[латекс]\БОЛЬШОЙ\dfrac{2}{8}-\dfrac{7}{8}=?[/latex]
В итоге мы получим ответ меньше нуля. Это не сработает для нас. Итак, как мы решим проблему? Ну, ответ заключается в заимствовании, а то, что мы заимствуем, — это целое число, 5. Скажем так, мы заимствуем 1 из 5. В результате у нас останется 4, а дальше что? Взгляните на следующую логику.
[латекс]\БОЛЬШОЙ5=4+1[/латекс]
[латекс]\БОЛЬШОЙ1=\dfrac{8}{8}[/латекс]
Если мы продолжим и разобьем 5 на 4 и 1 , а затем разделить эту 1 на части по 8, у нас есть гораздо больше восьмых для работы. Теперь мы можем собрать все вместе, чтобы получить следующее:
[латекс]\БОЛЬШОЙ5\dfrac{2}{8}=4+\dfrac{8}{8}+\dfrac{2}{8}=4\dfrac {10}{8}[/latex]
Теперь у нас есть числа, с которыми мы можем работать в исходном вопросе.
[латекс]\БОЛЬШОЙ4\dfrac{10}{8}-3\dfrac{7}{8}=?[/latex]
Выполняем те же действия, что и раньше.
Шаг 1 : Вычтите целые числа.
[латекс]\НАИБОЛЕЕ4-3=1[/латекс]
Шаг 2 : Вычтите дробную часть уравнения.


 Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скоростью, на 2 км/ч меньшей, чем по шоссе? Найдите t при s=10, v=6.
Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скоростью, на 2 км/ч меньшей, чем по шоссе? Найдите t при s=10, v=6.


 Найдите высоту, проведенную к основанию.
Найдите высоту, проведенную к основанию.
 Если к числителю этой дроби прибавить 7, а к знаменателю 5, то она увеличится на . Найдите эту дробь.
Если к числителю этой дроби прибавить 7, а к знаменателю 5, то она увеличится на . Найдите эту дробь. Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.
Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.



 Здесь числители 1 и 2, поэтому будет 1 + 2 = 3
Здесь числители 1 и 2, поэтому будет 1 + 2 = 3  Здесь знаменатель равен 5,9.0056
Здесь знаменатель равен 5,9.0056 Это будет 3/15 + 5/15 = 8/15
Это будет 3/15 + 5/15 = 8/15 Это будет 5/6 — 2/6 = 3/6. Это может быть дополнительно уменьшено до 1/2
Это будет 5/6 — 2/6 = 3/6. Это может быть дополнительно уменьшено до 1/2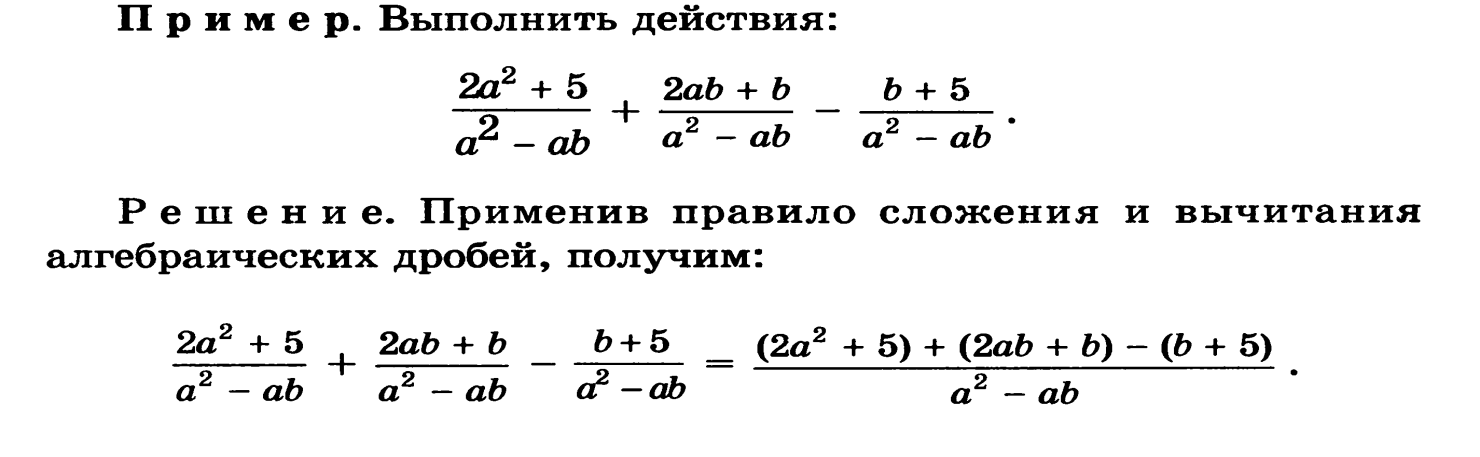 В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 7/4 + 5/1
В этом случае целое число равно 5, что можно записать как 5/1. Итак, теперь нам нужно сложить 7/4 + 5/1 Здесь НОК 1 и 5 равен 5. И после преобразования их в одинаковые дроби мы получаем (6 × 5)/(1 × 5) — (3 × 1)/(5 × 1) = 30/5 — 3/ 5
Здесь НОК 1 и 5 равен 5. И после преобразования их в одинаковые дроби мы получаем (6 × 5)/(1 × 5) — (3 × 1)/(5 × 1) = 30/5 — 3/ 5