Олимпиад по физике школьный тур 8 класс 2015-2016 уч год с решениями

Ответы к заданиям школьного этапа всероссийской олимпиады

школьников по физике в 2015 — 2016 учебном году

8 класс.

1. Велосипедист проехал первую половину пути со скоростью V₁ = 10 км/ч. Затем он поехал с большей скоростью, но проколол шину. После попытки ликвидировать прокол велосипедист был вынужден оставшуюся часть пути пройти пешком. Чему равна средняя скорость движения велосипедиста на всем пути, если первую треть времени, затраченного им на вторую половину пути, он ехал со скоростью V₂ = 20 км/ч, вторую треть занимался проколом и последнюю треть шел пешком со скоростью V₄ = 5 км/ч?

Решение. Средняя скорость на некотором участке пути, согласно определению, равна отношению пройденного пути ко времени, в течение которого этот путь пройден

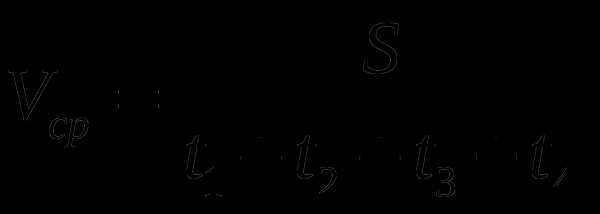.(1)

Согласно условиям задачи:

0,5S=V₁ t₁,

0,5S=V₂ t₂ +0∙t₃+ v₄t₄ ,

t₂=t₃=t₄ .

Отсюда можно найти:

t₁ = 0,5 S/V₁, (2)

t₂ = t₃ = t₄ = 0,5 S/(V₂ + V₄). (3)

Подставляя соотношения (2) и (3) в формулу (1), получаем:

.

Правильность (ошибочность) решения

Баллы

Полное верное решение

10

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

8

Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).

5-6

Найдено решение одного из двух возможных случаев.

5

Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.

2-3

Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).

0-1

Решение неверное, или отсутствует.

0

2. На рисунке изображены рычаги, на которых имеются крючки, прикрепленные через одинаковые расстояния. Крючки пронумерованы от -3 до 3, причем 0 приходится на середину рычага. К некоторым крючкам прикреплено по нескольку грузов одинаковой массы. Имеется еще один такой же не подвешенный груз. К крючку с каким номером

n его нужно подвесить, чтобы рычаг находился в равновесии? Решите задачу для каждого из трех случаев, представленных на рисунке.

Решение.

Обозначим через 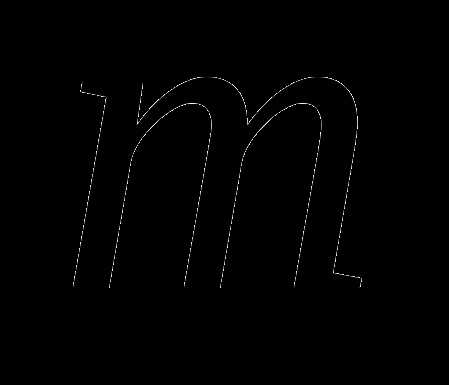массу одного груза, – расстояние между соседними крючками. Применим для каждого случая правило рычага:

(а) , отсюда ,

(б) , отсюда ,

(в) , отсюда

.

Правильность (ошибочность) решения

Баллы

Полное верное решение

10

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

8

Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).

5-6

Записаны уравнения моментов сил и получено решение – по 3 балла за случаи (а) и (б), 4 балла – случай (в).

Получен правильный ответ без уравнения моментов сил, за каждый рычаг

2

Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).

0-1

Решение неверное, или отсутствует.

0

3.С какой высоты должна падать вода, чтобы при ударе о землю она закипала? На нагрев воды идёт 50% расходуемой механической энергии, начальная температура воды 20⁰С.

Решение:

Согласно условию, на нагрев воды массой m расходуется энергия, равная mgh.

Поэтому по закону сохранения энергии: Е=Q; mgh =mc(t₂ — t₁),где t₂=100⁰С. Отсюда h=.

Вычисления дают: h = =70∙10³(м).

Полученный результат показывает, сколь велика энергия, выделяемая и поглощаемая в тепловых процессах.

Ответ: 70км.

Правильность (ошибочность) решения

Баллы

Полное верное решение

10

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

8

Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).

5-6

Записан закон сохранения энергии. Записана формула расчета потенциальной энергии и количества теплоты. Каждая формула по 1 баллу

Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.

2-3

Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).

0-1

Решение неверное, или отсутствует.

0

4. На вертолет мощностью 3000000 Вт загрузили 500 кг груза. Включив двигатель на 10% мощности, вертолет равномерно поднялся на высоту 100 м за время 5 секунд. Какова масса вертолета без груза?

масса груза.

Учитывая, что двигатели

1250 кг

Ответ: М=1250 кг.

Правильность (ошибочность) решения

Баллы

Полное верное решение

10

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

8

Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).

5-6

Записана формула мощности, записана формула работы силы тяжести, по 2 балла за каждую

Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.

2-3

Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).

0-1

Решение неверное, или отсутствует.

0

infourok.ru

Олимпиада по физике, 8 класс, школьный этап

Всероссийская олимпиада школьников по физике 2018-2019

Первый (школьный) этап.

8 класс

1.(10 баллов)Турист проехал на велосипеде за один день 40 км. При этом с 9.00 до 11.20 он  ехал со скоростью, которая равномерно возрастала со временем от 10 км/ч до 14 км/ч. Затем турист загорал на пляже. На оставшийся путь он потратил время с 18.30 до 20.00. Определите среднюю скорость туриста на вечернем участке поездки. Ответ дайте в км/ч.

2.(6 баллов)В то утро попугай Кешка, как обычно, собирался сделать доклад о пользе банановодства и бананоедства. Позавтракав 5 бананами, он взял мегафон и полез на «трибуну» — на верхушку пальмы высотой 20 м. На полпути он почувствовал, что с мегафоном ему не добраться до вершины. Тогда он оставил мегафон и полез дальше без него. Сумеет ли Кешка сделать доклад, если для доклада нужен запас энергии в 200 Дж, один съеденный банан позволяет совершить работу в 200 Дж, масса попугая 3 кг, масса мегафона 1 кг? (при расчетах принять g = 10Н/кг)

3. (10 баллов)В электрическом чайнике 1 литр воды нагревается на 10 градусов за 1 минуту. За какое время нагреются до кипения 500 г воды, взятые из ведра со смесью воды и льда? Потерями теплоты можно пренебречь. Плотность воды 1000 кг/м³.

4.(10 баллов)В цилиндрическом сосуде с водой находится  частично погружённое в воду тело, привязанное натянутой нитью ко дну сосуда. При этом тело погружено в воду на две трети своего объёма. Если перерезать нить, то тело всплывёт и будет плавать погружённым в воду наполовину. На сколько при этом изменится уровень воды в сосуде? Ответ дайте в метрах. Масса тела

m = 30 г, плотность воды ρ = 1,0 г/см³, площадь дна сосуда S = 10 см².

Ответы, указания, решения к олимпиадным задачам.

Физика, 8 класс

1. Турист проехал на велосипеде за один день 40 км. При этом с 9:00 до 11:20 он  ехал со скоростью, которая равномерно возрастала со временем от 10 км/ч до 14 км/ч. Затем турист загорал на пляже. На оставшийся путь он потратил время с 18:30 до 20:00. Определите среднюю скорость туриста на вечернем участке поездки. Ответ дайте в км/ч.

Вариант решения

С 9.00 до 11.20 турист ехал со средней скоростью (10 + 14)/2 = 12 км/ч (так как скорость возрастала равномерно со временем).

Время 11:20-9:00= 2:20=2 ч 20 мин = 2 ч.

Значит, за это время турист проехал расстояние:

За время с 18.30 до 20.00 велосипедист проехал 40 – 28  = 12 км.

Время 20:00-18:30 = 1: 30=1 ч 30 мин = 1,5 ч.

Следовательно, средняя скорость туриста на вечернем участке поездки равна:

Критерии оценивания:

• Средняя скорость туриста на утреннем участке поездки (12 км/ч): 4 балла

• Расстояние, которое проехал турист с 9.00 до 11.20 (28 км): 2 балла

• Расстояние, которое проехал турист с 18.30 до 20.00 (12 км): 2 балла

• Средняя скорость туриста на вечернем участке поездки (8 км/ч): 2 балла

Максимальное количество баллов – 10.

2.В то утро попугай Кешка, как обычно, собирался сделать доклад о пользе банановодства и бананоедства. Позавтракав 5 бананами, он взял мегафон и полез на «трибуну» — на верхушку пальмы высотой 20м. На полпути он почувствовал, что с мегафоном ему не добраться до вершины. Тогда он оставил мегафон и полез дальше без него. Сумеет ли Кешка сделать доклад, если для доклада нужен запас энергии в 200 Дж, один съеденный банан позволяет совершить работу в 200 Дж, масса попугая 3 кг, масса мегафона 1 кг?

Вариант решения

1. Запас энергии, который дают пять съеденных бананов:

2. Для того, чтобы попугаю Кеше забраться на пальму с мегафоном, потребовалось бы: Е= (M+m)∙g∙h. Так как Кешка на полпути оставил мегафон, то:

3)

4)

5)После этого у него оставалось 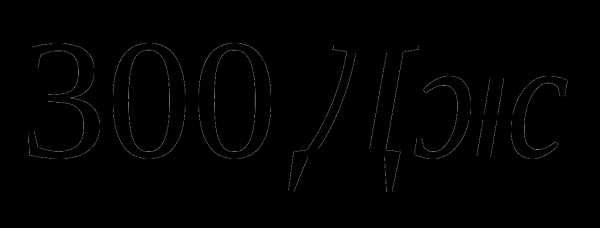энергии на то, чтобы сделать доклад.

6)Ответ: Кешка сумеет сделать доклад, он даже мог и не оставлять мегафон на полпути.

Критерии оценивания:

• Нахождение общего запаса энергии от съеденных бананов : 1 балл;

• Формула энергии, затраченной для поднятия тела на высоту h:

Е= (M+m)∙g∙h: 2 балла;

• Найдены энергии Е₁ и Е₂ : 2 балла;

• Математические расчеты, правильная формулировка окончательного ответа: 1 балл.

Максимальное количество баллов – 6.

3. В электрическом чайнике 1 литр воды нагревается на 10 градусов за 1 минуту. За какое время нагреются до кипения 500 г воды, взятые из ведра со смесью воды и льда? Потерями теплоты можно пренебречь. Плотность воды 1000 кг/м³.

Вариант решения

По условию за время τ₁ = 1 мин вода плотностью ρ = 1000 кг/м³, удельной теплоёмкостью c и объёмом V = 1 л нагревается на ∆t₁ = 10 °C. Получаемое количество теплоты при этом равно Q=c∙ρ∙V∙∆t₁, а мощность чайника оказывается равной P= c∙ρ∙V∙∆t₁/τ₁.

Во втором опыте масса воды m = 500 г нагревается от 0 °C до 100 °C, то есть на ∆t₂ = 100 °C. Получаемое при этом количество теплоты равно Q=c∙m∙∆t_2.

Время нагревания равно отношению данного количества теплоты к мощности чайника

τ = cm∆t₂

: (

cρV t₁

) = (

₁mt₂

) = 5 мин.

^

ρV t₁

Критерии оценивания:

• Отмечено, что мощность чайника в двух опытах одинаковая: 1 балл;

• Отмечено, что начальная температура воды во втором опыте составляет

0 °C, — 1 балл; отмечено, что конечная температура воды во втором опыте составляет

100 °C, — 1 балл.

• Правильно записана формула для расчёта времени нагревания τ : 2 балла;

• Математические расчёты верны, получен правильный ответ: 2 балла.

Максимальное количество баллов – 10.

4.В цилиндрическом сосуде с водой находится  частично погружённое в воду тело, привязанное натянутой нитью ко дну сосуда. При этом тело погружено в воду на две трети своего объёма. Если перерезать нить, то тело всплывёт и будет плавать погружённым в воду наполовину. На сколько при этом изменится уровень воды в сосуде? Ответ дайте в метрах. Масса тела m = 30 г, плотность воды ρ = 1,0 г/см³, площадь дна сосуда S = 10 см².

Вариант решения 1

Сила давления стакана на стол (после перерезания нити) не изменится, следовательно,

T = ρ·g·∆h·S, где T – сила реакции со стороны нити,  ∆h – изменение уровня воды. Запишем уравнение равновесия тела в первом случае:

Уравнение равновесия тела во втором случае: mg = ρg·(1/2)·V

Из последних двух уравнений находим, что T = 1/3 · mg

Окончательно получаем: 

Критерии оценивания:

• Уравнение равновесия тела в первом случае: 2 балла

• Уравнение равновесия тела во втором случае: 2 балла

• T = 1/3 · mg: 3 балла

• ∆h = T/(ρ·g·S): 2 балла

• ∆h = 0,01м: 1 балл

Вариант решения 2

Уравнение равновесия тела во втором случае:

mg = ρg · ½ · V  ⟹ V = 2m/ρ, где V – объём тела.

Изменение объёма погружённой части тела равно:

∆V = ∙2m/ρ= ∙m/ρ

Окончательно получаем:

Критерии оценивания

• Уравнение равновесия тела во втором случае: mg = ρg•(1/2)•V: 4 балла

• Изменение объёма : ∆V = 1/6 •V: 2 балла

• Запись формулы нахождения высоты ∆h = ∆V/S: 3 балла

• Математические вычисления: ∆h = 0,01 м: 1 балл

Максимальное количество баллов – 10.

В случае, если решение какой-либо задачи отличается от авторского, эксперт (учитель) сам составляет критерии оценивания в зависимости от степени и правильности решения задачи. Максимальное количество баллов остаётся таким, какое указано в примерных вариантах решения.

Всего за работу – 36 баллов.

18-23 балла (50%-65%) – отметка «3»

24-32 балла (66%-90%) – отметка «4»

33-36 баллов (91%-100%) – отметка «5»

infourok.ru

Олимпиада по физике школьный тур 8 класс

Школьный этап

Всероссийской олимпиады школьников по физике

(2017/18 учебный год)

8 класс

Количество задач – 4.

Время, отводимое на выполнение — 90 минут.

Каждая задача оценивается из 10 баллов.

Полное решение задачи оценивается в 10 баллов вне зависимости от того, совпадает выбранный школьником способ решения с авторским или нет.

Приведенные ниже критерии оценивания используются, если решение задачи не доведено до правильного ответа.

Задача 1.

В ртутном термометре Фаренгейта температура таяния льда (0ºC) равна 32ºF, а температура кипения воды (100ºC) равна 212ºF. Какова нормальная температура человеческого тела 36,6ºC по Фаренгейту?

Решение и ответ:

Интервал между температурами таяния льда и кипения воды по Фаренгейту равен 180ºF. Интервал между температурами таяния льда и кипения воды по шкале Цельсия равен 100ºC . Одному градусу по шкале Цельсия соответствует 180 / 100 = 1,8 градуса по шкале Фаренгейта (1°С=1,8°F). Температура t =0°C соответствует 32°F. Значит некая температура

Т °F = 32 ºF + t °С ∙ 1,8 °F
Нормальная температура человеческого тела по Фаренгейту будет равна

32ºF + 36,6 · 1,8ºF = 97,88 ºF.

Критерии оценивания:

Найден интервал между температурами таяния льда и кипения воды по шкале Фаренгейта — 2 балла

Найден интервал между температурами таяния льда и кипения воды по шкале Цельсия — 2 балла

Найдено соответствие одного градуса по шкале Цельсия количеству градусов по Фаренгейту — 2 балла

Сделано пояснение, что t =0°C соответствует 32°F — 1 балл

Записана формула и вычислена нормальная температура человеческого тела по шкале Фаренгейта -3 балла

Задача 2.

Колонна пехоты длиной L=400 м движется со скоростью u = 4км/ч. Командир, находящийся во главе колонны, послал адъютанта с приказом к замыкающему. Через какое время адъютант вернется, если он едет на лошади со скоростью v =20км/ч?

Решение и ответ:

Время движения против хода колонны , время движения по ходу колонны . Общее время движения .
После подстановки числовых данных получаем

Критерии оценивания:

Выбрана система отсчета, связанная с колонной — 1 балл

Найдена скорость движения против хода колонны -1 балл

Найдена скорость движения по ходу движения колонны — 1 балл

Найдено время t₁ движения против хода колонны-2 балла

Найдено время t₂ движения по ходу колонны-2 балла

Найдено общее время движения — 3 балла

Задача 3.

Последние исследования историков показали, что Буратино был изготовлен не из одного, а из двух поленьев. Его голову Папа Карло выточил из дуба, а остальные части тела выстругал из сосны. Известно, что плотность дуба 690 кг/м³, вес изготовленной из него части тела составляет треть от веса Буратино, а объём – только четверть. Найдите плотность соснового полена.

Решение и ответ:

Обозначим: m – массу Буратино; V – объем Буратино; ρ_д -плотность дуба; ρ_с — плотность сосны.

Тогда V и V. Выразим в каждом уравнении массу через плотность и объем, приравняем правые части. Получается равенство 3/4 ρ_д = 9/8 ρ_с . Выразим плотность сосны

Критерии оценивания:

Записана формула для вычисления массы головы — 2 балла

Записана формула для вычисления массы туловища — 2 балла

Проведены необходимые математические преобразования уравнения, выразили плотность сосны — 4 балла

Найдена плотность сосны и записан ответ — 2 балла

Задача 4.

«…Мимо бревно суковатое плыло,
Сидя и стоя, и лёжа пластом
Зайцев с десяток сидело на нём.

«Взял бы я вас — да потопите лодку!»
Жаль их, однако, да жаль и находку —
Я зацепился багром за сучок
И за собою бревно поволок…»

Н. А. Некрасов

При каком минимальном объёме бревна зайцы смогли бы на нём плыть? Считайте, что бревно погружено в воду наполовину. Масса одного зайца 3 кг, плотность древесины 400 кг/м³, плотность воды 1000 к г/м³.

Решение и ответ:

Масса одного зайца M_з = 3 кг, V_дер – объём бревна, m_дер – масса бревна, ρ_д – плотность дерева, ρ_в –плотность воды.

Приравняем выталкивающую силу Архимеда и силу тяжести
F_тяж = F_выт
M_общ ∙ g = ρ_в ∙ (V_дер / 2) ∙ g
(10∙M _з + m_дер) ∙ g =( ρ_в ∙ V_дер ∙ g) / 2
10∙ M_з ∙ + ρ_дер∙V_дер = (p_в∙ V_дер ) / 2

обе части уравнения умножим на 2
20∙M_з = ρ_в∙V_дер — 2∙ρ _дер∙V_дер

20∙M_з = V_дер ∙ (ρ_в — 2∙ρ _дер)
V_дер = (20∙M_з)/(ρ_в — 2ρ _дер)
V _дер = (20∙3кг) / (1000 — 2∙400) = 60 / 200 = 0,3м³
V_дер = 0,3 м³
Ответ: Объем бревна = 0,3 м³

Критерии оценивания.

Верно записана формула силы тяжести для десяти зайцев и бревна — 2 балла

Верно записана формула силы Архимеда для бревна и учтено, что бревно находится в воде наполовину — 2 балла

Верно записаны формула массы бревна — 1 балл

Верно составлено равенство силы Архимеда и силы тяжести — 2 балла

Верно выражена неизвестная величина (объём бревна) — 2 балл

Верно получен числовой ответ для объёма бревна — 1 балл

infourok.ru

Физика 8 класс, школьный (первый) этап, г. Москва, 2017-2018 год

Содержание

1. Задача 1
2. Задача 2
3. Задача 3
4. Задача 4

---

Задача 1

Содержание ↑

Турист проехал на велосипеде за один день 40 км. При этом с 9.00 до 11.20 он  ехал со скоростью, которая равномерно возрастала со временем от 10 км/ч до 14 км/ч. Затем турист загорал на пляже. На оставшийся путь он потратил время с 18.30 до 20.00. Определите среднюю скорость туриста на вечернем участке поездки.

Возможное решение

С 9.00 до 11.20 турист ехал со средней скоростью (10 + 14)/2 = 12 км/ч (так как скорость возрастала равномерно со временем). Значит, за это время турист проехал расстояние

За время с 18.30 до 20.00 велосипедист проехал 40 – 28  = 12 км. Следовательно, средняя скорость туриста на вечернем участке поездки равна:

Критерии оценивания

• Средняя скорость туриста на утреннем участке поездки (12 км/ч): 4 балла
• Расстояние, которое проехал турист с 9.00 до 11.20 (28 км): 2 балла
• Расстояние, которое проехал турист с 18.30 до 20.00 (12 км): 2 балла
• Средняя скорость туриста на вечернем участке поездки (8 км/ч): 2 балла

Максимум за задачу – 10 баллов.

Задача 2

Содержание ↑

Система, состоящая из двух однородных стержней разной плотности, находится в равновесии. Масса верхнего стержня m₁ = 1,4 кг. Трение пренебрежимо мало.

Определите, при какой массе m₂ нижнего стержня возможно такое равновесие.

Возможное решение

Так как нижний стержень подвешен за концы, находится в равновесии и его центр тяжести располагается посередине, то силы реакции нитей, действующие на него, одинаковы и равны по модулю m₂g/2. Запишем уравнение моментов для верхнего стержня относительно точки крепления левой (верхней) нити:

Критерии оценивания

Силы реакции нитей, действующие на нижний стержень, равны: 3 балла

Значения модулей этих сил реакций (m₂g/2): 2 балла

Уравнение моментов: 4 балла

m₂ = 1,2 кг: 1 балл

Максимум за задачу – 10 баллов.

Задача 3

Содержание ↑

В цилиндрическом сосуде с водой находится  частично погружённое в воду тело, привязанное натянутой нитью ко дну сосуда. При этом тело погружено в воду на две трети своего объёма. Если перерезать нить, то тело всплывёт и будет плавать погружённым в воду наполовину. На сколько при этом изменится уровень воды в сосуде? Масса тела m = 30 г, плотность воды ρ = 1,0 г/см³, площадь дна сосуда S = 10 см².

Возможное решение 1

Сила давления стакана на стол (после перерезания нити) не изменится, следовательно,

T = ρ·g·∆h·S, где ܶT – сила реакции со стороны нити,  ∆h – изменение уровня воды. Запишем уравнение равновесия тела в первом случае:

 

Уравнение равновесия тела во втором случае: mg = ρg·(1/2)·V

Из последних двух уравнений находим, что ܶT = 1/3 · mg

Окончательно получаем: 

Критерии оценивания

• Сила давления стакана на стол не изменится: 2 балла
• Уравнение равновесия тела в первом случае: 2 балла
• Уравнение равновесия тела во втором случае: 2 балла
• T = 1/3 · mg: 1 балл
• ∆h = T/(ρ·g·S): 2 балла
• ∆h = 0,01м: 1 балл

Возможное решение 2

Уравнение равновесия тела во втором случае:

mg = ρg · ½ · V  ⟹ V = 2m/ρ, где ܸV – объём тела.

Изменение объёма погружённой части тела равно:

 

Окончательно получаем:

Критерии оценивания

• mg = ρg · ½ · V: 4 балла
• ∆V = 1/6 · V: 2 балла
• ∆h = ∆V/S: 3 балла
• ∆h = 0,01 м: 1 балл

Максимум за задачу – 10 баллов.

Задача 4

Содержание ↑

Определите давление воздуха над поверхностью жидкости в точке А внутри закрытого участка изогнутой трубки, если ρ = 800 кг/м³, h = 20 см, p₀ = 101 кПа, g = 10 м/с². Жидкости плотностями ρ и 2ρ друг с другом не смешиваются.

Возможное решение

Давление в точке B равно: p_В = p₀ + ρg·4h

Давление в точке С равно:

p_C = p_A  + ρg·h + 2ρg·2h = p_A + 5ρgh

По закону Паскаля p_B = p_C, следовательно,

p_A + 5ρgh = p₀ + 4ρgh ⇒ p_A = P₀ – ρgh = 101 – 1,6 = 99,4 кПа

Критерии оценивания

• p_В = p₀ + ρg·4h: 3 балла
• p_C = p_A + 5ρgh: 3 балла
• p_В = p_C : 2 балла
• p_A = 99.4 кПа: 2 балла

В случае, если решение какой-либо задачи отличается от авторского, эксперт (учитель) сам составляет критерии оценивания в зависимости от степени и правильности решения задачи.

При правильном решении, содержащем арифметическую ошибку, оценка снижается на 1 балл.

Всего за работу – 40 баллов.

olimpiadnye-zadanija.ru

Олимпиада по физике 8 класс, задания с ответами

В этом разделе собраны примеры олимпиадных заданий по физике. Мы советуем обратить внимание на предложенный комплект заданий всем учителям и учащимся 8 класса. Используйте данный материал для того, чтобы подготовиться к олимпиаде. На уроках физики предложенные тесты и задачи могут использоваться для контроля и систематизации знаний, а во время домашней самоподготовки они помогут ученикам оценить свои силы.

К тестовым вопросам и задачам указаны правильные ответы и решения. Это очень удобно, ведь олимпиадные задания по физике с ответами можно решать без помощи учителя. Ответы расположены в самом низу страницы, чтобы ученик не увидел ответ до того, как попробует решить задание самостоятельно.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Тестовые задания

1. В каком состоянии вещество принимает форму сосуда?
А) в твердом
Б) в жидком
В) в газообразном
Г) в твердом и газообразном

2. В какой жидкости утонет кусок парафина?
А) в воде
Б) в ртути
В) в морской воде
Г) в бензине

3. Внутренняя энергия свинцового тела изменится, если:
А) сильно ударить по нему молотком
Б) поднять его над землей
В) бросить его горизонтально
Г) изменить нельзя

4. Какой вид теплопередачи наблюдается при обогревании комнаты батареей водяного отопления?
А) теплопроводность
Б) конвекция
В) излучение
Г) всеми тремя способами одинаково

5. Какая физическая величина обозначается буквой L и имеет размерность Дж/кг?
А) удельная теплоемкость
Б) удельная теплота сгорания топлива
В) удельная теплота плавления
Г) удельная теплота парообразования

6. В процессе кипения температура жидкости…
А) увеличивается
Б) не изменяется
В) уменьшается
Г) нет правильного ответа

7. Если тела взаимно отталкиваются, то это значит, что они заряжены …
А) отрицательно
Б) разноименно
В) одноименно
Г) положительно

8. В каком случае атом некоторого вещества превращается в отрицательный ион?
А) если атом приобретает «лишний» электрон
Б) если атом теряет свой собственный электрон

9. Сопротивление вычисляется по формуле:
А) R=I /U
Б) R = U/I
В) R = U*I
Г) правильной формулы нет

10. В каком состоянии вещества действуют наименьшие силы притяжения между молекулами?
А) силы притяжения одинаковы во всех состояниях
Б) в твердом
В) в жидком
Г) в газообразном

Открытые вопросы

Вопрос 1
Девочки сделали снеговика, а мальчики соорудили точную его копию, но в два раза большей высоты. Какова масса копии, если масса оригинала равна 50 кг? (Плотность снега в обоих снеговиках одинаковая)

Вопрос 2
Группа туристов, двигаясь цепочкой по обочине дороги со скоростью 3,6 км/ч, растянулась на 200 м. Замыкающий посылает велосипедиста к вожатому, который находится впереди группы. Велосипедист едет со скоростью 7 м/с; выполнив поручение, он тут же возвращается к замыкающему группы с той же скоростью. Через сколько времени после получения поручения велосипедист вернулся обратно?

Вопрос 3
В каком случае подъемная сила у самодельного бумажного воздушного шара, заполненного горячим воздухом, больше: когда ребята запускали его в помещении школы или на дворе школы, где было довольно прохладно?

Вопрос 4
В доску толщиной 5 см забили гвоздь длиной а=10 см так, что половина гвоздя прошла навылет. Чтобы вытащить его из доски, необходимо приложить силу 1,8 кН. Гвоздь вытащили из доски. Какую при этом совершили механическую работу?

Вопрос 5
Закрытый бидон из железа частично заполнен керосином. Предложите один из способов, позволяющих, не пользуясь никакими измерительными приборами (и не открывая бидон), определить примерный уровень керосина в бидоне.

Ответы на тесты

Тестовое задание	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	А	А	В	В	Б

Тестовое задание	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	В	А	Б	Б	А

Ответы на открытые вопросы

Ответ на вопрос 1:
При изготовлении точной копии все размеры (длина, ширина и высота) должны быть увеличены в 2 раза. Следовательно, объем снеговика, сделанного мальчиками, будет в 8 раз больше объема оригинала, а масса копии m =50 кг · 8=400 кг.

Ответ на вопрос 2:
Скорость велосипедиста в системе отсчета, связанной с группой, при движении к вожатому равна υ₂-υ₁ при возвращении обратно равна υ₂+υ₁. Поэтому время движения велосипедиста к вожатому t₁= L/ υ₂-υ₁ , а время возвращения велосипедиста к замыкающему t₂= L / υ₂+υ₁ , где L — длина цепочки. Общее время движения велосипедиста t= t₁+ t₂. Таким образом можно записать:
t= L / υ₂-υ₁+ L / υ₂+υ₁= 2 L · υ₂/ υ₂²-υ₁²
Подставив числовые значения величин, получим: t ≈58,3 с.

Ответ на вопрос 3:
Подъемная сила воздушного шара равна разности между весом воздуха в объеме шара и весом газа, заполняющего шар. Чем больше разница в плотностях воздуха и газа, заполняющего шар, тем больше подъемная сила. Поэтому подъемная сила шара больше на улице, где воздух менее прогрет.

Ответ на вопрос 4:
Чтобы переместить гвоздь на пути а, надо совершить работу А₁=F·а. При дальнейшем перемещении гвоздя сила будет убывать от F до 0. Поэтому работу надо находить для средней силы: А₂=1/2·F·а. Следовательно, полная работа
А= А₁+А₂=F·а +1/2·F·а= 3/2· F·а=1,5 · F·а
135 Дж

Ответ на вопрос 5:
Можно, например, вначале хорошо охладить бидон с керосином. Затем поместить его в теплое помещение. В помещении в результате конденсации пара бидон покроется капельками воды. По мере нагревания бидона в теплом помещении вода на нем будет испаряться. Так как масса воздуха и паров бензина в верхней части его значительно меньше массы керосина, находящегося в нижней части бидона, то при нагревании бидона в тёплом помещении испарение будет происходить быстрее с верхней части его. В результате в какой-то момент времени можно будет наблюдать резкую границу между сухой поверхностью бидона и частью его, еще покрытой капельками воды. Эта граница и укажет на уровень керосина в бидоне.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Другие классы

Обновлено: 16/06/2015 , автор: Валерия Токарева

ruolimpiada.ru

Физика 8 класс, муниципальный (второй) этап, г. Москва, 2016 год

Задача 1

Машина проехала расстояние L = 160 км от города до деревни за время T = 2 часа. Её скорость на первом, хорошем, участке пути была на ∆V = 10 км/час больше средней  скорости  на  всём  пути,  а  на  втором,  плохом,  участке –  на ∆V = 10 км/час  меньше  средней  скорости  на  всём  пути.  Чему  равна  длина  s плохого участка пути?

Возможное решение

Средняя  скорость  машины  на  всём  пути  V_ср = L / T = 80 км/ч.  Тогда  на  первом участке пути машина имела скорость V₁ = 90 км/ч, а на втором – V₂ = 70 км/ч.

Среднюю скорость на всём пути можно выразить через длины участков пути и скорости на них:

откуда

Ответ: S = 70 км

Критерии оценивания

Найдена средняя скорость на всём пути	1 балл
Найдены скорости на первом и втором участках	2 балла
Средняя скорость на всём пути выражена через длины участков	4 балла
Получено выражение для длины плохого участка	2 балла
Получено численное значение для длины плохого участка	1 балл

Задача 2

На  середину  плоской  льдины  толщиной  H = 60 см,  плавающей  в  воде,  ставят маленький  медный  кубик,  в  результате  чего  глубина  погружения  льдины увеличивается  на  Δh = 0,5 см.  Чему  станет  равна  глубина H_п  погружения  этой льдины, если на её середину вместо медного кубика поставить железный кубик с вдвое  большей  стороной?  Плотность  льда  ρ_л = 900  кг/м³,  плотность  воды ρ_в = 1000  кг/м³,  плотность  меди  ρ_м = 8900 кг/м³,  плотность  железа ρ_ж = 7800 кг/м³.

Возможное решение

В отсутствие кубиков сила тяжести, действующая на льдину, уравновешивается силой  Архимеда.  Над  водой  выступает  часть  льдины  высотой  h = H/10 = 6 см.

Это следует из условия плавания:

S∙H∙ρ_л = S∙ρ_в∙g∙(H-h),

где S – площадь льдины.

Сила  тяжести,  действующая  на  кубик,  уравновешивается  добавочной  силой Архимеда.  Запишем  условия  равновесия  только  для  добавочных  сил.  Для медного кубика:  S∙Δh∙ρ_{в =} ρ_м ∙a³∙g. Для железного кубика:  S∙ΔH∙ρ_в∙g ₌ ρ_ж ∙8a³∙g, где ΔH – добавочная  глубина  погружения  льдины  с  железным  кубиком.  Разделив  одно уравнение на другое, получим:

Отсюда H_п = (H – h) + ΔH = 57,5 см.

Это значение меньше толщины льдины, следовательно, она не утонет.

Критерии оценивания

Записано условие плавания льдины без кубиков	1 балл
Найдена высота выступающей части h (или глубина погружения)	2 балла
Записаны условия равновесия для плавания с кубиками (по 1 баллу)	2 балла
Правильно определено отношение масс кубиков	2 балла
Получено  выражение  для  добавочной  глубины  погружения  ΔH  льдины с железным кубиком	2 балла
Получено численное значение для новой глубины погружения льдины	1 балл

Задача 3

Рисунок 3.1

Сосуды,  частично  заполненные  ртутью,  над  которой находится  воздух,  сообщаются  трубками.  Левый верхний сосуд и верхняя трубка открыты в атмосферу. Ртуть  по  трубкам  не  перетекает.  Найдите  давление воздуха  в  точке  А,  ответ  выразите  в  мм рт. ст.

Определите  высоту  L  столба  ртути  в  верхней  трубке. Высота  h = 5  см.  Атмосферное  давление p₀ = 760 мм рт. ст.

Возможное решение

Так  как  жидкость  в  системе  находится  в  равновесии, можно  связать  друг  с  другом  гидростатические  давления  на  разных  глубинах.

Давление воздуха в нижнем сосуде равно давлению на поверхности граничащей с ним ртути: p₁ = p₀ + 8 ρ∙g∙h = 1160 мм рт. ст. (здесь ρ – плотность ртути). Такое же давление воздуха и в правом верхнем сосуде (то есть в точке А).

На  поверхности  жидкости  в  среднем  сосуде  давление  равно p₂ = p₀ + 11 ρ∙g∙h,  но иначе его можно выразить через высоту L следующим образом:  p₂ = p₀ +  ρ∙g∙(L + 4h)

Отсюда L = 7h = 35 см.

Ответ: L = 35 см

Задача 4

В калориметре смешали десять порций воды. Первая порция имела массу m = 1 г и температуру  t = 1 °С, вторая – массу 2m и температуру 2t, третья – 3m и 3t, и так далее, а десятая – массу 10m и температуру 10t. Определите установившуюся температуру смеси. Потерями теплоты пренебречь.

Возможное решение

Так  как  по  условию  система  теплоизолирована,  воспользуемся  законом сохранения  энергии.  Определим  количество  теплоты,  которое  выделится  при остывании всех порций воды до 0 °С.

Q = cmt + 2m∙c∙2t + … + 10m∙c∙10t = 385 cmt

Это  количество  теплоты  пустим  на  нагревание  всей  воды,  имеющей  массу m + 2m + … + 10m = 55m от 0 °С до искомой температуры t_x: Q = 55cmt_x = 385 cmt, откуда  t_x = 7 °С.

Ответ: t_x = 7 °С

Критерии оценивания

Составлено верное уравнение теплового баланса (в любом виде)	5 баллов
Получено выражение для установившейся температуры	3 балла
Найдено численное значение установившейся температуры	2 балла

Общие рекомендации по оцениванию работы

• За каждое верно выполненное действие баллы складываются.
• При  арифметической  ошибке (в  том  числе  ошибке  при  переводе  единиц измерения) оценка снижается на 1 балл.
• Максимум за 1 задание – 10 баллов.
• Всего за работу – 40 баллов.

olimpiadnye-zadanija.ru

Олимпиада по физике с решениями

8 класс

1. При помощи подвижного блока груз массой 20 кг был поднят на высоту 5 м. Определите КПД механизма, если к концу троса было приложено усилие 200 Н.

Решение

Для определения КПД необходимо найти полезную и совершенную работы. Полезная работа, необходимая для подъема груза, равна , где. Тогда . Совершенная работа определяется по формуле , где s – перемещение веревки. Так как используется подвижный блок, то согласно «золотому правилу механики» . Тогда . КПД найдем по формуле . Рассчитаем:

Критерий оценивания (по 1 баллу)

1)  Определение силы тяжести груза.

2)  Определение полезной работы, необходимой для подъема груза.

3)  Определение перемещения веревки.

4)  Определение совершенной работы.

5)  Записана формула для КПД.

6)  Расчет КПД.

2.  Дайте физическое обоснование пословице: «Коси коса пока роса, роса долой и мы домой».

Решение

Роса увеличивает массу стебля. Поэтому при ударе косой он в меньшей степени изгибается, и коса сразу срезает его.

Роса создает смазку и уменьшает силу трения, когда при обратном движении косы она скользит по траве.

Критерий оценивания (по 1 баллу)

1)  Установлена зависимость изменения скорости частей стебля от их массы.

2)  Установлена зависимость деформации стебля от изменения скорости его частей.

3)  Установлена зависимость результата действия силы от деформации стебля.

4)  Установлена зависимость силы трения от смазки.

5)  Установлено возникновение трения при обратном движении косы.

6)  Установлено скольжение косы по траве.

3.  Во льдах Арктики в центре небольшой плоской льдины стоит белый медведь массой m = 700 кг. Какой массы должна быть льдина, чтобы медведь не замочил своих лап?

Решение

Чтобы медведь не замочил лап, льдина должна быть на плаву, погрузившись полностью в воду. При этом сила тяжести, действующая на льдину с медведем, равна выталкивающей силе, действующей на льдину, т. е. FT1+FT2=FA, где . Объем льдины V можно определить по формуле .где mл и ρл – масса и плотность льдины. Сила тяжести, действующая на льдину с медведем равна . Применяя условие плавания тела, получим: . После алгебраических преобразований найдем массу льдины: . Расчеты дают:.

Критерий оценивания (по 1 баллу)

1)  Записано условие плавания тел.

2)  Записана формула для определения силы Архимеда.

3)  Определен объем круга.

4)  Записана формула для определения общей силы тяжести, действующей на круг с человеком.

5)  Получена расчетная формула для определения массы круга.

6)  Произведен расчет массы круга.

4.  Школьники побывали в музее-имении Л. Н. Толстого «Ясная поляна» и возвращались в Рязань на автобусах, которые ехали со скоростью v1 = 70 км/ч. Пошел дождь, и водители снизили скорость до v2 = 60 км/ч. Когда дождь кончился, до Рязани оставалось проехать S = 40 км. Автобусы поехали со скоростью v3 = 75 км/ч и въехали в Рязань в точно запланированное время. Сколько времени шел дождь? Чему равна средняя скорость автобуса? Для упрощения считайте, что автобусы в пути не останавливались.

Решение

Средняя скорость автобуса – это отношение пройденного пути к затраченному времени. Так как расстояние от «Ясной поляны» до Рязани из-за дождя не изменилось, и время, проведенное школьниками в автобусе, также не изменилось (потому что автобусы въехали в Рязань в точно запланированное время), то средняя скорость совпадает с начальной скоростью vср = 70 км/ч.

Пусть дождь шел в течение времени t. Тогда путь, пройденный за это время, составил v2·t. Время, за которое после дождя автобусы проехали оставшееся расстояние, равно S/v3. Ясно, что время, затраченное автобусами с момента начала дождя до прибытия в Рязань, должно равняться времени, которое потребовалось бы для преодоления того же расстояния с начальной скоростью v1:

.

Отсюда находим время, в течение которого шел дождь:

Критерий оценивания (по 1 баллу)

1)  Определена средняя скорость.

2)  Выражено время прохождения отдельных участков пути.

3)  Установлено равенство времени движения с момента начала дождя до прибытия в Рязань и времени, которое потребовалось бы для преодоления того же расстояния с начальной скоростью v1. (2 балла).

4)  Получена формула для расчета времени, в течение которого шел дождь.

5)  Расчет времени, в течение которого шел дождь.

9 класс

1.Найдите отношение масс спирта и бензина в смеси, удельная теплота сгорания которой q0=41 МДж/кг. Удельная теплота сгорания бензина, q1=44 МДж/кг, а удельная теплота сгорания спирта q2=26 МДж/кг.

Решение

Количество теплоты, выделяемое при сгорании смеси равно количеству теплоты, выделяемому при сгорании спирта и бензина, содержащихся в смеси, т. е. Q0=Q1+Q2. Смесь, сгорая, выделяет , бензин — , спирт . Тогда . Разделим обе части уравнения на m1 и получим . Расчет дают .

Критерий оценивания (по 1 баллу)

1.  Установлена связь между количествами теплоты, выделяемыми смесью, и компонентами её частей.

2.  Определена масса смеси как сумма масс её компонентов.

3.  Записаны формулы для количеств теплоты, выделенных при сгорании топлива.

4.  Выражена масса спирта или разделено уравнение на массу бензина.

5.  Получена формула отношения масс.

6.  Произведен расчет.

2.Сварочный аппарат присоединяют в сеть напряжением 380В медными проводами длиной 100 м и площадью поперечного сечения 50 мм2. Определите мощность сварочного аппарата, если сила тока в нем 125 А.

Удельное сопротивление меди равно 0,017 Ом мм2/м.

Решение.

Сопротивление проводов определяется по формуле . Напряжение на проводах равно Uп=IR. Тогда напряжение на сварочном аппарате Uc= U-Uп, и его мощность P=IUс, или

Произведенный расчет дает значение

Критерии оценивания (по 1 баллу)

1.  Определено сопротивление проводов

2.  Определено напряжение на проводах

3.  Определено напряжение на сварочном аппарате

4.  Определена мощность сварочного аппарата

5.  Получена расчетная формула

6.  Произведен расчет по формуле или по действиям.

3.Во льдах Арктики в центре небольшой плоской льдины площадью S = 70 м2 стоит белый медведь массой m = 700 кг. При этом надводная часть льдины выступает над поверхностью воды на высоту h = 10 см. На какой глубине под водой находится нижняя поверхность льдины? Плотность воды rв = 1000 кг/м3, плотность льда rл = 900 кг/м3.

Решение

Обозначим через x искомую глубину. Тогда масса льдины равна m=ρЛ∙V, где V=S(h+x). Сила тяжести, действующая на льдину с медведем, равна:

Fт =g[m + rлS(h + x)]. Она должна равняться силе давления воды на нижнюю поверхность льдины, находящуюся на глубине x (силе Архимеда): FА =rвgVп, где Vп=xS, поскольку льдина находится в состоянии равновесия. Отсюда получаем: . Произведенный расчет дает значение .

Критерии оценивания (по 1 баллу)

1.  Определена масса льдины

2.  Определена общая сила тяжести

3.  Определена сила Архимеда

4.  Применено условие плавания тел

5.  Получена расчетная формула

6.  Произведен расчет по формуле.

4. В калориметр с водой при температуре 20°С опустили тело массой 152 г при температуре 100°С. Температура поднялась до 30°С. Не вынимая тело, в сосуд налили 100 г воды при 100°С, при этом температура поднялась до 60°С. Определите удельную теплоемкость тела. Теплоемкостью калориметра не пренебрегать. Удельная теплоемкость воды 4200.

Решение

Калориметр с водой получают количество теплоты, равное , где С – теплоемкость калориметра, c, m – удельная теплоемкость и масса воды, находящейся в калориметре. Тело, опущенное в воду, отдает количество теплоты, равное , где c1, m1, t1 — удельная теплоемкость, масса и начальная температура тела. Запишем уравнение теплового баланса для первого процесса Q1+Q2=0, т. е.

(C+cm)(t-t0) = c1 m1 (t-t1). Отсюда можно выразить C+cm= (1).

После доливания горячей воды, которая отдаст количество теплоты, равное, где m2, t2 — масса и начальная температура горячей воды, а tk – конечная температура, содержимое калориметра получит количество теплоты, равное. Запишем уравнение теплового баланса для второго процесса Q3+Q4=0, т. е. (2).

Подставив первое выражение во второе, получим расчетную формулу:

. При расчете получим:

Критерии оценивания (по 1 баллу).

1.  Записаны уравнения количеств теплоты, которые получат калориметр с водой, и отдаст тело, опущенное в воду.

2.  Записано уравнение количества теплоты, которое отдаст после доливания горячая вода.

3.  Записано уравнение количества теплоты, которое получит после доливания горячей воды содержимое калориметра.

4.  Записано уравнение теплового баланса для первого и второго процессов.

5.  Получена расчетная формула.

6.  Произведен расчет по формуле.

10 класс

1. Мотоциклист, начав движение из состояния покоя, едет с постоянным ускорением 0,8 м/с2. Какой путь он пройдет за десятую секунду своего движения.

Решение

I способ

За десятую секунду мотоциклист прошел путь, равный разности путей, пройденных за десять и девять секунд, т. е. S =S10 – S9. Поскольку V0 = 0, ; , где t10 = 10 c, а t9 = 9 с. Тогда При расчете получим: S = 9,5∙0,8 = 7,6 (м).

II способ

Путь, пройденный мотоциклистом за десятую секунду, можно определить так: S = Vср∙t, где t=1 с, а Vср = , так как движение равноускореное.

V = at10 – скорость, приобретенная к концу десятой секунды,

V0 = at9 — скорость, приобретенная к концу девятой секунды, поскольку V0=0. Тогда . При расчете получим: S = 9,5∙0,8 = 7,6 (м).

Критерии оценивания (по 1 баллу).

I способ

1.  Выражение пути, пройденного мотоциклистом за 10-ю секунду через пути, пройденные за десять и девять секунд. (2 балла)

2.  Определение пути, пройденного за 10 с.

3.  Определение пути, пройденного за 9 с.

4.  Получение расчетной формулы.

5.  Произведен расчет по формуле или по действиям.

II способ (по 1 баллу)

1.  Выражение пути, пройденном мотоциклистом за 10-ю секунду через среднюю скорость.

2.  Определение средней скорости равноускоренного движения.

3.  Определение начальной скорости на последней секунде.

4.  Определение конечной скорости на последней секунде.

5.  Получена расчетная формула

6.  Произведен расчет по формуле или по действиям.

2. Найдите отношение масс спирта и бензина в смеси, удельная теплота сгорания которой q0=41 МДж/кг. Удельная теплота сгорания бензина, q1=44 МДж/кг, а удельная теплота сгорания спирта q2=26 МДж/кг.

Решение

Количество теплоты, выделяемое при сгорании смеси равно количеству теплоты, выделяемому при сгорании спирта и бензина, содержащихся в смеси, т. е. Q0=Q1+Q2. Смесь, сгорая, выделяет , бензин — , спирт . Тогда . Разделим обе части уравнения на m1 и получим . Расчет дают .

Критерий оценивания

1.  Установлена связь между количествами теплоты, выделяемыми смесью, и компонентами её частей.

2.  Определена масса смеси как сумма масс её компонентов.

3.  Записаны формулы для количеств теплоты, выделенных при сгорании топлива.

4.  Выражена масса спирта или разделено уравнение на массу бензина.

5.  Получена формула отношения масс.

6.  Произведен расчет.

3. Моток проволоки имеет сопротивление 1000 Ом. Максимальный ток, который выдерживает данная проволока, равен 1А. Какой максимальной тепловой мощности нагреватель можно изготовить из данной проволоки, если он будет включаться в розетку с напряжение 220В.

Решение

Максимальная тепловая мощность нагревателя опреднляется по формуле: , Минимальное сопротивление нагреватель будет иметь, если проводники, из которых он состоит соединить параллельно, т. е. , где R1 – сопротивление каждого из n кусков проволоки, которые соединены параллельно. Если моток разрезали на n частей, то сопротивление одной проволоки равно Тогда Т. к. извесен максимальный ток, который выдерживает данная проволока, то сила тока в нагревателе будет равна и , тогда .

т. е моток проволоки нужно разрезать на части.

Тогда .

Критерии оценивания (по 1 баллу).

1.  Записана формула площади с анализом max значения.

2.  Выяснение условий минимальности R. (2 балла).

3.  Учёт max значения тока в проволоке.

4.  Определения числа кусков, соединённых параллельно.

5.  Расчёт max мощности.

4.  В калориметр с водой при температуре 20°С опустили тело массой 152 г при температуре 100°С. Температура поднялась до 30°С. Не вынимая тело, в сосуд налили 100 г воды при 100°С, при этом температура поднялась до 60°С. Определите удельную теплоемкость тела. Теплоемкостью калориметра не пренебрегать. Удельная теплоемкость воды 4200.

Решение

Калориметр с водой получают количество теплоты, равное , где С – теплоемкость калориметра, c, m – удельная теплоемкость и масса воды, находящейся в калориметре. Тело, опущенное в воду, отдает количество теплоты, равное , где c1, m1, t1 — удельная теплоемкость, масса и начальная температура тела. Запишем уравнение теплового баланса для первого процесса Q1+Q2=0, т. е.

(C+cm)(t-t0) = c1 m1 (t-t1). Отсюда можно выразить C+cm= (1).

После доливания горячей воды, которая отдаст количество теплоты, равное, где m2, t2 — масса и начальная температура горячей воды, а tk – конечная температура, содержимое калориметра получит количество теплоты, равное. Запишем уравнение теплового баланса для второго процесса Q3+Q4=0, т. е. (2).

Подставив первое выражение во второе, получим расчетную формулу:

. При расчете получим:

Критерии оценивания (по 1 баллу).

1.  Записаны уравнения количеств теплоты, которые получат калориметр с водой, и отдаст тело, опущенное в воду.

2.  Записано уравнение количества теплоты, которое отдаст после доливания горячая вода.

3.  Записано уравнение количества теплоты, которое получит после доливания горячей воды содержимое калориметра.

4.  Записано уравнение теплового баланса для первого и второго процессов.

5.  Получена расчетная формула.

6.  Произведен расчет по формуле.

11 класс

1.  Груз массой m лежит на клине с углом наклона . С каким ускорением необходимо перемещать клин по горизонтальной поверхности, чтобы груз начал скользить по клину вверх? Коэффициент трения между грузом и поверхностью клина равен 0,1.

Решение

До скольжения сила трения покоя направлена вверх вдоль наклонной плоскости и не превышает максимального значения силы трения покоя, т. е.

Найдем значение ускорения а0. при котором груз еще не скользит по клину вверх при перемещении клина с ускорением по горизонтальной поверхности, По второму закону Ньютона:

.

Перейдя к проекциям на координатные оси и дописав уравнение для силы трения, получим:

Решая полученную систему уравнений, найдем а0:

Скольжение начнется при , т. е.

При расчете получим:

Критерии оценивания (по 1 баллу).

1.  Представлен чертеж с указанием сил и выбором системы отсчета.

2.  Определены условия скольжения и покоя, значение силы трения.

3.  Записан второй закон Ньютона в векторной форме.

4.  Записан второй закон Ньютона в проекциях на координатные оси.

5.  Решение полученной системы уравнений и неравенств.

6.  Произведен расчет по формуле.

2. С одноатомным газом совершен цикл, изображенный на рисунке 2.

Определите КПД цикла,

P

5p0 2 3

p0 1

0 V0 2V0 V

Рис. 2

Решение

КПД цикла определяется по формуле: .

Работа, совершенная газом, численно равна площади треугольника: .

Найдём, в каких процессах газ получает тепло:

1-2: , т. е. .

Температура возрастает, следовательно, Q поглощается.

2-3: p – const, V3>V2T3>T2 – Q поглощается.

3-1: V – const, p3>p1 T3>T1 — Q выделяется.

Таким образом, тепло полученное газом, равно: .

Из первого закона термодинамики

и .

Найдем изменение внутренней энергии одноатомного газа в процессе 1 — 2 — 3: , т. к. по закону Менделеева-Клапейрона .

Работа, совершенная газом на участке 1 — 2, численно равна площади трапеции

,

а на участке 2-3 равна площади прямоугольника ,

Тогда и

.

Критерии оценивания (по 1 баллу).

1.  Анализ процессов с указанием направления теплопередачи.

2.  Применение 1-го закона термодинамики для нахождения Q12 и Q23.

3.  Нахождение изменения внутренней энергии в этих процессах.

4.  Нахождение работы газа , .

5.  Определение работы, совершённой газом в циклическом процессе.

6.  Нахождения количества теплоты, полученной газом и расчёт КПД цикла.

3. Для зарядки конденсатора собрали электрическую цепь по следующей схеме (рис.3) и замкнули ключ. После зарядки энергия, запасенная конденсатором, оказалась равной 5 Дж. Сколько энергии выделилось в виде тепла в цепи?

E

R K

C

Рис. 3

Решение

После зарядки напряжение на конденсаторе равно U=E., а заряд q=cU=cE. Тогда энергия, запасенная конденсатором, будет равной .

Источник тока совершил работу по перемещению заряда .

С другой стороны, по закону сохранения энергии — энергии, выделившаяся в виде тепла в цепи. Подставляя соответствующие значения в формулу, получим .

Таким образом .

Критерии оценивания (по 1 баллу).

1.  Формула энергии конденсатора.

2.  Определение соотношения между напряжением на конденсаторе после окончания зарядки и E источника тока.

3.  Применение закона сохранения энергии в виде A=Q+Wc.

4.  Определение полной работы источника тока при зарядке.

5.  Определение заряда конденсатора.

6.  Определение количества теплоты, выделенной в цепи.

4. Моток проволоки имеет сопротивление 1000 Ом. Максимальный ток, который выдерживает данная проволока, равен 1А. Какой максимальной тепловой мощности нагреватель можно изготовить из данной проволоки, если он будет включаться в розетку с напряжение 220В.

Решение

Максимальная тепловая мощность нагревателя опреднляется по формуле: , Минимальное сопротивление нагреватель будет иметь, если проводники, из которых он состоит соединить параллельно, т. е. , где R1 – сопротивление каждого из n кусков проволоки, которые соединены параллельно. Если моток разрезали на n частей, то сопротивление одной проволоки равно Тогда Т. к. извесен максимальный ток, который выдерживает данная проволока, то сила тока в нагревателе будет равна и , тогда .

т. е моток проволоки нужно разрезать на части.

Тогда .

Критерии оценивания (по 1 баллу).

1. Записана формула площади с анализом max значения.

2. Выяснение условий минимальности R. (2 балла).

3. Учёт max значения тока в проволоке.

4. Определения числа кусков, соединённых параллельно.

5. Расчёт max мощности.

fiziku5.ru