Итоговая контрольная работа в 8 классе по математике – Итоговая контрольная работа по математике 8 класс в формате ОГЭ
Итоговая контрольная работа по математике для 8 класса
МАТЕМАТИКА
(оценка индивидуальных достижений обучающихся 8 класса за ___учебный год)
Итоговая контрольная работа по математике
I вариант
№1. Вычислите:
№2. Решите уравнение: . Если корней несколько, то в ответ запишите наибольший из корней.
№3. Укажите решение неравенства:
(2,5 ; +∞) 3) [ 2,5 ; + ∞)
(- ∞ ; 2,5] 4) ( — ∞ ; 2,5 )
№4. Решите уравнение: =
№5. Катеты прямоугольного треугольника равны 6 и 8. Найдите гипотенузу.
№6. Найдите среднюю линию трапеции, если её основания равны 16 и 32.
№7*. Найдите площадь трапеции, изображённой на рисунке:
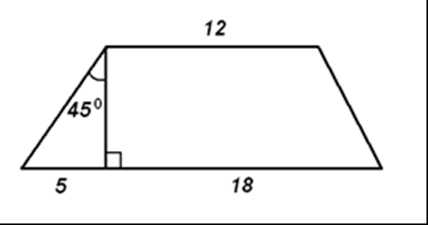
№7*. (для слепых обучающихся) Периметр параллелограмма равен 26. Одна сторона параллелограмма на 5 больше другой. Найдите меньшую сторону параллелограмма.
II вариант
№1. Вычислите:
№2. Решите уравнение: . Если корней несколько, то в ответ запишите наименьший из корней.
№3. Укажите решение неравенства:
( — ∞ ; 3,5 ) 3) [ 3,5 ; + ∞)
( — ∞ ; 3,5 ] 4) ( 3,5 ; + ∞)
№4. Решите уравнение:
№5. Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу данного треугольника.
№6. Найдите среднюю линию трапеции, если её основания равны 46 и 66.
№7*. Найдите площадь параллелограмма, изображённого на рисунке:
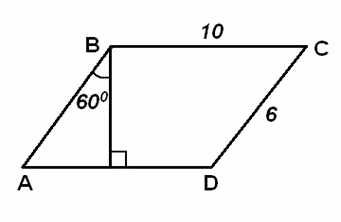
КОДИФИКАТОР
элементов содержания и требований к уровню подготовки обучающихся для оценки их индивидуальных достижений
Перечень умений, характеризующих достижение планируемых результатов
КОД | Проверяемые умения |
1. РАЗдел «Числа и вычисления» | |
1.1. | Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами, сравнивать действительные числа |
1.2. | Находить в несложных случаях значения степеней с целыми показателями и корней |
1.3. | Вычислять значения числовых выражений; переходить от одной формы записи чисел к другой |
2. РАЗдел «Алгебраические выражения» | |
2.1. | Составлять буквенные выражения и формулы по условиям задач, находить значения буквенных выражений, осуществляя необходимые подстановки и преобразования |
2.2. | Выполнять тождественные преобразования рациональных выражений |
3. РАЗдел «Уравнения и неравенства» | |
3.1. | Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним |
3.2. | Решать линейные неравенства с одной переменной |
3.3. | Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи |
4. РАЗДЕЛ «Координаты на прямой и плоскости» | |
4.1. | Различать числовые промежутки: интервал, отрезок, луч |
5.РАЗДЕЛ «Геометрия» | |
5.1. | Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) |
5.2. | Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи |
5.3. | Пользоваться основными единицами длины, площади. Осуществлять практические расчёты по формулам |
5.4. | Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений |
СПЕЦИФИКАЦИЯ
контрольной работы для оценки индивидуальных достижений обучающихся
Назначение КИМ
Работа предназначена для проведения процедуры промежуточного контроля ( уч. год)
Цель: проверка и оценка способности обучающихся применять полученные в процессе изучения математики знания для решения разнообразных задач учебного и практического характера
Документы, определяющие содержание КИМ
Содержание и структура итоговой работы по математике разработаны на основе следующих документов:
Федеральный компонент государственного стандарта основного общего образования по математике (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»)
Федеральный государственный образовательный стандарт основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования»)
Примерная общеобразовательная программа основного общего образования по математике, рекомендованная Минобрнауки РФ
Подходы к отбору содержания и разработке структуры КИМ. Структура КИМ
На основании документов, перечисленных в п.2 Спецификации, разработан кодификатор, определяющий в соответствии с требованиями ФГОС основного общего образования планируемые результаты освоения основной образовательной программы основного общего образования по математике для проведения итогового контроля индивидуальных достижений учащихся в образовательном учреждении.
В кодификатор включены планируемые результаты, которые относятся к блоку «Выпускник научится».
Полнота проверки обеспечивается за счет включения заданий, составленных на материале основных разделов курса: «Числа и вычисления»; «Алгебраические выражения»; «Уравнения и неравенства»; «Координаты на прямой и плоскости»; «Геометрия». Содержание заданий — проверка подготовки учащихся на базовом и повышенном уровнях сложности.
Распределение заданий КИМ по содержанию, видам умений и способам деятельности
Распределение заданий по основным разделам
Раздел курса | Число заданий |
Числа и вычисления Алгебраические выражения | 1 |
Уравнения и неравенства Координаты на прямой и плоскости | 3 |
Геометрия | 3 |
Итого: | 7 |
Распределение заданий КИМ по уровню сложности
Работа содержит две группы заданий, обязательных для выполнения всеми учащимися. Назначение первой группы – обеспечить проверку достижения учащимся уровня базовой подготовки, а второй – обеспечить проверку достижения повышенного уровня подготовки.
В работе используются виды заданий: с выбором верного ответа из нескольких предложенных, с развернутым ответом.
Уровень сложности заданий | № заданий | Число заданий | Виды заданий |
Базовый | 1 — 6 | 6 | Задания с развернутым ответом и задание с выбором верного ответов из предложенных вариантов. |
Повышенный | 7 | 1 | Задание с развернутым ответом |
Итого | 7 |
Система оценивания выполнения отдельных заданий и проверочной работы в целом
Критерии оценивания
Уровень | Минимальный балл | Максимальный балл | Критерии к баллу |
Базовый | 1 | 6 | Все верные ответы – 1 б. Нет верного ответа – 0 баллов. |
Повышенный | 1 — 2 | 2 | Задание считается выполненным верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то выставляется 1 балл. |
Шкала пересчёта первичного балла за выполнение проверочной работы в отметку по пятибалльной шкале
Уровни оценивания | Отметка | Количество баллов |
оптимальный | «5» | 8 |
допустимый | «4» | 6 — 7 |
критический | «3» | 3 — 5 |
недопустимый | «2» | 0 — 2 |
Результаты проверочной работы признаются удовлетворительными в случае, если обучающийся получил отметку не ниже удовлетворительной («3»).
Время выполнения варианта КИМ
Примерное время на выполнение заданий составляет:
1) для задания базового уровня сложности – 5 минут;
для задания повышенного уровня сложности – 10 минут;
На выполнение всей работы отводится 40 минут. (Для слепых обучающихся – 80 минут).
План варианта КИМ
Подробная информация о распределении заданий по разделам программы, по видам заданий и по уровню сложности приведена в плане работы.
Общий план работы
№ | Блок содержания | Объект оценивания | Код проверяемых умений | Тип задания | Уровень сложности | Максимальный балл за выполнение | Время выполнения (мин.) | ||
1 | Числа и вычисления Алгебраические выражения | Знание свойств степени с натуральным показателем. Умение возводить числа в степень. | 1.1 1.2 1.3 | РО | Б | 1 | 5 | ||
2 | Уравнения и неравенства Координаты на прямой и плоскости | Знание алгоритма решения квадратного уравнения, формул для нахождения дискриминанта и корней квадратного уравнения. Умение решать квадратное уравнение, выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами, находить значение квадратного корня, сравнивать действительные числа | 1.1 1.2 1.3 2.1 3.1 | РО | Б | 1 | 5 | ||
3 | Уравнения и неравенства Координаты на прямой и плоскости | Умение решать линейное неравенство с одной переменной. Знание свойств неравенств. Умение выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами. Различать числовые промежутки: интервал, отрезок, луч. | 1.1 1.3 3.2 4.1 | ВО | Б | 1 | 5 | ||
4 | Уравнения и неравенства Координаты на прямой и плоскости | Знание алгоритма решения дробного рационального уравнения. Умение решать дробное рациональное уравнение. Находить ОДЗ. Выполнять тождественные преобразования рациональных выражений. Умение решать линейное уравнение, выполнять арифметические действия с рациональными числами, проводить проверку корней. | 1.1 1.3 2.2 3.1 | РО | Б | 1 | 5 | ||
5 | Геометрия | Умение изображать геометрические фигуры; выполнять чертежи по условию задачи. Умение решать планиметрические задачи на нахождение геометрических величин (длины). Знание теоремы Пифагора и умение применять ее при решении планиметрической задачи. | 1.2 2.1 5.1 5.2 5.3 | РО | Б | 1 | 5 | ||
6 | Геометрия | Умение изображать геометрические фигуры; выполнять чертежи по условию задачи. Умение решать планиметрические задачи на нахождение геометрических величин (длины). Знание определения средней линии трапеции, формулы для ее нахождения и умение применять формулу при решении планиметрической задачи. | 1.2 2.1 5.1 5.2 5.3 | РО | Б | 1 | 5 | ||
7 | Геометрия | Умение решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей), распознавать геометрические фигуры на плоскости, различать их взаимное расположение, пользоваться основными единицами длины, площади, осуществлять практические расчёты по формулам. Умение проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, решать задачи алгебраическим методом, интерпретировать полученный результат. | 1.2 2.1 3.3 5.1 5.2 5.3 5.4 | РО | П | 2 | 10 | ||
ИТОГО | 8 баллов | 40 | |||||||
Условные обозначения: Б – базовый уровень сложности, П – повышенный уровень.
Тип задания: ВО – с выбором ответа, РО – с развернутым ответом.
Дополнительные материалы и оборудование
Дополнительные материалы для проведения работы: справочные материалы, выдаваемые на ГВЭ.
Условия проведения (требования к специалистам)
Проверочные работы проводят учитель класса и ассистент.
Контрольную работу анализирует учитель и ассистент, предоставляется протокол (анализ) проверочной работы.
Ключ
Уровень | № задания | Iвариант | II вариант |
Базовый | 1. 2. 3. 4. 5. 6. | 9 3 3 — 10 10 24 | 8 — 2 2 — 12,75 25 56 |
Повышенный | 7. | 87,5 4 (слепые учащиеся) | 30 |
Анализ проверочной работы в 8 классе
Число обуч-ся | % | |||||
Число обучающихся по списку | ||||||
Число обучающихся, выполнявших работу |
| 100 | ||||
| оптимальный уровень — 8 баллов | ||||||
допустимый уровень — 6 — 7 баллов | ||||||
критический уровень — 3- 5 баллов | ||||||
недопустимый уровень — 0-2 балла | ||||||
№ задания | Цель проверки | Допущенные ошибки | Число обуч-ся, допустивших ошибки | |||
1 | Знание свойств степени с натуральным показателем. Умение возводить числа в степень. | |||||
2 | Знание алгоритма решения квадратного уравнения, формул для нахождения дискриминанта и корней квадратного уравнения. Умение решать квадратное уравнение, выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами, находить значение квадратного корня, сравнивать действительные числа | |||||
3 | Умение решать линейное неравенство с одной переменной. Знание свойств неравенств. Умение выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами. Различать числовые промежутки: интервал, отрезок, луч. | |||||
4 | Знание алгоритма решения дробного рационального уравнения. Умение решать дробное рациональное уравнение. Находить ОДЗ. Выполнять тождественные преобразования рациональных выражений. Умение решать линейное уравнение, выполнять арифметические действия с рациональными числами, проводить проверку корней. | |||||
5 | Умение изображать геометрические фигуры; выполнять чертежи по условию задачи. Умение решать планиметрические задачи на нахождение геометрических величин (длины). Знание теоремы Пифагора и умение применять ее при решении планиметрической задачи. | |||||
6 | Умение изображать геометрические фигуры; выполнять чертежи по условию задачи. Умение решать планиметрические задачи на нахождение геометрических величин (длины). Знание определения средней линии трапеции, формулы для ее нахождения и умение применять формулу при решении планиметрической задачи. | |||||
7 | Умение решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей), распознавать геометрические фигуры на плоскости, различать их взаимное расположение, пользоваться основными единицами длины, площади, осуществлять практические расчёты по формулам. Умение проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, решать задачи алгебраическим методом, интерпретировать полученный результат. | |||||
Выводы:
Успеваемость (процент учащихся, имеющих оптимальный, допустимый и критический уровни): _________
Качество (процент учащихся, имеющих оптимальный и допустимый уровни): _______
Средний балл _________
Причины типичных ошибок:
Ф.И. учащихся | Допущенные ошибки | Коррекционные мероприятия |
Учитель: ___________________________
xn--j1ahfl.xn--p1ai
Методическая разработка по алгебре (8 класс) на тему: МЕТОДИЧЕСКАЯ РАЗРАБОТКА ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА по математике 8 КЛАССА
МЕТОДИЧЕСКАЯ РАЗРАБОТКА контрольной работы для проведения промежуточной аттестации в 8 классе
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ
ЗА КУРС 8 КЛАССА.
Вариант 1
1. Решите неравенство:
2. Упростите выражение: .
3. Постройте график функции . Найдите значения x, при которых функция принимает положительные значения.
4. Прямоугольный газон обнесён изгородью, длина которой 30 м. Площадь газона 56 м2 . Найдите длины сторон газона.
5. Решите неравенство : .
6. Основания равнобедренной трапеции равны 24 см и 40 см , а её площадь 480 см2 .Найдите периметр этой трапеции.
7. Диагонали ромба относятся как 2:3, а их сумма равна 25 см. Найдите площадь ромба.
8. Длина хорды окружности равна 30 см, а её расстояние от центра окружности до этой хорды равно 36 см. Найдите диаметр окружности.
Вариант 2
1. Решите неравенство: .
2. Упростить выражение: .
3. Постройте график функции . Найдите значения x, при которых функция принимает отрицательные значения.
4. Прямоугольный участок земли обнесён забором, длина которого 40 м. Площадь участка 96 м2. Найдите длины сторон участка.
5. Решите неравенство:
6. Основания равнобедренной трапеции равны 32 см и 42 см ,а её периметр равен 100 см. Найдите площадь этой трапеции.
7. Диагонали ромба относятся как 3:5, а их разность равна 8см.
Найдите площадь ромба.
8. В окружности, диаметр которой равен 50 см, проведена хорда такая, что расстояние от центра окружности до этой хорды равно 15 см. Найдите длину этой хорды.
№ п/п | Ответы варианта 1 | Ответы варианта 2 |
1 | Х | Х |
2 | 52 | 7 |
3 | Х > 3; Х –1 | (–3; –1 ) |
4 | 7 м; 8 м | 12 м; 8 м |
5 | Х > 1; Х –7 | (–4; –2) |
6 | 444 см2 | 98 см2 |
7 | 120 см2 | 75 см2 |
8 | 40 см | 78 см |
nsportal.ru
Итоговая контрольная работа по математике в 8 классе
Итоговая контрольная работа по математике в 8 классе
Демонстрационный вариант
Часть 1
Модуль «Алгебра»
Найти значение выражения

Ответ: _______________.
2. Какому промежутку принадлежит число 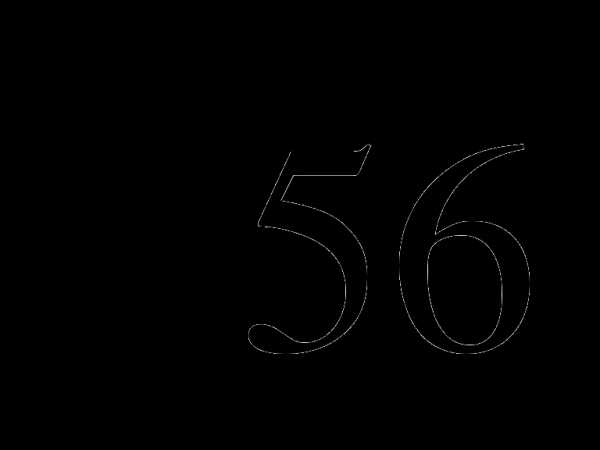 ?
?
1) [6;7]; 2) [7;8]; 3) [8;9]; 4) [9;10]
Ответ: _______________.
3. Решить квадратное уравнение: . В ответ записать меньший из корней.
Ответ: _______________.
4. Упростить выражение и найти его значение при х = 1,1; у = – 0,5.
Ответ: _______________.
5. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определить разность между наибольшей и наименьшей температурой воздуха за весь период.
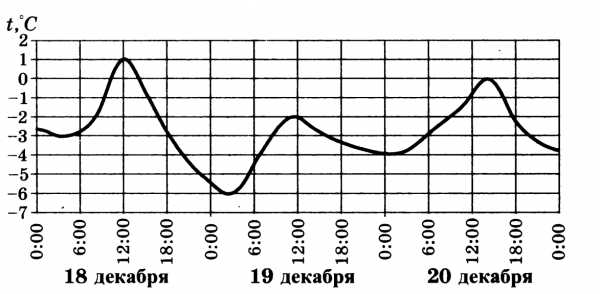
Ответ: _______________.
Модуль «Геометрия»
6. На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.
Ответ: _______________.
7. Найти тангенс угла А треугольника ABC,
изображенного на рисунке.
Ответ: _______________.
8. Какие из данных утверждений верны? Записать их номера.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Ответ: _______________.
9. Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определить высоту фонаря (в метрах).
Ответ: _______________.
Часть 2
Модуль «Алгебра»
10. Один из корней квадратного уравнения равен 5. Найти с и другой корень уравнения.
11. Первый рабочий за час делает на 13 деталей больше, чем второй, и выполняет заказ, состоящий из 208 деталей, на 8 часов быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Модуль «Геометрия»
12. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найти углы ромба.
Система оценивания
Верно выполненные задания 1 — 9 оцениваются одним баллом.
Задания, оцениваемые 1 баллом, считаются выполненными верно, если указан номер верного ответа (в заданиях с выбором ответа), или вписан верный ответ (в заданиях с кратким ответом), или правильно соотнесены объекты двух множеств и записана соответствующая последовательность цифр (в заданиях на установление соответствия).
Верно выполненные задания 10-12 оцениваются двумя баллами.
Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Максимальный балл за выполнение всей работы – 15. Из них – за модуль «Алгебра» — 9 баллов, за модуль «Геометрия» – 6 баллов.
Минимальный балл (оценка 3) — 5 баллов, набранные в сумме за выполнение заданий обоих модулей, при условии, что из них не менее 2 баллов получено по модулю «Геометрия».
Шкала перевода баллов в оценки
2
3
4
5
Общий балл
0 – 5
6 – 8
9 – 12
13 – 15
Время выполнения работы – 60 мин
1 вариант Ф.И.________________________
Часть 1
Найдите значение выражения

Ответ: _______________.
2. Между какими числами заключено число 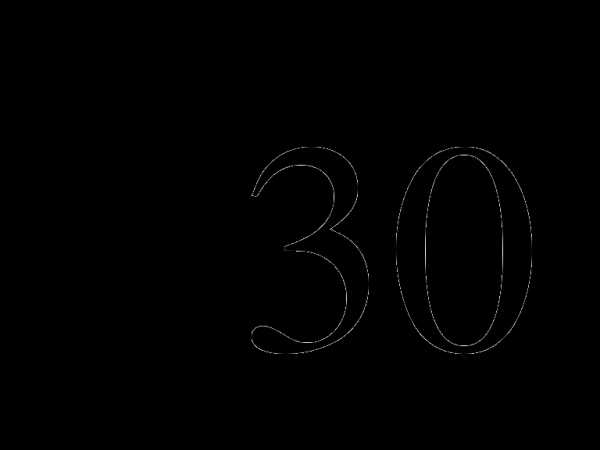 ?
?
1) 11 и 13; 2) 5 и 6; 3) 2 и 3; 4) 29 и 31.
Ответ: _______________.
3. Решите квадратное уравнение: . В ответ запишите меньший из корней.
Ответ: _______________.
4. Упростите выражение и найдите его значение при a = 6,5; b =0,7.
Ответ: _______________.
5. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите разность между наибольшей и наименьшей температурой воздуха за весь период.
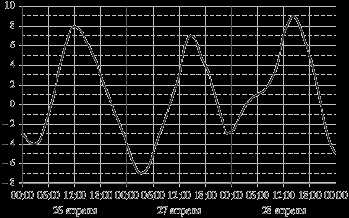
Ответ: _______________.
Модуль «Геометрия»
6. Найдите площадь трапеции.
Ответ: _______________.
7. Найдите тангенс угла С треугольника АВС, изображенного на рисунке.
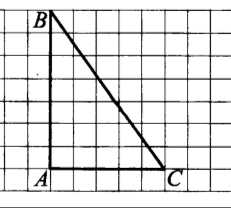
Ответ: _______________.
8. Какие из следующих утверждений верны?
1)
Площадь прямоугольного треугольника равна произведению катетов.
2)
Если в ромбе один из углов равен 90 градусам, то этот ромб является квадратом.
3)
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Ответ: _______________.
9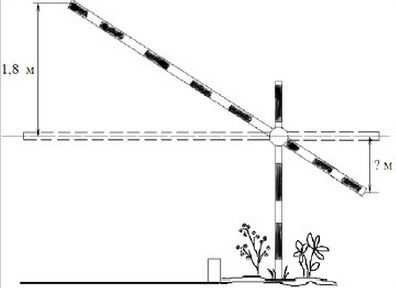 . Короткое плечо шлагбаума имеет длину м,
. Короткое плечо шлагбаума имеет длину м,
а длинное плечо — 3 м. На какую высоту (в метрах)
опустится конец короткого плеча, когда конец
длинного плеча поднимается на м?
Ответ: _______________.
Часть 2
Модуль «Алгебра»
10. Число 8 является корнем уравнения Найти значение p и второй корень уравнения.
11. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает каждый рабочий?
Модуль «Геометрия»
12. Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма.
Вариант 2 Ф.И.________________________
Часть 1
Модуль «Алгебра»
1. Найдите значение выражения 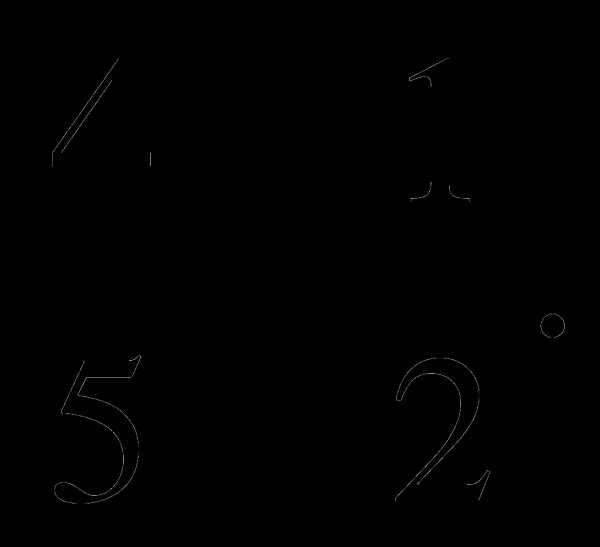
Ответ: _______________.
2. Какому промежутку принадлежит число 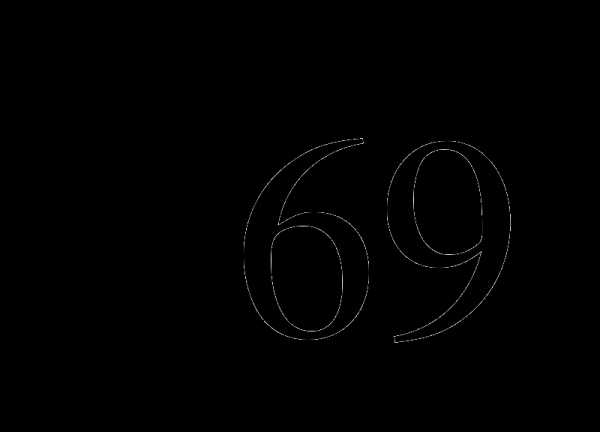 ?
?
1) [6;7]; 2) [7;8]; 3) [8;9]; 4) [9;10].
Ответ: _______________.
3. Решите квадратное уравнение В ответ запишите больший из корней.
Ответ: _______________.
4. Упростите выражение 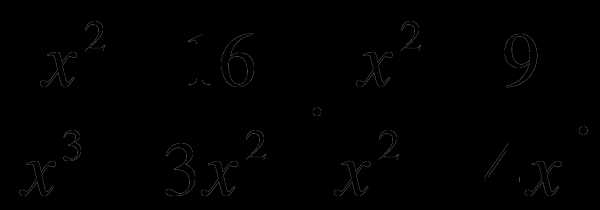 Найдите его значение при x = 2 .
Найдите его значение при x = 2 .
Ответ: _______________.
5. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значением температуры.
Ответ: _______________.
Модуль «Геометрия»
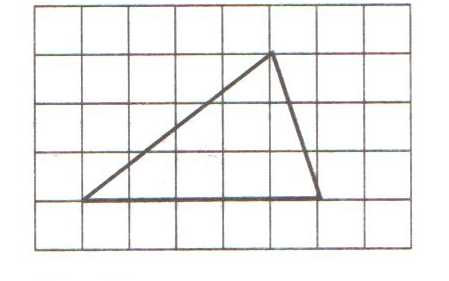
6. Найти площадь треугольника.
Ответ: _______________.
7. Найдите котангенс угла В треугольника АВС,
изображенного на рисунке.
Ответ: _______________.
8. Укажите в ответе номера верных утверждений.
1) Площадь параллелограмма равна произведению стороны на проведенную к ней высоту.
2) Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
3) Если в прямоугольнике диагонали перпендикулярны, то такой прямоугольник – квадрат.
Ответ: _______________.
9. На рисунке изображён колодец с «журавлём».
Короткое плечо имеет длину 2 м, а длинное плечо — 5 м.
На сколько метров опустится конец длинного плеча,
когда конец короткого поднимется на 1 м?
Ответ: _______________.
Часть 2
Модуль «Алгебра»
10. Число -12 является корнем уравнения Найти значение q и второй корень уравнения.
11. Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому 60 км он проезжает на 1 час быстрее второго велосипедиста. Найдите скорость каждого велосипедиста.
Модуль «Геометрия»
12. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Вариант 3 Ф.И.________________________
Часть 1
Модуль «Алгебра»
1. Найдите значение выражения 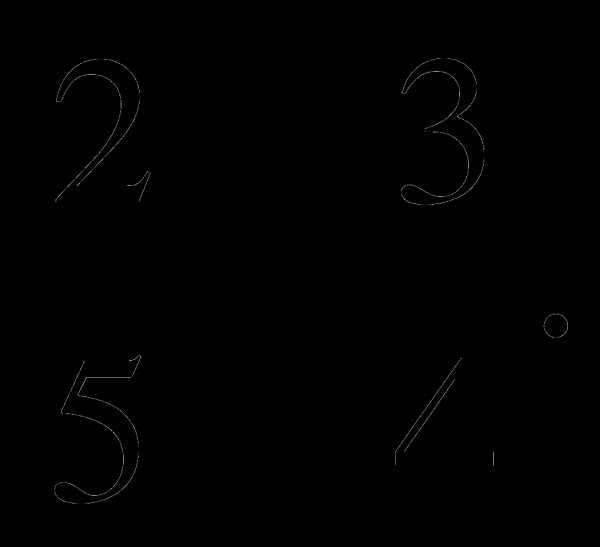
Ответ: _______________.
2. Между какими числами заключено число 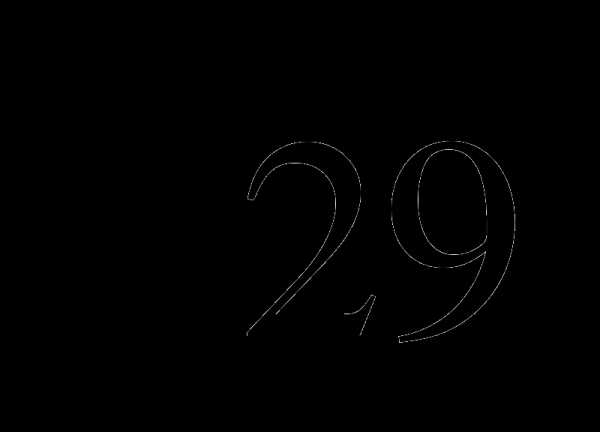 ?
?
1) 13 и 14; 2) 5 и 6; 3) 2 и 3; 4) 28 и 30.
Ответ: _______________.
3. Решите квадратное уравнение В ответ запишите больший из корней.
Ответ: _______________.
4. Упростите выражение 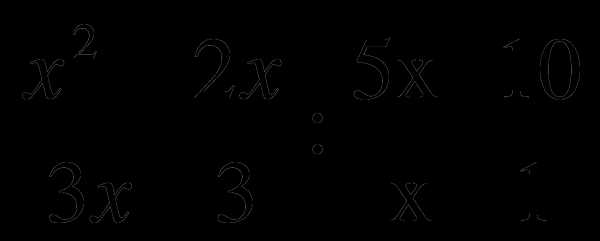 и найдите его значение при x = -55,5.
и найдите его значение при x = -55,5.
Ответ: _______________.
5. На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период.
Ответ: _______________.
Модуль «Геометрия»
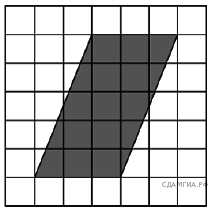
6. Найти площадь параллелограмма.
Ответ: _______________.
7. Найти котангенс угла А треугольника ABC,
изображенного на рисунке.
Ответ: _______________.
8. Укажите в ответе номера верных утверждений.
1) Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
2) Площадь треугольника равна произведению стороны на проведенную к ней высоту.
3) Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.
Ответ: _______________.
9. На рисунке изображён колодец с «журавлём».
Короткое плечо имеет длину 4 м, а длинное плечо — 6 м.
На сколько метров опустится конец длинного плеча,
когда конец короткого поднимется на 1 м?
Ответ: _______________.
Часть 2
Модуль «Алгебра»
10. Один из корней квадратного уравнения равен 5. Найдите с и другой корень уравнения.
11.Скорость первого автомобиля на 10 км/ч меньше скорости второго, поэтому 420 км он проезжает на 1ч дольше второго автомобиля. Найдите скорость каждого автомобиля.
Модуль «Геометрия»
12. Используя рисунок найдите угол 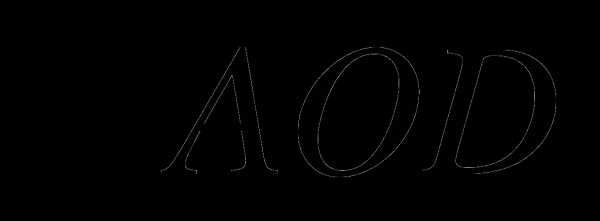
между диагоналями прямоугольника ABCD.
Ответы
1 вариант
1
2
3
4
5
6
7
8
9
10
11
12
ответ
0,7
2
3
0,1
16
28
1,4
23
0,6
-4; -4
20; 10
1,5
2 вариант
1
2
3
4
5
6
7
8
9
10
11
12
ответ
0,3
3
2
-1,25
9
7,5
3,5
13
2,5
36; -3
15; 12
5
3 вариант
1
2
3
4
5
6
7
8
9
10
11
12
ответ
1,15
2
4
-3,7
10
15
2,5
13
1,5
-8; 3
60; 70
110
infourok.ru
Итоговая контрольная работа по математике для 8 класса
Кодификатор требований к уровню подготовки обучающихся для проведения контрольной работы за 2015-2016 учебный год по математике (Кодификатор планируемых результатов) (КПРО)
Кодификатор требований к уровню подготовки по математике составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»).
В первом столбце таблицы указаны коды разделов, на которые разбиты требования к уровню подготовки по математике. Во втором столбце указан код умения, для проверки которого создаются контрольные задания. В третьем столбце сформулированы требования к уровню подготовки восьмиклассников.
Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы3.2
Решать линейные и квадратные неравенства с одной переменной и их системы.
3.3
Применять графические представления при решении уравнений, систем, неравенств.
3.4
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи.
4
Уметь строить и читать графики функций
4.1
Определять координаты точки плоскости, строить точки с заданными координатами.
4.2
Определять значение функции по значению аргумента при различных способах задания функции, решать обратную задачу.
4.3
Определять свойства функции по её графику (промежутки возрастания, убывания, промежутки знакопостоянства, наибольшее и наименьшее значения).
4.4
Строить графики изученных функций, описывать их свойства.
4.5
Решать элементарные задачи, связанные с числовыми последовательностями.
4.6
Распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов прогрессий
5
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
5.1
Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей)
5.2
Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи.
5.3
Определять координаты точки плоскости; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.
6
Уметь работать со статистической информацией, находить частоту и вероятность случайного события.
6.1
Извлекать статистическую информацию, представленную в таблицах, на диаграммах, графиках
6.2
Решать комбинаторные задачи путем организованного перебора возможных вариантов, а также с использованием правила умножения.
6.3
Вычислять средние значения результатов измерений.
6.4
Находить частоту события, используя собственные наблюдения и готовые статистические данные.
6.5
Находить вероятности случайных событий в простейших случаях.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели7.1
Решать несложные практические расчётные задачи; решать задачи, связанные с отношением, пропорциональностью величин, дробями.
7.2
процентами; пользоваться оценкой и прикидкой при практических расчётах; интерпретировать результаты решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых объектов.
7.3
Пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот. Осуществлять практические расчёты по формулам, составлять несложные формулы, выражающие зависимости между величинами.
7.4
Моделировать реальные ситуации на языке алгебры, составлять выражения, уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры.
7.4
Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимостей.
7.5
Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин
7.6
Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках.
7.7
Решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики.
7.8
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
Кодификатор
элементов содержания (КЭС) для проведения контрольной работы по математике в 8 классе.
Кодификатор элементов содержания для проведения контрольной работы по математике (далее -КЭС) является одним из документов, определяющих структуру и содержание контрольных измерительных материалов (далее — КИМ). Кодификатор является систематизированным перечнем требований к уровню подготовки учащихся и проверяемых элементов содержания, в котором каждому объекту соответствует определённый код.
Кодификатор элементов содержания по математике составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»),
В первом столбце таблицы указаны коды разделов и тем. Во втором столбце указан код элемента содержания, для которого создаются проверочные задания.
Кодраздела
Код
контролируемого элемента
Элементы содержания, проверяемые заданиями контрольной работы
1
Числа и вычисления
1.1
Натуральные числа
1.1.1
Десятичная система счисления. Римская нумерация
1.1.2
Арифметические действия над натуральными числами
1.1.3
Степень с натуральным показателем
1.1.4
Делимость натуральных чисел. Простые и составные числа, разложение натурального числа на простые множители
1.1.5
Признаки делимости на 2, 3, 5, 9, 10
1.1.6
Наибольший общий делитель и наименьшее общее кратное
1.1.7
Деление с остатком
1.2
Дроби
1.2.1
Обыкновенная дробь, основное свойство дроби. Сравнение дробей
1.2.2
Арифметические действия с обыкновенными дробями
1.2.3
Нахождение части от целого и целого по его части
1.2.4
Десятичная дробь, сравнение десятичных дробей
1.2.5
Арифметические действия с десятичными дробями
1.2.6
Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной
1.3
Рациональные числа
1.3.1
Целые числа
1.3.2
Модуль (абсолютная величина) числа
1.3.3
Сравнение рациональных чисел
1.3.4
Арифметические действия с рациональными числами
1.3.5
Степень с целым показателем
1.3.6
Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий
1.4
Действительные числа
1.4.1
Квадратный корень из числа
1.4.2
Нахождение приближенного значения корня
1.4.3
Запись корней с помощью степени с дробным показателем
1.4.4
Понятие об иррациональном числе. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби
1.4.5
Сравнение действительных чисел
Измерения, приближения, оценки
1.5
1.5.1
Единицы измерения длины, площади, объёма, массы, времени, скорости
1.5.2
Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире
1.5.3
Представление зависимости между величинами в виде формул
1.5.4
Проценты. Нахождение процента от величины и величины по её проценту
1.5.5
Отношение, выражение отношения в процентах
1.5.6
Пропорция. Пропорциональная и обратно пропорциональная зависимости
1.5.7
Округление чисел. Прикидка и оценка результатов вычислений. Выделение множителя — степени десяти в записи числа
Алгебраические выражения
2
Буквенные выражения (выражения с переменными)
2.1
2.1.1
Буквенные выражения. Числовое значение буквенного выражения
2.1.2
Допустимые значения переменных, входящих в алгебраические выражения
2.1.3
Подстановка выражений вместо переменных
2.1.4
Равенство буквенных выражений, тождество. Преобразования выражений
2.2.1
Свойства степени с целым показателем
2.2
Многочлены
2.3
2.3.1
Многочлен. Сложение, вычитание, умножение многочленов
2.3.2
Формулы сокращенного умножения: квадрат суммы и квадрат разности; формула разности квадратов
2.3.3
Разложение многочлена на множители
2.3.4
Квадратный трехчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители
2.3.5
Степень и корень многочлена с одной переменной
Алгебраическая дробь
2.4
2.4.1
Алгебраическая дробь. Сокращение дробей
2.4.2
Действия с алгебраическими дробями
2.4.3
Рациональные выражения и их преобразования
2.5.1
Свойства квадратных корней и их применение в вычислениях
2.5
Уравнения и неравенства
3
Уравнения
3.1
3.1.1
Уравнение с одной переменной, корень уравнения
3.1.2
Линейное уравнение
3.1.4
Решение рациональных уравнений
3.1.7
Система уравнений; решение системы
Неравенства
3.2
3.2.1
Числовые неравенства и их свойства
3.2.2
Неравенство с одной переменной. Решение неравенства
3.2.3
Линейные неравенства с одной переменной
Текстовые задачи
3.3
3.3.1
Решение текстовых задач арифметическим способом
3.3.2
Решение текстовых задач алгебраическим способом
Числовые последовательности
4
4.1.1
Понятие последовательности
4.1
Арифметическая и геометрическая прогрессии
Функции
Координаты на прямой и плоскости
6
Координатная прямая
6.1
6.1.1
Изображение чисел точками координатной прямой
6.1.2
Геометрический смысл модуля
6.1.3
Числовые промежутки: интервал, отрезок, луч
Декартовы координаты на плоскости
6.2
6.2.1
Декартовы координаты на плоскости; координаты точки
Геометрия
7
Геометрические фигуры и их свойства.
infourok.ru
Итоговая контрольная работа по математике 8 класс.
Итоговая контрольная работа по математике для 8 класса МБОУ «Конганурская средняя общеобразовательная школа»
Вариант 1
Часть 1
Решите квадратное уравнение:
х2 +1,5х = 0; (1 балл)
2х2 – 11х + 12 = 0. (1 балл)
Решите неравенство (1 балл)
Решите систему неравенств (1 балл)
Упростите выражение:
; (1 балл)
. (1 балл)
На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
(1 балл)
В треугольнике ABC угол C равен ,АВ = 30, ВС = 24 . Найдите cosA. (2 балла)
Упростите выражение . (1 балл)
Вычислите . (1 балл)
Часть 2
Упростите выражение . (2 балла)
Два велосипедиста одновременно отправились в 96-километровый пробег. Первый ехал со скоростью, на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. (3 балла)
Вариант 2
Часть 1
Решите квадратное уравнение:
х2 -5,7х = 0; (1 балл)
5х2 + 8х — 4 = 0. (1 балл)
Решите неравенство (1 балл)
Решите систему неравенств (1 балл)
Упростите выражение:
На клетчатой бумаге с клетками размером 1см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
(1 балл)
В треугольнике ABC угол C равен , АВ = 13, АС = 5 . Найдите tgA. (2 балла)
Упростите выражение . (1 балл)
Вычислите . (1 балл)
Часть 2
Упростите выражение . (2 балла)
Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. (3 балла)
Пояснения
к итоговой контрольной работе для 8класса
за 2014-2015 учебный год
Структура контрольной работы
Работа состоит из двух частей и содержит 10 заданий.
Часть I содержит 8 заданий базового уровня, причем две из них задачи по геометрии. Часть II содержит 2 задания, соответствующих уровню возможностей, но доступных учащимся с высоким уровнем математической подготовки, любящим занятия математикой. Это задания повышенной сложности – задания 2 части на экзамене в 9 классе.
Порядок проведения работы
На выполнение контрольной работы даётся 90 мин.
Оценивание
Правильное решение каждого из заданий 1-5,7,8 части I контрольной работы оценивается 1 баллом, задание 6 части 1 и задание 9 части 2 оценивается 2 баллами. Полное правильное решение задания 10 части 2 − 3 баллами оцениваются в 3 баллами.
Предполагается, что для получения положительной отметки необходимо преодолеть «порог», то есть набрать не менее восьми баллов за решение контрольной работы. Это отвечает минимальному уровню подготовки, подтверждающему освоение учеником 8 класса содержания основной общеобразовательной программы.
Нормы оценивания.
Для оценивания результатов выполнения работы применяются два количественных показателя: отметки «2», «3», «4», или «5» и рейтинг – сумма баллов за верно выполненные задания.
Оценка «2» выставляется, если ученик набрал менее 8 баллов.
Отметка «3» выставляется за 8 – 11 баллов.
Отметка «4» выставляется, если набрано от 12 до 14 баллов.
Для получения отметки «5» необходимо набрать 15-16 баллов.
С критериями оценивания и структурой работы необходимо ознакомить школьников до проведения итоговой работы. Текст работы выдаются каждому школьнику. Вывешивается за две недели до проведения работы демонстрационный вариант работы.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Примерные задания на итоговой контрольной работе по алгебре в 8 классе
Решите квадратное уравнение:
3х2 +4,5х = 0; (1 балл)
5х2 + 8х — 4 = 0. (1 балл)
Решите неравенство (1 балл)
Решите систему неравенств (1 балл)
Упростите выражение:
; (1 балл)
. (1 балл)
На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
(1 балл)
(1 балл)
В треугольнике ABC угол C равен , АВ = 35, ВС = 28 . Найдите cosA.
В треугольнике ABC угол C равен , АВ = 45, АС = 36 . Найдите tgА.
(2 балла)
Упростите выражение . (1 балл)
Вычислите . (1 балл)
Упростите выражение . (2 балла)
Два велосипедиста одновременно отправились в 195-километровый пробег. Первый ехал со скоростью, на 2 км/ч большей, чем скорость второго, и прибыл к финишу на 2 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. (3 балла)
Критерии оценок
Оценка «2» —менее 8 баллов
Оценка «3» — 8 -11 баллов
Оценка «4» — 12 -14 баллов
Оценка «5» — 15 -16 баллов
Литература
1. Макарычев Ю. Н., Миндюк Н.Г., Нешков К. И., Суворов С. Б. «Алгебра . 8 класс»: учеб. Для общеобразоват. Учреждений под ред. С. А. Теляковского-М.: Просвещение , 2009.
2. Макарычев Ю. Н., Миндюк Н.Г., Короткова Л. М Дидактические материалы по алгебре для 9 класса — М.: Просвещение , 2009.
3. Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 кл.
/Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.
– 3-е изд. – М.: Просвещение, 2008.
4. http://mathege.ru/or/ege/Main
Анализ итоговой контрольной работы по математике в 8 классе.
Май, 20, 2014 – 2015уч. г.
Критерии оценивания
Оценка «5» 15 — 16 баллов
Оценка «4» 12 — 14 баллов
Оценка «3» 8-11 баллов
Оценка «2» менее 8 баллов
На 5На 4
На 3
На 2
% качества
Учитель
Не знают формулу корней квадратного уравнения чел.Неверно подставляют числа в формулу корней квадратного уравнения чел.
При делении неравенства на отрицательное число чел.
При записи ответа при решении неравенства чел.
При раскрытии скобок чел.
При изображении графической модели решения неравенства чел.
При выборе и записи ответа при решении системы неравенств чел.
На применение формул сокращенного умножения чел.
На применение свойств квадратных корней чел.
Не знают формулу вычисления площади трапеции чел.
На применение теоремы Пифагора чел.
Не знают определение синуса, косинуса или тангенса острого угла прямоугольного треугольника чел.
На применение свойств степени с целым показателем в номер 7 чел.
На применение свойств степени с целым показателем в номер 8 чел.
На действия с алгебраическими дробями чел.
На применение формул сокращенного умножения в № 9 чел.
При составлении уравнения к задаче чел.
При решении дробно — рационального уравнения чел.
При выборе и записи ответа к решению задачи чел.
Учитель: ___________ / Войкова Р.Е./
infourok.ru
Итоговая контрольная работа по математике в 8 классе. Вариант 1. Часть I.
1) 1 и 0,8 2) -1 и -0,8 3) 1 и 0,6 4) -1 и -0,6
1)
1)
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник. 2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб. 3) Если один из углов, прилежащих к стороне параллелограмма, равен , то другой угол, прилежащий к той же стороне, равен . 4) Если сумма трех углов выпуклого четырехугольника равна , то его четвертый угол равен .
1) (-6; 6). 2) (6; +). 3) (-; -6). 4) (-; -6) (6; +). Итоговая контрольная работа по математике в 8 классе. Вариант 2. Часть I.
Ответ: ________________
1) 5 и — 3 2) 3 и – 5 3) 5 и 3 4) -5 и -3
1) 4(а+1) 2) 8(а2+1) 3) 4(а-1) 4) 8(а-1)
1) 2) 3) 4)
Ответ: _____________
1) 5,5 2) 5,5; 3) 5,5; 4) 5,5
1) (1; +). 2) (-; -1). 3) (-1; 1). 4) (-; -1) (1; +). | 10.Для каждой функции, заданной формулой укажите её график Формула А) y = х -1 Б) у = x2 – 1 В) у = — х+1 Г) ) у = — x2 + 1 График Часть 2
10.Для каждой функции, заданной формулой укажите её график Формула А) y = 2x2 – 4 Б) у = x – 4 В) у= х+4 График Часть 2
13.Расстояние между двумя пристанями по реке равно 21 км. Моторная лодка отправилась от одной пристани до другой и через 4 ч вернулась назад, затратив на стоянку 24 мин. Найдите собственную скорость моторной лодки, если скорость течения реки равна 2 км/ч. (4 балла) |
videouroki.net
Тест по алгебре (8 класс) на тему: Итоговая контрольная работа по математике 8 класс (в формате ОГЭ)
По теме: методические разработки, презентации и конспекты
Итоговая контрольная работа по математике 6 класс в формате ГИАДанный материал предназначен для проведения переводных экзаменов (итоговой контрольной работы в формате ГИА) по математики для учащихся 6 класса. Разработан по учебнику И.И.Зубарева, А.Г.Мордкович. Ра…
Итоговая контрольная работа по математике 5 класс в формате ГИАДанный материал предназначен для проведения переводных экзаменов (итоговой контрольной работы в формате ГИА) по математики для учащихся 5 класса. Разработан по учебнику И.И.Зубарева, А.Г.Мордкови…
Итоговая контрольная работа по математике 8 класс.Контрольная работа содержит задачи по алгебре и геометрии, составлена с использованием открытого банка задач ОГЭ и ЕГЭ….
Итоговая контрольная работа по математике 8 класс по материалам ОГЭ 1 вариантКонтрольная работа состоит из 5 варианто одинакового уровня сложности. Состоит из 8 заданий 1 части и одного задания 2 части. Контрольная работа расчитана на 45 минут. К контрольной работе прилагаются…
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА по математике 8 КЛАССАМЕТОДИЧЕСКАЯ РАЗРАБОТКА ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА по математике 8 КЛАССА…
итоговая контрольная работа по математике, 8 классработа состоит из трёх модулей : Алгебра, Геометрия и Реальная математика,к работе прилагается спецификация и кодиффикатор заданий….
Итоговая контрольная работа по математике 8 класс в формате ОГЭДанный материал представляет собой итоговую контрольную работу по математике ( алгебра и геометрия) за 8 класс. Контрольная работа состоит из двух частей с кратким ответом и представлением…
nsportal.ru


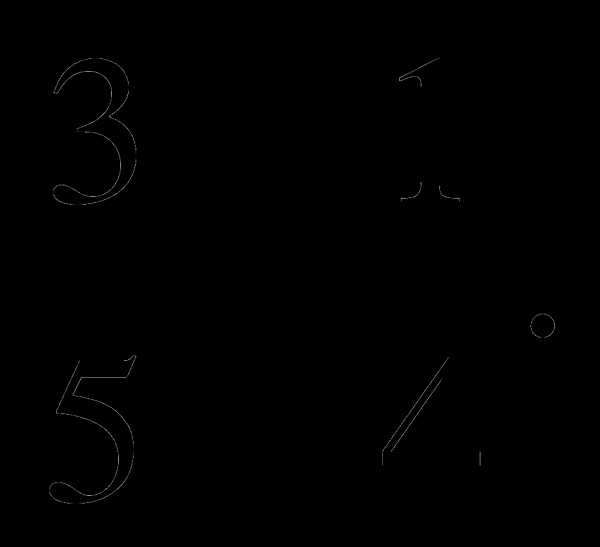
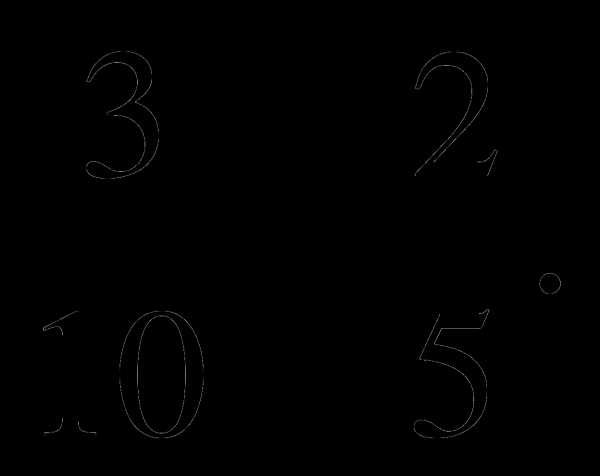
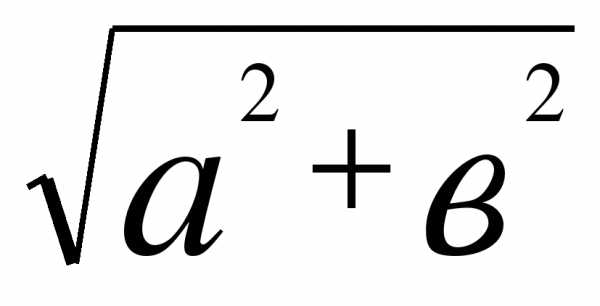 при а = 12 и в = -5 Ответ: ________________
при а = 12 и в = -5 Ответ: ________________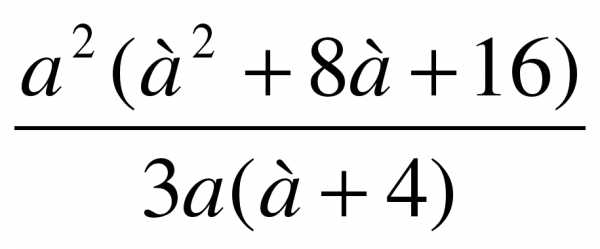 .
.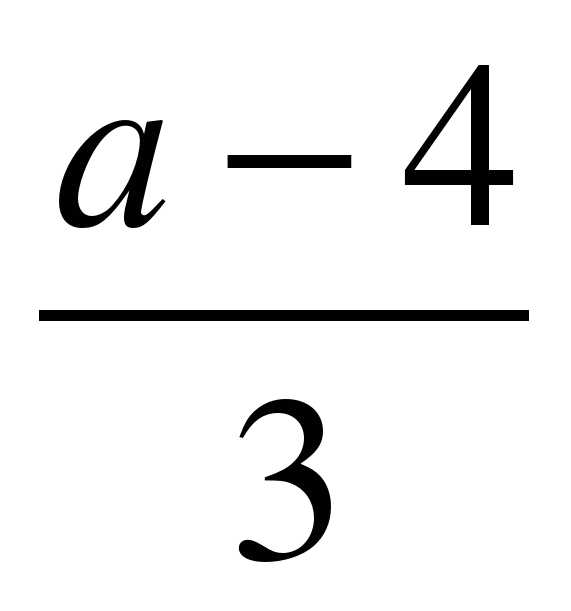 2)
2) 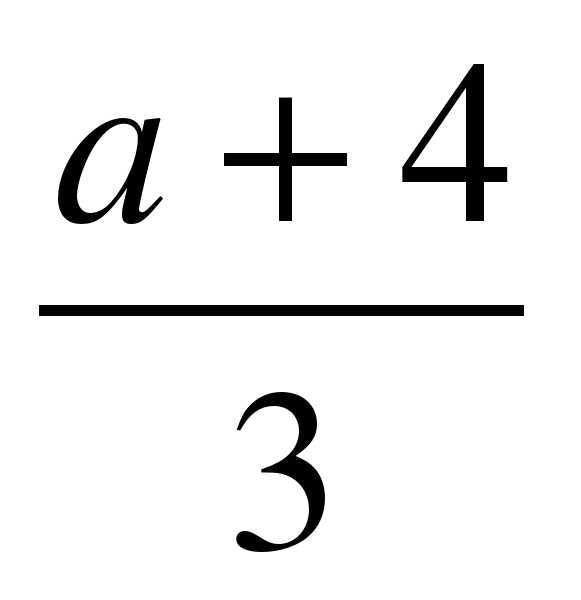 3)
3) 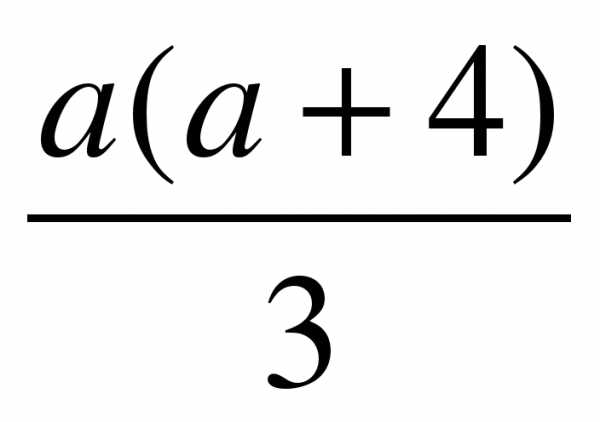 4)
4) 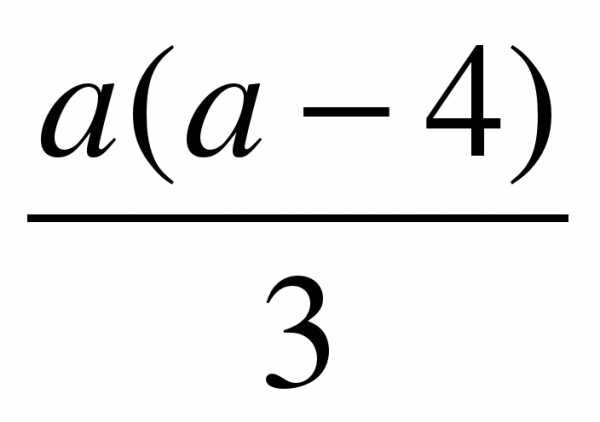
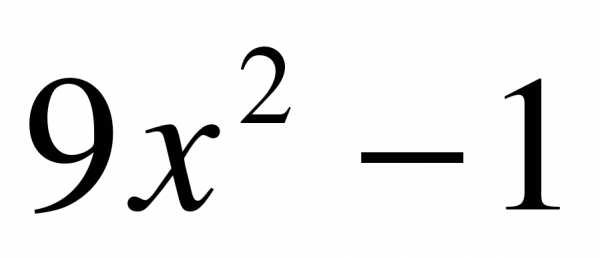 2)
2)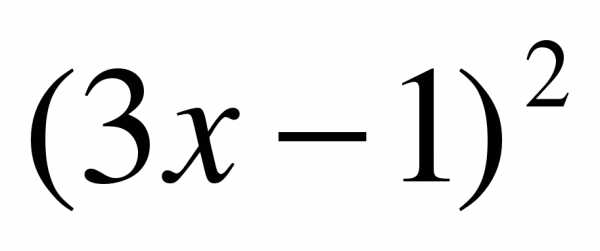 3)
3) 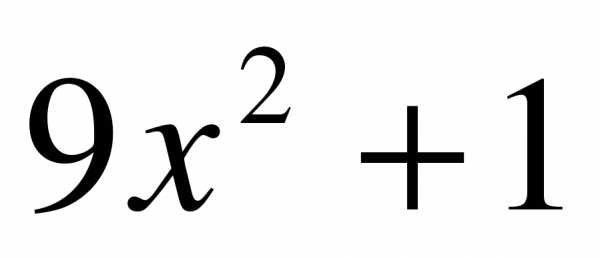 4)
4)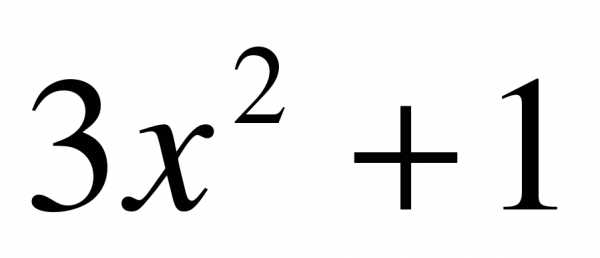
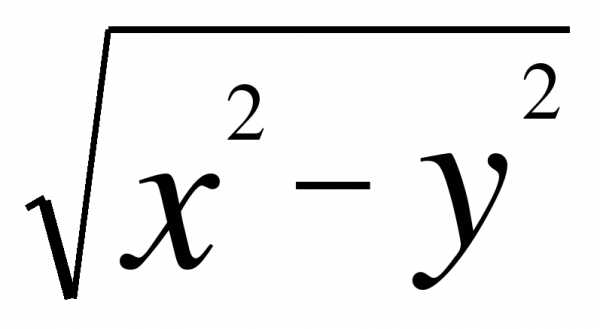 при х = 1,3 и у = 0,5.
при х = 1,3 и у = 0,5.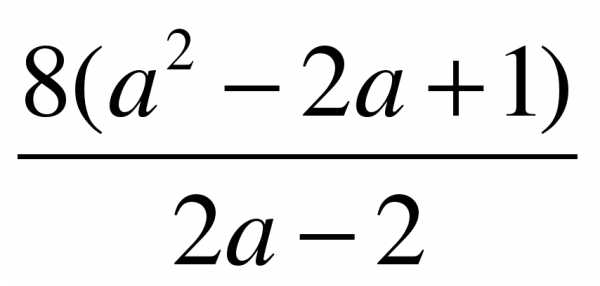 .
.