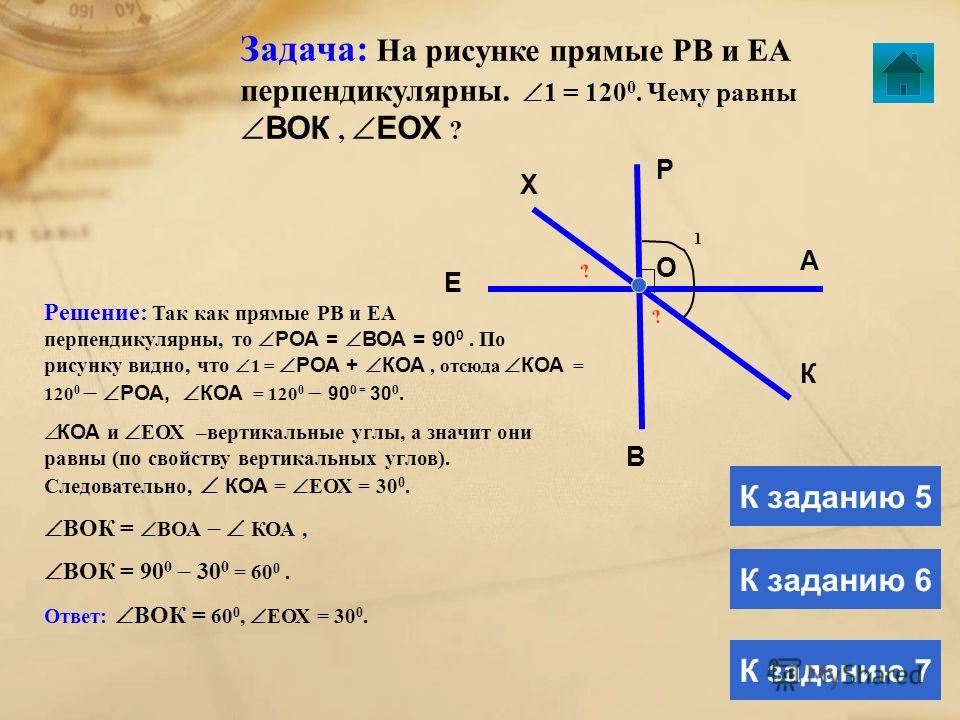
Урок геометрии перпендикулярные прямые 7 класс: Перпендикулярные прямые — урок. Геометрия, 7 класс.

Содержание

Перпендикулярные прямые | План-конспект урока по геометрии (7 класс) по теме:

Учитель ГБОУ школы-интерната № 28

Николаева Валентина Васильевна

Тема урока: «Перпендикулярные прямые» (ФГОС)

Учебник: «Геометрия 7-9», Л.С. Атанасян

Цели:

познакомить с определением перпендикулярных прямых
формировать и обосновать утверждение о двух прямых, перпендикулярных третьей
познакомить со способами построения на местности перпендикулярных прямых

Задачи:

создать условия для повторения понятий «смежные и вертикальные углы»
создать условия для введения понятия перпендикулярных прямых
формировать навык самостоятельного приобретения знаний
совершенствовать у учащихся навыки решения задач
расширять кругозор учащихся
воспитывать аккуратность, дисциплинированность, активность, умение

общаться, преодолевать трудности

развивать внимание, память, воображение, логическое мышление, умение

выделять главное, навыки самоконтроля

Тип урока: урок открытия нового знания

Методы обучения: проблемный, частично-поисковый

Ход урока:

Организационный момент (проверка готовности учащихся к уроку).
Актуализация опорных знаний:

Выясняем, удалось ли справиться с выполнением домашнего задания
Если большинство учащихся справились с домашним заданием, четырём

желающим предлагается показать свое решение №№ 61 (а, в, г), 64(б) на доске

устная работа

Совместно с ребятами, сидящими за партами, пытаемся устно ответить на следующие вопросы:

Каким – острым, тупым или прямым будет угол, смежный с углом в

300, 1300?

Сумма двух углов 2000. Смежные ли это углы?
Сумма двух углов 1800. Обязательно ли эти углы смежные?
Чему равен угол, если вертикальный с ним угол 340?
У двух углов общая вершина, каждый из них 600. Обязательно ли эти

углы вертикальные?

Один из четырёх углов, получившихся при пересечении двух прямых,

равен 1400. Чему равны остальные углы?

Стремимся, чтобы в обсуждении ответов на вопросы участвовало как можно больше ребят.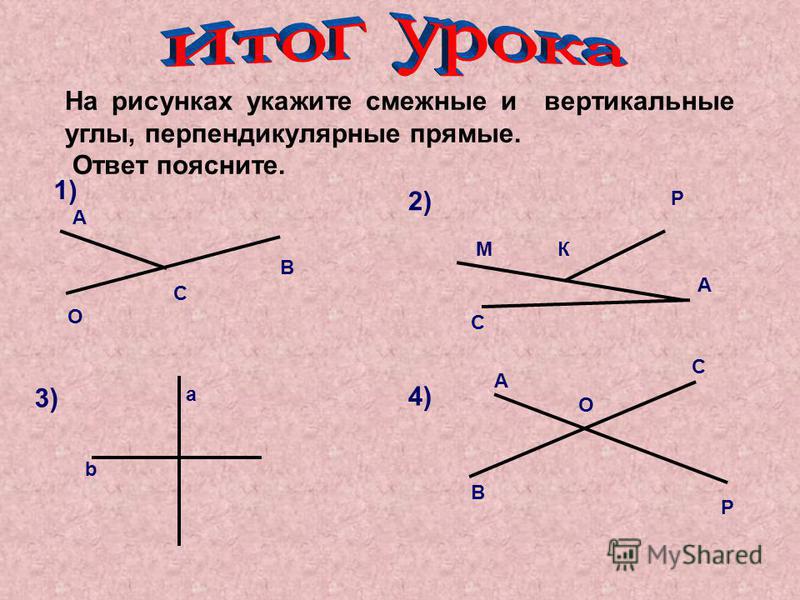 Для того чтобы в диалог вступали даже самые слабые ученики, ребятам предлагается проводить обсуждение в парах.

Совместно с учениками проверяем решение на доске.

Подробно разбираем решение задач, вызвавших затруднение дома (если таковые были).

Постановка проблемы:

Совместно с обучающимися класса рассматриваем рис. 42 учебника и

подводим их к самостоятельному обоснованию того факта, что, если при

пересечении двух прямых один из образовавшихся углов прямой, то и остальные углы прямые

Пытаемся ввести понятие перпендикулярных прямых

4. Объявление темы и цели урока:

Попробуйте сформулировать тему нашего урока («Перпендикулярные

прямые»).

Запишите в тетради.

Динамическая пауза

5. Построение новых знаний:

Фронтальная работа

Давайте попробуем сформулировать определение, какие прямые называются перпендикулярными?

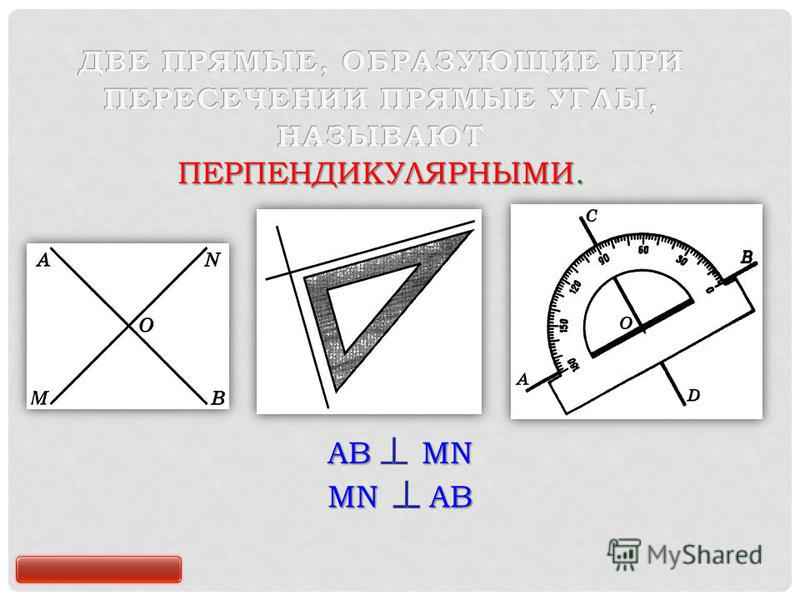
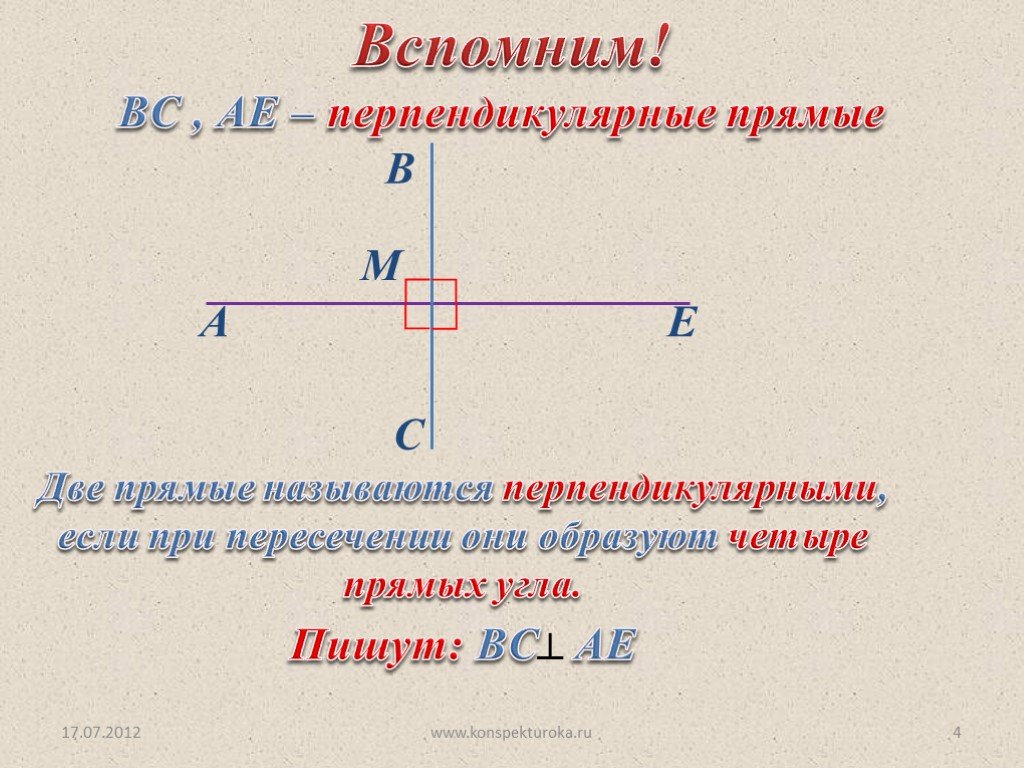
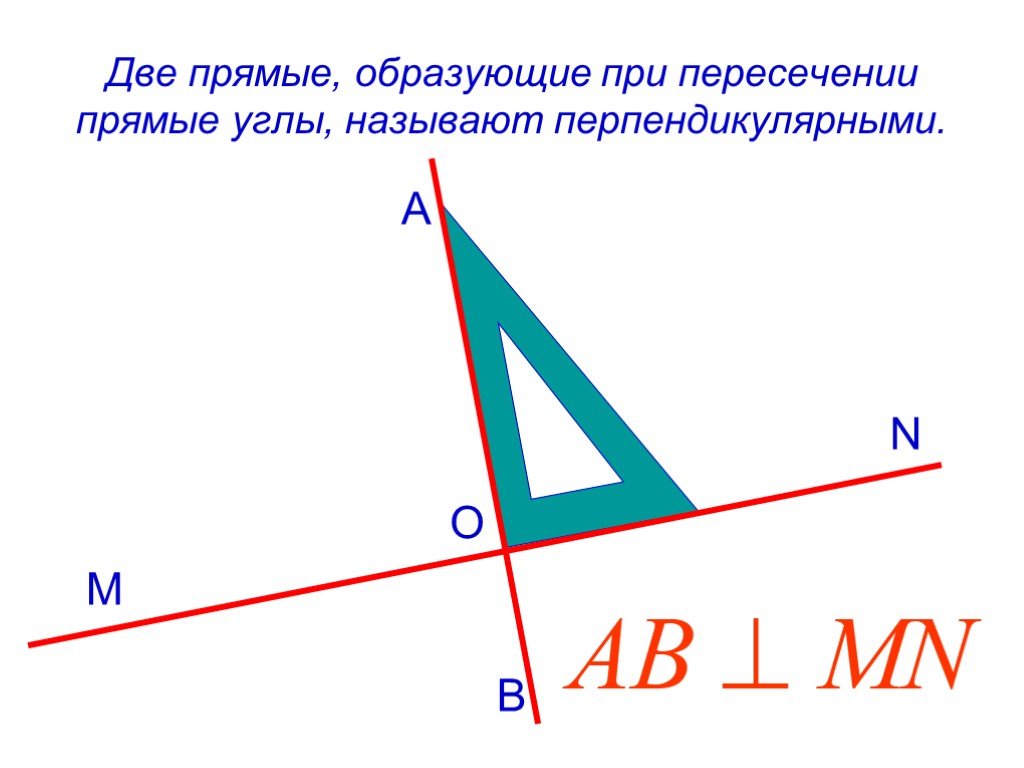
Две прямые называются перпендикулярными (или взаимно

перпендикулярными), если при пересечении они образуют четыре прямых угла.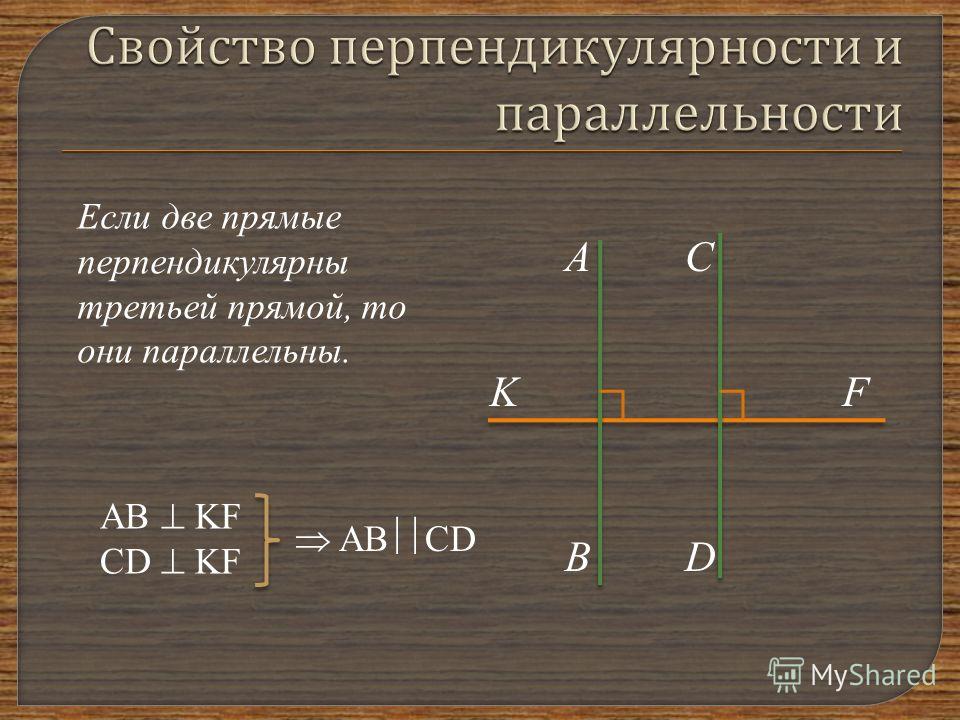

Запишите в тетради.

Используя математические символы, запишите в тетради: «Прямая АC

перпендикулярна прямой ВD». Выполните соответствующий рисунок:

Теперь попробуем ответить на вопрос «Пересекаются ли две прямые, перпендикулярные третьей?»

Для обоснования утверждения о том, что две прямые, перпендикулярные третьей, не пересекаются, используем наглядное пособие. Изобразим на картоне рис. 43 учебника. На верхнюю часть рисунка по прямой PQ приклеим кальку таким образом, чтобы её можно было перегнуть на глазах у учащихся.

Совместно с учениками обсуждаем проблему и делаем вывод, что «Две прямые, перпендикулярные третьей, не пересекаются».

Запишите в тетради это свойство перпендикулярных прямых.

Провести непродолжительную беседу о построении прямых углов на

местности.

Закрепление:

Попробовать самостоятельно выполнить практическое задание № 57.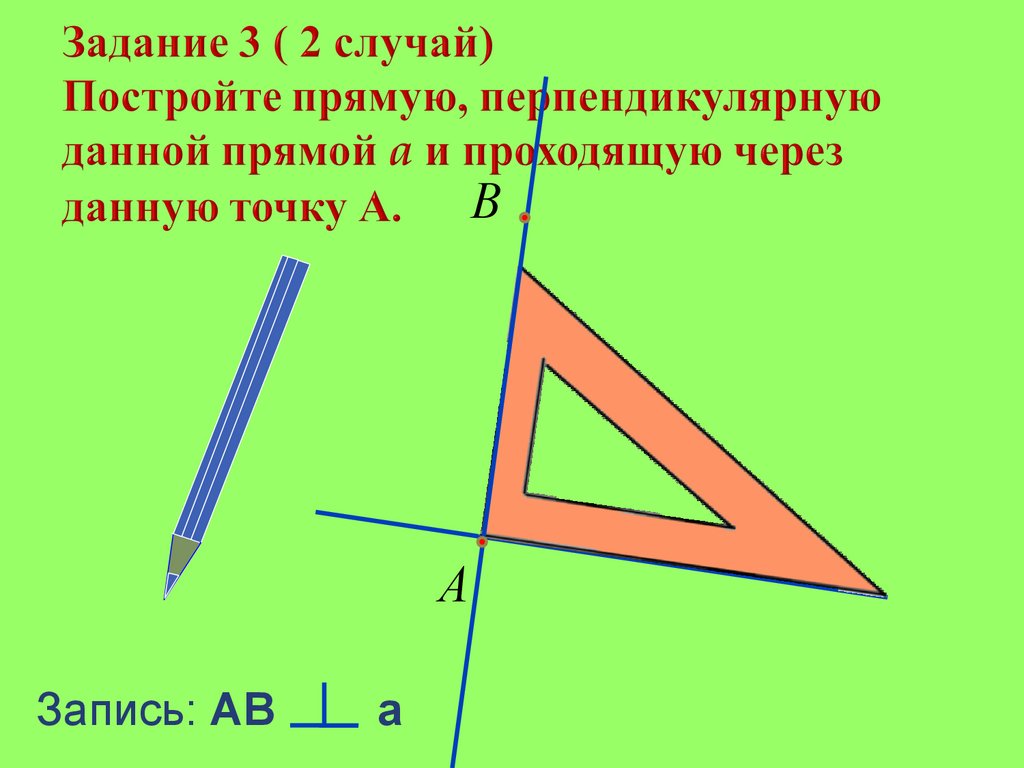

Ребятам, сидящим за одной партой, рекомендуется помогать друг другу. Учитель помогает всем, обратившимся за помощью.

Самостоятельная работа

Обучающимся предлагается решить задачи №№ 69,70.

Через 5-7 минут двум желающим предлагается объяснить свое решение.

Учитель обращается к классу с просьбой дополнить, уточнить или исправить ответ ученика, найти другое, более рациональное решение.

Итог урока:

Какие проблемы были поставлены в начале урока?

Определить,

– Какие прямые называются перпендикулярными?

– Пересекаются ли две прямые, перпендикулярные третьей?

Можно ли сказать, что мы их решили? Назовите.

– Две прямые называются перпендикулярными (или взаимно

перпендикулярными), если при пересечении они образуют четыре прямых угла.

– Две прямые, перпендикулярные третьей, не пересекаются.

Оцените Вашу работу на уроке:

все понятно – ничего не понял, понравилось – не понравилось, было

интересно – было скучно

ответы ребят у доски на этапе актуализации опорных знаний
ответы ребят, объяснявших решение задач № 69,70, на этапе

закрепления нового материала

Домашнее задание (стандартный минимум) и разъяснение методики

его выполнения:

§ 6, п. 11-13, вопросы 17-21 (стр. 26), задачи № 67, 68.

Перпендикулярные прямые — Математика — Уроки

Филиал МКОУ « Октябрьская СОШ» « Алексеевская ООШ»

Касторенского района Курской области

План-конспект урока

по геометрии в 7 классе

на тему: «Перпендикулярные прямые»

Разработала:

Якушева Татьяна Николаевна

учитель математикb I категории

2016 г.

Тема урока: Перпендикулярные прямые.

Цель: добиться усвоения учениками определения перпендикулярных прямых, понимания доказательства теоремы о двух прямых перпендикулярных к третьей.

Сформировать умения:

· воспроизводить названные выше определения и теоремы, доказательства теоремы;

· находить на готовом рисунке и строить, используя чертежные принадлежности, перпендикулярные прямые и параллельные прямые;

· решать задачи, предусматривающие применение определение и свойство перпендикулярных прямых отдельно и в комплексе со свойствами смежных и вертикальных углов.

Тип урока: усвоение знаний, умений и навыков.

Наглядность и оборудование: набор демонстрационных чертежных принадлежностей.

ХОД УРОКА

И. Организационный момент

II. Проверка домашнего задания

Проверку домашнего задания можно осуществить само — или взаимопроверкой тетрадей учащихся по образцам.

Математический диктант

Вариант 1 [2]

1. Прямые AM и CE пересекаются в точке O, лежащей между точками A и M и между точками C и E. Или образовались при этом вертикальные углы? Если да, то назовите их. [Ученик построил два вертикальные углы. Сколько пар прямых при этом образовалось?]

2. Какова градусная мера угла, если вертикальный с ним угол равен 34°? [У двух углов общая вершина, каждый из них имеет градусные мере 60°. Обязательно ли эти углы вертикальные? Изобразите это на рисунке.]

3. Один из 4-х углов, образовавшийся при пересечении двух прямых, равен 140° [40°]. Какую градусную меру имеет каждый из оставшихся углов?

4. Два угла с общей вершиной равны [не равны]. Обязательно ли они вертикальные? [эти вертикальные углы?]

5. У двух углов общая вершина. Один угол 40°, второй 140°. Или эти вертикальные углы? [Которую градусную меру имеет угол, что является вертикальным с прямым углом?]

После выполнения заданий математического диктанта, обязательная проверка и обсуждение.

Ответы

Вариант 1

1. Так: и ; и .

2. 34°.

3. 40°; 140°; 40°.

4. Не обязательно:

5. Нет, потому что не равны.

Вариант 2

1. Одна пара.

2. Нет.

3. 140°; 40°; 140°.

4. Нет, потому что не равны.

5. 90°.

III. Мотивация учебной деятельности. Формулировка цели и задач урока

Мотивация осуществляется, как во время проверки домашнего задания, так и во время проверки выполнение математического диктанта (вариант 2, № 5).

После обсуждения возможности «особого» способа пересечения прямых учитель формулирует дидактическую цель урока и задачи на урок.

IV. Актуализация опорных знаний

Выполнение устных упражнений

1. Что можно сказать каждый из вертикальных углов, если их сумма:

а) больше 180°; б) меньше 180°; в) равна 180°?

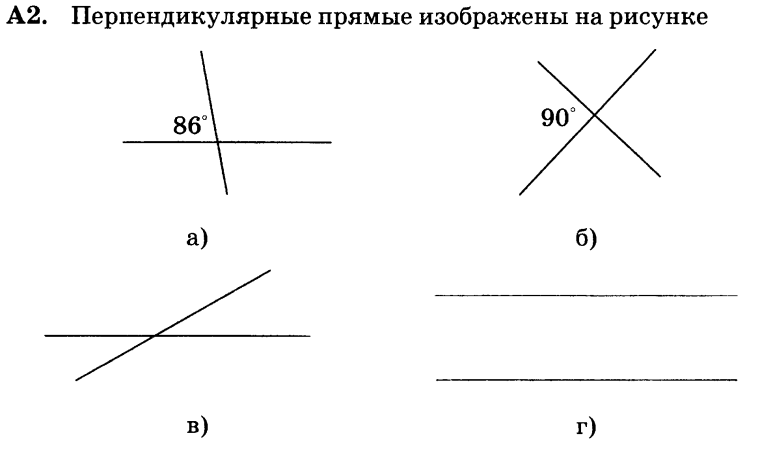
2. Есть ли на рисунке прямые углы? Сколько их на каждом изображении? Ответ проверьте с помощью транспортира и угольника.

3. Сформулируйте утверждение, противоположное данному: а) две прямые имеют общую точку; б) две прямые параллельны; в) через две точки можно провести прямую и только одну.

V. Усвоение новых знаний

План изучения нового материала

1°. Определение перпендикулярных прямых; перпендикулярные отрезки и лучи.

2°. Теорема о двух прямые, перпендикулярные к третьей.

3°. Применение теорема две прямые, параллельные третьей для построения параллельных прямых с помощью угольника и линейки.

Методический комментарий.

В учебнике тема «Перпендикулярные прямые» логически вытекает из темы «Смежные и вертикальные углы». Однако авторы считают не целесообразным рассматривание на этом этапе теоремы о существование и единственность прямой, перпендикулярной к данной, проходящей через данную точку данной прямого. Вместо неё, вполне оправдано изучается теорема двух прямых, перпендикулярных третьей. Поэтому доказательство теоремы о двух прямых, перпендикулярных третьей, в учебнике есть несколько в нестандартном виде (используется, кроме метода доказательства от противного, симметрия относительно прямой в неявном виде).

Поэтому, чтобы облегчить ученикам восприятие доказательства, можно организовать совместную работу учителя и учащихся «конструирования» соображений, приведенных в доказательстве теоремы, например, раздать ученикам прозрачные пленки, на которых они будут выполнять рисунок к теореме и его «перегиб».

VI. Проверка усвоения знаний

Выполнение графических упражнений

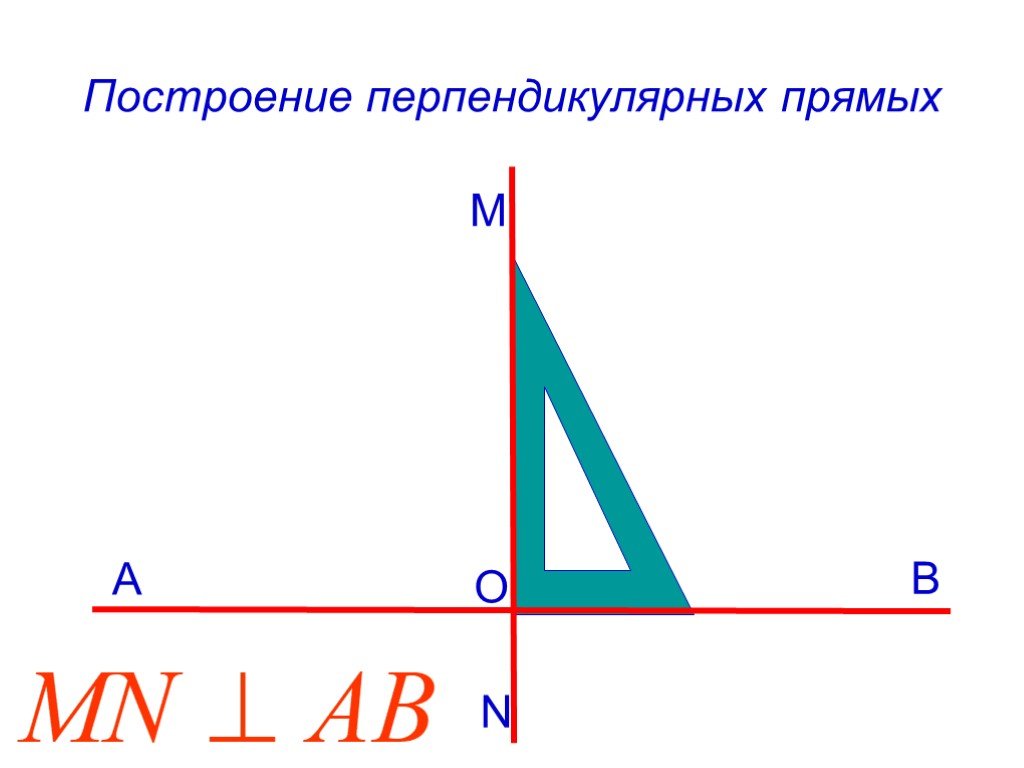
Начертите перпендикулярные прямые a и b, которые пересекаются в точке O.

а) Отметьте на прямой a точку B. С помощью угольника проведите через эту точку прямую c, перпендикулярную к прямой a.

б) параллельные прямые b и c? Почему?

Выполнение письменных упражнений

1. Прямые a и b перпендикулярны. Прямая c проходит через точку их пересечения и образует с прямой a угол 70°. Найдите угол между прямыми c и b.

2. Даны прямые a, b, c и d, причем , a||d. Докажите, что прямые b и d параллельны.

3. (Дополнительная). Через точку пересечения двух перпендикулярных прямых проведена третья прямая. Найдите самый маленький из тупых углов, образовавшихся в результате пересечения этих трех прямых, если наибольший из образованных тупых углов равен 165°.

VII. Усвоение умений и навыков

Одновременно с работой по усвоению новых знаний необходимо отрабатывать знания, умения и навыки, которые обучающиеся приобрели на предыдущих уроках.

Выполнение письменных упражнений

В результате пересечения двух прямых образовались 4 угла, каждый из которых меньше развернутого. Найдите градусную меру каждого угла, если:

а) сумма двух углов равна 78°;

б) разность двух углов равна 42°;

в) один из углов в 5 раз меньше другого;

г) один из углов в 2 раза меньше суммы двух других;

д) сумма трех углов равна 300°;

е) сумма трех углов больше четвертого на 100°.

VIII. Подведение итогов урока

1. Углы 1 и 2 образовавшиеся в результате пересечения двух не перпендикулярных прямых. Определите, каковы данные углы являются ли они смежными или вертикальными, если:

а) их сумма больше 180°;

б) только один из них острый;

в) их сумма меньше, чем сумма других двух полученных углов.

2. α и β-градусные меры двух смежных углов. Могут α и β быть градусными мерами двух вертикальных углов? В каком случае?

3. В результате пересечения двух прямых образовались четыре угла, ни один из которых не является острым. Под каким углом пересекаются данные прямые?

IX. Домашнее задание

Изучить теорию.

Повторить ранее изученную теорию с контрольными вопросами.

Контрольные вопросы

1. Назовите основные геометрические фигуры на плоскости. Как они обозначаются?

2. Сформулируйте аксиому прямой.

3. Какая фигура называется лучом (прямой)? Как обозначаются лучи?

4. Какие лучи называются дополнительными?

5. Дайте определение отрезка. Как обозначается отрезок?

6. Какие отрезки называются равными? Как сравнить два отрезка?

7. Сформулируйте аксиомы измерения и откладывания отрезков. Как сравнить два отрезка с заданными длинами?

8. Дайте определение середины отрезка.

9. Дайте определение угла. Как обозначаются углы?

10. Угол называется развернутым?

11. Какие углы называются равными? Как сравнить два угла?

12. Сформулируйте аксиомы измерения и откладывания углов. Как сравнить два угла с заданными градусными мерами?

13. Назовите единицу измерения углов. Какие углы называются острыми, прямыми, тупыми?

14. Дайте определение биссектрисы угла.

15. Дайте определение параллельных прямых. Назовите два случая взаимного расположения прямых на плоскости. Какие отрезки (лучи) называются параллельными?

16. Сформулируйте аксиому параллельных прямых. В чем заключается отличие от аксиом теорем? Наведите примеры аксиом из курса геометрии.

17. Сформулируйте и докажите теорему о двух прямых, параллельных третьей.

18. В чем заключается метод доказательства от противного? Опишите этапы рассуждений в ходе доведения от противного.

19. Дайте определение смежных углов.

20. Сформулируйте и докажите теорему о смежных углах.

21. Сформулируйте последствия теоремы о смежных углах.

22. Дайте определение вертикальных углов.

23. Сформулируйте и докажите теорему о вертикальных углах.

24. Дайте определение перпендикулярных прямых.

25. Сформулируйте и докажите теорему о двух прямых, перпендикулярных к третьей.

Выполните домашнюю самостоятельную работу.

Вариант 1

Начальный уровень

1. Угол, смежный с углом A, больше угла, смежного с углом B. Сравните углы A и B.

Средний уровень

2. Могут ли градусные меры углов, образовавшихся при пересечении двух прямых, относятся как 2 : 3 : 2 : 4?

Достаточный уровень

3. Углы 1 и 2 являются смежными, а углы 1 и 3 вертикальные. Сравните углы 2 и 3, если угол 1 острый.

Высокий уровень

4. Через точку пересечения двух перпендикулярных прямых проведено третью прямую. Сколько пар косвенных вертикальных углов при этом образовалось?

3.1 Отрезки, прямые и лучи | Геометрия прямых линий

Вы, наверное, точно знаете, что такое линия. В этой главе вы узнаете о отрезки и лучи и чем они отличаются от прямых. Вы также узнаете больше о параллельные и перпендикулярные прямые и как мы их обозначаем на диаграмме.

Отрезки, линии и лучи

Отрезки

Измерьте каждую сторону этот четырехугольник. Напишите размеры с каждой стороны.
Каждая сторона четырехугольника является отрезком .
Отрезок линии имеет определенную начальную точку и определенную конечную точку. Мы можем рисовать и измерять отрезки.
Нарисуйте отрезок длиной 12 см.

Линии и лучи

Мы можем думать о линиях, у которых нет концов, хотя мы не можем нарисовать их полностью. Мы рисуем отрезки для представления линий. Когда мы рисуем отрезок для представления линии, мы можем поставить стрелки на обоих концах, чтобы показать, что он продолжается бесконечно с обеих сторон.

Слово линия используется для обозначения линии, которая идет в обоих направлениях. Мы можем видеть и рисовать только часть линии. Линия не может быть измерена.

Проведите линию АВ.
Вы нарисовали вся линия АВ? Объяснять.

Мы также можем думать о линии, которая имеет определенную начальную точку, но бесконечно продолжается на другом конце. Это называется полулиния или луч .
Мы можем нарисовать начальную точку и часть луча, используя стрелку, чтобы указать, что он продолжается на одном конце.
Ray PQ идет вправо:
Ray DC идет влево:
Натяжной луч ЭФ.
Вы нарисовали весь луч EF? Объяснять.
Соответствуют ли отрезки XY и GH в любом месте?
Соответствуют ли линии KL и NP в любом месте?
Встречаются ли где-нибудь лучи AB и CD?
Встречаются ли где-нибудь лучи FT и MW?
Встречаются ли где-нибудь лучи JK и RS?

w3.org/1999/xhtml»> Параллельные и перпендикулярные прямые

Параллельные прямые

Две прямые, находящиеся на постоянном расстоянии друг от друга, называются параллельными прямыми . Линии AG и BH ниже параллельны. Символ || используется для обозначения параллельных прямых. Пишем: АГ || БХ.

Мера расстояние между двумя линиями:
1. в А и Б
2. в C и D
3. на E и F
Вот еще несколько параллельных линий:
Нарисуй два параллельные линии.
Нарисовать три линии которые параллельны друг другу.
Будет параллельно линии где-то встречаются?
Считаете ли вы, что прямые PQ и ST параллельны? Как можешь проверить?
1. Нарисуйте две линии, почти параллельные, но не довольно.
2. Опишите, что вы сделали для убедитесь, что ваши две линии не параллельны.
Могут ли два отрезка быть параллельно?
Отрезки DK и FS параллельны?
Отрезки MN и AB параллельны?
Что вы можете сделать, чтобы иметь возможность лучше проверить, параллельны ли два вышеупомянутых отрезка прямой или нет?
Может ли линия быть параллельной сама по себе?
Нарисуйте линию, которая параллельно линии XY выше.

Перпендикулярные линии

Строки CD и KL ниже перпендикулярны друг другу. Символ используется для обозначения перпендикулярные линии. Пишем: КД КЛ.

Сколько углы образуются в точке, где пересекаются две вышеуказанные линии?
Две прямые, образующие прямые углы, перпендикулярны друг другу.
Нарисуйте два луча с одинаковыми исходными точками.
Нарисуйте два луча, которые перпендикулярны друг другу и имеют одинаковую начальную точку.
Нарисуйте два луча которые встречаются, но не в своих начальных точках.
Нарисуй два лучи, которые встречаются, но не в своих начальных точках, и которые перпендикулярны друг друга.
Можете ли вы нарисуйте два луча, которые имеют одну и ту же начальную точку и параллельны каждому другой?

Уроки геометрии 1 и 2, параллельные и перпендикулярные линии

Альберта, 7 класс, раздел 8: уроки геометрии 1 и 2, параллельные и перпендикулярные линии

Комплекты модулей содержат все файлы в форматах Microsoft Word и PDF.

Вам только что вручили курс математики, и вы не знаете, с чего начать?

Расслабься, эта программа специально для тебя. Здесь вы найдете основы , которые помогут вам начать работу с и снимите груз со своих плеч.

Разработанные с учетом

начинающих учителей , но при этом значительно экономящие время для всех, эти уроки представляют собой полную кулинарную книгу для вашего класса. Подходящие планы уроков и раздаточные материалы облегчают начало работы и создают впечатление, что вы все знаете.

Каждый урок преподается на бесплатном видео на YouTube, если вам нужно освежить в памяти то, что вы узнали 10 лет назад.

Включены все викторины, ключи и итоговая оценка.

Если вы используете Западно-Канадский протокол с текстом Pearson’s Math Makes Sense Text, все остальное не составит труда. Не используете текст Пирсона? Не беспокойтесь, тексты используются только для заданий. Используй свой собственный!

Легко адаптируется к дистанционному обучению, отправьте учащимся раздаточный материал, и вы учите с урока на своем компьютере, и они могут следовать. Они даже могут посмотреть видео, если им нужен обзор. Математика больше не будет в вашем списке забот!

Вы получаете:

· 2 плана уроков

· 2 раздаточных материала для учащихся

· 1 викторина с ключом

Доступ к моему бесплатному каналу YouTube , на котором я провожу ВСЕ уроки, используя эти раздаточные материалы. Плейлисты позволяют легко и удобно находить уроки.

Посмотрите все мои уроки — я добавляю новые каждый день!

Ссылка на видео урока

Учащиеся используют мои видеоролики в качестве обзора для выпускных экзаменов и помогают лучше понять концепции.
Отсутствующие студенты могут заполнить примечания к этим видео и наверстать упущенное.
Заменить учителя ? Все, что они делают, это нажимают на видео и наблюдают за прогрессом класса у них на глазах.

Создать пакет домашних заданий очень просто: просто распечатайте раздаточные материалы к уроку и попросите их посмотреть видео на YouTube.
Родители и директора в восторге!

Как пользоваться моими уроками:

Этот пакет включает в себя все, что вам нужно. Он предназначен для сопровождения Pearson’s Математика имеет смысл текст. Учитель проецирует раздаточный материал и делает записи во время проведения урока. Учащиеся следуют и заполняют свои раздаточные материалы. Вопросы к заданиям есть в тексте, или вы можете создать свои.

Я использую Smart Board, но проецирование на белую доску работает нормально. Звон колоколов? Нет проблем, просто продолжайте с того места, на котором остановились в прошлый раз.

Учебная цель для этих уроков:

Учащиеся будут определять и строить параллельные и перпендикулярные линии с помощью инструментов.

Основные вопросы к этим урокам:

Что такое параллельные прямые?

Какие существуют способы построения параллельных линий?

Что такое перпендикулярные линии?

Какие существуют способы построения перпендикулярных линий?

УСЛОВИЯ ЛИЦЕНЗИИ. Эта покупка включает лицензию для одного учителя только для личного использования в классе. Лицензии не подлежат передаче, то есть их нельзя передавать от одного преподавателя к другому.