Степень с натуральным показателем 7 класс презентация – Презентация к уроку по алгебре (7 класс) по теме: Презентация на тему: Степень с натуральным показателем», 7 класс
Презентация к уроку по алгебре (7 класс) по теме: Презентация на тему: Степень с натуральным показателем», 7 класс
Слайд 1
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМСлайд 4
Обозначение: 5 2 Читается: «Пять в квадрате» Обозначение: 5 3 Читается: «Пять в кубе»
Слайд 5
( ) 3 = · · ( ) 4 = · · · 2 3 = 2 · 2 · 2 = ? Повторяющийся множитель называют основанием степени, а число повторяющихся множителей – показателем степени. 3 4 = 3 · 3 · 3 · 3 = ?
Слайд 6
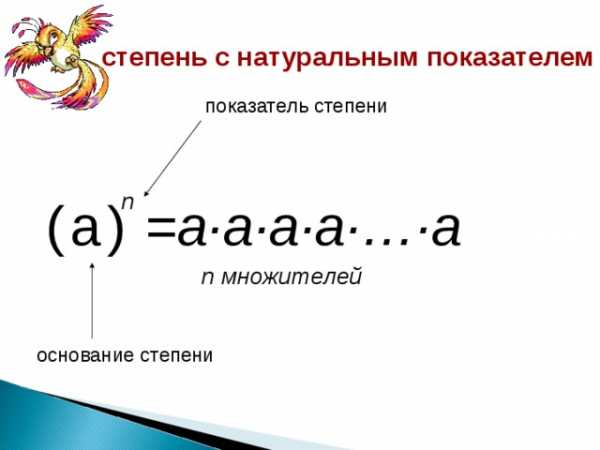
=a·a·a·a · … · a n множителей Теперь можно записать вывод: основание степени показатель степени ( а ) n Выражение читается так: «Степень числа a с показателем n » или кратко « a в степени n »
Слайд 7
Степенью числа а с натуральным показателем n , большим 1, называется произведение n множителей, каждый из которых равен a . Степенью числа a с показателем 1 называется само число a : a 1 =a
Слайд 8
Задание 1: Запишите произведение в виде степени, назовите основание и пока- затель степени: 1)0,3 · 0,3 · 0,3 · 0,3 · 0,3 · 0,3 2)(-ас) · (-ас) · (-ас) · (-ас) · (-ас) 3)5 · 5 · 5 · 5 · 5 · 5 · 5 · 5 · 5 · 5 4)(х+3) · (х+3) · (х+3) · (х+3) = (0,3) 6 =(-ас) 5 =5 10 =(х+3) 4
Слайд 9
Обратная задача: число в степени записать как произведение множителей: 1) 76 в степени 6 2) 89 в степени 4 3) X в степени 6 4) 100 в степени 5 = 76 6 =89 4 = x 6 = 100 5
Слайд 10
Вычисление значения степени называют действием возведения в степень. Например: = 2*2*2= 8 2 3 3 4 = 3*3*3*3 = 81 100 3 = 100*100*100= 1000000 (- 6 ) 4 = (- 6 ) * (- 6 ) * (- 6 ) * (- 6 ) =1296 (- 6 ) 3 = (- 6 ) * (- 6 ) * (- 6 ) = — 216
Слайд 11
Задание 2: Вычислите: 1) 7 3 2) 2 3 – 6 2 3) (-4) 2 + 5 3 4) 1 7 – 11 2 + 10 3 Задание 3: Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1. 1) 64 2)36 3)121 4)27 =343 = -28 =141 =880 =4 3 =6 2 =11 2 =3 3
Слайд 12
Задание 6: Запишите в виде произведения третью степень числа 4 и найдите ее числовое значение. Задание 7: Чему равна сумма кубов чисел 5 и 3. Задание 8: Вычислите квадрат куба числа 2. 4 3 =4 · 4 · 4=64 5 3 + 3 3 =125+27=152 (2 3 ) 2 =8 · 8 =64
Слайд 13
Упражнения, решаемые на этом уроке, можно условно разбить на группы: 1 группа : Задания на усвоение понятия степени. 2 группа : Задания на вычисление значения степени числа с натуральным показателем. 3 группа : Задания на вычисления значения числового выражения, содержащего степень.
Слайд 14
1 группа: №374, 375 (устно), №376 (а,б, д,е, и,к), №380 2 группа: № 382, № 381(а,б) 3 группа: №384, №385 (а,в,г), №386 (а,в,д,ж).
Слайд 15
Домашнее задание: 1. Придумать ребус по теме урока или сочинить сказку про «степень» 2. В учебнике: № 377, 379, 385 (б,г,е)
nsportal.ru
Презентация на тему «Степень с натуральным показателем»

СТЕПЕНЬ
С НАТУРАЛЬНЫМ
ПОКАЗАТЕЛЕМ

5 2=
5 3=
2•2=
2 •2 •2=
5•5
5 3= 5•5•5
2 2
2 3

Найдите закономерность в записи
5 · 5 · 5 · 5 · 5 · 5 · 5 5 7
(-3) · (-3) · (-3) · (-3) · (-3) · (-3) (-3) 6
8 · 8 · 8 8 3
(-19) · (-19) (-19) 2
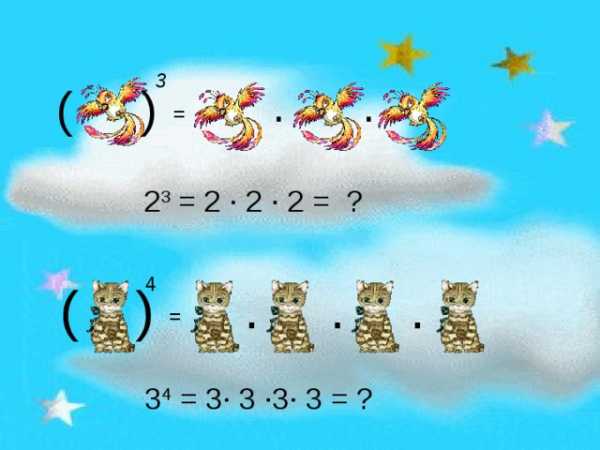
3
(
)
·
·
=
2 3 = 2 · 2 · 2 = ?
4
(
)
·
·
·
=
3 4 = 3 · 3 · 3 · 3 = ?
степень с натуральным показателем
показатель степени
n
=a·a·a·a · … · a
(
а
)
n множителей
основание степени

Задание 1: Запишите
произведение в виде степени,
назовите основание и пока-
затель степени:
1)0,3 · 0,3 · 0,3 · 0,3 · 0,3 · 0,3
2)(-ас) · (-ас) · (-ас) · (-ас) · (-ас)
3)5 · 5 · 5 · 5 · 5 · 5 · 5 · 5 · 5 · 5
4)(х+3) · (х+3) · (х+3) · (х+3)
= (0,3) 6
=(-ас) 5
=5 10
=(х+3) 4
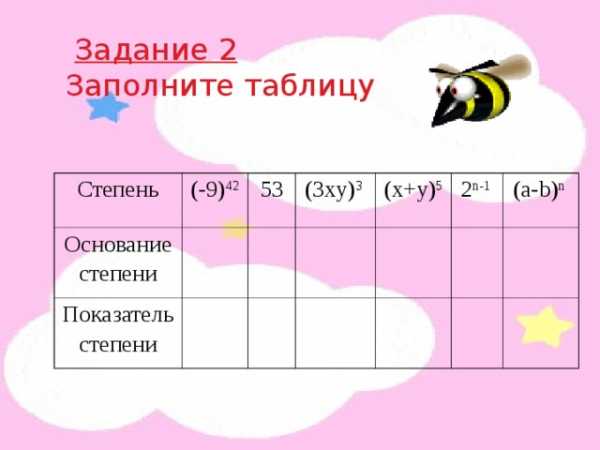 Задание 2
Задание 2Заполните таблицу
Степень
(-9) 42
Основание степени
53
Показатель степени
(3xy) 3
(x+y) 5
2 n-1
(a-b) n

Задание 3
Вычислите:
(-2 )5 = (- 2)•(-2)•(-2)•(-2)•(-2)=
(-2 )4 = (- 2)•(-2)•(-2)•(-2)=
(-2 )3 = (- 2)•(-2)•(-2)=
(-2 )2 = (- 2)•(-2)•=
Какую закономерность вы заметили?
3 ступень
2 ступень
1 ступень
степень

Задание 4: Вычислите:
1) 7 3
2) 2 3 – 6 2
3) (-4) 2 + 5 3
4) 1 7 – 11 2 + 10 3
Задание 5: Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1.
1) 64 2)36 3)121 4)27
=343
= -28
=141
=880
=4 3
=6 2
=11 2
=3 3

Задание 6: Запишите в виде произведения
третью степень числа 4 и найдите
ее числовое значение.
4 3 =4 · 4 · 4=64
Задание 7: Чему равна сумма кубов чисел 5 и 3.
5 3 + 3 3 =125+27=152
Задание 8: Вычислите квадрат куба числа 2.
(2 3 ) 2 =8 · 8 =64

САМОСТОЯТЕЛЬНАЯ РАБОТА
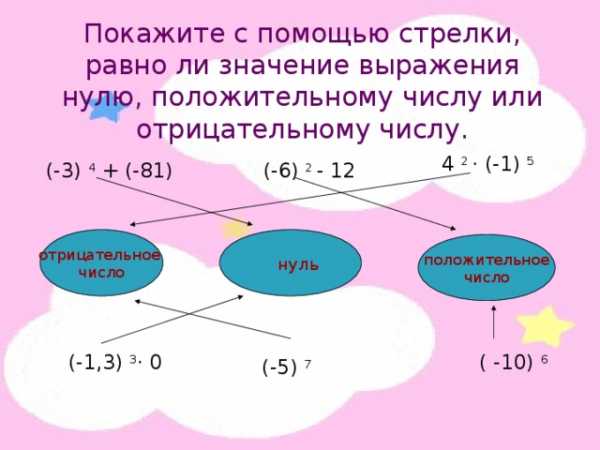
Покажите с помощью стрелки,
равно ли значение выражения
нулю, положительному числу или
отрицательному числу.
4 2 · (-1) 5
(-3) 4 + (-81)
(-6) 2 — 12
отрицательное
число
положительное
число
нуль
( -10) 6
(-1,3) 3 · 0
(-5) 7
videouroki.net
Степень с натуральным показателем. 7 класс.
Презентация к уроку алгебры в 7 классе. Сиепень с натуральным показателем. В презентации используются игровые технологии при формулировании темы и при закреплении основных понятий. урок можно отнести к урокам блочной системы изучения темы. Данная работа будет полезна при введении понятия степень с натуральным показателем. При знакомстве с свойствами степеней.
Просмотр содержимого документа
«Степень с натуральным показателем. 7 класс.»

натуральным
с
показателем
степень

Степень с натуральным
показателем и её
свойства

Пусть кто-нибудь
попробует вычеркнуть
из математики степени,
и он увидит, что
без них далеко
не уедешь.
М.В. Ломоносов

Как вы думаете, на какие вопросы мы будем отвечать?
- Что такое степень?
- Из чего состоит?
- Что с нею делать?
- Как будем считать?
- Какими свойствами обладает?

ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!
п
а
а*
а*
*а
=
•
•
•
n
раз
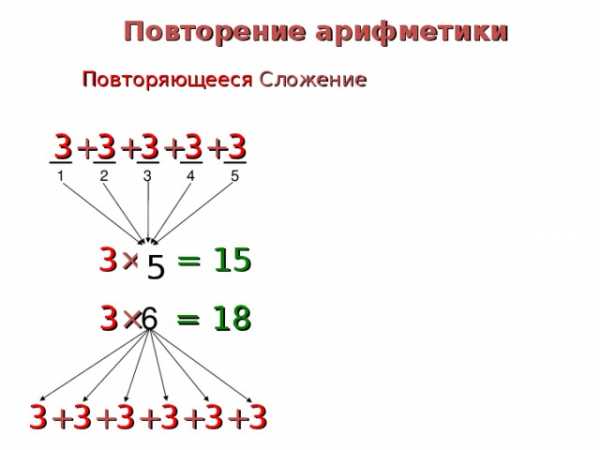
Повторение арифметики
Повторяющееся Сложение
3
3
3
3
+
+
+
+
3
1
5
4
3
2
×
= 15
3
?
5
6
×
3
= 18
3
+
+
+
+
+
3
3
3
3
3
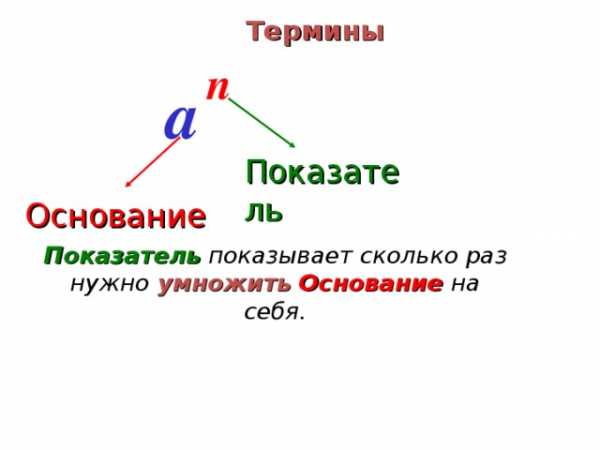
Термины
п
а
Показатель
Основание
Показатель показывает сколько раз нужно умножить Основание на себя.
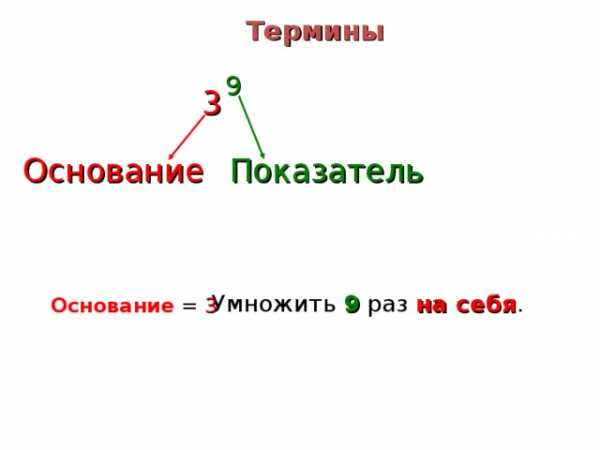
Термины
9
3
Основание
Показатель
Умножить 9 раз на себя .
Основание = 3

Вычислим на колькуляторе
9
3
= 19 683
3^9
19683.
3
×
3
3
3
×
×
×
×
3
×
3
×
×
3
3
3
^
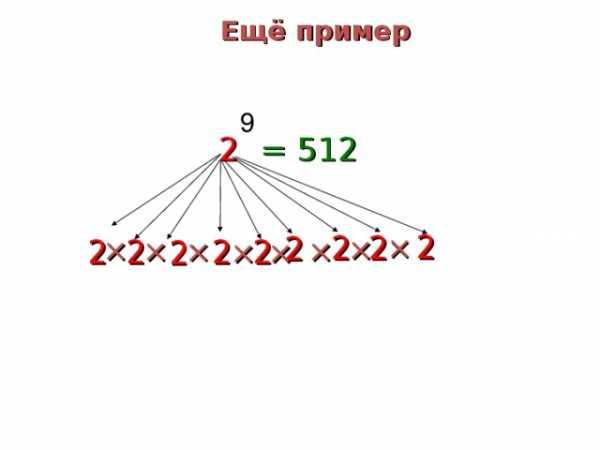
Ещё пример
9
= 512
2
2
×
2
2
2
×
×
×
×
×
2
2
2
2
×
×
2

Попрактикуемся ?
0 4
3 2
= 9
= 0
3 4
= 81
5 3
= 125
4 3
= 64
7 3
= 343
Замечательно!
10 3
= 1 000
15 1
= 15
2 6
= 64
1 9
= 1
Физминутка


Как читать степень
3
9
“ Три в девятой степени ”
4
5
“ Пять в четвертой степени ”
2
7
“ Семь во второй степени ”
“ или Семь в квадрате ”
3
10
“ Десять в третьей степени ”
“ или Десять в кубе ”

Найти показатель степени
показатель
6
2
3
4
5
1
6
5 × 5 × 5 × 5 × 5 × 5
= 5__
основание
4
= 8__
8 × 8 × 8 × 8
7
Выполнено!
= 2__
2 × 2 × 2 × 2 × 2 × 2 × 2
2
= 7__
7 × 7
5
= 1.5__
1.5 × 1.5 × 1.5 × 1.5 × 1.5
11
4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4
= 4__

1 . Запишите произведение в виде степени:
9·9·9 =
9³
(- х )(- х )(- х )(- х )(- х ) =
(- х )⁵
( а — с )( а — с ) =
( а – с )²
2. Найдите значение степени:
16
(-2)⁴ =
1
=
—
—
32
— 0,001
(- 0,1)³ =

Попрактикуемся без калькулятора
2
4
5
0
= 25
= 0
x
3
9
0
0
= 729
=
4
4
= 256
Все верно!
14
1
= 1
2
17
= 289
1
3
= 3
4
7
= 2 401

Составим таблицу основных степеней
7
1
2
= 2
2
= 128
8
2
2
2
= 4
= 256
9
3
2
= 512
= 8
2
10
4
2
= 16
2
= 1024
5
2
= 32
6
2
= 64

Составим таблицу основных степеней
1
1
1
7
3
= 3
= 7
= 5
5
2
2
5
= 25
2
7
3
= 9
= 49
3
3
5
= 125
3
3
= 27
= 343
7
5
= 625
5
4
3
= 81
5
3
= 242
6
3
= 729

3 . Вычислите:
10² — 3² =
100 – 9 =
91
7² =
49
(10 -3)² =
( -2)⁵ =
— 32
(6 — 8)⁵ =
— 70
10 — 5·16 = 10 — 80 =
10 — 5·2⁴ =
— 1 — 8 =
— 1³ + ( -2)³ =
— 9
— 37
— 36 — 1 =
— 6² — ( -1)⁴ =
 п ) 3 0 n n а 1 ,( а ≠ 0) ( а а = 6 n — — b b 0 ⁰ не имеет смысла b ≠ 0 ( )»
п ) 3 0 n n а 1 ,( а ≠ 0) ( а а = 6 n — — b b 0 ⁰ не имеет смысла b ≠ 0 ( )»
(
ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!
Показатели складываем
1
п
т + п
т
=
a
a
a
п
т
4
т п
( а ) = а
Показатели вычитаем
т
п
т — п
2
:
a
a
a
=
Показатели умножаем
n
n
n
( аb )
=
а b
5
( а ≠ 0, т п )
3
0
n
n
а
1
,( а ≠ 0)
(
а
а
=
6
n
—
—
b
b
0 ⁰ не имеет смысла
b
≠ 0
(
)
Все вычислительные примеры дети записывают в тетрадь
22

Верно ли выполнены действия?
— 8 х ³
5 ⁴
( — 2 х )³ = — 2 х ³
5·5·5·5 = 4⁵
9
(- 3)² = — 9
2¹⁰
2³ · 2⁷ = 2²¹
3 ¹⁰ : 3⁵ = 3²
12
2³ + 2² = 2⁵
5⁷
5³ · 5⁴ = 25⁷

Домашнее задание
Читать параграф 15, № 15.1(а, б ), 15.3(а,б), 15.4(а,б).
kopilkaurokov.ru
Степень с натуральным показателем (7 класс)
Презентация на тему: Степень с натуральным показателем (7 класс)Скачать эту презентацию
Скачать эту презентацию
№ слайда 1 Описание слайда:Обобщающий урок по теме: «Степень с натуральным показателем» В 7 «В» классе Учитель Эздекова Ф.Х. В 7 «В» классе Учитель Эздекова Ф.Х.
№ слайда 2 Описание слайда:«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов
№ слайда 3 Описание слайда:– Создать условия для овладения системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования. – Содействовать воспитанию нравственных знаний, положительного эмоционального отношения к окружающим, принятия ценностных ориентаций извне, воспитанию воли и настойчивости для достижения конечных результатов. – Способствовать развитию общеучебных умений, навыков и способов деятельности: навыки самоконтроля при выполнении самостоятельной работы; умение искать ответы на возникшие вопросы, используя разнообразные информационные источники; умение преобразовывать словесный и наглядный материал в алгебраические выражения и обратно и выполнять преобразования в нестандартных ситуациях. побуждать школьников логически мыслить, рассуждать, отстаивать свою точку зрения. – Создать условия для овладения системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования. – Содействовать воспитанию нравственных знаний, положительного эмоционального отношения к окружающим, принятия ценностных ориентаций извне, воспитанию воли и настойчивости для достижения конечных результатов. – Способствовать развитию общеучебных умений, навыков и способов деятельности: навыки самоконтроля при выполнении самостоятельной работы; умение искать ответы на возникшие вопросы, используя разнообразные информационные источники; умение преобразовывать словесный и наглядный материал в алгебраические выражения и обратно и выполнять преобразования в нестандартных ситуациях. побуждать школьников логически мыслить, рассуждать, отстаивать свою точку зрения. Цели урока:
План урока: Организация обучающихся 1 мин Сообщение темы, целей и задач урока. 1 мин Повторение свойств степени с натуральным показателем. 4 мин Устный счет. 4 мин Задания на вычисления. 6 мин Физкультурная пауза. 3 мин Самостоятельная работа по карточкам 5 мин Работа по учебнику 8 мин Тест 5 мин Сообщения детей 2 мин Рефлексия. 1 мин Постановка домашнего задания. 1 мин Организация обучающихся 1 мин Сообщение темы, целей и задач урока. 1 мин Повторение свойств степени с натуральным показателем. 4 мин Устный счет. 4 мин Задания на вычисления. 6 мин Физкультурная пауза. 3 мин Самостоятельная работа по карточкам 5 мин Работа по учебнику 8 мин Тест 5 мин Сообщения детей 2 мин Рефлексия. 1 мин Постановка домашнего задания. 1 мин
Свойства степени с натуральным показателем
№ слайда 6 Описание слайда:Повторяем формулы
№ слайда 7 Описание слайда:Повторяем формулы
№ слайда 8 Описание слайда:Устный счёт 1.Упростите выражение: а 6 а 7 ; (3х) 2 ; у 17 :у 5 ; х 2 х 8 :х; (хуz) 3 ; (b+1) 3 (b+1) 4 ;. 2.Вычислите :,,. 3.Представьте в виде степени с основанием 4 1; 4; 16; 256 1.Упростите выражение: а 6 а 7 ; (3х) 2 ; у 17 :у 5 ; х 2 х 8 :х; (хуz) 3 ; (b+1) 3 (b+1) 4 ;. 2.Вычислите :,,. 3.Представьте в виде степени с основанием 4 1; 4; 16; 256
№ слайда 9 Описание слайда:4.Какие числа нужно возвести в квадрат, чтобы получить: 121; ; ; -. 6. Какие числа нужно возвести в куб, чтобы получить : -8; 64; 125; 4.Какие числа нужно возвести в квадрат, чтобы получить: 121; ; ; -. 6. Какие числа нужно возвести в куб, чтобы получить : -8; 64; 125;
№ слайда 10 Описание слайда:Задания на вычисления 1.Представьте выражение в виде степени с основанием 7, 2.Решение уравнений: а) 1.Представьте выражение в виде степени с основанием 7, 2.Решение уравнений: а)
№ слайда 11 Описание слайда:б) с модулем. в)Найдите в равенстве k, если известно, что б) с модулем. в)Найдите в равенстве k, если известно, что
№ слайда 12 Описание слайда:«Поймай ошибку» 1. (-3b 4 y) 2 5b 7 y 8 = -3b 6 y 2 5b 7 y 8 = -15b 42 y 16 2. 1. (-3b 4 y) 2 5b 7 y 8 = -3b 6 y 2 5b 7 y 8 = -15b 42 y 16 2.
№ слайда 13 Описание слайда:Физкультминутка
№ слайда 14 Описание слайда:Самостоятельная работа Заполните пропуски, чтобы равенство было верным. 1. (y 2 ) 2 (…) 3 = y 10. 2. (…) 2 c 3 = c 13. 3. (-a) 3 (…) 2 = -4a 7. 4. b 2 (…) 3 = -27b 11. 5. (…) 2 a 18 = a 24. 6. (…) 4 : a 8 = a 4. Заполните пропуски, чтобы равенство было верным. 1. (y 2 ) 2 (…) 3 = y 10. 2. (…) 2 c 3 = c 13. 3. (-a) 3 (…) 2 = -4a 7. 4. b 2 (…) 3 = -27b 11. 5. (…) 2 a 18 = a 24. 6. (…) 4 : a 8 = a 4.
№ слайда 15 Описание слайда:Знаете ли вы ? Найдите верные неравенства. Из соответствующих им букв получите фамилию архитектора, по проекту которого в 1825 г. было построено здание Большого театра в Москве:
№ слайда 16 Описание слайда:Работа в тетрадях а) = ; б) = ; в) г) ( = а) = ; б) = ; в) г) ( =
№ слайда 17 Описание слайда:Тест Тест по теме: «Степень с натуральным показателем». 1. Представьте выражение к 7 к 5 в виде степени д.) к 5 р.) к 12 п.) к 13 2Вычислите значение выражения 2 3 2 4 а) 2 7 е) 128 я) 126. 3. Представьте в виде степени 5 80 : 5 40 р) 5² п) 1 40 н) 5. 40 4. Запишите в виде степени выражение 3 13 19 13 е) 57 13 а) 57 26 и) 22 13 Тест по теме: «Степень с натуральным показателем». 1. Представьте выражение к 7 к 5 в виде степени д.) к 5 р.) к 12 п.) к 13 2Вычислите значение выражения 2 3 2 4 а) 2 7 е) 128 я) 126. 3. Представьте в виде степени 5 80 : 5 40 р) 5² п) 1 40 н) 5. 40 4. Запишите в виде степени выражение 3 13 19 13 е) 57 13 а) 57 26 и) 22 13
№ слайда 18 Описание слайда:5. Запишите выражение, которое получится, если х² возвести в четвертую степень п) х² к) х 6 д) х 8 6. Выполните действие со степенями 3 5. 3 13 : 3 16 е) 9 а) 2 о) 1. 7. Выполните действие: (2а²в) 3 п)2а 6 в 3 к) 8а 6 в 3 д)8ав 8. Вычислите 2 1 3 1 е) 1/6о)6 2 а) 6. у) 2. 9. Вычислите :3 рт) 27. 3 2 пт) 9.сп) 40,5 5. Запишите выражение, которое получится, если х² возвести в четвертую степень п) х² к) х 6 д) х 8 6. Выполните действие со степенями 3 5. 3 13 : 3 16 е) 9 а) 2 о) 1. 7. Выполните действие: (2а²в) 3 п)2а 6 в 3 к) 8а 6 в 3 д)8ав 8. Вычислите 2 1 3 1 е) 1/6о)6 2 а) 6. у) 2. 9. Вычислите :3 рт) 27. 3 2 пт) 9.сп) 40,5
№ слайда 19 Описание слайда:РЕНЕ ДЕКАРТ Рене Декарт родился 21 марта 1596 года в маленьком городке Ла-Гэ в Турени. Род Декартов принадлежал к незнатному чиновному дворянству. Детство Рене провел в Турени. В 1612 году Декарт закончил школу. Он провел в ней восемь с половиной лет. Декарт далеко не сразу нашел свое место в жизни. Дворянин по происхождению, окончив коллеж в Ла-Флеше, он с головой окунается в светскую жизнь Парижа, затем бросает все ради занятий наукой. Декарт отводил математике особое место в своей системе, он считал ее принципы установления истины образцом для других наук. Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв х, у, zдля неизвестных; а, в, с-для коэффициентов,,, -для степеней. Интересы Декарта не ограничиваются математикой, а включают механику, оптику, биологию. В 1649 г. Декарт после долгих колебаний переезжает в Швецию. Это решение оказалось для его здоровья роковым. Через полгода Декарт умер от пневмонии. Рене Декарт родился 21 марта 1596 года в маленьком городке Ла-Гэ в Турени. Род Декартов принадлежал к незнатному чиновному дворянству. Детство Рене провел в Турени. В 1612 году Декарт закончил школу. Он провел в ней восемь с половиной лет. Декарт далеко не сразу нашел свое место в жизни. Дворянин по происхождению, окончив коллеж в Ла-Флеше, он с головой окунается в светскую жизнь Парижа, затем бросает все ради занятий наукой. Декарт отводил математике особое место в своей системе, он считал ее принципы установления истины образцом для других наук. Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв х, у, zдля неизвестных; а, в, с-для коэффициентов,,, -для степеней. Интересы Декарта не ограничиваются математикой, а включают механику, оптику, биологию. В 1649 г. Декарт после долгих колебаний переезжает в Швецию. Это решение оказалось для его здоровья роковым. Через полгода Декарт умер от пневмонии.
№ слайда 20 Описание слайда:Рефлексия -Что произошло с понятием степени в XVII веке, мы с вами можем предсказать сами. Для этого попробуйте ответить на вопрос: можно ли число возвести в отрицательную степень или дробную? Но это предмет нашего будущего изучения. Перед окончанием урока учащиеся сами оценивают свою работу. -Что произошло с понятием степени в XVII веке, мы с вами можем предсказать сами. Для этого попробуйте ответить на вопрос: можно ли число возвести в отрицательную степень или дробную? Но это предмет нашего будущего изучения. Перед окончанием урока учащиеся сами оценивают свою работу.
№ слайда 21 Описание слайда:Дети, знайте обязательно, степень с натуральным показателем! Слон живет у нас в квартире В доме 2, Подъезд 4. Каждый день привык питаться Утром в 8, Днем в 16. Без разбора всё глотает и калорий не считает. 32 свеклы сжевал и «спасибо» не сказал, 64 груши одним махом взял и скушал. Пирожков 128 в две минуты в рот забросил, 256 леденцов он схрустел за будь здоров. И вот 512 сушек съел, поглаживая уши. За год массы наел он себе 1024 кг.
№ слайда 22 Описание слайда:Домашнее задание Задание на дом: 1.Домашняя работа 4 1,2,5,6,7,9 2.Кроссворд. Задание на дом: 1.Домашняя работа 4 1,2,5,6,7,9 2.Кроссворд.
№ слайда 23 Описание слайда:Дополнительное задание: Найти значение выражения n 2 + k 2, если 2 n = 32 и 3 k = 9.
№ слайда 24 Описание слайда:ВСЕМ СПАСИБО ! УРОК ОКОНЧЕН
ppt4web.ru
Презентация и конспект на тему «Степень с натуральным показателем»

СТЕПЕНЬ
С НАТУРАЛЬНЫМ
ПОКАЗАТЕЛЕМ
ХАСИЕВА А.Х. ГБОУ СОШ г.БЕСЛАН 2015-2016 уч.год учебник « АЛГЕБРА,7 » Мерзляк А.Г.
 Цели урока:
Цели урока:
Закрепить и усовершенствовать навыки преобразования выражений, содержащих степени с натуральным показателем.
 План урока. Организационный момент:
План урока. Организационный момент:
-приветствие, проверка готовности; -сообщение темы, целей и задач урока.
Устная работа с классом.
1. Как можно сумму одинаковых слагаемых записать иначе: 3+3+3+3=…
(-5)+(-5)=…?
2. Как можно записать произведение одинаковых множителей
3×3×3×3=…
(-5)×(-5)=…?
3. Как называется выражение ?
Какое число n?
Какие ограничения накладываются на n ?
6. Если n=1, то =…
 Степень с натуральным показателем
Степень с натуральным показателем
( а)
n
показатель степени
степень числа
основание степени
 Определение степени с натуральным показателем
Определение степени с натуральным показателем
an a a …a
n раз
Степенью числа a с натуральным показателем n называется произведение n множителей, каждый из которых равен a.
an a a … a
n раз
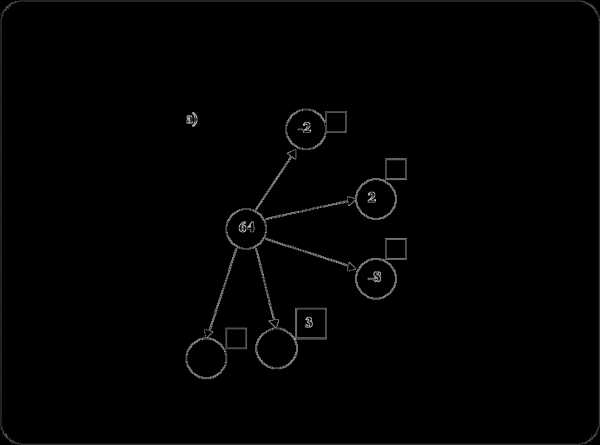 Заполните свободные места.
Заполните свободные места.
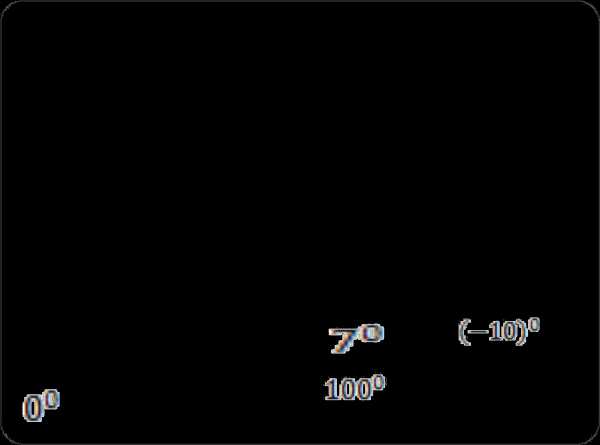 =
=
- Степень числа a,
a
0
1
не равного нулю,
с нулевым
показателем
=
=
равна единице
Выражение смысла не
=
имеет
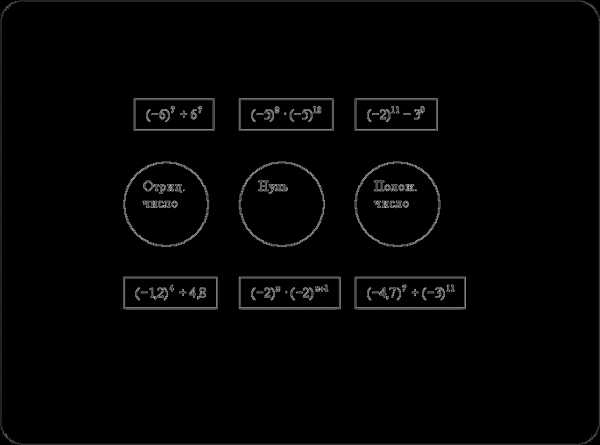
 Самостоятельная работа. 3-ий ряд (10-15 мин.)
Самостоятельная работа. 3-ий ряд (10-15 мин.)
Вариант 1 Вариант 2
1) Выполните действие:
 2) Вычислите значение выражения:
2) Вычислите значение выражения:
 Индивидуальная работа
Индивидуальная работа
Покажите с помощью стрелки, равно ли значение выражения нулю, положительному числу или отрицательному числу:
2)Вычислите значениевыраженияпри заданном значении х
125 х 4 при х 2.
 Работа с классом
Работа с классом
Свойства степени с натуральным показателем
an ak a n k
 Свойства степени с натуральным показателем
Свойства степени с натуральным показателем
an : ak a n k
a 0
n > k
 Свойства степени с натуральным показателем
Свойства степени с натуральным показателем
an k a nk
 Представьте в виде степени выражения (устно)
Представьте в виде степени выражения (устно)
a10 a15 ;
a6 a4 ;
a12 a5 .
a6 : a4 ;
a10 : a3 ;
a6 : a0 ;
a11 : a .
(a2 )2 ;
(a3 )3 ;
(a4 )5 ;
(a0 )2 .
Вычислить:79 75
;
516
54
12
518
7
 Найдите ошибки
Найдите ошибки
23 27 410
210
71 1
7
230 : 210 23 220
40 4
1 2х3 2х3 8х3
23 27 221 210 a 3 2 a 5 а6
 1)
1)
№3 Сравнить с нулем:
- 1)
…0
2)
…0
…0
…0
…0
…0
Сравните с нулём значение выражения.
нуль
положительное
число
число
(-1,3) 3· 0 (-5) 7 ( -10) 6
ТЕСТ
есть число …
+
—
+
 Возведение в степень произведения
Возведение в степень произведения
abn a n b n
При возведении в степень произведения возводят в эту степень каждый множитель и результаты
перемножают . №213
 Свойства степени с натуральным показателем
Свойства степени с натуральным показателем
a b cn an bn cn
Закрепление данного свойства:
№ 214(2;4).
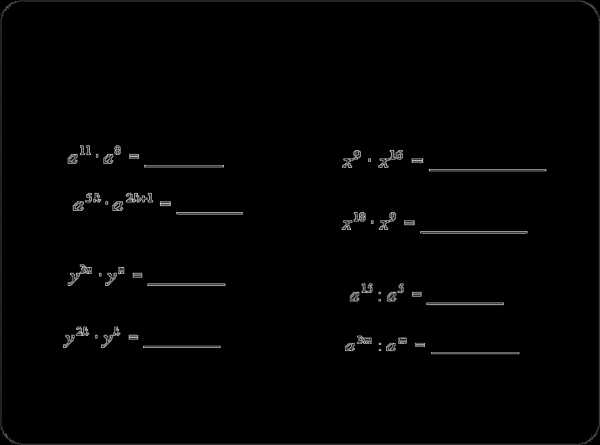
Подумайте, чем можно | ||||||||||||||||
заменить | ? (работа по | |||||||||||||||
рядам). | | |||||||||||||||
n15 : n5 | ||||||||||||||||
x5 x17 | a17 a17 | |||||||||||||||
: k 44 k11 | b2 b8 b24 | m25 : m10 | ||||||||||||||
20 | d | 49 | | |||||||||||||
t | t10 | d 19 | c15 | |||||||||||||
c30 | ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
712 719 | 512 53 519 | 212 2 217 | ||||||||||||||
a | a | | b | c | 1 | |||||||||||
3 * | b | |||||||||||||||
12 | * 4 | 16 | 136 | * | ||||||||||||

 Дополнительное задание:
Дополнительное задание:
Вариант 1 Вариант 2
1)Упростить(а4 )6 : (а3 )3 а) а б) а12 в)а15 2)При каком х выполняется
равенство 56 5х 510
а)125 б)25 в)4
Постановка домашнего задания № 223; 233;234;235.
Подведение итогов урока.
1)Упростить(х4 )3 : (х3 )2 а) х б) х6 в)а18 2)При каком х выполняется
равенство10х :102 10
а)100 б)10 в)1000
infourok.ru
Презентация по алгебре на тему «Степень с натуральным показателей и ее свойства» (7класс)
Эпиграф урока:
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь».
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:
an =
В выражении an :
— число а (повторяющийся множитель) называют основанием степени
— число n (показывающее сколько раз повторяется множитель) – показателем степени
Например:
25 = 2·2·2·2·2 = 32,
здесь:
2 – основание степени,
5 – показатель степени,
32 – значение степени
Отметим, что основание степени может быть любым числом.
Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 108
Каждое число большее 10 можно записать в виде: а · 10n , где 1 < a < 10 и n – натуральное число. Такая запись называется стандартным видом числа.
Например: 4578 = 4,578 · 103 ;
103000 = 1,03 · 105.
Свойства степени с натуральным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются
am · an = am + n
например: 71.7 · 7 — 0.9 = 71.7+( — 0.9) = 71.7 — 0.9 = 70.8
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются
am / an = am — n ,
где, m > n, a ? 0например: 133.8 / 13 -0.2 = 13(3.8 -0.2) = 133.6
3. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.
(am )n = a m · n
например: (23)2 = 2 3·2 = 26
4. При возведении в степень произведения в эту степень возводится каждый множитель
(a · b)n = an · b m ,
например:(2·3)3 = 2n · 3 m ,
5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель
(a / b)n = an / bn
например: (2 / 5)3 = (2 / 5) · (2 / 5) · (2 / 5) = 23 / 53
infourok.ru
Презентация к уроку по алгебре (7 класс) на тему: Свойства степени с натуральным показателем
Слайд 1
СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ. (урок обобщения и систематизации знаний по теме «Степень числа с натуральным показателем» в 7 классе) Разработка учителя математики Ермановой Ю.В.Слайд 2
ЦЕЛИ УРОКА: Обобщить знания о степени с натуральным показателем ; Закрепить и усовершенствовать навыки простейших преобразований выражений, содержащих степени с натуральным показателем Развивать память и логическое мышление
Слайд 3
ОПРЕДЕЛЕНИЕ: СТЕПЕНЬЮ ЧИСЛА А С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ N , БОЛЬШИМ 1, НАЗЫВАЕТСЯ СУММА N МНОЖИТЕЛЕЙ, КАЖДЫЙ ИЗ КОТОРЫХ РАВЕН А : a n = а + а + а + а… + а n раз a – показатель степени; n – основание степени a n =а • а • а • а…• а
Слайд 4
ВСПОМНИ! ГЕНИЙ СОЕДИНИ УСТНЫЙ СЧЕТ ЧЕРНЫЙ ЯЩИК НЕМНОГО ИСТОРИИ ВОТ ЭТО НОМЕР! А это СЛАБО! СЮРПРИЗ
Слайд 5
ВСПОМНИ СВОЙСТВА СТЕПЕНИ И ПРОДОЛЖИ ФОРМУЛЫ: m x : m c = m x-c (xy) a = x a y a (а m ) k = а mk a x a y = a x+y
Слайд 6
СОЕДИНИ СТРЕЛКАМИ СООТВЕТСТВУЮЩИЕ ЧАСТИ ВЫСКАЗЫВАНИЙ: При умножении степеней с одинаковыми основаниями… При делении степеней с одинаковыми основаниями… При возведении степени в степень… При возведении произведения в степень… … основание остается прежним, а показатели перемножаются. … в эту степень возводят каждый множитель и результаты перемножают. … основание остается прежним, а показатели складываются. … основание остается прежним, а показатели вычитаются.
Слайд 7
УСТНЫЙ СЧЕТ А Б В Г Д Е Ж 1 d 5 d 7 d 5 d 8 d 5 d 10 d 6 d 7 d 6 d 8 d 5 d 9 d 6 d 9 2 x 5 x 3 x 2 x 5 x 3 x 3 x 5 x 3 x 4 x 5 xx x 5 x 4 x xx 3 x x 2 xx 3 (x 3 ) 2 (x 3 ) 3 (x 3 ) 4 (x 3 ) 5 (x 2 ) 2 (x 2 ) 3 (x 2 ) 4 4 d k d 3 d 4 d 7 d k d 4 d k d 2 d d n d 2 d 5 d k d 3 d 6 d k d 9 d d 5 d n d 7 5 d 3 (d 3 ) 2 d(d 2 ) 3 d 3 (d 2 ) 3 d 3 (d 4 ) 5 d 2 (d 3 ) 2 d(d 5 ) 2 d 2 (d 3 ) 4 6 (d 2 d 4 ) 2 (dd 2 ) 3 (d 2 d) 2 (d 3 d 5 ) 2 (dd 3 ) 5 (d 3 d 3 ) 3 (dd 5 ) 4 7 p k p 2 p k p p 3 p k p 4 p 2k p k3 p k p 3 p 2k pp k 8 (cd) 3 (cd) 4 (cd) 5 (cd) 6 (c 2 d) 2 (c 3 d 3 ) 2 (c 4 d) 3 9 x 17 : x 9 x 3 : x x 8 : x 3 x 15 : x x 3 : x 3 x 7 : x 3 x 11 : x 8
Слайд 8
ВСЕ ГЕНИАЛЬНОЕ – ПРОСТО!!! НАЙДИ ЗНАЧЕНИЯ ЭТИХ С ВИДУ СЛОЖНЫХ ВЫРАЖЕНИЙ: = = = 3 2 = 9 = = = 3 4 3 9 : 3 8 =3 5 =32
Слайд 9
ВОТ ЭТО НОМЕР!!!
Слайд 10
ВОТ ЭТО НОМЕР!!!
Слайд 11
А ЭТО СЛАБО? 1 2 3 4 5 6 7 5 8 *25 5 7 *25 5 6 *25 5 5 *25 5 4 *25 5 3 *25 5 2 *25 3 12 *27 3 11 *27 3 10 *27 3 9 *27 3 8 *27 3 7 *27 3 6 *27 6 15 *36 6 14 *36 6 13 *36 6 12 *36 6 11 *36 6 10 *36 6 9 *36 32*2 9 32*2 8 32*2 7 32*2 6 32*2 5 32*2 4 32*2 3 5 6 : 5 4 5 7 : 5 4 5 8 : 5 4 5 9 : 5 4 5 6 : 5 3 5 7 : 5 3 5 8 : 5 3 81*3 6 81*3 7 81*3 8 81*3 9 81*3 10 81*3 11 81*3 12
Слайд 12
ДОМАШНЕЕ ЗАДАНИЕ : 1. ОТГАДАТЬ КРОССВОРД 2. СОСТАВИТЬ РЕКЛАМУ СТЕПЕНИ ИЛИ НАЙТИ ИСТОРИЧЕСКУЮ СПРАВКУ О СТЕПЕНИ 3. СОСТАВИТЬ И РЕШИТЬ 3-5 ПРОСТЫХ И СЛОЖНЫХ ЗАДАНИЙ С ИСПОЛЬЗОВАНИЕМ ВСЕХ СВОЙСТВ СТЕПЕНИ И РЕШИТЬ ИХ.
Слайд 13
ЛЮДИ ПРИДУМАЛИ СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ ОЧЕНЬ ДАВНО: Древнегреческий ученый Пифагор придумал, что каждое число можно представить в виде фигуры. Это интересно • • • • • • • • • • • • • • • • • • • • • • • • • • • • • 2 2 3 2 4 2
Слайд 14
Английский математик С. Стивин придумал запись для обозначения степени: 3(3) + 5(2) – 4 Современная запись: 3 3 + 5 2 – 4 . Индийские ученые открыли и оперировали степенями с натуральными показателями до 9, называя их с помощью комбинации трех слов: «ва» — 2 степень, от слова «варга» — квадрат; «гха» — 3 степень, от слова «гхана» — куб и « гхата», указывающую на сложение показателей. Напрмер , 4-я степень «ва-ва»; 5-я степень «ва-гха-гхата»; 6-я степнь — «ва-гха» Это интересно
Слайд 15
В 17 веке английским ученым Джоном Валленсом были придуманы современные обозначения. А вот заслуга в их признании и распространении принадлежит И. Ньютону. Он стал использовать их обозначения в своих работах, и таким образом они прижились . Для вычислительных машин использование 10 цифровых знаков оказалось очень неудобным по техническим причинам. Самой удобной и простой для ЭВМ оказалась двоичная позиционная система, использующая всего 2 цифры – 0 и 1. Например: 27 = 2 4 • 1 + 2 3 •1 + 2 2 • 0 + 2 1 •1 + 2 0 •1 = 11011 2 Это интересно
Слайд 16
СЮРПРИЗ. 1 парта 2 парта 3 парта
nsportal.ru

