как решаются системы уравнений в 7 классе

В 7 классе изучаются системы двух линейных уравнений с двумя неизвестными. Это системы вида a1x + b1y + c1 = 0 a2x + b2y + c2 = 0 Решением такой системы называется пара чисел (x0,y0), при подстановке которой вместо пары чисел (x,y), то есть x0 вместо x, y=0 вместо y получаются два верных числовых равенства. Любая такая система может иметь единственное решение, бесконечно много различных решений, не иметь решений. В 7 классе рассматриваются следующие способы решения системы двух линейных уравнений с двумя неизвестными: 1. Способ алгебраического сложения. Суть способа состоит в том, что каждое уравнение системы умножают на некоторое число так, чтобы при одной из неизвестной оказались коэффициенты, равные по модулю и противоположные по знаку. Затем, полученные уравнения складывают и получают уравнение с одним неизвестным, которое легко решается. Полученное значение неизвестного подставляют в любое из двух уравнений и решают его относительно второго неизвестного. Пример Решить систему 7х — 2у = 3 2х + 5у = 12 Умножим первое уравнение системы на 5, а второе на 2 35х — 10у = 15 4х + 10у = 24 Сложим полученные уравнения 35х — 10у + 4х + 10у = 15 + 24 39х = 39 х = 1 Подставим это значение х, например, в первое уравнение 7 — 2у = 3 4 = 2у у = 2 Ответ: х = 1, у = 2 2. Способ подстановки Суть способа состоит в том, что в одном из уравнений выражают одну из переменных через другую, т. е. преобразовывают его так, чтобы в левой части содержалась чистое неизвестное, без коэффициентов, а правая часть не зависела от этого неизвестного. Полученное выражение подставляют в другое уравнение вместо неизвестной и решают уравнение с одним неизвестным. По выражению для другой неизвестной через найденную определяют второе неизвестное. Данный способ является самым распространённым среди семиклассников. Пример Решить систему (та же самая система) 7х — 2у = 3 2х + 5у = 12 Выразим из первого уравнения у через х 2у = 7х — 3 у = (7х — 3)/2 Подставим это выражение вместо у во второе уравнение. 2х + 5*(7х — 3)/2 = 12 2х + 17,5х — 7,5 = 12 19,5х = 19,5 х = 1 Из выражения у = (7х — 3)/2 найдём н н = (7*1 — 3)/2 = 4/2 = 2 Ответ: х = 1, у = 2 3. Графический способ Суть способа состоит в том, что в каждом уравнении выражают одну переменную через другую, например, у через х, и строят в одной системе координат графики двух полученных линейных функций. Это будут две прямые. Координаты точки пересечения этих прямых (если они есть) составят ответ. Можно и не выражать одну переменную через другую, а просто выбрать два каких нибудь значения х, подставить каждое из них в первое уравнение и решить его относительно у. Получатся две точки, через которые можно провести прямую. Таким же способом построить и вторую прямую. Этот способ является самым наглядным, потому что он показывает, сколько решений имеет система. Пример Решить систему (та же самая система) 7х — 2у = 3 2х + 5у = 12 Пусть х =0, тогда из первого уравнения определяем у = -1,5, из второго — у = 2,4. Пусть х =2, тогда из первого уравнения определяем у = 5,5, из второго — у =1,6. Значит первая прямая проходит через точки (0; -1,5) и (2; 5,5), а вторая — через точки (0; 2,4) и (2; 1,6). Строим эти прямые на одном графике: <img src=»//otvet.imgsmail.ru/download/047da14d4f6ad70142043e9c6b0f5052_i-140.jpg» > Из полученного рисунка видно, что прямые пересекаются в единственной точке с координатами (1; 2), значит система имеет единственное решение х = 1; у = 2. Ответ: х = 1, у = 2.

touch.otvet.mail.ru

Решение линейных уравнений — Математика

Решение линейных уравнений, 7 класс

Разноуровневые карточки для проверки знаний учащихся по теме: «Линейные уравнения» содержат 5 уравнений разного уровня сложности. Их можно применять не только на уроках в данной теме, но и при повторении материала.

Вариант I (Уровень А)

Вариант II (Уровень В)

Вариант III (Уровень С)

Вариант I (Уровень А)

Вариант II (Уровень В)

Вариант III (Уровень С)

Вариант I (Уровень А)

Вариант II (Уровень В)

Вариант III (Уровень С)

 

 

 

Просмотр содержимого документа
«Решение линейных уравнений»

multiurok.ru

Презентация к уроку по алгебре (7 класс) по теме: Презентация «Способы решения систем уравнений» 7 класс

Слайд 1
СПОСОБЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ(7 класс)

Слайд 2
Презентация составлена учителем математики МОУ «СОШ» п. Аджером Корткеросского района Респубрики Коми Мишариной Альбиной Геннадьевной

Слайд 3
Способы решения:

Слайд 4
СПОСОБ ПОДСТАНОВКИСПОСОБ СЛОЖЕНИЯ

Слайд 5
СПОСОБ ПОДСТАНОВКИ

Слайд 6
ПРИ РЕШЕНИИ СИСТЕМЫДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ СПОСОБОМ ПОДСТАНОВКИ: 1. Из одного уравнения выражают одну переменную через другую2. Подставляют во второе уравнение найденное выражение;3. Решают полученное уравнение с одной переменной4. Находят соответствующее значение другой переменной.

Слайд 7
Например: 3х + 2у = 4 х – 4у = 6 Решение: из второго уравнения x = 4y+6Подставим данное выражение в первое уравнение: 3(4y+6)+2y=4 12y+18+2y=4 14y = -14 y=-1 Найдем х: x=4∙(-1)+6 x=2 Ответ: (2;-1)

Слайд 8
ПРИМЕР 1:Решим систему:

Слайд 9
5х – у = 16 10х – 3у = 27 Решение:Выразим из 1 уравнения: -у = 16-5x, тогда y = -16+5x = 5х-16Выражение у = (5х-16) подставим во второе уравнение системы вместо у: 10x — 3(5x-16)=27 10x — 15x + 48 = 27 — 5x = — 48 +27 — 5x = -21 х = 4,2 Найдем у: у = 5х-16 = 5· 4,2 – 16 =21-16= 5 ОТВЕТ: (4,2; 5)

Слайд 10
СПОСОБ СЛОЖЕНИЯ

Слайд 11
ПРИ РЕШЕНИИ СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ СПОСОБОМ СЛОЖЕНИЯ: 1. умножают левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в разных уравнениях стали противоположными числами;2. складывают почленно полученные уравнения;3. решают полученное уравнение с одной переменной;4. находят соответствующее значение второй переменной.

Слайд 12
ПРИМЕР 1:Решим систему:

Слайд 13
2х – 3у = 11 3х + 7у = 5Решение: первое уравнение умножим на (-3), а второе — на 2 — 6х + 9у = — 33 6х + 14у = 10 23y=-23 y=-1Найдем х: 2x — 3·(-1)=11 2x + 3 = 11 2х = -3 +11 2х = 8 х = 4 ОТВЕТ: (4;-1)

Слайд 14
ПРИМЕР 2:Решим систему:

Слайд 15
3х + 10у = 19 — 4х + 5у = -7 Решение: умножим второе уравнение на (-2) 3х + 10у = 19 8х – 10у = 14 11x=33 x=3Найдем у: -4∙3+5y=-7 5y=12 -7 5у = 5 у =1 ОТВЕТ: (3;1)

Слайд 16
Решить системы:

Слайд 17
1) 3х+4у =7 9х-4у = -7х-3у =6 2у-5х = -44х -6у =2 3у -2х =1-2х+3у =-1 4х +у =2 2х +у =6 -4х +3у =8

Слайд 18
3(х+у)+1=х+4у 7-2(х-у)=х-8у5+2(х-у)=3х-4у 10-4(х+у)=3у-3х2х — 7у = 3 3х + 4у = -105х + 2у = -9 4х – 5у = 6 5(х+у)-7(х-у) = 54 4(х+у)+3(х-у) = 51

Слайд 19
Проверим:

Слайд 20
1) х=0; у=7/42) (0; -2)3) любое число4) Х =0,5; у=05) х=1; у=46) (-1;-1)

Слайд 21
7) (6 1/9; 5/9)8) х = -2; у=-19) (-1;-2)10) (9; 6)

nsportal.ru

Линейные уравнения 7 класс | Алгебра

Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида

   

где a и b — числа, x — переменная.

Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на

число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).

Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.

   

Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки  не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:

   

Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

   

Ответ: -9.

   

Раскрываем скобки:

   

Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:

   

(Обратите внимание: хотя сумма слагаемых  с переменной равна нулю, результат записываем не как 0, а как 0x).

Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.

Ответ: x — любое число.

   

Раскрываем скобки:

   

Можно сначала привести подобные слагаемые, чтобы упростить уравнение:

   

а уже потом перенести: неизвестные — в одну сторону, известные — в другую:

   

   

Это уравнение не имеет корней.

Ответ: нет корней.

   

Раскрываем скобки:

   

Приводим подобные слагаемые:

   

Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

Ответ:

   

В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.

www.algebraclass.ru

Практика. Линейные уравнения и их системы. Видеоурок. Алгебра 7 Класс

Пример . Решить уравнение: .

Решение

Вспомним, что деление, по определению, операция, обратная умножению (деление на какое-либо число – это то же самое, что и умножение на обратное к этому числу):

Разделим обе части уравнения на  или умножим на :

Упростим выражение в левой части уравнения:

Упростим выражение в правой части уравнения:

Таким образом, решением уравнения будет:

Ответ: .

 

Пример . Решить уравнение: .

Решение

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Упростим уравнение – выполним действия в обеих частях уравнения: .

Разделим обе части уравнения на :

Решением уравнения является .

Ответ: .

 

Пример . Решить уравнение: .

Решение

Раскроем скобки в правой и левой частях уравнения. Для выражения в левой части уравнения используем распределительный закон: .

Тогда . Вспомним, что если перед скобками стоит знак минус, то при раскрытии скобок все знаки всех слагаемых внутри скобок меняются на противоположный: .

Перепишем уравнение после применения преобразований: .

Как и в предыдущем примере, перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Выполнив действия в обеих частях уравнения, получим тождество: .

Таким образом, данное равенство верно всегда, при любых значениях переменной.

Ответ:  – любое число.

 

Пример . Решить уравнение: .

Решение

Раскроем скобки в правой и левой частях уравнения, используя распределительный закон .

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Получаем .

Данное равенство неверно всегда, т.е. оно не выполняется ни при каких значениях переменной.

Ответ: нет решений.

 

Пример . Решить уравнение: .

Решение

Избавимся от знаменателей дробей – умножим обе части уравнения на общий знаменатель всех дробей, т.е. число :

Получим: .

Выполним сокращения и избавимся от знаменателей: .

Раскроем скобки:

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .

Выполнив действия в обеих частях уравнения, получим следующее уравнение: .

Найдем :

Ответ: .

В общем виде системы линейных уравнений выглядят следующим образом:  где  – переменные, – произвольные числа.

Есть несколько методов решения систем уравнений.

1. Метод подстановки.
2. Метод сложения.
3. Графический метод.

Пример . Решить систему: .

Решение (несколько способов)

1. Метод подстановки – необходимо в уравнении выразить одну переменную через другую и подставить во второе уравнение.

Из первого уравнения выразим , для этого перенесем  из левой части уравнения в правую: .

Затем умножим обе части первого уравнения на : .

Теперь подставим во второе уравнение полученное выражение: .

Теперь во втором уравнении только одна переменная , решим его (мы уже умеем это делать – получилось обычное линейное уравнение с одной переменной).

Раскроем скобки во втором уравнении: .

Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: .

Выполним действия в обеих частях второго уравнения: .

Найдем : .

Подставим в первое уравнение найденное значение переменной:

Решением системы будет: .

Ответ: .

 

2. Метод сложения – нужно преобразовать уравнения так, чтобы при одной переменной в разных уравнениях были противоположные коэффициенты, после этого нужно сложить правые и левые части уравнений.

Избавимся от переменной . Умножим первое уравнение на : .

Теперь система имеет вид: .

Сложим уравнения системы: .

Получим следующее уравнение: . Выполним действия: .

Найдем :

Подставим найденное значение в любое из уравнений исходной системы, например, в первое: .

Выразим : . Решением системы будет: .

Ответ: .

 

3. Графический метод

 

Сначала перепишем каждое из уравнений так, чтобы они задавали линейную функцию в привычном для нас виде , т.е. выразим  через :

Графиком линейной функции является прямая. Построим обе прямые по двум точкам. Вместо  возьмем произвольные значения и подставим их в соответствующие уравнения прямых:

Отметим точки на координатной плоскости и проведем через них прямые (Рис. 1).

Рис. 1. Иллюстрация к примеру 6

Видно, что точкой пересечения прямых является точка с координатами . Поскольку точка лежит на каждой из прямых, а прямая – это множество решений уравнения, то точка пересечения прямых является решением каждого из уравнений, т.е. является решением системы. Координаты точки пересечения и будут решением системы.

Дополнительно нужно подставить координаты точки в исходную систему, чтобы убедиться в правильности: .

Ответ: .

 

Пример . Решить систему: .

Решение

Сначала упростим уравнения системы – избавимся от знаменателей дробей. Для этого умножим каждое уравнение на общий знаменатель дробей, которые в него входят (чтобы найти это число, нужно рассмотреть наименьшее общее кратное чисел, которые стоят в знаменателе):

Получим:

Выполним сокращения и избавимся от знаменателей:

Раскроем скобки:

Приведем подобные слагаемые:

Умножим второе уравнение на :

Сложим уравнения системы:

Получим уравнение:

Выполним действия:

Найдем :

Подставим в первое уравнение найденное значение переменной:

Решением системы будет: .

Ответ: .

Задача

Провод длиной  метров разрезали на  части (Рис. 2), причем первая часть в  раза длиннее третьей, а вторая – на  метров длиннее третьей. Найти длину каждой части провода.

Рис. 2. Иллюстрация к задаче 1

Решение

1. Провод длиной  метров разрезали на  части:

Первая часть в  раза длиннее третьей:

Вторая часть на  метров длиннее третьей:

Теперь все выражено через часть , поэтому все замены можно переписать так:

2. Обозначим длину части  за :

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую:

Выполним действия:

Найдем

interneturok.ru

Решение систем линейных уравнений методом сложения. Номер №199

Вариант 1:

Контрольная работа №1. Тема. Линейное уравнение с одной переменной:

1; 2; 3; 4; 5;

Контрольная работа №2. Тема. Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов:

1; 2; 3; 4; 5; 6; 7; 8; 9;

Контрольная работа №3. Тема. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Разложение многочленов на множители:

1; 2; 3; 4; 5; 6; 7; 8;

Контрольная работа №4. Тема. Формулы сокращенного умножения:

1; 2; 3; 4; 5; 6; 7;

Контрольная работа №5. Тема. Сумма и разность кубов двух выражений. Применение различных способов разложения многочлена на множители:

1; 2; 3; 4; 5; 6;

Контрольная работа №6. Тема. Функции:

1; 2; 3; 4; 5;

Контрольная работа №7. Тема. Системы линейных уравнений с двумя переменными:

1; 2; 3; 4; 5; 6;

Контрольная работа №8. Тема. Обобщение и систематизация знаний учащихся:

1; 2; 3; 4; 5; 6;

Вариант 2:

Контрольная работа №1. Тема. Линейное уравнение с одной переменной:

1; 2; 3; 4; 5;

Контрольная работа №2. Тема. Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов:

1; 2; 3; 4; 5; 6; 7; 8; 9;

Контрольная работа №3. Тема. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Разложение многочленов на множители:

1; 2; 3; 4; 5; 6; 7; 8;

Контрольная работа №4. Тема. Формулы сокращенного умножения:

1; 2; 3; 4; 5; 6; 7;

Контрольная работа №5. Тема. Сумма и разность кубов двух выражений. Применение различных способов разложения многочлена на множители:

1; 2; 3; 4; 5; 6;

Контрольная работа №6. Тема. Функции:

1; 2; 3; 4; 5;

Контрольная работа №7. Тема. Системы линейных уравнений с двумя переменными:

1; 2; 3; 4; 5; 6;

Контрольная работа №8. Тема. Обобщение и систематизация знаний учащихся:

1; 2; 3; 4; 5; 6;

gdzplus.me

«Решение систем линейных уравнений способом подстановки»

Урок №

Тема: «Решение систем линейных уравнений способом подстановки».

Цель урока:

— обучающие: ввести алгоритм решения системы двух линейных уравнений с двумя переменными способом подстановки, сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки;

Этапы урока:

№

Этап урока

Время

Задачи этапа

1.

Организационный момент

1 мин.

2.

Проверка домашнего задания

3 мин.

Проверка правильности выполнения домашнего задания.

3.

Актуализация опорных знаний учащихся

5 мин.

Повторить основные определения; активизировать осознанность применения знаний при решении задач.

4.

Изучение нового материала

15 мин.

Знакомство учащихся с алгоритмом решения системы двух уравнений с двумя переменными методом подстановки (обратить внимание на оформление решений)

6.

Закрепления изученного материала

15 мин.

Сформировать умение решать системы уравнений методом подстановки

7.

Подведение итогов

4 мин.

Повторить изученное на уроке

8.

Домашнее задание

2 мин.

Инструктаж по домашнему заданию

Ход урока.

Этап №1

Слайд №1.

Приготовились к уроку, встали у своих мест.

-Здравствуйте, ребята. Сегодня у нас на уроке присутствуют гости, поздоровайтесь, пожалуйста, садитесь.

Слайд №2

Мы с вами начинаем очередной рабочий урок и эпиграфом к нему я подобрала следующее высказывание И. Гёте: «Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю». Так вот мы с вами сегодня будем пытаться стать настоящими учениками, чтобы хоть чуть-чуть почувствовать себя учителем.

Цель нашего урока – это вывести алгоритм решения системы двух линейных уравнений с двумя переменными способом подстановки, сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки.

Этап№2

На прошлом уроке мы с вами познакомились с новой математической моделью.

Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Перед нами стояла задача найти такие пары значений (х; у), которые одновременно удовлетворяют и первому, и второму уравнению.

-Кто может мне сказать:

Что называется решением системы двух линейных уравнений с двумя переменными?

Слайд№3. (открыть после ответа уч-ся).

—Хорошо.

-А что значит решить систему двух линейных уравнений с двумя переменными?

Слайд №4. (открыть после ответа уч-ся).

-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).

Проверим домашнее задание.

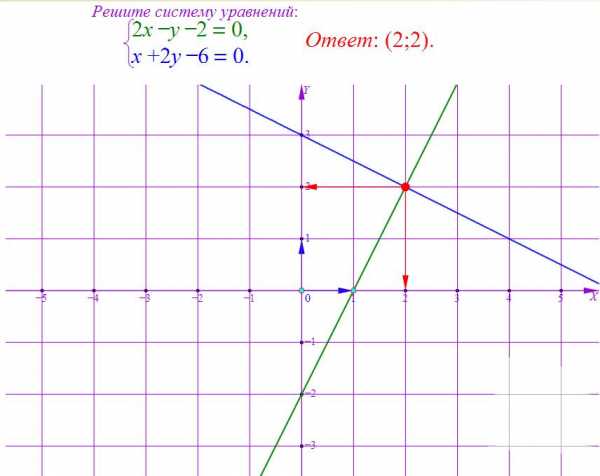
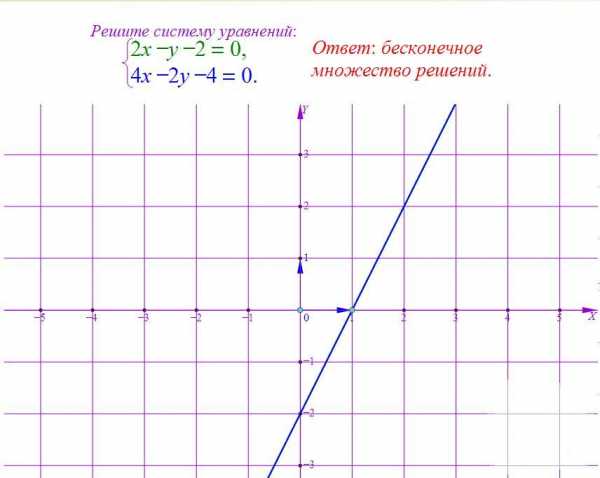
—Пока мы будем проверять домашнее задание, у доски нам решит систему графическим методом…(вызвать ученика к доске, задание на карточке).

Открыли тетради, взяли зеленую пасту, проверяем:

Слайды №5, №6, №7, №8, №9, №10.

-У кого не было ошибок, может поставить себе «5», у кого были помарки, исправления, неточности – зеленой пастой пишут: Домашнее задание проверено.

-Дома, я также просила поработать вас с текстом параграфа №27, и найти ответ на вопрос: «Какие важные выводы можно сделать с помощью графического способа решения систем уравнений?». Кто нашел ответ на этот вопрос? (стр.63 учебника).

Слайд №11. (строки «выпускать» по мере ответа уч-ся).

—ученик закончил решение системы. Сейчас он прокомментирует нам ее решение.

-Спасибо, садись.

Этап№3

-А сейчас, внимание на экран, я хочу показать вам решение графическим методом еще одной системы:

Слайд№12.

— На чертеже: построен синим цветом график первого линейного уравнения и зеленым цветом график второго уравнения. Как видите, графики пересекаются.

Координаты точки пересечения графиков и будут являться решением данной системы. Координаты данной точки являются решением и первого и второго линейных уравнений, т.к. точка принадлежит и первому и второму графикам функций. Однако, чему конкретно равны абсцисса и ордината точки, определить очень сложно. Точка «висит» внутри определенной клеточки.

Из этого примера видно, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с дробными значениями координат точки.

Этим мы и займемся сегодня на уроке.

Этап№4

-В тетрадях запишите, пожалуйста, число 17 апреля. Классная работа.

Тема урока: «Решение систем уравнений способом подстановки».

Слайд№13-14.

Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. И так:

№1.

Устный счет

Выразить у через х и х через у:

1. х + 3у = 10 3x-y = 3

2. х + у = 2 5x + 2y = 4

3. 2х + 7у = 8 4x + 2y = 6

4. 6х — 5у = 4 6x – 3y = 9

№2. Попробуем решить систему, которая была вам задана домой, другим способом: (учитель начинает рассуждение, затем продолжают ученики). Слайд №15

Выразим из 2 уравнения x через y:

Подставим в первое уравнение вместо x выражение, которое мы получили

Решаем первое уравнение с одной переменной

Ответ(2;2)

-Чем эти рассуждения отличались от тех, которые вы применяли дома при решении этой системы графическим методом?

-Откройте, пожалуйста, учебник на странице 236 и, прочитав текст, ответьте мне на этот вопрос.

-Как же мы рассуждали? Еще раз по учебнику прочитает нам………..

-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений — почему?

Итак: — выразили

— подставили

— решили

-нашли

-записали ответ

В учебнике найдите алгоритм решения и внимательно прочитайте его.

Слайд№17. («выпускать» строки по мере озвучения уч-ся)

-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.

Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.

Слайд №18.

-Давайте вернемся к системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске….)

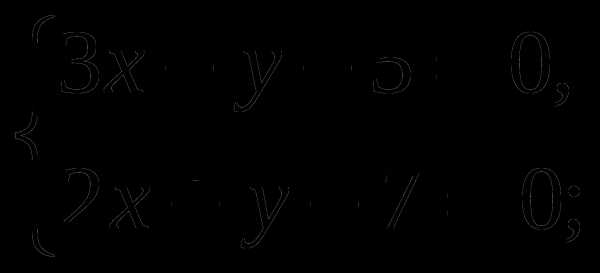
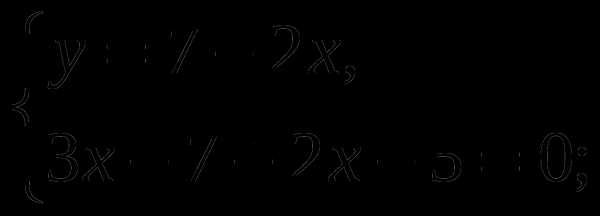
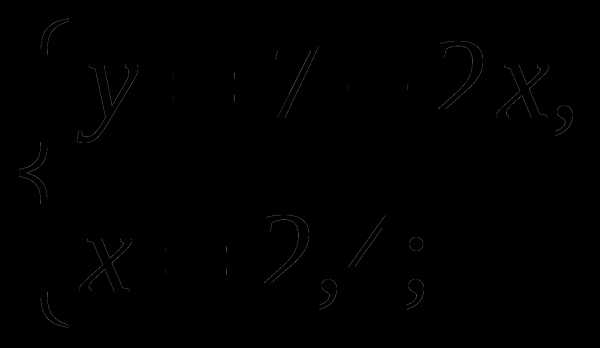
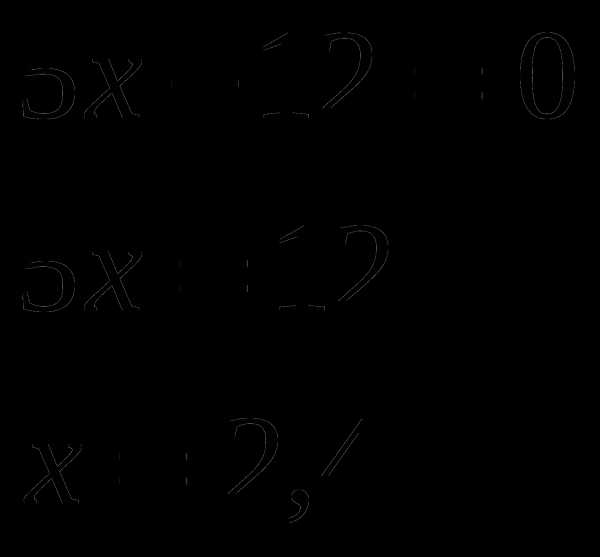
Ответ: ( 2,4 ;2,2)

Слайд №19.

Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа)

Теперь будем работать по учебнику стр. 238, № 1086 (а), 1088 (б), 1091 (б).

-Сегодня мы познакомились с вами с еще одним способом решения систем двух линейных уравнений с двумя переменными. Сформулировали алгоритм этого метода. На следующих уроках мы отработаем этот алгоритм на более сложных системах и познакомимся с еще одним очень интересным способом решения.

Домашнее задание: параграф 27 знать алгоритм № 1087, 1090, 1092*.

Оценки сегодня получили:……….

Спасибо за урок. До свидания.

infourok.ru