Медианы, биссектрисы и высоты треугольника. 7 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Презентация к уроку геометрии
«Медианы, биссектрисы и высоты
треугольника».
7 класс
Учитель математики МОБУ СОШ № 92 г. Сочи
Утёсова Е.А.
ТРИ ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ
ТРЕУГОЛЬНИКА
Медиана
Биссектриса
Высота
отрезок, соединяющий вершину треугольника с
серединой противолежащей стороны.
отрезок, который соединяет вершину

треугольника в точкой на противолежащей
стороне и делит внутренний угол пополам.
перпендикуляр, опущенный из вершины
треугольника на прямую, содержащую
противолежащую сторону треугольника.
ТРИ ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ
ТРЕУГОЛЬНИКА
Медиана
Биссектриса
Высота
отрезок, соединяющий вершину треугольника с
серединой противолежащей стороны.
отрезок, который соединяет вершину
треугольника в точкой на противолежащей
стороне и делит внутренний угол пополам.
перпендикуляр, опущенный из вершины
треугольника на прямую, содержащую
противолежащую сторону треугольника.
Три медианы пересекаются в
одной точке, которая всегда
находится внутри
треугольника (центр масс
треугольника)
Каждая медиана точкой пересечения
делится в отношении 2 : 1, считая
от вершины
c
b
Три медианы делят
треугольник на 6
равновеликих треугольников
(одинаковой площади)
a
Длина медианы
b
c
a1
a2
a
Три биссектрисы пересекаются в
одной точке, которая всегда
находится внутри треугольника.
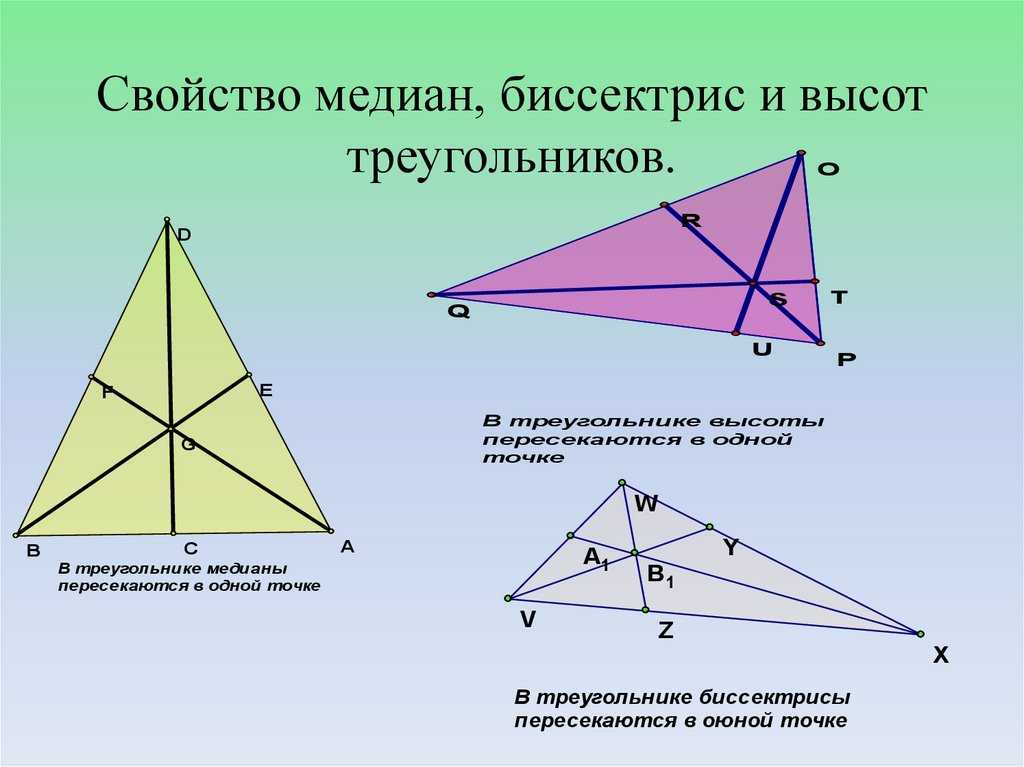
Эта точка является центром
вписанной окружности.
Биссектриса делит сторону
треугольника на отрезки,
пропорциональные двум
другим сторонам:
b
Длина биссектрисы
c
c
b
a
Прямые, содержащие высоты
треугольника, пересекаются в
одной точке. Эта точка
называется ортоцентром
Высоты треугольника
обратно пропорциональны
его сторонам:
c
b
a
Длина высоты
Три медианы пересекаются в одной
точке, которая всегда находится
внутри треугольника (центр масс
треугольника)
Каждая медиана точкой
пересечения делится в отношении
2 : 1, считая от вершины
Три медианы делят треугольник
на 6 равновеликих треугольников
(одинаковой площади)
c
b
a
Длина медианы
Три биссектрисы пересекаются в
одной точке, которая всегда
находится внутри треугольника.
Эта точка является центром
вписанной окружности.
b
a1
c
a2
a
Биссектриса делит сторону
треугольника на отрезки,
пропорциональные двум
другим сторонам:
b
Длина биссектрисы
c
Прямые, содержащие высоты
треугольника, пересекаются в
одной точке. Эта точка
называется ортоцентром
c
b
a
Высоты треугольника
обратно пропорциональны
его сторонам:
b
a
Длина высоты
c
Геометрия, 7 – 9. Учебник для общеобразовательных
учреждений./ Л.С.Атанасян, В.Ф. Бутузов и др.М.:Просвещение, 2010.-384с.
Поурочные разработки по геометрии к учебному
комплекту Л.С.Атанасян и др. 7 класс./Н.Ф.Гаврилова –
М.:ВАКО, 2009.- 368с.
Геометрия 7. Рабочая тетрадь./Ю.А.Глазков и др. –
М.:Просвещение, 2009. – 96с.
Дидактические материалы по геометрии для 7./Б.Г.Зив и
др. – М.:Просещение, 2009. – 144с.
Наглядный справочник по математике для 7-11
классов./Л.Э.Генденштейн. – М.:Илекса, 2010. – 96с.

English     Русский Правила

Презентация к уроку — Медианы, биссектрисы и высоты треугольника

7 класс

Медианы, биссектрисы и высоты треугольника.

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и соединенных попарно отрезками

Точки А, В и С – вершины треугольника

Отрезки АВ, ВС и АС –

стороны треугольника

В

АВС, ВАС, ВСА –

углы треугольника

А

С

Перпендикуляр к прямой

А  а, АН  а

Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а

, если прямые АН и а перпендикулярны.

А

н

а

2

Теорема о перпендикуляре

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

А

н

а

2

Медиана треугольника

А

СМ = МВ

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника .

В

С

М

АМ – медиана треугольника

2

Биссектриса треугольника

А

 АСА =  ВАА

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника .

В

С

А

1

АА1 – биссектриса треугольника

6

Высота треугольника

А

АН  СВ

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника .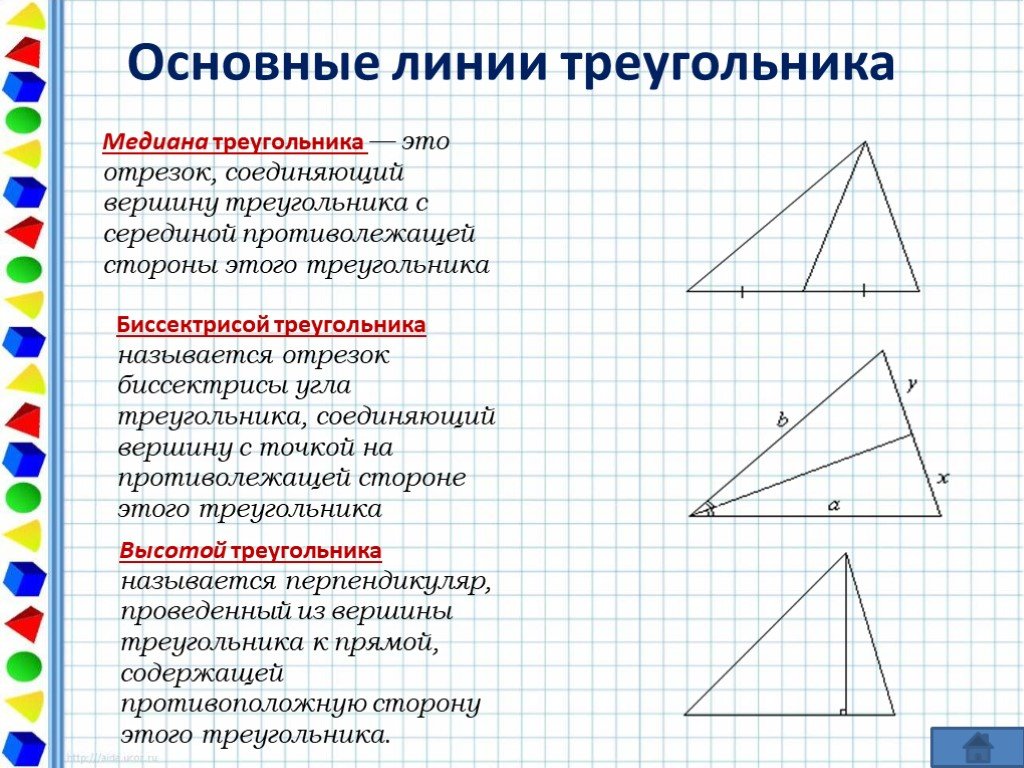

В

Н

С

АН – высота треугольника

6

Медианы в треугольнике

В любом треугольнике медианы пересекаются в одной точке.

6

Биссектрисы в треугольнике

В любом треугольнике биссектрисы пересекаются в одной точке.

6

Высоты в треугольнике

В любом треугольнике высоты или их продолжения пересекаются в одной точке

6

Замечательное свойство

В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются в одной точке.

6

Задание

С помощью чертежных инструментов найдите на рисунке:

а) медиану;

б) биссектрису;

в) высоту

треугольника MKT.

а) Медиана – отрезок .

б) Биссектриса – отрезок .

в) Высота – отрезок .

BT

AK

CH

6

Задание

Назвать элемент и дать его определение

Рефлексия

Выберите каждый по 1-2 предложения и закончите их.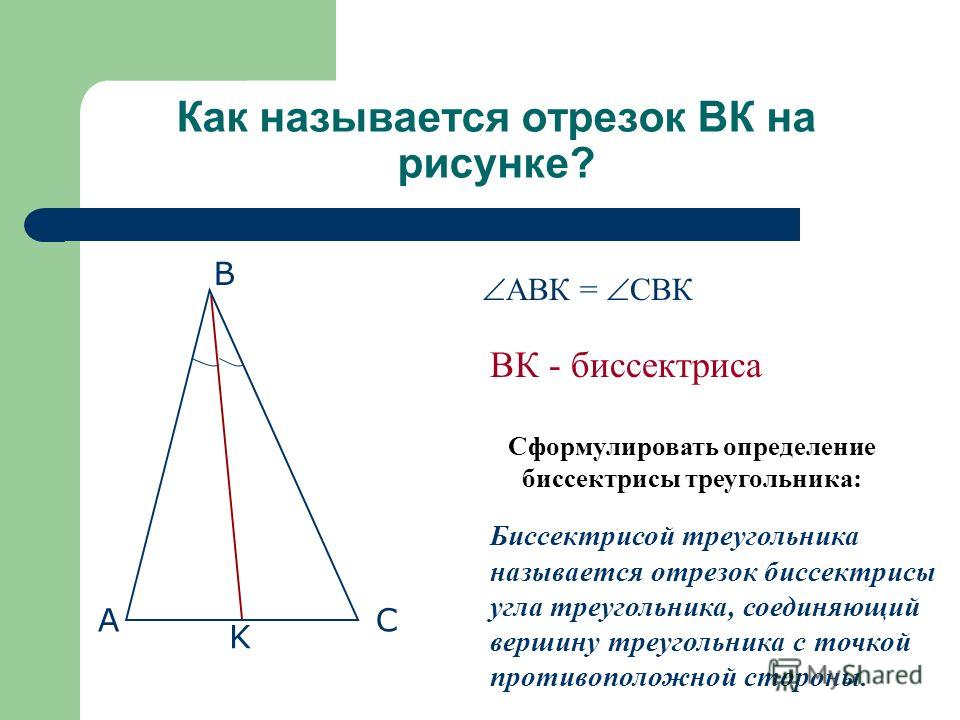

• Сегодня на уроке я узнал…
• Я понял, что…
• На уроке было трудно…
• На уроке я научился…
• Я смог…
• На уроке было интересно узнать, что…
• Меня удивило…
• Мне захотелось…

Спасибо за урок!

6

Высоты Медианы и биссектрисы углов

Точно так же, как существуют специальные имена для особых типов треугольников, существуют специальные имена для особых отрезков внутри треугольников. Разве это не особенное?

База и высота

Каждый треугольник имеет три оснований (любая из его сторон) и три высот (высот). Каждая высота представляет собой перпендикулярный отрезок от вершины к противоположной стороне (или продолжение противоположной стороны) (рис. 1).

Рисунок 1  Три основания и три высоты одного и того же треугольника.

Высоты иногда могут совпадать со стороной треугольника или иногда могут пересекаться с расширенным основанием за пределами треугольника. На рисунке 2 AC — это высота основания BC , а BC — высота основания AC .

Рисунок 2  В прямоугольном треугольнике каждый катет может служить высотой.

На рис. 3, AM — высота до базы BC .

Рисунок 3  Высота тупоугольного треугольника.

Интересно отметить, что в любом треугольнике три прямые, содержащие высоты, пересекаются в одной точке (рис. 4).

Рисунок 4  Три линии, содержащие высоты, пересекаются в одной точке, 

, который может быть или не быть внутри треугольника.

Медиана

А медиана в треугольнике — это отрезок, проведенный от вершины к середине противоположной стороны. Каждый треугольник имеет три медианы. На рисунке 5 E является средней точкой BC . Следовательно, БЭ = ЭК . AE является медианой Δ ABC.

Рисунок 5  Медиана треугольника.

В каждом треугольнике три медианы сходятся в одной точке внутри треугольника (рис. 6).

Рисунок 6  Три медианы сходятся в одной точке внутри треугольника.

Биссектриса угла

Биссектриса угла в треугольнике — это отрезок, проведенный из вершины, которая делит пополам (разрезает пополам) этот угол при вершине. У каждого треугольника есть три биссектрисы угла. На рисунке , представляет собой биссектрису угла в Δ ABC.

Рисунок 7  Биссектриса угла.

В каждом треугольнике три биссектрисы угла пересекаются в одной точке внутри треугольника (рис. 8).

Рисунок 8  Биссектрисы трех углов пересекаются в одной точке внутри треугольника.

Как правило, высоты, медианы и биссектрисы являются разными отрезками. Однако в некоторых треугольниках они могут быть одними и теми же сегментами.

На рисунке можно доказать, что высота, проведенная из угла при вершине равнобедренного треугольника, является медианой, а также биссектрисой угла.

Рисунок 9  Высота, проведенная из угла при вершине равнобедренного треугольника.

Пример 1: На основе маркировки на рисунке 10 назовите высоту Δ QRS, назовите медиану Δ QRS, и назовите биссектрису угла Δ QRS .

Рисунок 10  Нахождение высоты, медианы и биссектрисы угла.

RT является высотой до основания QS , потому что RT ⊥ QS .

SP является медианой базы QR , поскольку P является средней точкой QR .

QU является биссектрисой угла Δ QRS , поскольку делит пополам ∠ RQS.

Высота и медиана треугольника – свойства, примеры и примеры решения

Медиана треугольника – это отрезок прямой линии, проведенный от вершины треугольника к средней точке противоположной стороны. Он делит противоположную сторону треугольника на два равных отрезка. Это означает, что мы знаем, что это медиана, если у нас есть эти равные отрезки. Итак, на приведенной ниже диаграмме линия «AB» называется «медианой».

 

Давайте узнаем еще о двух терминах «высота и медиана треугольника» в следующей статье. Мы надеемся, что доступный контент поможет вам лучше понять медианы главы и высоты треугольников.

 

(Изображение будет загружено в ближайшее время)

Свойства медианы треугольника

1. В треугольнике может быть до трех медиан, по одной из каждой вершины. Обратитесь к следующему изображению.

2. Однако, когда мы рисуем три медианы, они всегда пересекаются в одной точке. И эта единственная точка известна как центр тяжести треугольника.

3. Медианы делят треугольники пополам. На самом деле два новых треугольника, образованные добавлением медианы, имеют равные площади.

4. Эти шесть (6) треугольников, образованных тремя (3) медианами, также состоят из равных площадей.

(Изображение будет загружено в ближайшее время)

Что такое высота треугольника?

Высота — это отрезок перпендикулярной линии, проведенный из вершины треугольника к противоположной стороне. В нашем треугольнике на приведенной выше диаграмме, если мы проведем линию из вершины А перпендикулярно противоположной стороне, она будет известна как высота. Однако мы могли бы сделать это из любой вершины, но чаще всего мы видим это сверху. Как и в случае с медианой, у нас также есть отношение к свойствам треугольника.

 

(Изображение будет загружено в ближайшее время)

 

Свойства высоты треугольника

• Каждый треугольник может иметь 3 высоты, т. е. по одной из каждой вершины, как вы можете ясно видеть на изображении ниже.

• Все 3 высоты треугольника всегда встречаются в одной точке, независимо от формы треугольника.

• На приведенной выше диаграмме также видно, что высота — это кратчайшее расстояние от вершины до ее противоположной стороны.

Разница между медианой и высотой треугольника 

Если вы запутались между этими двумя терминами: медианой и высотой треугольника и думаете, одинаковы они или нет, то позвольте мне разъяснить вам здесь.

 

Ответ: Нет. Высота и медиана в треугольнике не совпадают.

 

Высота – это биссектриса, лежащая на любой стороне треугольника, и она измеряет расстояние между вершиной и линией, являющейся противоположной стороной, тогда как медиана – это отрезок, соединяющий вершину с центральной точкой треугольника. Обратная сторона. Следовательно, медиана не обязательно должна быть перпендикулярна каждый раз. Однако в случае равностороннего треугольника медиана и высота всегда одинаковы.

 

Решенные примеры

Пример: 

Данные углы треугольника PQR относятся как 3 : 2 : 1. Вычислите все углы ΔPQR.

Решение: 

Пусть первый угол P равен x.

Следовательно, ∠B = 2x и ∠C = 3x

Мы знаем, что сумма всех углов треугольника = 180°

x + 2x + 3x = 180°

6x = 180°

x = 30

Итак, ∠P = 30°

∠Q = 2 × 30° = 60°,

∠R = 3 × 30° = 90°.

Таким образом, треугольник является разносторонним с тремя различными углами

 

Построение медианы треугольника с помощью компаса

Построение медианы треугольника с помощью компаса имеет очень простой метод.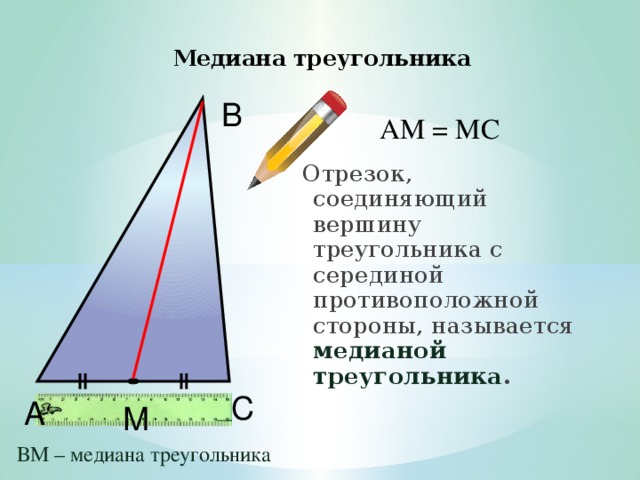 В этом методе ученики должны иметь весы, карандаш и циркуль. Во-первых, вы должны снять мерку с компаса и нарисовать дуги одинакового размера вверх с каждой стороны.

В точку, образованную пересечением дуг, проведите отрезок перпендикулярной линии к основанию треугольника. И так вы делаете медиану треугольника. Нарисовав отрезок с серединой, основание уже разделено на равные размеры.

Уникальные сведения о медиане и высоте

Высота и медиана треугольника во многих случаях могут совпадать. Хотя единственное различие между медианой и высотой, которое учащиеся могут заметить, заключается в том, как они нарисованы. Медиана проводится от вершины треугольника к середине основания. При этом высота проводится от любой вершины треугольника к противоположной стороне, перпендикулярной ей. Количество высот и медианы, которые может иметь треугольник, равно трем для обоих.

В равностороннем треугольнике медиана и высота равны. Это связано с тем, что перпендикулярная линия, проведенная из вершины треугольника к основанию, пересекает его одинаково.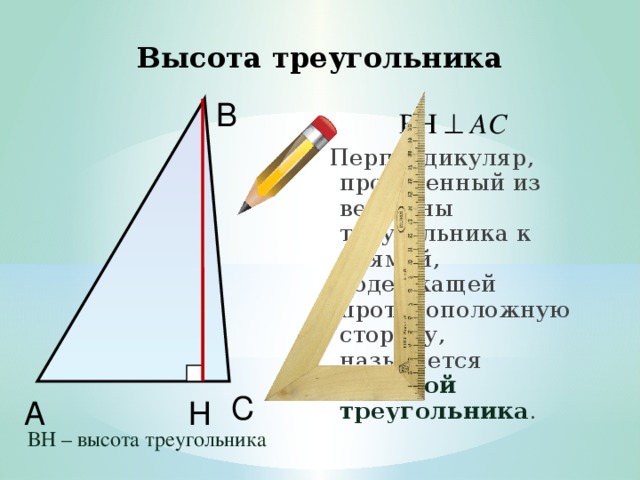 Также в равнобедренном треугольнике высота и медиана одинаковы. В этом случае высотный и срединный треугольники могут иметь три биссектрисы угла. И они всегда встречаются в одной и той же точке.

Как мы уже знаем о случае равносторонних треугольников и равнобедренных треугольников, высоты могут также находиться вне треугольника. Это происходит в основном для тупоугольных треугольников.

Параллелизм в медиане

Медианы в треугольниках не подчиняются правилу всегда быть перпендикулярными биссектрисами. Это не похоже на то, что каждая медиана не перпендикулярна. Они являются биссектрисами равносторонних треугольников. Точно так же он не делит пополам каждый треугольник, как равносторонний треугольник.

Существует способ доказательства параллелизма в медиане. И этот метод называется подходом координатной геометрии. В этом методе мы должны взять одну вершину в качестве начала координат. Так что одна сторона треугольника должна стать осью x.