Олимпиадные задания по алгебре (7 класс) по теме: сборник олимпиад для 7 класса по математике

Олимпиадные задачи для 7 класса 

Сумма двух чисел равна 13,5927. Если в большем из них перенести запятую на один знак влево, то получим меньшее число. Чему равны эти числа?

Вычислите: 2379 • 23782378 — 2378 • 23792379.

Один из четырёх гангстеров украл чемодан с деньгами. На допросе Алекс сказал, что чемодан украл Луи, Луи утверждал, что виновник Том, Том заверял следователя, что Луи лжёт. Жорж настаивал только на том, что он не виноват. В ходе следствия выяснилось, что только один из гангстеров сказал правду. Кто украл чемодан?                                                                          

Найдите площадь закрашенной фигуры:    

В каждой клетке шахматной доски 5×5 сидит жук. В некоторый момент по команде все жуки переползают на соседние (по горизонтали или по вертикали) клетки. Докажите, что при этом одна из клеток обязательно останется пустой.

Леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99 % сосен. Мы будем рубить только сосны. После их вырубки останется 98 % от всех деревьев». Какая часть леса будет вырублена?

Коза и корова съедают воз сена за 45 дней, корова и овца — за 60 дней, овца и коза — за 90 дней. За сколько дней съедят воз сена коза, овца и корова вместе?

Делится ли число  44444…44 на 8?

       2005штук

Докажите, что число 2 делится на 9.

Два поезда движутся навстречу друг другу по параллельным путям — один со скоростью 60 км\ч, а другой со скоростью 80 км\ч. Пассажир, сидящий во втором поезде, заметил, что первый поезд шел мимо него в течение 6 с. Какова длина первого поезда?

Магазин продал третью часть полученных апельсин и ещё 32 кг, третью часть остатка и ещё 32 кг отпустил школьной столовой, третью часть нового остатка и ещё 32 кг передали детскому саду, после чего осталась третья часть нового остатка и ещё 32 кг. Сколько кг апельсин было в магазине первоначально?

Имеется 9 пластинок и двухчашечные весы без гирь. По виду все пластинки одинаковые, но одна из них легче других. Как с помощью двух взвешиваний найти более лёгкую пластинку?

В приёмной 10 кресел. Сколькими способами в них могут разместиться 4 посетителей?

У звезды ACFBD равны углы при вершинах А и В, углы при вершинах F и С, а также длины отрезков АС и ВF. Докажите, что AD = BD.                                                  

Малыш и Карлсон поочерёдно берут конфеты из одного пакета. Малыш берёт    одну конфету, Карлсон — две, затем Малыш берёт 3 конфеты, Карлсон — 4, и так далее. Когда количество оставшихся в пакете конфет станет меньше необходимого, тот, чья очередь наступила, заберёт все оставшиеся конфеты. Сколько конфет было в пакете первоначально, если у Малыша в итоге оказалось 101 конфета?

Вычислите: ;

Два джентльмена одновременно отправились на прогулку по аллее длиной 100 метров. Мистер Смит за час проходит 1 км, мистер Джонс идёт помедленнее — всего 600 метров в час. Дойдя до конца аллеи, каждый поворачивает и с прежней скоростью идёт обратно. Встречаясь, они каждый раз раскланиваются. Сколько раз они раскланиваются на протяжении первых 25 минут? Сколько времени из этих 25 минут они шли в одном направлении?

В бутылке, стакане, кувшине и банке находится молоко, лимонад, квас, вода. Известно, что вода и молоко находятся не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?

Сколько белых грибов надо собрать для получения 1 кг сушеных, если при переработке свежих грибов остаётся 50 % их массы, а при сушке остаётся 10 % массы обработанных грибов?

Углы 60° и 40° имеют общую сторону. Найдите отношение меры угла, образованного не общей стороной угла 40° и биссектрисой большего угла, к мере большего угла.

Сколько рыб в пруду? Некий ихтиолог хотел определить, сколько в пруду рыб, годных для улова. Для этого он забросил сеть с заранее выбранным размером ячеек и, вытащив её, обнаружил 30 рыб, отметил каждую из них меткой и бросил в пруд. На другой день забросил ту же самую сеть и поймал 40 рыб, на 2 из которых были его метки. Как по этим данным он приблизительно вычислил сколько рыб в пруду?

 Найти все такие целые числа х и у,  такие   что    (1 +у)(ху — 1) = 3.

Число х при делении на 10 даёт в остатке 3, а число у при делении на 10 даёт в остатке 2. Доказать, что сумма (х + у) делится нацело на 5.

Среднее арифметическое шести чисел равно 345, а среднее арифметическое четырёх других чисел равно 555. Чему равно среднее арифметическое всех десяти чисел?

В комнате стоят табуретки и стулья, у каждой табуретки 3 ножки, у каждого стула 4 ножки. Когда на всех табуретках и стульях сидят люди, в комнате 39 ног. Сколько стульев и табуреток в комнате?

Теплоход проходит путь от А до В по течению за 3 часа, а возвращается обратно за 4 часа. За какое время путь от А до В преодолевает плот?

Решите уравнение:  || х — 674| -1| = 4.

В классе учатся 40 человек. Из них по русскому языку имеют «3» 19 человек, по математике — 17 человек и по физике — 22 человека. Только по одному предмету имеют «3»: по русскому языку — 4 человека, по математике — 4 человека и по физике 11 человек. Семь человек имеют «3» и по математике, и по физике, из них пятеро имеют «3» и по русскому языку. Сколько человек учатся без троек?

В шестизначном числе первая цифра совпадает с четвёртой, вторая — с пятой, третья — с шестой. Докажите, что это число кратно 7, 11, 13.

Докажите, что если треугольники АВМ и АВМ равны, то треугольники CDMи CDM тоже равны.

nsportal.ru

Задания олимпиад по математике для 7 класса (школьный тур)

Задания для школьного этапа олимпиады по математике

2017-2018 учебный год

1. класс

1. Даны числа: 5, 10, 15, 20, 25, 30, 35, 40, 45. Впишите их в клетки девятиклеточного квадрата так, чтобы получилось в сумме одно и то же число по любой вертикали, горизонтали и диагонали.

1. Решить уравнение: 2 (х² + х) – (х² + 3х – 12 )= х².

1. Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили?

2. Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра, в Петропавловске-Камчатском полдень. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?

3. Цена товара дважды увеличивалась: сначала на 20%, потом – на 30%. На сколько процентов увеличилась цена товара в результате двойного повышения?

Решение

для школьного этапа олимпиады по математике

2017-2018 учебный год

7 класс

1. Даны числа: 5, 10, 15, 20, 25, 30, 35, 40, 45. Впишите их в клетки девятиклеточного квадрата так, чтобы получилось в сумме одно и то же число по любой вертикали, горизонтали и диагонали.

Ответ:

20	45	10
15	25	35
40	5	30

2.

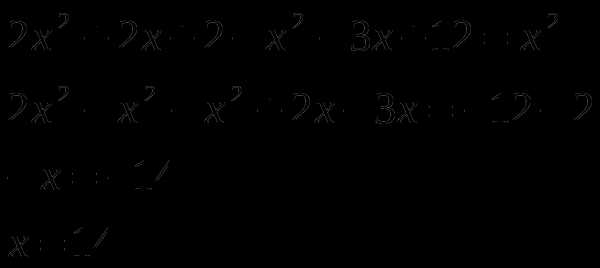
Ответ: 14

3. Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили?

Из условия следует, что 100 – 4 = 96 делится на искомое число.
Также 90-18=72 делится на искомое число.
Их разность также делится на искомое число: 96 – 72 = 24. 
Следовательно, искомое число — 24, так как на него делится и 96, и 72. 

Ответ: 24

4. Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра, в Петропавловске-Камчатском полдень. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?

Москва Чикаго Петропавловск-Камчатский

12-00 03-00(т.е Москва – 9 час) —

03-00 — 12-00(т.е. Москва + 9 час)

? 03-00

03-00 – 9 час = 18-00 (в Москве)

18-00 – 9 час = 09-00 (в Чикаго)

Ответ 9 часов утра

1. Цена товара дважды увеличивалась: сначала на 20%, потом – на 30%. На сколько процентов увеличилась цена товара в результате двойного повышения?

Пусть x – первоначальная цена товара,

1,2 x – цена после первого повышения,

1,3(1,2x)- цена после второго повышения, 1,3*1,2x=1,56x, значит на 56%.

Ответ: на 56 %.

videouroki.net

Задания по математике 7 класс

1. Вставьте вместо букв цифры так, чтобы получилось верное равенство:

ДУБОК+ДУБОК+ДУБОК+ДУБОК+ДУБОК+ДУБОК+ДУБОК+ДУБОК+ДУБОК=ЛЕСОК.
Одинаковым буквам должны соответствовать одинаковые цифры, а разным буквам — разные цифры. Постарайтесь найти все возможные решения ребуса.

Ответ: Ребус имеет 2 решения: Д=1, У=0, Б=4, О=2, К=5, Л=9, Е=3, С=8, и Д=1, У=0, Б=8, О=2, К=5, Л=9, Е=7, С=4 Легко определить Д, У и Л (9 пятизначных чисел дают пятизначное, значит ДУБОК — маленький, а ЛЕСОК — большой). Ясно также, что ОК=25. Остальное небольшим перебором.

 

2. На сколько частей могут разделить плоскость три прямые? Укажите все возможные варианты.

Ответ: Небольшой перебор показывает, что количество частей может быть: 4 (все прямые параллельны), 6 (две прямые параллельны, или все три пересекаются в одной точки) или 7 (нет параллельных и нет общей для всех трех прямых точки). Ответ: 4, 6, 7.

 

3. Найдите все четверки (x, y, z, t), состоящие из простых чисел, удовлетворяющих уравнению:

xyz + 1 = t²

Ответ: t не может быть равно 2, так как t² ≥ 2 · 2 · 2 + 1 = 9. Следовательно, t — нечетное. Но тогда t² −1 = (t−1)(t+1) — произведение двух подряд идущих четных чисел, и, следовательно, xyz = t² −1 делится на 2 · 4 = 8. Ответ: x = y = z = 2, t = 3.

 

4. Какой угол образуют часовая и минутная стрелки часов в 20 часов 12 минут?

Ответ: 12 минут — это пятая часть часа. Следовательно, угол между минутной стрелкой и направлением на 12 часов («вверх») в рассматриваемый момент времени равен 360◦ /5 = 72◦ . Угол между часовой стрелкой и направлением «вверх» равен (8 + 1/5) · 360◦ /12 = 246◦ . Искомый угол: 246◦ − 72◦ = 174◦ . Ответ: 174◦ .

 

5. 2012 конфеток «Чудесная алгебра» весят x кг, а 2013 конфеток «Волшебная геометрия» весят y кг. За победу в олимпиаде по алгебре Таня получила от жюри 2012 конфеток «Чудесная алгебра» и одну конфетку «Волшебная геометрия». За победу в олимпиаде по геометрии Петя получил от жюри 2013 конфеток «Волшебная геометрия» и одну конфетку «Чудесная алгебра». Оказалось, что призы Тани и Пети имеют одинаковый вес. Что больше: x или y?

Ответ: Пусть Таня съест из своего набора две разные конфетки, и так же поступит Петя. У Тани останется 2011 конфеток «Чудесная алгебра», а у Пети 2012 конфеток «Волшебная геометрия», вес же останется равный. Из этого ясно также, что конфетка «Чудесная алгебра» тяжелее конфетки «Волшебная геометрия». Добавим Тане «Чудесную алгебру», а Пете «Волшебную геометрию». Теперь у Тани набор тяжелее, чем у Пети, при этом у нее x кг, а у Пети y кг. Ответ: x > y.

Вконтакте

Facebook

Twitter

Google+

Одноклассники

olimpotvet.ru

Олимпиада по математике 7 класс с ответами 2017-2018 школьный этап

1. Две лошади начали пить воду из одного бака, до верху наполненного водой. Гнедая лошадь выпила половину трети четверти половины бака, а вороная – четверть половины трети половины бака. Какая лошадь выпила больше воды?

6 баллов)

2. Замените буквы цифрами так, чтобы получилось верное равенство

АААА + ВВВ + С = 2005,

если известно, что одинаковые буквы соответствуют одинаковым цифрам, разные – разным.

(7 баллов)

3. Дедушка решил подарить внукам по новогоднему подарку, состоящему из конфеты, яблока, апельсина, шоколадки и книги. На те же деньги он мог купить одни конфеты и их оказалось бы 224, яблоки– их было бы 112, апельсины – 56, шоколадки – 32, а книг – 16. Сколько внуков у дедушки?

(10 баллов)

4. Огород квадратной формы 5 м × 5 м нужно разделить несколькими кусками ячеистой сетки на 5 равных по площади «клетчатых» участков. Это легко сделать, используя 20 м сетки, как показано на рисунке.

        Хватит для этой цели 16 м сетки? Выполните рисунок.

(8 баллов)

5. Каждый из трех мальчиков либо всегда говорит правду, либо всегда лжет. На вопрос «Есть ли хотя бы один лжец среди двух остальных?» первый ответил: «Нет», второй ответил: «Да». Какой ответ дал третий мальчик. Ответ объясните.

(9 баллов)

Ответы, указания, решения

VII класс

1. Ответ: лошади выпили равное количество воды.

Решение.

1)  – такую часть воды из бака выпила гнедая лошадь,

2)  – такую часть воды из бака выпила вороная лошадь.

2. Ответ: 1111+888+6=2005.

3. Ответ: 8 внуков.

Решение. Замечаем, что яблоко «стоит» 2 конфеты, апельсин – 4 конфеты, шоколадка – 7 конфет, книга – 14 конфет. Значит, «цена» подарка равна 1+2+4+7+14=28 (конфет). Следовательно, внуков у дедушки 224:28=8.

4. Ответ: хватит.

Решение. Одно из возможных решений показано на рисунке.

5. Ответ: «Нет».

Решение. Если предположить, что первый мальчик сказал правду, то оказывается, что все трое правдивы, а второй мальчик солгал, т.е. получаем противоречие. Значит, первый мальчик лжец, а второй сказал правду.

Предполагая, что третий мальчик всегда говорит правду, получаем, что первый ученик сказал правду, т.е. получаем противоречие. Значит, третий мальчик – лжец, т.е. он солгал и ответил: «Нет».

konspekt-v-gruppe.ru

Олимпиадные задачи по математике в 7 классе |

В серию математических задач-игр входит несколько типов игровых задач. Среди них  есть и игры-шутки. На олимпиадах по математике разного уровня игровые задачи предлагаются не только в 7 классе. 

Но цель данной статьи – рассмотреть примеры олимпиадных задач для 7 класса типа “игра-шутка”, причем эти задачи можно использовать в качестве допрофильной подготовки семиклассников к обучению в классах с углубленным изучением математики.

Игры-шутки.

Рассмотрим вначале те игры, результат которых не зависит от того, как играют соперники, а зависит только от начальных условий игры. Такие игры называют еще играми-шутками.
Разберем несколько задач этого типа.

Задача 1.

В мешке лежат 73 конфеты. Двое берут из мешка по очереди конфеты от 1 до 10. Когда разобраны все конфеты, игроки подсчитывают, кто сколько набрал конфет. Если эти числа взаимно простые — выигрывает первый игрок, в противоположном случае выигрывает второй.

Решение.
Число 73 — простое. Все конфеты разделили на две кучки по а и b конфет в каждой, т.е. а + b = 73.
Могут ли а и b быть всегда взаимно простыми (НОД (а; b) = 1)? Не знаем. А могут а и b быть не взаимно простыми? Если НОД (а; b) = c; с ≠1, то а + b делится на с, но тогда 73 должно делится на с, a 73 — простое. Противоречие. Следовательно, при любом разбиении 73 на два слагаемые, они взаимно простые. Всегда выигрывает первый.

Теперь можно составить сколько угодно таких задач. Следует брать количество предметов (конфет, камней и т.д.) — простое число, правила игры (по сколько предметов игроку брать каждый раз) не играют роли. Всегда а и b получим взаимно простыми.

Попутно мы «открыли» важное свойство простых чисел:

Простые числа можно представить в виде суммы двух, трех и т.д. слагаемых, но обязательно эти слагаемые взаимно простые между собой.

Примеры
17 = 2 +15 = 3 + 14 = 4+13 ит.д.
НОД (12; 15) = 1; НОД (3; 14) = 1; НОД (4; 13) = 1 и т.д.

Кроме того, если слагаемых два, то они не могут быть одинаковой четности.
Если они четные, сумма четная, а значит, число составное.
Если они оба нечетные, то их сумма снова четная.

Следовательно, простое число представить легко в виде сумы двух взаимно простых чисел разной четности.

19 = 2+17 = 3+ 16 = 4+15 и т.д.

Задача 2.

На доске написано n чисел в строку. Игроки расставляют по очереди между ними знаки “+” или “-“. После того, как все места заполнены, подводится итог. Если результат четный, то выигрывает 1-й игрок, если нечетный, – выигрывает 2-й игрок.

Решение.
Пусть игра окончена. Обозначим четные числа «r», а нечетные — «n». Проанализируем, от чего зависит результат (четность, нечетность полученной суммы). Так как r ± r =>r; n ± n => r; r ± n => n, то результат зависит только от числа нечетных чисел, записанных на доске. Если количество нечетных чисел четно, то сумма четная и выигрывает 1-й игрок, в противном же случае выигрывает 2-й игрок.

А вот игра, где результат зависит только от количества ходов.

Задача 3.

Есть три кучи камней. В первой — 25, во второй — 30, в третьей — 36 камней. За один ход разрешается любую кучу разделить на две меньшие. Проигрывает тот, кто не сможет сделать ход.

Решение.
Вначале посчитаем, сколько всего камней в трех кучах. 25 + 30 + 36 = 91. В конце игры получим 91 кучку камней по одному в кучке, 91 — нечетное число. После каждого очередного хода любого игрока одна куча исчезает, а вместо нее появляются две, следовательно, общее число куч увеличивается на 1. Изначально есть уже 3 кучи, чтобы получить 91 кучку, надо сделать 91 – 3 = 88 ходов. Игра будет закончена на 88 ходу — четное число. Четные ходы делает второй игрок. Он всегда выигрывает.
А как обеспечить выигрыш первому? (Сумма числа камней в трех кучах должна быть четной).

Задача 4 и ее решение (кликните по картинке).

Итак, олимпиадные задачи по математике для учащихся 7 класса в виде игры-шутки могут служить мощным инструментом в развитии интеллекта школьника. Они формируют не столько знания, сколько умение рассуждать логически, ориентироваться в нестандартных ситуациях, предвидеть результат  и конечно смело действовать.

Уместно вспомнить слова русского математика В.П. Ермакова:

В математике следует помнить не формулы, а процесс мышления .

Олимпиадные задачи по математике для учащихся 7 класса в виде игр-шуток достигают именно таких целей.

repetitor-problem.net

«10 задач для подготовки к Всероссийской олимпиаде школьников по математике. 7 класс».

«10 задач для подготовки к Всероссийской олимпиаде школьников по математике»

7 класс.

Условия задач.

1. Расставьте скобки, чтобы равенство стало верным: 0,5 + 0,5 : 0,5 + 0,5: 0,5 = 5.

2. На листке написано выражение: 4 − 5− 7 −11−19 = 22. Расставьте знаки модуля так, чтобы получилось верное равенство.

3. Замените буквы цифрами так, чтобы получилось верное равенство: ГОЛ * ГОЛ = ФУТБОЛ,

если известно, что одинаковые буквы соответствуют одинаковым цифрам, разные – разным.

4. Сократите дробь: .

5. Из натурального числа вычли сумму его цифр и получили 2016. Найдите наибольшее возможное исходное число.

6. В ящике 24 кг гвоздей. Как на чашечных весах без гирь и без стрелки отмерить 9 кг?

7. Пять кошек и четыре котёнка весят 19 кг. Четыре кошки и пять котят весят 17 кг. Сколько весит кошка и сколько весит котёнок?

8. Маугли попросил своих друзей-обезьян принести ему орехов. Обезьяны набрали поровну орехов и понесли Маугли. Но по дороге они поссорились, и каждая обезьяна бросила в каждую по ореху. В результате Маугли досталось лишь 35 орехов. Сколько орехов собрали обезьяны, если известно, что каждая из них принесла больше одного ореха?

9. Нарисовать треугольник, который можно разделить на 5 равных треугольников.

10. На рисунке изображена часть крепостной стены. Один из камней имеет столь причудливую форму, что если его вытащить из стены и положить иначе, то стена станет ровной. Изобразите этот камень.

Ответы и решения задач:

1. Расставьте скобки, чтобы равенство стало верным: 0,5 + 0,5 : 0,5 + 0,5: 0,5 = 5.

Ответ: ((0,5 + 0,5) : 0,5 + 0,5) : 0,5 = 5 .

2. На листке написано выражение: 4 − 5− 7 −11−19 = 22. Расставьте знаки модуля так, чтобы получилось верное равенство.

Решение: | |4 – 5| −| 7 −11−19|| = 22. Ответ: 22.

3. Замените буквы цифрами так, чтобы получилось верное равенство: ГОЛ * ГОЛ = ФУТБОЛ,

если известно, что одинаковые буквы соответствуют одинаковым цифрам, разные – разным.

Решение:

425 • 425 = 180625.

Ответ: Б – 6, Г – 4, Л – 5, О  2, Т  0, У  8, Ф  1.

4. Сократите дробь: .

Решение: . Ответ: .

5. Из натурального числа вычли сумму его цифр и получили 2016. Найдите наибольшее возможное исходное число.

Решение:

Исходное число не может быть двух- и трёхзначным, так как в этом случае разность числа и суммы его цифр будет значительно меньше, чем 2016. Не может оно быть и пятизначным, так как в этом случае разность числа и суммы его цифр будет значительно больше, чем 2016. Выходит, искомое число  четырёхзначное.

Представим искомое число как = 1000a + 100b + 10c + d.

Если мы вычтем из него сумму его цифр, то получим

1000a +100b +10c + d −(a +b +c +d) = 999a + 99b +9c = 9(111a + 11b + c) = 2016.

Тогда 111a + 11b + c = 2016 : 9 = 224.

Очевидно, что a не может быть равно 3 и больше (111• 3 = 333).

Также a ≠0, a≠1.

Даже если b и c имеют максимально возможные значения (то есть 9), равенства не получается: 111 • 0 + 11 • 9 + 9 = 108, а 111•1+ 11 • 9 + 9 = 219. Значит, a = 2.

В этом случае b не может быть равно единице и больше, т.к. 111•2+11•1=244. Значит, b = 0, отсюда с = 2. При этом d может быть любым. Максимальным исходное число будет при d = 9, то есть искомое число равно 2029.

Ответ: 2029.

6. В ящике 24 кг гвоздей. Как на чашечных весах без гирь и без стрелки отмерить 9 кг?

Решение:

Разделим 24 кг на две части, отмерив на весах по 12 кг гвоздей. Отложим одну кучу гвоздей, а вторую поделим поровну. Получим две кучи по 6 кг. Одну из них поделим пополам. Всего у нас будет четыре кучи гвоздей по 12, 6, 3, 3 кг. Сложим вторую и третью, получим ровно 9 кг.

7. Пять кошек и четыре котёнка весят 19 кг. Четыре кошки и пять котят весят 17 кг. Сколько весит кошка и сколько весит котёнок?

Решение:

5 кошек + 4 котенка = 19 кг
4 кошки + 5 котят = 17 кг.
Значит, кошка тяжелее котенка на 19 — 17 = 2 кг.

Зная это, заменим при первом взвешивании всех 5 кошек котятами:
у нас тогда будет 5 + 4 = 9 котят, а стрелка весов, вместо 19 кг, покажет на 2 • 5=10 кг меньше (т.к. масса котенка на 2 кг. меньше массы кошки).
Значит, 9 котят весят 19 — 10 = 9 кг.
Отсюда ясно, что котенок весит 1 кг, а взрослая кошка 1 + 2 = 3 кг.

Ответ: котенок весит 1кг, кошка – 3 кг.

8.Маугли попросил своих друзей-обезьян принести ему орехов. Обезьяны набрали поровну орехов и понесли Маугли. Но по дороге они поссорились, и каждая обезьяна бросила в каждую по ореху. В результате Маугли досталось лишь 35 орехов. Сколько орехов собрали обезьяны, если известно, что каждая из них принесла больше одного ореха?

Решение:

Так как обезьяны собрали орехов поровну и поровну бросили, то принесли они поровну. Имеем 35 = 5∙7 . Возможны два случая:

1) обезьян было 5, принесли по 7, бросили по 4 ореха, значит, каждая собрала 11 = 7 + 4; 2) обезьян было 7, принесли по 5, бросили по 6 орехов, значит, каждая собрала 11 = 5+ 6 .

Ответ: 11 орехов

9. Нарисовать треугольник, который можно разделить на 5 равных треугольников.

Решение:

Очевидно, что треугольник можно разделить на 4 равные части. Далее к этому треугольнику требуется «приставить» его четвертую часть, при этом снова должен получиться треугольник. Это возможно только в том случае, когда треугольник является прямоугольным, так как только тогда сумма двух прямых углов даст развернутый угол (отрезок, который является стороной треугольника, при этом будет суммой сторон большого треугольника и его «четвертушки»).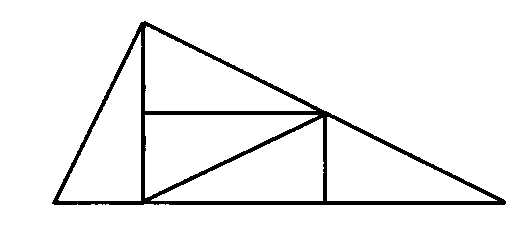

5. На рисунке изображена часть крепостной стены. Один из камней имеет столь причудливую форму, что если его вытащить из стены и положить иначе, то стена станет ровной. Изобразите этот камень.

Решение:

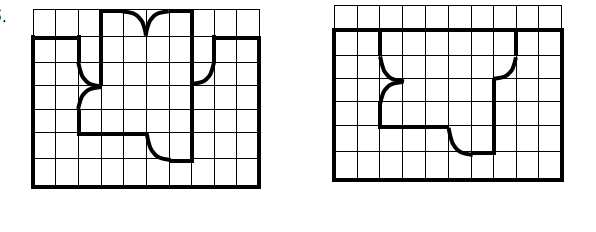
infourok.ru

Олимпиадные задачи муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 7 класс

Транскрипт

1 Олимпиадные задачи муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 7 класс 1. Дети парами выходят из лесу, где они собирали орехи. В каждой паре идут мальчик и девочка, причем у мальчика орехов либо вдвое больше, либо вдвое меньше, чем у девочки. Могло ли так случиться, что у всех вместе 2014 орехов? 2. На доске было написано трехзначное число без нулевых цифр. Из него получили три двузначных числа: первое вычеркиванием первой цифры (из исходного числа), второе вычеркиванием второй цифры (из исходного числа), третье вычеркиванием третьей цифры (из исходного числа). Найдите исходное число, если сумма трех полученных чисел равна В городе живут рыцари и лжецы. Рыцари говорят всегда только правду, а лжецы всегда лгут. Однажды в автобусе ехало несколько человек. «Сейчас остановка А. Следующая остановка Б», — произнес 1-й пассажир. «Сейчас остановка Б, — сказал 2-й. Предыдущая была В». «Предыдущая была В, — вступил в спор 3-й пассажир. Сейчас остановка А!». Определите, сколько из этих троих пассажиров рыцарей. 4. В клетках квадратной таблицы произвольным образом расставлены числа от 1 до 100. Пусть ли оказаться так, что среди чисел ровно на 1? — суммы чисел, стоящих в столбцах таблицы. Могло любые два соседних числа различаются 5. Встретились два математика, А и В, А спросил: «Сколько лет твоим четырем сыновьям?» На что В ответил, что произведение их возрастов равно 36, а сумма равна номеру проезжающего мимо автобуса. Подумав немного, А сказал, что этой информации ему недостаточно. Тогда В добавил: «Да, я забыл сказать, что мой старший сын занимается плаванием», и А назвал возраст детей. Как это ему удалось?

2 Олимпиадные задачи муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 8 класс 1. Докажите, что число не делится на Докажите, что если к произведению четырех последовательных натуральных чисел прибавить удвоенное произведение двух средних из них, то получится квадрат натурального числа. 3. В олимпиаде по математике участвовали двое близнецов. На вопрос о том, есть ли у них еще братья и какого они возраста, близнецы ответили: «У нас есть брат, его возраст записывается двумя одинаковыми цифрами, а суммарный возраст всех нас троих двузначное число, у которого вторая цифра вдвое больше первой». Определите возраст братьев. 4. Точка К середина гипотенузы АВ прямоугольного равнобедренного треугольника АВС. Точки L и М выбраны на катетах ВС и АС соответственно так, что ВL = СМ. Докажите, что треугольник LMK также прямоугольный равнобедренный. 5. Каждый житель острова Гдетотам рыцарь, всегда говорящий правду, лжец, который всегда лжет, или хитрец, который может и лгать, и говорить правду. Однажды собрались трое жителей острова. Первый сказал: «Я лжец». Второй сказал: «Среди нас есть хитрец». Третий сказал: «Среди нас есть лжец». Сколько хитрецов могло быть среди собравшихся?

3 Олимпиадные задачи муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 9 класс 1. Произведение трех натуральных чисел оканчивается на Докажите, что их сумма не может равняться Верно ли, что если квадратные уравнения и не имеют корней, то и уравнение также не имеет корней? 3. Докажите, что не существует двух натуральных чисел, таких, что их сумма равна 201, а произведение делится на На сторонах AB, BC, CD, DA квадрата ABCD (AB=1) взяты соответственно точки K, L, M и N так, что AK+LC+CM+NA=2. Докажите, что отрезки KM и LN перпендикулярны. 5. Двое по очереди выписывают на доску натуральные числа от 1 до Первым ходом первый игрок выписывает на доску число 1. Затем очередным ходом на доску можно выписать либо число 2а, либо число а + 1, если на доске уже написано число а. При этом запрещается выписывать числа, которые уже написаны на доске. Выигрывает тот, кто выпишет на доску число Кто выигрывает при правильной игре?

4 Олимпиадные задачи муниципального этапа Всероссийской олимпиады школьников по математике ( уч. год) 10 класс 1. Коля отправился за грибами между восемью и девятью часами утра в момент, когда часовая и минутная стрелки его часов были совмещены. Домой он вернулся между двумя и тремя часами дня, при этом часовая и минутная стрелки его часов были направлены в противоположные стороны. Сколько времени продолжалась Колина прогулка? 2. Найдите все такие простые p и q, что уравнение имеет целые корни. 3. Существует ли такое число x, что все три числа, и являются целыми? 4. В окружность вписан прямоугольный треугольник АВС с гипотенузой АВ. На большем катете ВС взята точка D так, что АС = ВD, а точка Е середина дуги АВ, содержащей точку С. Найдите угол DEC. 5. Двое играют в следующую игру. Есть три кучки камней. В первой из них лежит 7 камней, во второй 9 камней, в третьей 11 камней. Ходят по очереди. За один ход разрешается либо взять из любой кучки камень, либо взять по одному камню из любых двух кучек. Проигрывает тот, кто не может сделать ход. Кто может выиграть в этой игре независимо от ходов соперника?

5 Олимпиадные задачи муниципального этапа Всероссийской олимпиады школьников по математике ( уч. год) 11 класс 1. Существует ли такое число х, что значения выражений и — целые числа? 2. Назовем число почти квадратом натурального числа. Докажите, что произведение почти квадратов двух последовательных натуральных чисел также является почти квадратом натурального числа. 3. В треугольнике АВС проведена медиана ВМ. Может ли радиус окружности, вписанной в треугольник ВСМ, быть в 2 раза меньше радиуса окружности, вписанной в треугольник АВС? 4. Сколько положительных членов есть среди 2014 членов последовательности:,…? 5. Два игрока играют в следующую игру: сначала на доске написаны числа 2,4,6,8,,2014. За один ход можно уменьшить на 1 любое из написанных чисел. При этом с доски стираются нули и числа, совпадающие с какими то из уже написанных на доске чисел. Проигрывает тот, после чьего хода на доске не останется ни одного числа. Кто выигрывает при правильной игре?

6 Ответы и решения задач муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 7 класс 1. Ответ: не могло. Решение. Заметим, что число орехов у каждой пары детей делится на 3. Это означает, что суммарное число орехов должно делиться на 3. Однако число 2014 на 3 не делится. 2. Ответ: 998. Решение. Из представления следует, что либо два из слагаемых равны 98, а одно 99 (тогда исходное число было 998), либо два слагаемых равны 99, а одно 97 (это невозможно, потому что любая цифра по условию встречается хотя бы в двух из полученных чисел). 3. Ответ: все лжецы. Решение. Заметим, что 2-й и 3-й высказываются о текущей остановке по-разному, а о предыдущей одинаково. Это означает, что среди них нет ни одного рыцаря, т.е. 2-й и 3-й лжецы. Но 3-й и 1-й говорят о текущей остановке одинаково, значит, 1-й тоже лжец. 4. Ответ: не могло. Решение. Предположим, что требуемая расстановка чисел существует. Тогда, так как суммы чисел, стоящих в соседних столбцах, отличаются на единицу, то в пяти столбцах сумма чисел четна, а в пяти других нечетна, т.е. сумма чисел во всей таблице нечетна. Однако = 5050 четное число противоречие. 5. Ответ: 1, 2, 2 и 9. Решение. Число 36 можно разложить на 4 натуральных сомножителя девятью способами. При этом получаются 8 различных сумм этих сомножителей. Но раз второй математик сказал, что этой информации недостаточно, то это означает, что возможно больше одного варианта решения, то есть или — в обоих случаях сумма сомножителей равна 14. После последней подсказки (про старшего сына) становится ясно, что детям первого математика 1, 2, 2 и 9 лет.

7 Ответы и решения задач муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 8 класс 1. Решение. Рассмотрим сумму ( ) ( ) ( ) = ( ). В последней сумме первое слагаемое делится на 3, а второе слагаемое не делится на 3. Поэтому и вся сумма не делится на Решение. Имеем ( )( )( ) ( )( ) ( )( )( )= ( ) 3. Ответ: 13, 13 и 22 года. Решение. Из условия получаем, ( ) откуда следует, что — четная цифра, т.е. (теоретически возможно и, но тогда уже не является цифрой). Значит Первое невозможно, так как тогда возраст каждого из близнецов — ( ), и они не могли участвовать в олимпиаде, во втором случае их возраст ( ). 4. Решение. Медиана СК треугольника АВС является также высотой и биссектрисой, так как треугольник равнобедренный. Поэтому KBC = KCB = KCA = 45. Отсюда КС = КВ, и, значит, треугольники КВL и КСМ равны по двум сторонам (KC =KB, BL = CM) и углу между ними. Поэтому КL =КМ, и из равенства ВКL = СКМ следует LKM = LKC + CKM = LKC + BKL = BKC = 90. Значит, треугольник LMK прямоугольный равнобедренный. 5. Ответ: два или три. Решение. Если первый рыцарь, то он солгал, а если лжец, то сказал правду. Ни то ни другое невозможно. Поэтому первый хитрец. Значит, второй сказал правду. Он может быть рыцарем или хитрецом. Если третий сказал правду, то он хитрец или рыцарь. Но тогда лжеца среди собравшихся на самом деле нет противоречие. Поэтому третий солгал, и лжецов среди собравшихся действительно нет. Следовательно, третий хитрец.

8 Ответы и решения задач муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 9 класс 1. Решение. Если сумма трех целых чисел равна 9999, то либо они все нечетны (и тогда их произведение оканчивается на нечетную цифру), либо два из них четны, а одно нечетно (тогда их произведение делится на 4, а число, оканчивающееся на 14, на 4 не делится). 2. Ответ: верно. Решение. Первое решение. По условию Покажем, что тогда ( ) ( ) Имеем ( ) ( ) ( ( ) ) ( ) ( ). (Мы использовали неравенство ( ).) Второе решение. Пусть По условию при всех так как Но тогда и значит, уравнение не имеет корней. 3. Решение. Предположим, что нашлись такие два числа, что а делится на 201. Так как то одно из чисел, для определенности, делится на 3, но тогда и делится на 3. Аналогично и, и делятся на 67, т.е. каждое из них не меньше, т.е. их сумма больше 201 противоречие. 4. Решение. Проведем CP MK и DQ NL, тогда CMKP и DQLN параллелограммы, значит, KP = CM и LQ = DN. Тогда AK+LC+CM+NA = AK+LQ+CQ+CM+NA = AK+KP+DN+NA+CQ = = AP+AD+CQ = 2 BP+CQ. Итак, CQ = BP и, значит, DQC = CPB. Отсюда QDC= PCB=90 PCD, т.е. DQ перпендикулярен CP, и, значит, LN перпендикулярен KM. 5. Ответ: второй. Решение. Заметим, что если какой-то из игроков выпишет на доску число 500 или 999 (назовем такой ход проигрышным), то его противник следующим ходом выпишет число 1000 и выиграет. Какие числа могут быть выписаны на доску до появления чисел 500 и 999? Во-первых, это все числа от 1 до 449 (их 449). Во-вторых, это все числа от 502 до 998 (их 497), так как 502 можно получить удвоением из числа 251. Заметим также, что число 501 может получиться только из числа 500, т.е. перед появлением числа 500 или 999 будет сделано не более =996 непроигрышных ходов. При этом если сделано менее 996 непроигрышных ходов, то можно сделать еще один. Действительно, все числа от 2 до 499 можно получить из 1 операцией а + 1. Число 502 получается из 251. А из 502 можно получить все числа от 503 до 998. Таким образом, можно сделать четное число непроигрышных ходов. Это означает, что проигрышный ход сделает первый игрок.

9 Ответы и решения задач муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 10 класс 1. Ответ: 6 часов. Решение: По прошествии 6 часов минутная стрелка находится в исходном положении, а часовая поворачивается на 2. Ответ: p = q = 2 Решение: Пусть x 1, x 2 корни уравнения. Тогда по теореме Виета x 1 x 2 =, x 1 + x 2 = — q. Отношение простых чисел целое, значит, p = q и x 1 x 2 = 1, откуда x 1 = x 2 = — 1 и p = q = 2 3. Ответ: Не существует. Решение: Предположим, что существует такое число x, что все три числа, данные в условии, целые. Тогда их сумма, равная x, тоже целая. Первое число будет целым тогда, когда x целое и целое. Но из равенства следует:. Однако разность между двумя квадратами целых чисел не может равняться 2, поскольку между и разность равна 1, а между любыми двумя другими квадратами она хотя бы равна 3. Таким образом, первое число не может быть целым. 4. Ответ: 90. Решение: Точка Е середина дуги АВ (см. рисунок), поэтому АЕ = ВЕ. Кроме того, вписанные углы САЕ и ЕВС, опирающиеся на одну дугу, равны. Также по условию АС = ВD. Значит, треугольники АСЕ и ВDЕ равны, откуда СЕА = ВЕD. Но тогда DЕС = ВЕА 90, так как ВЕА = ВСА. 5. Ответ: Выиграет второй Решение: Выигрывает тот, после чьего хода в кучках не осталось камней. Опишем выигрышную стратегию второго игрока. Если первый игрок первым ходом взял 1 камень из какой-нибудь кучки, то второму следует взять по 1 камню из двух других кучек. Если же первый игрок первым ходом взял по 1 камню из каких-то двух кучек, то второму следует взять 1 камень из оставшейся кучки. Таким образом, после хода второго в первой кучке будет лежать 6 камней, во второй 8 камней, в третьей 10 камней, т.е. в каждой кучке будет лежать четное число камней. Каждым следующим ходом второй должен брать столько же камней и из тех же кучек, что и первый, т.е. после каждого хода второго в каждой кучке будет оставаться четное число камней. Второй всегда сможет сделать ход, так как после хода первого в тех кучках, из которых он брал камни, будет оставаться нечетное число камней, т.е. хотя бы по одному. А так как второй всегда сможет сделать ход, то именно он и заберет последние камни из кучек и выиграет.

10 Ответы и решения задач муниципального этапа Всероссийской олимпиады школьников по МАТЕМАТИКЕ ( уч. год) 11 класс 1. Ответ: Не существует. Решение: Пусть и, где n и m целые числа. Тогда =,, следовательно, ( )( ), откуда ( ). Число иррационально, поэтому это равенство возможно лишь в случае. Полученное равенство возможно только для иррациональных n и m ( ) 2. Доказательство: Утверждение следует из цепочки равенств: (( ) ) ( ) ( ) ( ) ( ) ( ) 3. Ответ: Не может Первое решение: Пусть — данные окружности (см. рисунок), их радиусы,. Тогда из формулы S=rp и равенства следует, что периметры треугольников АВС и ВМС должны быть равны. Но ( ) В С Второе решение: Построим треугольник АDC, в котором ВМ средняя линия. Он подобен треугольнику ВМС с коэффициентом 2, т.е радиус r вписанной в него окружности равен, но r > (окружности вписаны в один угол С, но окружность касается более удаленной от вершины угла С, чем АВ, прямой АD). 4. Ответ: 3 положительных члена Решение: При имеем ( ) ( ) ( ) делится на 9, значит, ( ) делиться на 360. Поэтому все члены последовательности, начиная с четвертого, совпадают с ( ). Таким образом, в последовательности 3 положительных члена. 5. Ответ: Выигрывает первый игрок. Решение: Выигрышная стратегия для первого игрока такова: каждый раз выбирать для своего хода наименьшее из написанных на доске нечетных чисел, а если таковых нет произвольное (четное) число. Если первый игрок следует своей стратегии, то после первого хода образуется одно нечетное число, после хода второго игрока 0 или 2 нечетных. Следовательно, после хода первого вновь будет ровно одно нечетное число. При этом не может появиться пара ( ) так как она может возникнуть только из пары ( ) а первый игрок выбирает для хода меньшее из двух написанных нечетных чисел. Значит, после хода второго игрока вновь будет 0 или 2 нечетных числа (ровно одно могло бы появиться, если бы перед каждым ходом была пара ( )) и т.д. Значит, после каждого хода первого игрока число нечетных чисел равно 1 и он не проигрывает.

11

docplayer.ru