Олимпиадная задача по математике 7 класс – 7
Олимпиада по математике 7 класс, задания, уравнения, задачи с ответами
Усвоить школьную программу по математике могут только те, кто проявляет достаточно упорства. На уроках 7 классе учащиеся знакомятся с такими разделами, как степень с натуральным показателем, одночлен и многочлен, линейная функция, системы линейных уравнений с двумя переменными.
Принимая участие в олимпиадах, ученики углубляют свои знания и совершенствуют навыки, приобретенные на уроках. Но, чтобы добиться высокого результата, нужно долго и усердно готовиться.
На нашем сайте вы найдете олимпиадные задания по математике с ответами и решениями. Предложенные задания помогут подготовиться к олимпиаде. Мы советуем вам использовать их в качестве тренажера как на уроках, так и в ходе внеклассной самостоятельной подготовки.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Уравнения
1. Оба корня уравнения x2
2. Решите в натуральных числах уравнение:
zx + 1 = (z + 1)2
3. Решите уравнение:
12 – (4х – 18) = (36 + 5х) + (28 – 6х)
4. Найдите решение уравнения:
7x + 3 (x+0,55) = 5,65
5. Решите уравнение:
10у – 13,5 = 2у — 37,5.
6. Преобразуйте в многочлен:
(4х – 5у)2
7. Представьте выражение в виде квадрата двучлена:
4у2 — 12у + 9
8. Решите уравнение:
8у – (3у + 19) = -3(2у — 1)
9. Решите уравнение:
5х2 – 4х = 0
10. Решите систему уравнений:
{ x+2*y = 12
{ 2*x-3*y = -18
Задачи
Задача №1
Из чисел A, B и C одно положительно, одно отрицательно и одно равно 0. Известно, что A = B (B – C). Какое из чисел положительно, какое отрицательно и какое равно 0? Почему?
Задача №2
Последовательность строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на 1. Какое число стоит на 2000 месте?
Задача №3
В XIX-XX веках Россией правили 6 царей династии Романовых. Вот их имена и отчества по алфавиту: Александр Александрович, Александр Николаевич, Александр Павлович, Николай Александрович, Николай Павлович, Павел Петрович. Один раз после брата правил брат, во всех остальных случаях после отца — сын. Как известно, последнего русского царя, погибшего в Екатеринбурге в 1918 году, звали Николаем. Найдите порядок правления этих царей.
Задача №4
Сколько чисел от 1 до 90 делятся на 2, но не делятся на 4?
Задача №5
В трех мешках 114 кг сахара. В первом на 16 кг меньше, чем во втором, а в третьем на 2 кг меньше, чем во втором. Сколько килограммов сахара во втором мешке?
Задача №6
Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не повторяются.
Задача №7
Точка D — середина основания AC равнобедренного треугольника ABC. Точка E — основание перпендикуляра, опущенного из точки D на сторону BC. Отрезки AE и BD пересекаются в точке F. Установите, какой из отрезков BF или BE длиннее.
Задача №8
Пол в гостиной барона Мюнхгаузена вымощен одинаковыми квадратными каменными плитами. Барон утверждает, что его новый ковер (сделанный из одного куска ковролина) закрывает ровно 24 плиты и при этом каждый вертикальный и каждый горизонтальный ряд плит в гостиной содержит ровно 4 плиты, покрытых ковром. Не обманывает ли барон?
Задача №9
Саша выписал первые миллион натуральных чисел, не делящихся на 4. Рома подсчитал сумму 1000 подряд идущих чисел в Сашиной записи. Могло ли у него получиться в результате 20012002?
Задача №10
Автомобиль из A в B ехал со средней скоростью 50 км/ч., а обратно возвращался со скоростью 30 км/ч.. Какова его средняя скорость?
Математические загадки
Загадка №1
Не пользуясь калькулятором и компьютером (в уме) вычислите сумму всех чисел от одного до ста?
Загадка №2
Позавчера Васе было 17 лет. В следующем году ему будет 20 лет. Как такое может быть?
Загадка №3
Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
Загадка №4
На острове живут два племени: молодцы. Которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник встретил островитянина, спросил его, кто он такой, и когда услышал, что он из племени молодцов, нанял его в проводники. Они пошли и увидели вдали другого островитянина, и путешественник послал своего проводника спросить его, к какому племени он принадлежит. Проводник вернулся и сказал, что тот утверждает, что он из племени молодцов. Спрашивается: был проводник молодцом или лгуном?
Загадка №5
В двух футбольных лигах в сумме 39 команд. Команда играет с каждой командой из своей лиги по одному разу; при этом никаких матчей между лигами не происходит. За победу полагается 3 очка, за ничью — 1 очко, за проигрыш — 0. В прошлом году в одной лиге состоялось на 171 матч больше, чем в другой. Команда «Чемпионы», входящая в одну из лиг, проиграла всего три матча и набрала 32 очка.
Вопрос: со сколькими командами играли «Чемпионы» и сколько раз они сыграли вничью?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | a = 3 | z = 2 x = 3 | x = — 15¹/₃ | x = 0,4 | y = -3 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | 16х2 — 40ху + 25у2 | (2у — 3)2 | y = 2 | x = 0 x=0,8 | x = 0,6 |
Ответы к задачам
Задача 1
Если A = 0, то либо B = 0, либо B – C = 0. Ни то, ни другое невозможно. Поэтому A не 0. Если B = 0, то и A = 0. Это тоже невозможно. Поэтому B не 0. Следовательно, C = 0, и равенство из условия задачи можно переписать в виде A = B. Отсюда следует, что B > 0. Значит, B положительно, а A – отрицательно.
Задача 2
Так как 2000 = 3 x 666 + 2, то 2000-м месте стоит число 5.
Задача 3
Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.
Задача 4
23
Задача 5
44 кг
Задача 6
60 чисел
Задача 7
Отрезок BE длиннее
Задача 8
Примером такой клетчатой фигуры может служить квадрат 6 на 6 без двух подходящих обобщенных диагоналей. Конечно, если трактовать это как ковер в гостиной, получится нечто экстравагантное, но ведь барон не зря слыл незаурядным человеком.
Задача 9
Задача 10
37,5 км/ч
Ответы на загадки
Загадка 1
5050
Загадка 2
Если нынешний день 1 января, а у Васи день Рождения тридцать первого декабря. Позавчера, т.е. тридцатого декабря ему было еще семнадцать лет. Вчера, т.е. тридцать первого декабря исполнилось восемнадцать лет. В этом году исполнится девятнадцать лет, а в следующем году двадцать лет.
Загадка 3
Всего деливших было трое: дед, его сын и внук
Загадка 4
На острове на данный вопрос никто не мог ответить ничего, кроме того, что он молодец. Так как проводник воспроизвел правильно этот единственно возможный ответ, то ясно, что он молодец.
Загадка 5
«Чемпионы» играли с 23 командами (следовательно, в их лиге 24 команды, а в другой — 15) и сыграли вничью 14 матчей из 23.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Другие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
Олимпиадные задания по математике для 7 класса
1. Произведение цифр трёхзначного числа равно 25. Найдите такие числа.
Ответ: 551; 155; 515.
2. Поставить вместо звёздочек такие цифры, чтобы число 32*35717* делилось на 72.
Решение: Чтобы число делилось на 72, необходимо и достаточно, чтобы оно делилось на 8 и на 9. Чтобы число делилось на 8, необходимо и достаточно, чтобы на 8 делилось число, составленное из трех последних его цифр в том же порядке. Для числа 17* это 176, то есть последняя цифра 6. Для делимости на 9 необходимо и достаточно, чтобы сума цифр числа делилась на 9. Вместо оставшейся звездочки может стоять только 2.
Ответ: 322357176.
3. Как от куска материи в метра отрезать 2/3 полметра, не имея под рукой метра?
Решение: Сложить пополам, ещё раз пополам и отрезать одну часть. В остатке — 1/2 метра.
4. Мальчики в классе составляют 2/5 учащихся всего класса. 1/7 их числа составляют отличники. Сколько в классе девочек?
Ответ: 21 девочка
5. Какой угол образуют стрелки часов в 12 часов 20 минут?
Решение: В 12.00 стрелки сходятся вместе. После этого за 20 минут минутная стрелка проходит 1/3 окружности, то есть описывает угол в 120º. Часовая стрелка движется в 12 раз медленнее минутной (так как описывает круг за 12 часов). Поэтому она за 20 минут опишет угол в 120º : 12=10º и будет образовывать с минутной стрелкой угол в 120º -10º=110º
6. Попробуйте найти семь различных способов деления данной фигуры на четыре равные части. 
Ответ: 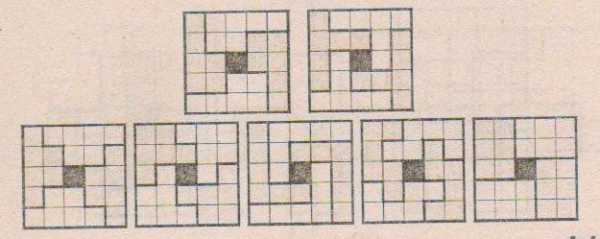
Вконтакте
Google+
Одноклассники
olimpotvet.ru
Олимпиадные задания по математике (7 класс): Решение олимпиадных задач 7 класс.
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ТУЧКОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3
С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ
Региональный мастер-класс
«Методика обучения учащихся математическому моделированию при решении задач повышенного уровня сложности».
мастер -класс
«Решение олимпиадных задач». Лекция № 2.
Математическая школа «Пифагореец» 7 класс
Составитель: учитель высшей квалификационной категории
Уханова Анастасия Владимировна
16.02.2019г
п.N
Основные цели:
Образовательная — обучение различным способам решения нестандартных задач, углубление знаний по предмету;
Воспитательная — воспитание творческой активности учащихся, повышение математической культуры,
Развивающая — развитие математического мышления, интеллектуального уровня, оригинальности и изобретательности, развитие навыков самостоятельной работы и стремления к обучению и самообучению.
Задачи:
- Решение олимпиадных задач, предложенных на олимпиадах прежних лет;
- Решение задач творческого характера, имеющие практические применения.
- Подготовка к математическим предметным олимпиадам разных уровней.
Тип занятия: применения и совершенствования знаний
Методы обучения: частично – поисковый, использование принципа «от простого к сложному»
Оборудование: мультимедийный проектор, компьютер, доска.
Ход занятия
Организационный момент.
Формулировка темы и целей урока.
Тема: «Олимпиадные задачи.»
Олимпиадные задачи в системе изучения математики направлены на расширение кругозора и повышения математической культуры, развитие смекалки, сообразительности, находчивости, настойчивости в поиске оригинального решения.
Устная работа.
- Найти наибольшее значение отношения трехзначного числа к сумме его цифр.
Решение. Ответ: 100.
2.Сколько существует трехзначных чисел- квадратов, у которых сумма цифр совпадает с двумя первыми цифрами исходного числа?
Решение. Единственное число 169. Ответ: 169.
3.Вычислить . Ответ:
4. Три последовательных натуральных числа дают в сумме 111. Найти эти числа.
Решение. (х+1) + х + (х− 1) =111,
3х = 111
х=37.
Ответ: 36, 37, 38.
5. Найти хотя бы одно натуральное число n , при котором число +3 будет составным.
Решение. Если n= 5, то +3 =32+3= 35 = 5· 7 – составное число.
Решение задач.
- Разложить многочлен на два множителя с целыми коэффициентами.
Решение. = ( + + + +++ +− + ++ + х+ =+ х+ + х+ + + х+ − + х+ ++ х+ + х+(− ++1).
- Доказать, что при любых х0, у значение выражения+ху + 0.
Решение. +ху +=( +2х· у +) + = + 0.
- Найти двузначные числа, равные квадрату суммы своих цифр.
Решение. По условию имеем: 10 + = , или 9 =. Далее учесть, что в правой части произведение двух последовательных целых чисел, откуда =8 и =9, т.е. =1, и, искомое число 81=.
- Из канистры отлили часть бензина, потом 10 % ее общей емкости. После этого в канистре осталось 26 л бензина. Какова емкость канистры?
Решение. Пусть х л- емкость канистры, тогда
( х −0,25х) – 0,1х = 26
х= 40.
Ответ: емкость канистры 40л.
- Найти х,у, z для которых справедливо равенство
+ +│х+у+ z│= 0.
Решение.
Сумма двух и более неотрицательных выражений равна нулю одновременно, если каждое из них равно нулю.
Тогда =0,
= 0 ,
х+у+ z=0. Откуда у= -1, х= -4, z=5.
- C Дано: АС=ВС, АД- медиана,=2м, АВ=8м.
Найти: АС и ВС.
Решение. По условию АС= ВС , то
СД=ДВ ( по условию). Пусть АС=2х, СД=ДВ = х,
АВ=8м. Тогда =3х+ АД, =8+АД + х.
По условию =2м, значит
А В 3х+ АД− (8+АД + х ) =2, или 2х-8=2, откуда 2х=10, т.е. АС=ВС=10м.
Ответ: 10 м и 10м.
7.Доказать, что квадрат нечетного числа 2n +3 при делении на 8 всегда дает в остатке 1.
Решение. = 4. Так как слагаемое в скобке делится на 8, то остаток равен 1.
8.Доказать, что если х+у=2007z и 2007z u= у(z +u), где z o, u o, то верно равенство = .
Решение. Перемножим левые и правые части данных равенств, тогда получим 2007z u(х+у) =2007z у(z +u),
теперь разделим обе части равенства на 2007z o, имеем
u (х+у) = у(z +u),
ux + uy = yz +yu
ux = yz, по правилу пропорции имеем:
= .
9. Внутри АВС взята точка К так, что АВК =, КАВ =,
АСВ= и АС= ВС . Найти АКС.
Решение.Пусть Е -точка пересечения высоты CD и прямой ВК.
Так как ABC—равнобедренный и CD — высота, проведенная к основанию АВ, то АЕ = BE и
EAК = EAB− KAB = 30° -10° =20°, ACD= ACВ =40°,
EAC=
KE = KAB + KBA = 10° + 30° = 40° =>
=> AEK = ACE (по стороне и прилежащим к ней углам)
АК =АС, AKC= ACK=(180°-CAK) =(180° -40°) = 70°.
Ответ: 70° С
А В
10.На доске написаны в строку 2007 целых чисел. Доказать, что из них можно стереть одно число так, что сумма оставшихся чисел будет четной. Верно ли это для 2006 чисел?
Решение. Если количество нечетных чисел нечетно, то можно стереть любое из них.
Если же количество чисел четно, то, очевидно, на доске есть хотя бы одно четное число( всего чисел 2007), его и стираем.
Если же на доске написаны 2006 нечетных чисел, то при стирании любого из них, сумма оставшихся будет нечетна.
11. В некотором году три месяца подряд содержали всего по 4 воскресенья. Доказать, что один из этих месяцев — февраль.
Решение. Из условия следует, что три месяца содержат всего 12 воскресений. А поскольку один из любых семи подряд идущих дней является воскресеньем, то эти месяцы насчитывали вместе меньше чем 13·7=91 день.
Остается заметить, что любые три подряд идущих месяца, среди которых нет февраля, насчитывают вместе не меньше , чем 91 день.
Работа в группах.
- Торт имеет форму равнобедренной трапеции, у которой верхнее основание и боковые стороны в 2 раза меньше нижнего основания. Можно ли торт разделить на 4 равные части?
Ответ : можно
nsportal.ru
Олимпиадные задания по математике для 7 класса (школьный этап)
ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ
ПО МАТЕМАТИКЕ 2015-2016 ГГ.
ШКОЛЬНЫЙ ЭТАП
7 КЛАСС
1. В ящике 25 кг гвоздей. Как с помощью чашечных весов и одной гири в 1кг за два взвешивания отмерить 19 кг гвоздей?
2. На часах половина девятого. Чему равен угол между часовой и минутной стрелками?
3. Написав контрольную работу, ученики Володя, Саша и Петя сообщили дома:
Володя: «Я написал на 5».
Саша:«Я написал на 3».
Петя: «Я написал не на 5».
После проверки выяснилось, что один из мальчиков получил 3, другой 4, третий 5. Какую оценку получил каждый, если известно что из трех сделанных высказываний одно ложно, а два других истинны?
4. В примере a ∙ b + c ∙ d + e ∙ f , a увеличили на 20%, b уменьшили на 20%, c увеличили на 60%, d уменьшили на 40%, e увеличили на 50%, f уменьшили на 36%. После этого пример решили и получили 80. Найти a ∙ b + c ∙ d + e ∙ f
.5. Проведите шесть прямых и отметьте на них 11 точек так, чтобы на каждой прямой было отмечено ровно четыре точки.
Каждое задание оценивается в 7 баллов. Всего – 35 баллов.
РЕШЕНИЕ ОЛИМПИАДНЫХ ЗАДАЧ ПО МАТЕМАТИКЕ 7 КЛАСС
1. В ящике 25 кг гвоздей. Как с помощью чашечных весов и одной гири в 1кг за два взвешивания отмерить 19 кг гвоздей?
Решение: При первом взвешивании в одну из чашек весов кладем гирю и все гвозди раскладываем по чашкам так, чтобы установилось равновесие. Получим 13 и 12 кг гвоздей. Первую кучку откладываем, а остальные гвозди делим пополам, взвешивая без гири: 12 = 6 + 6. Получили искомое количество гвоздей: 19 = 13 + 6.
2. На часах половина девятого. Чему равен угол между часовой и минутной стрелками?
Решение: В момент, когда часы показывают половину девятого, минутная стрелка указывает на цифру 6, а часовая на середину дуги между цифрами 8 и 9 (см. рисунок). Если из центра часов провести два луча к соседним цифрам циферблата, то между ними будет угол 360
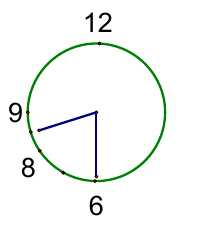
3. Написав контрольную работу, ученики Володя, Саша и Петя сообщили дома:
Володя: «Я написал на 5».
Саша:«Я написал на 3».
Петя: «Я написал не на 5».
После проверки выяснилось, что один из мальчиков получил 3, другой 4, третий 5. Какую оценку получил каждый, если известно что из трех сделанных высказываний одно ложно, а два других истинны?
Решение:
Володя
Л 4 или 3
П 5
П 5
Саша
П 3
П 3
Л 4
Петя
П 4 или 3
Л 5
П 3
―
―
ОТВЕТ: Володя — 5; Петя — 3; Саша — 4.
4. В примере a ∙ b + c ∙ d + e ∙ f , a увеличили на 20%, b уменьшили на 20%, c увеличили на 60%, d уменьшили на 40%, e увеличили на 50%, f уменьшили на 36%. После этого пример решили и получили 80. Найти a ∙ b + c ∙ d + e ∙ f.
Решение: 1,2a∙0,8b + 1,6c ∙ 0,6d + 1,5e ∙ 0,64f = 0,96a ∙ b + 0,96c ∙ d + 0,96e ∙ f = 0,96 (a ∙ b + c ∙ d + e ∙ f) = 80
a ∙ b + c ∙ d + e ∙ f =
ОТВЕТ:
5. Проведите шесть прямых и отметьте на них 11 точек так, чтобы на каждой прямой было отмечено ровно четыре точки.
Решение:

infourok.ru
ОЛИМПИАДНЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ 7 КЛАСС (с решениями)
Задача № 1 :
В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.
Решение:
Пусть AD = a, BC = b, AC = a + b. Продолжим AD за точку D на расстояние DM = BC. Тогда очевидно, что ?АСМ — равносторонний.
Но это значит, что ?АОD и ?ВОС — тоже равносторонние.
Отсюда непосредственно следует, что ?АОВ = ?СОD, откуда имеем, что AB = CD.
Задача № 2 :
Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
Решение:
Просчитав несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды. Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/ 2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k+1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Задача № 3 :
Решите уравнение : x² + 2005x – 2006 = 0.
Решение:
Исходное уравнение имеет очевидный корень 1. Второй корень найдем по формулам Виета. Так как x1∙x2 = -2006 и x1= 1, то x2 = 2006.
Задача № 4:
Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
Решение:
Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные шесть выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков. Что возможно при единственной комбинации 8+9+9=26. Итак, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, в девятку – 3 раза.
Задача № 5:
Сколько всего есть четырехзначных чисел, которые делятся на 19 и оканчиваются на 19?
Ответ : 5 .
Решение :
Пусть — такое число. Тогда N – 19 тоже кратно 19. Но Поскольку 100 и 19 взаимно просты, то двузначное число делится на 19. А таких всего пять: 19, 38, 57, 76 и 95. Легко убедиться, что все числа 1919, 3819, 5719, 7619 и 9519 нам подходят.
Задача № 6:
У даты 12.04.1961 (то есть 12 апреля 1961 года) сумма цифр равна 24. Найдите ближайшую дату после 01.01.2008, у которой сумма цифр равна: а) 35; б) 7.
Решение :
а) Наибольшая сумма цифр числа равна 11 для 29-го числа. Наибольшая сумма цифр месяца равна 9 для сентября, то есть для 09. Значит, наибольшая сумма цифр в текущем году будет у даты 29.09.2008. Она равна 30, что меньше 35. Следовательно, надо менять и год. Последняя цифра года не более 9, и если мы сохраняем первые две цифры, то придется цифру десятилетий увеличить до 4.
б) Для 2008 года сумма цифр года уже больше 27, поэтому год придется изменить. Ближайший год в будущем с меньшей суммой цифр — 2010-й. Соответственно, ближайшая подходящая дата 03.01.2010.
Ответ : а) 29.09.2049; б) 03.01.2010.
Задача №7:
Сумма квадратов n простых чисел, каждое из которых больше 5, делится на 6. Докажите что и n делится на 6.
Решение.
Если сумма нескольких чисел делится на шесть, то и сумма их остатков при делении на шесть тоже будет делится на 6. Простое число, большее пяти, может иметь при делении на 6 только остатки 1 или 5 (иначе это число будет делиться на 2 или 3). Следовательно, квадрат любого простого числа, большего чем 5, имеет при делении на 6 остаток 1. Так как сумма этих остатков равна количеству чисел n, значит n делится на 6.
Задача №8:
Петя и Вася сделали в тире по 5 выстрелов. Первыми тремя выстрелами они выбили поровну, а последними тремя Петя выбил в три раза больше очков, чем Вася. На мишени остались пробоины в 10, 9, 9, 8, 8, 5, 4, 4, 3, 2 очков. Куда попал каждый из них третьим выстрелом? Приведите все возможные варианты ответа и докажите, что других нет.
Ответ. Третьим выстрелом Петя выбил 10, а Вася — 2 очка.
Решение.
Последними тремя выстрелами Вася не мог выбить больше, чем 9 очков (иначе Петя бы выбил последними тремя выстрелами не меньше 30). Меньше 9 очков Вася тоже выбить не мог, так как наименьшая сумма за три выстрела 2+3+4 = 9. Следовательно, Вася выбил 2, 3 и 4 очка а Петя 10, 9 и 8 очков (других вариантов набрать 27 очков тремя выстрелами нет). Значит первыми двумя выстрелами мальчики выбили 9, 8, 5 и 4 очка. При этом Петя третьим выстрелом выбил не меньше, чем 8, а Вася — не больше, чем 4 очка. Так как сумма очков после первых трех выстрелов была равной, значит, первыми двумя выстрелами Петя выбил по крайней мере на четыре очка меньше, чем Вася. Единственная возможность — Вася выбил 9 и 8, а Петя 5 и 4 очка, следовательно, третьим выстрелом Вася выбил 2, а Петя 10 очков.
Задача № 9:
Если дату 10 февраля 2001 года записать в виде 10.02.2001, а затем убрать точки, то получится палиндром (т.е. число, читающееся слева направо и справа налево одинаково). Найдите ближайшую к 10.02.2001 дату, обладающую тем же свойством. Рассмотрите два случая:
1) требуемая дата еще не наступила,
2) требуемая дата уже прошла.
Ответ обосновать.
Ответ. 1) 20 февраля 2002 2) 29 ноября 1192 года.
Решение.
При условии, что дата записывается как палиндром, день и месяц однозначно находятся по заданному году.
пункт (1): в 2001 году других палиндромов быть не может, а в следующем (2002) году это должен быть 20 день второго месяца.
Пункт (2): Чтобы дата была как можно ближе к 2001 году, необходимо брать самый большой возможный год, меньший 2001. Вторая цифра года должна быть первой цифрой месяца, то есть 0 или 1, т.к. месяцев не больше 12. В 2000 году палиндрома быть не может (нулевого дня не бывает), следовательно, первые две цифры года — 11 (соответственно, месяц — ноябрь). Третью цифру года нужно взять максимально возможную, т.е. девять, тогда четвертой (так как в ноябре не больше 31 дня) может быть два. Получится дата-палиндром 29.11.1192.
Задача № 10:
В выпуклом четырехугольнике ABCD стороны AB и CD параллельны, а диагонали AC и BD перпендикулярны. Докажите, что AD+BC = AB+CD.
Решение.
Впишем четырехугольник ABCD в прямоугольник EFGH со сторонами, параллельными диагоналям (EF || AC и EH ||BD) — смотри рисунок. Пусть L — точка пересечения прямых DC и EF, а M — точка на прямой HG такая, что LM || FG . Тогда ABLC — параллелограмм, следовательно, AB = CL. Так как GM = FL = EB = HD и AH = CG, то \triangle AHD = \triangle CGM , следовательно, AD = CM. В силу неравенства треугольника BM £ BC+CM = BC+AD . Но BM = DL как диагонали прямоугольника BLDM, и DL = DC +CL = DC+AB. Следовательно, AD+BC ³ DL = DC +CL = DC+AB, что и требовалось доказать.
multiurok.ru
Олимпиадные задачи по математике (7 класс) с решением
Просмотр содержимого документа
«Олимпиадные задачи по математике (7 класс) с решением»
Олимпиадные задачи по математике (7 класс) с решением
ЗАДАЧА 1. Один из углов равнобедренного треугольника равен 108°. Найти отношения длин двух биссектрис неравных углов.
Решение.
По условию задан равнобедренный треугольник, то есть такой треугольник, у которого равны две стороны. Согласно свойствам треугольников: против равных сторон лежат равные углы.
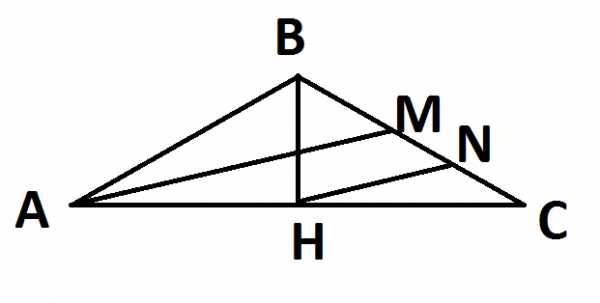 Обозначим данный равнобедренный треугольник ABC, проведем АМ параллельно НN, получаем, что ⦟ C = 180° — 108°= 72/2 = 36°
Обозначим данный равнобедренный треугольник ABC, проведем АМ параллельно НN, получаем, что ⦟ C = 180° — 108°= 72/2 = 36°
⦟HBC = 108°/2 = 54°. Далее проведем НN параллельно АМ, тогда ⦟ САМ = 36°/2 = 18°
⦟BHN = 90° — 18° = 72°. Получается, что ⦟HNB = 180° — (72°+54°) = 180°-126° = 54°. Треугольник BHN равнобедренный, следовательно, BH = HN = ½ АМ,
таким образом, отношения длин двух биссектрис BH : АМ = 1 : 2
Ответ: отношения длин двух биссектрис неравных углов будут
1 : 2
ЗАДАЧА 2. Решите в целых числах уравнение
71х + 13у = ху – 14
Решение.
xy -13y – 71x -14 = 0 (*)
ВНИМАНИЕ ЗАПОМНИ:(х – 13)∙(у – 71) = ху – 13у – 71х +923, сравним с (*)
у нас не +923, а -14, поэтому (х – 13)∙(у – 71) = 937 (923 + 14 = 937)
Так как число 937 простое, то запишем системы уравнений:
Ответ: (14;1008), (950;72)
ЗАДАЧА 3. На боковой стороне равнобедренного треугольника АВС взяты точки М и N (М лежит между В и N) так, что AN = MN и угол ВАМ = углу NAC. Доказать, что угол МАС = 60°.
Решение.
В равнобедренном треугольнике углы при основании равны.
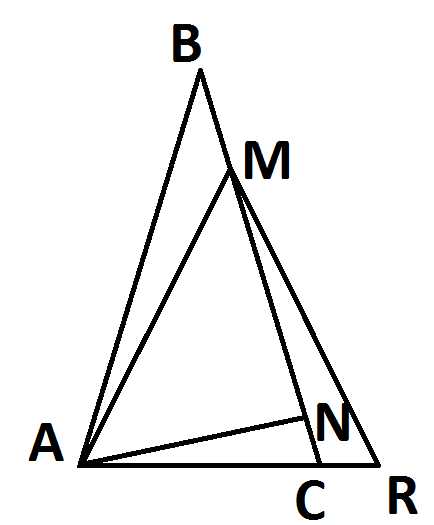
Пусть ⦟MAN=⦟AMN=α, ⦟ВАМ=⦟NAC=β, ⦟ANM=γ. Продлим АС до длины АМ (до точки R), соединим М и R. В полученном треугольнике AMR ⦟CMR=β, ⦟ARM=α+β, получается в треугольнике CMR ⦟MCR=180°-γ+β, → ⦟ MCR+⦟CRM+⦟CMR=180°=180°-γ+β+α+β+β.
γ=3β+α
В треугольнике AMN ⦟MAN=⦟AMN=α, ⦟MNA=γ, следовательно, γ=180°-2α.
3β+α=180°-2α
β=60°-α
α+β = 60°= ⦟MAC, что и требовалось доказать.
Ответ: угол МАС = 60°

multiurok.ru
Олимпиадные задания по математике в 7 классе
Олимпиадные задания предназначены для проведения школьного тура математической олимпиады школьников.Задания среднего уровня сложности.
Задачами олимпиады школьников является
переориентация образования на запросы личности, его индивидуализацию, превращение в средство жизненного и профессионального самоопределения, самореализации, самовыражения и самоутверждения личности подрастающего поколения, что придаст ей социальную устойчивость, обеспечит адаптацию в динамично меняющихся социально-экономических условиях, сохранит здоровье и будет способствовать улучшению качества среды обитания в условиях современного экологического кризиса;
развитие общей культуры подрастающего поколения посредством формирования у школьников научных форм системного мышления, которое станет основой для творческого подхода к собственной деятельности;
обеспечение условий для практической реализации триады «воспитание — просвещение — образование» на основе личного опыта творческой познавательной деятельности;
повышение креативности образования, переориентация процесса обучения на теоретические способности учащихся, что сделает эффективной их подготовку к жизни в различных образовательных средах, то есть сделает образование развивающим;
переориентация процесса обучения на превращение знаний в инструмент творческого освоения мира, а образования — в источник процедурных знаний, знаний о том, как и где при необходимости самостоятельно получить новое знание, а затем эффективно его использовать.
Просмотр содержимого документа
«Олимпиадные задания по математике в 7 классе»
Олимпиада по математике (школьный тур) для 7 класса
Задача № 1
В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?
Задача № 2
Будет ли сумма чисел 1 + 2 + 3 + ……+ 2005 + 2006 + 2007 делиться на 2007?
Задача № 3
Из квадрата со стороной 100 тетрадных клеточек вырезали квадрат со стороной 80. Оставшийся кусок разрезали на единичные квадратики (это можно сделать), из которых Андрей хочет сложить новый квадрат.
Чему будет равна его сторона?
Задача № 4
Девочка заменила каждую букву в своём имени её номером в русском алфавите и получила 2011533. Как её зовут?
Задача № 5
Задуманное число добавили к числу, большему его на единицу.
Затем из суммы вычли число, на единицу меньшее задуманного.
В итоге получилось 23. Какое число было задумано?
Задача № 6
Нюша , Бараш, Копатыч и Лосяш играли с мячами синим, зелёным, жёлтым и красным. Каким из мячей играл каждый из них, если мяч Бараша не синий, у Нюши не синий и не красный, а у Копатыча желтый мяч?
Задача № 7
Терпеливая Маша обшивает квадратную салфетку тесьмой по краю за 1 час.
Сколько часов ей понадобится, чтобы обшить квадратную салфетку,
площадь которой в 4 раза больше?
Задача № 8
Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.
Задача № 9
Квадрат числа состоит из цифр 0, 2, 3, 5. Найти его.
Задача № 10
Есть два ведра емкостью 4 и 9 литров.
Как с их помощью принести из речки ровно 6 литров воды?
Задача № 11
Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра,
в Петропавловске-Камчатском полдень.
Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?
kopilkaurokov.ru

