График функции 7 класс макарычев презентация – Презентация «График функции» 7 класс скачать
Презентация к уроку алгебры в 7 классе по теме «График функции»

Урок алгебры в 7 Б классе
06.03.2018

«хочу» «могу» «умею» «делаю»
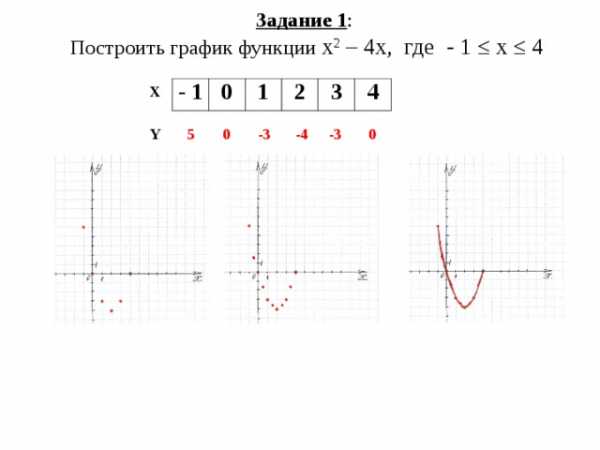
Задание 1 : Построить график функции х 2 – 4х, где — 1 ≤ х ≤ 4
Х
— 1
0
1
2
3
4
0
-3
-4
-3
0
5
Y
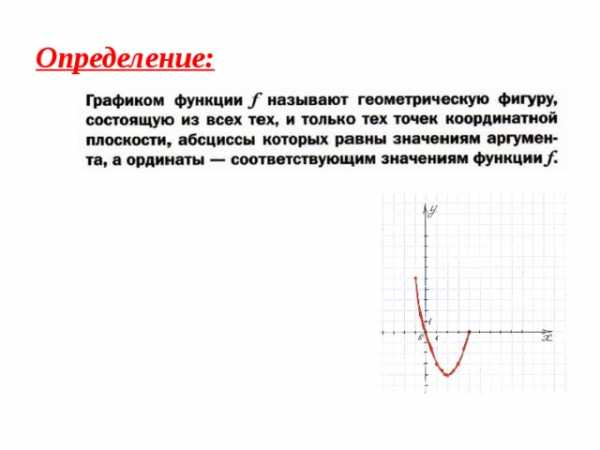
Определение:

Тема урока «График функции»
Цели и задачи урока:
Научиться строить график функции, заданной с помощью формулы.
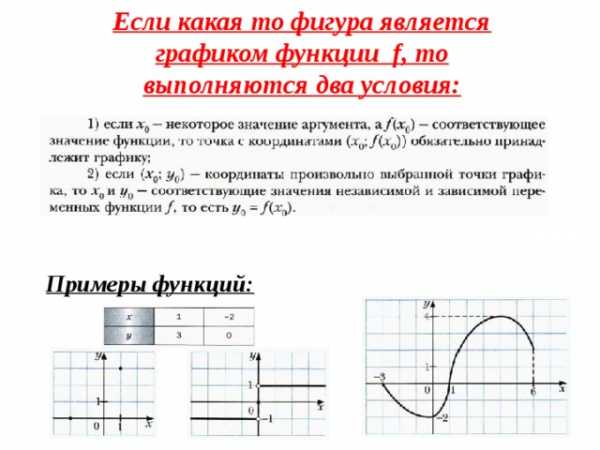
Если какая то фигура является графиком функции f , то выполняются два условия:
Примеры функций:
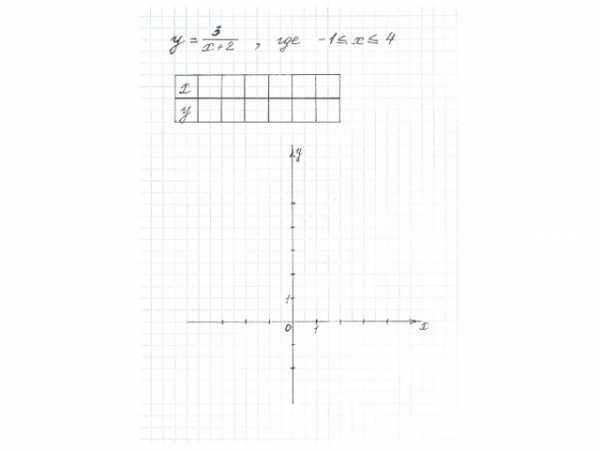
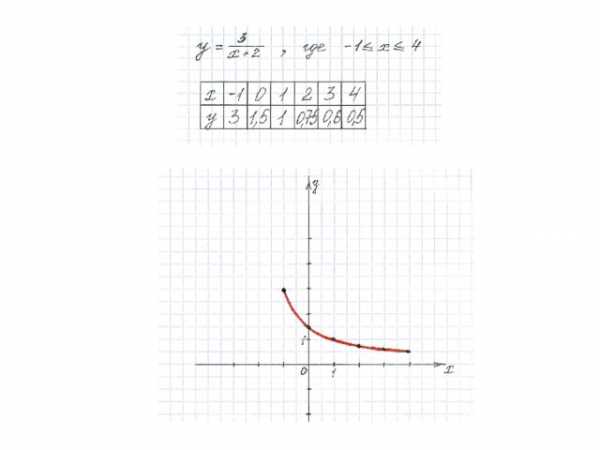

Алгоритм построения графика функции
1) На заданной области определения функции взять допустимые значения аргумента функции.
2) Для выбранных значений аргумента функции вычислить соответствующие им значения функции.
3) Перенести полученные пары чисел как координаты (х; у) точек на координатную плоскость.
4) Соединить полученные точки плавной линией.
5) Получили график данной функции
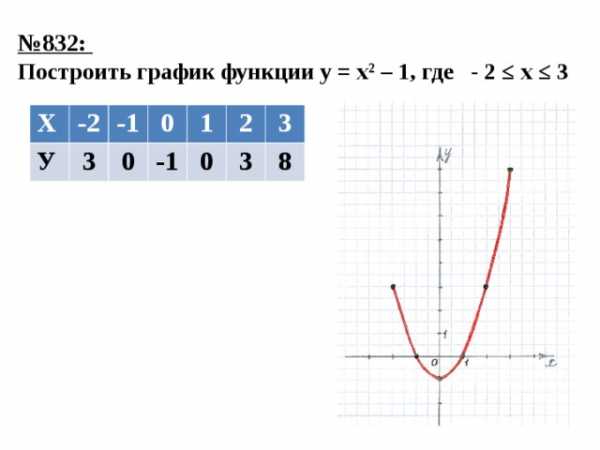
№ 832: Построить график функции у = х 2 – 1, где — 2 ≤ х ≤ 3
Х
-2
У
-1
3
0
0
1
-1
2
0
3
3
8

0
2
3
2
0
-2
-3
-2
0

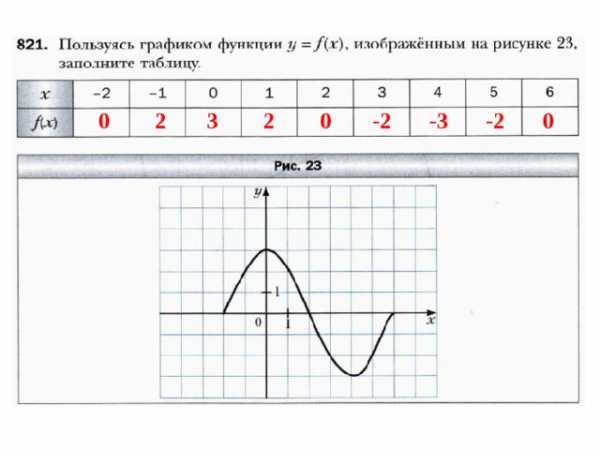
Задание 2: Постройте график функции у = х(6 – х), где -1 ≤ х ≤ 5
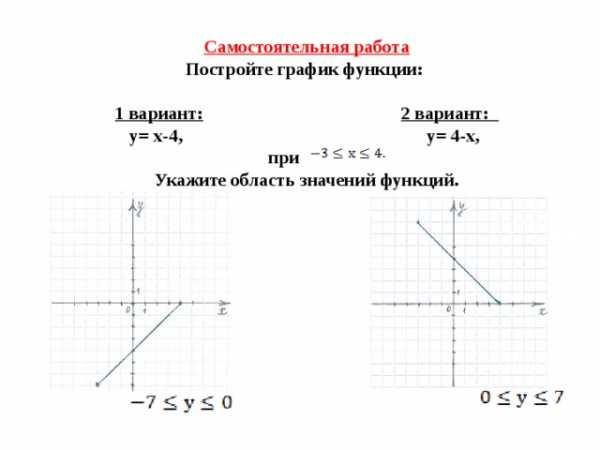
Самостоятельная работа
Постройте график функции:
1 вариант: 2 вариант:
у= х-4, у= 4-х,
при
Укажите область значений функций.
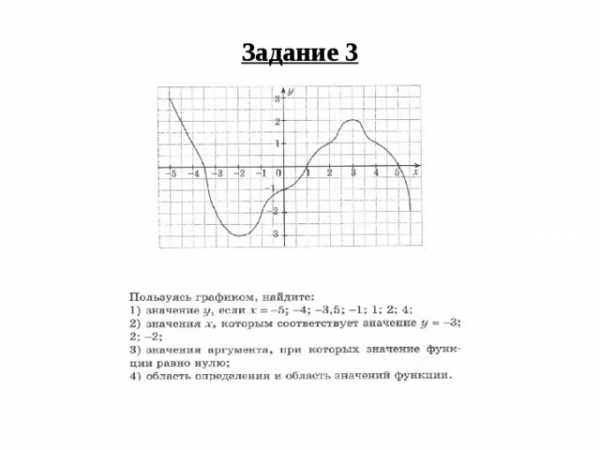
Задание 3

Домашнее задание:
- Постройте график функции, задающей результаты вашей успеваемости по математике за период обучения с 1 по 7 классы. (ось Х – класс, ось У – отметка)
- № 823, 833

-Назовите тему урока. -Расскажите, чему вы научились на уроке? -Что было самым интересным на ваш взгляд на уроке? -Мне понравилось… -Оцените свою деятельность, всё ли у вас получилось?

Спасибо, ребята, вам всем за урок!
Пусть все эти знания будут вам впрок!
Теперь говорю я вам всем “до свидания”,
Окончен урок. Благодарю за внимание.
Урок алгебры в 7 классе «График функции»
Урок алгебры в 7 классе «График функции»АРХИВ МАТЕРИАЛОВ ПРОШЛЫХ ЛЕТ. Поддержка прекращена.
| Урок алгебры в 7 классе «График функции» |
|
Фестиваль —
Педагогические идеи и технологии: среднее образование |
| Постоянный адрес работы (URL): https://educontest.net/component/content/article/49785 |
|
Автор работы: Иванова Ирина Анатольевна, МБОУ «Шигалинская ООШ» Урмарского района Чувашской Республики |
| Дата публикации: 19.11.14 20:20 |
| Просмотров работы участниками: 267 |
| Пояснительная записка: Урок алгебры в 7 классе «График функции» — урок изучения новой темы. На этапе объяснения нового материала и первичного закрепления используются ресурсы Единой коллекции цифровых образовательных ресурсов (http://school-collection.edu.ru) к учебнику «Алгебра», 7 класс, Макарычев Ю.Н., Миндюк Н.Г. и др., глава II п.12.Урок сопровождается презентацией. |
Файл работы не опубликован в надлежащем виде в соответствии с техническими требованиями. Публикатору работы необходимо отредактировать работу и правильно загрузить файл или обратиться в оргкомитет.
Если просмотр приложенных файлов не поддерживается, работу можно загрузить и просмотреть на компьютере.
educontest.net
Презентация к уроку «График функции»

График функции.

Что называют функцией?
Как называется независимая переменная?
Как называется зависимая переменная?
Перечислите способы задания
функций

Функция задана формулой Заполните пустые клетки таблицы
х
у
-0,5
-2
0
4,5
9
0
-3
3
6
Какова область определения функции?
Какова область значений функции?

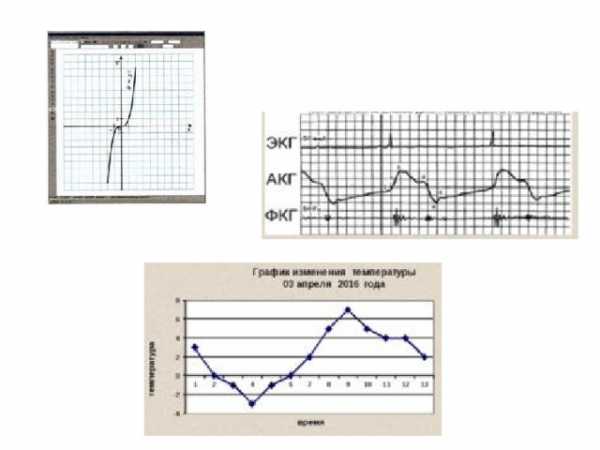
Где мы встречаемся с графиками ?
Как построить график функции?
Используется гиперссылки для перехода в необходимый раздел
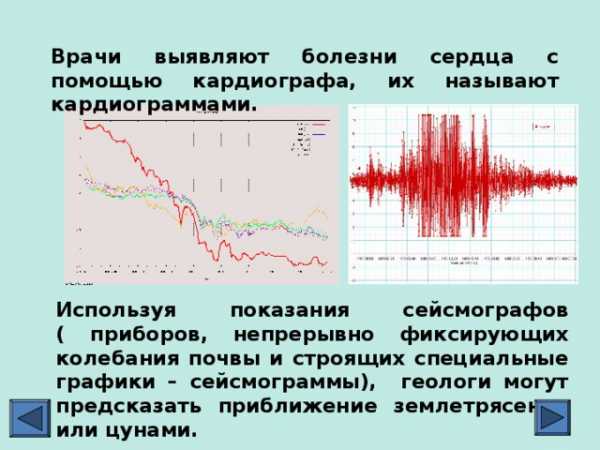
Врачи выявляют болезни сердца с помощью кардиографа, их называют кардиограммами.
Используя показания сейсмографов ( приборов, непрерывно фиксирующих колебания почвы и строящих специальные графики – сейсмограммы), геологи могут предсказать приближение землетрясение или цунами.
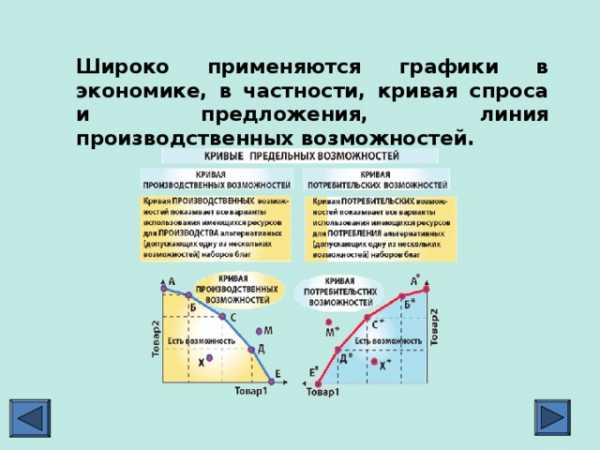
Широко применяются графики в экономике, в частности, кривая спроса и предложения, линия производственных возможностей.
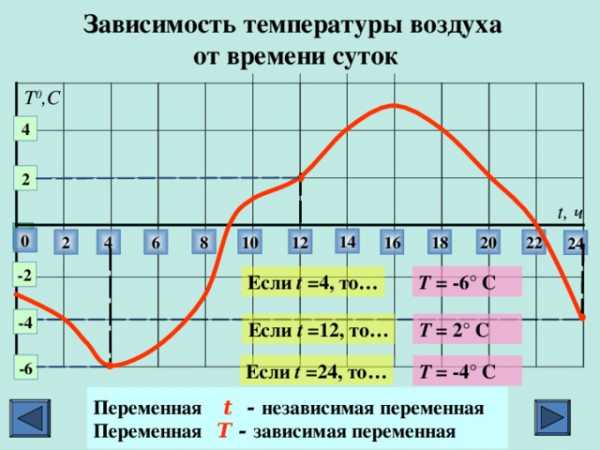
Зависимость температуры воздуха от времени суток
Т 0 ,С
4
2
t, ч
0
14
8
10
12
20
18
2
4
6
16
22
24
-2
Если t =4, то…
T = -6 ° C
-4
Если t =12, то…
T = 2 ° C
-6
Если t =24, то…
T = -4 ° C
Переменная t — независимая переменная
Переменная T — зависимая переменная

v, км/ч
График скорости машины v в зависимости от времени t
50
Из графика можно найти скорость
машины v в любой момент времени t :
9
7
6
0
t, ч
1
4
3
-80
Если t = 0,5, то…
v = 25
v = 0
Если t = 5, то…
Если t = 1,5, то…
v = 50
Если t = 6,5, то…
v = -40
Если t = 3,5, то…
v = 25
t – выбираем произвольно.
t – независимая переменная.

Построим график функции
у = х(4 – х), где -1 ≤ х ≤ 5
х
у
-1
0
1
2
3
4
5
3
0
4
0
3
-5
-5
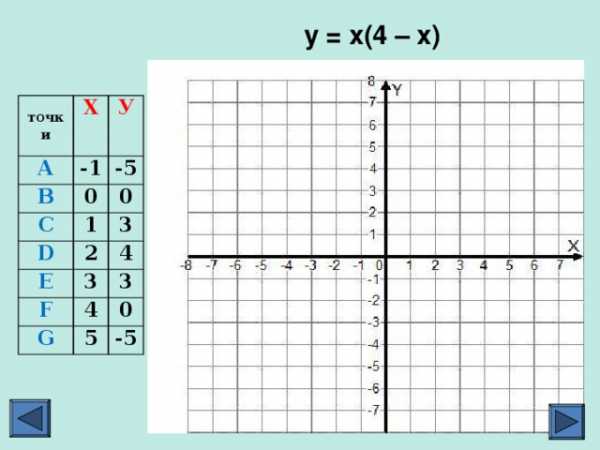
у = х(4 – х)
точки
Х
А
У
-1
В
0
-5
С
1
D
0
2
3
Е
F
4
3
4
3
G
0
5
-5
Используется перо и выделение для построения точек и графика функции

Определение:
Графиком функции называется множество всех точек координатной плоскости,
абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции
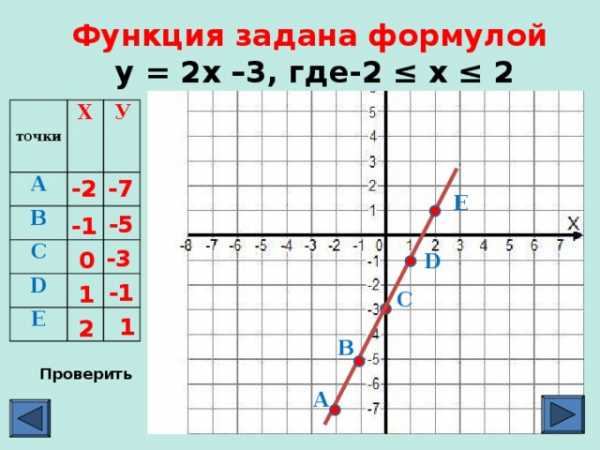
Функция задана формулой
у = 2х –3, где-2 ≤ х ≤ 2
точки
Х
А
У
В
С
D
Е
-7
-2
E
-5
-1
-3
0
D
-1
1
C
1
2
B
Проверить
А
М
К
О
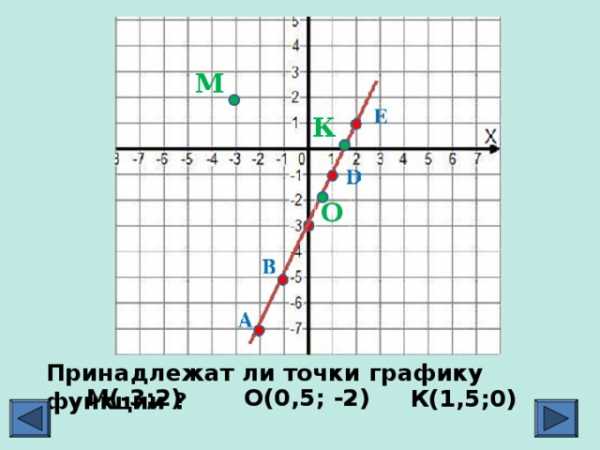
Принадлежат ли точки графику функции ?
М(-3;2)
О(0,5; -2)
К(1,5;0)
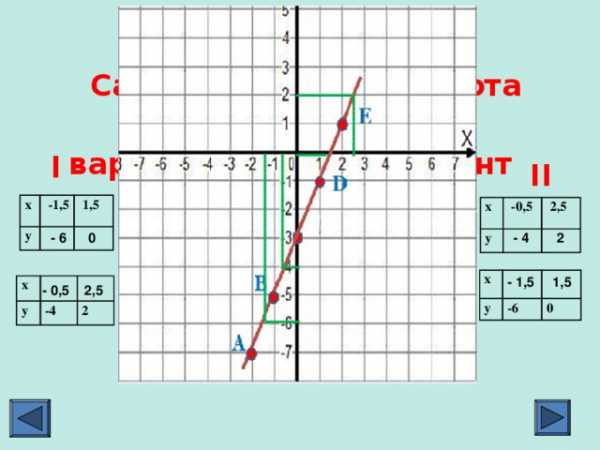
Самостоятельная работа
II
вариант
I
вариант
I
II
х
у
-1,5
1,5
х
у
-0,5
2,5
2
— 6
0
— 4
1,5
— 1,5
х
у
-6
0
х
у
-4
2
2,5
— 0,5
Проверить

Контрольные вопросы:
На примере объясните, как построить точку на координатной плоскости.
Что называется графиком функции?
Как определить, принадлежит ли точка А(a, b) графику функции или нет?

Домашнее задание
№ 284
№ 285
№ 286
Мини-проект:
Придумать свой пример функциональной зависимости одной переменной от другой, исследовать и построить график. Разработки представить в классе на обсуждение.

Выполнила:
учитель математики МОБУ СОШ №100 г. Сочи
Рылькова Наталья Валерьевна
multiurok.ru
Презентация к уроку по алгебре (7 класс) на тему: Презентация «Линейная функция и её график»
Шарабарина Галина Гавриловна — учитель математики,МБОУ «Солоновская средняя общеобразовательная школаимени Матренина А.П.»Смоленского районаАлтайского края7 классалгебра
1 2 3 4 5 6 7 Х
-7 -6 -5 -4 -3 -2 -1 0
У654321
-1 -2 -3 -4 -5 -6
Найти координаты точек
Линейные функции.
Верно!
у = к х + в
Функции прямой пропорциональности.
у = kx
Правильно!
Графики каких функций находятся в
у = 2х
у = -5х
I и III координатных четвертях
II и IV координатных четвертях
у = -6х
у = х
у = 8х
у = -1,5х
у = -(-3х)
-у = 4х
k = 5; b = 8
k = -3; b = 2
k =-1; b = 4
k =- 7; b = 0
k = 0; b = 6
Назовите коэффициенты k и b в указанных на доске линейных функциях у = 5х + 8у = -3х + 2у = 4-ху =-7ху = 6 У
Х
3.
у=-х-1
У
Х
2.
у=1,5х
У
Х
1.
у=1/3х+2
Ученик допустил ошибку при построении графика одной из функций. На каком рисунке эта ошибка ?
2
У
Х
3.
2.
1.
На рисунке изображены графики следующих функций:У = 3х; у = — 3х; у = х-3; Под каким номером изображен график функции ?
у = — 3х
Проблемная ситуация Взаимное расположение графиков линейных функций Цели: рассмотреть случаи взаимного расположения графиков линейных функций, отработать понятие углового коэффициента k; развивать самостоятельность мышления, умение выделять главное, видеть общую закономерность и делать обобщающие выводы. Выяснить зависимость расположения графиков линейных функций от значений k и b. Научиться по внешнему виду определять взаимное расположение графиков линейных функций. У=4х-1
У=-5х+3
У=5х+3
У=-2х+2
У=-0,5х-4
У=0,5х-4
У=2х+1
У=-3х+2
У=3х+2
3
2
1
Коэффициент k называют угловым коэффициентом прямой, т.к. он характеризует угол, который образует прямая с положительным направлением оси Ox. Задание № 1 Постройте графики функций и отметьте углы, которые образуют прямые с положительным направлением оси Ox.Сделайте вывод о возможной связи между углом наклона прямой и коэффициентом «к»Влияние углового коэффициента k на положение графика линейной функции на координатной плоскости. 1.Коэффициент k называют угловым коэффициентом прямой, т.к. он характеризует угол, который образует прямая с положительным направлением оси Ox.Если k>0, то график линейной функции «идет вверх» (угол острый), если kα
α
k>0
Делаем выводы
Если k >0,то график расположен в направлении от I к III координатной четверти.
I
III
II
IY
Если k Введение в тему «Взаимное расположение графиков линейных функций»Ресурс содержит материалы по теме «Взаимное расположение графиков линейных функций»[Карточка ресурса]exe3.67 мб
Сделайте вывод о взаимном расположении построенных вами графиков линейных функций, если у них к1=к2, в1= в2
Задание № 2
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
1
2
3
1
2
3
ПОДУМАЙ!
ПОДУМАЙ!
ВЕРНО!
1 2 3 4 5 6 7
7 6 5 4 3 2 1
-7 -6 -5 -4 -3 -2 -1
-1 -2 -3 -4 -5 -6 -7
1
2
3
4
у= –2х+2
у= 2х+1
у= –3х+1
у= 3х+1
y
x
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
График какой функции изображен на рисунке
у
0
х
Составить формулы для функций,изображенных графиков.
у = х + 2
у = х
у = х — 3
у
х
0
Составить формулы для функций,изображенных графиков.
у = 3
у = х +2
у = -х +1
Х = -2
3
2
1
1
4
3
2
nsportal.ru
-4 | -3 | -2 | -1 | 0 | 1 | 2 | |
у |
doc4web.ru
Презентация к уроку математики в 7 классе по теме «Линейная функция»
Презентация к уроку математики в 7 классе по теме «Линейная функция».
Линейной функцией называется функция вида у = кх + в, где к и в — заданные числа. графиком линейной функции является прямая.
1 способ построения — по 2 точкам.
2 способ построения — с помощью параллельного переноса.
Примеры построения графиков. решение задач.
Просмотр содержимого документа
«Презентация к уроку математики в 7 классе по теме «Линейная функция» »

7 КЛАСС. АЛГЕБРА.
Линейная функция. y = kx+b
Обратная пропорциональность. y =
k
x

Линейной функцией называется функция вида
у = kx + b
где k и b – заданные числа
у = kx + b
Графиком линейной функции является прямая
1 способ построения – по двум точкам
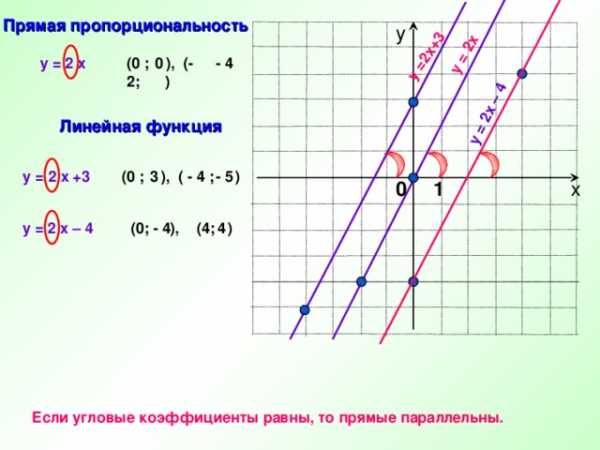
y = 2 x
y = 2 x +3
y = 2x – 4
Прямая пропорциональность
у
y = 2 x
— 4
(0 ; ), (- 2; )
0
Линейная функция
(0 ; ), ( — 4 ; )
y = 2 x +3
3
— 5
1
х
0
(0; ), (4; )
y = 2 x – 4
— 4
4
Если угловые коэффициенты равны, то прямые параллельны.
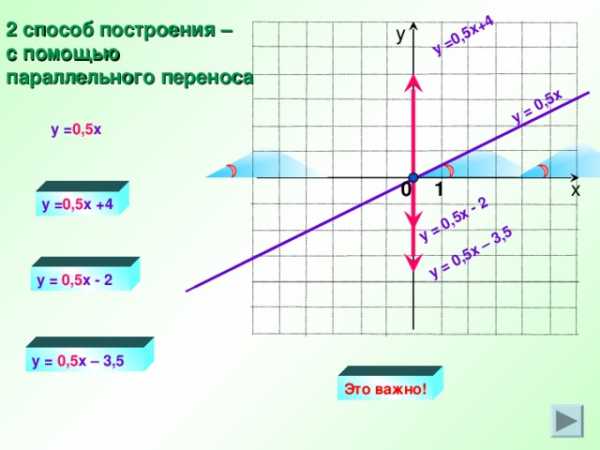
y = 0,5 x
y = 0,5 x +4
y = 0,5 x — 2
y = 0,5 x – 3,5
2 способ построения –
с помощью
параллельного переноса
у
y = 0,5 x
х
0 1
y = 0,5 x +4
y = 0,5 x — 2
y = 0,5 x – 3,5
Это важно!
 0 х 0 1 b 0″
0 х 0 1 b 0″
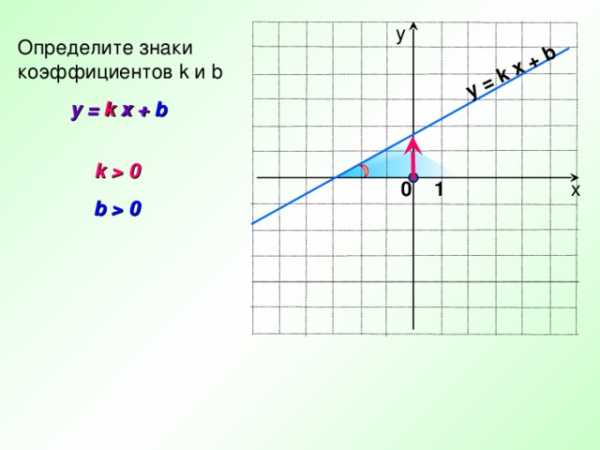
y = k x + b
у
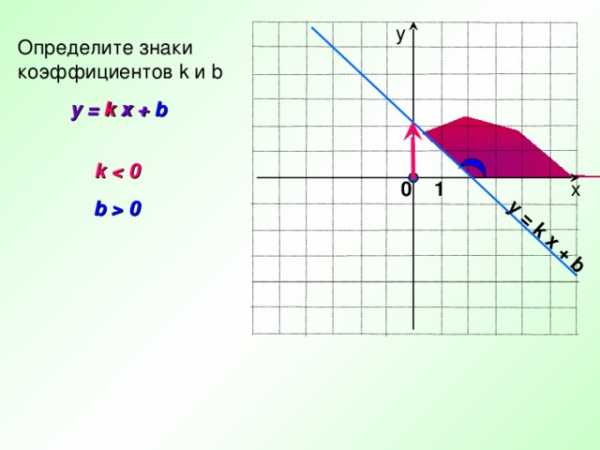
Определите знаки
коэффициентов k и b
y = k x + b
k 0
х
0 1
b 0
 0 х 0 1 b»
0 х 0 1 b»
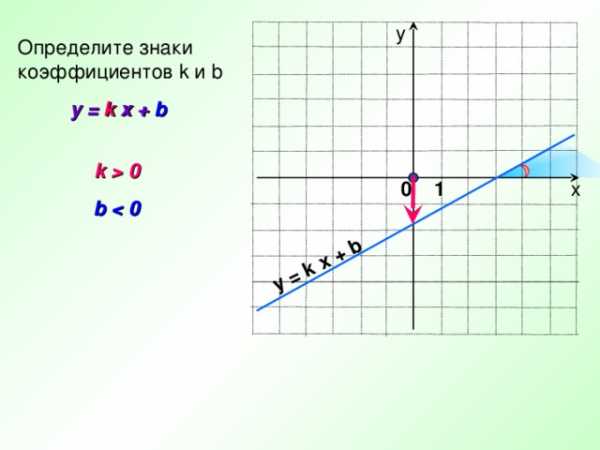
y = k x + b
у
Определите знаки
коэффициентов k и b
y = k x + b
k 0
х
0 1
b
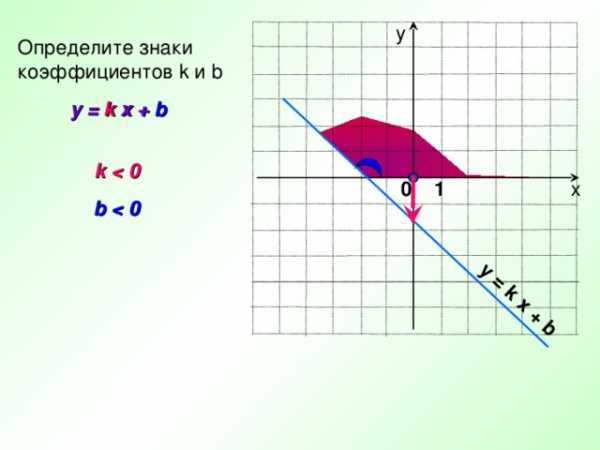
y = k x + b
у
Определите знаки
коэффициентов k и b
y = k x + b
k
х
0 1
b
 0″
0″
y = k x + b
у
Определите знаки
коэффициентов k и b
y = k x + b
k
х
0 1
b 0
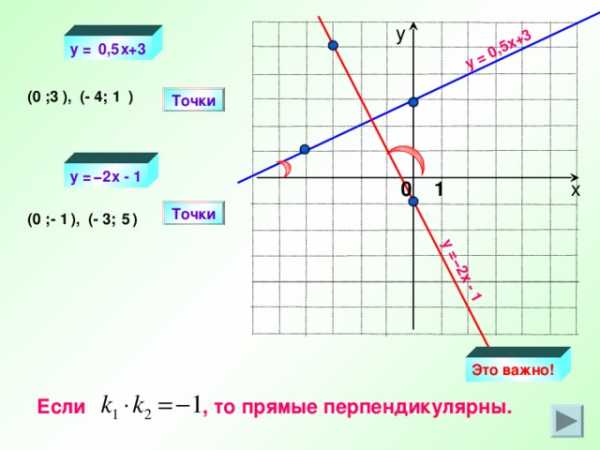
y = 0,5 x +3
y = − 2х — 1
у
y = x +3
0,5
3
(0 ; ), (- 4; )
1
Точки
− 2
y = х — 1
0 1
х
Точки
(0 ; ), (- 3; )
— 1
5
Это важно!
Если , то прямые перпендикулярны.
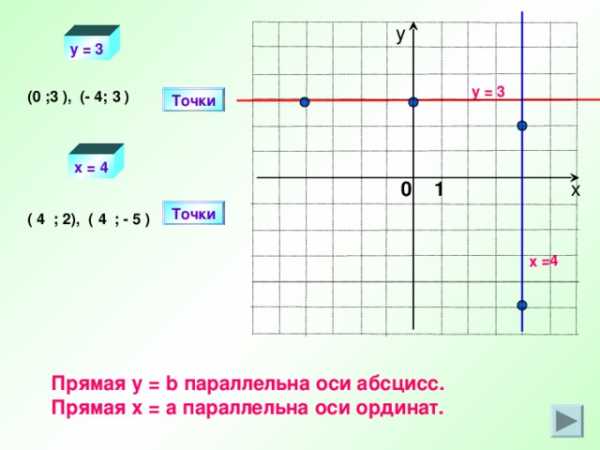
x = 4
у
y = 3
y = 3
(0 ; ), (- 4; )
3
3
Точки
x = 4
х
0 1
Точки
4
4
( ; 2 ), ( ; — 5 )
Прямая y = b параллельна оси абсцисс.
Прямая х = а параллельна оси ординат.
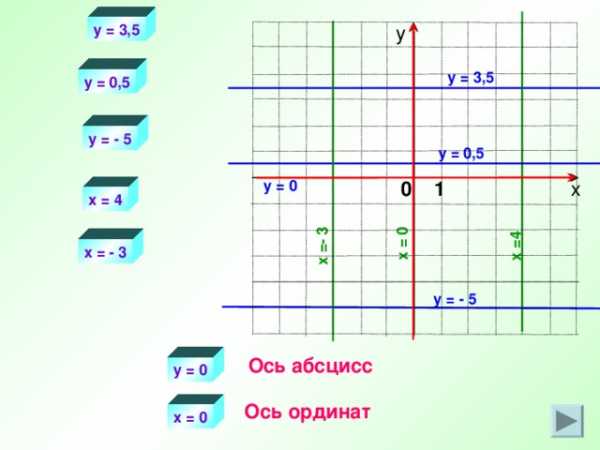
x = 4
x = — 3
x = 0
y = 3,5
у
y = 3,5
y = 0,5
y = — 5
y = 0,5
х
0 1
y = 0
x = 4
x = — 3
y = — 5
Ось абсцисс
у = 0
Ось ординат
х = 0
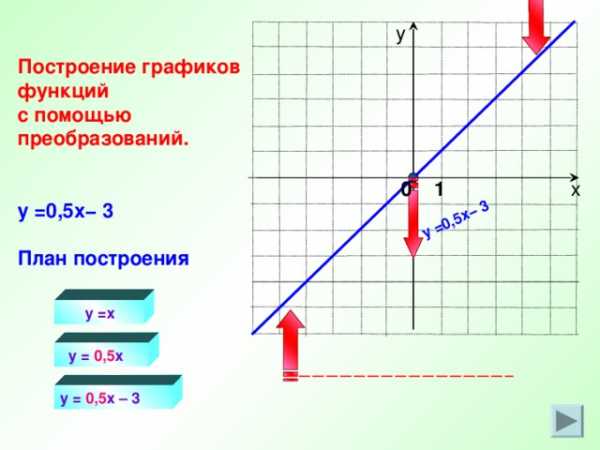
y = 0,5 x − 3
у
Построение графиков функций
с помощью преобразований.
y = 0,5 x − 3
План построения
х
0 1
y =x
y = 0,5 x
y = 0,5 x – 3
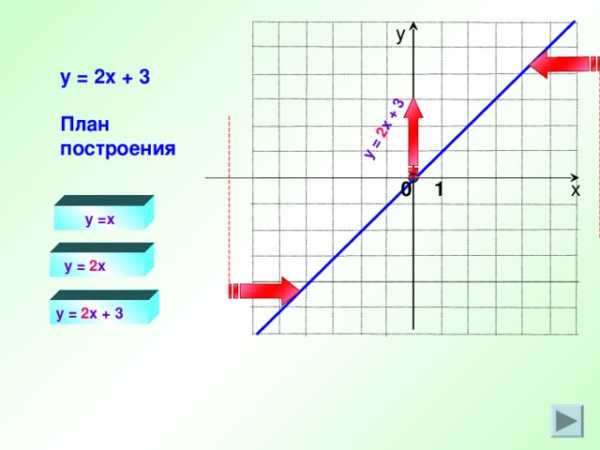
y = 2 x + 3
у
y = 2 x + 3
План построения
х
0 1
y =x
y = 2 x
y = 2 x + 3
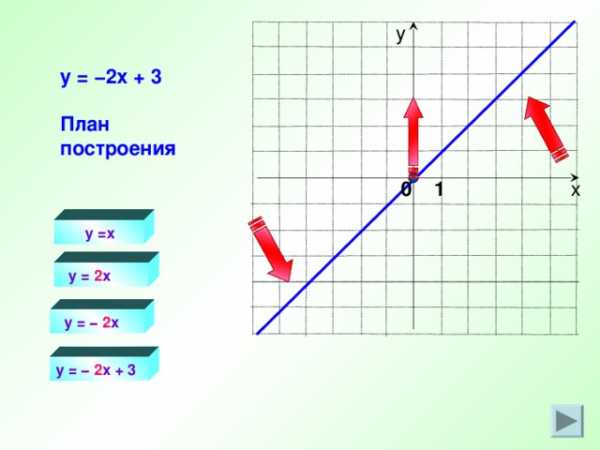
у
y = −2 x + 3
План построения
0 1
х
y =x
y = 2 x
y = − 2 x
y = − 2 x + 3
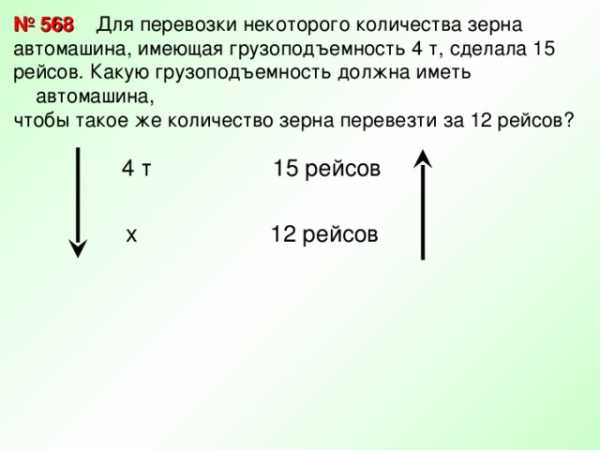
№ 568 Для перевозки некоторого количества зерна
автомашина, имеющая грузоподъемность 4 т, сделала 15
рейсов. Какую грузоподъемность должна иметь автомашина,
чтобы такое же количество зерна перевезти за 12 рейсов?
15 рейсов
4 т
х
12 рейсов

Поезд движется из Москвы в Санкт-Петербург со скоростью v км/ч. За какое время поезд пройдет путь 700 км?
700
t =
v
Москва
700
t ( v ) =
Санкт-Петербург
v
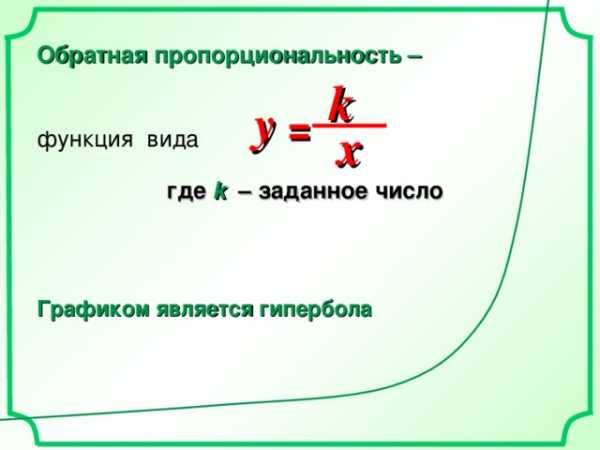
Обратная пропорциональность –
функция вида
где k – заданное число
k
y =
x
Графиком является гипербола
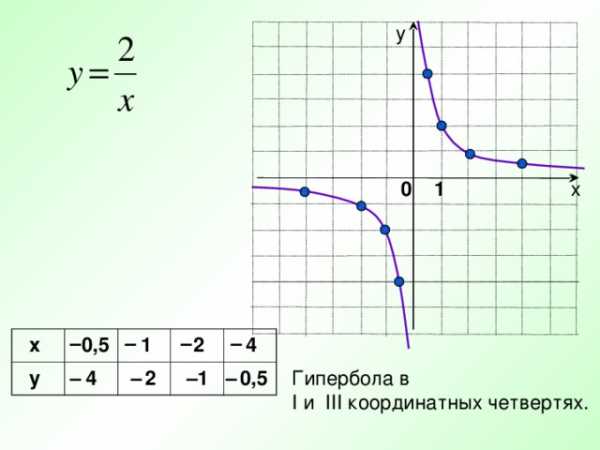
у
х
0 1
– – – –
х
у
0,5
1
2
4
4
Гипербола в
I и III координатных четвертях.
1
2
0,5
– – – –
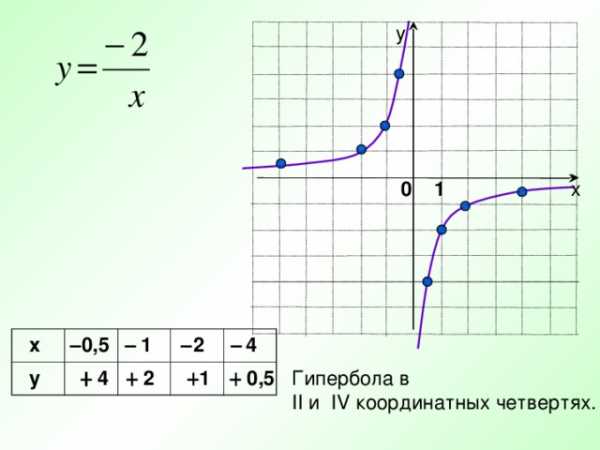
у
х
0 1
– – – –
х
у
0,5
1
2
4
– 4
Гипербола в
II и IV координатных четвертях.
– 2
– 1
– 0,5
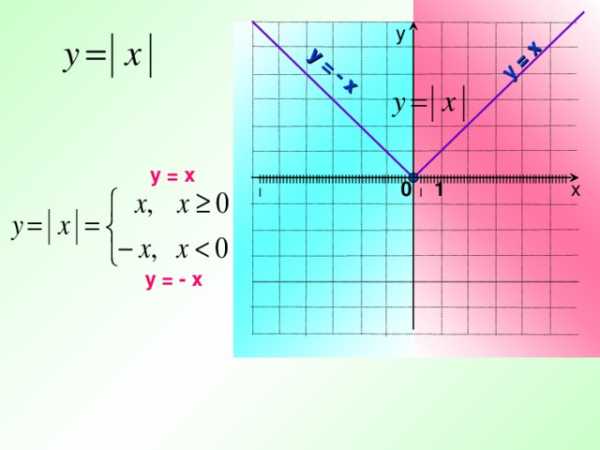
у = х
у = — х
у
у = х
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
х
0 1
у = — х

у
х
0 1
kopilkaurokov.ru
Презентация к уроку «Линейная функция» 7 класс

Обобщающий урок по теме: «Линейная функция»

Линейная функция

ЦЕЛЬ УРОКА:
Обобщение и закрепление знаний по теме «Линейная функция».
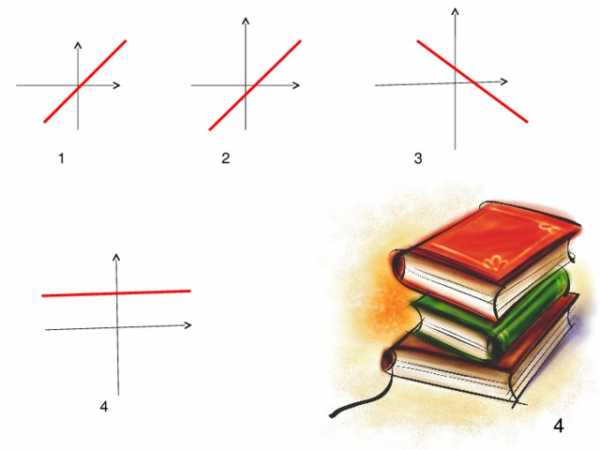
3
1
2
4

Устная разминка

Назовите функции, графики которых пересекаются?
Параллельны?
у=3х-5,
у=х+8,
у=3х+1,
у=-2х+8
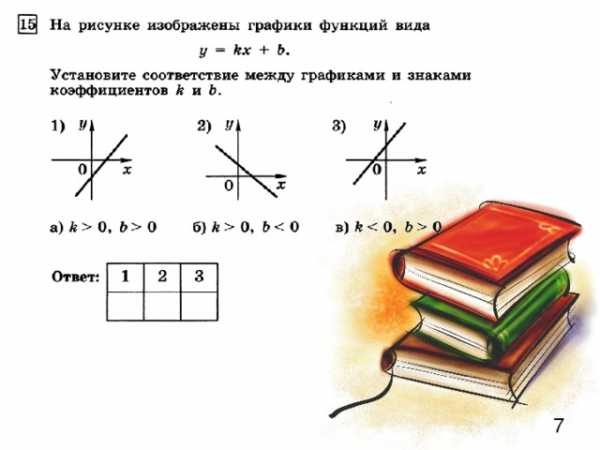
6

Физкульт-минутка

Работа с классом
1) Поезд находится в 30 км от города и удаляется от него со скоростью 40км/ч.
Задайте формулой расстояние от города до поезда в
зависимости от времени
движения t .Найдите S,
если t=2,3.

2) График функции у=кх+ b проходит через точки А(0;-3) и В(2;0). Определите k и b и постройте график .
10

Самостоятельная работа по вариантам Вариант 1
1.Соотнесите функции с
их графиками
1)у=2х+2 2)у=-2х-2 3)у=2х
2.Даны три прямые у=3х-2, у=3х,у=3х+0,7
Сколько у них общих точек? Ответ___
3.Не выполняя построений,
найдите общую точку графиков
функций у=4х-5 и у=2,4х-5
Ответ_____
4.Напишите уравнение прямой,
проходящей через точку К(2;3)
и параллельно прямой у=1,5х+7.Постройте график этой функции.

Вариант2
1.Соотнесите функции с их графиками
1)у=3х, 2)у=1-х, 3)у=2х-3
2.Сколько общих точек имеют графики функций
У=3х-7,у=-х-7 и у=-7?
3.Пересекает ли ось абсцисс
график функции У=-6?
4.График функции у= k х+1
параллелен графику у=-3х.
Найдите k . Проходит ли он
через точку М(-5;4)?
Постройте график этой функции.

Викторина .
1. Любое число можно изобразить точкой на числовой прямой. Что называется модулем числа «а»?
2. | x | = 17. Чему равно значение « x »?
3. Задайте линейную функцию с числом k 0.
4. Что является графиком прямой пропорциональности?
5. | x | = 7, a |- x | =?
6. y = | x — 3|. Чему равен подмодульный нуль?
7. Назовите числовые промежутки, которые получаются при раскрытии модуля функции y = | x — 3|?
8. Какова область определения линейной функции?

Подведение итогов урока.

Домашнее задание:

Молодцы, ребята!
Спасибо за урок.
videouroki.net


 овторим основные понятия, которые мы изучили:
овторим основные понятия, которые мы изучили: