Конспект урока геометрии в 7 классе по теме «Перпендикулярные прямые»

Тема урока геометрии в 7 классе: «Перпендикулярные прямые»

Учитель Венжик Тамара Дмитриевна

Математике должно учить в школе еще с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни. 

Н.И. Лобачевский — русский математик, один из создателей неевклидовой геометрии

Цель:

1. Повторить понятие перпендикулярные прямые;

2. Рассмотреть свойство перпендикулярных прямых;

3. Совершенствовать у учащихся умение решать задачи.

Используемое помещение и оборудование: сенсорная комната, 2 рабочих места для детей-инвалидов, оборудованных ПК, интерактивная доска, экранная лупа, сканер-распознаватель текста, видеокамера, клавиатура для слабовидящих, релакс-оборудование – пузырьковая колонна, тактильная дорожка.

ХОД УРОКА

1. Организационный момент. Проверить готовность к уроку: наличие учебника, тетради, дневника, карандаша, угольника, транспортира и циркуля.

Сегодня у нас не совсем обычный урок геометрии – на нем присутствуют гости из других школ и отдела образования. Ребята, поприветствуйте гостей.

Начать с эпиграфа – презентация.

2. Определение темы урока.

Картинка Пизанской башни в Италии (колокольни).

Что изображено на картинке?

Падает Пизанская Башня уже на протяжении восьми столетий. Из-за этого сами итальянцы и называют ее «затянувшимся чудом». На сегодняшний день отклонение башни составляет 4м 4см.

Что не так с этим зданием?

Что может произойти, если башня рухнет?

А как правильно нужно было построить башню, чтобы она не упала?

Перпендикулярно земле. Это и есть тема нашего сегодняшнего урока – «Перпендикулярные прямые».

3. Актуализация опорных знаний.

Сколько прямых можно провести через две точки? (2 рисунка на листе).

Сколько общих точек могут иметь две прямые? Сделайте необходимые рисунки. Обозначьте прямые и точки. Опишите их взаимное расположение.

1. С помощью лупы читает текст. Отвечает на вопросы теста, используя клавиатуру для слабовидящих – Павлюкова В.

2. Грязнов В. – сканированный текст слушает и воспроизводит услышанное, потом пересказывает классу. Далее – работа в паре. Проверяет у Павлюковой ответы на тест.

4. Изучение новой темы – определение перпендикулярных прямых и способов их построения.

ОПРЕДЕЛЕНИЕ ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ

1. 1. открыть тему урока.

В 6-м классе мы уже проходили эту тему, давайте сегодня вспомним, какие две прямые называются перпендикулярными? Чему равна градусная мера остальных трех углов?

1. 2. Дать определение. Записать в тетрадь.

Определение: Две прямые называются перпендикулярными, если они образуют четыре прямых угла.

1. 3. Где в природе мы сталкиваемся с перпендикулярными прямыми? (Рисунок бабочки, рисунок птички — презентация).

   4. Учащиеся приводят свои примеры. Для обозначения перпендикулярности имеется общепринятый символ:

      ┴, предложенный в 1634 году французским математиком Пьером Эригоном.

   5. Стихотворение «Гордый перпендикуляр» — ВИДЕОФИЛЬМ.

1. 6. Даны две пересекающиеся прямые. Как я могу убедиться, что прямые пересекаются под прямым углом, т.е. перпендикулярны? Кто мне поможет?

   7. Как построить две перпендикулярные прямые? (Построить прямой угол и продолжить каждую из сторон угла).

   8. С помощью каких чертежных инструментов еще можно построить перпендикулярные прямые?

ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ

1. 9. С помощью каких чертежных инструментов я могу построить перпендикулярные прямые? Вызвать к доске …….. Параллельно показываю это на сенсорной доске.

а) с помощью угольника

б) с помощью транспортира

в) с помощью циркуля.

1. 10. Как построить перпендикулярные прямые с помощью чертежного угольника? – 1 чел у доски Обозначаем прямые. Делаем запись АВ_┴СD

   11. Как построить перпендикулярные прямые с помощью транспортира? – 1 чел у доски

   12. Как построить перпендикулярные прямые с помощью циркуля?…..

Параллельно с детьми произвожу построения на сенсорной доске с помощью чертежных инструментов.

Вызвать детей к сенсорной доске для обозначения перпендикулярных прямых и записи АВ_┴СD.

ФИЗКУЛЬТМИНУТКА, РЕЛАКС

1. 13. Поискать глазами перпендикулярные прямые на потолке, на стена, на столе. Изобразить перпендикуляры глазами, глазами и головой.

   14. Релакс-минутка. Павлюкова – тактильная дорожка + посидит в кресле. Пузырьковая колонна. Минутка покоя.

СВЯЗЬ С ДРУГИМИ ПРЕДМЕТАМИ

Конференц-связь с кабинетом физики – учитель физики Голотина Ирина Васильевна сказала нам о давлении тел на поверхность земли, объяснение проводит используя презентацию.

Связь с краеведением –

Я комментирую услышанное: вы знаете, что в Ростовской области очень много шахт по выработке угля. То есть под нами в земле образовались пустоты. И очень важно при строительстве домов таким образом рассчитать силу давления зданий на поверхность земли, чтобы дома не провалились под землю.

Второй пример надежного строительства – это Останкинская башня в Москве. В отличие от Пизанской башни она построена строго перпендикулярно основанию. И несмотря на то, что ее высота 540м 74см, состоит она из 45 этажей, туристы смело взбираются на самый верх, чтобы обозреть окрестности Москвы.

5. Проверка выполненных индивидуальных заданий.

3. Грязнов В. – ПРАКТИЧЕСКАЯ РАБОТА.

Дать отвес: Для того, чтобы построить крепкие и прочные дома строители проверяют перпендикулярность стены дома к основанию дома с помощью отвеса, то есть грузика на веревке. Отсюда и произошло название перпендикуляра: латинское «перпендикулярис» означает «отвесной».

4. 2 чел, работавшие по рисункам дают ответы на вопрос: Сколько прямых можно провести через две точки? (2 рисунка на листе).

5. 1 чел. — Сколько общих точек могут иметь две прямые? Сделайте рисунок.

Все эти знания нам сейчас пригодятся при изучении свойства перпендикулярных прямых.

6. Свойство перпендикулярных прямых. Показать видеофильм – доказательство свойства перпендикулярных прямых, потом рисунок.

Что было непонятно?

Проговорить основные этапы доказательства еще раз.

Дать определение перпендикулярных отрезков.

Вызвать ученика к сенсорной доске

Задача. С помощью какого чертежного инструмента можно определить, являются ли отрезки перпендикулярными. Как это сделать?

7. Закрепление изученного.

   1. Практическое задание: построить прямую а┴в, в┴с, с┴d. Что вы можете сказать о взаимном расположении прямых а и d? Опишите взаимное расположение прямых в и d.

   2. Изобразите в тетради два отрезка, построенные вот таким способом. Как проверить, перпендикулярны ли эти отрезки?

   3. № 69, 70.

№69. Решение. Обе прямые АР и АQ не могут быть перпендикулярны прямой а, так как АР и АQ пересекаются.

№70. Решение. Допустим обратное (метод от противного): что все эти три прямые перпендикулярны а, то тогда эти три прямые не пересекаются. А по условию они все проходят через одну точку А. Значит все эти три прямые одновременно перпендикулярными быть не могут. Следовательно только одна прямая из трех может быть перпендикулярна а.

8. Итог урока.

Итак, давайте подведем итог сегодняшнего урока. С чем мы сегодня познакомились?

Какие прямые называются перпендикулярными? С помощью каких инструментов можно построить перпендикулярные прямые? Какие чертежные инструменты при этом используются? Назовите свойство перпендикулярных прямых. Какие отрезки называются перпендикулярными?

Вы хорошо поработали на уроке, вижу, что тему сегодняшнего урока вы усвоили, поняли важность соблюдения принципов перпендикулярности в строительстве, поэтому, надеюсь, в будущем из вас получатся хорошие специалисты, которые не допустят обрушения домов. И мы можем не бояться за свою жизнь.

Похвалить. Выставить отметки.

Дома. П.12-13, вопр.19-21 стр.26 № 80, 82а.

infourok.ru

Перпендикулярные прямые. Видеоурок. Геометрия 7 Класс

Рассмотрим частный случай смежных углов, если они оба равны.

                                

Рис. 1. Угол ∠АОС

На рисунке изображены смежные углы ∠АОВ и ∠ВОС. α + β = 180^o.

                                          

Рис. 2. Перпендикулярные прямые

Определение: Если пересекающиеся прямые образуют угол 90^о, то они называются перпендикулярными. На рисунке 2 изображены перпендикулярные прямые АС и BD.

Обозначение перпендикулярных прямых следующее: .

Очевидно, что существует множество прямых, которые перпендикулярны данной прямой. Рассмотрим 2 из них.

                                          

Рис. 3. Перпендикулярные прямые

На рисунке 3 изображена прямая PQ и две прямые, которые перпендикулярны ей,  AA₁ и BB₁. Докажем, что данные прямые не пересекаются между собой.

Докажем методом «от противного». Предположим, что прямые  AA₁  и BB₁ пересекаются в точке , тогда существует и другая точка пересечения М в другой полуплоскости относительно прямой PQ. Соответственно, через 2 точки проходит две прямых, а это противоречит аксиоме. Наше изначальное предположение неверно, прямые AA₁ и BB₁ не пересекаются.

 и .

То есть две прямые, перпендикулярные третьей, не имеют общих точек между собой.

Рассмотрим следующие задачи:

Пример 1: Градусная мера угла ∠АОВ равна 90^о. Луч СО делит данный угол на два. Найти градусную меру угла между биссектрисами образовавшихся ∠СОА и ∠ВОС.

Решение:

Выполним пояснительный рисунок:

                               

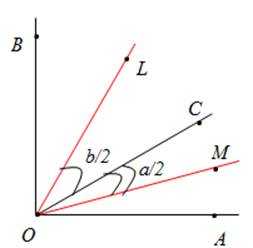
Рис. 4. Чертеж к примеру 1

Пусть ∠ВОС = β, тогда ∠LOC =  (OL – биссектриса). Пусть ∠СОА = α, тогда ∠СОМ =   (OМ – биссектриса). ∠LOM = ∠LОС + ∠СОM =  +  = ^o.

Ответ: 45^о.

Пример 2: Докажите, что биссектрисы вертикальных углов лежат на одной прямой.

Решение:

                 

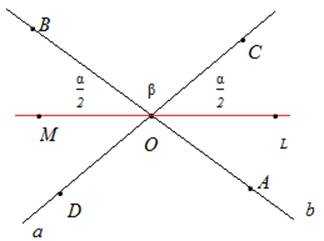
Рис. 5. Чертеж к примеру 2

Рассмотрим вертикальные углы ∠BOD и ∠СОА. Биссектрисы этих углов соответственно ОМ и ОL. Поскольку вертикальные углы равны, то пусть  ∠BOD = ∠СОА = α. Тогда ∠МОВ  = ∠СОL = . Угол ∠ВОС = β. Поскольку α и β – смежные, то α + β = 180^о. Очевидно, чтобы доказать, что ОL и ОМ лежат на одной прямой, необходимо доказать, что угол ∠МОL – развернутый. Для этого выполним алгебраическое сложение: ∠ МОL = ∠МОВ + ∠ВОС + ∠СОL = ^о.

Доказано.

Пример 3: Могут ли прямые AP и AQ быть перпендикулярными к прямой a?

Решение:

                                                                 

Рис. 6. Чертеж к примеру 3

Сама по себе прямая AQ может быть перпендикулярной прямой a. Также прямая АР тоже может быть перпендикулярна a. Поскольку прямые AP и AQ пересекаются, то одновременно перпендикулярными прямой a они быть не могут.

Ответ: Соотношение невозможно.

 

Список рекомендованной литературы

1. Александров  А.Д., Вернер А. Л., Рыжик В. И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Обобщающий урок по геометрии в 7-м классе (Источник).
2. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. № 15. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

2. Постройте перпендикулярные прямым прямые, проходящие через заданные точки.

3. Сколько пар прямых углов образуется при пересечении в одной точке трех пар взаимно перпендикулярных прямых?

4. Прямая ОС перпендикулярна прямой АВ. Углы 1 и 2 равны. Докажите, что углы АОЕ и КОВ равны.

interneturok.ru

Урок геометрии в 7 классе «Перпендикулярные прямые»

ГЕОМЕТРИЯ 7 КЛАСС «ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ»

Цели: ввести понятия смежных и вертикальных углов; рассмотреть их свойства; ввести понятие перпендикулярных прямых и показать, как применяются эти понятия при решении задач.

Наглядные пособия: таблицы «Смежные углы», «Вертикальные углы», «Перпендикулярные прямые».

Ход урока

I.  Анализ результатов самостоятельной работы.

 

II. Изучение нового материала. Решение задач.

1. Ввести понятие смежных углов и их свойства (сумма смежных углов равна 180°) с помощью таблицы «Смежные углы».

2. Выполнение практического задания № 55 (на доске и в тетрадях).

3. Устно решить задачи № 58, 59, 60, 63, 62 (по рис. 46).

4. Письменно решить задачу № 61 (в; г):

в) Дано: ∠hk и ∠kl — смежные; ∠hk больше ∠kl на 47° 18′.

Найти: ∠hk и ∠kl.

 

 

Решение: Пусть ∠kl = х, тогда ∠hk = х + 47°18′. По свойству о сумме смежных углов ∠kl + ∠hk = 180°.

х + х + 47°18′ = 180°;

2х = 180° — 47°18′;

2х — 179°60′ — 47° 18′; 

2х = 122°42′;

х = б6°21′.

∠kl = 66°2Г; ∠hk = 66°21′ + 47°18′ = 113°39′.

Ответ: 113°39′ и 66°21′.

г)  Пусть ∠kl = х, тогда ∠hk = 3х

х + 3х = 180°; 4х = 180°; х = 45°; ∠kl = 45°; ∠hk = 135°.

Ответ: 135° и 45°.

5. Понятие вертикальных углов можно ввести, выполняя следующее задание:

1) Начертите неразвернутый ∠AOB и назовите лучи, являющиеся сторонами этого угла.

2) Проведите луч ОС, являющийся продолжением луча ОА, и луч ОД, являющийся продолжением луча ОВ.

3) Запишите в тетради: углы АОВ и СОД называются вертикальными.

6. На таблице «Вертикальные углы» показать, что при пересечении двух прямых образуются две пары вертикальных углов с вершиной в точке пересечения этих прямых.

7. Определение вертикальных углов (рис. 41).

8. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере, записав его на доске и в тетрадях учащихся.

Задача. Прямые АВ и СД пересекаются в точке О так, что ∠AOД = 35°. Найдите углы АОС и ВОС.

 

 

Решение:

1) Углы АОД и АОС смежные, поэтому ∠BOC = 180° — 35° = 145°.

2) Углы АОС и ВОС также смежные, поэтому ∠BOC = 180° — 145° = 35°.

Значит, ∠BOC = ∠АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?

9. Самостоятельное доказательство учащимися свойства вертикальных углов (рис. 41) и запись этого доказательства в тетрадях.

10. Устно решить задачу № 65 (использовать таблицу «Вертикальные углы»).

11. Устно решить задачу № 67 по рисунку 47.

12. Ввести понятие перпендикулярных прямых (использовать таблицу «Перпендикулярные прямые» (рис. 42).

13. Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.

14. Выполнение практического задания № 57.

15. Беседа о построении прямых углов на местности (п. 13) с демонстрацией изготовленного учащимися экера.

 

III. Самостоятельная работа.

Вариант I

1.  Один из смежных углов на 27° меньше другого. Найдите оба смежных угла.

2.  Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 226°.

Вариант II

1.  Один из смежных углов в девять раз больше другого. Найдите оба смежных угла.

2.  Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 81° больше другого.

 

IV. Итоги урока.

Домашнее задание: изучить пункты 11

infourok.ru

План-конспект урока по геометрии (7 класс) по теме: Перпендикулярные прямые

Учитель ГБОУ школы-интерната № 28

Николаева Валентина Васильевна

Тема урока: «Перпендикулярные прямые» (ФГОС)

Учебник:  «Геометрия 7-9»,  Л.С. Атанасян

Цели:

• познакомить с определением перпендикулярных прямых
• формировать и обосновать утверждение о двух прямых, перпендикулярных  третьей
• познакомить со способами построения на местности  перпендикулярных прямых

Задачи:

• создать условия для повторения понятий «смежные и вертикальные углы»
• создать условия для введения понятия перпендикулярных прямых
• формировать навык самостоятельного приобретения знаний
• совершенствовать у учащихся навыки решения задач
• расширять кругозор учащихся
• воспитывать аккуратность, дисциплинированность, активность, умение

общаться, преодолевать трудности

• развивать внимание, память, воображение, логическое мышление, умение

выделять главное, навыки самоконтроля

Тип урока: урок открытия нового знания

Методы обучения: проблемный, частично-поисковый

Ход урока:

1. Организационный момент (проверка готовности учащихся к уроку).
2. Актуализация опорных знаний:

• Выясняем, удалось ли справиться с выполнением домашнего задания
• Если большинство учащихся справились с домашним заданием,  четырём

желающим предлагается показать свое решение №№ 61 (а, в, г), 64(б) на доске

устная работа

     Совместно с ребятами, сидящими за партами, пытаемся устно ответить на следующие вопросы:

1. Каким – острым, тупым или прямым будет угол, смежный с углом  в

300, 1300?

2. Сумма двух углов 2000. Смежные ли это углы?
3. Сумма двух углов 1800. Обязательно ли эти углы смежные?
4. Чему равен угол, если  вертикальный с ним угол 340?
5. У двух углов общая вершина, каждый из них 600. Обязательно ли эти

углы вертикальные?

6. Один из четырёх углов, получившихся при пересечении двух прямых,

равен 1400. Чему равны остальные углы?

Стремимся, чтобы в обсуждении ответов на вопросы участвовало как можно больше ребят. Для того чтобы в диалог вступали даже самые слабые ученики, ребятам предлагается проводить обсуждение в парах.

       Совместно с учениками проверяем решение на доске.

       Подробно разбираем решение задач, вызвавших затруднение дома (если таковые были).

3. Постановка проблемы:

• Совместно с обучающимися класса рассматриваем рис. 42  учебника и

подводим их к самостоятельному обоснованию того факта, что, если при

пересечении двух прямых один из образовавшихся углов прямой, то и остальные углы прямые

• Пытаемся ввести понятие перпендикулярных прямых

4.   Объявление темы и цели урока:

Попробуйте сформулировать тему нашего урока («Перпендикулярные

прямые»).

Запишите в тетради.             

Динамическая пауза

5.   Построение  новых знаний:

      Фронтальная работа

• Давайте попробуем сформулировать определение, какие прямые называются перпендикулярными?

Две прямые называются перпендикулярными    (или взаимно

перпендикулярными), если при пересечении они образуют четыре прямых угла.

     Запишите в тетради.

• Используя математические символы, запишите в тетради: «Прямая АC 

перпендикулярна прямой ВD». Выполните соответствующий рисунок:

                  

•   Теперь попробуем ответить на вопрос «Пересекаются ли две прямые, перпендикулярные третьей?»

Для обоснования утверждения о том, что две прямые, перпендикулярные третьей, не пересекаются,  используем наглядное пособие.  Изобразим на картоне рис. 43 учебника. На верхнюю часть рисунка по прямой PQ приклеим кальку таким образом, чтобы её можно было перегнуть на глазах у учащихся.

            Совместно с учениками обсуждаем проблему и делаем вывод, что «Две прямые, перпендикулярные третьей, не пересекаются».

         Запишите в тетради это свойство перпендикулярных прямых.

• Провести непродолжительную беседу о построении прямых углов на

местности.

6. Закрепление:

Попробовать самостоятельно выполнить практическое задание № 57.

Ребятам, сидящим за одной партой,  рекомендуется помогать друг другу. Учитель помогает всем, обратившимся за помощью.

Самостоятельная работа

Обучающимся предлагается решить задачи №№ 69,70.

Через 5-7 минут двум желающим предлагается объяснить свое решение.

Учитель обращается к классу с просьбой  дополнить, уточнить или исправить ответ ученика, найти другое, более рациональное решение.

7. Итог урока:

      Какие проблемы были поставлены в начале урока?

     –  Какие прямые называются перпендикулярными?

     –  Пересекаются ли две прямые, перпендикулярные третьей?

• Можно ли сказать, что мы их решили? Назовите.

–     Две прямые называются перпендикулярными (или взаимно

перпендикулярными), если при пересечении они образуют четыре прямых угла.

                 –     Две прямые, перпендикулярные третьей, не пересекаются.

• Оцените Вашу работу на уроке:

• все понятно – ничего не понял, понравилось – не понравилось, было

интересно – было скучно

• ответы ребят у доски на этапе актуализации опорных знаний
• ответы ребят, объяснявших решение задач № 69,70, на этапе

       закрепления нового материала

8. Домашнее задание (стандартный минимум) и разъяснение методики

его выполнения:

§ 6, п. 11-13, вопросы 17-21 (стр. 26), задачи № 67, 68.

nsportal.ru

Урок-проект геометрия 7 класс, «Параллельные и перпендикулярные прямые»

УРОК

«Проектная работа на уроке геометрии в 7 классе по теме: «Параллельные и перпендикулярные прямые».

Цели урока:

• обобщение и систематизация учебного материала по теме;

• проверка умений самостоятельной работы школьников с разными источниками информации, их умения самостоятельно ориентироваться в информационном пространстве, отбора необходимого, анализа полученной информации и её применения к решению проблем;

• повторить алгоритм решения типичных задач на применение изученной теории;

• оценивать и самооценивать приобретённые знания;

• развитие творческих способностей, обучение совместным интеллектуальным действиям в группе.

Оборудование:

• портреты Евклида и Лобачевского;

• презентация к уроку;

• памятка для учащихся;

• кроссворд.

Тип урока: обобщение и систематизация знаний и умений.

Ход урока.

1. Сообщение темы урока, целей урока.

Учитель. В этом году вы начали изучение геометрии, каждый из вас уже сумел убедиться в том, какой это интересный и многогранный раздел математики. Мы ознакомились с понятиями аксиомы и теоремы, изучили некоторые из них. Для работы над этим проектом у нас были созданы группы, каждая из которых имела своё задание:

• историки – собрать сведения о учёных, которые создавали геометрию в частности изучали вопросы параллельности и перпендикулярности прямых;

• теоретики – систематизировали и обобщили теоретический материал по теме;

• практики – показали практическое применение параллельных и перпендикулярных прямых, выполнили подборку типичных задач;

• информатики – составили презентацию к теме урока.

Девиз урока:

«Математике должно учить в школе еще с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни.»

Н.И. Лобачевский

2. Систематизация и обобщение знаний.

Учитель. Этот урок есть последним перед тематической контрольной работой поэтому мы должны систематизировать знания, повторить алгоритмы решения типичных задач, подготовиться к контрольной работе. Я подготовила для вас памятку работы над изученным материалом, т.к. вы сегодня не просто ученики, а соавторы проведения этого урока, потому что урок не просто урок, а урок-проект. Вы подбирали к уроку практические задания, вопросы теории, исторический материал, работали над составлением презентации, изучали практические способы построения параллельных прямых и их применение в жизненных ситуациях. Поэтому помните: 1) цените приобретённые знания, время; 2) будьте настойчивы и внимательны; 3) продемонстрируйте грамотность при выполнении заданий; 4) воспринимайте информацию вдумчиво, с интересом; 5) не бойтесь ошибиться; 6) поверьте в свои силы. Желаю успеха.

В этом году вы начали изучать новый раздел математики – геометрию, вы уже смогли убедиться в том, что он очень интересный и многогранный. Мы ознакомились с новыми для вас понятиями, понятиями аксиомы и теоремы, выучили некоторые из них. Ребята из группы историков познакомят вас с историческим материалом, связанным с этими понятиями.

Первый ученик. Аксиома – с греческого дословно «внимание, авторитет», в переносном значении – то, что в следствии своего авторитета не подлежит сомнению. Впервые этот термин применил Аристотель. Он говорил: «…Аксиомы имеют самую высокую ступень обобщённости и представляют основы всего». Аксиома – это утверждение, которое принимается без доказательства, позволяет доказать все дальнейшие факты науки. Аксиомы также называли постулатами. Совокупность аксиом (систему) называют аксиоматикой. Аксиоматический взгляд на математику впервые встречается у древнегреческого учёного Евклида в книге «Начала».

Первая ученица. Евклид (третий век до н. э.) выдающийся древнегреческий математик. Наука имеет не много сведений о его жизни и деятельности. Известно, что он родом из Афин, был учеником Платона. Как свидетельствует Папп Александрийский, Евклид был человеком мягкого характера. очень скромным и независимым его сочинение «Начала» наиболее широкий научный трактат в мире. Он состоит из 13 книг – сувоев; первые 6 посвящены планиметрии. Работа Евклида интересна не только своим богатым содержанием, но и формой изложения. В ней сначала сформулированы определения и аксиомы, а все последующие утверждения доказаны как теоремы.

Второй ученик. Евклид не сам открыл и доказал все изложенные им теоремы. Многие сделали его предшественники, но Евклид настолько удачно систематизировал известные ему математические знания, что его «Начала» были основным учебником по математике в течение двух тысяч лет. Насколько популярные «Начала», можно судить из того, что в английских школах и теперь изучают геометрию по некоторым из этих книг. Интересный факт из биографии Евклида. однажды царь спросил математика, нет ли в геометрии короче пути, чем тот, который предлагает Евклид в своих книгах. На что Евклид ответил: «Нет, в математике даже для царей нет других путей!». После Евклида для развития геометрии много сделали Архимед, Аполлоний и другие древнегреческие математики.

Вторая ученица. Евклидова геометрия построена на базе аксиом абсолютной геометрии и аксиомы Евклида о параллельных прямых. Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов. Именно эта аксиома стала «камнем преткновения» для ещё одного известного математика – Лобачевского Николая Ивановича (1792-1856). Этот великий русский математик родился в Нижнем Новгороде. Был профессором Казанского университета. Он первый человек, который отважился выступить с новой, отличной от Евклидовой, теорией геометрии, завоевав себе звание «Коперника геометрии». В 1826 году он передал в университет рукопись «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных». М. И. Лобачевский опередил своё время, и его идеи нашли полное признание и применение как в математике, так и в физике, а в геометрии началась новая эра.

Третий ученик. В древние века, буквально 2500 лет тому назад, в известной школе Пифагора греческое слово «параллелос» начали употреблять как геометрический термин, хотя определение параллельных прямых в те времена ещё не знали. Но исторические факты говорят о том, что Евклид всё же раскрыл смысл такого понятия как параллельные прямые. Термин «параллелос» в переводе с греческого языка обозначает рядом идущий или проведённый друг возле друга. В математике для обозначения параллельных прямых существует специальный знак. Правда, не всегда знак параллельности имел теперешний вид. Древнегреческий математик Папп для обозначения параллельности пользовался знаком «равно». И лишь в 18 веке благодаря Уильяму Отреду для обозначения параллельных прямых стали использовать нынешний знак параллельности.

Учитель. Слово имеет группа теоретиков.

Ученик. Сейчас мы предлагаем вам поучаствовать в игре «ты мне, я тебе» (смысл: ребята задают вопросы одни другому, выбирая сами своих «коллег» заслушивают ответ, если он правильный принимают его, неправильный – отвечают сами. После игра переходит к другому ученику).

Вопросы для проведения игры:

1. Сформулируйте:

1. Определение параллельных прямых;

2. Определение перпендикулярных прямых;

3. Определение аксиомы;

4. Определение теоремы;

2. Сколько существует перпендикуляров, проведённых к данной прямой в данной точке?

3. Назовите пары углов, которые образуются при пересечении двух прямых третьей?

4. Какие свойства этих углов используем, для доказательства параллельности прямых, пересечённых третьей?

5. Как называются только что сформулированные свойства?

6. Сформулируйте свойства двух прямых, перпендикулярных третьей.

7. Объясните понятие «теорема прямая» и «теорема обратная».

8. Сформулируйте определение аксиомы параллельных прямых.

9. Сформулируйте изученные вами другие аксиомы.

Учитель. Я предлагаю вам заслушать определение параллельных прямых данных в своё время Евклидом и Посидонием.

Ученица. Формулирует определение параллельных прямых данное Евклидом:

• «Параллельные суть прямые, которые находясь в одной плоскости и будучи продолжены в обе стороны неограниченно ни с той, ни с другой стороны между собой не встречаются.

• Определение данное Посидонием (первый век до н. э.): «Две прямые, лежащие в одной плоскости, равно отстоящие друг от друга.

3. Обобщение и систематизация умений.

Учитель. Слово для освещения результатов своей работы имеет группа практиков.

Ученица. Сейчас мы предлагаем вам подборку задач с применением изученных аксиом и теорем о параллельных и перпендикулярных прямых.

Задача 1. На модели куба укажите параллельные и перпендикулярные прямые.

Задача 2. Какие названия имеют пары углов, полученные при пересечении двух прямых с секущей?

Задача 3. Прямые a и b пересекаются с секущей так, что сумма внутренних односторонних углов равна 200 градусов. Сколько общих точек имеют прямые a и b?

Задача 4. Чему равна сумма внутренних односторонних углов, если внутренние накрест лежащие углы равны?

Задача 5. №186, с. 58.

C

B

А

D

2

1

4

3

Задача 6. Назовите параллельные прямые на рисунке, если: 1) ;

2);

Задача 7. На рисунке . Какие из приведённых равенств правильные?

1

2

3

4

a

b

c

6

5

7

8

1);

2)

3);

4)

a

b

B

А

2

1

Задача 8. №202, с. 66, рис. 116.

Задача 9. №203, с. 66.

Задача10.

Найти .

Ученик. Мы работали над проектом «Способы построения параллельных прямых»: 1) способ построения с помощью линейки и угольника рассмотрим при решении задачи №195, с. 59; 2) способ построения параллельных прямых с помощью одной линейки; 3) способ построения параллельных прямых с помощью рейсшины при выполнении чертежей, рисунок 104 учебника; 4) при выполнении столярных работ разметку параллельных прямых проводят с помощью малки (малка – две деревянные планки, скреплённые шарниром, рисок 105 учебника).

Учитель. Можете ли вы рассказать о практическом применении параллельных и перпендикулярных прямых в окружающей жизни, приведите примеры их использования.

Ответы учащихся.

4. Подведение итогов урока, рефлексия.

Учитель. На протяжении урока вы сознательно и критически пересмотрели изученный материал, определили для себя, что усвоено хорошо, а что требует дополнительной доработки.

Ученик. Я предлагаю вам разгадать кроссворд (см. приложение 1)

Учитель.

— Чему вы научились, работая над проектом?

— Понравилась ли вам работа в группах?

— Чему новому вы научились?

— Подтвердились ли ваши ожидания от урока?

Ученик.

Стихотворение «Параллельные прямые»

Эти линии все знают

Направление храня,

Они дружно убегают

В бесконечность от меня

Мы частенько из встречаем,

Невозможно всё назвать

Пара рельсов у трамвая,

В нотоносце целых пять.

Даже если линий много

Не смешать одну с другой,

Они держат очень строго

Расстоянье меж собой.

Параллельные прямые –

Славный, вежливый народ

Ни одна из них другие —

никогда не зачеркнёт.

5. Домашнее задание.

Повторить: глава 3, §1 и §2, №213, 216

6. Литература к уроку.

1. Атанасян Л. С. Геометрия 7-9 классы: учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев // — 19-е издание – М.: Просвещение, 2009 г., — 384 с.

2. Гузеев В. В. Преподавание. От теории к мастерству, -М.: Школьные технологии, 2009 г.

3. Рафальська О. Д. Метод проектів / О. Д. Рафальська // Математика в школах України. – 2012 р. – №9(21). – с. 5-11

Приложение 1

Кроссворд «Параллельность прямых»

⁶

¹

⁵

²

³

⁸

⁷

⁹

⁴

По горизонтали:

По вертикали:

1. Углы, образованные при пересечении прямых секущей;

4. То, что в теореме дано;

7. Исходное положение, на основании которого доказываются теоремы;

9. Теорема в которой условие является заключением, а заключение условием;

2. Эти углы образовались при пересечении двух прямых третьей;

3. То, что в теореме требуется доказать;

5. Какая геометрия изложена в началах?

6. Как располагаются углы, из равенства которых вытекает параллельность двух прямых, пересечённых третьей;

8. Прямые, которые лежат в одной плоскости и не пересекаются.

По горизонтали:

По вертикали:

1. соответственные

4. условие

7. аксиома

9. обратная

2. односторонние

3. заключение

5. евклидова

6. накрест

8. параллельные

infourok.ru

Перпендикуляр к прямой. Видеоурок. Геометрия 7 Класс

Для начала вспомним важный факт: две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

                                  

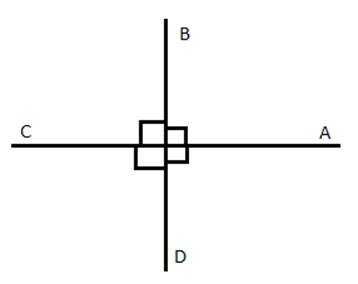
Рис. 1. Перпендикулярные прямые

АС⊥ВD, поскольку четыре угла по 90°. Напомним также, что при пересечении любых прямых образуются четыре угла: 2 вертикальных, которые равны между собой, еще пара равных вертикальных углов. a и b – смежные углы. И по теореме о смежных углах a + b = 180°.

Рис. 2. Пересечение прямых

В единственном случае a = b = 90°. В этом случае прямые АС и ВD называются перпендикулярными.

Теорема 1: Две прямые, перпендикулярные к третьей, не пересекаются.

         

Рис. 3. Чертеж к теореме 1

Отсюда следует, что AA₁ и BB₁ не имеют общих точек. Прямые  AA₁ и BB₁ можно продлить бесконечно, но при этом они не пересекутся. В этом заключается смысл теоремы.

Определение: Пусть прямые АН и a перпендикулярны. Мы знаем, что чтобы все четыре угла при этих прямых были по 90°, необходимо, чтобы один из них был прямым. Отрезок АН называют перпендикуляром, проведенным из точки А к прямой a, если прямые АН и a перпендикулярны. При этом точка Н называется основанием перпендикуляра.

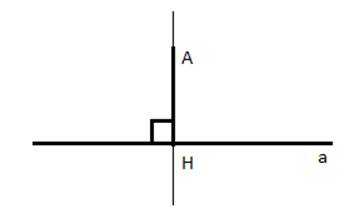
Рис. 4. Чертеж к определению перпендикуляра

В данном случае перпендикуляр – это отрезок. Значит, перпендикуляр к прямой – это отрезок.

Теорема 2: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Рис. 5. Чертеж к теореме 2

Существует множество точек, которые не лежат на прямой a. Из любой точки А, не лежащей на данной прямой, можно провести перпендикуляр к прямой. К тому же этот перпендикуляр единственный.

Дано: точка А не принадлежит прямой a.

Доказать: существует единственный отрезок АН, где АН.

Доказательство:

1. Проведем 2 равных угла. ∠АВС =∠МВС или ∠1 = ∠2.

2. Равные углы можно совместить наложением. При этом точка А перейдет в точку A₁. ВА = ВA₁(перегибание по прямой ВС).

3. Соединим точки А и A₁. Получим точку Н. Углы ∠ВНА = ∠3, ∠ВНA₁ = ∠4.

4.

Следовательно, треугольники ВНА = ВНA₁ по первому признаку равенства треугольников, то есть по углу и двум прилежащим сторонам. Из равенства треугольников следует равенство всех элементов. А значит, ∠3 = ∠4. Эти углы лежат против равных сторон. Два смежных равны только в случае, если каждый из них равен по 90°. А значит, АН^ВС. Мы доказали, что из точки А можно провести перпендикуляр к прямой a.

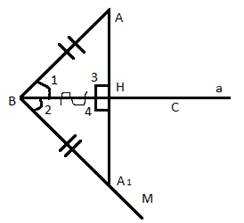
Рис. 6. Чертеж к доказательству теоремы 2(1)

Единственность перпендикуляра, проведенного из точки А к прямой, докажем методом «от противного».

5. Предположим, что из точки А можно провести к прямой a два разных перпендикуляра.

АН ⊥ a, АH₁ ⊥ a.

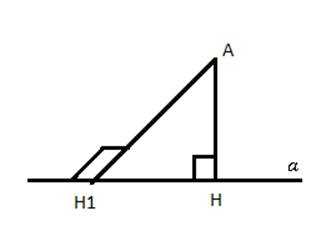
Рис. 7. Чертеж к доказательству единственности перпендикуляра

Это невозможно, поскольку из разных точек прямой a проведены 2 перпендикуляра, которые имеют общую точку А. Мы получили противоречие, значит, наше предположение неверно. Из точки А можно провести лишь один перпендикуляр к прямой a.

Пример 1: Точки А и С лежат по одну сторону от прямой a. Перпендикуляры АВ и СD к прямой a равны.

1. Докажите, что АВD = ∠CDВ.

2. Найдите ∠АВС, если ∠АDВ = 44°.

Дано: А) АВ⊥ a, CD ⊥ a.

Доказать: ∠ADB = ∠CDB.

Доказательство:

Выполним пояснительный рисунок:

Рис. 8. Чертеж к примеру 1(а)

Доказательство основано на понятии перпендикуляра из точки к прямой. Отсюда следует, что ADB = CDB, что и требовалось доказать.

Дано: Б) АВ⊥ a, CD⊥ a. AB = CD, ∠ADB = 44°. Найти ∠АВС.

Доказательство:

Выполним пояснительный рисунок:

Рис. 9. Чертеж к примеру 1(б)

1. ∆ABD = ∆CDB. (AB = CD, BD – общая, ∠ABD = ∠CDB). Из равенства треугольников следует равенство их соответствующих элементов. AD = CB.

2. ∠ADB = ∠CBD = 44°. Поскольку эти углы лежат против равных сторон AB и CD соответственно.

3. ∠АВС = 90° — 44° = 46°

Ответ: 46°.

На сегодняшнем уроке мы рассмотрели понятие перпендикуляра к прямой и доказали теорему об этом перпендикуляре. На следующем уроке мы познакомимся с медианой, биссектрисой, высотой треугольника.

 

Список рекомендованной литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.

2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5 изд. – М.: Просвещение.

3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Обобщающий урок по геометрии в 7-м классе (Источник).
2. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание:

1. №13(б). Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

2. Один из смежных углов в 3 раза больше другого. Найдите эти углы.

3. Прямые BH и AH взаимно перпендикулярны и ∠BHM = ∠AHC. Докажите, что НМ⊥НС.

4. № 14(г). Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

interneturok.ru

Поурочный план по геометрии для 7 класса Тема урока: «Перпендикулярные прямые». » Мир учителя

Поурочный  план по геометрии для  7 класса

Тема урока:«Перпендикулярные  прямые».

               Девиз: « Дорогу осилит идущий, а  математику – мыслящий»

Цели урока:

— познакомить учащихся с определением перпендикулярных  прямых, перпендикуляра  к  данной  прямой;

— формирование умений анализировать изученный материал и навыков применения его для решения задач;

— показать значимость изучаемых понятий;

— развитие познавательной активности и самостоятельности получения знаний;

— воспитание интереса к предмету.

Тип урока:  урок введения новых знаний.

Формы работы:  устная, письменная, индивидуальная, групповая.

Методы: словесные, проблемно – поисковые.

Оборудование:  презентация, интерактивная доска.

ХОД УРОКА

  1.Организационный момент.

  2. Мотивация урока.

Удивительная страна — Геометрия!

Фигуры и линии в ней живут,

Меряют, чертят и узнают:

Периметр, площадь, длину, ширину,

Диаметр, радиус и высоту.

Скорей собирай своих знаний багаж!

Готовь поскорее простой карандаш!

3. Актуализация опорных знаний.

Устный опрос:

— Что называют вершиной угла, сторонами угла?

— Какие углы называются равными?

— Как сравнить два угла?

— Как называется луч, делящий угол пополам?

— Какие виды углов вы знаете?

— Где встречается прямой угол?

— Какому углу равна сумма двух прямых углов?

— При помощи какого инструмента измеряют углы?

— Какая фигура называется прямой?

4. Проверка усвоения, изученного  ранее материала. Игра  «Найдите ошибку»:

Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными прямыми.

Сумма смежных сторон равна 180 градусам ?

Если два угла равны, то совместные с ними углы равны.

Вертикальные углы различны.

Если прямые пересекаются, значит, они перпендикулярны.

5. Изучение нового материала.

Изучая геометрические фигуры, вы уже не раз встречались с перпендикулярными  прямыми. Например, смежные стороны прямоугольника перпендикулярны. Как убедиться в том, что две линии (прямые) перпендикулярны? С древних пор строители проверяли перпендикулярность стены основанию дома с помощью отвеса, то есть грузика на веревке. Отсюда и произошло название перпендикуляра: латинское “перпендикулярис” означает “отвесной”. Чтобы построить перпендикуляр  к  прямой, достаточно построить прямой угол.

Итак, давайте выясним, какие  же  прямые называются  перпендикулярными?

Про перпендикулярные линии часто говорят, что каждая из них – «перпендикуляр»  к  другой. Если при пересечении двух прямых образуется один прямой угол, то и три остальных угла тоже будут прямыми.

Итак, перпендикулярными называются две прямые, при пересечении которых образуется четыре прямых угла.

Пришло время научиться строить перпендикулярные прямые. И начнем мы с построение перпендикулярной прямой через точку, лежащую на  данной прямой. (Слайд)

Теперь самостоятельно попробуйте построить две перпендикулярные прямые через точку, не лежащую  на  данной прямой.

Проверим ваш алгоритм построения:

Строим произвольную прямую.

Отмечаем точку вне  прямой.

Прикладываем чертежный треугольник.

Проводим перпендикулярную прямую.

Теорема. Через  каждую  точку прямой  можно провести  перпендикулярную ей прямую, и только одну. 

(Слайд).

Определение. Перпендикуляром к данной прямой называется отрезок прямой, один из концов которого является  точкой пересечения прямых.

Эта точка пересечения прямых называется  основанием перпендикуляра.

Построим перпендикуляр из точки М к прямой АВ с помощью чертежного угольника.

6. Первичное закрепление изученного материала

– Теперь давайте проведем взаимопроверку полученных знаний и умений, для этого поработаем в парах.

– Начертите на глаз две перпендикулярные прямые. Поменяйтесь листочками и проверьте, действительно ли  прямые перпендикулярны.

Подведем мини-итог  «Вставьте пропущенные слова».

 Если прямые перпендикулярны, то…

 Если при пересечении двух прямых образуются четыре прямых угла, то …

 Если при пересечении прямых ….

7. Математическая сказка «О точке» в исполнении учащихся класса.

8.  Устный опрос класса:

1. Сформулируйте определение  перпендикулярных прямых?

2. С  помощью  каких  инструментов строятся перпендикулярные прямые?

3. Приведите примеры  перпендикулярных прямых в окружающей обстановке?

9. Практическая работа.

1.Используя разлиновку тетради, проведите

перпендикулярные прямые. Обозначьте их, запишите, что данные прямые перпендикулярны.

2. Отметьте  две точки на одной прямой и две точки на другой и запишите полученные  отрезки.

3. Опишите взаимное расположение  точек и прямых.

4.Запишите  полученные отрезки. Можно ли назвать их перпендикулярными?

5.Запишите все прямые углы, которые вы видите на  рисунке.

10. Проверка практической работы  (в парах  обменив тетрадями — оценив.)

11.  Закрепление нового материала.                                                                      Письменно  решение задач №72, 75. (по учебнику  А.Н. Шыныбекова ).

12. Игра «Найди пару»

Вертикальные                       прямые

Перпендикулярные                углы

Стороны                                к прямой

Прямой                                 треугольника

Перпендикуляр                        угол

13.  Синквейны на слово «Геометрия».                          

14. Подведение итогов урока.  

– Подведем итоги. Что мы узнали? (Понятие «перпендикулярные прямые», историю его возникновения, как построить  перпендикуляр к  данной  прямой)

– Чему научились? (Строить перпендикулярные прямые, решать задачи, применяя знания о перпендикулярных  прямых)

15. Домашнее  задание.      

Заключительные слова учителя:

           К геометрии способность проявляй,

                                            Не ленись, а ежедневно развивай,

           Повторяй, учи, трудись, соображай

 

                                            С геометрией дружить не забывай.

скачать dle 12.1

worldofteacher.com