Экзамен 7 класс по геометрии 7 класс: Билеты для переводного экзамена по геометрии
Зачеты и экзамен по геометрии. 7-й класс
Зачеты и экзамен по геометрии. 7-й класс- Воробьева Елена Георгиевна, учитель
Разделы: Математика
Класс: 7
Введение
В данной работе я предлагаю вопросы для зачётов, задачи к этим зачётам и билеты к экзамену за курс геометрии 7 класса. Практический материал на экзамене можно предложить из задач к зачётам.
Надеюсь, что данная работа поможет преподавателю математики проверить знания по данной дисциплине на начальной стадии её усвоения.
Для учащихся полезно будет по вопросам к зачётам готовить учебный материал
самостоятельно, решая задачи, усваивать теоретические знания на практике, тем
самым делая учебу интересной и успешной.
В 7 классе у наших детей появляется новый учебный предмет, который поначалу
может показаться простым и не очень серьезным. Но это далеко не так. В былые
годы наличие обязательного экзамена по геометрии с первых дней изучения новой
дисциплины настраивало на серьёзный лад. Сейчас наличие задач по геометрии в ГИА
и ЕГЭ по математике помогает убедить учащихся в насущности и значимости
предмета. Необходимость теоретических знаний понимается большинством учащихся
при решении задач, доказательстве теорем, везде, где не обойтись без
аргументированных объяснений. Задача учителя не только донести знания по
предмету, но и заставить овладеть ими. Готовясь к зачётам дети вынуждены
самостоятельно разбирать, заучивать учебный материал, а также консультироваться
у учителя, друг у друга, доказывая друзьям теоремы и решая задачи на
дополнительных занятиях и консультациях по математике. Этот процесс – объяснение
товарищу – очень нравится ребятам, они при этом повышают свою самооценку,
мотивацию к учебе, повышают качество собственных знаний.
ЗАЧЕТ № 1
- Основные геометрические фигуры на плоскости. Их изображение и обозначение. Основные свойства принадлежности точек и прямых на плоскости.
- Понятие «точка лежит между точками». Отрезок. Концы отрезка. Равные отрезки. Основное свойство расположения точек на прямой.
- Основное свойство измерения отрезков.
- Основное свойство расположения точек относительно прямой.
- Полупрямая. Начальная точка полупрямой.
 Дополнительные полупрямые.
Дополнительные полупрямые. - Угол. Вершина угла. Стороны угла. Виды углов. Равные углы. Понятие «луч проходит между сторонами угла». Основные свойства измерения углов.
- Основные свойства откладывания отрезков и углов.
- Треугольник. Вершины треугольника. Стороны треугольника. Угол треугольника. Равные треугольники. Основное свойство существования треугольника, равного данному.
- Параллельные прямые. Изображение и обозначение. Основное свойство параллельных прямых.
ЗАДАЧИ К ЗАЧЕТУ № 1
- На отрезке AB длиной 23 см взята точка C так, что отрезок AC на 7 см меньше отрезка CB. Найдите длины отрезков BD, если AC и BC.
- На отрезке AB длиной 17 см отмечена точка C так, что отрезок AC равен 9 см. Найдите длину отрезка BC.
- На отрезке AB взяты точки C
и D. Найдите длину отрезка CD,
если AB= 22 см, AC= 13 см,
BD= 7см.

- На отрезке AB взята точка C, а на отрезке CB – точка D. Найдите длину отрезка BD, если AB= 17 см, CD= 8 см, AC= 7см.
- На отрезке AB взяты точки C и D. Известно, что AB= 22 см, AC= 18 см, CD= 7см. Найдите длину отрезка BD.
- На отрезке AB длиной 28 см взята точка K. Найдите длины отрезков AK и BK, если AK больше BK на 6 см.
- На отрезке AB длиной 56 см взята точка K. Найдите длины отрезков AK и BK, если AK : BK=2:7.
- Луч с проходит между сторонами угла (аb), равного 62?. Найдите угол ( ас), если угол (bс) равен 43?.
- Луч с проходит между сторонами угла (аb), равного 62?. Найдите углы (ас) и (bс), если угол (ac) на 27? больше угла (bc).
- Луч ОС проходит между сторонами угла АОВ, равного 160?. Найдите углы АОС
и СОВ, если угол АОС меньше угла СОВ в 3 раза.

- Луч ОС проходит между сторонами угла АОВ, равного 140?. Найдите углы АОС и СОВ, если угол АОС на 50? больше угла СОВ.
- Может ли луч с проходить между сторонами угла (ab), если угол (ab) равен 45?, угол (aс) равен 130?, угол (сb) равен 85??
Дано: угол АОВ равен 137?, угол AOD равен 28?, угол COB равен 34?
Найти: угол COD.- Треугольники АВС и MNK равны. Известно, что АВ= 17 см, АС= 11 см. Чему равны соответствующие стороны треугольника MNK?
- Треугольники АВС и MNK равны. Известно, что угол М равен 69?, угол K равен 28?. Чему равны соответствующие углы треугольника АВС?
ЗАЧЕТ № 2
- Угол. Вершина угла. Стороны угла. Виды углов. Равные углы. Понятие «луч проходит между сторонами угла». Основные свойства измерения углов. Биссектриса угла.
- Смежные углы. Теорема о смежных углах.
 Свойства из теоремы о смежных
углах.
Свойства из теоремы о смежных
углах. - Вертикальные углы. Теорема о вертикальных углах.
ЗАДАЧИ К ЗАЧЕТУ № 2
- Найдите углы смежные с углами 39?, 83?, 90?, 157?.
- Найдите смежные углы, если один из них на 27? больше другого.
- Найдите смежные углы, если один из в 2 раза меньше другого.
- Смежные углы относятся как 3:2. Найдите эти смежные углы.
- Один из смежных углов составляет 0,5 другого угла. Найдите эти смежные углы.
- Один из углов, образованных при пересечении двух прямых, равен 37?. Найдите остальные углы.
- Один из углов, образованных при пересечении двух прямых, в 3 раза больше
другого. Найдите все образовавшиеся при этом углы.

- Один из углов, образованных при пересечении двух прямых, на 36? меньше другого. Найдите все образовавшиеся при этом углы.
- Сумма двух углов, которые получаются при пересечении двух прямых, равна 86?. Найдите все получившиеся при этом углы.
- Сумма трех углов, образовавшихся при пересечении двух прямых, равна 235?. Найдите эти углы.
ЗАЧЕТ № 3
- Треугольник. Вершины треугольника. Стороны треугольника. Угол треугольника.Равные треугольники. Основное свойство существования треугольника, равного данному.
- Первый признак равенства треугольников.
- Второй признак равенства треугольников.
- Третий признак равенства треугольников.
- Равнобедренный треугольник. Боковые стороны. Основание. Свойство углов равнобедренного треугольника.
- Равнобедренный треугольник. Высота, биссектриса, медиана треугольника.

- Равнобедренный треугольник. Признак равнобедренного треугольника.
ЗАДАЧИ К ЗАЧЕТУ № 3
- Дано: ΔАВС и ΔСBD, AB= CD, угол ABD равен углу CBD. Докажите, что ΔАВС=ΔСBD.
- Дано: ΔАВС и ΔАDС, угол ВAС равен углу DАС, угол ВСА равен углу DCA. Докажите, что ΔАВС=ΔСBD.
- Дано: ΔАВС и ΔСBD, AB= CD, угол ABD равен углу CBD. Докажите, что АD=СD.
- Равные отрезки AB и CD точкой пересечения М делятся пополам. Докажите равенство треугольников AMC и BMD.
- Равные отрезки AB и CD точкой пересечения М делятся пополам. Докажите равенство отрезков AC и BD.
- Отрезки AB и CD пересекаются в точке O. Отрезки CO и OD равны, угол ACO равен 90?, угол BDO равен 90?. Докажите, что Δ AOС=ΔBOD.
- Отрезки AB и CD
пересекаются в точке O. Отрезки CO
и OD равны, углы ACO и
BDO прямые.
 Докажите, что углы CAO
и DBO равны.
Докажите, что углы CAO
и DBO равны. - Треугольники MNK и MNR равнобедренные с общим основанием MN. Докажите, что ΔMKR=Δ NKR.
- В равнобедренном треугольнике угол при основании равен 47?. Найдите угол при вершине данного треугольника.
- В равнобедренном треугольнике один из углов равен 91?. Найдите остальные углы треугольника.
- Периметр равнобедренного треугольника равен 34см, основание – 10см. Найдите длины остальных сторон этого треугольника.
- Периметр равнобедренного треугольника 39см. Основание на 6см меньше боковой стороны. Найдите стороны треугольника.
- В ΔCDF проведены медианы CA, DB, FN. AF=6см, BC=8см, DN=4см. Найдите периметр ΔFCD.
- Дано ΔABK, AB=
KB, точки M и
N принадлежат сторонам АВ и КВ, BM=BN,
BC – медиана треугольника.
 Докажите, что
MC=NC.
Докажите, что
MC=NC.
ЗАЧЕТ № 4
- Параллельные прямые. Изображение и обозначение. Основное свойство параллельных прямых. Теорема о параллельности двух прямых третьей.
- Внутренние односторонние углы. Внутренние накрест лежащие углы. Соответственные углы. Изображение и обозначение. Признак параллельности прямых. Свойства из теоремы.
- Треугольник. Вершины треугольника. Стороны треугольника. Угол треугольника.. Сумма углов треугольника. Следствие из теоремы.
- Треугольник. Вершины треугольника. Стороны треугольника. Угол треугольника. Внешний угол треугольника. Теорема о внешнем угле треугольника. Следствие из теоремы.
- Прямоугольный треугольник. Признак равенства прямоугольных треугольников.
- Существование и единственность перпендикуляра к прямой. Расстояние от точки до прямой.
ЗАДАЧИ К ЗАЧЕТУ № 4
- Отрезки MN и PK
пересекаются в точке A и делятся ею пополам.
 Докажите, что прямые MK ║ PN.
Докажите, что прямые MK ║ PN. - Угол MBA равен 69?, угол BAN равен 111?. Параллельны ли прямые MB и AN? Обоснуйте ответ.
- Прямые AB и CD пересечены секущей MN. Точка O– точка пересечения АВ и MN, точка P – точка пересечения прямых CD и MN. Сумма углов AOP и DPN равна 180?. Докажите, что прямые AB и CD параллельны.
- Один из углов, которые получаются при пересечении двух параллельных прямых секущей равен 49?. Найдите остальные углы.
- Сумма двух внутренних накрест лежащих углов при двух параллельных прямых и секущей равна 138?. Чему равны эти углы?
- Найдите углы треугольника, если они пропорциональны числам 2, 3, 4.
- Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании равен 53?.
- Дано ΔABC, AB =
BC, внешний угол при вершине В равен 72?. Найдите
внутренние углы ΔАВС.
 Укажите тип данного треугольника.
Укажите тип данного треугольника. - Внутренние углы треугольника пропорциональны числам 8, 5, 2. Найдите внешние углы этого треугольника.
- Один из внутренних углов треугольника на 16? больше другого, а внешний угол, смежный с третьим внутренним углом треугольника, равен 110?. Найдите все внутренние углы треугольника.
- Дано ΔMNR – равнобедренный с основанием MR. Биссектрисы углов при основании пересекаются в точке B. Угол MBR равен 102?. Найдите угол MNR.
- Дано ΔACB, угол C – прямой, CD – высота ΔACB, угол DCB равен 75?. Найти угол CAB.
- Дано ΔABC, высоты AH и CM пересекаются в точке D, угол BAC равен 60?, угол BCA равен 70?. Найти угол ADC.
ЗАЧЕТ № 5
- Окружность. Центр, радиус, хорда, диаметр окружности. Описанная
окружность. Теорема о центре окружности описанной около треугольника.

- Касательная к окружности. Виды касания окружностей. Окружность, вписанная в треугольник. Теорема о центре окружности, вписанной в треугольник.
- Построение треугольника по трем сторонам.
- Построение угла, равного данному.
- Построение биссектрисы угла.
- Деление отрезка пополам.
- Построение перпендикулярной прямой.
- Геометрическое место точек. Окружность как геометрическое место точек. Теорема о точках равноудаленных от двух данных точек.
ЗАДАЧИ К ЗАЧЕТУ № 5
-
Дано: окружность с центром О. ОА – радиус, ВС – хорда, ОА и ВС пересекаются в точке К, ОА перпендикулярен ВС. Докажите, что ВК = КС.
-
Дано: окружность с центром О, СА и СВ касательные. Докажите, что СО – биссектриса угла АСВ.
-
Дано: окружность с центром О, АС – диаметр, ОВ – радиус, градусная мера угла АОВ равна 42?.
 Найдите углы треугольника ВОС.
Найдите углы треугольника ВОС. -
Дано: окружность с центром О, АВ – касательная, угол ОАВ равен 36?. Найти углы ΔОАВ.
-
Найдите расстояние между центрами двух окружностей в случае внешнего касания, если их радиусы 19см и 27см.
-
Найдите расстояние между центрами двух окружностей в случае внутреннего касания, если их радиусы 23см и 17см.
-
Постройте треугольник АВС, если угол А равен 35?, угол В равен 70?, АВ = 4,5см.
-
Постройте ΔCDF, если CD = 5см, CF = 6см, угол DCF равен 45?.
-
Постройте прямоугольный треугольник по гипотенузе и острому углу.
-
Постройте прямоугольный треугольник по гипотенузе и катету.
-
Дана окружность с центром О и хорда АВ.
 На окружности
найдите точки, равноудаленные от точек А и В.
На окружности
найдите точки, равноудаленные от точек А и В. -
Постройте геометрическое место точек, равноудаленных от точек А, В и С.
БИЛЕТЫ ПО ГЕОМЕТРИИ 7 КЛАСС
№ 1
- Основные геометрические фигуры. Обозначение. Изображение. Основные свойства, связанные с этими понятиями.
- Смежные углы.
- Задача.
№ 2
- Отрезок. Обозначение. Изображение. Основные свойства, связанные с этим понятием.
- Вертикальные углы.
- Задача.
№ 3
- Измерение отрезков. Основные свойства, связанные с этим понятием.
- Первый признак равенства треугольников.
- Задача.
№ 4
- Полуплоскость. Основные свойства, связанные с этим понятием.
- Признак равнобедренного треугольника.

- Задача.
№ 5
- Полупрямая. Угол. Основные свойства, связанные с этими понятиями.
- Свойство углов равнобедренного треугольника.
- Задача.
№ 6
- Откладывание отрезков и углов. Основные свойства, связанные с этими понятиями.
- Свойство медианы равнобедренного треугольника.
- Задача.
№ 7
- Треугольник. Основные свойства, связанные с этим понятием.
- Признак параллельности прямых.
- Задача.
№ 8
- Равные треугольники. Основные свойства, связанные с этим понятием.
- Теорема о двух прямых, параллельных третьей прямой.
- Задача.
№ 9
- Параллельные прямые. Основные свойства, связанные с этим понятием.
- Сумма углов треугольника.

- Задача.
№ 10
- Перпендикулярные прямые.
- Внешний угол треугольника.
- Задача.
№ 11
- Биссектриса треугольника.
- Свойство углов, образованных при пересечении параллельных прямых секущей.
- Задача.
№ 12
- Высота треугольника.
- Существование и единственность перпендикуляра к прямой.
- Задача.
№ 13
- Медиана треугольника.
- Теорема о центре окружности, описанной около треугольника.
- Задача.
№ 14
- Биссектриса треугольника.
- Теорема о центре окружности, вписанной в треугольник.
- Задача.
ГДЗ Геометрия 7 класс Глазков Рабочая тетрадь
Подробные решения по геометрии за 7 класс авторы Глазков, Камаев, Атанасян
Школьная программа для учащихся 7 класса не так проста, как может показаться. Поэтому к урокам геометрии необходимо отнестись весьма серьезно. К сожалению, не все школьники осознают всю серьезность ситуации и иногда подходят к обучению несознательно. Такое отношение может негативно сказаться на оценках и на качестве полученных знаний. Потому, что большинство родителей, зачастую, не могут помочь своим детям, гдз по геометрии рабочая тетрадь за 7 класс Глазков станет полезной настольной книгой всех школьников. Учебный год в 7 классе станет не сложным испытанием. Усложнение материала и ввод дополнительных понятий не станут проблемой – данный ресурс поможет успешно справиться со всеми задачами.
Поэтому к урокам геометрии необходимо отнестись весьма серьезно. К сожалению, не все школьники осознают всю серьезность ситуации и иногда подходят к обучению несознательно. Такое отношение может негативно сказаться на оценках и на качестве полученных знаний. Потому, что большинство родителей, зачастую, не могут помочь своим детям, гдз по геометрии рабочая тетрадь за 7 класс Глазков станет полезной настольной книгой всех школьников. Учебный год в 7 классе станет не сложным испытанием. Усложнение материала и ввод дополнительных понятий не станут проблемой – данный ресурс поможет успешно справиться со всеми задачами.
Кому могут быть полезны быстрые ответы к рабочим тетрадям?
Наверняка создание сборника решений к рабочей тетради по геометрии 7 класс авторы Глазков, Камаев оценят:
- семиклассники, участвующие в олимпиадах и конкурсах по географии, для получения больших способностей и знаний по данному предмету;
- родители, у которых совершенно нет лишнего свободного времени, для того чтобы помочь своему ребёнку не только объяснить материал, но и проверить домашнее задание и быть уверенным, что сделал это правильно;
- преподаватели, имеющие дефицит свободного времени.
 Сейчас актуально меньше времени проводить за проверкой контрольных, самостоятельных или проверочных работ, гораздо лучше это время уделить ученикам;
Сейчас актуально меньше времени проводить за проверкой контрольных, самостоятельных или проверочных работ, гораздо лучше это время уделить ученикам; - отличники, желающие получить самую высшую оценку по данному предмету. Такие ребята хотят быть безусловными лидерами, и поэтому используют справочник для проверки своих знаний и умений;
- ученики, обучающиеся на дистанционном или домашнем обучении. Они используют готовые ответы для изучения, повторения пройденного материала, а также, пути выполнения действий и решений сложных заданий;
- дети, не имеющие временной возможности после школьных занятий посещать платные курсы или репетитора, для более детального изучения данного предмета;
- ребята, которые постоянно принимают участие в спортивных соревнованиях и международных выступлениях. Для них необходимы быстрые ответы, чтобы проверить свои знания и освоить упущенный материал;
- те, кто довольно медленно усваивают материал по географии. Не все дети легко понимают и вникают в тему с первого раза;
- ученики, желающие самостоятельно, не прибегая к сторонней помощи изучить материал, который пропустили.
 Это актуально для детей, которые, например, пропустили много тем по причине болезни.
Это актуально для детей, которые, например, пропустили много тем по причине болезни.
Безусловные преимущества применения решебника к рабочей тетради по геометрии 7 класс Глазкова, Камаева
Использование справочника на еуроки ГДЗ обладает рядом преимуществ, таких как:
- они круглосуточно доступны в любое время дня и ночи с любого устройства;
- не просто дают вам правильный ответ, но и подскажут алгоритм действий и решений;
- прояснят самые сложные и невыполнимые задания;
- экономят время школьникам, но и родителям и педагогам;
- дают возможность проверить ответ, перед сдачей работы учителю;
- имеют актуальные ответы и решения;
- учат самостоятельно анализировать и делать выводы.
Теперь для всех станет понятно, что использование готовых ответов – это цепь одних только преимуществ.
Общий базовый тест по математике для 7 класса (примеры вопросов)
Общий базовый экзамен по математике для 7 класса с практическими вопросами
1.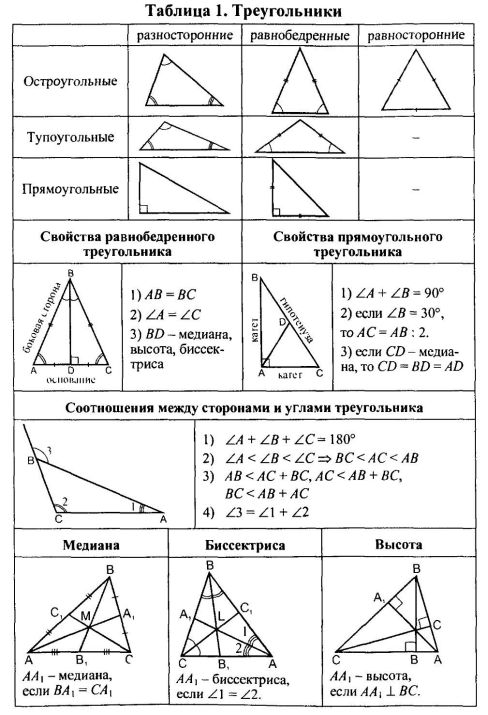 Изучите рисунок ниже. Если треугольник расширить в 2 раза, каков периметр нового треугольника?
Изучите рисунок ниже. Если треугольник расширить в 2 раза, каков периметр нового треугольника? - 19
- 32
- 44
- 76
- ¼
- 1 / 3
- 3
- 4
- Три острых угла
- Два острых угла и один прямой угол
- Два острых угла и один тупой угол
- Два прямых угла и один острый угол
- Параллелограмм
- Прямоугольник
- Ромб
- Квадрат
 Кевин сажает овощи в своем саду. Если сад имеет форму круга диаметром 10 футов, какова площадь сада?
Кевин сажает овощи в своем саду. Если сад имеет форму круга диаметром 10 футов, какова площадь сада? - 15,7 футов2
- 31,4 футов2
- 78,5 футов2
- 314 футов2
- 9,42 фута
- 18,8 фута
- 28,3 фута
- 113 футов
- 4
- 6
- 15
- 21
- 10°
- 20°
- 40°
- 50°
 Если Джейсон использует размеры, показанные на рисунке ниже, сколько квадратных футов фанеры ему понадобится для изготовления столешницы?
Если Джейсон использует размеры, показанные на рисунке ниже, сколько квадратных футов фанеры ему понадобится для изготовления столешницы? - 5 футов2
- 6 футов2
- 9 футов2
- 12 футов 2
- 64 см 2
- 192 см 2
- 384 см 2
- 512 см 2
1. D: Поскольку исходный треугольник расширен в 2 раза, длина каждой стороны будет умножена на 2, чтобы получить длины сторон нового треугольника. Следовательно, 8×2=16, 12×2=24 и 18×2=36. Тогда 16+24+36=76. Ответ A получается, если каждая из длин сторон была неправильно разделена на 2. Ответ B получается, если 2 было неправильно вычтено из каждой из длин сторон. Ответ C получается, если к длине каждой стороны было неправильно прибавлено 2.
2. A: Чтобы определить коэффициент масштабирования, возьмите длины сторон масштабированного прямоугольника и разделите их на соответствующие стороны исходного прямоугольника: 1 / 4 = 1 / 4 и 3 / 12 = 1 / 4 . Следовательно, масштабный коэффициент, используемый для масштабирования прямоугольника, равен 1/4. Ответ B получается, если масштабный коэффициент был неправильно определен путем деления сторон внутри каждого прямоугольника в следующем порядке: 4 / 12 = 1 / 3 и 1 / 3 =

3. D: Чтобы построить треугольник, сумма трех углов должна составлять 180°. В ответе D два прямых угла сами по себе дадут в сумме 180°, поэтому добавление к этому значению острого угла сделает сумму больше 180°. Следовательно, треугольник не может быть построен с двумя прямыми углами. Ответы A, B и C — это все возможные варианты углов для построения треугольника.
4. D: Горизонтальное разрезание правой прямоугольной призмы создаст срезы, параллельные основанию призмы. Поскольку основание призмы представляет собой квадрат со стороной 4, каждый из горизонтальных срезов также будет иметь форму квадрата. Ответы A и C — это формы, которыми выглядит основание, если не принимать во внимание рисунок трехмерного изображения и то, что призма представляет собой правильную прямоугольную призму. Ответ B — двумерная фигура, полученная в результате вертикального разреза призмы.
5. C: Формула площади круга: A=pr 2 . Поскольку диаметр сада равен 10 футам, радиус сада равен 5 футам. Следовательно, A=3,14(5 «футов») 2 = 78,5 дюймов 2 . Ответ А — это результат, если радиус не был возведен в квадрат, т. е. ?r. Ответ B — это результат, если была рассчитана окружность сада. Ответ D является результатом использования диаметра в формуле площади.
Следовательно, A=3,14(5 «футов») 2 = 78,5 дюймов 2 . Ответ А — это результат, если радиус не был возведен в квадрат, т. е. ?r. Ответ B — это результат, если была рассчитана окружность сада. Ответ D является результатом использования диаметра в формуле площади.
6. B: Расстояние вокруг каждой шины равно длине окружности: C=2pr=2(3,14)(3 фута)=18,84 фута. Ответ А — это результат, если бы радиус не удваивался. Ответ C – площадь внутри шины. Ответ D — это результат, если в формуле площади использовался диаметр.
7. C: Два угла, показанные на рисунке, являются дополнительными. Чтобы найти x, необходимо использовать следующее уравнение: 10x-5+35=180. Это уравнение упрощается: 10x+30=180. После вычитания 30 с обеих сторон уравнение становится 10x=150. Наконец, после деления обеих частей на 10, решение x=15. Ответ A получается, если считать углы равными и составить уравнение как 10x-5=35. Ответ B получается в результате рассмотрения углов как дополнительных и составления уравнения в виде 10x-5+35=9. 0. Ответ D получается, если уравнение было правильно составлено как 10x+30=180, но затем к обеим частям было неправильно добавлено 30, чтобы получить 10x=210.
0. Ответ D получается, если уравнение было правильно составлено как 10x+30=180, но затем к обеим частям было неправильно добавлено 30, чтобы получить 10x=210.
8. C: Прежде чем мы сможем найти меру ?DBC, нам сначала нужно найти x. Поскольку ?ABD и ?DBC дополняют друг друга, нам нужно использовать уравнение m ?ABD + m ?DBC = 90. Подставляя значения m ?ABD и m ?DBC, уравнение принимает вид 5x+4x=90. Это уравнение упрощается: 9x=90. Наконец, после деления обеих частей уравнения на 9 результат x=10. Чтобы найти меру ?DBC, подставим x=10 в (4x)°, чтобы получить (4(10))°=40°. Ответ А — это значение х. Ответ B — это значение x, если бы углы рассматривались как дополнительные и были установлены как 5x+4x=180. Ответ D является мерой ?ABD. 92. В ответе А при расчете использовалась только база 5 футов. В ответе C для высоты использовалось значение 3 фута. В ответе D 1/2 была исключена из формулы, поэтому площадь была рассчитана неправильно: A=h(b_1+b_2).
10. C: Количество ткани, необходимое для покрытия шкатулки, равно площади поверхности шкатулки. Формула площади поверхности куба: SA=6 2 , где s — длина одной стороны. Следовательно, площадь поверхности шкатулки для драгоценностей равна SA=6(8 см) 2 = 6(64см) 2 =384 см 2 . В ответе А вычислялась площадь только одной стороны коробки. В ответе Б периметр одной стороны ящика умножался на 6. В ответе Г вычислялся объем ящика.
Формула площади поверхности куба: SA=6 2 , где s — длина одной стороны. Следовательно, площадь поверхности шкатулки для драгоценностей равна SA=6(8 см) 2 = 6(64см) 2 =384 см 2 . В ответе А вычислялась площадь только одной стороны коробки. В ответе Б периметр одной стороны ящика умножался на 6. В ответе Г вычислялся объем ящика.
7-й класс Wisconsin Forward Math Worksheets: БЕСПЛАТНО и для печати
Хотите завершить процесс обучения для 7-го класса Wisconsin Forward Math Test? Используйте наши рабочие листы по математике для 7-го класса штата Висконсин!
Wisconsin Forward Exam — это стандартный тест, который можно использовать для оценки успеваемости учащихся 3–8 классов. В настоящее время использование учебных пособий для подготовки к экзаменам стало очень важным и играет важную роль в завершении учебного процесса. Одним из наиболее практичных учебных пособий, доступных в настоящее время для теста Wisconsin Forward, являются рабочие листы Wisconsin Forward Math для 7-го класса, которые в этой статье предоставляются учащимся 7-го класса бесплатно. Целенаправленные упражнения, включенные в эти всеобъемлющие рабочие листы Wisconsin Forward Math для 7-го класса, способствуют развитию навыков и позволяют учащимся достичь высокого уровня подготовки к экзаменам.
Целенаправленные упражнения, включенные в эти всеобъемлющие рабочие листы Wisconsin Forward Math для 7-го класса, способствуют развитию навыков и позволяют учащимся достичь высокого уровня подготовки к экзаменам.
ВАЖНО: УСЛОВИЯ АВТОРСКОГО ПРАВА: Эти листы предназначены для личного использования. Рабочие листы нельзя загружать в Интернет в любой форме, включая классные/личные веб-сайты или сетевые диски. Вы можете скачать рабочие листы и распечатать столько, сколько вам нужно. У вас есть разрешение на распространение печатных копий среди ваших учеников, учителей, наставников и друзей.
У вас НЕТ разрешения на отправку этих листов кому бы то ни было (по электронной почте, текстовым сообщениям или другим способом). Они ДОЛЖНЫ загрузить рабочие листы самостоятельно. Вы можете отправить адрес этой страницы своим ученикам, репетиторам, друзьям и т.д.
Related Topics
- Grade 4 Wisconsin Forward Math Worksheets
- Grade 5 Wisconsin Forward Math Worksheets
- Grade 6 Wisconsin Forward Math Worksheets
- 8 класс Wisconsin Forward Рабочие листы по математике
7 -й класс в Висконсине, концепции математики,
Фракции и десятичные десятки
- Упрощающие фракции
- Добавление и вычитание фракций
- Умножение и разделение фракций
- Добавленные и подложки смешивания
- .
 Десятичные дроби
Десятичные дроби - Умножение и деление десятичных дробей
- Сравнение десятичных дробей
- Округление десятичных дробей
- Факторинговые номера
- Наибольший общий фактор
- Наименее распространенное множество
Реальные числа и целые числа
- Добавление и вычитание целых чисел
- Multipling and Dividing Integers
- Заказы
- -й Интеллекционеры
- Обратные номера
- Обравы
- Обратные номера
- и порядок
- и порядок
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- Обравы
- .
Пропорции, отношения и проценты
- Упрощение отношений
- Пропорциональные отношения
- Подобие и отношения
- Соотношение и ставки Проблемы с словом
- Процентные расчеты
- Проблемы
- Дисконтирование, налог и кончик
- процент изменения
- Простые проценты
Algebraic Experious
Algebraic Experision
 Преобразование фраз в алгебраическое выражение
Преобразование фраз в алгебраическое выражениеEquations and Inequalities
- One-Step Equations
- Multi-Step Equations
- Graphing Single–Variable Inequalities
- One-Step Inequalities
- Multi-Step Inequalities
- Системы уравнений
- Системы уравнений Словесные задачи
- Квадратное уравнение
Линейные функции
- Нахождение наклона
- Графические линии с использованием линейного уравнения
- Написание линейных уравнений
- Графические линейные неравенства
Экспоненты и радикалы
- Свойство Умножения
- Zero и отрицательные экспоненты
- .
- Отрицательные экспоненты и отрицательные основания
- Научное обозначение
- Квадратные корни
Геометрия и объемные фигуры
- Angles
- Pythagorean Relationship
- Triangles
- Polygons
- Trapezoids
- Circles
- Cubes
- Rectangular Prism
- Cylinder
- Pyramids and Cone
Statistics and Probability
- Mean and Median
- Mode и диапазон
- Гистограммы
- График ствола и листьев
- Круговая диаграмма
- Вероятностные задачи
- Комбинации и перестановки
7 -й класс по математике.



 Дополнительные полупрямые.
Дополнительные полупрямые.
 Свойства из теоремы о смежных
углах.
Свойства из теоремы о смежных
углах.

 Докажите, что углы CAO
и DBO равны.
Докажите, что углы CAO
и DBO равны. Докажите, что
MC=NC.
Докажите, что
MC=NC.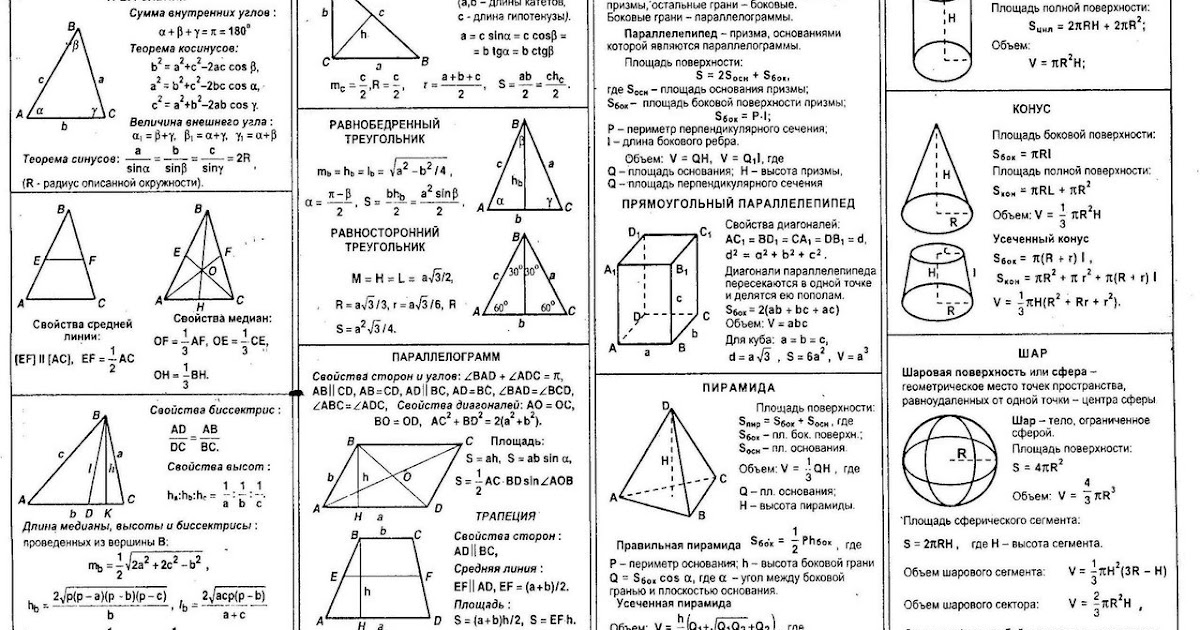 Докажите, что прямые MK ║ PN.
Докажите, что прямые MK ║ PN.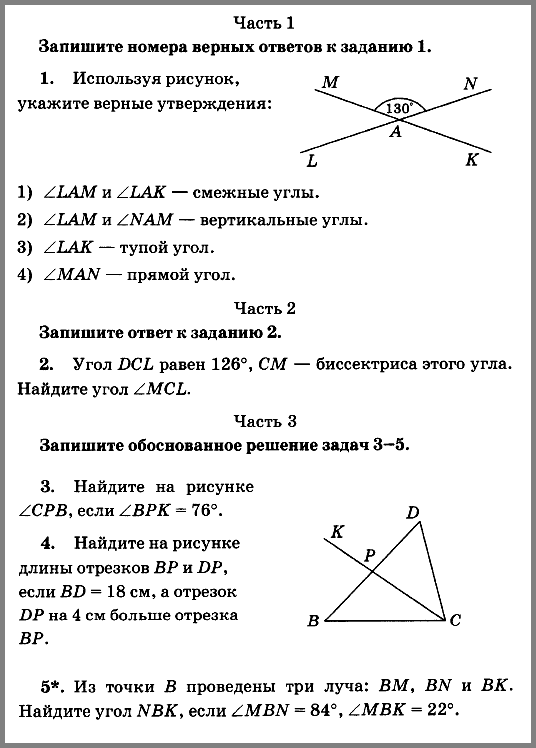 Укажите тип данного треугольника.
Укажите тип данного треугольника.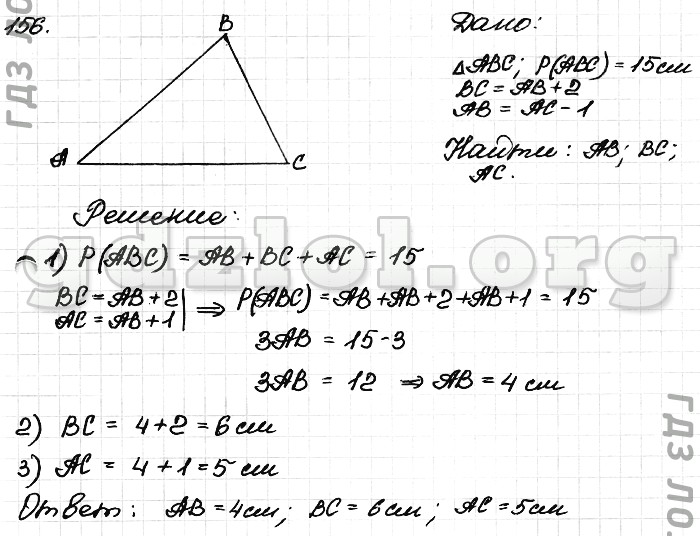
 Найдите углы треугольника ВОС.
Найдите углы треугольника ВОС.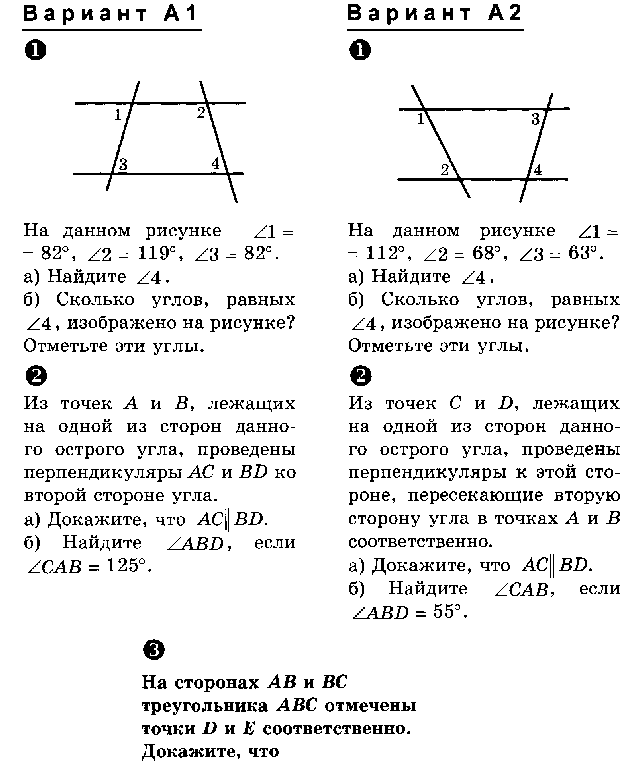 На окружности
найдите точки, равноудаленные от точек А и В.
На окружности
найдите точки, равноудаленные от точек А и В.

 Сейчас актуально меньше времени проводить за проверкой контрольных, самостоятельных или проверочных работ, гораздо лучше это время уделить ученикам;
Сейчас актуально меньше времени проводить за проверкой контрольных, самостоятельных или проверочных работ, гораздо лучше это время уделить ученикам; Это актуально для детей, которые, например, пропустили много тем по причине болезни.
Это актуально для детей, которые, например, пропустили много тем по причине болезни. Десятичные дроби
Десятичные дроби