Задания и ответы олимпиада по математике 6 класс – Олимпиадные задания по математике, 6 класс

Содержание

Олимпиадные задания по математике, 6 класс

ОЛИМПИАДНЫЕ задания по математике для 6 класса

1. Расшифруйте числовой ребус

СЕЛ ^xСЕЛ = ПОДСЕЛ

Одинаковым буквам соответствуют одинаковые цифры.

2. К празднику были срезаны розы: белых и розовых – 400 штук, розовых и красных – 300, белых и красных – 440. Сколько роз каждого цвета было срезано?

3. Сколько потребуется отдельных металлических цифр для нумерации 113 комнат гостиницы «Русский дом»?

4. Сейчас Коле 11 лет, а Пете 1 год. Сколько лет будет Коле и Пете, когда Коля будет втрое старше Пети?

5. В зоопарке одного города жили три кенгуру: Луиза, Дженни и Алекс. А потом родился крошка Ку. Всё это семейство съедает 28 кг моркови в неделю. Причём Ку съедает ровно вдвое меньше, чем любой из старших кенгуру. Сколько моркови в неделю съедало это семейство до рождения крошки Ку?

1) 25 кг 2) 24 кг 3) 26 кг

4) 23 кг 5) 22 кг 6) правильного ответа нет

6. На доске было написано двузначное число. Саша переставил цифры, и полученное число увеличилось в 4,5 раза. Какое двузначное число было записано первоначально?

7. За весну Винни-Пух сбавил в весе на 25%, а за лето прибавил 20%, за осень похудел на 10%, за зиму прибавил 20%. Похудел он или поправился за год?

8. Володя придумал интересный ребус. Расшифруйте его

ПЧЁЛКА · 7 = ЖЖЖЖЖЖ

9. Из двух городов, расстояние между которыми 320 км, одновременно навстречу друг другу выходят два поезда. Один идёт со скоростью 45 км/час, другой – 35 км/час. Вместе с первым поездом вылетает ласточка со скоростью 50 км/час и летит навстречу второму поезду. Встретив этот поезд, ласточка поворачивает обратно и летит навстречу первому поезду. Встретив этот поезд, она летит опять навстречу второму и так далее. Какое расстояние пролетит ласточка, пока поезда не встретятся?

1) 180 км 2) 200 км 3) 210 км

4) 140 км 5) 150 км 6) правильного ответа нет

10. Сколько процентов от часа составляют 12 минут?

1) 20% 2) 12% 3)2% 4)25%

11. При каком значении b выражение 2b+3 не является простым числом?

1) 1 2) 2 3) 3 4) 4

12. Среднее арифметическое десяти чисел равно 8, а среднее арифметическое девяти из них равно 7 . Чему равно десятое число?

1) 4 2) 3) 12 4) 9

13. 12% числа х составляют 28% числа 420. Чему равен х?

14. Какому числу кратно выражение:

4(1,5 – 3х) – 1,2(2,5 – 15х) при любом натуральном значении х?

15. Длины сторон треугольника относятся как 2 : 3 : 4. Чему равен периметр треугольника, если разность наибольшей и наименьшей сторон равна 6 см?

1) 27 2) 9 3) 18 4) 36

16. Сумма длин всех рёбер куба равна 36 см. Чему равен его объём?

1) 216 см² 2) 64 см² 3) 729 см² 4) 27 см²

17. В записи 52*2* замените звёздочки цифрами так, чтобы полученное число делилось на 36. Укажите все возможные решения.

18. Выразите число 16 с помощью четырёх пятёрок, соединяя их знаками действий.

19. Найдите два корня уравнения

| — 0,63 | : | х | = | — 0,9 |

20. В классе 35 учеников. Из них: 20 школьников занимаются в математическом кружке, 11 – в экологическом, 10 ребят не посещают эти кружки. Сколько экологов увлекается математикой?

Ответы, рекомендации, решения.

1. Решение: 625 ^х625 = 390625

2. Ответ: к празднику были срезаны розы: белых – 270, розовых – 130, красных – 170.

3. Ответ: 231.

4. Решение: через Х лет Коля будет втрое старше Пети, составим уравнение 11+х=(1+х)х3, решив его получим х=4, тогда 11+4=15(лет) – Коле, 1+4=5(лет) – Пете.

5. Ответ: 2) 24 кг

6. Ответ: 18

7. Ответ: Винни — Пух похудел за год.

8. Решение: 142857х7=999999

9. Решение: 45км/ч + 35 км/ч = 80 км/ч,

320 км : 80 км/ч = 4 ч,

50 км/ч · 4 ч = 200 км

10. Ответ: 2) 20%

11. Ответ: 3) 3

12. Ответ: 3) 12

13. Решение: 0,12х=420·0,28; х=980

14. Решение: 4(1,5 – 3х) – 1,2(2,5 – 15х)=6 – 12х – 3 + 18х=3+6х=3(1+2х), данное выражение кратно 3.

15. Ответ: 1) 27

16. Решение: 36 см : 12 = 3см, V=3³=27(см³)

17. Рекомендации. Число делится на 36, если оно делится и на 4 и на 9. Так как сумма цифр 5, 2, 2 равна 9, то сумма двух недостающих цифр должна равняться 0, 9 или 18. Учитывая, что число должно делиться на 4, а предпоследняя цифра равна 2, то последняя цифра может быть лишь 0 или 4 или 8. Тогда ответ будет: 52524, 52128, 52020, 52920.

18. Решение: 55 : 5 + 5 = 16

19. Ответ: х=0,7 и х=-0,7

20. Решение: 35 – 10 = 25 (уч) – посещают кружки

25 – 20 = 5 (уч) – посещают экологический кружок

11 – 5 = 6 (уч) – посещают оба кружка

Ответ: 6 экологов увлекаются математикой.

www.metod-kopilka.ru

Олимпиада по математике 6 класс, задания с ответами

На уроках математики в 6 классе ученики знакомятся с множеством новых тем, а также углубляют и расширяют знания, полученные ранее. В частности, на уроках ребята знакомятся с положительными и отрицательными числами, учатся выполнять арифметические действия с ними, а также узнают про отношения и пропорции, координаты на плоскости.

Чтобы определить самых способных учеников, учителя проводят разнообразные тестовые и контрольные работы. Но особое место занимают олимпиады по математике. Мы предлагаем вам задания для 6 класса с ответами, которые могут использовать на уроках или во время самостоятельной подготовки.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Уравнения

1. Решить уравнение:
5x + 13 = 3x – 3

2. Найдите решение уравнения:
2x + 5x = –14

3. Найдите решение уравнения:
4x – 5х = 20

4. Найдите решение уравнения:
–5x + 3x = 16

5. Найдите решение уравнения:
х : 2 = –8

6. Найдите решение уравнения:
4х + 3 = 2х + 13

7. Найдите решение уравнения:
((x : 2 − 3) : 2 − 1) : 2 − 4 = 3

8. Найдите решение уравнения:
11 — 5x = 12 — 6x

9. Найдите решение уравнения:
4 • (х + 5) = 12

10. Найдите решение уравнения:
5x = 2x + 6

Задачи

Задача №1
Гравировщик делает таблички с буквами. Одинаковые буквы он гравирует за одинаковое время, разные — возможно, за разное. На две таблички «ДОМ МОДЫ» и «ВХОД» вместе он потратил 50 минут, а одну табличку «В ДЫМОХОД» сделал за 35 минут. За какое время он сделает табличку «ВЫХОД»?

Задача №2
Раньше называли число, равное миллиону миллионов , словом «легион». Если разделить миллион легионов на легион миллионов, то получится:
A) легион
B) миллион
C) миллион миллионов
D) легион легионов

Задача №3
В магазин доставили 6 бочонков с квасом, в них было 15, 16, 18, 19, 20 и 31 литр. В первый же день нашлось два покупателя: один купил два бочонка, другой – три, причем первый купил вдвое меньше кваса, чем второй. Не пришлось даже раскупоривать бочонки. Из шести бочонков на складе остался всего лишь один. Какой?

Задача №4
Молодой человек согласился работать с условием, что в конце года он получит автомобиль «Запорожец» и 2600. Но по истечении 8 месяцев уволился и при расчёте получил «Запорожец» и 1000. Сколько стоил «Запорожец»?

Задача №5
На окраску деревянного кубика затратили 4 г краски. Когда она высохла, кубик распилили на 8 одинаковых кубиков меньшего размера. Сколько краски потребуется для того, чтобы закрасить образовавшиеся при этом неокрашенные поверхности?

Задача №6
Гриша с папой ходил в тир. Уговор был такой: Гриша делает 5 выстрелов и за каждое попадание в цель получает право сделать ещё два выстрела. Всего Гриша сделал 17 выстрелов. Сколько раз Гриша попал в цель?

Задача №7
Ученик Вовочка любит решать математические задачи. Известно, что вчера он решил на 11 задач меньше, чем позавчера и на 32 задачи меньше, чем позавчера и сегодня вместе. Сколько задач решил Вовочка сегодня?

Задача №8
Чтобы сжить с белого света Змея Горыныча, которому исполнилось 40 лет, Кощей Бессмертный придумал приучить его к курению. Кощей Бессмертный подсчитал, что если Змей Горыныч каждый день в течение года будет выкуривать по 17 сигарет, то он умрет через 5 лет, если же он будет выкуривать по 16 сигарет, то умрет через 10 лет. До скольких лет доживет Змей Горыныч, если он не будет курить?

Задача №9
В затруднительном положении оказались однажды трое пеших разведчиков, которым необходимо было перебраться на противоположный берег реки при отсутствии моста. Правда, по реке катались в лодке два мальчика, готовые помочь солдатам, Но лодка была так мала, что могла выдержать вес только одного солдата; даже солдат и один мальчик не могли одновременно сесть в нее без риска ее потопить. Плавать солдаты совсем но умели. Казалось бы, при таких условиях мог переправиться через реку только один солдат. Между тем все три разведчика вскоре благополучно переправились на противоположный берег и возвратили лодку мальчикам. Как это они сделали?

Задача №10
Один из пяти братьев – Андрей, Витя, Дима, Толя или Юра разбил окно. Андрей сказал: “Это сделал или Витя, или Толя”. Витя сказал: “Это сделал не я и не Юра”. Дима сказал: “Нет, один из них сказал правду, а другой – неправду”. Юра сказал: “Нет, Дима, ты не прав”. Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто же из братьев разбил окно?

Математические загадки

Загадка №1
У 28 человек 5 «Ы» класса на собрание пришли папы и мамы. Мам было — 24, пап — 18. У скольких учеников на собрание пришли одновременно и папа и мама?

Загадка №2
В ящике лежат 100 синих, 100 красных, 100 зелёных и 100 фиолетовых карандашей. Сколько карандашей необходимо достать, не заглядывая в ящик, чтобы среди них обязательно нашлись по крайней мере 1 красный и 1 фиолетовый.

Загадка №3
На сколько нулей оканчивается произведение 1•2•3•4•…•37?

Загадка №4
Два невисокосных года идут подряд. В первом из них больше понедельников, чем сред. Какой из семи дней чаще всего встречается во втором году?

Загадка №5
Разбейте число 186 на три попарно различных натуральных слагаемых, сумма любых двух из которых делится на третье.

Ответы к уравнениям

Уравнение	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	x = – 8	x = –2	х = 4	x = 8	х = 16

Уравнение	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	х = –5	x = 66	x = 1	х = -2	х = 2

Ответы к задачам

Задача 1
20 минут

Задача 2
Вариант А

Задача 3
Первый покупатель купил 15-литровый и 18-литровый бочонки. Второй – 16-литровый, 19-литровый и 31-литровый. Остался не проданным 20-литровый бочонок.

Задача 4
2200

Задача 5
4 грамма

Задача 6
6 раз

Задача 7
21 задачу

Задача 8
130 лет

Задача 9
9 цифр

Задача 10
Толя разбил окно

Ответы на загадки

Загадка 1
14 учеников

Загадка 2
301 карандаш

Загадка 3
8 нулей

Загадка 4
Вторник

Загадка 5
31+62+93

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

ruolimpiada.ru

Олимпиада по математике 6 класс

Вариант 1 Вариант 2 Вариант 3

Задание 1.

Все натуральные числа раскрасили в три цвета.
Число 1 стало красным, 2 — синим,
3 — зеленым, 4 — красным, 5 — синим, 6 — зеленым, и так далее.
Какого цвета может быть сумма красного и синего чисел?

А — только зеленого Б — только красного В — только синего
Г — красного или синего Д — может быть любого цвета

Задание 2.

Два велосипедиста одновременно выехали навстречу друг другу по одной и той же дороге,
соединяющей два села.
Одному на весь путь требуется 1 час, а другому полтора часа.
Через сколько минут они встретятся?

А — 20 Б — 24 В — 30 Г — 36 Д — 40

Задание 3.

Петя хочет разрезать прямоугольник 6 х 7 на квадраты с целыми сторонами.
Какое наименьшее число квадратов может при этом получиться?

А — 4 Б — 5 В — 7 Г — 9 Д — 42

Задание 4.

На доске написано несколько натуральных чисел.
Сумма этих чисел равна их произведению и равна 2012.
Какое самое маленькое количество чисел может быть на доске?

А — 1006 Б — 1507 В — 1508 Г — 1556 Д — 2012

Задание 5.

В войске 5555 человек.
На 10 солдат приходится 1 капрал, на 5 капралов — 1 офицер, на 9 офицеров — 1 генерал.
Сколько в войске солдат?

А — 505 Б — 4950 В — 5000 Г — 5050 Д — 5500

Ответы к заданиям:

1 — А 2 — Г 3 — Б 4 — А 5 — Б

Олимпиада по математике 6 класс с решением

Задание 1.

На некотором острове необычайно регулярный климат :
по понедельникам и средам всегда идут дожди,по субботам — туман, зато в остальные дни — солнечно.
Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней?
A — в понедельник; B — в среду; C — в четверг; D — в пятницу; E — во вторник

Решение :

Выясним, сколько полных недель в 44 днях.
Получим 6 недель. В течении этих недель число солнечных дней не зависит от того, когда начнется отдых.
В качестве оставшихся двух дней выбираем четверг и пятницу — солнечные дни.
Следовательно, отправляем туристов утром в четверг.
То есть верный ответ — (С).

Задание 2.

У двузначного числа «n» цифра десятков в два раза больше, чем цифра единиц.
Тогда число «n» обязательно: A — четное; B — нечетное; C — меньше 20; D — делится на 3; E — делится на 6.

Решение :

Ищем число «n» среди ряда чисел: 10 — 99.
По условию, у всех подозреваемых чисел — десятки четны (2,4,6,8), а единицы — в два раза меньше (1,2,3,4,).
Перечислим все эти числа: 21, 42, 63, 84. Все они делятся на 3.
Следовательно верен ответ (D).

Задание 3.

Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? A — 18; B — 32; C — 24; D — 36; A — 48;

Решение :

Из условия следует, что 100-4=96 делится на искомое число.
Также 90-18=72 делится на искомое число.
Их разность также делится на искомое число: 96-72=24.
Следовательно, искомое число — 24, так как на него делится и 96, и 72.
Верен ответ (С).

Задание 4.

Раньше называли число, равное миллиону миллионов , словом «легион».
Если разделить миллион легионов на легион миллионов,
то получится : A — легион; B — миллион; C — миллион миллионов; D — легион легионов; E — 1

Решение :

Перепишем заново:
делимое: миллион легионов — это миллион миллионов миллионов,
делитель: легион миллионов — это миллион миллионов миллионов,
следоватально частное равно 1.
Верен ответ (Е).

Задание 5.

Есть 10 монет, среди них ровно две фальшивые.
Детектор R7 за одну операцию исследует три монеты и указывает на одну из них.
Известно, что детектор не может указать на настоящую монету,
если среди тестируемых монет есть хотя бы одна фальшивая.
Как за шесть тестов выявить обе фальшивые монеты?

Решение:

Выберем три кучки по три монеты, протестируем каждую из них,
и возьмём те три монет, на которые указал детектор.
Среди них, очевидно есть хоть одна фальшивая.
Протестируем эти монеты и таким образом определим одну из фальшивых.
Вторая фальшивая монета может быть только среди тех четырёх монет,
с которыми тестировалась найденная фальшивая или быть той монетой, которая ещё не была задействована.
Среди этих пяти монет за два теста определить одну фальшивую уже совсем легко
(каждый тест выявляет две настоящие монеты).

Задание 6.

На доске написано пять двузначных натуральных чисел.
Чебурашка каждую минуту прибавляет ко всем числам единицу или (тоже ко всем числам) двойку.
После того, как Чебурашка увеличивает числа, К. Гена может стереть какое-нибудь число,
делящееся на 13, или число, сумма цифр которого делится на 7 (если, конечно, такое число на доске есть).
Докажите, что при любых действиях Чебурашки,
Гена через некоторое время сумеет стереть с доски все числа.

Решение:

Гена может найти пять пар не более чем пятизначных соседних чисел,
так, чтобы в каждой паре он мог стереть любое число.
Чебурашка сможет «провести» через одну такую пару не более одного числа,
а значит все пять чисел Гена сможет стереть.Подобных пар очень много,
например годятся пары 142 и 143, 312 и 313, 3120 и 3121, 1312 и 1313, 69999 и 70000…

Вариант 1 Вариант 2 Вариант 3

eruditu.ru

Олимпиада по математике 6 класс

Математика олимпиада 6 класс задания

ЗАДАНИЕ №1.

Число 1000 вырази 8 восьмёрками (кроме цифр можно использовать знаки математических действий)

ЗАДАНИЕ №2.

На плоскости расположены четыре фигуры: два треугольника и две прямые. Они могут пересекаться и не пересекаться. Найди наибольшее возможное количество точек пересечения между собой всех этих четырёх фигур.

ЗАДАНИЕ №3.

Число 361*** делится на 9 и на 13. Восстанови неизвестные цифры.

ЗАДАНИЕ №4.

Рыночная цена 1 кг картофеля составляет 2 гривны. В связи с ненастной погодой цена 1 кг картофеля повысилась на 20%. Через некоторое время цена понизилась на 20%. На сколько копеек 1 кг картофеля подорожает или подешевеет по сравнению с первоначальной ценой.

ЗАДАНИЕ №5.

Можно ли ходом коня обойти все клетки шахматной доски, начав с клетки а1, закончив на клетке h8 и на каждой клетке доски побывав ровно один раз?

Математика олимпиада 6 класс ответы и решения на задания

6 класс

ЗАДАНИЕ №1.

888+88+8+8+8=1000.

ЗАДАНИЕ №2.

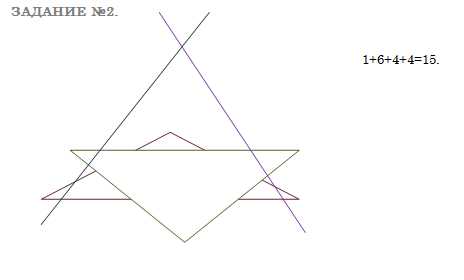
1+6+4+4=15.

ЗАДАНИЕ №3.

36153.

ЗАДАНИЕ №4.

Цена картофеля понизилась на 8 копеек по сравнению с первоначальной ценой.

ЗАДАНИЕ №5.

Не может (подсказка: чтобы оказаться на клетке того же цвета, конь должен сделать чётное число ходов).

Олимпиада по математике 6 класс — 4.0 out of 5 based on 46 votes

Добавить комментарий

zadachi-ru.com.ua

Олимпиадные задания для 6 классов с решениями.

Олимпиадные задания по математике

для 6 классов.

№1. ( 2 балла) Используя шесть раз цифру 2, знаки действий и скобки, напишите выражение, значение которого равно 100.

№2. (2 балла) На полке в один ряд стоят книги. Энциклопедия стоит пятой слева и семнадцатой справа. Сколько книг на полке?

№3. (4 балла) По углам и сторонам квадрата вбиты колышки на расстоянии 2 метра друг от друга. Сколько колышков вбито, если сторона квадрата равна 10 метрам? Показать решение на рисунке.

№3. (4 балла) В забеге участвовало 37 человек. Число спортсменов, прибежавших раньше Игоря, в 5 раз меньше числа тех, кто прибежал позже. Какое место занял Игорь?

№4. (3 балла) В коробке 14 белых и 14 чёрных шариков. Какое минимальное количество шариков нужно достать из коробки, чтобы среди них наверняка оказалось 2 черных шарика?

№5. (5 баллов) В семье четверо детей, им 5,8,13и 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на 3?

№6. (5 баллов) Младший брат Насти во время игры вырвал из книги 3 листа. Настя сложила номера всех вырванных 6 страниц и получила 2016. Докажите, что при сложении девочка допустила ошибку.

Максимальное количество баллов – 25 баллов

Задания с решениями

Ответ: возможное решение (222-22) : 2 = 100

2 балла, если записано верное равенство

Ответ: 21 книга. (4 + 1 + 16 = 21)

2 балла – приведено решение задачи, получен верный ответ.

1 балл – записан верный ответ

Ответ: 20 колышков.

4 балла – на рисунке верно представлено решение задачи

2-3 балла – решение, представленное на рисунке, имеет недочеты

1 балл – записан верный ответ без рисунка

Ответ: 7 место. (х+5х+1=37; 6х = 36; х=6, 7место у Игоря)

4 балла – приведено обоснованное решение задачи, получен верный ответ

2-3 балла – приведено решение задачи, содержащее неточности

1 балл – записан верный ответ

Ответ: 16.(14+2 = 16)

2-3 балла – приведено решение задачи, получен верный ответ.

1 балл – записан верный ответ

Ответ: Вере-5 лет; Боре-8 лет, Ане-13 лет; Гале-15 лет.

5 баллов – приведено верное обоснованное решение задачи

3-4 балла – при верных рассуждениях получен неточный ответ

2 балла – записан верный ответ

Ответ: сумма номеров страниц на одном листе число нечетное, тогда сумма номеров 3-х листов тоже нечетное число.

5 баллов – приведено верное обоснованное решение задачи

Максимальное количество баллов – 25 баллов

intolimp.org

Олимпиадные задачи по математике, 6 класс.

Олимпиадные задачи по математике, 6 класс.

1.На некотором острове необычайно регулярный климат: по понедельникам и средам идут дожди, по субботам – туман, зато в остальные дни – солнечно. Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней? ( 3 балла )

А- в понедельник, В- в среду, С- в четверг, Д- в пятницу, Е – во вторник.

2.Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? ( 3 балла )

А – 18, В – 32, С – 24, Д – 36, Е – 48.

3.Если кенгуру научится прыгать в 1,5 раза дальше, чем умеет, ему понадобится ровно 6 прыжков, чтобы добраться до тенистого дерева. За сколько прыжков кенгуру может это сделать сейчас? ( 3 балла )

А – 3, В -4, С – 6, Д – 9, Е – невозможно определить.

4.На каждой кочке в маленьком болотце сидят не меньше, чем по 3 лягушки, а всего лягушек 145. Тогда число кочек в этом болотце не может равняться: ( 3 балла )

А – 1, В – 23, С – 31, Д – 44, Е – 55.

5.Выполните действия рациональным способом

354 * 73 + 23 *25 + 354 * 27 +17 * 25 ; ( 5 баллов )

6.На одной чашке весов лежат шесть одинаковых пачек чая и гиря массой 50 г, а на другой – одна пачка чая и две гири массой 100 г и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая? ( 6 баллов )

7.Из 40 учащихся 6 класса 32 ходят на кружок «Умелые руки», 21 посещают спортивную секцию, 15 учащихся ходят и на кружок и на секцию. Сколько учащихся не ходят на этот кружок, ни на эту секцию? ( 6 баллов )

Ответы. 1.- С; 2.- С; 3.- Д; 4.- Е; 5.-36400; 6.-50 г; 7.- 2 уч.

Олимпиадные задачи по математике, 6 класс, 2 тур.

1.Гусеница ползёт по стволу яблони. За первый час она поднялась на 10 см, за второй час опустилась на 4 см, за третий час вновь поднялась на 10см, а за четвёртый опустилась на 4 см. Так она продолжала подниматься и опускаться в течение нескольких часов. На сколько сантиметров поднимется гусеница за 11 ч? (5 баллов)

2.Решите уравнение |2x|*|-3,5|=|-28|. (3 балла)

3.В детский летний лагерь приехали три друга: Миша, Володя, Петя. Известно. Что каждый из них имеет одну из фамилий: Иванов, Семёнов, Герасимов. Миша не Герасимов. Отец Володи инженер. Володя учится в 6 классе. Ребёнок с фамилией Герасимов учится в 5 классе. Отец с фамилией Иванов – слесарь. Какая фамилия у каждого из друзей? (4 балла)

4.Запиши число 100 девятью различными цифрами, соединёнными знаками действий. (4 балла)

5.У фермера было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Мальчик спросил фермера, сколько весит один поросёнок и один ягнёнок. Фермер ответил, что 3 поросёнка и 2 ягнёнка весят 22 кг, а 2 поросёнка и 3 ягнёнка весят 23 кг. Как узнать, сколько весит один поросёнок и сколько весит один ягнёнок? (5 баллов)

infourok.ru

Олимпиадные задания по алгебре (6 класс) на тему: 10 олимпиадных заданий по математике для 6 класса( с решением)

Банк олимпиадных заданий

по математике для 6 класса

Авторы:

Филонова Лариса Ивановна, МБОУ Платоновская СОШ Рассказовского района;

Тумакова Елена Семеновна, МБОУ Платоновская СОШ;

Ильичева Ирина Николаевна, МБОУ Платоновская СОШ;

Богданова Людмила Александровна, Саюкинский филиал МБОУ Платоновской СОШ;

Дьякова Эугения Станиславовна, Рождественский филиал МБОУ Платоновской СОШ

Место прохождения стажировки: МАОУ «Лицей № 29», г. Тамбов

Организатор стажировки: Калужина Татьяна Николаевна

Задача 1. Расшифруйте запись примера на сложение, где одинаковыми буквами обозначены одинаковые цифры:

А Б В Д

+ А Б Г Д

В Д Г А Д

Ответ:

5 2 1 0

+ 5 2 4 0

1 0 4 5 0

Задача 2. Докажите, что если цифры десятизначного числа выписать в обратном порядке, то полученное число не будет в три раза больше исходного.

Решение.

Предположим, что такое число нашлось. Его первая цифра может быть 1, 2 или 3 (потому что иначе в три раза большее число будет одиннадцатизначным).

Если первая цифра 1, то последняя – 7 (так как иначе при умножении на три на конце получится другое число – см. таблицу умножения на 3). Но тогда обращённое число получается более чем в три раза превосходит исходное.

Если первая цифра – 2 или 3, то последняя – 4 или 1, поэтому обращённое число получается слишком мало.

Задача 3. Кассир продал все билеты в первый ряд кинотеатра, причем по ошибке на одно из мест было продано два билета. Сумма номеров мест на всех этих билетах равна 857. На какое место продано два билета?
Решение.

Сколько мест могло быть в первом ряду. Во-первых, их не больше 40, так как сумма натуральных чисел от 1 до 41 равна 861. Во-вторых, их не меньше 40, так как сумма натуральных чисел от 1 до 39 равна 780, и даже после прибавления к ней 39, результат будет меньше 857. Значит в первом ряду ровно 40 мест. Теперь несложно определить, на какое место был продан лишний билет: 1 + … + 40 = 820; 857 – 820 = 37.
Ответ: на тридцать седьмое место

Задача 4. Есть 10 монет, среди них ровно две фальшивые. Детектор R7 за одну операцию исследует три монеты и указывает на одну из них. Известно, что детектор не может указать на настоящую монету, если среди тестируемых монет есть хотя бы одна фальшивая. Как за шесть тестов выявить обе фальшивые монеты?

Решение.

Выберем три кучки по три монеты, протестируем каждую из них, и возьмём те три монет, на которые указал детектор. Среди них, очевидно есть хоть одна фальшивая. Протестируем эти монеты и таким образом определим одну из фальшивых. Вторая фальшивая монета может быть только среди тех четырёх монет, с которыми тестировалась найденная фальшивая или быть той монетой, которая ещё не была задействована. Среди этих пяти монет за два теста определить одну фальшивую уже совсем легко (каждый тест выявляет две настоящие монеты).

Задача 5. Яйцо варится 9 минут. Как отсчитать это время с помощью двух песочных часов по 5 минут и 7 минут?

Решение.

1 способ: Одновременно запускаем часы по 5 минут и 7 минут. Через 5 мин. (когда кончится песок в 5 мин. часах) начинаем варить яйцо. Через 2 мин. кончится песок в7 мин. часах; перевернем их. Когда в них опять кончится песок, яйцо будет готово.

2способ: Варить яйцо начинаем одновременно с запуском двух песочных часов по 5 минут и 7 минут. Через 5 минут переворачиваем пяти минутные часы, а еще через 2 минуты (когда семи минутные часы станут пустыми) переворачиваем пяти минутные часы еще раз.

Задача 6. На каждом километре между селами Марьино и Рощино стоит столб с табличкой, на одной стороне которой написано расстояние до Марьино, на другой – расстояние до Рощино. Останавливаясь у каждого столба, Бобик заметил, что если сложить все цифры, записанные на обеих сторонах таблички, то получится 13. Найдите расстояние между селами.

Решение.

Расстояние между селами не может быть больше, чем 49 километров, так как тогда на одном из столбов будет написано с одной стороны 49, а с другой – не 0, то есть, сумма цифр будет больше 13. На первых девяти столбах с одной стороны записаны однозначные числа от 1 до 9, поэтому числа, записанные с другой стороны, также должны быть из одного десятка (чтобы суммы цифр были одинаковы). Следовательно, искомое расстояние выражается числом, оканчивающимся на 9. Числа 9, 19, 29 и 39 решениями не являются, так как на первом столбе сумма цифр не будет равна 13. Таким образом, искомое расстояние равно 49 километрам.

Ответ: 49 километров.

Задача 7. На доске написано пять двузначных натуральных чисел. Чебурашка каждую минуту прибавляет ко всем числам единицу или (тоже ко всем числам) двойку. После того, как Чебурашка увеличивает числа, К. Гена может стереть какое-нибудь число, делящееся на 13, или число, сумма цифр которого делится на 7 (если, конечно, такое число на доске есть). Докажите, что при любых действиях Чебурашки Гена через некоторое время сумеет стереть с доски все числа.

Решение.

Гена может найти пять пар не более чем пятизначных соседних чисел, так, чтобы в каждой паре он мог стереть любое число. Чебурашка сможет «провести» через одну такую пару не более одного числа, а значит все пять чисел Гена сможет стереть.

Подобных пар очень много, например годятся пары 142 и 143, 312 и 313, 3120 и 3121, 1312 и 1313, 69999 и 70000…

Задача 8. На одной стороне улицы разбитых фонарей стояло 150 фонарей, причём среди любых трёх фонарей, стоящих подряд, хотя бы один был разбит. После того, как электрик Петров починил несколько фонарей, среди любых четырёх фонарей, стоящих подряд, осталось не более одного разбитого. Докажите, что электрик починил не менее 25 фонарей.

Решение.

1 способ. Разобьём фонари на 25 шестёрок подряд стоящих, и докажем, что в каждой из них был починенный фонарь. Предположим, что в какой-то шестёрке ни один фонарь не был починен. В такой шестёрке не менее двух разбитых фонарей (поскольку в каждой из двух троек, составляющих шестёрку, был разбитый фонарь), между которыми не менее трёх работающих фонарей (так как иначе можно будет указать четыре фонаря, среди которых хотя бы два разбитых). Но как раз трёх работающих фонарей подряд стоять и не может.

2 способ. Посмотрим на фонари до прихода электрика. В каждой тройке подряд стоящих фонарей есть хотя бы один испорченный, значит всего испорченных фонарей не менее 50. Пронумеруем первые 50 испорченных фонарей слева направо и разобьём на пары: 1-й со 2-м, 3-й с 4-м, и т.д. (всего 25 пар) Между фонарями одной пары все фонари целые, а значит их не более двух. Поэтому один из испорченных фонарей, входящих в одну пару, надо починить.

Задача 9. На острове Невезения отменили понедельники: у них за воскресеньем сразу следует вторник. За последний год (то есть, с 15 декабря 2002 года по 14 декабря 2003 года) воскресенья на острове совпадали с нашими воскресеньями ровно восемь раз. Какой день недели на острове сегодня?
Решение.

Так как обычная неделя состоит из семи дней, а неделя на острове – из шести, то совпадение воскресений происходит один раз в 6 х 7 = 42 дня. Значит, за 378 дней происходит 9 совпадений. Поскольку 378 – 365 = 13, то девятое совпадение должно произойти в течение ближайших тринадцати дней (с 15 по 27 декабря). Единственное воскресенье в этот период – 21 декабря. Непосредственным подсчетом получаем, что сегодня на острове – суббота.
Ответ: суббота.

Посмотрим на фонари до прихода электрика. В каждой тройке подряд стоящих фонарей есть хотя бы один испорченный, значит всего испорченных фонарей не менее 50. Пронумеруем первые 50 испорченных фонарей слева направо и разобьём на пары: 1-й со 2-м, 3-й с 4-м, и т.д. (всего 25 пар) Между фонарями одной пары все фонари целые, а значит их не более двух. Поэтому один из испорченных фонарей, входящих в одну пару, надо починить.

Задача 10 . Каждый из трёх приятелей либо всегда говорит правду, либо всегда лжёт. Им был задан вопрос: «Есть ли хотя бы один лжец среди двух остальных?» Первый ответил: «Нет», второй ответил: «Да». Что ответил третий?
Решение. Так как первый и второй приятели дали различные ответы, то один из них – лжец, а другой – рыцарь. Кроме того, рыцарь не мог ответить «Нет» на предложенный ему вопрос, так как в этом случае он бы сказал неправду (среди двух оставшихся точно есть лжец). Следовательно, первый – лжец. Он солгал, значит, среди двух оставшихся должен быть лжец, и им может быть только третий приятель. Значит, третий ответил «Нет».
Ответ: «Нет».

Критерии оценивания.

Все задания оцениваются, исходя из 7 баллов.

7 баллов – верное решение,

6 баллов – решение с недочетами,

4-5 баллов – в основном решение верно, но неполно или содержит непринципиальные ошибки,

1-3 балла – решение в целом неверно, но содержит более или менее существенные продвижения в верном направлении.

0 баллов – решении неверно или отсутствует.

nsportal.ru