Решение задач с помощью пропорций 6 класс: Презентация к уроку по алгебре (6 класс) на тему: «Решение задач с помощью пропорции», 6 класс
«Решение задач с помощью пропорций»
Тип урока: комбинированный.
Цели урока:
- научить учащихся выделять в условиях задач две величины;
- устанавливать вид зависимости между ними;
- научить их делать краткую запись условия задачи и составлять пропорцию;
- развить воображение, математическую интуицию, память, мышление, сформировать правильную математическую речь;
- активизировать познавательную и творческую активность учащихся.
Оборудование: плакаты, индивидуальные карточки, сигнальные карточки
ХОД УРОКА
Организационный момент
- Проверка готовности класса к уроку;
- Сообщение темы и цели урока.
Устные задания (тест с использованием сигнальных карточек):
Найти отношение:
а) [8]; б) [6].
Верна ли пропорция:
а) [2]; б) [1].
3. Решить пропорцию:
а) 12,5:Х = 1,2 : 0,6 [4]
б) [0]
Ответы: 1) да; 2) нет; 3) 2; 4) 6,25; 5); 6) ; 7)12,05; 8); 9); 0) ?.
Вопросы:
- Что называется отношением двух чисел?
- Что показывает отношение двух чисел?
- Что такое пропорция?
- Сформулируйте основное свойство пропорции?
Решение задач
На предыдущем уроке учащимся были введены понятия прямой и обратной пропорциональности, отработаны данные понятия на задачах. На данном уроке решаем задачи с помощью пропорций. Рассматриваемые задачи – это задачи с целыми значениями величин, отношение которых тоже целое число. Для этого составляем краткую запись условия задачи. В процессе устного обсуждения выделяем 2 величины, устанавливаем вид зависимости. Уменьшение величины показываем стрелкой вниз, а увеличение — стрелкой вверх. Затем составляем пропорцию и решаем её.
1. За 6 ч поезд прошел 480 км. Какой путь прошел поезд за первые 2 ч, если его скорость была постоянна.
Решение.
I способ (“по-старому”).
1) 480 : 6 = 80 (км/ч)
2) 80 • 2 = 160 (км)
II способ
Составим краткую запись условия задачи:
Краткая запись заранее оформляется на плакате. В процессе устного обсуждения выясняем, что время и путь уменьшились в одно и то же число раз, так как при постоянной скорости эти величины прямо пропорциональны.
Затем, составляем пропорцию и решаем её: ; Х= 160 (км)
2. Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песку. Сколько килограмм сахарного песку надо взять на 12 кг ягод? [8 кг]. (Задача дается на самостоятельное решение, но перед этим устное обсуждение задачи).
3. Расстояние между городами пассажирский поезд прошел со скоростью 80 км/ч за 3 ч. За сколько часов товарный поезд пройдет то же расстояние, со скоростью 40 км/ч?
Решение.
В процессе устного обсуждения выясняем, что скорость уменьшилась, а время увеличилось в одно и то же число раз, следовательно, эти величины при одном и том же расстоянии являются обратно пропорциональными.
(ч)
4. Пять маляров могли бы покрасить забор за 8 дней. За сколько дней покрасят тот же забор 10 маляров? [4 дня] (Для самостоятельного решения).
В этой задаче предполагается, что все
работники трудятся с одинаковой
производительностью. Для того, чтобы учащиеся
лучше освоили прием составления пропорций,
постоянно задаём вопрос: “Во сколько раз
увеличилась (уменьшилась) первая величина?”.
Тогда число, дающее ответ, будет находиться
делением большего значения величины на меньшее
(в направлении стрелок).
Чтобы у учащихся не сложилось впечатление, будто
зависимость бывает только двух видов – прямой
или обратной пропорциональностью, —
рассматриваем провокационные задачи, в которых
зависимость имеет другой характер.
5.
1) За 2 ч поймали 12 карасей. Сколько карасей
поймали за 3 ч?
2) Когда Вася прочитал 10 страниц книги, то ему
осталось прочитать ещё 90 страниц. Сколько
страниц ему останется прочитать, когда он
прочитает 30 страниц?
Затем, рассматриваем задачу, в которой
зависимость между величинами часто принимают за
прямую пропорциональность.
6. * Пруд зарастает лилиями, причём за неделю площадь, покрытая лилиями, удваивается. За сколько недель пруд покрылся лилиями наполовину, если полностью он покрылся лилиями за 8 недель? [7 недель]
IV. Задача на смекалку (на “совместную работу”).
За пять недель пират Ерёма
Способен выпить бочку рома.
А у пирата у Емели
Ушло б на это две недели
За сколько дней прикончат ром
Пираты, действуя вдвоем? [10 дней]
V. Задание на дом
1) В 100 граммах раствора содержится 4 грамма соли.
Сколько граммов соли содержится в 300 граммах
раствора?
2) 4 комбайна могут убрать пшеницу с поля за 10 дней.
За сколько дней уберут это поле 8 комбайнов?
3) Три петуха разбудили 6 человек. Сколько человек
разбудят пять петухов?
4) По учебнику № 803 (а).
VI. Подведение итогов урока
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:«Решение задач с помошью пропорции»
2 слайд Описание слайда:
Описание слайда:Что означает слово «пропорция»?
3 слайд
№ 1: Задача на прямую пропорциональность ( Чем больше одна величина, тем больше другая) ( Чем меньше …, тем меньше…) №2 :Задача на обратную пропорциональность ( Чем больше одна величина, тем меньше другая) Творческое задание
4 слайд Описание слайда:
Описание слайда:Что называется отношением?
5 слайд Описание слайда:
Описание слайда:Что показывает отношение?
6 слайд Описание слайда:
Описание слайда:Что называется пропорцией?
7 слайд Описание слайда:
Описание слайда:Сформулиро-вать основное свойство пропорции
 Описание слайда:
Описание слайда:Какая зависимость между величинами называется прямой?
9 слайд Описание слайда:
Описание слайда:Какая зависимость между величинами называется обратной?
10 слайд Описание слайда:
Описание слайда:1. Какие из равенств являются пропорциями? а) 25 : 5 = 45 : 9; б) 2,5 : 0,5 = 3 + 2; в) 0,5 x 12 = 24 : 4. 2. а) Прочитайте пропорцию: а) 18 : 6 = 24 : 8 б) 30 : 5 = 42 : 7 в)36 : 9 = 50 :10.
11 слайд Описание слайда:
Описание слайда:2. Найдите отношение 2 часа к 1 суткам.
12 слайд
1) 10 : 120 2) 2 : 24 Равны или нет эти отношения? Можем составить ……
13 слайд Описание слайда: 14 слайд
Описание слайда: 14 слайд  Описание слайда:
Описание слайда:Десять золотых уроков, которые вы можете использовать в своей повседневной жизни 1. Человек, который никогда не ошибался, никогда не пробовал сделать что-нибудь новое. 2. Образование — это то, что остается после того, когда забываешь все, чему учили в школе. 3. В своем воображении я свободен рисовать как художник. Воображение важнее знания. Знание ограничено. Воображение охватывает весь мир. 4. Секрет творчества состоит в умении скрывать источники своего вдохновения. 5. Ценность человека должна определяться тем, что он дает, а не тем, чего он способен добиться. Старайтесь стать не успешным, а ценным человеком.
15 слайд Описание слайда:
Описание слайда:6. Есть два способа жить: вы можете жить так, как будто чудес не бывает и вы можете жить так, как будто все в этом мире является чудом. 7. Когда я изучаю себя и свой способ думать, я прихожу к выводу, что дар воображения и фантазии значил для меня больше, чем любые способности к абстрактному мышлению. 8. Чтобы стать безупречным членом стада овец, нужно в первую очередь быть овцой. 9. Нужно выучить правила игры. А затем, нужно начать играть лучше всех. 10. Очень важно не перестать задавать вопросы. Любопытство не случайно дано человеку.
16 слайд Описание слайда:
Описание слайда:1)18:х = 54:6 2) х:5 = 38:19 3)3,6:4,8=х:2,4 4) 17:5 = х:25
17 слайд Описание слайда:
Описание слайда:1) Х = 2 2) Х = 10 3) Х = 1,8 4) Х = 85 Если твой ответ не совпал с данными – НЕ ОТЧАИВАЙСЯ ! Просто придумай другое уравнение, для которого это число будет КОРНЕМ!!!
18 слайд Описание слайда:
Описание слайда:Профилактика шейного остеохондроза Творческий Агрессивный Ответственный Невнимательный Целеустремлённый Мало читает Коммуникабельный
19 слайд Описание слайда:
Описание слайда:На изготовление24 утюгов кузнецу требуется 72 кг. металла. Сколько таких же утюгов может изготовить кузнец из 48 кг. металла? ! Чугун – сплав железа с углеродом
20 слайд Описание слайда:
Описание слайда:24 садовода за 6дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 садоводов, если будут работать с той же производительностью? С англ. яз.клубника – strawberry – переводится как «соломенная ягода».
21 слайд Описание слайда:
Описание слайда:10 кондитеров за смену могут изготовить 30 тортов. Сколько таких же тортов могут изготовить 3 кондитера за смену? ! Торт (от итал. torta, ранее от лат. tōrta, круглый хлеб)
22 слайд Описание слайда:
Описание слайда:Для получения 20,3 г сульфата бария химики взяли 12,2 г серной кислоты. Сколько сульфата бария получат химики если возьмут 36,6 г серной кислоты?
23 слайд Описание слайда:
Описание слайда:СУЛЬФАТ БАРИЯ 20,3 г. Х г. СЕРНАЯ КИСЛОТА 12,2 г. 36,6 г. Х= Х = 60,9(г.)сульфата бария получится. Ответ: 60,9 г.
24 слайд Описание слайда:
Описание слайда:1. Укажите пропорции, составленные верно: 1)5:10=2:4 3)6:4=3:2 5) 6:3=2:4 2)5:10=10:5 4)8:4=6:3 6)3:2=6:4 2.Найдите неизвестный член пропорции 15:7=х:28. 3. 6 учеников пропололи грядку за 8 часов. За сколько часов выполнят эту работу 4 ученика? 4. 4 девочки посадили 12 кустов роз. Сколько кустов роз посадят за то же время 6 девочек? Выберите и решите любые два задания. Остальные – дополнительно на двойных листах!
25 слайд Описание слайда:
Описание слайда:Задача№1. За два дня Ваня прочитал 63 страницы книги. В первый день он прочитал 4 ⁄ 9 всей книги. Сколько страниц прочитал Ваня каждый день? Задача №2. Дети за два дня посадили 64 дерева.Сколько деревьев было посажено каждый день, если число дер. пропорционально числам 3 и 5 ?
26 слайд Описание слайда:
Описание слайда:1. Найдите отношение: а) 63 к 3; б) 4 к 20. 2. В классе 25 учащихся. Из них 15 мальчиков, остальные девочки. Какую часть учащихся составляют мальчики, а какую – девочки? 3. Урок – 40 мин. Самостоятельная работа длилась 10 мин. Какую часть урока заняла самостоятельная работа? 4. Из пункта А в пункт В автомобиль ехал 1 час 20 минут, обратный путь он проехал с той же скоростью за 80 минут. Почему? 5. Что идет не двигаясь?
27 слайд Описание слайда: 28 слайд
Описание слайда: 28 слайд  Описание слайда: 29 слайд
Описание слайда: 29 слайд  Описание слайда:
Описание слайда:внимание!!! До скорых встреч !!!

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Краткое описание документа:
Древние греки использовали законы пропорции для строительства зданий. Красивейшее произведение древнегреческой архитектуры – Парфенон – построено в V в. до н. э. При строительстве фасада этого здания использовано золотое сечение. Египтяне использовали золотое сечение при строительстве пирамид. Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей.
Древнегреческие математики с помощью пропорций решали задачи, которые в настоящее время решают с помощью уравнений, выполняли алгебраические преобразования, переходя от одной пропорции к другой.
Роль теории пропорции заметно уменьшилась после того, как было осознано, что отношение величин является числом (может быть, иррациональным), а поэтому пропорция – это равенство чисел. Это позволило вместо пропорции использовать уравнения, а вместо преобразований пропорций – алгебраические преобразования.
Общая информация
Номер материала: 399888
Похожие материалы
Оставьте свой комментарий
МКОУ «Гимназия №1 г. Майский», КБР
6 класс
Учитель математики высшей категории:
Гейваронская М.М.
2017-2018г
Дата: 16.04.2018
Тема: Решение задач с помощью пропорций.
Предварительная подготовка к уроку: Учащиеся должны знать следующие темы:
«Отношения», «Пропорции», «Прямая пропорциональная зависимость», «Обратная пропорциональная зависимость»; владеть навыками работы с пропорциями..
Тип урока: урок освоения и систематизации полученных знаний.
Технологии: здоровьесбережения, поэтапного формирования умственных действий, развития исследовательских умений, дифференцированного подхода в обучении.
Решаемые проблемы: 1) Выработка навыков решения задач, содержащих обратно пропорциональные величины 2) Закрепление навыков и умений решения пропорций.
Виды деятельности: фронтальная работа с классом, работа с текстом учебника, работа в четверках, текущий тестовый контроль, работа у доски, комментирование домашнего задания.
Планируемые результаты: выработать схему решения задач с помощью пропорций; правильно использовать при решении задач либо пропорцию, либо равенство произведений соответствующих величин.
Оборудование: примеры для устной работы на доске, листы с заданиями (без решения), задания для работы в четверках, интердоска, карточки с тестами.
…Владение математикой – умение решать задачи,
причем не только стандартные, но и требующие…
оригинальности, изобретательности.
Д. Пойа.
Ход урока.
I Дети, как вы думаете, какая тема сегодня нашего урока? Давайте проведём фрагмент игры к доске (выходят 3 человека как в телепередаче «Своя игра»). На доске перечень тем:
«Животный мир КБР»
«Обыкновенные дроби»
«Монеты государств»
«Делимость чисел на 3, 9 и 25»
«Музыкальные инструменты»
«Решение задач с помощью пропорций»
«Отношение двух чисел».
Ученики поочереди выбрасывают темы.
Исключить темы, которые не относятся к математике, отбросить те, которые вы изучили. Почему вы думаете, что эта тема сегодня на уроке? Какие задачи вы уже умеете решать, где встречаются пропорции?
Как вы думаете, какие задачи вы должны решить для достижения цели урока. Выработаем алгоритм для решения задач, где встречаются обратно – пропорциональные величины, научимся строить логические цепочки рассуждений, попытаться составить схему решения задач с помощью пропорций.
II Устная работа.
Ну – ка в сторону карандаши
Ни костяшек, ни ручек, ни мела!
Устный счет мы творим это дело,
Только силой ума и души.
Цифры сходятся где то во тьме
И глаза начинают светится
И кругом только умные лица
Потому что считаем в уме!
Задача №1. В корзине 15 яблок и 30 груш. Какую часть всех фруктов составляют яблоки? Какую часть от числа груш, составляют яблоки?
Задача №2 Указать верные пропорции (на доске пропорции)
А) 2 : 7= 5 : 16 В) 4 : 9 = 8 : 18 Д) 8 : 3 = 16 : 6
Б) 6: 5= 3 : 4 Г) 3 : 2 = 15 : 10
Задача №3. Найти неизвестный член пропорции.
А) 2 / 20 = X / 40 Б) X / 18 = 0,1 / 6
Задача №4. Указать какие величины являются прямо – пропорциональными:
А) Рост ребенка и его возраст
Б) Масса бруска и его объем
В) Периметр квадрата и длина его стороны.
III Работа с учебником. Откройте учебник п. 36 № 1053
Вопросы к задаче: 1) О каких величинах идёт речь?
2) Обозначить искомую величину через Х и составить уравнение.
3) Решить уравнение и ответить на вопрос задачи.
16 с. — 21 чел.
Х с. — 14 чел.
16 * 21 = х * 14
Х = (16* 21)/ 14 = 24 с.
Ответ: 24 солдата
IV Дополнительный материал. (Учитель читает условие задачи). Для перевозки груза потребовалось 14 машин грузоподъемностью 4, 5 т. Сколько потребуется машин грузоподъемностью 7 т. для перевозки этого же груза?
Учитель задает вопросы по условию задачи.
14 м. — 4, 5 т.
Х м. — 7т.
14 * 4, 5 = х * 7
Х = ( 14 * 4,5) / 7 = 9 м.
Ответ: 9 машин.
V Физкультминутка
VI Тесты (на партах задания тестов для каждого ученика по вариантам. Взаимопроверка тестов в парах.)
А1 Найти отношение
7 г к 2 кг. 7 см к 3 м.
1) 7 : 200 3) 7 : 200 1) 7 : 3 3) 300 : 7
2) 7 : 2 4) 2000 : 7 2) 7 : 30 4) 7 : 3000
А2 Какие из чисел являются крайними членами пропорции
3/5=15/25 7/11=14/22
- 3 и 25 1) 7 и 22
- 5 и 15 2) 11 и 14
- 3 и 15 3) 7 и 14
- 5 и 25 4) 11 и 22
А3 Найти процентное отношение
3,6 к 6 2,5 к 20
1) о,6% 1) 8%
2) 60% 2) 1/8%
3) 1,7% 3) 12,5%
4) 50% 4) 125%
В1 В классе 17 мальчиков и 12 девочек. Какую часть класса составляют девочки?
В хоре 35 девочек и 19 мальчиков. Какую часть хора составляют мальчики?
С1 При каком значении х верна пропорция?
Х+1 2 3 х+2
6 3 4 8
Работа в четверках.
1)Из следующих равенств составьте пропорции:
А) 45*2=15*6
Б) 8*9=24*3
В)6*8=12*4
Г)2*42=21*4
Д)10*6=15*4
Е)15*3=4*9
2) Из данных чисел составить пропорцию
A) 7,3,21,9,15
Б) 40,15,4,10,16
В) 9,1,9,81,12
Г) 7,8,35,40,11
Д) 0,4; 1,6; 8; 2; 7
Е) 24,5,8,12,4
3 Решить пропорцию:
А) 0,3/ х= 0,6/10
Б) 7/3=21/х
В) х/40= 7/35
Г) 1,6/8=х/2
Д) 28/х=7/5
Е) 36/х=90/180
Обобщение урока:
Дети вернемся к нашей задаче в начале урока. Давайте попробуем составить схему решения задач на пропорции.
Схема решения задач ( вставить лист)
Рефлексия
Ребята, вам понравился сегодня урок? Что нового вы узнали на уроке? Давайте назовем самых активных учеников на уроке. Кто сегодня работал лучше всех? Как себя оцениваете( учитель поднимает учеников). А над чем надо поработать дома. Какие вопросы отработать с учебником.
Учитель отмечает активных и средне активных, слабых учеников, указывает ошибки ответов. Выставляет оценки детям.
Домашнее задание: п36, №1055, 1063. Творческое задание:придумать одну задачу с обратно пропорциональными величинами( В-1), с прямо пропорциональными величинами ( В-2) и оформить ее с рисунком. Подготовить презентацию по теме «Отношения вокруг нас» 4-5 слайдов.
Дети, спасибо за урок. Звенит звонок
Окончен урок
Но помни всегда
Ученье- свет,
А не учение- тьма.
Литература
- Мастерская учителя математики. Н.Л. Барсукова
- «Открытые уроки математики 5-6 кл.» М: ООО «Вако» 2010г
- «Математика. Итоговые уроки» 5-9 классы О.В. Бощенко. Волгоград 2008г
- Л. Короткова, Н. Савинцева Математика 6 кл. рабочая тетрадь. Тесты Москва 1999
- ФГОС контрольно-измерительные материалы. Математика 6 кл Л.П. Попова М: ООО «Вако» 2012г
- Библиотека «Первое сентября» Я иду на урок математики. 6 кл Москва 2001г
- А.В. Шевкин «Сборник задач по математике 5-6 кл. Москва «Русское слово- РС» 2011г
- И.И. Зубарева. А.Г. Мордкович математика 6 кл. Мнемозина 2017 г.
Тестовая работа
В-I
А1 Найти отношение
7 г к 2 кг.
1) 7 : 2000 2) 7 : 2 3) 7 : 200 4) 2000 : 7
А2 Какие из чисел являются крайними членами пропорции
=
- 3 и 25 2)5 и 15 3)3 и 15 4)5 и 25
А3 Найти процентное отношение
3,6 к 6
1) 0,6% 2) 60% 3) 1,7% 4) 50%
В1 В классе 17 мальчиков и 12 девочек.
Какую часть класса составляют девочки?
С1 При каком значении х верна пропорция?
=
_________________________________________________________
Тестовая работа
В-II
А1 Найти отношение
7 см к 3 м.
1) 7 : 3 2) 7 : 300 3) 300 : 7 4) 7 : 3000
А2 Какие из чисел являются крайними членами пропорции
=
1) 7 и 22 2) 11 и 14 3) 7 и 14 4) 11 и 22
А3 Найти процентное отношение
2,5 к 20
1) 8% 2) 1/8% 3) 12,5% 4) 125%
В1. В хоре 35 девочек и 19 мальчиков. Какую часть хора составляют мальчики?
С1 При каком значении х верна пропорция?
=
Работа в группах
Группа I
1)Из следующих равенств составьте пропорции:
45*2=15*6
2) Из данных чисел составить пропорцию
7, 3, 21, 9, 15
3) Решить пропорцию:
=
_________________________________________________________
Группа II
1)Из следующих равенств составьте пропорции:
8*9=24*3
2) Из данных чисел составить пропорцию
40, 15, 4, 10, 16
3) Решить пропорцию:
=
__________________________________________________________
Группа III
1)Из следующих равенств составьте пропорции:
6*8=12*4
2) Из данных чисел составить пропорцию
9, 1, 9, 81, 12
3) Решить пропорцию:
=
Группа IV
1)Из следующих равенств составьте пропорции:
2*42=21*4
2) Из данных чисел составить пропорцию
7, 8, 35, 40, 11
3) Решить пропорцию:
=
Группа V
1)Из следующих равенств составьте пропорции:
10*6=15*4
2) Из данных чисел составить пропорцию
0,4; 1,6; 8; 2; 7
3) Решить пропорцию:
=
_________________________________________________________
Группа VI
1)Из следующих равенств составьте пропорции:
12*3=4*9
2) Из данных чисел составить пропорцию
24, 5, 8, 12, 4
3) Решить пропорцию:
=
Устная работа | Проверьте верность равенств: 1). (Б) 4,4 : 2/7=7 : 5/11 2) (У) 8/9 : 11/3 = 0,2 : 0,3 3) (М) 7,2 : 0,08 = 63:0,7 4) (И) 0,48/0,06 =24/3 5) (Ё) 1,2 : 0,04 = 15:0,5 6) (С) 1,5:5=0,6:2 Что за равенства записаны на доске? Что такое пропорция? Какие вы знаете пропорциональные величины? Это какие величины? А еще? Это что за величины? Где применяются понятия прямой и обратной пропорциональности? А как вы думаете, как будет называться тема нашего с вами урока? Молодцы? А чем мы будем заниматься на уроке? Открываем тетради записываем число и тему урока: «Решение задач с помощью пропорций» А теперь давайте вернемся к нашим равенствам, поставьте результаты вычислений в порядке убывания. А теперь поставьте под вычислениями буквы соответствующих примеров, какое слово вы получили? Вы знаете кто такой Мёбиус? А́вгуст Фердина́нд Мёбиус — немецкий математик, механик и астроном-теоретик. Давайте послушаем сообщение об этом замечательном ученом и его открытиях, а так же где они используются и применяются. |
Все равенства верные. -Пропорции. Пропорция – это верное равенство двух отношений. -обратно пропорциональные. — это величины такие, что при увеличении одной вторая уменьшается и наоборот. -прямо пропорциональные — это величины такие, что при увеличении одной вторая тоже увеличивается, а при уменьшении одной вторая тоже уменьшается. — эти понятия применяются в математике, точнее в задачах. — «Решение задач с помощью пропорций» — решать задачи. Открывают тетради и записывают число итему урока. 90, 30, 15,4; 8, 2/3, 0,3 М Ё Б И У С — нет — ребята слушают и кратко фиксируют интересные моменты сообщения в тетради. | Работа в группах. | А теперь давайте решим с вами несколько задач. Вы слышали из сообщения, что открытие Мёбиуса «Лента или лист Мёбиуса» используется авторами фантастических литературных произведений. Например, «Двери на песке» (линию метро построили в форме ленты Мёбиуса и поезда там пропадали по два месяца). ЗАДАЧА №1. Поезд №86 проехал 120 километров со скорость 40км/ч, а поезд №143 ехал со скорость 50 км/ч. Какое расстояние проехал поезд №143 за тоже время, что и поезд №86? ЗАДАЧА №2. Поезд №86 ехал со скорость 40 км/ч и за 3,5 часа проехал такое же расстояние, что и поезд №143. Найти время в пути поезда №143 если он ехал со скоростью 50 км/ч. Эти задачи вы решаете в группах с помощью пропорций и строите диаграмму к задаче на обратную пропорциональность. Но сначала давайте вспомним алгоритм решения задач с помощью пропорций. Ребята к какой задаче составляем диаграмму? Давайте вспомним алгоритм построение диаграмм в программе XL. Капитаны групп оцените вклад каждого участника в достижение целей вашей группы. Мы решали с вами задачи о блуждающих поездах, а давайте попробуем представить этот путь. У вас на столах лежат листы бумаги с разметкой. Необходимо склеить лист, соединив стрелочки. Поставьте точку на получившейся фигуре и начинайте вести линию, что вы заметили? | -1. Внимательно прочитать условие и вопрос задачи. 2. Установить вид зависимости. 3. Проверить соответствие единиц. 4. Обозначить неизвестное за Х. 5. Составить таблицу по условию. 6. Записать пропорцию. 7. Решить получившееся уравнение. 8. Ответить на вопрос задачи. №1 120 км — 40 км/ч Х — 50 км/ч 120/х = 40/50 х=120*50/40 х=150 Ответ: 150 км. №2. 40 км/ч —-3,5 ч 50 км/ч ——х 40/50 =х/3,5 х=2,8 Ответ: 2,8 часа. — ко второй.
Строят диаграммы. Оцениваю с комментированием. — склеивают. — линия проходит непрерывно по двум сторонам, заканчиваясь в начальной поставленной точке. | Рефлексия. | Что нового вы узнали на уроке? Составьте синквейн к нашему уроку. Оцените свою работу на уроке. Давайте запишем домашнее задание: попробуйте разукрасить свой лист Мёбиуса и придумайте две задачи из материала сегодняшнего урока. | Синквейн:
Выставляют оценки в виде карточек «все понял» — зеленая «понял, но есть затруднения » — желтая «не понял» — красная. |
Устная работа | Проверьте верность равенств: 1). (Б) 4,4 : 2/7=7 : 5/11 2) (У) 8/9 : 11/3 = 0,2 : 0,3 3) (М) 7,2 : 0,08 = 63:0,7 4) (И) 0,48/0,06 =24/3 5) (Ё) 1,2 : 0,04 = 15:0,5 6) (С) 1,5:5=0,6:2 Что за равенства записаны на доске? Что такое пропорция? Какие вы знаете пропорциональные величины? Это какие величины? А еще? Это что за величины? Где применяются понятия прямой и обратной пропорциональности? А как вы думаете, как будет называться тема нашего с вами урока? Молодцы? А чем мы будем заниматься на уроке? Открываем тетради записываем число и тему урока: «Решение задач с помощью пропорций» А теперь давайте вернемся к нашим равенствам, поставьте результаты вычислений в порядке убывания. А теперь поставьте под вычислениями буквы соответствующих примеров, какое слово вы получили? Вы знаете кто такой Мёбиус? А́вгуст Фердина́нд Мёбиус — немецкий математик, механик и астроном-теоретик. Давайте послушаем сообщение об этом замечательном ученом и его открытиях, а так же где они используются и применяются. |
Все равенства верные. -Пропорции. Пропорция – это верное равенство двух отношений. -обратно пропорциональные. — это величины такие, что при увеличении одной вторая уменьшается и наоборот. -прямо пропорциональные — это величины такие, что при увеличении одной вторая тоже увеличивается, а при уменьшении одной вторая тоже уменьшается. — эти понятия применяются в математике, точнее в задачах. — «Решение задач с помощью пропорций» — решать задачи. Открывают тетради и записывают число итему урока. 90, 30, 15,4; 8, 2/3, 0,3 М Ё Б И У С — нет — ребята слушают и кратко фиксируют интересные моменты сообщения в тетради. | Работа в группах. | А теперь давайте решим с вами несколько задач. Вы слышали из сообщения, что открытие Мёбиуса «Лента или лист Мёбиуса» используется авторами фантастических литературных произведений. Например, «Двери на песке» (линию метро построили в форме ленты Мёбиуса и поезда там пропадали по два месяца). ЗАДАЧА №1. Поезд №86 проехал 120 километров со скорость 40км/ч, а поезд №143 ехал со скорость 50 км/ч. Какое расстояние проехал поезд №143 за тоже время, что и поезд №86? ЗАДАЧА №2. Поезд №86 ехал со скорость 40 км/ч и за 3,5 часа проехал такое же расстояние, что и поезд №143. Найти время в пути поезда №143 если он ехал со скоростью 50 км/ч. Эти задачи вы решаете в группах с помощью пропорций и строите диаграмму к задаче на обратную пропорциональность. Но сначала давайте вспомним алгоритм решения задач с помощью пропорций. Ребята к какой задаче составляем диаграмму? Давайте вспомним алгоритм построение диаграмм в программе XL. Капитаны групп оцените вклад каждого участника в достижение целей вашей группы. Мы решали с вами задачи о блуждающих поездах, а давайте попробуем представить этот путь. У вас на столах лежат листы бумаги с разметкой. Необходимо склеить лист, соединив стрелочки. Поставьте точку на получившейся фигуре и начинайте вести линию, что вы заметили? | -1. Внимательно прочитать условие и вопрос задачи. 2. Установить вид зависимости. 3. Проверить соответствие единиц. 4. Обозначить неизвестное за Х. 5. Составить таблицу по условию. 6. Записать пропорцию. 7. Решить получившееся уравнение. 8. Ответить на вопрос задачи. №1 120 км — 40 км/ч Х — 50 км/ч 120/х = 40/50 х=120*50/40 х=150 Ответ: 150 км. №2. 40 км/ч —-3,5 ч 50 км/ч ——х 40/50 =х/3,5 х=2,8 Ответ: 2,8 часа. — ко второй.
Строят диаграммы. Оцениваю с комментированием. — склеивают. — линия проходит непрерывно по двум сторонам, заканчиваясь в начальной поставленной точке. | Рефлексия. | Что нового вы узнали на уроке? Составьте синквейн к нашему уроку. Оцените свою работу на уроке. Давайте запишем домашнее задание: попробуйте разукрасить свой лист Мёбиуса и придумайте две задачи из материала сегодняшнего урока. | Синквейн:
Выставляют оценки в виде карточек «все понял» — зеленая «понял, но есть затруднения » — желтая «не понял» — красная. |
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Решение задач с помощью пропорции Разработка урока: Султанова Светлана Альбертовна, учитель математики МБОУ лицей г.Янаул муниципального района Янаульский район Республики Башкортостан
2 слайд Описание слайда:
Описание слайда:Базовый учебник: Математика 6 класс: учебник для общеобразовательных учреждений/ Н.Я.Виленкин и др.– М.: Мнемозима, 2009. Тип урока: урок закрепления знаний. Формы работы учащихся: фронтальная, индивидуальная. Необходимое техническое оборудование: компьютер, мультимедийный проектор, интерактивная доска. Цель урока: закрепление алгоритма решения задач с помощью пропорций, формирование навыка решения задач данного типа.
3 слайд Описание слайда:
Описание слайда:Задачи: — обучающие: Повторить алгоритм решения задач с помощью пропорций. Формирование навыка определения типа пропорциональной зависимости, описываемой в задаче. -развивающие: Развитие умений в применении знаний в конкретной ситуации. Развитие логического мышления, умения выделять главное, проводить обобщение, делать верные логические выводы. Развитие умений сравнивать, правильно формулировать задачи и излагать мысли. Развитие самостоятельной деятельности обучающихся. Развитие познавательного интереса. -воспитательные : Воспитание умения работать в коллективе, культуры общения, взаимопомощи. Воспитывать ответственность за результаты своего труда.
4 слайд Описание слайда:
Описание слайда:Что такое пропорция? Сформулируйте основное свойство пропорции. Как найти неизвестный крайний член пропорции? Как найти неизвестный средний член пропорции?
5 слайд Описание слайда:
Описание слайда:Повторим, какие величины называются прямо пропорциональными и обратно пропорциональными: Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
6 слайд Описание слайда:
Описание слайда:Задача 1. Из 6 кг помидоров получают 2 л томатного соуса. Сколько литров соуса можно получить из 54 кг помидоров? 6 кг помидоров – 2 л соуса 54 кг помидоров – х л соуса Решение: 54 : 6 = х : 2 х = 54 * 2 : 6 х = 18. Ответ: 18 л соуса.
7 слайд Описание слайда:
Описание слайда:Задача 2. 8 одинаковых труб заполняют бассейн за 25 минут. За сколько минут заполнят бассейн 10 таких труб? 8 труб – 25 минут 10 труб – х минут Решение: 10 : 8 = 25 : х х = 8 * 25 : 10 х = 20. Ответ: за 20 минут.
8 слайд Описание слайда:
Описание слайда:Решите самостоятельно. Задача 3. Из 5 кг свежих слив получается 1,5 кг чернослива. Сколько чернослива получится их 17 кг свежих слив? Ответ: 5,1 кг чернослива. Задача 4. Шесть маляров могут выполнить некоторую работу за 18 дней. Сколько еще маляров надо пригласить, чтобы работа была выполнена за 12 дней? Ответ: трех маляров нужно пригласить.
9 слайд Описание слайда:
Описание слайда:Решаем вместе – задачи на движение. Задача 5. Велосипедист за 3ч проезжает 75 км. За сколько времени проедет велосипедист 125 км с той же скоростью? Ответ: за 5 часов. Задача 6. На путь от одного поселка до другого со скоростью 12,5 км/ч велосипедист затратил 0,7 ч. С какой скоростью он должен ехать, чтобы преодолеть этот путь за 0,5 ч? Ответ: 17,5 км/ч.
10 слайд Описание слайда:
Описание слайда:Физкультминутка Из-за парт мы быстро встали И на месте зашагали. А потом мы улыбнулись, Выше-выше потянулись. Сели – встали, сели – встали За минутку сил набрались. Плечи ваши распрямите, Поднимите, опустите, Вправо, влево повернитесь И за парту вновь садитесь.
11 слайд Описание слайда:
Описание слайда:Решаем вместе – задачи на проценты. Задача 7. Весной при проведении работ по озеленению города на улице посадили липы. Принялось 95% всех посаженных лип. Сколько посадили лип, если принялось 57 лип? Ответ: посадили 60 лип. Задача 8. Содержание соли в растворе составляет 32%. а) Сколько килограммов соли содержится в 75 кг раствора? б) Сколько килограммов раствора необходимо взять, чтобы он содержал 12,8 кг соли? Ответ: а) 24 кг соли. б) 40 кг раствора.
12 слайд Описание слайда:
Описание слайда:Задачи на части. Решаем вместе. Задача 9. В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5 т железа? Ответ: 31,5 т примесей Решите самостоятельно. Задача 10. В кулинарной книге написано, что для варенья из малины на 3 части ягод надо взять 2 части сахара. Сколько сахара надо взять на 9 кг ягод? Ответ: 6 кг сахара.
13 слайд Описание слайда:
Описание слайда:Решите самостоятельно. Задача 11. Воду из котлована планировалось откачать за 30 дней с помощью 24 насосов. а) сколько таких же насосов необходимо добавить, чтобы откачать воду за 20 дней? б) На сколько дней замедлится работа, если 6 насосов вышли из строя? Ответ: а) 12 насосов нужно добавить; б) на 10 дней замедлится работа.
14 слайд Описание слайда:
Описание слайда:Домашнее задание. Придумайте две задачи: одну на прямую и одну на обратную пропорциональные зависимости.
15 слайд Описание слайда:
Описание слайда:Интернет-ресурсы: Источник шаблона: Ранько Елена Алексеевна, учитель начальных классов МАОУ лицей №21 г.Иваново, http://pedsovet.su/ Источники рисунков: http://zance.ru/docs/2800/index-2115843.html http://www.ipgg.nsc.ru/CONFERENCES/Pages/default.aspx http://vector-images.com/clipart/clp497585/?lang=rus http://alik.forumrpg.ru/viewtopic.php?id=587 http://ru.123rf.com/photo_8757480_painter-with-and-paint-illustration-isolated-on-white-background.html http://picsfab.com/image/similars?id=50392

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-402721
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Урок – игра.
Урок в 6 классе по теме: Решение задач с помощью пропорции.
Цель урока:
повторить и закрепить правила решения задач на прямиую и обратную пропорциональности;
проверить умение учащихся решать задачи на данную тему;
проверить умение находить член пропорции
Задачи урока:
обучающая: повторить и закрепить понятие «пропорция», систематизировать знания по теме;
воспитывающая: воспитывать ответственность, организованность, трудолюбие, аккуратность
развивающая: развивать познавательный интерес учащихся, желание познавать новое
Методы: словесный, наглядный, практический.
Тип урока: комплексного применения знаний, умений и навыков
Оборудование урока: мультимедиа, презентация Power Point
План урока:
Организационный момент
Вступительное слово учителя
Устная работа
Решение задач
Физкультминутка
Решение задач (продолжение)
Самостоятельная работа
Итог урока
Домашнее задание.
Ход урока.
I.Организационный момент.
II.Вступительное слово учителя.
Здравствуйте, ребята! Сегодня у нас необычный урок, урок-путешествие.
Слайд №1
А про какой стране мы будем путешествовать, узнаем, разгадав ребус.
Слайд№2
Это слово «пропорция» и путешествовать мы будем по стране «Пропорция».
Тема урока: (записать в тетрадь)Решение задач с помощью пропорции.
Слайд №3
Цель урока: Проверить умение находить неизвестный член пропорции и решать задачи с помощью пропорции.
Данная тема служит основой для решения многих задач практического характера. Путешествуя сегодня, мы встретимся с людьми различных профессий, с различных предприятий, познакомимся с продукцией этих предприятий, ведь задачи, решения которых сводятся к составлению пропорции, встречаются у людей любой профессии.
Поэтому девиз нашего урока: ЧЕМ БОЛЬШЕ Я ЗНАЮ, ТЕМ БОЛЬШЕ УМЕЮ
Слайд №4
План путешествия: Слайд№5
Край математических знаний
Станция «Хлебокомбинат»
Станция «Строительная»
Станция «Сахарный завод»
Математическая таможня (с/р)
Итак, в путь!
III.Устная работа.
Край математических знаний Слайд №6
Устная работа.
1.Кроссворд. Решите кроссворд и вы узнаете, что означает слово «пропорция» 
Слайд№7
1. Частное двух чисел. (отношение)
2. Равенство двух отношений. (пропорция)
3. Члены а и d пропорции а:b = c:d называются… (крайние)
4. Члены b и с пропорции = называются… (средние)
5. Часть прямой. (отрезок)
6. Результат деления . (частное)
7. Результат сложения. (сумма)
2.Какие из данных равенств являются пропорциями? Слайд№8
Вопросы: Почему первое равенство не является пропорцией?
Как проверить, что второе равенство является пропорцией?
3. Верните в окошко «сбежавшее» число, чтобы получилась верная пропорция
Слайд№9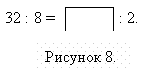
Вопросы: — прочитайте пропорцию
— проверьте верна ли пропорция двумя способами
— назовите крайние и средние члены
4. Проверьте, правильно ли найден неизвестный член пропорции: слайд№10
25∶3=3∶у
у=
у=25
Вопросы: — как найти неизвестный крайний член пропорции? (нужно найти
произведение средних членов и разделить на известный крайний)
— Найдите правильный ответ ()
Учитель: так как следующие станции связаны с решением задач практического характера, давайте вспомним:
— Какие величины называются прямо пропорциональными?
— Какие величины называются обратно пропорциональными?
VI.Решение задач.
Следующий пункт путешествия:
Станция «Хлебокомбинат» Слайд №11
Решает ученик у доски, остальные в тетрадях.
Задача. При выпечке хлеба из килограмма ржаной муки пекарь получает 1,4 кг хлеба. Сколько килограммов муки расходуется на выпечку 21 ц хлеба?
Решение. Пусть х кг муки расходуется на выпечку 21 ц хлеба.
1кг – 1,4 кг
Х кг – 2100 кг
= ,
Х = 1500.
Ответ: 15 ц.
Учитель. Итак. Где мы побывали ? О какой профессии вы узнали из этой задачи?
V.Физкультминутка.
Ребята, давайте с вами отдохнем.
Раз — подняться, потянуться,
Два — нагнуть, разогнуться,
Три — в ладоши, три хлопка,
Головою три кивка.
На четыре — руки шире,
Пять — руками помахать,
Шесть — на место тихо сесть
Продолжаем решать задачи
VI.Решение задач (продолжение).
Станция «Строительная» Слайд №12
Один ученик решает на откидной доске, остальные самостоятельно в тетрадях.
Задача. Пять каменщиков могут закончить работу за 9 дней . За какое время закончат эту же работу 15 каменщиков, считая, что все они будут работать с одинаковой производительностью?
Решение. Пусть за х дней каменщики закончат работу.
5 кам. — 9 дн.
15 кам – х дн.
= .
х = 3.
Ответ: 3 дня.
Вопрос к классу: — Каким свойством пользовались при решении задачи? (свойством обратно пропорциональных величин)
— Сформулируйте.(если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины)
— В какой организации мы с вами побывали?
— Чем занимается эта организация?
— С какой профессией мы познакомились?
Станция «Сахарный завод» Слайд №13
Один ученик решает у доски с объяснением.
Задача. В сахарной свекле содержится 18,5 % сахара. Сколько сахара содержится в 50 т сахарной свеклы?
Решение. Пусть х т сахара содержится в 50 т сахарной свеклы.
50 т – 100%
х т – 18,5%
=
х = 9,25.
Ответ: 9,25 т.
Учитель. — Где мы с вами побывали?
— Какой продукт там изготавливается?
— Из чего получается сахар?
Мы подошли к последнему пункту нашего путешествия и чтобы его пройти нужно решить самостоятельную работу.
VII.Самостоятельная работа.
Математическая таможня Слайд №14
Самостоятельная работа с последующей проверкой, ответы спроецировать на экран.
1 вариантНайдите неизвестный член пропорции:
2,8∶3,2=2,1∶х
На 20 км пути автомашина расходует л горючего. Сколько горючего автомашина израсходует на 50 км пути?
2 вариант
Найдите неизвестный член пропорции:
у∶2,1=4,5∶3,5
Участок клубники 24 человека пропололи за 6 дней. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?
Слайд №15
Ответы:
х=2,48 литров
у=2,7
4 дня
VIII.Итог урока.
С какими профессиями мы познакомились на уроке?
Что такое пропорция?
Сформулируйте основное свойство пропорции?
Какие величины называются прямо пропорциональными?
Какие величины называются обратно пропорциональными?
IX.Домашнее задание Слайд №16
Придумайте дома две новые станции, две задачи и решите их.
А закончим урок словами С. Маршака: Слайд №17
Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будет ум у вас,
А сердце умным будет.
С. Маршак
Резерв.
Переставьте буквы в словах так, чтобы получились слова, связанные с математикой. Слайд №18
ТИР три
СЛЮП плюс
СОЛИЧ число
Найдите общую час трех слов, которая состоит из 2 букв. Слайд № 19
Ответ: ВА
Учащиеся решают задачи, используя уравнения вида x + p = q и px = q , а также задачи, связанные с пропорциями.
Учащиеся расширят свои знания о написании выражений для написания уравнений. Уравнение — это утверждение, что два выражения эквивалентны. Студенты напишут два эквивалентных выражения, которые представляют одинаковое количество.Одно выражение будет числовым, а другое — переменной.
Важно, чтобы, когда студенты пишут уравнение, они точно определяли переменную. Например, n представляет количество минут, которые Aiko побежал, или x представляет количество ящиков на полке.
Затем ученики решают уравнения и тем самым решают задачи.
Студенты будут решать проблемы пропорций, решая уравнения. Это имеет смысл, потому что такая пропорция, как xa = bc, на самом деле является просто уравнением вида xp = q , где p = 1a и q = bc.
Учащиеся также сравнят свои алгебраические решения с арифметическим решением задачи. Они увидят, например, что проблема, которая может быть решена арифметически путем вычитания 5 из 78, также может быть решена алгебраически путем решения x + 5 = 78, где 5 вычитается с обеих сторон — параллельное решение вычитания 5 из 78.
- Для решения задач используйте уравнения вида x + p = q и xp = q .
- Решить проблемы пропорций, используя уравнения.
ELL: ELL могут испытывать трудности с вербализацией своих рассуждений, особенно из-за того, что проблемы со словами сильно зависят от языка. Приспособьте ELLs, предоставляя им дополнительное время для обработки информации. Обратите внимание, что эта проблема является хорошей возможностью для ELLs развить свои навыки грамотности, поскольку она включает в себя навыки чтения, письма, аудирования и разговорной речи. Призовите студентов бросить вызов идеям друг друга и обосновать свое мышление, используя академический и специализированный математический язык.
,Решения Пропорций: Слово Проблемы | Purplemath
Purplemath
Многие проблемы со словом «пропорция» могут быть решены с помощью других методов, поэтому они могут быть вам знакомы. Например, если вы узнали об уравнениях прямой, то вы узнали о наклоне прямой линии и о том, как этот наклон иногда называют «подъемом над бегом».
Но это слово «над» подсказывает, что да, мы говорим о дроби. А это значит, что «превышение скорости» можно обсуждать в контексте пропорций.
MathHelp.com

Вы устанавливаете водосточные желоба в задней части вашего дома.В указаниях сказано, что желоба должны уменьшаться на 1 / 4 дюймов на каждые четыре фута бокового хода. Водостоки будут простираться на тридцать семь футов. Насколько ниже, чем начальная точка (то есть, насколько ниже, чем верхний предел) должен быть нижний конец желобов?
Водосточные желоба должны быть слегка наклонными, чтобы дождевая вода стекала в водосточную трубу, а затем в нее.Когда я иду от верхнего края желоба к нижнему краю, на каждые четыре фута длины, которые я иду вбок, желоба должны уменьшаться (быть ниже) на четверть дюйма. Итак, насколько должен уменьшиться водосточный желоб за тридцать семь футов? Я установлю пропорцию, используя « d », чтобы обозначить расстояние, которое мне нужно найти.
Существует переменная только в одной части моей пропорции, поэтому я могу использовать метод быстрого доступа для решения.
d = [(37) (1/4)] / 4
д = 9.25/4
д = 2,3125
Для удобства (поскольку моя рулетка не помечена в десятичных числах), я преобразую этот ответ в форму смешанного числа:
Нижний конец должен быть на 2 5 / 16 дюймов ниже верхнего конца.
Как всегда в случае с «решением» упражнений, мы можем проверить наши ответы, включив их обратно в исходную задачу.В этом случае мы можем проверить размер «капли» от одного конца дома к другому, проверяя произведения средних и крайних значений (то есть, подтверждая, что перекрестные умножения совпадают) законченной пропорции :
Преобразовав «одну четвертую» в «0,25», получим:
(0,25) (37) = 9,25
(4) (2,3125) = 9,25
Поскольку значения совпадают, пропорциональность должна быть решена правильно, и решение должно быть правильным.
Биологам необходимо приблизительно знать, сколько рыб обитает в определенном озере, но они не хотят подчеркивать или иным образом вредить рыбе, осушая или осушая озеро. Вместо этого они спустили маленькие сети в нескольких разных местах вокруг озера, поймав, пометив и выпустив 96 рыб. Неделю спустя, после того, как помеченная рыба имела возможность тщательно перемешаться с населением в целом, биологи возвращаются и снова подводят свои сети.Они ловят 72 рыбы, из которых 4 помечены. Предполагая, что улов является репрезентативным, сколько рыб живет в озере?
Насколько я знаю, биологи и управляющие парками фактически используют эту технику для оценки популяций. Идея заключается в том, что после того, как выделенное время (как мы надеемся) достаточно для циркуляции помеченной рыбы по всему озеру, эти рыбы будут равномерно смешиваться с общей популяцией.Когда исследователи поймают немного рыбы позже, отношение помеченной рыбы в образце к непомеченной представляет соотношение 96 рыб, которые они пометили, с общей популяцией.
Я буду использовать « f », чтобы обозначить общее количество рыб в озере, и установлю мои соотношения с количеством «помеченных» рыб на верху. Тогда я настрою и решу пропорцию:
Поскольку переменная находится только в одной части пропорции, я могу использовать быстрый метод для ее решения.
f = [(96) (72)] / 4
f = 6912/4
f = 1728
Это говорит мне о том, что численность населения составляет:
Еще один тип проблемы слова «пропорция» — это преобразование единиц измерения, которое выглядит следующим образом:
Сколько футов в секунду эквивалентно 60 милям в час?
Чтобы выполнить это упражнение, мне понадобятся коэффициенты пересчета, которые являются просто отношениями.(Если вы решаете проблему такого рода, то у вас должен быть доступ — например, в учебнике или в раздаточном материале — к основным коэффициентам преобразования. Если нет, то ваш инструктор, вероятно, ожидает, что вы запомните эти факторы.)
Я настрою все в длинном умножении, чтобы единицы отменялись:
Тогда мой ответ:
Обратите внимание на то, как я устанавливаю коэффициенты пересчета для моего мультипликатора (см. Выше) не обязательно стандартными способами.Например, обычно говорят «шестьдесят минут в час», а не «один час за шестьдесят минут». Так почему же я ввел коэффициент преобразования час-минута (во второй строке моих вычислений выше) как «один час на шестьдесят минут»?
Потому что при этом выстраивались дроби так, что единица «часы» в моем коэффициенте конверсии была бы отменена с «часами» в исходных «60 милях в час». Эта вещь об отмене юнитов является важной техникой, и вы должны рассмотреть ее дальше, если вам не удобно с ней.
Конкретный рецепт печенья требует 225 грамм муки для одной партии из тридцати печенья. Джейд хотел бы приготовить как можно больше печенья для предстоящей вечеринки, и единственным препятствием для него является мука (у него много сахара, яиц и т. Д.). Если у него есть 1,206 килограмма муки, и если предположить, что все печенья имеют одинаковый размер, сколько приблизительно он может сделать? (Округлить до целого числа.)
У меня есть два элемента для моей пропорции: грамм муки и количество печенья. Сначала я прочитал «граммы», когда читал упражнение, поэтому я положу «граммы» сверху в моей пропорции.
Так как отношения даны мне в терминах граммов, а не килограммов, мне нужно будет также преобразовать имеющуюся меру Джейд в «1,206 грамма». Я буду использовать « с «, чтобы обозначить число, которое я пытаюсь разобраться за «печеньки».
(грамм) / (печенье): 225/30 = 1206/ c
Поскольку у меня есть неизвестный только в одной точке в этой пропорции, я могу использовать метод быстрого доступа для решения.
с = [(1206) (30)] / 225
с = 36180/225
с = 160.8
Оооо! Теперь я понимаю, почему в инструкции сказано округлить до «подходящего» целого числа: Джейд может делать только целые куки; «восьмая точка» печенья будет маленьким кусочком, который он съест, прежде чем отправиться на вечеринку.
В то время как обычно я округлял бы это число до , чтобы получить мой полный номер ответа, в этом случае мне нужно округлить до ; другими словами, в этом контексте (а именно, что все файлы cookie имеют одинаковый размер), я должен игнорировать дробную часть (то есть десятичную часть целого числа восемь), чтобы получить желаемый ответ.
Кумар живет в Хорватии и посещает родственников в Индии. Текущий обменный курс составляет один евро (1 евро) к 80,45 индийских рупий (80,45)). Он хочет купить им подарок, который стоит 3759 фунтов стерлингов. Сколько евро будет стоить ему этот подарок? (Укажите свой ответ с точностью до двух знаков после запятой.)
Они дали мне обменный курс, который, по сути, является еще одним фактором пересчета, таким как упражнение «миль в час» выше.Так что я установлю свою пропорцию, с евро сверху, и буду использовать e , чтобы обозначить количество евро, которое ему понадобится.
(евро) / (рупии): 1 / 80,45 = и /3759
Я буду использовать ярлык для решения:
и = [(3759) (1)] / 80,45
и = 46.72467371 …
Округляя до двух знаков после запятой, Кумар будет тратить:
За исключением вышеописанного упражнения по преобразованию ставок, мы смогли решить все пропорции с помощью метода ярлыков. Скорее всего, вы также найдете это в своей домашней работе. Но всегда возможно, что у вас возникнет вопрос, где вам лучше использовать кросс-умножение.
Джордж слышал из двух разных источников о диапазоне заработной платы в конкретной компании. Один источник говорит, что отношение самой низкой заработной платы к самой высокой заработной плате составляет 3: 7. Другой источник говорит, что самый высокий заработок ежегодно приносит на 57 000 долларов больше, чем самый низкий заработок. Каковы приблизительные зарплаты для самых высоких и самых низких заработков? (Округлить до ближайшей тысячи.)
Я знаю, что соотношение составляет 3: 7, поэтому я буду использовать дробь 3/7 для одной части моей пропорции.Если самая низкая ставка заработной платы в тысячах долларов составляет л , то самая высокая — л + 57. Моя пропорция:
(низший) / (высший): 3/7 = L / ( L + 57)
Поскольку в двух частях этой пропорции есть переменные, метод ярлыков не будет столь же полезен, как перекрестное умножение, чтобы очистить все дроби. Так что я буду кросс-умножить:
3/7 = L / ( L + 57)
3 ( L + 57) = 7 L
3 L + 171 = 7 L
171 = 4 L
42.75 = L
Вспоминая, что я отбросил конечные нули и считаю тысячи, приведенное выше число означает, что самая низкая зарплата (округленная до ближайшей тысячи) составляет приблизительно 43 000 долларов. Тогда самая высокая зарплата, составляющая около 57 тыс. Долларов, составляет примерно 100 тыс. Долларов.
, наименьшее: $ 43 000,
, наивысшее: $ 100 000,
URL: https: // www.purplemath.com/modules/ratio5.htm
,Пропорции Решения
Этот урок посвящен решению пропорций с помощью перекрестного произведения для поиска неизвестных терминов.Мы также покажем некоторые принципы, специальные приемы или ярлыки, которые можно использовать для быстрого решения пропорции.
Условия, которые необходимо знать:
x, y или любая другая буква используется для обозначения неизвестного числа.
Неизвестный термин: пропущенное или неизвестное число в пропорции.
Мы увидели в уроке о пропорциях, которые мы можем использовать для перекрестных произведений, чтобы определить, пропорциональны ли доли или соотношения.
Перекрестные продукты могут также использоваться, чтобы найти неизвестный термин в пропорции. Вот как!
с / d тогда a × d = b × c |
с / d тогда a × d = b × c |
Мы проиллюстрируем это на нескольких примерах.
Пример №1:
Используя перекрестное произведение, мы получим:
5 × 16 = x × 10
80 = 10x
Если вы знаете свою таблицу умножения, вы можете быстро получить ответ.
Если 10 × x = 80, то x должно быть 8, потому что 10 × 8 равно 80.
x = 8
| Пропорция становится 5 / 8 |
Обратите внимание, что 5 × 16 = 8 × 10 = 80
Вы также можете разбить проблему на несколько этапов, если хотите, как показано ниже:
Первый перекрестный продукт: 5 × 16 = 80
Второй перекрестный продукт: 10 × x
Если равные перекрестные продукты равны, мы получим:
10 × x = 80
Существует более быстрый способ получить ответ при решении пропорций.Посмотрите на пропорцию снова:
Обратите внимание, что чтобы получить 10, 5 умножили на 2. По тому же токену, чтобы получить 16, нужно умножить что-то или число на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Пример № 2:
Используя перекрестное произведение, мы получаем:
8 × 25 = 10 × n
200 = 10n
Вместо того, чтобы спрашивать себя «10 раз, что равно 200?», Мы на этот раз решим уравнение, чтобы показать вам другое способ получить.
Разделите обе стороны на 10
200, деленное на 10 — это 20, а 10, деленное на 10 — это 1
20 = 1n
20 = n
Полезные эквивалентные пропорции, которые можно использовать при определении пропорций.
Принцип № 1:
Доказательство:
Добавьте 1 к обеим сторонам уравнения и выполните математические расчеты, как показано:
Выше может быть полезно, если вы решите
Вышеупомянутое уравнение становится
или
Вышесказанное, конечно, намного проще решить
Принцип # 2:
| знак равно Икс / 4 тогда у = 4 |
| знак равно 50 / 100 тогда у = 100 |
| знак равно Икс / Y тогда х = 18 |
Принцип № 3:
Доказательство:
Перемножение:
b × c = a × d
bc = ad
Добавьте ab к обеим сторонам уравнения
ab + bc = ab + ad
Коэффициент b слева сторона.Фактор с правой стороны.
b (a + c) = a (b + d)
Перепишите вышеприведенное как пропорцию. Это как отмена перекрестного умножения.
Почему принцип # 3 полезен при определении пропорций?
| Скажи, что у тебя есть х + 2 / 8 + 4 |
| Это эквивалентно Икс / 8 |
Опять же, последний формат выглядит дружелюбно, и его можно решить быстрее.
Просто помните эти 3 принципа при определении пропорций, и это облегчит вам упражнение с пропорциями. Спасибо за прочтение!
Мы проиллюстрируем это на нескольких примерах.
Пример №1:
Поскольку эти две доли или соотношения находятся в пропорциях, мы знаем, что перекрестное произведение должно быть равным.
Используя перекрестный продукт, мы получим:
5 × 16 = x × 10
80 = 10x
Если вы знаете свою таблицу умножения, вы можете быстро получить ответ.
Если 10 × x = 80, то x должно быть 8, потому что 10 × 8 равно 80.
x = 8
| Пропорция становится 5 / 8 |
Обратите внимание, что 5 × 16 = 8 × 10 = 80
Вы также можете разбить проблему на несколько этапов, если хотите, как показано ниже:
Первый перекрестный продукт: 5 × 16 = 80
Второй перекрестный продукт: 10 × x
Если равные перекрестные продукты равны, мы получим:
10 × x = 80
Существует более быстрый способ получить ответ при решении пропорций.Посмотрите на пропорцию снова:
Обратите внимание, что чтобы получить 10, 5 умножили на 2. По тому же токену, чтобы получить 16, нужно умножить что-то или число на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Пример № 2:Используя перекрестное произведение, мы получаем:
8 × 25 = 10 × n
200 = 10n
Вместо того, чтобы спрашивать себя «10 раз, что равно 200?», Мы на этот раз решим уравнение, чтобы показать вам другое способ получить
разделить обе стороны на 10
200, деленное на 10 — это 20, а 10, деленное на 10 — это 1
20 = 1n
20 = n
Полезные эквивалентные пропорции, которые можно использовать при определении пропорций:
Принцип # 1:
Доказательство:
Добавьте 1 к обеим сторонам уравнения и выполните математические расчеты, как показано:
Выше может быть полезно, если вы решите
Вышеупомянутое уравнение становится
или
Вышесказанное, конечно, намного проще решить
Принцип # 2:
| знак равно Икс / 4 тогда у = 4 |
Например,
| знак равно 50 / 100 тогда у = 100 |
| знак равно Икс / Y тогда х = 18 |
Принцип № 3:
Доказательство:
Перемножение:
b × c = a × d
bc = ad
Добавьте ab к обеим сторонам уравнения
ab + bc = ab + ad
Коэффициент b слева сторона.Коэффициент a с правой стороны
b (a + c) = a (b + d)
Перепишите вышеприведенное как пропорцию. Это как отмена перекрестного умножения
Почему принцип # 3 полезен при определении пропорций?
| Скажи, что у тебя есть х + 2 / 8 + 4 |
| Это эквивалентно Икс / 8 |
Опять же, последний формат выглядит дружелюбно, и его можно решить быстрее.
Просто помните эти 3 принципа при определении пропорций, и это облегчит вам упражнение с пропорциями. Спасибо за чтение
Решение викторины пропорций. Можете ли вы получить 100% по этой викторине?
Используйте этот калькулятор пропорций для решения задач пропорции
Новые уроки математики
Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.
,
