Расстояние между точками на координатной прямой | Презентация к уроку по математике (6 класс) по теме:

Слайд 1

Расстояние между точками на координатной прямой х 0 1 А В АВ = ρ (А, В)

Слайд 2

Расстояние между точками на координатной прямой Цель урока: — Найти способ (формулу, правило) для нахождения расстояния между точками на координатной прямой. — Научиться находить расстояние между точками н а координатной прямой, используя найденное правило.

Слайд 3

1. Устный счет 15 -22 +8 -31 +43 -27 -14

Слайд 4

2 . Устно решите задание с помощью координатной прямой: сколько целых чисел заключено между числами: а ) – 8,9 и 2 б ) – 10,4 и – 3,7 в ) – 1,2 и 4,6? а ) 10 б ) 8 в ) 6

Слайд 5

0 1 2 7 п оложительные числа -1 -5 о трицательные числа Расстояние от дома до стадиона 6 Расстояние от дома до школы 6 Координатная прямая

Слайд 6

0 1 2 7 -1 -5 Расстояние от стадиона до дома 6 Расстояние от школы до дома 6 Нахождение расстояния между точками на координатной прямой ρ ( -5 ; 1 )=6 ρ ( 7 ; 1 )=6 Расстояние между точками будем обозначать буквой ρ ( ро )

Слайд 7

0 1 2 7 -1 -5 Расстояние от стадиона до дома 6 Расстояние от школы до дома 6 Нахождение расстояния между точками на координатной прямой ρ ( -5 ; 1 )=6 ρ ( 7 ; 1 )=6 ρ (a; b) = ? | a-b |

Слайд 8

Расстояние между точками a и b равно модулю разности координат этих точек. ρ ( a; b)= | a-b | Расстояние между точками на координатной прямой

Слайд 9

Геометрический смысл модуля действительного числа a b a a=b b x x x Расстояние между двумя точками

Слайд 10

0 1 2 7 -1 -5 На йдите расстояния между точками на координатной прямой — 2 — 3 — 4 3 4 5 6 -6 ρ (-6 ; 2 )= ρ (6 ; 3 )= ρ (0 ; 7 )= ρ (1 ; -4 ) = 8 3 7 5

Слайд 11

0 1 2 7 -1 -5 На йдите расстояния между точками на координатной прямой — 2 — 3 — 4 3 4 5 6 -6 ρ (2 ; -6 )= ρ (3 ; 6 )= ρ (7 ; 0 )= ρ (-4 ; 1 ) = 8 3 7 5

Слайд 12

Вывод : значения выражений | a – b | и | b – a | равны при любых значениях а и b =

Слайд 13

–16 –2 0 –3 +8 0 +4 +17 0 ρ(–3; 8) = 11; |(–3) – (+8)| = 11; |(+8) – (–3)| = 11. ρ(–16; –2) = 14; |(–16) – (–2)| = 14; |(–2) – (–16)| = 14. ρ(4; 17) = 13; |(+4) – (+17)| = 13; |(+17) – (+4)| = 13. Расстояние между точками координатной прямой

Слайд 14

Найдите ρ(х; у) , если : 1 ) x = – 14, у = – 23; ρ( х ; у )=| х – у |=|–14–(– 23 )|=|–14+23|=| 9 |=9 2 ) x = 5,9 , у = –6,8; ρ( х ; у )=|5, 9 –(– 6,8 )|=|5,9+6,8|=| 12,7 |=12,7

Слайд 15

Продолжить предложение 1. Координатная прямая – это прямая с указанными на ней … 2. Расстояние между двумя точками — это … 3. Противоположные числа – это числа, … 4. Модулем числа Х называют … 5. — Сравните значения выражений a – b V b – a сделайте вывод … — Сравните значения выражений | a – b | V | b – a | c делайте вывод …

Слайд 16

Винтик и Шпунтик идут по координатному лучу. Винтик находится в точке В(236), Шпунтик – в точке Ш(193) На каком расстоянии друг от друга находятся Винтик и Шпунтик ? ρ (B, Ш ) = 43

Слайд 17

Найдите расстояние между точками А(0 ), В(1 ) А(2 ), В(5 ) А(0 ), В (- 3) А(- 10), В(1 ) АВ = 1 АВ = 3 АВ = 3 АВ = 11

Слайд 18

Найдите расстояние между точками А(- 3,5), В(1,4 ) К(1,8 ), В(4,3 ) А(- 10), С(3 )

Слайд 19

Проверка АВ = КВ = АС =

Слайд 20

С( – 5 ) С(– 3 ) Найдите координату точки — середины отрезка ВА

Слайд 21

На координатной прямой отмечены точки А (–3,25) и В (2,65). Найдите координату точки О – середины отрезка АВ. Решение : 1) ρ(А;В )= |–3,25 – 2,65| = |–5,9| = 5,9 2) 5,9 : 2 = 2,95 3) –3,25 + 2,95 = – 0,3 или 2,65 – 2,95 = – 0,3 Ответ : О(–0,3 )

Слайд 22

На координатной прямой отмечены точки С( – 5,17) и D(2,33). Найдите координату точки А – середины отрезка CD. Решение: 1 ) ρ(С; D )= |– 5 , 17 – 2, 33 | = |– 7 , 5 | = 7 , 5 2 ) 7 , 5 : 2 = 3 , 7 5 3) – 5 , 17 + 3 , 7 5 = – 1 , 42 или 2, 33 – 3 , 7 5 = – 1 , 42 Ответ: A (– 1 , 42 )

Слайд 23

Вывод: Алгоритм нахождения координаты точки – середины данного отрезка: 1. Найти расстояние между точками – концами данного отрезка = 2. Разделить результат-1 на 2 (половина величины) = с 3. Прибавить результат-2 к координате а или вычесть результат-2 из координаты а + с или — с 4. Результат-3 есть координата точки — середины данного отрезка

Слайд 24

Работа с учебником: §19, с.112, А. № 573, 575 В. № 578, 580 Домашнее задание: §19, с.112, А. № 574, 576, В. № 579, 581 подготовиться к КР «Сложение и вычитание рациональных чисел. Расстояние между точками на координатной прямой»

Слайд 25

Сегодня я узнал… Было интересно… Я понял, что… Теперь я могу… Я научился… У меня получилось… Я попробую… Меня удивило… Мне захотелось…

Слайд 26

До новых встреч!

Конспект урока математики для 6 класса «Соотношение: время, скорость, расстояние»

 

Тема: «Соотношение: скорость, время, расстояние»

Цель — закрепить умение дифференцировать нахождение времени, скорости и расстояния

Задачи:

— упражняться в нахождении скорости, времени и расстояния ;

— развивать память, внимание, мышление; расширять кругозор, обогащать словарный запас, осуществлять взаимосвязь с уроками географии;

— прививать интерес к изучению математики.

 

Оборудование: мультимедийные средства, карточки для самостоятельной работы.

План урока

I.Организационный момент.

II. Проверка домашнего задания.

III. Повторение.

IV. Устный счёт.

V. Работа с новым числовым материалом.

1.Решение задачи на нахождение расстояния.

2. Решение задачи на нахождение скорости.

3. Решение задачи на нахождение времени

4. Задание на развитие логического мышления

5.Самостоятельная работа.

VI. Домашнее задание.

VII. Итог урока. Отметки.

 

 

Ход урока.

I.Организационный момент.

— Сядут те, кто родился весной.

— Сядут те, кто родился летом.

— Сядут те, кто родился осенью.

-Ребята, которые стоят – когда вы родились? (зимой)

Запись числа, темы урока.

— Какой главный зимний праздник?

-Сегодня на уроке мы отправимся в путешествие по нашей стране.

Мы поедим в гости к Деду Морозу в Великий Устюг. (находим на карте Вологодскую область и город Великий Устюг).

СЛАЙД №1

 

II. Проверка домашнего задания. СЛАЙД №2 (стр. 131, №487(4) )

— Какое задание вы выполняли дома?

— Как вычислить расстояние?

— Какое число получилось?

III. Повторение.

Как найти расстояние, если известна скорость и время? СЛАЙД №3

2.Как найти скорость, если известно расстояние и время ? СЛАЙД №4

3. Как найти время, если известно расстояние и скорость? СЛАЙД №5

 

IV. Устный счёт.

Вычислите расстояние. Кто движется со скоростью 4 км в час?

 

 

Вычислите скорость.

 

 

— Что движется со скоростью 60 км в час? (поезд)

3. Вычислите время. Кто движется со скоростью 9 км в час? (лыжник)

 

 

V. Работа с новым числовым материалом.

 

1.Решение задачи на нахождение расстояния.

— Мы отправляемся из Саранска в Москву на поезде

Задача.

Школьники ехали из Саранска в Москву 9 часов на поезде

 со скоростью 73 км в  час. Какое расстояние прошёл поезд?

— Прогулка по Москве( просмотр слайдов №№ 14-20).

Физ. минутка.

 

2. Решение задачи на нахождение скорости. СЛАЙД №29, №30

— Из Москвы мы летим на самолёте в Великий Устюг.

 

— СЛАЙД №30, 31. Мы прилетели в Великий Устюг. Где же Дед Мороз?

— Дед Мороз живёт в своей резиденции в сосновом бору.

— Каким транспортом мы будем добираться до резиденции Деда Мороза?

— Какой транспорт используют народы севера? (олени)

 

3.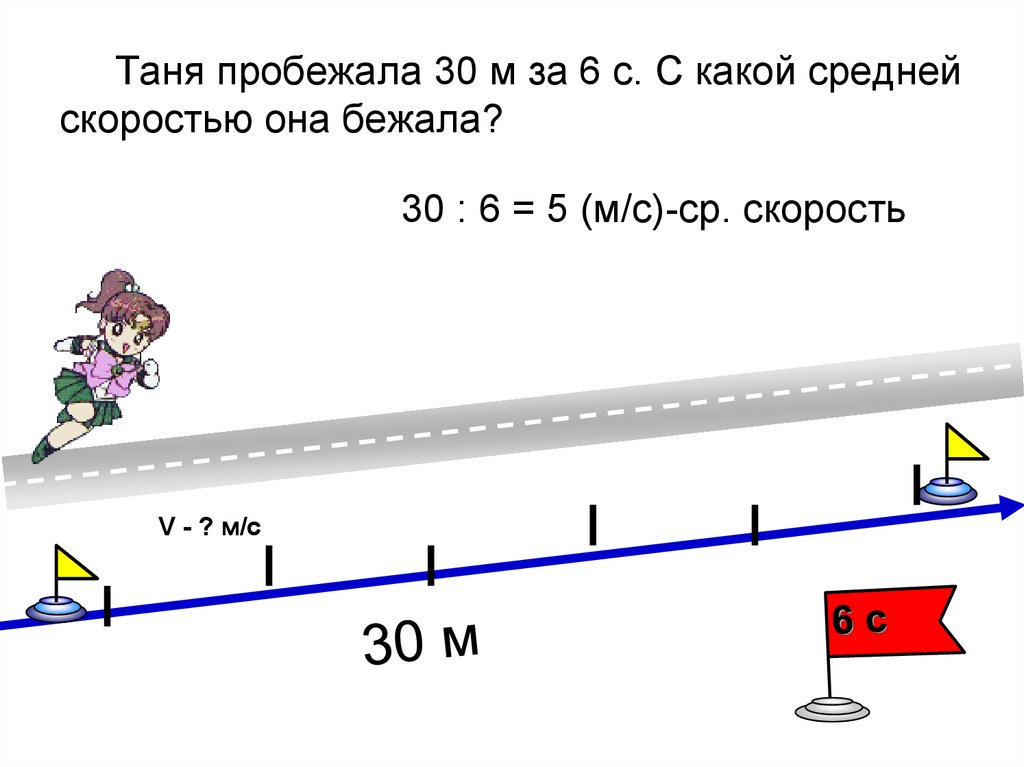 Решение задачи на нахождение времени.

4.Задание на развитие логического мышления.

— Вот Дед Мороз встречает нас в своей резиденции. Он приготовил для вас интересное задание.

 

5. Самостоятельная работа. СЛАЙД №37

 

 

Проверка самостоятельной работы.

 

VI. Домашнее задание.

VII. Итог урока. Отметки.

 

 

Математика, 6 класс, Оценка, Использование нормы для определения скорости и расстояния

CCSS.Math.Content.6.RP.A.3d 6 класс, Соотношения и пропорциональные отношения

Кластер: понимание концепций отношений и использование рассуждений об отношениях для решения задач

Стандарт: использование рассуждений об отношениях для преобразования единиц измерения; правильно манипулировать и преобразовывать единицы при умножении или делении величин.

Степень выравнивания: Без рейтинга (0 пользователей)

CCSS.Math.Content.6.RP.A.3b 6 класс, Отношения и пропорциональные отношения

Кластер: Понимание концепций соотношений и использование рассуждений об отношениях для решения задач

Стандарт: Решение задач по расценкам за единицу, в том числе связанных с ценообразованием за единицу и постоянной скоростью. Например, если на стрижку 4 газонов ушло 7 часов, то при такой скорости сколько газонов можно косить за 35 часов? С какой скоростью косили газоны?

Степень выравнивания: Без рейтинга (0 пользователей)

CCSS.Math.Content.6.RP.A.2 6 класс, Отношения и пропорциональные отношения

Кластер: Понимание концепций отношений и использование рассуждений об отношениях для решения задач к нулю) и использовать язык ставок в контексте отношений отношения. Например, «В этом рецепте соотношение 3 стакана муки и 4 стакана сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки». «Мы заплатили 75 долларов за 15 гамбургеров, что составляет 5 долларов за гамбургер». (Ожидания по удельным расходам в этом сорте ограничены несложными фракциями.)

Степень выравнивания: Без рейтинга (0 пользователей)

CCSS.Math.Content.6.RP.A.3 6 класс, Отношения и пропорциональные отношения

Кластер: понимание концепций отношений и использование рассуждений об отношениях для решения задач

Стандарт: использование рассуждений об отношениях и пропорциях для решения реальных и математических задач, например, путем рассуждений о таблицах эквивалентных отношений, ленты диаграммы, линейные диаграммы с двойным числом или уравнения.

Степень выравнивания: Без рейтинга (0 пользователей)

MCCRS.Math.Content.6.RP.A.3 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций отношений и использование рассуждений об отношениях для решения задач

Индикатор: Использование рассуждений об отношениях и пропорциях для решения реальных и математических задач, например, путем рассуждений о таблицах эквивалентные отношения, ленточные диаграммы, линейные диаграммы с двойным числом или уравнения.

Степень выравнивания: Без рейтинга (0 пользователей)

MCCRS.Math.Content.6.RP.A.2 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций соотношения и использование рассуждений об отношении для решения задач

Индикатор: Понимание концепции удельной скорости a/b, связанной с отношением a:b с b ‰äĘ 0 (b не равно нулю) и использовать язык ставок в контексте отношений отношения. Например, «В этом рецепте соотношение 3 стакана муки и 4 стакана сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки». «Мы заплатили 75 долларов за 15 гамбургеров, что составляет 5 долларов за гамбургер». (Ожидания по удельным расходам в этом сорте ограничены несложными фракциями.)

Степень выравнивания: Без рейтинга (0 пользователей)

MCCRS.Math.Content.6.RP.A.3d 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций отношений и использование рассуждений об отношениях для решения задач

Индикатор: Использование рассуждений об отношениях для преобразования единиц измерения; правильно манипулировать и преобразовывать единицы при умножении или делении величин.

Степень выравнивания: Без рейтинга (0 пользователей)

MCCRS.Math.Content.6.RP.A.3b 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций соотношений и использование рассуждений об отношениях для решения задач

Индикатор: Решение задач по расценкам за единицу, в том числе связанных с ценообразованием за единицу и постоянной скоростью. Например, если на стрижку 4 газонов ушло 7 часов, то при такой скорости сколько газонов можно косить за 35 часов? С какой скоростью косили газоны?

Степень выравнивания: Без рейтинга (0 пользователей)

WY.Math.6.RP.A.3b 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций отношений и использование рассуждений об отношениях для решения задач.

Индикатор: решение проблем со стоимостью единицы продукции, в том числе связанных с ценообразованием единицы продукции и постоянной скоростью.

Степень выравнивания: Без рейтинга (0 пользователей)

WY.Math.6.RP.A.3d 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций отношений и использование рассуждений об отношениях для решения задач.

Индикатор: используйте соотношение для преобразования единиц измерения; правильно преобразовывать единицы при умножении или делении величин.

Степень выравнивания: Без рейтинга (0 пользователей)

WY.Math.6.RP.A.3 6 класс

Область обучения: Отношения и отношения пропорциональности

Стандарт: Понимание концепций отношений и использование рассуждений об отношениях для решения задач.

Индикатор: используйте рассуждения об отношении и скорости для решения реальных и математических задач.

Степень выравнивания: Без рейтинга (0 пользователей)

WY.

Math.6.RP.A.2 6 класс

Область обучения: соотношения и пропорциональные отношения

Стандарт: Понимание концепций пропорций и использование рассуждений о пропорциях для решения проблем.

Индикатор: понимание концепции удельной ставки a/b, связанной с отношением a:b, где b ≠ 0, и использование языка ставок в контексте отношений отношения.

Степень выравнивания: Без рейтинга (0 пользователей)

Математика, 6 класс, Оценка, Использование скорости для определения скорости и расстояния

Обзор

На этом уроке учащиеся смотрят видео с бегуном и выражают его скорость в метрах в секунду. Затем учащиеся используют скорость, чтобы определить, сколько времени требуется бегуну, чтобы пройти любое расстояние.

Скорость — скорость, которая выражается как пройденное расстояние за единицу времени. Мили в час, круги в минуту и ​​метры в секунду — все это примеры единиц измерения скорости.

Меры скорости, расстояния и времени взаимосвязаны. Связь может быть выражена тремя способами: d = rt ,  r = dt ,  t = dr .

• Исследуйте скорость как скорость, которая измеряет взаимосвязь между двумя аспектами ситуации: расстоянием и временем.
• Сравнивая расстояние, скорость и время, поймите, как использовать любые две из этих мер, чтобы найти третью меру.

Предложите учащимся просмотреть видео и попытаться ответить на вопросы. Учащимся, возможно, придется посмотреть его более одного раза, чтобы понять два аспекта ситуации, отслеживаемой двойной числовой линией.

Обсудите вопросы в классе.

ELL: Помогите ELL создать свой математический словарь, постоянно моделируя использование новых терминов в контексте работы и занятий в классе. Если позволяет время, дайте возможность ELL строить свои собственные предложения, используя новый словарь.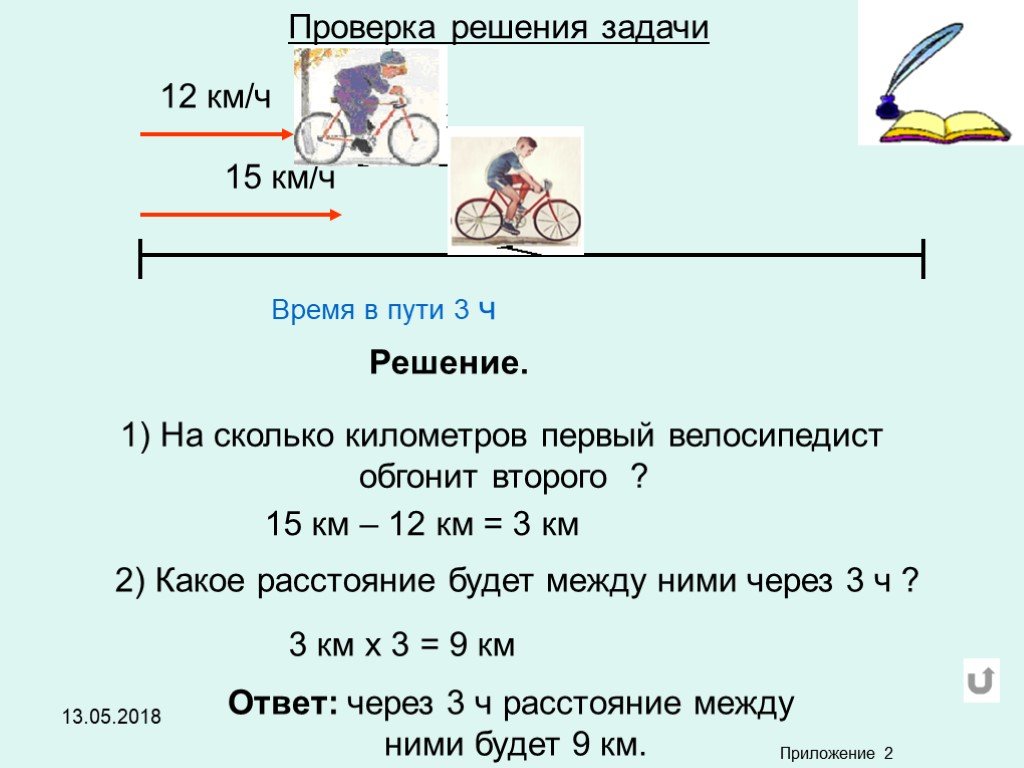

Чтобы успешно решить задачи на рабочее время, учащиеся должны быть в состоянии ответить и понять все три следующих вопроса:

1. Какие две величины вы видите в этом видео (отслеживаются числовыми линиями)?
   • Одна числовая линия показывает расстояние, которое пробегает Джейсон.
   • Другая числовая линия показывает время, которое он бежит.
2. Как двойная числовая линия показывает отношение между двумя величинами?
   • Двойная числовая линия показывает, сколько времени прошло для каждого заданного расстояния, а также расстояние, которое Джейсон пробежал за каждое заданное время.
   • Разделив любое расстояние в метрах по двойной числовой прямой на соответствующее время в секундах, мы получим следующую скорость: Джейсон бежит со скоростью 5 метров в секунду.
3. Какова скорость Джейсона в метрах в секунду?
   • 5 метров в секунду.

Обсудите эти вопросы с классом. Обсуждение должно быть коротким, но убедитесь, что все учащиеся понимают, что скорость Джейсона составляет 5 метров в секунду. Они будут использовать эту ставку в течение рабочего времени.

Открытие

Посмотрите видео и подумайте над следующими вопросами.

• Какие две величины в этом видео можно измерить?
• Как двойная числовая линия отслеживает взаимосвязь между количествами?

ВИДЕО: Джейсон бежит

Обсудить математическую миссию.

Учащиеся будут использовать скорость Джейсона, выраженную как скорость 5 метров в секунду, чтобы найти, сколько времени ему потребуется, чтобы пройти любое расстояние.

SWD: У учащихся с ограниченными возможностями могут возникнуть трудности с выполнением этой математической миссии. Подумайте, как вы можете предоставить всем учащимся доступ к этой информации управляемым способом. Один из вариантов состоит в том, чтобы разбить задачу на отдельные последовательные шаги (сначала учащиеся найдут соотношение, затем они будут использовать это соотношение, чтобы рассчитать время, необходимое для прохождения заданного расстояния).

Открытие

Объясните, как использовать скорость Джейсона, чтобы определить, сколько времени ему потребуется, чтобы пройти любое расстояние.

Учащиеся, которые закончат раньше:

• Приготовьтесь представить свою работу классу.
• Найдите другой способ решения этой задачи или покажите их решение, используя другое представление.

ELL: Для задания «Рабочее время» обязательно продемонстрируйте и устно объясните задание шаг за шагом, чтобы убедиться, что ELL понимают, что от них требуется.

Математическая практика 1: Разбираться в задачах и настойчиво решать их.

• Пока учащиеся работают, ищите учащихся, которые понимают проблемную ситуацию и понимают взаимосвязь между скоростью, расстоянием и временем.

Математическая практика 5: Стратегическое использование соответствующих инструментов.

• Определите учащихся, которые надлежащим образом используют инструмент двойной числовой линии или таблицу для представления взаимосвязи между расстоянием и временем.

Математическая практика 6: внимание к точности.

• Часы для учащихся, которые обращают внимание на точность при вычислениях или при маркировке строк и таблиц с двойными числами.

Студенту трудно начать.

• Опишите проблему своими словами своему партнеру.
• Какую информацию вы знаете?
• Что вы пытаетесь найти?
• Что означает скорость 5 метров в секунду?
• Можете ли вы использовать двойную числовую строку или таблицу, чтобы помочь вам?
• Можешь попробовать решить более простую задачу?

Ученик неправильно решил.

• Умножает 5 метров в секунду на 240 метров:
  • Ваш ответ 1200 секунд имеет смысл? Сколько минут равняется 1200 секундам?
  • Можете ли вы использовать двойную числовую строку или таблицу, чтобы подтвердить свой ответ?
  • Объясните, почему вы умножили скорость 5 метров в секунду на 240 метров.

Ученик нашел решение.

• Объясните свою стратегию решения проблемы.
• Где в вашем [диаграмме, двойной числовой строке, таблице] вы видите курс?
• Где вы видите ответ в своей [диаграмме, двойной числовой строке, таблице]?
• Можно ли было решить эту проблему другим способом? Объяснять.

• Джейсону понадобится 48 секунд, чтобы пробежать 240 метров.
• Джейсон может пробежать 275 метров за 55 секунд.
• Ответы учащихся должны включать оценку, задействованные величины, представление их решения, уравнения и два полных предложения.

Рабочее время

Джейсон бежит с постоянной скоростью 5 метров в секунду.

• Сколько времени потребуется Джейсону, чтобы пробежать 240 метров?
• Сколько метров Джейсон пробежит за 55 секунд?
• Включите в свои ответы следующее:
  • Оценка того, что, по вашему мнению, могут быть ответы
  • Величины, участвующие в задаче
  • Диаграмма, таблица, двойная числовая линия или другое представление, показывающее, почему ваше решение имеет смысл
  • Ваши уравнения, ваша работа и ваши решения
  • Два полных предложения, которые отвечают на вопросы

Подсказка:

Умножьте скорость 5 метров в секунду на количество времени, чтобы найти пройденное расстояние. Например, чтобы найти расстояние, пройденное за 20 секунд, умножьте 5 метров в секунду на 20 секунд:

20 секунд • 5 метров в секунду = 100 метров

Пока учащиеся работают, ищите ответы, в которых учащиеся:

• Умножьте скорость на расстояние. 5 метров 1 секунда⋅240 метров = 1200 секунд
• Правильно разделите расстояние на скорость. 240 метров ÷ 5 метров 1 секунда = 48 секунд
• Найдите скорость 0,2 секунды на метр и используйте ее для решения первой задачи.
  1 секунда 5 метров = 0,2 секунды на метр
  0,2 секунды 1 метр⋅240 метров = 48 секунд

Ответы

Рабочее время

Подготовьте презентацию о вашем методе решения проблемы.

• Объясните, что вы сделали по-другому, чтобы найти время по сравнению с определением расстояния.
• Используйте свою работу для подтверждения своего объяснения.

На Олимпийских играх 1996 года Майкл Дуэйн Джонсон установил мировые рекорды в беге на 200 и 400 метров. Он пробежал 200 метров за 19,32 секунды и 400 метров за 43,49 секунды.

• Рассчитайте его скорость для каждой гонки, используя коэффициент.
• В какой гонке он показал наибольшую скорость? Обоснуйте свое мышление.

Выберите различные студенческие работы с целью установления соответствия между разумными методами. К концу обсуждения учащиеся должны понять методы друг друга и понять, почему некоторые методы не сработали.

SWD: Представление о том, что три разных представления данных представляют одну и ту же информацию, может вызвать затруднения у учащихся с ограниченными возможностями. Повторяйте и закрепляйте эту идею всякий раз, когда это возможно, чтобы помочь учащимся понять и вспомнить эту важную концепцию.

Попросите студентов, которые использовали другие методы (например, таблицу, числовую прямую или деление по скорости), представить. В рамках обсуждения предложите учащимся сравнить свои представления о проблеме.

• Как [Имена] поняли суть проблемы и как математически смоделировали проблемную ситуацию? Что общего в их подходах? Что отличается?
• Какой метод помогает вам лучше всего увидеть структуру математики? Какой метод имеет для вас наибольшее значение?
• [Имя] умножить 0,2 секунды на метр на 240 метров. Почему этот метод работает? Как этот метод соотносится с делением 240 метров на 5 метров в секунду?
• Как найти расстояние, используя скорость 0,2 метра в секунду? Как этот подход соотносится с использованием скорости 5 метров в секунду для определения расстояния?
• Если учащиеся не заметят, вы можете указать, что деление любого числа в строке с числами расстояния на 5 дает соответствующее число в строке с числами времени.

В конце обсуждения напомните учащимся, что, когда скорость используется много раз, иногда у нее есть специальное название. Скорость — это скорость, которая представляет расстояние во времени. Плотность населения — это показатель, который представляет численность населения на единицу площади.

Задание на выполнение

• Во время обсуждения в классе делайте заметки о том, как решить как расстояние, так и время.
• Ответьте на вопросы о методах, которые вы использовали для решения проблемы.

Подсказка:

В присутствии одноклассников задайте такие вопросы, как:

• Где вы видите скорость 5 метров в секунду в своих методах? Где ты видишь ответ?
• Какую операцию вы использовали и почему?
• Можете ли вы объяснить свое решение с точки зрения единиц измерения: каковы единицы скорости и как уравновешиваются секунды?

Студенту трудно начать.

• Опишите проблему своими словами своему партнеру.
• Какую информацию вы знаете?
• Что вы пытаетесь найти?
• Можете ли вы использовать двойную числовую строку или таблицу, чтобы помочь вам?
• Можешь попробовать решить более простую задачу?

Ученик нашел решение.

• Объясните свою стратегию решения проблемы.
• Где в вашем [диаграмме, двойной числовой строке, таблице] вы видите курс?
• Где вы видите ответ в своей [диаграмме, двойной числовой строке, таблице]?
• Можно ли было решить эту проблему другим способом? Объяснять.

• Скорость ходьбы Эммы составляет 1/20 мили в минуту или 20 минут за милю.
• Эмма может пройти 4,5 мили за 90 минут.
• Эмма может пройти 0,75 мили за 15 минут.
• Учащиеся должны построить двойную числовую линию, чтобы показать взаимосвязь между числами.

Рабочее время

Эмма прошла 3 мили за 60 минут.

• Какова была ее скорость ходьбы в пересчете на скорость?
• Если она пройдет 4,5 мили с той же скоростью, сколько времени она пройдёт?
• Если она будет идти 15 минут с той же скоростью, какое расстояние она пройдёт?
• Сделайте двойную числовую линию, чтобы показать взаимосвязь между числами.

Подсказка:

• Каковы количества в ситуации?
• Как найти скорость ходьбы с точки зрения скорости?
• Вы использовали выражение d = rt , чтобы помочь вам найти время или расстояние?

Скорость — это показатель, который рассчитывается путем деления расстояния на время. Вы можете умножить время на скорость, чтобы найти любое расстояние. Величины скорость, расстояние и время связаны между собой. Отношение может быть выражено тремя способами: d = rt ,  r = dt ,  t = dr .

Скорость — это показатель, который выражается в виде пройденного расстояния в единицу времени.