Прямая и обратная пропорциональность. Формулы, обозначение, примеры

​ ​

Поможем понять и полюбить математику

Начать учиться

184.6K

Чем старше дерево, тем оно выше. Чем медленнее темп, тем дольше идти до школы. Эти и другие процессы можно описать математическим языком в виде прямой и обратной пропорциональной зависимости. Как это делать — расскажем в этой статье.

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Виды зависимостей:

• Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.

• Обратная зависимость.

  Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

• Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одного числа ведет к уменьшению другого во столько же раз.

• Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

a и d называются крайними членами, b и c — средними.

Основное свойство пропорции

Произведение крайних членов равно произведению средних членов.

Свойство прямо пропорциональной зависимости:

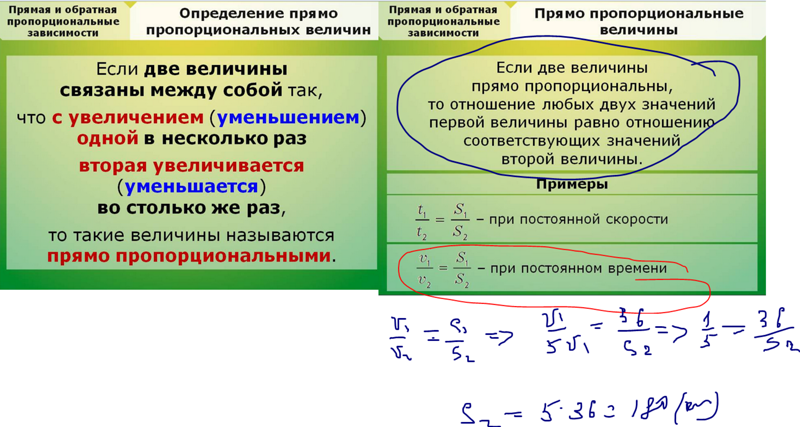
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

• при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;

• периметр квадрата и его сторона — прямо-пропорциональные величины;

• стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности y = kx, где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Как решаем:

1. Вспомним формулу для определения пути через скорость и время:

2. Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений:

3. Найдем скорость второго автомобиля:

Ответ: 20 км/ч.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней, если они пишут с такой же скоростью?

Как рассуждаем:

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

1. Составим пропорцию:

   14 (постов) / 8 (дней) × х (блогеров) = 420 (постов) / 12 (дней)

2. Вспомним основное свойство пропорции, согласно которому:

   14x × 12 = 420 × 8

   х = (420 × 8) / (14 × 12)

3. х = 20

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

• время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;

• при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;

• количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.

Формула обратной пропорциональности где y и x — это переменные величины, k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.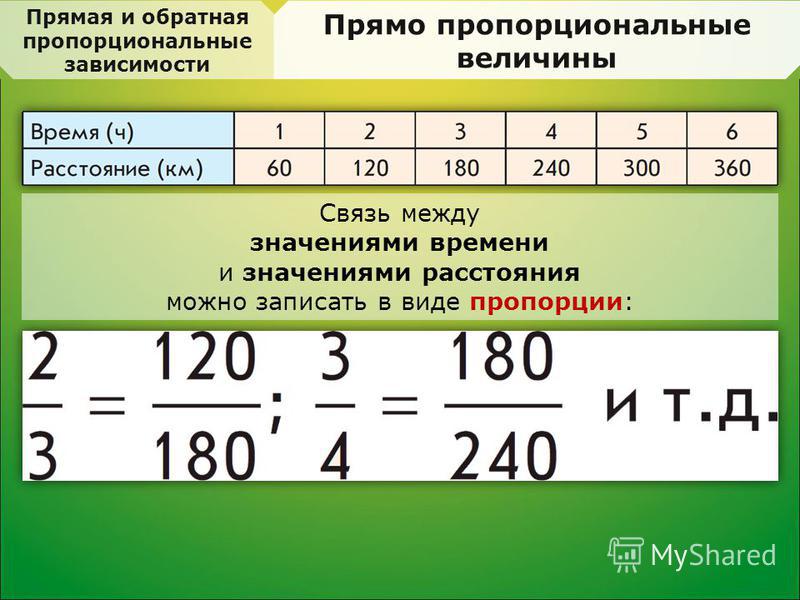

Формула коэффициента обратной пропорциональности:

xy = k.

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

1. Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

   30 : 24 = 5 : х

2. Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

   х = 24 * 5 : 30

   х = 4

3. Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

v₁ = 75 км/ч

v₂ = 52 км/ч

t₁ = 13 ч

t₂ = х

Как решаем:

1. Составим пропорцию:

   Соотношения равны, но перевернуты относительно друг друга.

2. Подставим известные значения:

   18 ч 45 мин

Ответ: 18 часов 45 минут.

 

Шпаргалки по математике родителей

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

116.7K

Теорема синусов

К следующей статье

Площадь прямоугольного треугольника

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

6.1.3. Прямо пропорциональные величины.

Главная » 6 класс. Математика. » 6.1.3. Прямо пропорциональные величины

Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 6.2k. Опубликовано 29 января 2013

I. Прямо пропорциональные величины.

Пусть величина y зависит от величины х. Если при увеличении х в несколько раз величина у увеличивается во столько же раз, то такие величины х и у называются прямо пропорциональными. 

Примеры.

1. Количество купленного товара и стоимость покупки (при фиксированной цене одной единицы товара — 1 штуки или 1 кг и т. д.) Во сколько раз больше товара купили, во столько раз больше и заплатили.

2. Пройденный путь и затраченное на него время (при постоянной скорости). Во сколько раз длиннее путь, во столько раз больше потратим времени на то, чтобы его пройти.

3. Объем какого-либо тела и его масса. (Если один арбуз в 2 раза больше другого, то и масса его будет в 2 раза больше)

II. Свойство прямой пропорциональности величин.

Если две величины прямо пропорциональны, то отношение двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.

Задача 1.  Для малинового варенья взяли 12 кг малины и 8 кг сахара. Сколько сахара потребуется, если взяли 9 кг  малины?

Решение.

Рассуждаем так: пусть потребуется х кг сахара на 9 кг малины. Масса малины и масса сахара — прямо пропорциональные величины: во сколько раз меньше малины, во столько же раз нужно меньше сахара. Следовательно, отношение  взятой (по массе) малины (12:9) будет равно отношению взятого сахара (8:х). Получаем пропорцию:

12:9=8:х;

х=9·8:12;

х=6.   Ответ: на 9 кг малины нужно взять 6 кг сахара.

Решение задачи можно было оформить и так:

Пусть на 9 кг малины нужно взять х кг сахара.

(Стрелки на рисунке направлены в одну сторону, а вверх или вниз — не имеет значения. Смысл: во сколько раз число 12 больше числа 9, во столько же раз число 8 больше числа х, т. е. здесь прямая зависимость).

 

 

Ответ: на 9 кг малины надо взять 6 кг сахара.

Задача 2. Автомобиль за 3 часа проехал расстояние 264 км. За какое время он проедет 440 км, если будет ехать с той же скоростью?

Решение.

Пусть за х часов автомобиль пройдет расстояние 440 км.

Ответ: автомобиль пройдет 440 км за 5 часов.

Задача 3. Из трубы поступает вода в бассейн. За 2 часа она заполняет 1/5 бассейна. Какая часть бассейна заполняется водой за 5 часов?

Решение. 

Отвечаем на вопрос задачи: за 5 часов наполнится 1/х часть бассейна. (Весь бассейн принимается за одну целую).

задачи на пропорцию прямая пропорциональность прямо пропорциональные величины

( 2 оценки, среднее 3 из 5 )

Что такое пропорция — определение, формула, примеры

Пропорция объясняется в основном на основе соотношения и дробей. Дробь, представленная в виде a/b, а отношение a:b, то пропорция утверждает, что два отношения равны. Здесь a и b — любые два целых числа. Соотношение и пропорция являются ключевыми основами для понимания различных концепций в математике, а также в естественных науках.

Пропорция находит применение в решении многих повседневных жизненных проблем, например, в бизнесе при совершении транзакций или при приготовлении пищи и т. д. Она устанавливает отношение между двумя или более величинами и, таким образом, помогает в их сравнении.

1.	Что такое пропорция?
2.	Продолжение пропорций
3.	Соотношения и пропорции
5.	Формула пропорции с примерами
6.	Типы пропорций
7.	Свойства пропорции
8.	Разница между отношением и долей
9.	Часто задаваемые вопросы о пропорции

Что такое пропорция?

Доля, как правило, называется частью, долей или числом, рассматриваемым в сравнительном отношении к целому. Определение пропорции гласит, что когда два отношения эквивалентны, они пропорциональны. Это уравнение или утверждение, используемое для изображения равенства двух отношений или дробей.

Пропорция — Определение

Пропорция — это математическое сравнение двух чисел. Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же отношении, то говорят, что отношения прямо пропорциональны друг другу. Пропорции обозначаются символом «::» или «=».

Пропорция. Пример

Два отношения называются пропорциональными, если они равны. Например,   время, необходимое поезду для прохождения 50 км в час, равно времени, затраченному им на преодоление расстояния 250 км за 5 часов. Например, 50 км/час = 250 км/5 часов.

Непрерывные пропорции

Говорят, что любые три величины находятся в непрерывной пропорции, если отношение между первой и второй равно отношению между второй и третьей. Точно так же четыре количества в непрерывной пропорции будут иметь отношение между первым и вторым, равным отношению между третьим и четвертым.

Например, рассмотрим два соотношения: a:b и c:d. Чтобы найти непрерывную пропорцию для двух заданных членов отношения, мы преобразуем их средние значения в один член/число. В общем случае это будет НОК средних, и для данного отношения НОК b и c будет bc. Таким образом, умножая первое отношение на c, а второе отношение на b, мы имеем

• Первое соотношение- ca:bc
• Второе соотношение- bc:bd

Таким образом, непрерывную пропорцию для данных отношений можно записать в виде ca:bc:bd.

Соотношения и пропорции

Соотношение — это способ сравнения двух величин одного вида с помощью деления. Формула соотношения для двух чисел a и b задается как a:b или a/b. Умножение и деление каждого члена соотношения на одно и то же число (не ноль) не влияет на отношение.

Когда два или более таких отношения равны, говорят, что они находятся в пропорции .

Четвертая, третья и среднепропорциональная

Если a : b = c : d, то:

• d называется четвертой пропорциональностью a, b, c.
• с называется третьим пропорциональным числам а и b.
• Среднее пропорциональное между a и b равно √(ab).

Советы и рекомендации по пропорциям

• a/b = c/d ⇒ ad = bc
• a/b = c/d ⇒ b/a = d/c
• a/b = c/d ⇒ a/c = b/d
• a/b = c/d ⇒ (a + b)/b = (c + d)/d
• a/b = c/d ⇒ (a – b/b = (c – d)/d
• a/(b + c) = b/(c + a) = c/(a + b) и a + b + c ≠0, тогда a = b = c.
• a/b = c/d ⇒ (a + b)/(a — b) = (c + d)/(c — d), что известно как правило компонендо-дивидендо
.
• Если оба числа a и b умножить или разделить на одно и то же число в отношении a:b, то полученное соотношение останется таким же, как исходное соотношение.

Формула пропорции с примерами

Формула пропорции — это уравнение, которое можно решить, чтобы получить сравнительные значения. Для решения задач на пропорции мы используем концепцию, согласно которой пропорция — это два отношения, равные друг другу. Мы имеем в виду это в том смысле, что две дроби равны друг другу.

Формула отношения

Предположим, что у нас есть любые две величины (или два объекта) и мы должны найти отношение этих двух, тогда формула отношения определяется как a:b ⇒ a/b , где

• a и b могут быть любыми двумя величинами.
• «а» называется первым термином или предшествующим .
• «b» называется вторым членом или консеквентом .

Например,  в соотношении 5:9 представлено 5/9, где 5 предшествует, а 9 последует. 5:9 = 10:18 = 15:27

Формула пропорции

Теперь предположим, что в пропорции два отношения равны a:b и c:d.   Два термина «b» и «c» называются «среднее значение или средние термины», тогда как термины «a» и «d» известны как «крайние или крайние термины».

a/b = c /d или a:b::c:d. Например, рассмотрим еще один пример количества учащихся в 2 классах, где отношение количества девочек к количеству мальчиков равно. Наше первое отношение количества девочек к мальчикам равно 2:5, а другое — 4:8, тогда пропорция может быть записана как: 2:5::4:8 или 2/5 = 4/8. Здесь 2 и 8 — крайние значения, а 5 и 4 — средние значения.

Типы пропорций

В зависимости от типа отношения, в котором участвуют два или более количества, пропорция может быть разделена на различные типы. Существует два типа пропорций.

• Прямая пропорция
• Обратная пропорция

Прямая пропорция

Этот тип описывает прямую зависимость между двумя величинами. Проще говоря, если увеличивается одна величина, увеличивается и другая величина, и наоборот. Например, если скорость автомобиля увеличивается, он преодолевает большее расстояние за фиксированный промежуток времени. В обозначениях прямая пропорция записывается как y ∝ x.

Обратная пропорция

Этот тип описывает косвенную зависимость между двумя величинами. Проще говоря, если одна величина увеличивается, другая величина уменьшается, и наоборот. В обозначениях обратная пропорция записывается как y ∝ 1/x. Например, увеличение скорости автомобиля приведет к преодолению фиксированного расстояния за меньшее время.

Важные примечания

• Пропорция — это математическое сравнение двух чисел.
• Основные пропорции бывают двух типов: прямые пропорции и обратные пропорции.
• Мы можем применять понятия пропорций к географии, сравнивая количества в физике, диетологии, кулинарии и т. д.

Свойства пропорции

Пропорция устанавливает эквивалентное отношение между двумя соотношениями. Свойства пропорции, за которой следует это отношение:

• Дополнение – Если a : b = c : d, то значение каждого отношения равно a + c : b + d
• Subtrahendo – Если a : b = c : d, то значение каждого отношения равно a – c : b – d
• Дивидендо – Если a : b = c : d, то a – b : b = c – d : d
• Componendo – Если a : b = c : d, то a + b : b = c + d : d
• Альтернатива – Если a : b = c : d, то a : c = b: d
• Invertendo – Если a : b = c : d, то b : a = d : c
• Компонендо и дивидендо – Если а : b = с : d, то а + b : а – b = с + d : с – d

Разница между отношением и долей

Соотношение и пропорция являются тесно связанными понятиями. Пропорция означает равное соотношение между двумя или более отношениями. Чтобы понять концепцию отношения и пропорции, просмотрите разницу между соотношением и пропорцией, приведенную здесь.

Серийный номер	Соотношение	Доля
1	Соотношение используется для сравнения размера двух вещей с одной и той же единицей измерения.	Пропорция используется для выражения отношения двух соотношений.
2	Выражается двоеточием (:) или косой чертой (/).	Выражается двойным двоеточием (::) или равен символу (=)
3	Это выражение.	Это уравнение.
4	Ключевое слово для различения соотношения в задаче — «ко всем».	Ключевое слово, позволяющее различать пропорции в задаче, — «из».

Пропорция Связанные темы

Ниже приведен список тем, которые тесно связаны с пропорцией в коммерческой математике. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.

Часто задаваемые вопросы о пропорции

Что вы подразумеваете под отношением?

Отношение — это математическое выражение, записанное в форме a:b, которое выражает дробь в форме a/b, где a и b — любые целые числа. Например, дробь 1/3 может быть выражена как 1:3 в форме соотношения.

Что такое пропорция в математике?

Пропорция — это математическое сравнение двух чисел. Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же отношении, то говорят, что отношения прямо пропорциональны друг другу. Пропорции обозначаются с помощью символа  ‘::’ или ‘=’. Например, 2:5 :: 4:8 или 2/5 = 4/8. Здесь 2 и 8 — крайние значения, а 5 и 4 — средние значения.

Как соотношение и пропорция используются в повседневной жизни?

Соотношения и пропорции используются ежедневно. Соотношения и пропорции используются в деловых операциях при работе с деньгами, сравнении количества по цене при совершении покупок и т.  д. Например, у бизнеса может быть коэффициент для суммы прибыли, полученной за продажу определенного продукта, например 5 : 1, в котором говорится, что бизнес получает 2,50 доллара за каждую продажу.

Как узнать, образуют ли два отношения пропорцию?

Если два отношения эквивалентны друг другу, то говорят, что они пропорциональны. Например, соотношения 1:2, 2:4 и 3:6 являются эквивалентными соотношениями.

Как рассчитать пропорцию?

Пропорция рассчитывается по формуле пропорции: a:b::c:d или a:b = c:d. Мы читаем это как «а» для «б», как «с» для «d».

Какие существуют типы пропорций?

В зависимости от типа отношений между двумя или более величинами пропорция может быть разделена на разные типы. Существует два типа пропорций.

• Прямая пропорция — описывает прямую зависимость между двумя величинами. Проще говоря, если увеличивается одна величина, увеличивается и другая величина, и наоборот.
• Обратная пропорция — описывает косвенную связь между двумя величинами. Проще говоря, если одна величина увеличивается, другая величина уменьшается, и наоборот.

Каковы различные свойства пропорции?

Пропорция устанавливает эквивалентное отношение между двумя соотношениями. Свойства пропорции, за которыми следует это отношение:

• Дополнение – Если a : b = c : d, то значение каждого отношения равно a + c : b + d
• Subtrahendo – Если a : b = c : d, то значение каждого отношения равно a – c : b – d
• Дивидендо – Если a : b = c : d, то a – b : b = c – d : d
• Componendo – Если a : b = c : d, то a + b : b = c+d : d
• Альтернатива – Если a : b = c : d, то a : c = b: d
• Invertendo – Если a : b = c : d, то b : a = d : c
• Компонендо и дивидендо – Если а : b = с : d, то а + b : а – b = с + d : с – d

Формула пропорции — Что такое формула пропорции? , Примеры

Прежде чем мы начнем с формулы пропорции, давайте сначала вспомним понятие пропорции. Если два отношения равны, то говорят, что они пропорциональны. Если a, b, c, d пропорциональны четырем элементам, то это означает, что a/b = c/d. Элементы a и d называются крайними, а b и c — средними членами. В этом отношении произведение средних равно произведению крайностей. Любые два отношения называются равными, если их перекрестные произведения равны. Давайте поймем формулу пропорции, используя решенные примеры.

Что такое формула пропорции?

В соответствии с определением пропорции, когда два соотношения эквивалентны, они пропорциональны. Формула пропорции используется для отображения равенства двух отношений или дробей. Формула пропорции может быть представлена ​​следующим образом:

a : b :: c : d = a/b = c/d

Формула пропорции

a : b :: c : d = a/b = c/d

где,

• a, d = крайние условия
• b, c = средние значения

Другие формулы, связанные с пропорцией:

• Произведение средних = произведение крайностей. Это можно записать как ad = bc
.
• Существуют еще две пропорциональные формулы, основанные на прямой или косвенной вариации. Если две величины x и y находятся в прямой зависимости, то y = kx, а если две величины x и y находятся в прямой зависимости, то y = k/x, где k – константа пропорциональности.

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами

Закажите бесплатный пробный урок

Примеры использования формулы пропорции

Пример 1. Чему равно значение x в 12 : x :: 4 : 5?

Решение:

Используя формулу пропорции,

a : b :: c : d = a/b = c/d

12/x = 4/5

x = 15

Следовательно, значение x = 15

Пример 2: Сэм пробегает 6 миль за 30 минут. С такой скоростью, какое расстояние он сможет пробежать за 45 минут?

Решение:

Предположим, что неизвестная величина равна x.

Используя формулу пропорции,

6 : 30 :: x : 45 = 6/30 = x/45

x = 9 миль

Следовательно, расстояние, пройденное Сэмом за 45 минут, = 9 милям.

Пример 3: Джейн прошла 4 мили за 30 минут. С такой скоростью, какое расстояние она могла бы пройти за 60 минут?

Решение:

Предположим, что неизвестная величина равна x.

Используя формулу пропорции,

4 : 30 :: x : 60

4/30 = x/60

x = 8

Следовательно, расстояние, пройденное Джейн за 60 минут, равно 8 милям Формула пропорции 

Что означает формула пропорции?

Любое уравнение называется пропорциональным, если элементы в нем пропорциональны. Это означает, что если элементами уравнения являются a, b, c и d, то уравнение будет пропорциональным, когда пропорциональны a, b, c и d. Элементы a и d называются крайними, а b и c — средними членами. В этом отношении произведение средних равно произведению крайностей.