НОД и НОК

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое

12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить, какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

12 : 3 = 4

9  : 3 = 3

Значит НОД (12 и 9) = 3

---

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

2 × 3 = 6

Значит НОД (24 и 18) = 6

---

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения:  и 

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

28 : 4 = 7

16 : 4 = 4

 НОД (28 и 16) = 4

---

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

100 : 20 = 5

40 : 20 = 2

 НОД (100 и 40) = 20.

---

Пример 3. Найти НОД чисел 72 и 128

Раскладываем на множители число 72

Раскладываем на множители число 128

Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

72 : 8 = 9

128 : 8 = 16

 НОД (72 и 128) = 8

---

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18,  24  и  36

Разложим на множители число 18

Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

18 : 6 = 3

24 : 6 = 4

36 : 6 = 6

 НОД (18, 24 и 36) = 6

---

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

Разложим на множители число 36

 

Разложим на множители число 42

Получили четыре разложения:

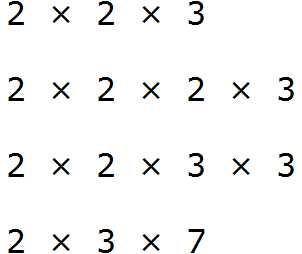
Теперь найдём и подчеркнём общие множители:

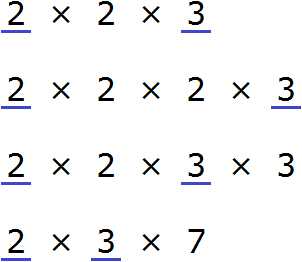
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

12 : 6 = 2

24 : 6 = 4

36 : 6 = 6

42 : 6 = 7

 НОД (12, 24 , 36 и 42) = 6

---

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно

a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

Теперь выпишем кратные обоих чисел:

 

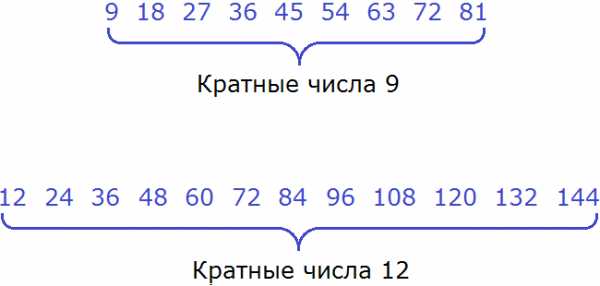
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

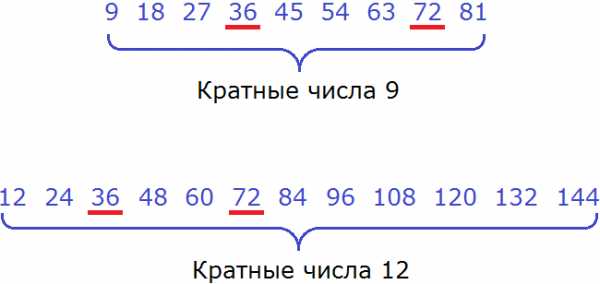
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

---

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

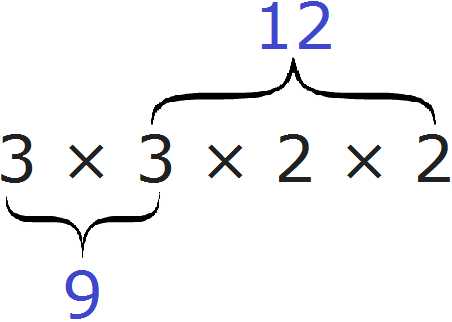
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12

---

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

900 : 50 = 18

900 : 180 = 5

НОК (50 и 180) = 900

---

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

Разложим на множители число 15

Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

1320 : 8 = 165

1320 : 15 = 88

1320 : 33 = 40

НОК (8, 15 и 33) = 1320

---

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

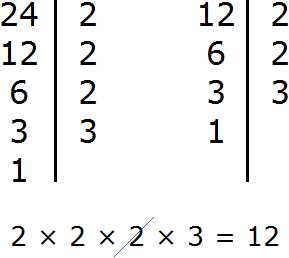
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

НОК (24 и 12) = 24

---

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

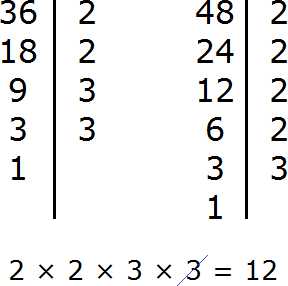
Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

НОК (36 и 48) = 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

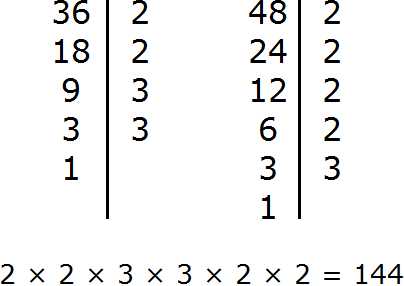
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

---

Задания для самостоятельного решения

Задание 1. Найдите НОД чисел 12 и 16

Решение:

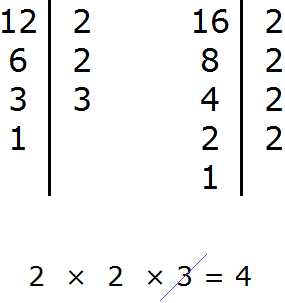
Задание 2. Найдите НОК чисел 12 и 16

Решение:

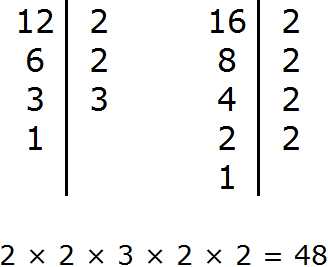
Задание 3. Найдите НОД чисел 40 и 32

Решение:

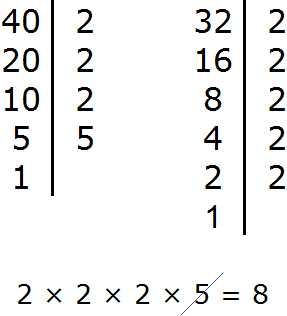
Задание 4. Найдите НОК чисел 40 и 32

Решение:

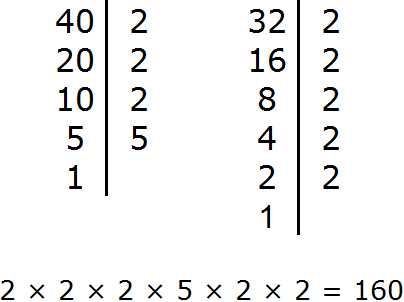
Задание 5. Найдите НОД чисел 54 и 86

Решение:

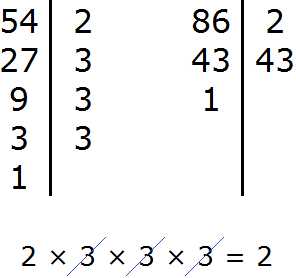
Задание 6. Найдите НОК чисел 54 и 86

Решение:

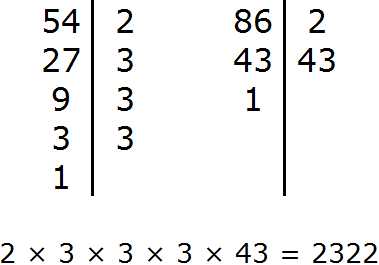
Задание 7. Найдите НОД чисел 98 и 35

Решение:

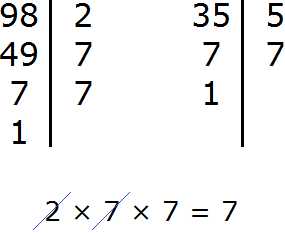
Задание 8. Найдите НОК чисел 98 и 35

Решение:

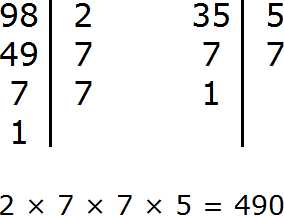
Задание 9. Найдите НОД чисел 112 и 82

Решение:

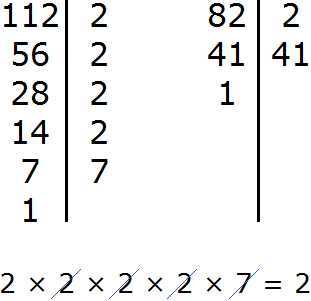
Задание 10. Найдите НОК чисел 112 и 82

Решение:

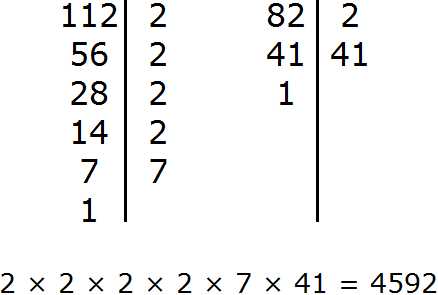
Задание 11. Найдите НОД чисел 24, 48, 64

Решение:

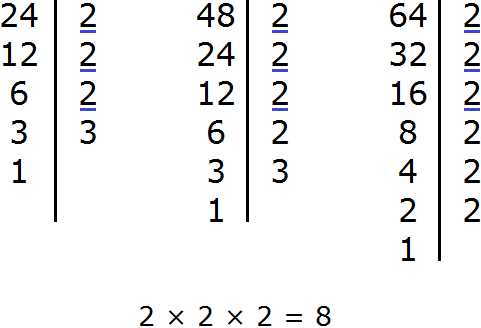
Задание 12. Найдите НОК чисел 24, 48, 64

Решение:

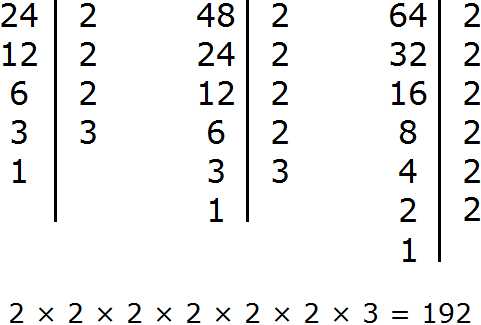
Задание 13. Найдите НОД чисел 18, 48, 96

Решение:

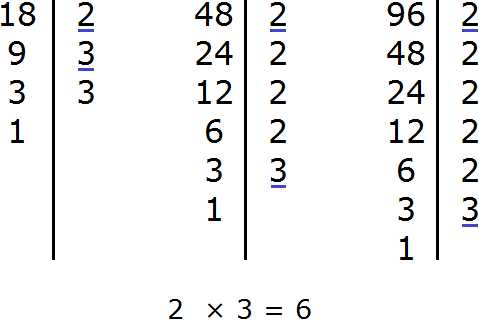
Задание 14. Найдите НОК чисел 18, 48, 96

Решение:

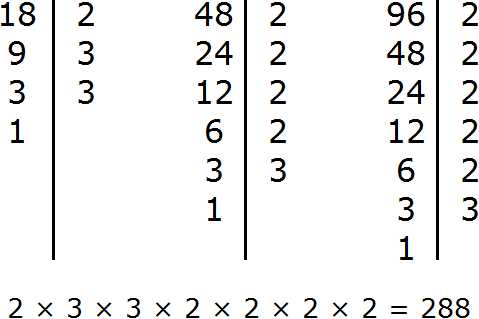
Задание 15. Найдите НОД чисел 28, 24, 76

Решение:

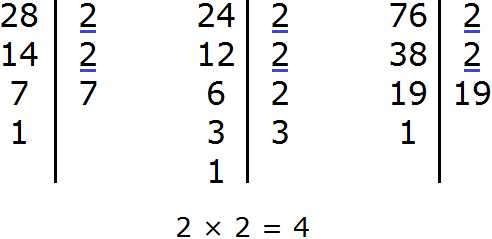
Задание 16. Найдите НОК чисел 28, 24, 76

Решение:

---

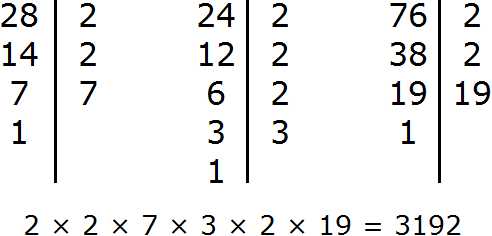
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ, алгоритм как найти НОД

Наибольший общий делитель чисел – это наибольшее число, на которое делятся все заданные числа.

Алгоритм поиска НОД

Вычисление НОД похоже на поиск НОК. Чтобы найти наибольший общий делитель, нужно использовать следующий алгоритм:

1. Разложить все числа на простые множители, используя признаки делимости чисел.
2. Найти совпадающие множители во всех числах и выписать их.
3. Перемножить совпадающие множители.

Если среди множителей чисел не были найдены одинаковые, числа являются взаимно простыми.

Примеры поиска наибольшего общего делителя

Рассмотрим, как найти НОД с помощью алгоритма на нескольких примерах.

Пример 1:

Найдите наибольший общий делитель чисел 420 и 990.

Решение:

Разложим оба числа на простые множители:

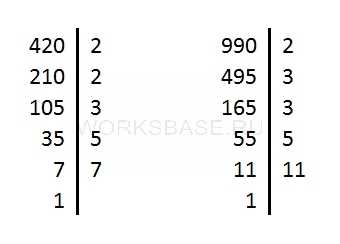
Получили, что:

420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7

990 = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 11

Выпишем все совпадающие множители для обоих чисел и перемножим их:

НОД = 2 ⋅ 3 ⋅ 5 = 30

Ответ: 30

Пример 2:

Найдите наибольший общий делитель чисел 588 и 1820.

Решение:

Разложим оба числа на простые множители:

Получили, что:

588 = 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 7

1820 = 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 13

Выпишем все совпадающие множители для обоих чисел и перемножим их:

НОД = 2 ⋅ 2 ⋅ 7 = 28

Ответ: 28

Пример 3:

Найдите наибольший общий делитель чисел 1000 и 3267.

Решение:

Разложим оба числа на простые множители:

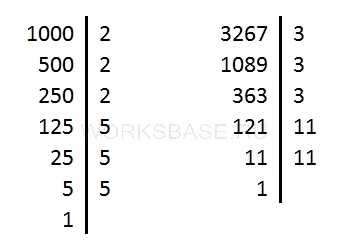
Получили, что:

1000 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5

3267 = 3 ⋅ 3 ⋅ 3 ⋅ 11 ⋅ 11

Совпадающих множителей у этих 2 чисел нет, поэтому они являются взаимно простыми, то есть

Ответ: 1

worksbase.ru

Наибольший общий делитель (НОД): определение, как найти, схема

 

Решим задачу. У нас есть  два типа печенья. Одни шоколадные, а другие простые. Шоколадных 48 штук, а простых 36. Необходимо составить из этого печенья максимально возможное число подарков, при этом надо использовать их все.

Для начала выпишем все делители каждого из этих двух чисел, так как оба эти числа должны делиться на количество подарков.

Получаем, 

• 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
• 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.

Найдем среди делителей общие, которые есть как у первого, так и у второго числа.

Общими делителями будут: 1, 2, 3, 4, 6, 12.

Наибольшим из всех общих делителей является число 12. Это число называют наибольшим общим делителем чисел 36 и 48.

Исходя из полученного результата, можем заключить, что из всего печенья можно составить 12 подарков. В одном таком подарке будет 4 шоколадных печенья и 3 обычных печенья.

Определение наибольшего общего делителя

• Наибольшее натуральное число, на которое делятся без остатка два числа a и b, называют наибольшим общим делителем этих чисел.

Иногда для сокращения записи используют аббревиатуру НОД.

Некоторые пары чисел имеют в качестве наибольшего общего делителя единицу. Такие числа называют взаимно простыми числами. Например, числа 24 и 35. Имеют НОД =1.

Как найти наибольший общий делитель

Для того чтобы найти наибольший общий делитель не обязательно выписывать все делители данных чисел.

Можно поступить иначе. Сначала разложить на простые множители оба числа.

• 48 = 2*2*2*2*3,
• 36 = 2*2*3*3.

Теперь из множителей, которые входят в разложение первого числа, вычеркнем все те, которые  не входят в разложение второго числа. В нашем случае это две двойки.

• 48 = 2*2*2*2*3,
• 36 = 2*2*3*3.

Останутся множители 2, 2 и 3. Их произведение равно 12. Это число и будет являться наибольшим общим делителем чисел 48 и 36. 

Это правило можно распространить на случай с тремя, четырьмя и т.д. числами.

Общая схема нахождения наибольшего общего делителя

• 1. Разложить числа на простые множители.
• 2. Из множителей,  входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.
• 3. Посчитать произведение оставшихся множителей.

Нужна помощь в учебе?

Предыдущая тема: Простые и составные числа: разложение чисел на простые множители
Следующая тема:&nbsp&nbsp&nbspНаименьшее общее кратное (НОК): определение, как найти, общая схема

Все неприличные комментарии будут удаляться.

www.nado5.ru

Как найти наибольший общий делитель (НОД)

Рассмотрим два способа нахождения наибольшего общего делителя.

Нахождение путём разложения на множители

Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.

Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.

Пример 1. Найдём НОД (84, 90).

Раскладываем числа 84 и 90 на простые множители:

Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой: 1 · 2 · 3 = 6.

Таким образом, НОД (84, 90) = 6.

Пример 2. Найдём НОД (15, 28).

Раскладываем 15 и 28 на простые множители:

Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель – единица.

НОД (15, 28) = 1.

Алгоритм Евклида

Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.

Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.

Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.

Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно, НОД (27, 9) = 9.

В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:

1. Из двух данных чисел большее число делят на меньшее.
2. Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
3. Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
4. Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
5. Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.

Пример 2. Найдём наибольший общий делитель чисел 140 и 96:

1) 140 : 96 = 1 (остаток 44)

2) 96 : 44 = 2 (остаток 8)

3) 44 : 8 = 5 (остаток 4)

4) 8 : 4 = 2

Последний делитель равен 4 – это значит, что НОД (140, 96) = 4.

Последовательное деление так же можно записывать столбиком:

Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:

1. Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
2. Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
3. Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.

Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа – 48:

1) 48 : 4 = 12

48 делится на 4 без остатка. Таким образом, НОД (140, 96, 48) = 4.

naobumium.info

Нахождение НОД — 6 класс — Математика — Каталог статей

Нахождение НОД
    

•     Если натуральное число делится только на 1 и на само себя, то оно называется простым.

Любое натуральное число всегда делится на 1 и на само себя.

Число 2 — наименьшее простое число. Это единственное чётное простое число, остальные простые числа — нечётные.

Простых чисел много, и первое среди них — число 2. Однако нет последнего простого числа. 

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Например:
•    число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
•    число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа.
    

• Делитель натурального числа a — это такое натуральное число, которое делит данное число a без остатка.

Натуральное число, которое имеет более двух делителей называется составным.

Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12.

Общий делитель двух данных чисел a и b — это число, на которое делятся без остатка оба данных числа a и b.
    

• Наибольший общий делитель (НОД) двух данных чисел a и b — это наибольшее число, на которое оба числа a и b делятся без остатка.

Кратко наибольший общий делитель чисел a и b записывают так:

НОД (a; b).
Пример: НОД (12; 36) = 12.
Делители чисел в записи решения обозначают большой буквой «Д».
Пример.
Д (7) = {1, 7}

Д (9) = {1, 9}

НОД (7; 9) = 1

Числа 7 и 9 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми числами.
    

• Взаимно простые числа — это натуральные числа, которые имеют только один общий делитель — число 1. Их НОД равен 1.

Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел нужно:
1.    разложить делители чисел на простые множители;

Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.

Поясним сразу на примере. Разложим на простые множители числа 28 и 64.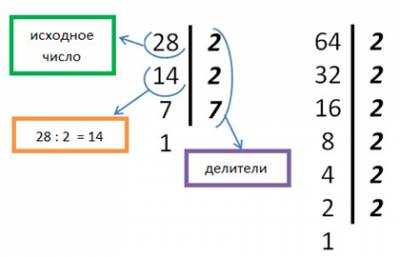
 
2.    Подчёркиваем одинаковые простые множители в обоих числах. 
28 = 2 • 2 • 7 

64 = 2 • 2 • 2 • 2 • 2 • 2
3.    Находим произведение одинаковых простых множителей и записать ответ; 
НОД (28; 64) = 2 • 2 = 4 

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД
Найти НОД 48 и 36.

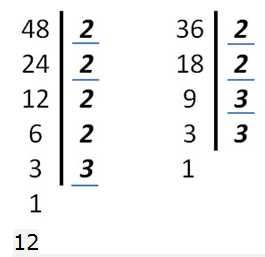
 НОД (48; 36) = 2 • 2 • 3 = 12

Второй способ записи НОД
Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.
Д (10) = {1, 2, 5, 10}

Д (15) = {1, 3, 5, 15}

Д (10, 15) = {1, 5}

НОД (10; 15) = 5
    
 

matematik.3dn.ru

НОД. Наибольший общий делитель чисел.

• Наибольшим общим делителем данных натуральных чисел называют наибольшее натуральное число, на которое делится каждое из этих чисел.
•  Наибольший общий делитель данных чисел равен произведению общих простых множителей в разложениях этих чисел. Пример. НОД(24, 42)=2·3=6, т. к. 24=2·2·2·3, 42=2·3·7, их общие простые множители 2 и 3.
•  Если натуральные числа имеют только один общий делитель-единицу, то эти числа называют взаимно простыми.

Пример 1. Найти НОД(15; 35).

Решение.

Разложим данные числа на простые множители.

 15=3∙5,               35=5∙7

Общий делитель чисел 15 и 35 – это число 5.

Ответ: НОД(15; 35)=5.

 

Пример 2. Найти НОД(72; 64).

Решение.

 Разложим числа 72 и 64 на простые множители.

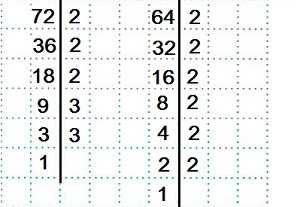72=2∙2∙2∙3∙3 или 72=2³∙3²,          64=2∙2∙2∙2∙2∙2 или 64=2⁶

Нужно взять произведение общих множителей: 2∙2∙2=2³=8.

Ответ: НОД(72; 64)=2³=8.

Примечание: из разложений данных чисел нужно брать общие множители с наименьшими показателями. У нас в первом разложении было 2³, а во втором 2⁶, поэтому, взяли 2³.

 

Пример 3. Найдите наибольший общий делитель разности чисел 69 и 19 и суммы чисел 36 и 39.

Решение.

Требуется найти НОД(50; 75). Разложим эти числа на простые множители.

50=2∙5² ;              75=3∙5²

Общий делитель 5 берем во второй степени.

НОД(50; 75)=5²=5∙5=25.

Ответ: НОД(50; 75)=25.

 

 

Запись имеет метки: НОД

www.mathematics-repetition.com

Урок математики на тему «Наибольший общий делитель. Взаимно простые числа». 6-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (183,1 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Данная работа предназначена для сопровождения объяснения новой темы. Практические и домашние задания учитель подбирает на свое усмотрение.

Оборудование: компьютер, проектор, экран.

Ход объяснения

Слайд 1. Наибольший общий делитель.

Устная работа.

1. Вычислите:

а) 0,7 * 10 : 2 — 0,3 : 0,4 _________ ?

б) 5 : 10 * 0,2 + 2 : 0,7 _______ ?

Ответы: а) 8; б) 3.

2. Опровергните утверждение: Число “2” является общим делителем всех чисел”.

— Очевидно, что нечетные числа не делятся на 2.

3. Как называются числа, кратные 2?

— Четные.

4. Назовите число, которое является делителем любого числа.

— 1.

Письменно.

1. Разложите число 2376 на простые множители.

Решение.

Слайд 2.

2. Найдите все общие делители чисел 18 и 60.

Решение.

Делители числа 18: 1; 2; 3; 6; 9; 18.

Делители числа 60: 1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60.

Далее учащиеся называют общие делители: 1; 2; 3; 6.

— Назовите наибольший общий делитель чисел 18 и 60.

— Число 6.

— Попробуйте сформулировать, какое число называют наибольшим общим делителем двух натуральных чисел

Правило. Наибольшее натуральное число, на которое делятся без остатка числа , называют наибольшим общим делителем.

Пишут: НОД (18; 60) = 6.

— Скажите, пожалуйста, удобен ли рассмотренный способ нахождения НОД?

— Нет.

— Почему?

— Числа могут быть слишком большие и для них трудно перечислить все делители.

Слайд 3.

Давайте попытаемся найти другой способ нахождения НОД.

Разложим числа 18 и 60 на простые множители:

18 =

— Приведите примеры делителей числа 18.

— Числа: 1; 2; 3; 6; 9; 18.

— Приведите примеры делителей числа 60.

— Числа: 1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60.

— Приведите примеры общих делителей чисел 18 и 60.

— Числа: 1; 2; 3; 6.

— Как можно найти наибольший общий делитель 18 и 60?

Алгоритм.

1. Разложить данные числа на простые множители.

2. Сравнить множители чисел и вычеркнуть разные.

3. Вычислить произведение оставшихся множителей.

Слайд 4. Взаимно простые числа.

Задание. Найдите НОД чисел 24 и 35.

Решение.

Правило. Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.

Это интересно!

• Делители числа 18: 1; 2; 3; 6; 9; 18.
• Делители числа 60: 1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60.
• НОД (18;60) = 6.
• Делители числа 6: 1; 2; 3; 6.
• Заметим, что числа 1; 2; 3; 6 являются общими делителями чисел 18 и 60.
• Например, НОД (108;196) = 4. Значит, сразу можно сказать, что общие делители чисел 108 и 196 – это делители числа 4, то есть 1; 2; 4.

Каждый делитель числа НОД (a;b) является общим делителем чисел a и b и, наоборот, каждый их общий делитель является делителем числа НОД (a;b).

3.01.2015

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai