Приведение дробей к общему знаменателю 6 класс онлайн-подготовка на Ростелеком Лицей

47. Приведение дробей к общему знаменателю

Можно ли сравнить дроби 34и 24? 27 и38?

Первые две дроби имеют одинаковый знаменатель, значит можно их сравнить: 34 > 24. Дроби 27 и 38 имеют разные знаменатели, поэтому также сравнить не получится. Если умножить числитель и знаменатель дроби 34 на одно и тоже число 2, то получим равную ей дробь 68.

В этом случае говорят, что мы привели дробь 34 к знаменателю 8.

Таким образом, дробь можно привести к любому знаменателю.

Дополнительным множителем называют число, на которое надо умножить знаменатель дроби.

Если привести дроби к новому знаменателю, то ее числитель и знаменатель умножают на дополнительный множитель.

Пример 1. Приведем дробь 27 к знаменателю 35.

Число 35 кратно 7, так как 35:7 = 5.

Дополнительным множителем является число 5.

Умножим числитель и знаменатель дроби на 5, получим:

27=2∙57∙5=1035.

Любые две дроби можно привести к общему знаменателю.

Например, 23=1015 и 45=1215.

Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.

Пример 2. Приведем к наименьшему общему знаменателю дроби 34 и 56.

Наименьшим общим кратным чисел 4 и 6 является число 12. Чтобы получить в знаменателе 12, числитель и знаменатель дроби 34 умножаем на 3, а числитель и знаменатель дроби 56 умножаем на 2.

Значит, 3∙34∙3=912; 5∙26∙2=1012.

Чтобы привести дроби к наименьшему общему знаменателю, надо:

1. Найти наименьший общий знаменатель этих дробей.
2. Разделить наименьший общий знаменатель на знаменатели данных дробей таким образом, найти для каждой дроби дополнительный множитель.
3. Умножить числитель и знаменатель каждой дроби на дополнительный множитель.

В других случаях дополнительные множители находят с помощью разложения на простые множители.

Пример 3. Приведем дроби 1160 и 31168 к наименьшему общему знаменателю.

Разложим знаменатели данных дробей на простые множители: 60 = 2·2·3·5, 168 = 2·2·2·3·7.

Найдем НОК, которое и будет наименьшим общим знаменателем: 2·2·2·3·5·7 = 840.

Для дроби 1160 дополнительным множителем является 14. Получим 154840.

Для дроби 31168дополнительным множителем является 5. Получим 155840.

6 класс. Математика. Приведение дробей к общему знаменателю — Приведение дробей к общему знаменателю

Комментарии преподавателя

По­смот­ри­те: это две книги или одна (см. рис. 1, 2)? Книга одна, формы раз­ные. В одних слу­ча­ях удоб­на одна форма, в дру­гих дру­гая. Се­год­ня мы будем го­во­рить об эк­ви­ва­лент­ных обо­зна­че­ни­ях од­но­го и того же ко­ли­че­ства.

Рис. 1. «Вол­шеб­ник Изу­мруд­но­го го­ро­да»

Рис. 2. «Вол­шеб­ник Изу­мруд­но­го го­ро­да» (из­да­ние 1984 года)

Оди­на­ко­вую ин­фор­ма­цию можно по­да­вать в раз­ном виде, на­при­мер, число «три­на­дцать» будет вы­гля­деть так: 13, ХIII, три­на­дцать.

Если по­тре­бу­ет­ся вы­пол­нить сло­же­ние. До­пу­стим, при­ба­вить два­дцать семь.

Три­на­дцать + два­дцать семь = сорок

ХIII + XXVII = ХL

13 + 27 = 40

Удоб­нее всего вы­пол­нять вы­чис­ле­ния, если ис­поль­зу­ет­ся де­ся­тич­ная за­пись. На­при­мер, есть два мешка (см. рис. 3). В одном 2 пуда зерна, в дру­гом 32 кг. Это одно и то же ко­ли­че­ство, обо­зна­че­ния раз­ные. До­ба­вим в каж­дый мешок по 3 кг. В пер­вом мешке у нас 2 пуда и 3 кг. Во вто­ром – 35 кг (см. рис. 4). Какая за­пись проще? По­нят­но, вто­рая.

Рис. 3. Мешки с зер­ном

Рис. 4. Мешки с зер­ном

Пред­став­лять не целые числа удоб­нее с по­мо­щью дро­бей. Ин­те­рес­но то, что оди­на­ко­вое ко­ли­че­ство числа можно пред­ста­вить с по­мо­щью эк­ви­ва­лент­ных дро­бей. Так, по­ло­ви­ну торта мы можем по­лу­чить, раз­де­лив торт на две части и взяв из них одну, а можно раз­де­лить на 6 ча­стей и взять 3 (см. рис. 5).

Рис. 5. Эк­ви­ва­лент­ные дроби

Мы по­лу­чим эк­ви­ва­лент­ные дроби . Пусть те­перь нам нужно сло­жить  торта и  торта (см. рис. 6). В таком виде нам это сде­лать не уда­ет­ся (это все равно как скла­ды­вать пуды и ки­ло­грам­мы). Мы можем скла­ды­вать оди­на­ко­вые части, на­при­мер, ше­стые. За­ме­ним  эк­ви­ва­лент­ной дро­бью  (см. рис. 7).Те­перь мы скла­ды­ва­ем оди­на­ко­вые дроби (ше­стые),  (см. рис. 8).

Рис. 6. Сло­же­ние дро­бей 

Рис. 7. За­ме­на  эк­ви­ва­лент­ной дро­бью

Рис. 8. Сумма дро­бей

Рас­смот­рим еще несколь­ко при­ме­ров.

При­мер 1. Сло­же­ние и вы­чи­та­ние дро­бей с раз­ны­ми зна­ме­на­те­ля­ми с по­мо­щью эк­ви­ва­лент­ных дро­бей.

Вы­чис­ли­те: .

Ре­ше­ние

За­пи­шем для каж­дой дроби по несколь­ко эк­ви­ва­лент­ных до тех пор, пока не встре­тим два оди­на­ко­вых зна­ме­на­те­ля в раз­ных рядах.

Те­перь легко вы­пол­нять вы­чис­ле­ния.

Так,при­ве­де­ние дро­бей к об­ще­му зна­ме­на­те­лю – за­ме­на дро­бей на такие эк­ви­ва­лент­ные дроби, ко­то­рые со­дер­жат оди­на­ко­вый зна­ме­на­тель.

Чтобы срав­нить, сло­жить или вы­честь дроби, нам нужно при­ве­сти их к об­ще­му зна­ме­на­те­лю.

Для при­ве­де­ния дро­бей к об­ще­му зна­ме­на­те­лю можно вы­пи­сать це­поч­ку эк­ви­ва­лент­ных, а потом вы­брать такие дроби, у ко­то­рых оди­на­ко­вые зна­ме­на­те­ли.

1)      Вы­пол­нить сло­же­ние: 

Ре­ше­ние

Сна­ча­ла за­пи­шем це­поч­ку эк­ви­ва­лент­ных дро­бей для , для этого чис­ли­тель и зна­ме­на­тель дроби до­мно­жим на 2, 3, 4 и т. д.

То же самое про­де­ла­ем для дроби : .

Как видим, есть сов­па­де­ние зна­ме­на­те­лей ( и ). За­ме­ня­ем те­перь ис­ход­ные дроби эк­ви­ва­лент­ны­ми и вы­пол­ня­ем вы­чис­ле­ния: .

Опре­де­лить зна­че­ние раз­но­сти: .

Ре­ше­ние

В ка­че­стве об­ще­го зна­ме­на­те­ля можно также ис­поль­зо­вать про­из­ве­де­ние зна­ме­на­те­лей ис­ход­ных дро­бей. При­ве­дем дроби  и  к зна­ме­на­те­лю . Для этого до­мно­жим чис­ли­тель и зна­ме­на­тель пер­вой дроби на 12, а вто­рой – на 16.

Точно так же, как мы умно­жа­ли чис­ли­тель и зна­ме­на­тель дроби на одно и то же число, мы можем и по­де­лить их на одно и то же число. В нашем при­ме­ре чис­ли­тель и зна­ме­на­тель де­лят­ся на 8, вы­пол­ним де­ле­ние: .

Такое де­ле­ние, как мы вы­пол­ни­ли, на­зы­ва­ет­ся со­кра­ще­ни­ем дроби. Со­кра­тить дробь – озна­ча­ет раз­де­лить и чис­ли­тель, и зна­ме­на­тель на оди­на­ко­вое число (не рав­ное 0).

Найти зна­че­ние вы­ра­же­ния: .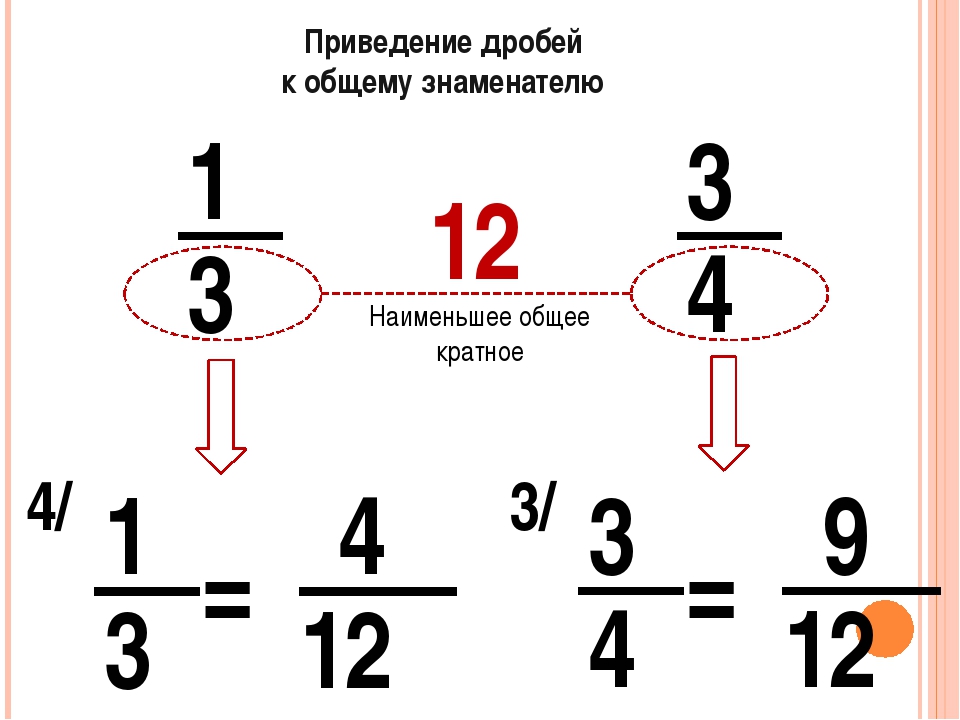

1 спо­соб – вос­поль­зу­ем­ся нашим пра­ви­лом: про­из­ве­де­ние зна­ме­на­те­лей яв­ля­ет­ся общим зна­ме­на­те­лем дро­бей. До­мно­жим чис­ли­тель и зна­ме­на­тель пер­вой дроби на 105, а вто­рой – на 70.

Как мы видим, числа 595 и 105 за­кан­чи­ва­ют­ся на 5, а зна­чит, де­лят­ся на 5, то есть мы можем со­кра­тить дробь: .

Также за­ме­тим, что чис­ли­тель и зна­ме­на­тель де­лят­ся на 7, и со­кра­тим дробь:

2 спо­соб – вы­пи­шем це­поч­ки эк­ви­ва­лент­ных дро­бей для  и :

Уже на этом этапе име­ет­ся сов­па­де­ние зна­ме­на­те­лей. За­ме­ним дроби им эк­ви­ва­лент­ны­ми:

Как ви­ди­те, вто­рой спо­соб дал нам ответ быст­рее, чем пер­вый.

Да­вай­те те­перь по­ду­ма­ем, сколь­ко су­ще­ству­ет общих зна­ме­на­те­лей для двух дро­бей.

Какой общий зна­ме­на­тель дро­бей  и ? Вы­пи­шем це­поч­ку эк­ви­ва­лент­ных дро­бей для  и :

Мы видим несколь­ко пар дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми ( и ,  и ,  и ).

Если мы про­дол­жим даль­ше це­поч­ки эк­ви­ва­лент­ных дро­бей, то по­лу­чим бес­ко­неч­ное мно­же­ство таких сов­па­де­ний зна­ме­на­те­лей. То есть у двух дро­бей су­ще­ству­ет бес­ко­неч­ное мно­же­ство общих зна­ме­на­те­лей, и нам под­хо­дит любой из них.

На­при­мер, про­из­ве­де­ние зна­ме­на­те­лей ис­ход­ных дро­бей  – это общий зна­ме­на­тель, од­на­ко не самый мень­ший, мы видим общий зна­ме­на­тель, ко­то­рый мень­ше, – 12.

Есть ли спо­соб отыс­ка­ния наи­мень­ше­го об­ще­го зна­ме­на­те­ля? Да, такой спо­соб су­ще­ству­ет.

Да­вай­те рас­смот­рим сле­ду­ю­щий при­мер.

При­мер 4. Вы­чис­ли­те зна­че­ние вы­ра­же­ния: .

Ре­ше­ние

Будем сле­до­вать рас­смот­рен­но­му ал­го­рит­му и вы­пи­шем це­поч­ки эк­ви­ва­лент­ных дро­бей:

Можем ли мы как-то упро­стить наш ал­го­ритм? Да, можем. Це­поч­ка с бОль­шим зна­ме­на­те­лем ко­ро­че, по­это­му с ней и будем ра­бо­тать. Возь­мем бОль­ший зна­ме­на­тель и будем скла­ды­вать его са­мо­го с собой (таким об­ра­зом, мы не про­пу­стим число 180), про­ве­ряя на каж­дом шаге, де­лит­ся ли число на мень­ший зна­ме­на­тель (45).

60 не де­лит­ся на 45, зна­чит, не будет яв­лять­ся общим зна­ме­на­те­лем для ис­ход­ных дро­бей.

60 + 60 = 120, снова не де­лит­ся на 45. Про­дол­жа­ем при­бав­лять 60.

120 + 60 = 180 де­лит­ся на 45, 180 : 45 = 4.

Тогда общий зна­ме­на­тель 180.

Вы­чис­ли­те зна­че­ние вы­ра­же­ния: .

Ре­ше­ние

Берем бОль­ший зна­ме­на­тель (35) и скла­ды­ва­ем его с самим собой до тех пор, пока ре­зуль­тат не будет де­лить­ся на мень­ший зна­ме­на­тель (21).

35 не де­лит­ся на 21.

35 + 35 = 70 не де­лит­ся на 21.

70 + 35 = 105 де­лит­ся на 21 (105 : 21 = 5), зна­чит, 105 – общий зна­ме­на­тель.

При­ве­дем обе дроби к зна­ме­на­те­лю 105, для этого чис­ли­тель и зна­ме­на­тель пер­вой дроби до­мно­жим на 5, а вто­рой – на 3: .

При­мер 5

Вы­чис­ли­те зна­че­ние вы­ра­же­ния: .

Ре­ше­ние

Когда зна­ме­на­те­ли боль­шие, при­ме­нить преды­ду­щие ме­то­ды до­ста­точ­но слож­но. Тогда раз­мыш­ля­ем так, чтобы число  де­ли­лось на 210, оно долж­но со­дер­жать мно­жи­тель 210. При этом само число рас­кла­ды­ва­ет­ся на мно­жи­те­ли: .

Так все мно­жи­те­ли числа 210 со­дер­жат­ся и в числе .

Нам нужно найти такое число, ко­то­рое со­дер­жит все мно­жи­те­ли числа 210 и числа 1155.

Скон­стру­и­ру­ем необ­хо­ди­мое число, со­дер­жа­щее все мно­жи­те­ли и пер­во­го, и вто­ро­го чисел: .

Ни один из мно­жи­те­лей убрать нель­зя – это и есть наи­мень­шее число, ко­то­рое од­но­вре­мен­но де­лить­ся на 210, и на 1155. Это наи­мень­ший общий зна­ме­на­тель. Раз­ло­же­ние на про­стые мно­жи­те­ли не толь­ко поз­во­ля­ет найти наи­мень­ший общий зна­ме­на­тель, но и под­ска­зы­ва­ет, на какой мно­жи­тель необ­хо­ди­мо до­мно­жить каж­дую дробь. Так, в пер­вом зна­ме­на­те­ле до об­ще­го зна­ме­на­те­ля не хва­та­ет мно­жи­те­ля 11, а во вто­ром – 2.

Вы­чис­ли­те зна­че­ние вы­ра­же­ния: .

Ре­ше­ние

Рас­кла­ды­ва­ем каж­дый зна­ме­на­тель на мно­жи­те­ли.

Общий зна­ме­на­тель: .

Вы­чис­ли­те зна­че­ние вы­ра­же­ния: .

Ре­ше­ние

Сна­ча­ла раз­ло­жим каж­дый зна­ме­на­тель на мно­жи­те­ли:

Кон­стру­и­ру­ем наи­мень­ший общий зна­ме­на­тель, он дол­жен со­дер­жать все мно­жи­те­ли каж­до­го зна­ме­на­те­ля.

Зна­чит, у пер­во­го зна­ме­на­те­ля не хва­та­ет мно­жи­те­лей 5 и 7, а у вто­ро­го – 2 и 11.

Чтобы срав­нить, сло­жить или вы­честь дроби с раз­ны­ми зна­ме­на­те­ля­ми, их необ­хо­ди­мо све­сти к об­ще­му зна­ме­на­те­лю. Так можно со­став­лять эк­ви­ва­лент­ные дроби, ра­бо­тать с бóльшим зна­ме­на­те­лем, вы­чис­лять про­из­ве­де­ние на­чаль­ных зна­ме­на­те­лей, а также на­хо­дить наи­мень­ший общий зна­ме­на­тель, путём раз­ло­же­ния на мно­жи­те­ли ис­ход­ных зна­ме­на­те­лей.

 

Рис. 1. Срав­не­ние дро­бей с раз­ны­ми зна­ме­на­те­ля­ми

Да­вай­те по­про­бу­ем разо­брать на при­ме­ре, как можно срав­нить две дроби с раз­ны­ми зна­ме­на­те­ля­ми (рис. 1). 

Если су­дить по кар­тин­ке, то может по­ка­зать­ся, что пер­вая дробь од­но­знач­но боль­ше, да­вай­те про­ве­рим это пред­по­ло­же­ние ма­те­ма­ти­че­ским спо­со­бом. Для на­ча­ла да­вай­те вспом­ним, что: при срав­не­нии дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми боль­ше та дробь, чис­ли­тель ко­то­рой боль­ше (рис. 2).

Рис. 2. Срав­не­ние дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми

Зна­чит, для того чтобы срав­нить две дроби с раз­ны­ми чис­ли­те­ля­ми и зна­ме­на­те­ля­ми, нам нужно при­ве­сти их к об­ще­му зна­ме­на­те­лю. Как же это сде­лать? Вер­нем­ся к нашим дро­бям  и  и вос­поль­зу­ем­ся ос­нов­ным свой­ством дро­бей. Нам нужно умно­жить и чис­ли­тель, и зна­ме­на­тель на одно и то же число и по­лу­чим дробь, рав­ную дан­ной. Да­вай­те умно­жим чис­ли­тель и зна­ме­на­тель пер­вой дроби на зна­ме­на­тель вто­рой. А потом чис­ли­тель и зна­ме­на­тель вто­рой дроби на зна­ме­на­тель пер­вой. (6 и 8 – до­пол­ни­тель­ные мно­жи­те­ли). Те­перь у нас есть две дроби с оди­на­ко­вы­ми зна­ме­на­те­ля­ми и мы можем их срав­нить.

Учи­ты­ва­ем уже зна­ко­мое нам пра­ви­ло, что из двух дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми боль­ше та, чис­ли­тель ко­то­рой боль­ше.

Да­вай­те рас­смот­рим дру­гой спо­соб при­ве­де­ния к об­ще­му зна­ме­на­те­лю, его удоб­нее ис­поль­зо­вать в слу­чае, если зна­ме­на­те­ля­ми вы­сту­па­ют очень боль­шие числа. Он ос­но­ван на опре­де­ле­нии об­ще­го зна­ме­на­те­ля дро­бей.

Возь­мем уже зна­ко­мую нам пару дро­бей  и . Для того чтобы найти общий зна­ме­на­тель, нам нужно найти наи­мень­шее общее крат­ное для 8 и 6. , зна­чит, и обе дроби нам нужно при­ве­сти к зна­ме­на­те­лю 24.

Чтобы при­ве­сти дробь  к зна­ме­на­те­лю 24, ее нужно умно­жить на 3. Дробь  – на 4.

• Найти наи­мень­ший общий зна­ме­на­тель (НОЗ). Для этого нужно опре­де­лить НОК зна­ме­на­те­лей этих дро­бей, оно и будет НОЗ ис­ход­ных дро­бей.
• Опре­де­лить до­пол­ни­тель­ный мно­жи­тель для каж­до­го из ис­ход­ных дро­бей.
• Умно­жить чис­ли­тель и зна­ме­на­тель ис­ход­ных дро­бей на со­от­вет­ству­ю­щий до­пол­ни­тель­ный мно­жи­тель.

При­ве­сти к об­ще­му зна­ме­на­те­лю дроби  и .

Ре­ше­ние

Ответ:  и .

Не все­гда легко можно по­до­брать НОК чисел, и в таком слу­чае вам по­мо­жет уме­ние рас­кла­ды­вать числа на про­из­ве­де­ние про­стых мно­жи­те­лей.

За­да­ние

При­ве­сти к об­ще­му зна­ме­на­те­лю дроби  и .

Ре­ше­ние

Ответ:  и .

Мы на­учи­лись при­во­дить дроби к об­ще­му зна­ме­на­те­лю.

По­вто­ре­ние. Ос­нов­ное свой­ство дроби.

Если чис­ли­тель и зна­ме­на­тель дроби умно­жить или раз­де­лить на одно и то же на­ту­раль­ное число, то по­лу­чит­ся рав­ная ей дробь.

На­при­мер, чис­ли­тель и зна­ме­на­тель дроби   можно раз­де­лить на 2. По­лу­чим дробь  . Эту опе­ра­цию на­зы­ва­ют со­кра­ще­ни­ем дроби. Можно вы­пол­нить и об­рат­ное пре­об­ра­зо­ва­ние, умно­жив чис­ли­тель и зна­ме­на­тель дроби  на 2. В этом слу­чае го­во­рят, что мы при­ве­ли дробь к но­во­му зна­ме­на­те­лю. Число 2 на­зы­ва­ют до­пол­ни­тель­ным мно­жи­те­лем.

Вывод. Дробь можно при­ве­сти к лю­бо­му зна­ме­на­те­лю крат­но­му зна­ме­на­те­лю дан­ной дроби. Для того чтобы при­ве­сти дробь к но­во­му зна­ме­на­те­лю, ее чис­ли­тель и зна­ме­на­тель умно­жа­ют на до­пол­ни­тель­ный мно­жи­тель.

1.     При­ве­ди­те дробь    к зна­ме­на­те­лю 35.

Число 35 крат­но 7, то есть 35 де­лит­ся на 7 без остат­ка. Зна­чит, это пре­об­ра­зо­ва­ние воз­мож­но. Най­дем до­пол­ни­тель­ный мно­жи­тель. Для этого раз­де­лим 35 на 7. По­лу­чим 5. Умно­жим на 5 чис­ли­тель и зна­ме­на­тель ис­ход­ной дроби.

2.   При­ве­ди­те дробь    к зна­ме­на­те­лю 18.

Най­дем до­пол­ни­тель­ный мно­жи­тель. Для этого раз­де­лим новый зна­ме­на­тель на ис­ход­ный. По­лу­чим 3. Умно­жим на 3 чис­ли­тель и зна­ме­на­тель дан­ной дроби.

3.     При­ве­ди­те дробь    к зна­ме­на­те­лю 60.

Раз­де­лив 60 на 15, по­лу­чим до­пол­ни­тель­ный мно­жи­тель. Он равен 4. Умно­жим чис­ли­тель и зна­ме­на­тель на 4.

4.     При­ве­ди­те дробь    к зна­ме­на­те­лю 24

В неслож­ных слу­ча­ях при­ве­де­ние к но­во­му зна­ме­на­те­лю вы­пол­ня­ют в уме. При­ня­то толь­ко ука­зы­вать до­пол­ни­тель­ный мно­жи­тель за ско­боч­кой чуть пра­вее и выше ис­ход­ной дроби.

Дробь   можно при­ве­сти к зна­ме­на­те­лю 15 и дробь   можно при­ве­сти к зна­ме­на­те­лю 15. У дро­бей  и    общий зна­ме­на­тель 15.

Общим зна­ме­на­те­лем дро­бей может быть любое общее крат­ное их зна­ме­на­те­лей. Для про­сто­ты дроби при­во­дят к наи­мень­ше­му об­ще­му зна­ме­на­те­лю. Он равен наи­мень­ше­му об­ще­му крат­но­му зна­ме­на­те­лей дан­ных дро­бей.

При­мер. При­ве­сти к наи­мень­ше­му об­ще­му зна­ме­на­те­лю дроби  и  .

Сна­ча­ла най­дем наи­мень­шее общее крат­ное зна­ме­на­те­лей дан­ных дро­бей. Это число 12. Най­дем до­пол­ни­тель­ный мно­жи­тель для пер­вой и для вто­рой дроби. Для этого 12 раз­де­лим на 4 и на 6. Три – это до­пол­ни­тель­ный мно­жи­тель для пер­вой дроби, а два – для вто­рой. При­ве­дем дроби к зна­ме­на­те­лю 12.

Мы при­ве­ли дроби  и   к об­ще­му зна­ме­на­те­лю, то есть мы нашли рав­ные им дроби, у ко­то­рых один и тот же зна­ме­на­тель.

Пра­ви­ло. Чтобы при­ве­сти дроби к наи­мень­ше­му об­ще­му зна­ме­на­те­лю, надо

Во-пер­вых, найти наи­мень­шее общее крат­ное зна­ме­на­те­лей этих дро­бей, оно и будет их наи­мень­шим общим зна­ме­на­те­лем;

Во-вто­рых, раз­де­лить наи­мень­ший общий зна­ме­на­тель на зна­ме­на­те­ли дан­ных дро­бей, т. е. найти для каж­дой дроби до­пол­ни­тель­ный мно­жи­тель.

В-тре­тьих, умно­жить чис­ли­тель и зна­ме­на­тель каж­дой дроби на ее до­пол­ни­тель­ный мно­жи­тель.

а) При­ве­сти к об­ще­му зна­ме­на­те­лю дроби  и  .

Наи­мень­ший общий зна­ме­на­тель равен 12. До­пол­ни­тель­ный мно­жи­тель для пер­вой дроби – 4, для вто­рой – 3. При­во­дим дроби к зна­ме­на­те­лю 24.

б) При­ве­сти к об­ще­му зна­ме­на­те­лю дроби  и  .

Наи­мень­ший общий зна­ме­на­тель равен 45. Раз­де­лив 45 на 9 на 15, по­лу­чим, со­от­вет­ствен­но, 5 и 3. При­во­дим дроби к зна­ме­на­те­лю 45.

в) При­ве­сти к об­ще­му зна­ме­на­те­лю дроби  и  .

Общий зна­ме­на­тель – 24. До­пол­ни­тель­ные мно­жи­те­ли, со­от­вет­ствен­но, – 2 и 3.

Ино­гда бы­ва­ет труд­но по­до­брать устно наи­мень­шее общее крат­ное для зна­ме­на­те­лей дан­ных дро­бей. Тогда общий зна­ме­на­тель и до­пол­ни­тель­ные мно­жи­те­ли на­хо­дят с по­мо­щью раз­ло­же­ния на про­стые мно­жи­те­ли.

При­ве­сти к об­ще­му зна­ме­на­те­лю дроби  и  .

Раз­ло­жим числа 60 и 168 на про­стые мно­жи­те­ли. Вы­пи­шем раз­ло­же­ние числа 60 и до­ба­вим недо­ста­ю­щие мно­жи­те­ли 2 и 7 из вто­ро­го раз­ло­же­ния. Умно­жим 60 на 14 и по­лу­чим общий зна­ме­на­тель 840. До­пол­ни­тель­ный мно­жи­тель для пер­вой дроби – это 14. До­пол­ни­тель­ный мно­жи­тель для вто­рой дроби — 5. При­ве­дем дроби к об­ще­му зна­ме­на­те­лю 840.

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/slozhenie-i-vychitanie-drobej-s-raznymi-znamenatelyami/privedenie-drobey-k-obschemu-znamenatelyu-slupko-m-v

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/slozhenie-i-vychitanie-drobej-s-raznymi-znamenatelyami/privedenie-drobey-k-obschemu-znamenatelyu-terentieva-i-g

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/slozhenie-i-vychitanie-drobej-s-raznymi-znamenatelyami/privedenie-drobey-k-obschemu-znamenatelyu-moskalenko-m-v

источник видео — http://www.youtube.com/watch?v=AQcsPkqBK-w

источник видео — http://www.youtube.com/watch?v=xmvU6-N8CZo

источник ивдео — http://www.youtube.com/watch?v=Mgj3uV5G95Q

источник видео — http://www. youtube.com/watch?v=1orzNXFOTSg

источник видео — http://www.youtube.com/watch?v=4nGcI1eO198

источник видео — http://www.youtube.com/watch?v=ks8spHhfS2E

источник презентация — http://ppt4web.ru/matematika/privedenie-drobejj-k-obshhemu-znamenatelju-klass.html

 

Приведение дробей к общему знаменателю

Поможет нам разобраться с этой темой основное свойство дроби, которое, напомню, звучит следующим образом:

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Например

Напомним, что дроби можно приводить только к тем знаменателям, которые кратны исходным.

Обратите внимание, мы можем обе дроби привести к знаменателю 12.

Говорят, можно  и  можно привести к общему знаменателю.

То есть если у нас есть две дроби с разными знаменателями, мы можем сделать так, чтобы знаменатели стали одинаковыми.

Приведение к общему знаменателю понадобится для сложения и вычитания обыкновенных дробей. Кроме того, сравнивать дроби с одинаковыми знаменателями очень просто.

Примеры

Кстати, число, на которое мы умножаем числитель и знаменатель, называется дополнительным множителем.

В математике существует много способов нахождения общего кратного чисел, а значит общего знаменателя для дробей.

Поэтому, если перед вами стоит задача приведения дробей к общему знаменателю, не торопитесь. Правильно выбранный способ может сократить ваше решение.

Пример

Этот примем помогает намного сократить вычисления, но, к сожалению, применяется он только в случае, когда один знаменатель делится на другой.

Существует способ, который работает для любых дробей. Суть способа заключается в нахождении наименьшего общего кратного знаменателей. Этот способ используется чаще всего.

Пример

Приведём к общему знаменателю дроби

Последний этап – умножение дробей на дополнительные множители.

Если вам сложно раскладывать числа на множители, находить наименьший общий знаменатель, то следующий способ для вас.

Пример

В результате знаменатели обеих дробей стали равными произведению исходных знаменателей.

Этот способ простой для понимания. Но приготовьтесь много считать, если используете этот способ для дробей с большими числами в числителе и знаменателе.

Итоги

Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.

Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.

Тест по математике 6 класс «Приведение дробей к общему знаменателю»

Тест по теме «Приведение дробей к общему знаменателю»

6 класс

Вариант I

1. Общий знаменатель дробей – это:

а) наибольшее общее кратное знаменателей дробей;

б) наименьшее общее кратное знаменателей дробей;

в) наибольшее натуральное число, на которое делятся без остатка знаменатели дробей;

г) наибольшее натуральное число, которое делится без остатка на знаменатели дробей.

2. Какую дробь можно привести к знаменателю 50?

а) б) в) г)

3. Приведите дробь к знаменателю 49:

а) б) в) г)

4. Наименьшим общим знаменателем дробей и является число:

а) 150 б) 70 в) 25 г) 60

5. Сколько сотых содержит дробь ?

а) пять б) десять в) двенадцать г) двадцать

6. Приведите дроби и к знаменателю 35.

а) и б) и в) и г) и

7. Можно ли привести дробь к знаменателю 30?

а) да б) нет

8. Выразите ч в шестидесятых долях часа.

а) ч б) ч в) ч г) ч

9. Какой десятичной дроби равна дробь ?

а) 0,19 б) 1,9 в) 0,095 г) 0,95

10. Выразите в минутах часа:

а) 20 мин б) 45 мин в) 30 мин г) 40 мин

Вариант II

1. Дополнительный множитель дробей – это:

а) наибольшее натуральное число, на которое делят знаменатели дробей;

б) наименьшее натуральное число, на которое делят знаменатели дробей;

в) наибольшее натуральное число, на которое делятся без остатка знаменатели дробей;

г) наименьшее натуральное число, полученное при делении общего знаменателя на знаменатели дробей.

2. Какую дробь можно привести к знаменателю 60?

а) б) в) г)

3. Приведите дробь к знаменателю 35:

а) б) в) г)

4. Наименьшим общим знаменателем дробей и является число:

а) 48 б) 70 в) 24 г) 460

5. Сколько сотых содержит дробь ?

а) две б) десять в) сто г) восемнадцать

6. Приведите дроби и к знаменателю 72.

а) и б) и в) и г) и

7. Можно ли привести дробь к знаменателю 100?

а) да б) нет

8. Выразите мин в шестидесятых долях минуты.

а) мин б) мин в) мин г) мин

9. Какой десятичной дроби равна дробь ?

а) 0,09 б) 0,36 в) 0,095 г) 3,6

10. Выразите в граммах кг:

а) 250 г б) 800 г в) 750 г г) 500 г

Ключи

Вариант I	Вариант II
1-б 2-б 3-в 4-г 5-в 6-б 7-б 8-г 9-г 10-б	1-г 2-в 3-а 4-в 5-г 6-а 7-б 8-в 9-б 10-в

Урок 51.

приведение дробей к общему знаменателю — Математика — 5 класс

Математика

5 класс

Урок № 51

Приведение дробей к общему знаменателю

Перечень рассматриваемых вопросов:

• основное свойство дроби;
• общий знаменатель дробей;
• дополнительный множитель;
• НОК двух чисел;
• наименьший общий знаменатель.

Тезаурус

Общий знаменатель – это число всегда положительное, на которое делятся знаменатели данных дробей.

Наименьший общий знаменатель – это наименьшее положительное число, кратное знаменателям данных дробей.

Дополнительный множитель – это число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель.

Обязательная литература:

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Вы уже знаете, что дробь в математике – это число, состоящее из одной или нескольких частей единиц, и умеете определять и называть часть целого.

Вопрос: какая часть яблока на картинке?

Ответ:

Вопрос: какая часть пиццы осталась на тарелке?

Ответ: .

Или, например, круг разделили на восемь частей. Четыре части закрасили в другой цвет: значит, закрашено части круга.

Но, если посмотреть внимательнее, четыре доли круга, разделённого на восемь частей, – это ровно половина. Значит, дробь равна дроби .

Вспомним основное свойство дроби.

Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.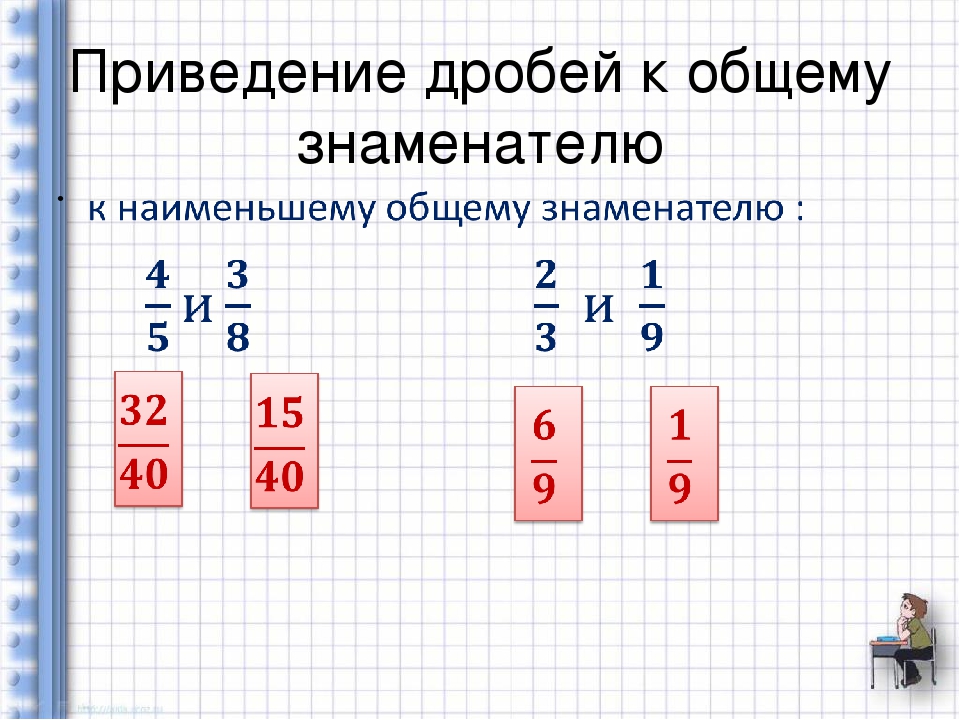

Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю.

Для этого найдём число, которое делится на 8 и 3, – например, число 24.

Дополнительный множитель обычно пишут слева над числителем:

Приведём дроби к знаменателю 24. Для этого умножим числитель и знаменатель дроби на дополнительный множитель 3.

Теперь умножим числитель и знаменатель дроби на дополнительный множитель 8.

Дробииприведены к общему знаменателю.

Далее приведём дроби и к наименьшему общему знаменателю.

Так как наименьшее общее кратное (НОК) чисел 36 и 54 равно 108, то наименьший общий знаменатель этих дробей также равен 108.

Соответственно, чтобы привести дробь к знаменателю 108, необходимо и числитель, и знаменатель дроби умножить на 3:

Чтобы привести дробь к тому же знаменателю, умножаем и числитель, и знаменатель этой дроби на 2:

Таким образом, алгоритм приведения дробей к наименьшему

1. деление на простые множители знаменателей дробей;
2. поиск наименьшего общего кратного(НОК)для знаменателей этих дробей;
3. приведение дроби к общему знаменателю, то есть умножение и числителя, и знаменателя дроби на множитель.

Итак, сегодня мы научились находить наименьший общий знаменатель дробей двумя способами:

• первый способ – перемножить знаменатели этих дробей;
• второй способ – найти наименьшее общее кратное этих дробей.

Тренировочные задания

№ 1. Для дроби выберите из представленных равную ей дробь со знаменателем 6; 15; 102:

Чтобы привести дробь к знаменателю 6, нужно числитель и знаменатель дроби умножить на дополнительный множитель 2:

Чтобы привести дробь к знаменателю 15, нужно числитель и знаменатель дроби умножить на дополнительный множитель 5:

Чтобы привести дробь к знаменателю 102, нужно числитель и знаменатель дроби умножить на дополнительный множитель 34:

Следовательно, правильный ответ:

№ 2. Какое число является наименьшим общим знаменателем дробей и ?

12

24

96

35

Чтобы найти наименьший общий знаменатель дробей и , нужно:

1. разложить на простые множители знаменатели дробей: 8 = 2 ∙ 2 ∙ 2 и 12 = 2 ∙ 2 ∙ 3;
2. найти НОК (8, 12) = 24.

Следовательно, правильный ответ: 24.

Приведение дробей к общему знаменателю

Учитель: Мсоева З.И.

Класс : 6

Тема урока «Приведение дробей к общему знаменателю».

Цель урока:

Познакомиться с правилом приведения дробей к общему знаменателю и сформировать способность к его практическому использованию.

Задачи:

образовательные — познакомиться с правилом приведения дробей к общему знаменателю и сформировать способность к его практическому использованию;

развивающие— развитие логического мышления, доказательной математической речи, наблюдательности, смекалки;

воспитательные— воспитание взаимоуважения, целеустремленности, самостоятельности; создание благоприятных условий, эмоционального и психологического климата в классе для восприятия учебного материала.

Тип урока: урок изучения нового материала.

Оборудование : мультимедийный проектор (интерактивная доска), напечатанные на карточках дополнительные задания, напечатанные на карточках правила для учащихся, учебник «Математика 6 класс», автор Мерзляк А.Г.

Ход урока

1. Самоопределение к деятельности:

Прозвенел звонок веселый,
Мы начать урок готовы?
Будем слушать, рассуждать
И друг другу помогать.

Здравствуйте, садитесь.

Мы спокойны, добры и приветливы. Глубоко вдохните. Выдохните вчерашнюю обиду, злость, беспокойство. Вдохните в себя тепло солнечных лучей. Я желаю вам хорошего настроения. Я надеюсь, хорошее настроение сохранится у вас до конца урока.

2. Актуализация знаний:

Чтоб ошибки не лезли в тетрадь,

Надо правила помнить и знать.

— О чем мы говорили на предыдущих уроках?

— Что значить сократить дробь?

— Всякую ли дробь можно сократить?

— На чем основано сокращение дробей?

— Сформулируйте основное свойство дроби.

— Пришло время проверить ваше домашнее задание. (Откройте тетради и поменяйтесь друг с другом). Проверка по слайду. Выставление оценок. Кто получил 5? 4? 3?

Устная работа:

— Предлагаю найти ошибки в ваших вычислениях и дать правильный ответ:

1.

2. Найти НОК чисел:

5 и 7

8 и 4

6 и 9

Повторить правила

1. Чему равен НОК взаимно простых чисел

2. Чему равен НОК, если одно из чисел является делителем другого

3. Вместо х подставь такое число, чтобы равенство было верным

3. Постановка учебной задачи:

— Сегодня мы продолжим работать над преобразованием дробей.

1. Умножить числитель и знаменатель дроби

— Как на ваш взгляд можно назвать такое преобразование дробей? (Приведение к новому знаменателю)

2. Приведите дробь к знаменателю 18, 33, 25. Почему нельзя привести к знаменателю 25?( Потому, что 25 не делиться на 3)

— Значит новый знаменатель должен быть для предыдущего …(кратным)

3. Выполни действия

— Что надо сделать предварительно, чтобы можно было выполнить действие? (Привести дроби к одинаковому знаменателю(общему)).

-А мы умеем это делать? (Нет).

— Сформулируйте пожалуйста тему урока. (Приведение дробей к общему знаменателю)

— А какие цели мы можем себе поставить на урок?

(…)

— Познакомиться с правилом приведения дробей к общему знаменателю и сформировать способность к его практическому использованию.

4. Открытие нового знания:

-Умножьте числитель и знаменатель дроби , а дроби

— Что можно заметить? (У дробей стал одинаковый знаменатель).

— Говорят , что дроби привели к общему знаменателю.

— А чем является этот знаменатель для чисел 3 и 5. (Кратным)

— Общим знаменателем дробей может быть любое общее кратное их знаменателей, но обычно дроби приводят к наименьшему знаменателю.

— Давайте найдем НОК(3,5)=15. Приведем дроби к знаменателю 15.

— Что необходимо для этого?

— Дробь умножить на 3 , а дробь на 5.

— 3 и 5 называются дополнительными множителями.

— Давайте попытаемся вывести правило приведения дробей к общему знаменателю. (…)

Приведение дробей к наименьшему общему знаменателю (НОЗ)

Чтобы привести несколько дробей к наименьшему общему знаменателю, надо:

1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;

2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;

3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Пример: Привести дроби к наименьшему общему знаменателю

и

НОК (6; 8) = 24

24 : 6 = 4; 24 : 8 = 3

= и =

Физпауза.

Потрудились славно, отдохнем исправно,

Вот минутка для игры или физзарядки.

Мы при счете раз, два, три,

Встали попорядку.

Ученик проводит зарядку.

5. Первичное закрепление:

№ 236, 237 (1-4)

Дополнительные карточки для тех кто выполнил быстрее.

Приведи дроби к наименьшему общему знаменателю. Если возможно, вначале сократи их.

6. Первичная проверка усвоение материала:

(самостоятельная работа с самопроверкой в классе)

Вариант 1 1. Приведите дробь к знаменателю 24. 2. Приведите дробь к знаменателю 39. 3. Приведите к наименьшему общему знаменателю дроби: а) б) в)

Вариант 2 1. Приведите дробь к знаменателю 36. 2. Приведите дробь к знаменателю 49. 3. Приведите к наименьшему общему знаменателю дроби: а) б) в)

7. Включение знаний в систему:

1. № 246

2. Из ряда чисел назови те, которые могут быть общими знаменателями для указанных дробей:

6, 12, 24, 40, 48

20, 30, 45, 50, 60

8.Домашнее задание:

Учитель: Пришло время для нового домашнего задания.

п.9 № 239, № 300242 (5 — 8).

9. Итог урока.

Учитель: Каким сегодня был для нас урок (закрепление или открытие) и почему?

Учитель: Что нам помогало на уроке?

10. Рефлексия

— Вы сегодня хорошо работали, помогали друг другу и справились со всеми заданиями. Благодарю всех за активную работу. Предлагаю оценить свою работу на уроке.

Сейчас – за окном осень. А давайте закроем глаза и представим, что сейчас – лето, мы с вами на цветущей поляне. Попытаться вспомнить наш урок, и ответить на 3 вопроса:

Как я себя чувствовал на уроке и доволен ли собой?

Легко ли вам было работать на уроке?

Трудно ли было выполнять задание?

Откройте глаза, перед вами лежат 3 лошадки-облака (зелёная, жёлтая, красная), выберите одну из них.

Зелёная обозначает: “Я удовлетворён уроком, я хорошо работал на уроке, понимал всё и получил заслуженную оценку”.

Жёлтая обозначает: “ Урок был интересен, я принимал в нём участие, но что-то осталось еще не понятным”.

Красная шарик обозначает: “ Пользы от урока я получил мало, многое не понял”.

Уходя из класса, прикрепите на доску одну из них.

Урок окончен. До свидания.

Онлайн урок: Приведение дробей к общему знаменателю по предмету Математика 6 класс

Общим знаменателем дробей может быть любое общее кратное их знаменателей (например, произведение знаменателей).

Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.

 

Пример 1

Приведем к наименьшему общему знаменателю дроби \(\mathbf{\frac{3}{4}}\) и \(\mathbf{\frac{5}{6}}\)

Решение:

Наименьшим общим кратным чисел 4 и 6 является 12

Чтобы привести дробь \(\mathbf{\frac{3}{4}}\) к знаменателю 12, надо умножить числитель и знаменатель этой дроби на дополнительный множитель 3 (12 : 4 = 3)

Получим \(\mathbf{\frac{3}{4} = \frac{3\cdot3}{4\cdot3} = \frac{9}{12}}\)

Чтобы привести дробь \(\mathbf{\frac{5}{6}}\) к знаменателю 12, надо числитель и знаменатель этой дроби умножить на дополнительный множитель 2 (12 : 6 = 2)

Получим \(\mathbf{\frac{5}{6} = \frac{5\cdot2}{6\cdot2} = \frac{10}{12}}\)

Итак, \(\mathbf{\frac{3}{4} = \frac{9}{12}}\), а \(\mathbf{\frac{5}{6} = \frac{10}{12}}\)

 

Чтобы привести дроби к наименьшему общему знаменателю, надо:

1. Найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем
2. Разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель
3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель

В сложных случаях наименьший общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.

 

Пример 2

Приведем дроби \(\mathbf{\frac{11}{60}}\) и \(\mathbf{\frac{31}{168}}\) к наименьшему общему знаменателю.

Решение:

Разложим знаменатели данных дробей на простые множители:

\(\mathbf{60 = 2\cdot2\cdot3\cdot5}\)

\(\mathbf{168 = 2\cdot2\cdot2\cdot3\cdot7}\)

Найдем наименьший общий знаменатель: \(\mathbf{2\cdot2\cdot2\cdot3\cdot5\cdot7 = 840}\)

Дополнительными множителями для дроби \(\mathbf{\frac{11}{60}}\) является произведение \(\mathbf{2\cdot7}\), т.е. тех множителей, которые надо добавить к разложению числа 60, чтобы получить разложение общего знаменателя 840.

Поэтому \(\mathbf{\frac{11}{60} = \frac{11\cdot2\cdot7}{60\cdot2\cdot7} = \frac{154}{840}}\)

Для дроби \(\mathbf{\frac{31}{168}}\) таким же способом находим дополнительный множитель 5.

Значит, \(\mathbf{\frac{31}{168} = \frac{31\cdot5}{168\cdot5} = \frac{155}{840}}\)

 

Пример 3

Приведите к наименьшему общему знаменателю дроби:

А) \(\mathbf{\frac{1}{3}}\) и \(\mathbf{\frac{2}{9}}\)

Б) \(\mathbf{\frac{1}{9}}\) и \(\mathbf{\frac{7}{30}}\)

В) \(\mathbf{\frac{1}{10}}\) и \(\mathbf{\frac{3}{4}}\)

Г) \(\mathbf{\frac{8}{15}}\) и \(\mathbf{\frac{7}{12}}\)

Решение:

А)

\(\mathbf{НОК (3;9) = 9}\)

\(\mathbf{\frac{1}{3} = \frac{1\cdot3}{3\cdot3} = \frac{3}{9}}\)

\(\mathbf{\frac{2}{9} = \frac{2\cdot1}{9\cdot1} = \frac{2}{9}}\)

Б)

\(\mathbf{НОК (9;30) = 90}\)

\(\mathbf{\frac{1}{9} = \frac{1\cdot10}{9\cdot10} = \frac{10}{90}}\)

\(\mathbf{\frac{7}{30} = \frac{7\cdot3}{30\cdot3} = \frac{21}{90}}\)

В)

\(\mathbf{НОК (10;4) = 20}\)

\(\mathbf{\frac{1}{10} = \frac{1\cdot2}{10\cdot2} = \frac{2}{20}}\)

\(\mathbf{\frac{3}{4} = \frac{3\cdot5}{4\cdot5} = \frac{15}{20}}\)

Г)

\(\mathbf{НОК (15;12) = 60}\)

\(\mathbf{\frac{8}{15} = \frac{8\cdot4}{15\cdot4} = \frac{32}{60}}\)

\(\mathbf{\frac{7}{12} = \frac{7\cdot5}{12\cdot5} = \frac{35}{60}}\)

 

Пример 4

Приведите дроби к общему знаменателю и сравните их:

А) \(\mathbf{\frac{2}{3}}\) и \(\mathbf{\frac{5}{7}}\)

Б) \(\mathbf{\frac{2}{5}}\) и \(\mathbf{\frac{1}{6}}\)

Решение:

А)

\(\mathbf{НОК (3;7) = 21}\)

\(\mathbf{\frac{2}{3} = \frac{2\cdot7}{3\cdot7} = \frac{14}{21}}\)

\(\mathbf{\frac{5}{7} = \frac{5\cdot3}{7\cdot3} = \frac{15}{21}}\)

\(\mathbf{\frac{14}{21} < \frac{15}{21}}\)

Б)

\(\mathbf{НОК (5;6) = 30}\)

\(\mathbf{\frac{2}{5} = \frac{2\cdot6}{5\cdot6} = \frac{12}{30}}\)

\(\mathbf{\frac{1}{6} = \frac{1\cdot5}{6\cdot5} = \frac{5}{30}}\)

\(\mathbf{\frac{12}{30} > \frac{5}{30}}\)

Общий знаменатель

Это самый простой из известных нам методов сложения и вычитания дробей!

Что такое знаменатель?

Знаменатель — это нижнее число в дроби.

Показывает, на сколько равных частей разделен предмет.

Что такое общий знаменатель?

Когда знаменатели двух или более дробей равны и одинаковому , они равны Общим знаменателям .

Почему это важно?

Прежде чем мы сможем сложить или вычесть дроби, дроби должны иметь общий знаменатель

Другими словами, знаменатели должны совпадать с .

Делаем знаменатели одинаковыми

Чтобы сделать знаменатели одинаковыми, мы можем:

Умножьте верхнюю и нижнюю часть каждой дроби на знаменатель другой.

Как в этом примере (нажмите кнопку воспроизведения) :

Это всегда работает, но нам часто нужно впоследствии упростить дробь, как в этом примере (нажмите кнопку воспроизведения) :

Мы упростили дробь 20 32 до 10 16 , затем до 5 8 , разделив верхнюю и нижнюю части на 2 каждый раз, и это очень просто!

Что мы сделали?

1. Мы умножили каждую дробь на знаменатель другой. Давайте использовать буквы вместо цифр, чтобы показать это:

2. И поскольку теперь у них одинаковый знаменатель, мы можем сложить их:

За один шаг!

Мы могли бы сделать эти две вещи за один шаг следующим образом:

Что мы можем использовать так:

Пример: Что такое

2 3 + 4 5 ?

2 3 + 4 5 = 2 × 5 + 3 × 4 3 × 5 = 10 + 12 15 = 22 15

(Примечание: a было 2, b было 3, c было 4 и d было 5.)

Так делают специалисты!

Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея

Результаты обучения

• Определить наименьший общий знаменатель двух дробей
• Преобразование двух дробей в эквивалентные дроби на ЖК-дисплее
• Сложить две дроби с разными знаменателями

В предыдущем разделе мы объяснили, как складывать и вычитать дроби с общим знаменателем. Но как мы можем складывать и вычитать дроби с разными знаменателями?

Давайте снова подумаем о монетах. Можете ли вы добавить четверть и одну копейку? Можно сказать, что есть две монеты, но это не очень полезно. Чтобы найти общую стоимость одной четверти плюс одна копейка, вы меняете их на одну и ту же единицу — центы. Одна четверть равна [латексу] 25 [/ латексу] центов, а одна десятицентовая монета равна [латексу] 10 [/ латексу] центов, поэтому сумма составляет [латекс] 35 [/ латекс] центов. См. Изображение ниже.

Вместе четверть и десять центов стоят [латекс] 35 [/ latex] центов или [latex] \ frac {35} {100} [/ latex] доллара.

Точно так же, когда мы складываем дроби с разными знаменателями, мы должны преобразовать их в эквивалентные дроби с общим знаменателем. Что касается монет, когда мы конвертируем их в центы, знаменатель будет [латекс] 100 [/ латекс]. Поскольку в одном долларе [латекс] 100 [/ latex] центов, [latex] 25 [/ latex] центов — это [latex] \ frac {25} {100} [/ latex] и [latex] 10 [/ latex] центов — это [латекс] \ frac {10} {100} [/ latex]. Итак, мы добавляем [latex] \ frac {25} {100} + \ frac {10} {100} [/ latex], чтобы получить [latex] \ frac {35} {100} [/ latex], то есть [латекс] 35 [/ латекс] центов.

Вы попрактиковались в сложении и вычитании дробей с общим знаменателем. Теперь давайте посмотрим, что вам нужно делать с дробями с разными знаменателями.
Сначала мы будем использовать дробные плитки для моделирования поиска общего знаменателя для [latex] \ frac {1} {2} [/ latex] и [latex] \ frac {1} {3} [/ latex].

Начнем с одной плитки [latex] \ frac {1} {2} [/ latex] и плитки [latex] \ frac {1} {3} [/ latex]. Мы хотим найти общую дробную плитку, которую мы можем использовать для точного сопоставления как [latex] \ frac {1} {2} [/ latex], так и [latex] \ frac {1} {3} [/ latex].
Если мы попробуем кусочки [latex] \ frac {1} {4} [/ latex], [latex] 2 [/ latex] из них точно совпадут с [latex] \ frac {1} {2} [/ latex] кусок, но они не совсем соответствуют куску [latex] \ frac {1} {3} [/ latex].

Если мы попробуем кусочки [латекса] \ frac {1} {5} [/ latex], они не будут полностью покрывать кусок [латекса] \ frac {1} {2} [/ latex] или [латекс] \ frac {1} {3} [/ latex] кусок.

Если мы попробуем кусочки [latex] \ frac {1} {6} [/ latex], то увидим, что ровно [latex] 3 [/ latex] из них покрывают [латекс] \ frac {1} {2} [/ latex] кусок, и ровно [latex] 2 [/ latex] из них покрывают [latex] \ frac {1} {3} [/ latex] кусок.

Если бы мы попробовали кусочки [latex] \ frac {1} {12} [/ latex], они тоже подействовали бы.

Плитка даже меньшего размера, такая как [латекс] \ frac {1} {24} [/ latex] и [latex] \ frac {1} {48} [/ latex], также точно покрывает [латекс] \ frac Элемент {1} {2} [/ latex] и кусок [latex] \ frac {1} {3} [/ latex].

Знаменатель наибольшего куска, покрывающего обе дроби, является наименьшим общим знаменателем (ЖКД) этих двух дробей. Итак, наименьший общий знаменатель для [латекса] \ frac {1} {2} [/ latex] и [latex] \ frac {1} {3} [/ latex] является [latex] 6 [/ latex].

Обратите внимание, что все плитки, покрывающие [латекс] \ frac {1} {2} [/ latex] и [latex] \ frac {1} {3} [/ latex], имеют нечто общее: их знаменатели являются общими кратными of [latex] 2 [/ latex] и [latex] 3 [/ latex], знаменатели [latex] \ frac {1} {2} [/ latex] и [latex] \ frac {1} {3} [ /латекс]. Наименьшее общее кратное (НОК) знаменателей — [латекс] 6 [/ латекс], поэтому мы говорим, что [латекс] 6 [/ латекс] является наименьшим общим знаменателем (ЖКД) дробей [латекс] \ frac { 1} {2} [/ latex] и [латекс] \ frac {1} {3} [/ latex].

Выполнение манипулятивного математического задания «Поиск наименьшего общего знаменателя» поможет вам лучше понять ЖК-дисплей.

Наименьший общий знаменатель

Наименьший общий знаменатель (ЖКД) двух дробей — это наименьшее общее кратное (НОК) их знаменателей.

Чтобы найти ЖКД двух дробей, мы найдем НОК их знаменателей. Мы следуем процедуре, которую использовали ранее, чтобы найти НОК двух чисел. При нахождении ЖК-дисплея мы используем только знаменатели дробей, а не числители.

Пример

Найдите ЖК-дисплей для фракций: [latex] \ frac {7} {12} [/ latex] и [latex] \ frac {5} {18} [/ latex]

Решение:

Разложите каждый знаменатель на его простые числа.
Перечислите простые числа [латекс] 12 [/ латекс] и простые числа [латекс] 18 [/ латекс], выровняв их по столбцам, когда это возможно.
Обрушьте колонны.
Умножьте множители.Продукт — LCM.	[латекс] \ text {LCM} = 36 [/ латекс]
LCM [latex] 12 [/ latex] и [latex] 18 [/ latex] — это [latex] 36 [/ latex], поэтому ЖК-дисплей [latex] \ frac {7} {12} [/ латекс] и [латекс] \ frac {5} {18} [/ latex] — 36.	LCD из [латекса] \ frac {7} {12} [/ latex] и [latex] \ frac {5} {18} [/ latex] — 36.

Чтобы найти ЖКД двух дробей, найдите НОК их знаменателей. Обратите внимание на то, что шаги, показанные ниже, аналогичны шагам, которые мы предприняли для поиска LCM.

Найдите наименьший общий знаменатель (ЖКД) двух дробей

1. Разложите каждый знаменатель на простые числа.
2. Перечислите простые числа, по возможности сопоставив простые числа в столбцах.
3. Обрушьте колонны.
4. Умножьте множители. Произведение — это НОК знаменателей.
5. НОК знаменателей — это ЖКД дробей.

Пример

Найдите наименьший общий знаменатель для дробей: [latex] \ frac {8} {15} [/ latex] и [latex] \ frac {11} {24} [/ latex]

Показать решение

Решение:
Чтобы найти ЖКД, находим НОК знаменателей.
Найдите НОК [латекс] 15 [/ латекс] и [латекс] 24 [/ латекс].

LCM [латекс] 15 [/ латекс] и [латекс] 24 [/ латекс] — это [латекс] 120 [/ латекс]. Итак, ЖК-экран [latex] \ frac {8} {15} [/ latex] и [latex] \ frac {11} {24} [/ latex] равен [latex] 120 [/ latex].

Ранее мы использовали дробные плитки, чтобы увидеть, что ЖК-экран [latex] \ frac {1} {4} \ text {и} \ frac {1} {6} [/ latex] — это [latex] 12 [/ latex] . Мы видели, что три [латекса] \ frac {1} {12} [/ latex] куска точно покрывают [латекс] \ frac {1} {4} [/ latex] и два [латекса] \ frac {1} {12} [/ latex] детали точно покрывают [латекс] \ frac {1} {6} [/ latex], поэтому

[латекс] \ frac {1} {4} = \ frac {3} {12} \ text {и} \ frac {1} {6} = \ frac {2} {12} [/ latex].

Мы говорим, что [latex] \ frac {1} {4} \ text {и} \ frac {3} {12} [/ latex] являются эквивалентными дробями, а также что [latex] \ frac {1} {6} \ text {и} \ frac {2} {12} [/ latex] — эквивалентные дроби.

Мы можем использовать свойство Equivalent Fractions Property, чтобы алгебраически преобразовать дробь в эквивалентную. Помните, что две дроби эквивалентны, если имеют одинаковое значение. Свойство эквивалентных дробей повторяется ниже для справки.

Эквивалентные дроби Свойство

Если [латекс] a, b, c [/ latex] — целые числа, где [latex] b \ ne 0, c \ ne 0, \ text {then} [/ latex]

[латекс] \ frac {a} {b} = \ frac {a \ cdot c} {b \ cdot c} \ text {и} \ frac {a \ cdot c} {b \ cdot c} = \ frac { а} {b} [/ латекс]

Чтобы сложить или вычесть дроби с разными знаменателями, нам сначала нужно преобразовать каждую дробь в эквивалентную дробь с помощью ЖК-дисплея.Давайте посмотрим, как заменить [latex] \ frac {1} {4} \ text {и} \ frac {1} {6} [/ latex] на эквивалентные дроби со знаменателем [latex] 12 [/ latex] без использования моделей.

Пример

Преобразуйте [латекс] \ frac {1} {4} \ text {и} \ frac {1} {6} [/ latex] в эквивалентные дроби со знаменателем [латекс] 12 [/ latex], их ЖК-дисплей.

Решение:

Найдите ЖК-дисплей.	ЖК-дисплей [латекс] \ frac {1} {4} [/ latex] и [латекс] \ frac {1} {6} [/ latex] — [latex] 12 [/ latex].
Найдите число, чтобы умножить [латекс] 4 [/ латекс], чтобы получить [латекс] 12 [/ латекс].	[латекс] 4 \ cdot \ color {красный} {3} = 12 [/ латекс]
Найдите число, чтобы умножить [латекс] 6 [/ латекс], чтобы получить [латекс] 12 [/ латекс].	[латекс] 6 \ cdot \ color {красный} {2} = 12 [/ латекс]
Используйте свойство «Эквивалентные дроби» для преобразования каждой дроби в эквивалентную дробь с помощью ЖК-дисплея, умножая числитель и знаменатель каждой дроби на одно и то же число.	[латекс] \ frac {1} {4} [/ latex] [латекс] \ frac {1} {6} [/ latex] [латекс] \ frac {1 \ cdot \ color {красный} {3}} {4 \ cdot \ color {красный} {3}} [/ latex] [латекс] \ frac {1 \ cdot \ color {красный} {2}} {6 \ cdot \ color {красный} {2}} [/ латекс]
Упростите числители и знаменатели.	[латекс] \ frac {3} {12} [/ latex] [латекс] \ frac {2} {12} [/ latex]

Полученные дроби не уменьшаем. Если бы мы это сделали, мы бы вернулись к нашим исходным дробям и потеряли бы общий знаменатель.

Преобразование двух дробей в эквивалентные дроби с их ЖК-дисплеем в качестве общего знаменателя

1. Найдите ЖК-дисплей.
2. Для каждой дроби определите число, необходимое для умножения знаменателя, чтобы получить ЖК-дисплей.
3. Используйте свойство Equivalent Fractions Property, чтобы умножить числитель и знаменатель на число, которое вы нашли на шаге 2.
4. Упростите числитель и знаменатель.

Пример

Преобразуйте [латекс] \ frac {8} {15} [/ latex] и [latex] \ frac {11} {24} [/ latex] в эквивалентные дроби со знаменателем [latex] 120 [/ latex], их ЖКД.

Показать решение

Решение:

ЖК-дисплей [латекс] 120 [/ латекс]. Начнем с шага 2.
Найдите число, которое должно умножить [latex] 15 [/ latex], чтобы получить [latex] 120 [/ latex].	[латекс] 15 \ cdot \ color {красный} {8} = 120 [/ латекс]
Найдите число, на которое нужно умножить 24, чтобы получить 120.	[латекс] 24 \ cdot \ color {красный} {5} = 120 [/ латекс]
Используйте свойство «Эквивалентные дроби».	[латекс] \ frac {8 \ cdot \ color {красный} {8}} {15 \ cdot \ color {красный} {8}} [/ latex] [латекс] \ frac {11 \ cdot \ color {красный} {5}} {24 \ cdot \ color {красный} {5}} [/ латекс]
Упростите числители и знаменатели.	[латекс] \ frac {64} {120} [/ latex] [латекс] \ frac {55} {120} [/ латекс]

В нашем следующем видео мы покажем еще два примера того, как использовать метод столбца, чтобы найти наименьший общий знаменатель двух дробей.

Рабочий лист

дробей

Добро пожаловать на страницу рабочих листов для дробей на Math-Drills.com, где чашка наполовину заполнена! Скорее всего, это одна из самых популярных наших страниц, потому что изучение дробей невероятно важно в жизни человека, и это математическая тема, к которой многие подходят с трепетом из-за плохой репутации на протяжении многих лет.Освоить дроби на самом деле не так сложно, особенно с поддержкой нашего широкого выбора рабочих листов.

Эта страница включает в себя рабочие листы дробей для понимания дробей, включая моделирование, сравнение, упорядочение, упрощение и преобразование дробей и операции с дробями. Начнем с очевидного: моделирование дробей. Это отличная идея, если студенты действительно могут понять, что такое дробь, поэтому, пожалуйста, уделите немного времени аспекту моделирования. Связь моделирования с реальной жизнью тоже очень помогает, так как гораздо легче связать половину печенья, чем половину квадрата.Спросите у большинства студентов, что вы получите, если добавите половину печенья и половину печенья, и они, вероятно, дадут вам знать, что из этого получится одна вкусная закуска.

Другие рабочие листы на этой странице посвящены тому, чтобы помочь студентам понять концепцию дробей. От сравнения и упорядочения до упрощения и преобразования … к тому времени, когда студенты усвоят материал на этой странице, операции с дробями будут похожи на прогулку по парку.

Задание на самые популярные дроби на этой неделе

Распечатки с дробями общего назначения

Дробные круги

Черные и белые круги дробей можно использовать в качестве манипулятора для сравнения дробей.Сделайте фотокопию рабочего листа на слайд с проекцией сверху. Карандашом слегка закрасьте соответствующий кружок, чтобы изобразить первую дробь на бумажной копии. Используйте непостоянную ручку над головой, чтобы раскрасить соответствующий круг, чтобы обозначить вторую дробь. Положите слайд на бумагу и сравните два круга. Вы легко сможете определить, какая дробь больше или меньше или равны две дроби. Используйте оба листа повторно, стирая карандаш и смывая маркер.

Фракционные полосы

Полоски с дробями можно ламинировать для повышения прочности и вырезать для сравнения, упорядочивания, сложения и вычитания дробей.Они очень полезны для сравнения дробей. Вы также можете скопировать полоски с дробями на слайды проекции и вырезать их. Они будут не только долговечными, но и прозрачными, что полезно при использовании в сочетании с бумажными версиями (например, для сравнения дробей).

Рабочие листы моделирования дробей

Помимо использования приведенных ниже таблиц, вы также можете попробовать еще несколько интересных способов моделирования дробей. Здоровые закуски могут стать отличными моделями для дробей.Можно ли разрезать огурец пополам? Помидор на четвертинки? Можно ли сделать две трети винограда красными, а одну треть — зелеными?

Моделирование фракций с группами фигур

Дроби могут представлять части группы или части целого. В этих таблицах дроби моделируются как части группы.

Моделирование дробей прямоугольниками

Моделирование фракций с окружностями

Таблицы соотношений и пропорций

Соотношение сторон изображения

Эквивалентные фракции

Рабочие листы моделей эквивалентных фракций включают только «фракции выпечки» в версиях A.Чтобы увидеть более сложные и разнообразные дроби, выберите версии от B до J после загрузки версии A.

Эквивалентные соотношения

Таблицы сравнения и сортировки дробей

Сравнение простых дробей

Есть много разных стратегий, кроме просмотра страницы, которые помогут в сравнении дробей. Попробуйте начать с чего-нибудь наглядного, что будет изображать рассматриваемые дроби.Мы настоятельно рекомендуем наши дробные полоски (прокрутите немного вверх). Использование линейки, такой как линейка, книга или складка, поможет учащимся легко увидеть, какая дробь больше или равна ли они. Следует также отметить, что сравниваемые вещи должны быть одинаковыми. Например, каждая фракционная полоска имеет одинаковый размер, тогда как если вы возьмете треть арбуза и половину винограда, арбуз, вероятно, победит.

Сравнение простых и неправильных дробей

Другая стратегия, которую можно использовать при сравнении дробей, — использовать числовую линию и использовать контрольные цифры, такие как 0, 1, 1/2, чтобы выяснить, куда идет каждая дробь, а затем посмотреть, какая из них больше.Студенты на самом деле делают это все время, так как они часто могут сравнивать дроби, осознавая, что одна меньше половины, а другая больше половины. Они также могут увидеть, что одна фракция намного ближе к целому, чем другая фракция, даже если они обе могут быть больше половины.

Сравнение простых, неправильных и смешанных дробей

Другая стратегия сравнения дробей — преобразовать каждую дробь в десятичную дробь и сравнить десятичные дроби.Десятичные преобразования можно запомнить (особенно для обычных дробей), рассчитанные путем деления в столбик, с помощью калькулятора или справочной таблицы. Мы предлагаем последнее, поскольку использование справочной таблицы часто приводит к мысленному вспоминанию.

Заказ дробей по числовой строке

Многие из тех же стратегий, которые работают для сравнения дробей, также работают для упорядочивания дробей. Использование таких манипуляторов, как полоски дробей, использование числовых линий или поиск десятичных эквивалентов, заставит ваших учеников быстро расставить дроби в правильном порядке.Мы, вероятно, говорили об этом раньше, но убедитесь, что вы подчеркнули, что при сравнении или упорядочивании дробей учащиеся понимают, что целое должно быть одинаковым. Сравнение половины населения Канады с третью населения Соединенных Штатов не поможет. Попробуйте использовать визуальные эффекты, чтобы усилить эту важную концепцию. Несмотря на то, что мы включили числовые линии ниже, вы можете свободно использовать свои собственные стратегии.

Заказ дробей

Рабочие листы с упорядочением дробей в этом разделе не включают числовую линию, чтобы студенты могли использовать различные стратегии сортировки.

Рабочие листы по упрощению и преобразованию дробей

Округление дробей

Округление дробей помогает учащимся немного лучше понимать дроби и может применяться для оценки ответов на вопросы о дробях. Например, если нужно было оценить 1 4/7 × 6, они, вероятно, могли бы сказать, что ответ был около 9, так как 1 4/7 составляет около 1 1/2, а 1 1/2 × 6 — 9.

Упрощение дробей

Изучение того, как упрощать дроби, значительно облегчает жизнь студента в дальнейшем, когда он будет изучать операции с дробями.Это также помогает им узнать, что дроби, которые выглядят по-разному, могут быть эквивалентными. Один из способов продемонстрировать это — разделить две эквивалентные дроби. Например, 3/2 и 6/4 при делении дают частное 1,5. Будем надеяться, что практикуя упрощение дробей, студенты будут распознавать неупрощенные дроби, когда они начнут складывать, вычитать, умножать и делить на дроби.

Преобразование из неправильной дроби в смешанную

Преобразование между дробями, десятичными знаками, процентами и отношениями

Преобразование дробей в завершающие десятичные дроби Преобразование дробей в завершающие и повторяющиеся десятичные дроби Преобразование завершающих десятичных знаков в дроби Преобразование завершающих и повторяющихся десятичных знаков в дроби Преобразование дробей в сотые Преобразование дробей в десятичные числа, проценты и частичное- частичное соотношения (, завершающие десятичные дроби) Преобразование дробей в десятичные дроби, проценты и частичные к целые соотношения (, завершающие десятичные дроби) Преобразование десятичных дробей в дроби, проценты и частичное- частичное соотношения (, завершающие десятичные дроби) Преобразование десятичных дробей в дроби, проценты и целые соотношения целые ( только с завершением десятичных знаков) Преобразование процентов в дроби, десятичные дроби и частичные и частичные соотношения (, завершающие десятичные дроби) Преобразование процентов в дроби, десятичные дроби и целые соотношения целые ( только завершающие десятичные числа) Преобразование соотношений частей к частям в дроби, десятичные дроби и проценты ( только завершающие десятичные дроби ) Преобразование отношения части к целому в дроби, десятичные дроби и проценты ( только с завершением десятичных знаков) Преобразование различных дробей, десятичных дробей, процентов и дробных частей в частичных соотношений (, завершающие десятичные дроби) Преобразование различных дробей, десятичных знаков, процентов и дробных чисел в целых отношений ( завершает десятичные дроби) Преобразование дробей в десятичные числа, проценты и дробные части Части отношения Преобразование дробей в десятичные числа, проценты и частичные к целые соотношения Преобразование десятичных дробей в дроби, проценты и частичное- частичное соотношения Преобразование десятичных знаков в дроби, проценты и частичные к целые соотношения Преобразование процентов в дроби, десятичные дроби и частичные- частичные соотношения Преобразование процентов в дроби, десятичные дроби и целые отношения Преобразование отношения частей к частям в дроби, десятичные дроби и проценты Преобразование целого числа частей к целому в дроби, десятичные дроби и проценты Преобразование различных дробей, десятичных знаков, процентов и дробных частей к частям отношений Преобразование различных дробей, десятичных знаков, процентов и дробных чисел целых отношений Преобразование различных дробей, десятичных знаков, процентов и дробей в Части отношений с 7-ми и 11-ю Преобразование различных дробей, десятичных знаков, процентов и частей в- Целые отношения с 7-ми и 11-ми числами (СТАРЫЙ) Преобразование дробей, десятичных знаков, процентов и соотношений

Рабочие листы операций с дробями

Умножение дробей

Умножение дробей обычно менее запутанно с операционной точки зрения, чем любая другая операция, и может быть менее запутанным в концептуальном плане при правильном подходе.Алгоритм умножения — это просто умножение числителей, а затем знаменателей. Волшебное слово в понимании умножения дробей — «из». Например, что составляет две трети ОТ шести? Что такое треть от половины? Когда вы используете слово «из», становится намного легче визуализировать умножение дробей. Пример: разрезать буханку хлеба пополам, затем половину разрезать на три части. Одна треть полбуханки хлеба такая же, как 1/3 x 1/2, и вкусная с маслом.

На дроби

По идее, деление на дроби, вероятно, самая сложная из всех операций, но мы собираемся помочь вам.Алгоритм деления дробей аналогичен умножению дробей, но вы находите обратное значение второй дроби или производите перекрестное умножение. Это даст вам правильный ответ, что чрезвычайно важно, особенно если вы строите мост. Мы рассказали вам, как концептуализировать умножение дробей, но как оно работает с делением? Легкий! Вам просто нужно выучить волшебную фразу: «Сколько ____ в ______? Например, в вопросе 6 & div; 1/2 вы спросите:« Сколько половинок в 6? »Становится немного больше. трудно, когда оба числа являются дробными, но это не гигантский скачок, чтобы понять это.1/2 & div; 1/4 — довольно простой пример, особенно если вы думаете о монетах США или Канады. Сколько четвертей в полдолларе?

Сложение дробей

Для сложения дробей нужен надоедливый общий знаменатель. Упростите жизнь своих учеников, сначала обучив их понятиям эквивалентных дробей и наименьших общих кратных. Как только учащиеся знакомы с этими двумя концепциями, идея поиска дробей с общими знаменателями для сложения становится намного проще.Время, потраченное на моделирование дробей, также поможет учащимся понять сложение дробей. Связь дробей с знакомыми примерами, безусловно, поможет. Например, если вы добавите 1/2 банана и 1/2 банана, вы получите целый банан. Что произойдет, если вы добавите 1/2 банана и 3/4 другого банана?

Сложение смешанных фракций Рабочие листы

Обычная стратегия, которую используют при добавлении смешанных фракций, состоит в том, чтобы преобразовать смешанные фракции в неправильные фракции, завершить сложение, а затем переключиться обратно.Другая стратегия, требующая немного меньших умственных способностей, — рассматривать целые числа и дроби по отдельности. Сначала сложите целые числа. Добавьте доли секунды. Если полученная дробь неправильная, ее нужно преобразовать в смешанное число. Часть целого числа может быть добавлена ​​к исходной части целого числа.

Вычитание Дроби

Нет большой разницы между сложением и вычитанием дробей.Оба требуют общего знаменателя, что требует некоторых предварительных знаний. Единственная разница в том, что второй и последующие числители вычитаются из первого. Существует опасность того, что вы можете получить отрицательное число при вычитании дробей, поэтому учащимся, возможно, потребуется узнать, что это означает в этом случае. Когда дело доходит до любого понятия в дробях, всегда полезно связать его с знакомой или простой для понимания ситуацией. Например, 7/8 — 3/4 = 1/8 может иметь значение в контексте гонки.Первый бегун шел на 7/8 по трассе, а второй бегун на 3/4 по трассе. Как далеко впереди был первый бегун? (1/8 трека).

Вычитание смешанных дробей Рабочие листы

Рабочие листы с дробями различных операций

Смешение знаков операций с рабочими листами с дробями заставляет учащихся уделять больше внимания тому, что они делают, и позволяет хорошо проверить свои навыки в более чем одной операции.

Сложение и вычитание дробей

Умножение и деление на дроби

Смешанные операции с дробями

Операции с

Отрицательными дробями

Хотя некоторые из этих листов представляют собой отдельные операции, было бы полезно иметь все они в одном месте.При выполнении операций с отрицательными дробями следует учитывать некоторые особенности. Обычно очень полезно перед тем, как продолжить, заменить любые смешанные числа на неправильную дробь. Важно обращать внимание на знаки и знать правила умножения положительных и отрицательных (++ = +, + — = -, — + = — и — = +).

Рабочие листы для операций с дробями

Порядок операций с листами дробей с опциями как положительных, так и отрицательных дробей различной сложности.

Порядок действий с дробями

Как и другие рабочие листы с порядком операций, рабочие листы с порядком дробей требуют некоторых предварительных знаний. Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций / навыков, прежде чем продолжить.В противном случае приведенные ниже рабочие листы должны содержать довольно простые ответы и не должны приводить к чрезмерному выпадению волос.

Порядок операций с

десятичными и смешанными дробями

Добавление дробей

Эта страница содержит ссылки на бесплатные рабочие листы по математике для задач сложения дробей. Нажмите одну из кнопок ниже, чтобы увидеть все рабочие листы в каждом наборе. Вы также можете использовать меню «Рабочие листы» сбоку на этой странице, чтобы найти рабочие листы по другим математическим темам.

Общий знаменатель, без целых частей

---

Общий знаменатель, смешанные ответы

---

Смешанные дроби с общим знаменателем

---

Половинки, четверти, восьмые

---

20 Рабочие листы сложения дробей

Эти рабочие листы дробей обеспечивают практическое сложение общих дробей с половинками, четвертями и восьмыми.

Половинки, четверти, восьмые

Различные знаменатели

---

24 Рабочие листы сложения дробей

Эти рабочие листы имеют практические проблемы для сложения дробей с разными знаменателями..

Разные знаменатели

Неправильно с тем же знаменателем

---

Неправильно с другим знаменателем

---

Как сложить дроби

Шаги по сложению дробей могут быть очень простыми, если проблема настроена правильно. Рабочие листы на этой странице содержат примеры задач, которые иллюстрируют возрастающие уровни сложности для развития навыков, необходимых для решения любых задач сложения дробей.

В простейших случаях у двух дробей уже будет общий знаменатель.В этом случае сложите числители, а затем уменьшите полученную дробь.

Если числитель ответа больше знаменателя, то ответ является неправильной дробью. Эту дробь следует превратить в правильную дробь, вычеркнув из числителя целые числа, пока числитель не станет меньше знаменателя.

При сложении дробей без общего знаменателя перед сложением числителей необходимо найти общий знаменатель. Найдите две эквивалентные дроби, определив наименьшее общее кратное двух знаменателей и используя его в качестве знаменателя для обеих дробей.

Эти шаги кажутся более сложными, чем кажется, но очень хороший способ визуализировать процесс сложения дробей — использовать калькулятор дробей по ссылке ниже.

Сложение и вычитание дробей с разными знаменателями

Чтобы сложить или вычесть дроби с разными знаменателями, нам нужно проделать несколько дополнительных шагов. Общий подход обсуждается ниже. В этом уроке мы рассмотрим несколько примеров, чтобы убедиться, что вы освоили эту процедуру.

---

шагов, как сложить или вычесть дроби с разными знаменателями

Шаг 1: Даны две разные дроби, знаменатели которых НЕ совпадают.

Шаг 2: Сделайте знаменатели одинаковыми, найдя наименьшее общее кратное (НОК) их знаменателей. Этот шаг точно такой же, как поиск наименьшего общего знаменателя (LCD).

Шаг 3: Перепишите каждую дробь в эквивалентную дробь со знаменателем, равным наименьшему общему кратному, найденному на шаге №2..

Шаг 4: Теперь добавьте или вычтите «новые» дроби из шага №3. Всегда сокращайте ответ до минимума.

---

Примеры сложения и вычитания дробей с разными знаменателями

Пример 1: Сложите дроби с разными знаменателями.

Знаменатели двух дробей не равны . Нам нужно сделать их равными, найдя их наименьшее общее кратное, которое будет служить их наименьшим общим знаменателем (LCD).

Начните с перечисления кратных каждого знаменателя и определите наименьшее общее для них обоих число.

У первой дроби уже есть знаменатель, равный НОК = 15, поэтому мы оставим его в покое.

Вторая дробь требует некоторой корректировки, чтобы знаменатель стал равным 15. Для этого нужно умножить числитель и знаменатель на число 3.

• После того, как их знаменатели станут равными, сложите дроби, сложив их числители и затем скопировав общий знаменатель.

Дробь {{11} \ over {15}} — наш окончательный ответ, потому что она уже находится в наименьшем члене.

---

Пример 2: Сложите дроби с разными знаменателями.

Мы пока не можем сложить две дроби, потому что у них разные знаменатели, а именно 5 и 9. Начните с перечисления их кратных и выберите наименьшее общее число. Это станет их общим знаменателем.

Теперь преобразуйте каждую дробь в эквивалентную дробь с НОК в качестве знаменателя, затем продолжите обычное сложение.

Ищите возможность сократить ответ до самого низкого члена. Числитель и знаменатель числа {{33} \ over {45}} делятся на 3 .

---

Пример 3: Сложите дроби с разными знаменателями.

Иногда нет необходимости находить наименьший общий знаменатель методом списка. Мы можем сразу найти его, если оба числа являются простыми числами.

• Простое число — это число, которое делится только на 1 и само себя.

Обратите внимание, что знаменатели 3 и 5 — простые числа. ЖК-дисплей будет просто их продуктом, то есть 3 x 5 = 15.

---

Пример 4: Сложите дроби с разными знаменателями.

Решение :

Найдите наименьшее общее кратное знаменателей.

Внесите необходимые изменения в знаменатель и действуйте как обычно. Сократите свой окончательный ответ до самого низкого члена.

---

Пример 5: Сложите дроби с разными знаменателями.

Решение :

Поскольку знаменатели 11 и 13 являются простыми числами, наименьшим общим знаменателем будет их произведение.

Преобразуйте текущие знаменатели двух дробей в ЖК-дисплей и продолжайте регулярное сложение.

---

Пример 6: Вычтите дроби с разными знаменателями.

Вычитание дробей с неравными знаменателями очень похоже на сложение.

Уравнять их знаменатели, используя принцип наименьшего общего кратного.Затем соответственно вычтите их числители.

Перепишите каждую дробь в ее эквивалентную дробь со знаменателем, равным НОК = 30 , затем вычтите их числители. Обязательно сократите свой ответ до самого низкого члена.

---

Пример 7: Вычтите дроби с разными знаменателями.

Поскольку оба знаменателя являются простыми числами, их НОК — это просто их произведение, поэтому 7 x 5 = 35.

---

Пример 8: Вычтите дроби с разными знаменателями.

Решение :

Найдите наименьший общий знаменатель, определив НОК знаменателей.

Записываем две дроби с общим знаменателем, равным НОК = 42 . Вычтите их числители и, если возможно, сократите ответ до наименьшего члена.

---

Пример 9: Вычтите дроби с разными знаменателями.

Решение :

Найдите наименьший общий знаменатель, решив найти наименьшее общее кратное знаменателей.

Мы вносим поправки в существующие дроби, чтобы их знаменатель был равен LCD = 40 . После этого вычтите их числители и скопируйте общий знаменатель.

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Сложение и вычитание дробей с одинаковым знаменателем
Умножение дробей
Деление дробей
Упрощение дробей
Эквивалентные дроби
Обратное значение дроби

Дроби для заказа — пояснения и примеры

Как заказать дроби?

Упорядочивание дробей означает упорядочение дробей от наименьшей к наибольшей (в возрастающем порядке) или от наибольшей к наименьшей (в порядке убывания).

Существует два распространенных метода упорядочивания дробей.

Это:

• Использование общего знаменателя.
• Преобразование дробей в десятичные и последующее упорядочение.

Порядок дробей с использованием общего знаменателя

Дроби можно сравнить и упорядочить, определив их эквивалентные дроби с общим знаменателем. Общие знаменатели создаются путем использования общих кратных двух чисел. Например, 24 — это наименьшее общее кратное 8 и 12.

8 x 3 = 24

12 x 2 = 24

Однако 8 и 12 имеют несколько других общих кратных; однако 24 — это самый низкий показатель.

Преобразование дробей в десятичные с последующим упорядочиванием

Преобразование дробей в десятичные — это еще один метод упорядочивания дробей.

Пример 1

Расположите следующие дроби в порядке возрастания.

3/4, 1/2, 4/5, 3/8

Решение

Сначала преобразуйте всю дробь в десятичные числа, как показано ниже:

3/4 = 0.75

1/2 = 0,5

4/5 = 0,8

3/8 = 0,375

Поскольку все дроби имеют ноль в цифре единицы, сравните их, проверив разряд десятых.

Теперь расположите десятичные дроби в порядке убывания.

0,8, 0,75, 0,5, 0,375,

Там окончательный ответ: 4/5, 3/4, 1/2 и 3/8

Существуют и другие методы упорядочивания дробей, например, вычисление их процентов.

Например, мы можем решить проблему, выразив ее в процентах.

Порядок 1/10, 1/5, 1/4, 1/2, 1/3

Дробь	Десятичный	Процент
1/10	0,1	10%
1/5	0,2	20%
1/4	0,25	25%
1/2	0,5	50%
1/3	0,3 ¯	33,3 ¯%

Упорядочение дробей от наименьшей к наибольшей (h3)

Давайте разберемся в этом на примерах.

Пример 2

Расположите следующие дроби в порядке возрастания:

1/2, 2/3, 7/12, 5/6, 1/4

Решение

• Сначала определите все знаменатели дробей. В данном случае знаменатели равны 2, 3, 12, 6 и 4.
• Вычислите наименьшее общее кратное всех знаменателей. Вы посмотрите на L.C.M. двух чисел за раз и проверьте, являются ли другие знаменатели множителями вычисленного L.СМ.
• Наименьшее общее кратное знаменателей 2, 3, 12, 6 и 4 равно 12
• Следующий шаг — переписать каждую дробь как эквивалентную дробь со знаменателем 12.

1/2 x 6/6 = 6 / 12

2/3 x 4/4 = 8/12

7/12 x 1/1 = 7/12

5/6 x 2/2 = 10/12

1/4 x 3/3 = 3/12

Теперь, когда все дроби имеют общий знаменатель, проще расположить дроби в порядке возрастания, сравнивая их числители.

При сравнении числителей окончательный ответ становится 1/4, 1/2, 7/12, 2/3, 5/6.

Дополнительные примеры

1. Расположите следующее в порядке возрастания:

1/2, 1/4, 3/4

Решение

Найдите НОК 2, 4, которое 4

Умножение 1/2 = 1/2 × 2/2 = 2/4

Поскольку числитель 4 остается во всех дробях, упорядочьте дроби следующим образом:

1/4 <1/2 <3/4

2.Расположите дроби ниже в порядке возрастания:

3/5, 3/7, 9/25

Решение

Определите НОК 5, 7 и 25, что составляет 175

Умножьте каждую дробь на НОК как :

3/5 = 3/5 × 35/35 = 105/175

3/7 = 3/7 × 25/25 = 75/175

9/25 = 9/25 × 7/7 = 63 / 175

Теперь расположите дроби в порядке возрастания:

9/25, 3/7, 3/5

3. Упорядочите дроби от наименьшей к наибольшей.

2/5, 4/7, 5/6

Решение

Найдите НОК 5, 7 и 6 = 210

2/5 = 2/5 × / 42/42 = 84/210

4/7 = 4/7 × 30/30 = 120/210

5/6 = 5/6 × 35/35 = 175/210

Теперь дроби в порядке возрастания = 2/5 <4/7 < 5/6

4. Расположите следующие дроби в порядке возрастания

1/3, 6/9, 9/18

Решение

Определите НОК знаменателей как 18.

1/3 = 1/3 × 6/6 = 6/18

6/9 = 6/9 × 2/2 = 12/18

Сейчас,

6/18 <9/18 <12 / 18 и, следовательно, дробь в порядке возрастания;

1/3 <9/18 <6/9

5. Упорядочите дроби ниже от наименьшей к наибольшей.

3/9, 9/25, 5/20

Решение

Начните с вычисления НОК знаменателей 4, 20 и 25 = 100

3/4 = 3/4 × 25/25 = 75 / 100

9/25 = 9/25 × 4/4 = 36/100

5/20 = 5/20 × 5/5 = 25/100

Таким образом;

25/100 <36/100 <75/100

Следовательно, дробь от наименьшей к наибольшей составляет

5/20 <9/25 <3/4

6.Расположите эти дроби в порядке возрастания:

2/15, 3/18, 9/10

Решение

Рассчитайте НОК знаменателей 15, 18 и 10 как 90

2/15 = 2/15 × 6/6 = 12/90

3/18 = 3/15 × 5/5 = 15/90

9/10 = 9/10 × 9/9 = 81/90

Таким образом, дроби в По возрастанию: 2/15 <3/18 <9/10

7. Перечислите следующие дроби в порядке возрастания

16/15, 15/14, 14/12

Решение

Рассчитайте НОК 15, 14 и 12 как 420

16/15 = 16/15 × 28/28 = 448/420

15/14 = 15/14 × 30/30 = 450/420

14/12 = 14 / 12 × 35/35 = 490/420

Таким образом,

448/420 <450/420 <4 90/4200420 И отсюда дроби в порядке возрастания:

16/15 <15/14 <14/12

8.Расположите эти дроби в порядке возрастания:

2/3, 3/4, 4/5

Решение

Начните с вычисления НОК знаменателей 3, 4 и 5 как 60

2/3 = 2 / 3 × 20/20 = 40/60

3/4 = 3/4 × 15/15 = 45/60

4/5 = 4/5 × 12/12 = 48/60

Теперь расставьте дроби как:

40/60 <45/60 <48/60 Таким образом, дроби от наименьшего к наибольшему:

2/3 <3/4 <4/5

Практические вопросы

1. Учитель делит своим ученикам мешок с теннисными мячами.Он отдает 2/9 мячей Мэри, 1/3 Харишу, 7/27 Джеймсу и оставляет 5/27 себе. Упорядочьте долю их доли от наибольшей к наименьшей.
2. На прошлой неделе Педро слушал 2/3 своей любимой музыки, а Адам и Филипп слушали 3/5 и 4/7 своей любимой музыки соответственно. Расположите эти дроби в порядке убывания.
3. Сала участвовал в 4 различных спортивных мероприятиях. Он потратил 9/10 часа на плавание, 2/3 часа на футбол, 1/3 и 2/4 часа на бег трусцой и прыжки, соответственно.Закажите время, которое он потратил на занятия различными видами спорта, от самого большого до самого маленького.

Предыдущий урок | Главная страница | Следующий урок

Общий знаменатель: поиск и дроби — класс естественных наук [видео 2021 года]

Наименьший общий знаменатель

Есть два способа найти общий знаменатель для двух или более дробей. Первый метод включает нахождение наименьшего общего знаменателя или наименьшего целого числа, которое делится на оба знаменателя.Чтобы найти наименьший общий знаменатель, перечислите кратные каждого знаменателя, а затем выберите наименьший.

Рассмотрим пример:

Сначала мы найдем кратные каждому знаменателю.

Кратные 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.. .

Кратные 7: 7, 14, 21, 28, 35, 42.. .

Наименьшее общее число 3 и 7 — 21. Следовательно, 21 — наименьший общий знаменатель.

Второй метод нахождения общего знаменателя для двух или более дробей — это умножение знаменателей друг на друга.

Рассмотрим другой пример:

Знаменатели 6 и 8. Итак, 6 * 8 = 48; следовательно, общий знаменатель — 48. Хотя этот метод может показаться более простым, общий знаменатель может не быть наименьшим общим знаменателем, а это означает, что в конце задачи сложения или вычитания дробь должна быть уменьшена до самой простой формы.

Сложение дробей

После нахождения общего знаменателя двух или более дробей мы можем использовать эту информацию для сложения или вычитания дробей и решения задачи. Вернемся к нашему первому примеру:

Сначала мы умножим числитель и знаменатель каждой дроби на те же числа. В данном случае 7/7 и 3/3.

Затем мы сложим их вместе.

Не забудьте убедиться, что дробь имеет наименьшую форму. В данном случае дробь 13/21 представлена ​​в простейшем виде.

Вычитание дробей

Теперь вернемся ко второму примеру:

Здесь общий знаменатель равен 48. И снова, следующий шаг — умножить числитель и знаменатель каждой дроби на одинаковые числа.В данном случае 8/8 и 6/6.

5/6 * 8/8 = 40/48

3/8 * 6/6 = 18/48

Теперь решаем задачу вычитания.

40/48 — 18/48 = 22/48

Эта дробь должна быть уменьшена на путем деления каждого числа на наибольший общий множитель, который в данном случае равен 2:

22/48 сокращается до 11/24 , что является нашим окончательным ответом.

Пример задачи

Попробуем еще один пример. Найдите общий знаменатель для:

Кратные 2: 2, 4, 6, 8, 10, 12, 14.. .

Кратные 5: 5, 10, 15, 20.. .

Наименьший общий знаменатель равен 10.

В качестве альтернативы мы можем умножить два знаменателя вместе (2 * 5 = 10), а затем использовать умножение, чтобы получить общие знаменатели дробей:

Наконец, складываем дроби вместе:

Итоги урока

Давайте рассмотрим.