Задачи по математике 5 класс задачи на части: Задачи на части. | Тренажёр по математике (5 класс):

Содержание

Задачи «на части» в 5-м классе, на ВПР и итоговых экзаменах

Если вы решили заниматься летом с ребёнком математикой, но с трудом вспоминаете школьную программу, наш блогер Александр Шевкин поможет вам всё наверстать. Сегодня он приводит примеры задач «на части» и объясняет, как их решать.

Задачи «на части» являются классическим типом задач, решаемых как арифметически, так и при помощи уравнения. Такие задачи встречаются в учебниках для пятого класса, в ВПР и на выпускном экзамене.

Для развития мышления и речи детей начинать лучше с арифметического способа решения. Рассмотрим решения двух задач из учебника «Математика, 5» (Просвещение, С. М. Никольский и др.) В первых задачах части упоминаются явно.

Задача 1. Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара следует взять на 6 кг ягод?

Решение: По условию задачи ягод 6 кг, и это количество составляет 2 части, поэтому на каждую часть приходится:

6: 2 = 3 кг.

Сахара надо взять 3 такие же части, то есть:

3 ∙ 3 = 9 кг.

Ответ: 9 кг.

В следующей задаче некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.

Задача 2. На двух полках стоит 120 книг — на первой полке в 3 раза больше, чем на второй. Сколько книг стоит на каждой полке?

Решение: Если книги, стоящие на второй полке, составляют 1 часть, то на первой полке — 3 такие части. Выполним схематический рисунок.

1) Сколько частей составляют 120 книг?

1 + 3 = 4 (части).

2) Сколько книг приходится на 1 часть?

120: 4 = 30 (книг).

3) Сколько книг приходится на первую полку?

30 ∙ 3 = 90 (книг).

Ответ: 90 и 30 книг.

Следующая задача была предложена на экзамене «Математическая грамотность» (Казахстан). Это аналог нашего ЕГЭ базового уровня для выпускников средней школы.

Задача 3. Когда отцу был 31 год, сыну было 8 лет. Сейчас отец в 2 раза старше сына.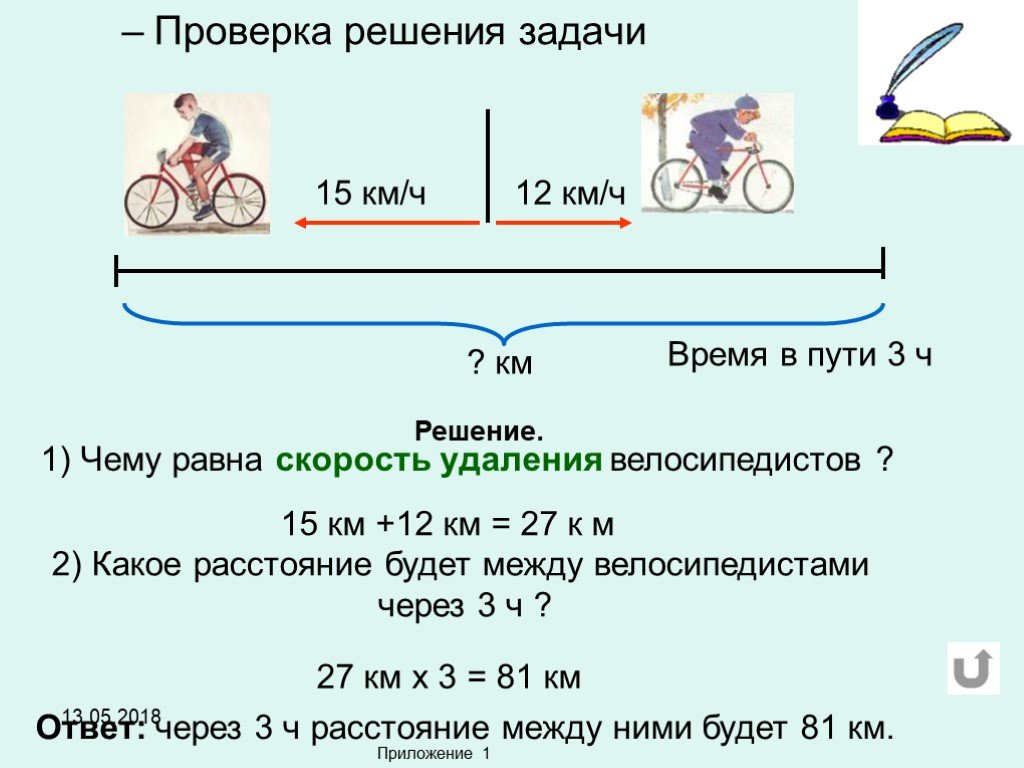 Сколько лет сыну сейчас?

Решение: Отец старше сына на 31 — 8 = 23 года. Пусть сейчас возраст сына составляет 1 часть, тогда возраст отца — 2 такие же части. Выполним схематический рисунок.

Замечание. Эту задачу преподаватель из ютьюба, обучавший выпускников казахстанских школ, решал при помощи уравнения, приняв за x число лет, прошедших между описанными в задаче событиями.

В заключение задача посложнее.

Задача 4. Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши 3 части, а сливы 2 части общего веса сухофруктов. Сейчас граммов яблок, груш и слив было в отдельности?

Решение:

1) 4 + 3 + 2 = 9 (частей) — приходится на 1800 г,

2) 1800: 9 = 200 (г) — приходится на 1 часть,

3) 200 ∙ 4 = 800 (г) — было яблок,

4) 200 ∙ 3 = 600 (г) — было груш,

5) 200 ∙ 2 = 400 (г) — было слив.

Ответ: 800, 600 и 400 г.

Отметим, что приём решения задач «на части» может использоваться при решении более сложных составных задач.

Задача 5. На двух полках стояли 36 книг. Когда с первой полки на вторую переставили 3 книги, то книг на второй полке стало в 2 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?

Решение: Пусть количество книг на первой полке после перестановки трёх книг составляет 1 часть, тогда на второй полке — 2 части.

1) 1 + 2 = 3 (части) — приходится на 36 книг,

2) 36: 3 = 12 (книг) — приходится на 1 часть (стало на 1-й полке),

3) 36 — 12 = 24 (книг) — стало на 2-й полке.

Вернём три книги на первую полку.

4) 12 + 3 = 15 (книг) — было на первой полке первоначально,

5) 24 — 3 = 21 (книга) — была на второй полке первоначально.

Ответ: 15 и 21 книга.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Математика 5 класс. Решение задач на части.

Математика 5 класс

Урок по теме: «Задачи на части».

Цели урока: знакомство обучающихся с новым типом задач, методами решения задач на части.

Задачи урока:

Личностные:

содействовать формированию интереса к изучаемому материалу на уроке;
развивать умения извлекать необходимую информацию, формулировать выводы, обосновывать суждения.

Метапредметные:

регулятивные:

принимать и сохранять учебную задачу;
находить вариант решения учебной задачи;
уметь самостоятельно ставить цели и задачи;
понимать сущности алгоритмических предписаний и уметь действовать в соответствии с предложенным алгоритмом;
оценивать правильность выполнения действий на уровне адекватной оценки;

коммуникативные:

выражать свои мысли, обосновывая суждения;
расширять кругозор, содействовать воспитанию интереса к математике, активности, мобильности, умению общаться, общей культуры;
работать самостоятельно;
развивать навыки взаимоконтроля;

познавательные:

выполнять учебные действия в письменной и устной форме;
осуществлять поиск нужной информации, используя предоставленные источники;
осуществлять анализ объекта, делать выводы;

Предметные:

изучить основные приемы решения задач на части;
расширить знания о видах текстовых задач решаемых арифметическим способом

Ход урока

1. Мотивационно — ориентировочный этап.

Слайд №1

Добрый день, дорогие друзья, мне приятно видеть вас и я очень хочу начать наш урок. Желаю вам позитивных эмоций на уроке, радости общения, интересной и плодотворной работы.

Слайд №2

Марк Иванович Башмаков, математик, ученый-педагог, как-то заметил: «Главная сила математики состоит в том, что вместе с решением одной конкретной задачи она создаёт общие приёмы и способы, применимые во многих ситуациях, которые даже не всегда можно предвидеть».

Ребята, а как короче можно выразить эту мысль, что здесь главное? (Решая конкретную задачу мы учимся решать разные задачи).

Как вы думаете, о чем сегодня пойдет речь на уроке? (О задачах, решении задач).

Верно. А вот о каких задачах, узнаем далее. Давайте мы с вами сегодня в процессе решения математических задач постараемся открыть новые идеи, приемы и разобраться, как нам добытые знания смогут пригодиться в жизни.

Откройте тетради и запишите число, классная работа.

2.Актуализация опорных знаний.

Ребята, а какие самые главные умения мы развиваем на уроках математики? Что мы обязательно должны уметь делать? (Вычислять, считать).

Нужны нам эти умения при решении задач? (Да)

Тогда давайте проведем вычислительную работу.

Устная работа Эстафета по рядам

Перед вами на партах лежат заготовки-таблички.

Задание:

— вычислите значение двух числовых выражений и запишите полученный результат;

— найдите полученное число в таблице;

— впишите букву, соответствующую данному числу в таблицу;

— передайте листок следующей парте.

(Работа выполняется в парах. Каждая парта выполняет вычисления двух примеров, затем передает по цепочке следующей парте ряда. Первая парта вычисляет и называет конечный результат).

Г. 15·2+14=	Н. 3+9·7=	М. 17·3-18=	И. 51+12·4=	А. 17+4·5=
Ц. 8+8·10=	К. 9+39:3=	И. 36:4+2=	Й. 11·9-44=

33	37	44	66	11	88	22	99	55

Какой же ряд справился первый? Что же у вас получилось?

Ответ: Магницкий.

А кто это? Чем он знаменит?

Автор первого учебника по арифметике, который содержал много интересных задач.

Ну, что же с заданием на вычисление вы успешно справились, а теперь я предлагаю нам с вами также обратиться к решению задач.

3. Подготовка к восприятию нового материала

Постановка проблемы

Слайд №3

Выполните задания:

1) прочитайте задачи и сравните условия задач

№1. В первой пачке 40 тетрадей, а во второй — в 2 раза меньше. Сколько всего тетрадей?

№2. В двух пачках 60 тетрадей. Во второй пачке тетрадей в 2 раза меньше, чем в первой. Сколько тетрадей в каждой пачке?

Чем они похожи и чем отличаются?

Сходство: речь о тетрадях, всего 2 пачки.

Отличия: в первой задаче известно количество тетрадей в одной из пачек, но неизвестно, сколько всего тетрадей; во второй задаче известно количество тетрадей в двух пачках, но неизвестно, сколько в каждой.

б) составьте устно план решения каждой задачи;

Возникли у вас трудности с составлением плана решения какой-либо задачи?

Как вы думаете, почему они возникли? (Потому, что мы пока не умеем решать такие задачи).

Как мы можем выйти из затруднения? (научиться решать такие задачи)

Для чего нам это нужно?

Ребята, а что нам очень помогает при решении задач? Дает наглядное представление об условии? (Схематический рисунок). Я предлагаю выполнить вам небольшую лабораторную работу в парах.

Перед вами на столе листок №1. На нем представлены схематические рисунки. Выберите рисунок, который может соответствовать условию задачи № 2 и ответьте письменно на поставленные вопросы.

? тетр. 60 тетр.

1 пачка 1пачка

60 тетр.

?тетр.

2 пачка 2 пачка

? тетр.

Рис.1 Рис.2

1) Какой рисунок соответствует условию задачи? (1 рисунок)

2) Что мы видим по рисунку? На что, на какие элементы можно разделить условно все тетради? (все тетради можно условно разделить на равные части).

3) Сколько частей приходится на 60 тетрадей? (три части)

4) Что мы можем узнать из этого? (Сколько тетрадей приходится на одну часть, а значит и количество тетрадей во второй пачке).

5) Какое действие будет следующим? (Узнаем, сколько тетрадей в первой пачке).

6) Ответив на все поставленные вопросы, смогли мы решить задачу? (Да).

А теперь давайте послушаем, какие же ответы вы записали на поставленные вопросы.

(Дети читают свои ответы, а учитель в это время последовательно записывает решение на доске)

1)1+2=3 (части) — приходится на все тетради

2) 60:3=20 (тетр.) – приходится на одну часть (количество тетрадей во второй пачке)

3) 20·2=40 (тетр.) – приходится на две части (количество тетрадей в первой пачке)

Ответ: 20 и 40 тетрадей.

Давайте запишем решение данной задачи в тетрадь.

Итак, ребята, смогли мы с вами решить задачу, с решением которой возникли вначале затруднения? (Да)

Это новая была для вас задача? (Да)

4. Объявление темы урока, постановка цели и задач урока

Что нового встретилось вам при решении задач? (Понятие части, распределение всех объектов на части).

Как же мы можем сформулировать тему урока? (Задачи на части)

Слайд №4

Запишем в тетради «Задачи на части».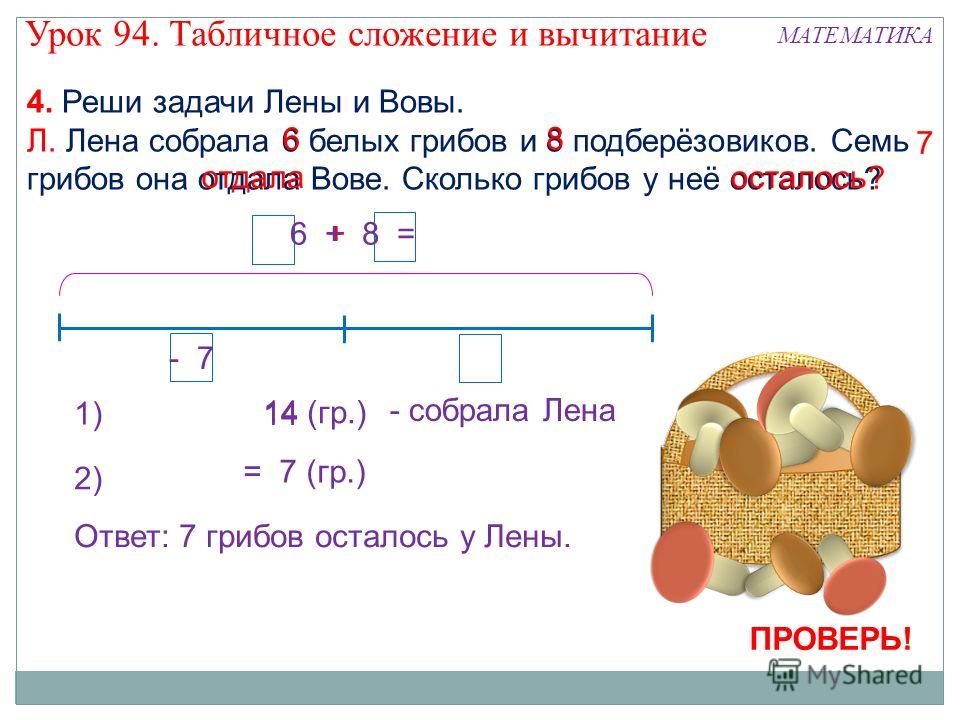

Какие цели и задачи мы с вами поставим к уроку?

(Ученики предлагают, учитель записывает на доске возможные задачи урока, затем производят отбор требуемых к уроку)

Возможные вопросы:

Условия задач на части отличаются от других типов задач? (Да)

— научиться распознавать по условию задачи данный тип задач;

Как вы думаете, задачи на части все одинаковые или могут отличаться друг от друга? (Отличаются)

— познакомиться с видами задач на части;

А для чего мы рассматриваем новый тип задач? (Чтобы научиться их решать)

-научиться решать задачи на части.

На доске:

— научиться распознавать задачи на части;

— познакомиться с видами задач на части;

— научиться решать задачи на части.

5. Изучение нового материала

Одну из задач на части мы с вами решили. Что помогло нам в решении задачи? (схематический рисунок)

Как вы думаете, поможет нам рисунок при решении других задач такого вида? (Да)

Откройте учебник на странице 48. Давайте решим задачу № 221 (б). Я вам предлагаю самостоятельно выполнить схематический рисунок к задаче, после этого я покажу свой рисунок и мы сравним их.

Слайд №5 (часть1)

№221 (б)

Яблоки

Груши 1600 г

Сливы

Ребята, смогли вы выполнить рисунок? Есть различия с выполненным мною рисунком?

Давайте составим план решения задачи:

1.Найдем, сколько всего частей ;

2. Узнаем, сколько граммов приходится на одну часть;

3. Узнаем, сколько граммов составляют 7 частей яблок;

4. Узнаем, сколько граммов составляют 4 части груш;

5. Узнаем, сколько граммов составляют 5 частей слив .

Запишем решение:

Слайд №5 (часть 2)

7+4+5=16 (частей) – всего
1600: 16=100(г)– приходится на одну часть;

3) 7∙100=700(г) составляют7 частей яблок;

4) 4 ∙100=400г) составляют 4 части груш;

5) 5∙ 100= 500(г) составляют 5 частей слив.

Ответ: 700 граммов яблок, 400 граммов груш, 500 граммов слив.

А теперь давайте мы с вами посмотрим презентацию, как авторы учебника предлагают решать задачу на части и сравним с нашим решением. (Просмотр флэш-презентации).

В чем сходство наших решений с авторским? (Схематический рисунок, деление на части, нахождение количества объекта, приходящегося на одну часть).

В таком случае, можно сделать вывод, что вы самостоятельно смогли правильно придумать способ решения задач на части.

А сейчас я предлагаю вам немного отдохнуть и выполнить упражнения для снятия утомляемости и напряжения глаз.

Физкультминутка

6. Работа по закреплению изученного материала

Вернемся к решению задач

1. Решение задач из учебника

Слайд №6 (часть 1)

Задание: придумайте по рисунку задачу на части

А теперь давайте сравним ваши задачи с предложенной в учебнике. Прочитаем № 219б на с. 49.

Решим эту задачу по предложенному плану.

Слайд №6 (часть 2)

Свинец Учитель на доске, дети в тетради

1) 5 – 2 = 3 (части) – составляют 360 г

? 360 г 2) 360 : 3 = 120 (г) –приходится на одну часть

3) 120 · 2 = 240 (г) — свинца в сплаве

4) 120 · 5 = 600 (г) — олова в сплаве

? Ответ: 240 граммов и 600 граммов.

Олово

Вернемся к задачам урока. Какие из задач мы рассмотрели?

Раз мы научились решать задачи, выполним самостоятельную работу.

2. Работа с текстом (устно, текст задачи распечатан на парту)

Прочитайте задачу:

Задача: Мальчик и девочка рвали в лесу орехи. Всего они сорвали 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов было у мальчика и девочки в отдельности?

Эта задача взята из повести Н. Носова «Витя Малеев в школе и дома», где описаны размышления главного героя над решением задачи. Вот как он размышлял.

«Прочитал я задачу, и даже смех разобрал. «Вот так задача! – думаю. – Чего тут не понимать? Ясно, 120 надо поделить на два, и получится 60 орехов. Теперь нужно узнать, сколько орехов сорвал мальчик:120 отнять 60, тоже будет 60… Только как же это так? Получается, что они сорвали поровну, а в задачнике сказано, что девочка сорвала в два раза меньше орехов. Ага! – думаю. – Значит 60 надо поделить на два, получится 30. Значит, мальчик сорвал 60, а девочка 30 орехов». Посмотрел в ответ; а там: мальчик 80, а девочка 40».

Ответьте устно на вопросы:

1) Возможно в задачнике опечатка и Витя верно решил задачу?

2) Предложите свой вариант решения.

(Оказывается, Витя смог решить задачу лишь тогда, когда нарисовал девочку в переднике с одним карманом, а мальчика в курточке с двумя карманами. «Все 120 орехов теперь лежали у них в трех карманах: в двух карманах у мальчика и в одном кармане у девочки, а всего, значит, в трех.

И вдруг у меня в голове, будто молния, блеснула мысль: «Все 120 орехов надо делить на три части!»

Ребята, давайте вернемся к целям и задачам, которые мы ставили на урок и посмотрим, что мы должны были сделать и что сделали?

7. Контроль полученных знаний

Самостоятельная работа

1. Установите соответствие между условиями задач и схематическими рисунками, выполненными по условию задач.

Задачи:

1) Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши – 3 части и сливы – 2 части общего веса сухофруктов. Сколько граммов яблок, груш и слив было в отдельности?

2) Для приготовления салата «Африканского» потребуется 5 частей ананасов и две части сыра, причем сыра на 120 г меньше. Сколько граммов сыра и ананасов нужно взять для салата?

3) Мангеймское золото – сплав, состоящий из 16 частей меди, 3 частей цинка и 1 части олова, имеет цвет золота. Сколько граммов меди в сплаве, если олова с цинком 32 грамма?

Схематические рисунки:

А.

? г

? г 120 г

Б.

? г

32 г

В. ? г

? г

1800 г

? г

Ответ:	1	2	3
Ответ:

2. Решите задачу №1 (решение запишите на листе).

А теперь давайте проверим, как вы справились с самостоятельной работой.

Поменяйтесь листочками с соседом по парте и выполните проверку работы.

Слайд №7

Верните работы друг другу.

Ребята, поднимите руки те, кто правильно выполнил все задания. Молодцы!

А теперь поднимите руки, кто верно выполнил только одно задание работы.

А кто совсем не справился с самостоятельной работой, то есть все задания выполнил неверно.

Какую цель мы можем сформулировать на следующий урок? Что нам предстоит?

8. Домашнее задание

Слайд №8

У: с. 48-49, №218 (а), 220.

Выяснить и подготовиться к ответу: кто и в каких сферах деятельности решает задачи на части?

9. Подведение итогов урока. Рефлексия

Слайд №9

Цель: подведение итогов урока, обсуждение того, что узнали, и того, как работали – т. е. каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы.

Закончи предложение:

Сегодня я узнал…

Было интересно…

Было трудно…

Я выполнял задания…

Я понял, что…

Теперь я могу…

Я почувствовал, что…

Я приобрел…

Я научился…

У меня получилось …

Я смог…

Я попробую…

Меня удивило…

Урок дал мне для жизни…

Мне захотелось…

Вопросы:

Какое важное условие должно выполняться в задачах на части? Какими должны быть все части? (Все части, о которых идет речь в задаче, равные).

Что первым делом надо найти при решении задач на части? (Сколько составляет одна часть).

Задачи математической производительности — пятый класс г -на Боуэна

Номер разговоры

Math Talk Boarks
Talk Stems для учащих
Math Talks Обзор
Number Talks Обзор
Что такое Number Talk? (Математические решения)

Математические заблуждения

Сбор из 22 общих математических неправильных представлений
ошибочные представления и общие ошибки

Коллекции задач.
Расширенные подсказки с ответами (по месяцам)
Задания CRA
Открытые вопросы (3–6 классы)
База данных Heinemann
Учебные процедуры для 5 класса
Открытые математические задачи (новые ежемесячно)
Сборник задач на успеваемость FCIT (сгруппирован по стандарту CCSS)
Сборник задач на успеваемость RDA (3–5 классы)
Вперед, математика! Задачи производительности
Задачи сбалансированной оценки производительности
Задания производительности Inside Mathematics
Задачи MARS (по классам)
Задания производительности NC
Задачи EDM RSA
Задачи OKC 7th EDM Grade 9 Write
0000008
OKC 5 -й класс. Десятичные дроби
Числа и операции — дроби
Конфеты (дроби и соотношения)
Фруктовые дроби (эквивалентность)
Пицца с друзьями (часть/целиком)
Где печенье? (сложение/вычитание дробей, работа в обратном порядке)
Time for Recess
Дроби плитки шоколада (эквивалент 4 степени)
Пицца с начинкой (эквивалент 5 степени)
Фермер Фред (4 степень, части целого)
Стандарты Джорджии Операции с дробями
Геометрия
Объем (призмы)
Стандарты Грузии Геометрия и координатная плоскость
Georgia Standards 2-мерные рисунки
Измерение и данные
График круга Открытый ответ
Двойной платок открытый ответ
мешки для покупок (преобразования измерений)
Объем стандартов GEORGIA и алгебраическое мышление
Сборник стандартов Джорджии
Массивы и головоломки с числами
Бусины под облаком (числовые шаблоны, таблицы ввода/вывода)
Кнопки (схемы номера)
Гороховный суп (схемы номеров)
Everyday Math Resources
EDM Math Box Propts
EDM RSA Подсказки
Виртуальное обучение сообщество
Оценка дифференциации. Учебное пособие по обзору системы дифференциации оценок
Учебное пособие по работе с EDM
Achievethecore.org :: Mathematics — Mathematics Tasks
Результаты (29)
Сортировать по
Самые загружаемыеДата добавленияНазвание (A-Z)
24.09.20
2 ФАЙЛА
Задания «Сделай сейчас» — это разминка, которую можно использовать в классах средней школы, чтобы улучшить понимание учащимися…
6–8 классы
17.02.16
5 ФАЙЛОВ
Что нам нравится в этой задаче Математически: Стандарты адресов: 4.NF.A.2 и MP3. Позволяет учащимся рассуждать о размере фр…
Класс 4
17. 02.16
4 ФАЙЛА
Что нам нравится в этой задаче Математически: Позволяет учащимся сравнивать дроби, используя общие числители, общий номинал…
Класс 3
18.03.15
1 ФАЙЛ
Что нам нравится в этом наборе заданий Математически: Стандарты адресов: 1.OA.C.6 и MP.5. Использует отношение между add…
Класс 1
26.02.15
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 7.NS.A.2d, MP.3 и MP.6. Ориентирован на преобразование десятичных чисел…
7 класс
25.02.15
2 ФАЙЛА
Что нам нравится в этой задаче Математически: Стандарты адресов: 5.
NF.A, 5.NF.B.3 и 4.NF.B.3d. Предоставляет возможность…
5 класс
25.02.15
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 4.ОА.А, 4.НБТ.Б, 4.ОА.А.3, 4.НБТ.Б.6, МП.1…
Класс 4
16.07.14
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов:  5.NF.B.7 и MP.2 Предоставляет возможность использо…
5 класс
05.06.14
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: K.CC.A.3, K.OA.A.2 Дает возможность попрактиковаться в сложении ф…

Марка К
25. 04.14
2 ФАЙЛА
Что нам нравится в этой задаче Математически: Стандарты адресов: 3.NF.A и MP.3 Требует от учащихся построить жизнеспособную…
Класс 3
11.02.14
4 ФАЙЛА
Что нам нравится в этой задаче Математически: Стандарты адресов: 2.NBT.A.1, 2.NBT.B.5 и MP.8. Предлагает возможность т…
Класс 2
01.11.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: A-SSE.A.1, A-SSE.B.3 и MP.7. Предлагает учащимся проанализировать …

9–12 классы
01.11.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 7. RP.A.2 и MP.8 Исследует несколько аспектов про…
7 класс
01.11.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 8.F.B.4, MP.2, MP.4 и MP.6. Требуется, чтобы студенты имели…
8 класс
31.10.13
1 ФАЙЛ

Что нам нравится в этой задаче Математически: Стандарты адресов: 3.NF.A.2a, 3.NF.A.1 и MP.2. Помогает учащимся в…
Класс 3
31.10.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 6.RP.A.1, 6.RP.A.2, MP.5 и MP.6. Обеспечивает си…
6 класс
31. 10.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 6.RP.A.2, 6.RP.A.3, MP.2 и MP.6. Предоставляет сим…
6 класс
31.10.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 3.NF.A.3d и MP.3 Представлены две дроби с одинаковым числом…

Класс 3
10.10.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: F-LE, F-IF.C.7,F-BF.B.3, A-CED.A.1, A-REI.B.4 и MP.4 Требуется…
9–12 классы
02.10.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: A-REI. B.4 и MP.7 Вознаграждает практика поиска и м…
9–12 классы
01.10.13

1 ФАЙЛ
Что нам нравится в этом наборе заданий Математически: Стандарты адресов: 3.OA.C.7, 3.OA.B.6, 3.OA.B.5, Часть …
Класс 3
08.09.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 1.OA.A.2, 1.OA.C.5, 1.OA.D.7, 1.NBT.B.2 Развивает учёбу…
Класс 1
08.09.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 8.EE.B, MP.1, MP.3 и MP.6. Представляет u…
8 класс
08. 09.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 6.NS.A.1, 5.NF.B.7 и MP.3. Включает понятия, …
6 класс
08.09.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 4.OA.A.1, 4.OA.A.2 и MP.4. Многократно выделяет…
Класс 4
08.09.13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 3.NF.A.2a и MP.1. Помогает учащимся понять дробь…
Класс 3
09/08/13
1 ФАЙЛ
Что нам нравится в этой задаче Математически: Стандарты адресов: 5.