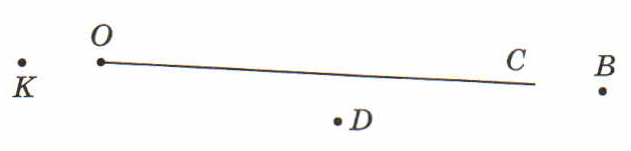Точка прямая плоскость луч отрезок 5 класс: Плоскость, прямая, луч, треугольник, угол. Видеоурок. Математика 5 Класс

Конспект урока по математике «Прямая, луч, отрезок» (5 класс)

План-конспект урока математики № 45

Класс: 5-Б

Дата: 13.11.2017

Учитель: Кольцова Н.А.

Тема:

Прямая, луч, отрезок

Тип урока:

Урок усвоения новых знаний, умений и навыков

Место урока в разделе:

Первый урок в теме «Измерение величин»

Оборудование:

Мультимедийный комплекс

Формы работы на уроке

Фронтальная, групповая, индивидуальная

Цели:

обучающие

(ориентированные на достижение предметных результатов обучения)

Ввести понятия «плоскость», «луч», «прямая», «отрезок»; установить свойства изучаемых объектов; научить строить и распознавать данные фигуры.

развивающие (ориентированные на достижение метапредметных результатов обучения)

Развивать внимание, память, образное мышление; формировать самостоятельность и коммуникативность; создавать условия для проявления познавательной активности.

воспитательные (ориентированные на достижение личностных результатов обучения)

Воспитывать умение слушать, вступать в диалог, участвовать в коллективном обсуждении проблем;

УУД:

познавательные

Поиск и выделение необходимой информации;

анализ объектов с целью выделения признаков; выделение и формулирование познавательной цели, рефлексия способов и условий действий.

регулятивные

Прогнозирование своей деятельности; планирование своей деятельности для решения поставленной задачи.

коммуникативные

Умение слушать и вступать в диалог; умение с достаточной полнотой и точностью выражать свои мысли.

личностные

Установление связи между целью деятельности и ее мотивом; проявление внимания и терпения; проявление доброжелательности в дискуссии, доверия к собеседнику.

Ход урока

I.Организационный момент

Приветствие учителя, проверка готовности учащихся к уроку.

II. Мотивация учебной деятельности

1. Сообщение темы (устный счет).

Решив все примеры и расположив ответы в порядке возрастания, вы сможете прочитать три слова, которые являются темой нашего урока (прямая, луч, отрезок).

15х0= (П)

44+150= (Р)

120:2= (Л)

32:32= (Р)

16-14= (Я)

25х4= (Ч)

160-80= (У)

90:10= (М)

11х10= (О)

920-800= (Т)

12+18= (А)

1000х15= (К)

1000:2= (О)

90-35= (Я)

50х4= (Е)

450-150= (З)

2. Формулирование цели урока.

3. Актуализация опорных знаний, полученных в начальной школе.

(Вспомнить понятия точки, прямой, отрезка)

III. Восприятие и первичное осознание нового материала

1. Определение плоскости.

Поверхность стола, стена, классная доска, оконное стекло могут служить примером части плоскости. Всю плоскость невозможно изобразить потому, что она бесконечна, но ее можно представить себе (привести примеры части плоскости).

2. Определение и обозначение прямой.

— прямая не имеет ни начала, ни конца – она бесконечна;

— прямую обозначают одной строчной латинской буквой или двумя заглавными;

— через любые две точки можно провести только одну прямую;

— две прямые на плоскости могут пересекаться или быть параллельными.

3. Определение луча.

Точка А, лежащая на прямой, делит ее на две части. Каждую их этих частей называют лучом с началом в точке А, обозначают луч двумя заглавными буквами.

4. Определение отрезка.

— определение отрезка;

— обозначение отрезка;

— определение равных отрезков.

IV. Первичное применение новых знаний

Решение упражнений №342, 354, 355, 356, 359.

V. Физминутка

VI. Применение знаний в стандартных условиях с целью усвоения навыков

1. Фронтальный опрос (1 группа):

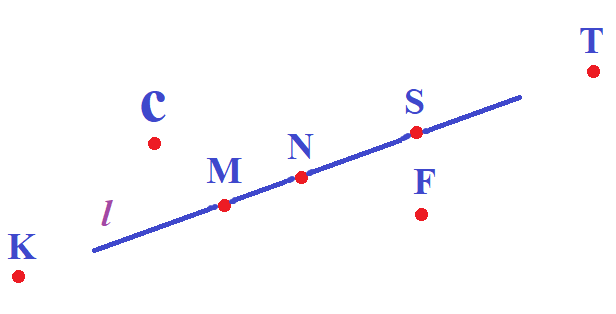
— Какие точки лежат на прямой l ?

— Какие точки не лежат на прямой

l ?

— Назовите все лучи с вершиной в точках M, N, S?

— Какие точки не лежат на луче MS?

— Перечислите все отрезки, изображенные на рисунке.

2. Индивидуальная работа по карточкам (2 группа):

Тест (Приложение 1).

Начало формы

Конец формы

VII. Итог урока.

Сообщение домашнего задания:

Прочитать п.2.1. стр. 77-79, выполнить №353,357 – 1 группа;

№358,360 – 2 группа.

Рефлексия:

— Сегодня на уроке я научился…

— Мне было интересно…

— Мне было трудно…

— Я понял, что…

— Больше всего мне понравилось…

— Своей работой на уроке я доволен (не совсем, не доволен), потому что…

Приложение 1

ТЕСТ

Как правильно записать обозначение луча?

А) АМ

Б) МА

Сколько лучей на рисунке?

А) один

Б) два

В) три

Г) четыре

Какие из обозначенных точек не лежат на луче АС?

А) К, D, В

Б) D, К

В) О, В

Г) К, О

Какая из фигур, изображенных на рисунке, является прямой?

А) ВА

Б) АС

В) ВС

Г) ВМ

Укажите пару пересекающихся фигур.

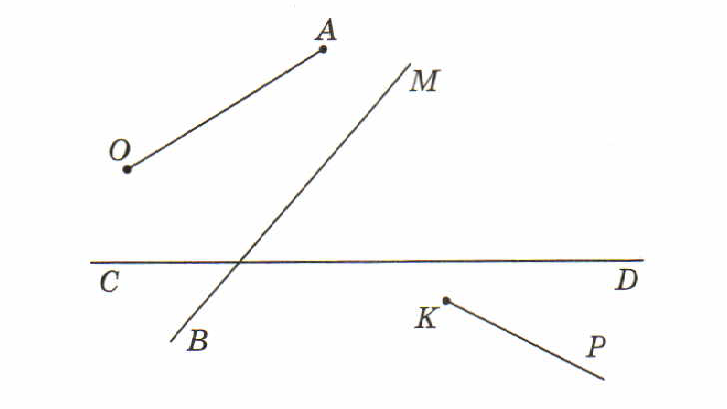
А) отрезок ОА и прямая СD

Б) луч КР и прямая ВМ

В) прямые СD и ВМ

Г) луч КР и отрезок ОА

Что является общей частью лучей АС и ВС?

А) отрезок АВ

Б) луч ВС

В) точка А

Г) точка В

Пересекаются ли прямые CD и АВ?

А) да

Б) нет

Пересекаются ли лучи АВ и СD?

А) да

Б) нет

9. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость?

Дата____________________ ФИ _____________________________________ Класс__________

Приложение 2

Технологическая карта урока

Деятельность учителя

Деятельность ученика

Время

(в мин.)

Формируемые УУД

Познавательные

Регулятивные

Коммуникативные

Личностные

Организационный момент

Приветствие; проверка готовности класса к уроку; организация внимания.

Осознанное и произвольное построение речевого высказывания

Прогнозирование своей деятельности

Умение слушать и вступать в диалог

Умение выделять нравственный аспект поведения

Мотивация учебной деятельности

Вместе с учениками определяет тему урока (Слайд 2-3).

Вспомнить понятия точки, прямой, отрезка, полученные ранее.

Задает учащимся наводящие вопросы

(Слайд 4-5)

Выполняют задание, решая примеры.

Записывают тему урока в тетрадь.

Участвуют в определении цели урока.

Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы.

Поиск и выделение необходимой информации.

Анализ объектов с целью выделения признаков.

Выдвижение гипотез.

Постановка цели.

Выделение и осознание того, что уже пройдено.

Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог

Установление связи между целью деятельности и ее мотивом

Восприятие и первичное осознание нового материала

Знакомит учащихся с определением плоскости, прямой, луча, отрезка.

Задает вопросы, подводящие к определению понятий (Слайды 6-10)

Слушают, задают вопросы.

Анализ объектов с целью выделения признаков.

Умение слушать и вступать в диалог

Проявление внимания и терпения

Первичное применение новых знаний

Решают упражнения из учебника №342, 354, 355, 356, 359.

Выполняют задания, отвечая на вопросы

проверяют правильность выполнения.

Поиск и выделение необходимой информации.

Структурирование знаний.

Подведение под понятие

Планирование своей деятельности для решения поставленной задачи

Умение слушать и вступать в диалог.

Коллективное обсуждение проблем (при необходимости)

Проявление

терпения и аккуратности при построении чертежей

Физминутка

Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.

Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.

Осознание ценности здоровья

Применение знаний в стандартных условиях с целью усвоения навыков

Комментирует, направляет работу учащихся.

Постановка проблемного вопроса.

1 группа работает с учителем, выполняя задания у доски (Слайд 11-12).

2 группа работает индивидуально с тестовыми заданиями на карточках с последующей самопроверкой (Слайд 13)

Выделение и формулирование познавательной цели, рефлексия способов и условий действия

Анализ объектов и синтез

Контроль изученного материала

Умение с достаточной полнотой и точностью выражать свои мысли

Проявление доброжелательности в дискуссии, доверия к собеседнику

Подведение итогов

Сообщает домашнее задание. Подводит итог урока

Дает возможность самим ученикам оценить себя, затем оценивает учащихся с комментированием.

Рефлексия.

Записывают домашнее задание в дневник

Подводят итог урока, оценивают себя своих товарищей.

Осознанное и произвольное построение речевого высказывания

Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог

Ориентация в межличностных отношениях

Онлайн урок: Плоскость. Прямая. Луч по предмету Математика 5 класс

Важно отметить, что в начале разбора приходится некоторые понятия принимать как нечто, что не требует определения, к таким понятиям относятся понятия прямой и точки.

Немецкий учений Гильберт как-то сказал на эту тему, что “точкой можно назвать хоть стул”, тем самым говоря, что вся наша модель строится на некоторых условностях.

С этим пониманием приступим к первой теме урока.

Для начала нам нужно понять, что такое поверхность.

Есть много строгих математических формулировок, но они уместны скорее в высших учебных заведениях, пока будет достаточно обиходного понятия поверхности.

Будем понимать под поверхностью непрерывное множество точек, границу, отделяющую геометрическое тело от внешнего пространства.

Представьте себе поверхность рабочего стола, футбольного мяча или любого другого предмета.

Также известно, что некоторые поверхности, например, рабочего стола, плоские.

Так мы подходим к понятию плоскости. Плоскость — плоская, бесконечная поверхность.

Плоская в данном случае обозначает, что если через любые две точки, принадлежащие этой плоскости, провести прямую, то она будет лежать в этой плоскости.

В самом деле, если нарисовать две точки на поверхности стола и соединить их прямой, то эта прямая будет лежать в плоскости стола.

Если же отметить две точки на шаре, то (тут нужен некоторый мысленный эксперимент) прямая, соединяющая их, будет проходить внутри шара, а не по его поверхности. Таким образом, поверхность шара не плоская, не является плоскостью.

Сейчас очень важно понять, что плоскость — это некоторое математическое понятие, соответствующее нашим бытовым плоским поверхностям с главным отличием в том, что у плоскости нет края.

Обычно на рисунках плоскость обозначается конечной, в крайнем случае лист бумаги или экран компьютера конечен.

Но это лишь обозначения, сама плоскость бесконечна.

Поверхности и плоскости принято обозначать двумя способами: с помощью трех латинских букв, соответствующих трем точкам плоскости, или одной греческой.

Выше изображена четырехугольная пирамида. В ней можно насчитать 5 плоскостей:

AEB
BED
BDC
ABC
AED (которую можно еще записать как AEC, ECD и ADC)

Согласись, две точки слишком мало, чтобы обозначить плоскость: на данном рисунке, например, есть две плоскости, проходящие через точки A и E, а четыре точки уже несут избыточную информацию, поэтому плоскости обозначают тремя точками.

Иногда плоскость обозначают одной строчной греческой буквой, например, так:

Содержание

Урок 21. прямая, луч, отрезок — Математика — 5 класс

Математика

5 класс

Урок №21

Прямая, луч, отрезок

Перечень рассматриваемых вопросов:

— понятия «прямая», «луч», «отрезок»;

— отличия прямой, луча, отрезка;

— прямая, луч, отрезок на чертежах, рисунках и моделях.

Тезаурус

Отрезок – часть прямой, ограниченный двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.

Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).

Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.

Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.

Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.

Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.

Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.

Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.

Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.

Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя.

Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.

Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.

В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.

Заметим, что два отрезка называются равными, если они совмещаются при наложении.

Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.

Это интересно

Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.

Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: добавление подписей к изображениям.

Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.

Правильные ответы:

1) а – это прямая.

2) АВ – это отрезок.

3) А – это луч.

№ 2. Тип задания: подстановка элементов в пропуски в тексте.

Вставьте в текст нужные слова.

Через__________ две____________ можно провести только одну _________.

Слова: любые; точки; прямую; ломаную.

Правильный ответ: через любые две точки можно провести только одну прямую.

Конспект урока математики в 5 классе по теме «Плоскость, прямая, луч»

Конспект урока математики в 5 классе

по теме «Плоскость. Прямая. Луч»

Содержание:

1. Введение ……………………………………………………………………… стр. 3

2. Основная часть – конспект урока «Плоскость. Прямая. Луч»…………… стр. 4

3. Заключение…………………………………………………………………… стр. 10

4. Список использованных источников………………………………………. стр. 10

5. Приложения………………………………………………………………….. стр. 11

1. Введение

Данный конспект урока «Плоскость. Прямая. Луч» является первым в изучаемой теме, составлен мной в этом году для проведения урока математики в 5-х классах.

Тип урока: первичное усвоение нового материала.

Дидактическая задача: создать условия для осознания и осмысления блока новой учебной информации.

Цели урока:

Образовательная – способствовать формированию понятий «плоскость», «прямая», «луч»; создать условия для усвоения основных свойств данных геометрических понятий.

Развивающая – развитие чертежных навыков, умения устанавливать причинно-следственные связи.

Воспитательная – способствовать пониманию того, что уважительное взаимодействие в процессе выполнения задания приводит к успеху каждого ученика.

Методы обучения: наглядный, словесный, репродуктивный, исследовательский, частично-поисковый.

Формы организации познавательной деятельности: фронтальная, коллективная, индивидуальная.

Методические рекомендации: данный конспект составлен для проведения без использования технических средств во время урока, для обеспечения наглядности и экономии времени на уроке на доске можно заранее сделать необходимые чертежи. Также при проведении урока можно использовать распечатанные картинки (см. добавленную в приложение). Для проведении рефлексии у учителя готовы небольшие листочки.

Оборудование: доска, мел, линейка/треугольник для выполнения чертежей на доске.

Технические средства: использовались при подготовке к уроку: компьютер, интернет, принтер. Другими техническими средствами не оснащен кабинет математики.

2. Основная часть:

Конспект урока по теме «Плоскость. Прямая. Луч»

Основные понятия: плоскость, прямая, луч

Ресурсы: учебник.

Деятельность учителя

Деятельность учеников

I. Организационный момент (2 мин.)

Подготовка к уроку, приветствие, сбор тетрадей с домашней работой/раздача проверенных тетрадей.

Подготовка тетрадей к уроку.

II. Устный счет (2 мин.)

Решить/определить какие знаки нужно поставить:

193*10 =

86+115 115+68

86+115 115+86

68+151 151+86

Устно решают задания, записанные на доске.

III. Определение темы урока (3 мин).

Отгадайте загадки:

1. В математике она пригождается всегда:

Без хвоста от запятой всем нам кажется простой.

И в конце, закончив строчку,

Мы поставим, братцы… (точку)

2. Линию прямую, ну-ка,

Сам нарисовать сумей-ка!

Это сложная наука!

Пригодится здесь… (линейка)

3. Он ограничен с двух сторон

И по линейке проведён.

Длину его измерить можно,

И сделать это так несложно! (Отрезок)

4. Он от солнца прилетает,

Пробивая толщу туч,

И в тетрадочке бывает,

А зовётся просто… (луч)

Но в загадке говорится, что он бывает и в тетрадке. Как луч может оказаться в тетрадке? Об этом мы узнаем сегодня на уроке по теме «Плоскость. Прямая. Луч» (записать тему на доске).

Слушают учителя, отвечают на вопросы, записывают тему урока в тетрадях.

IV. Объяснение нового материала (10 мин)

1) Начертить отрезок АВ на доске.

Мы с вами уже научились строить отрезки в тетради. Но скажите, на сколько большой отрезок вы сможете построить в своей тетради? Измерьте отрезок, который можно построить.

Как видите, размеры тетради ограничивают нас и не дают нам строить отрезки очень большой длины. А давайте попробуем представить себе, что тетрадный лист с помощью волшебного заклинания вырос до размеров поверхности стола. Длина вашего большого отрезка как-то поменялась?

А теперь представьте себе, что этот тетрадный лист стал ещё больше, например, размером с футбольное поле. Что стало с длиной вашего отрезка?

Поверхности тетрадного листа, стола, футбольного поля дают нам представление о плоскости. Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях.

Запомните! Плоскость бесконечна. Поэтому эту геометрическую фигуру нельзя изобразить, но её можно вообразить.

2)Если плоскость бесконечна, то что мы можем сказать о длине отрезка?

Давайте построим отрезок АВ. Напоминаю, что отрезок – это кратчайшая линия, соединяющая две точки.

3) Если этот отрезок с помощью линейки продлить в обе стороны, то мы получим ещё одну геометрическую фигуру, которую называют прямой.

Запомните! Прямая не имеет концов. Она бесконечна. Поэтому на рисунке мы можем изобразить только часть прямой, но мысленно мы должны понимать, что прямая продолжается в обе стороны бесконечно.

А теперь давайте отметим на листе бумаги две точки – А и В. Проведём через них прямую. Задание: Попробуйте через эти же две точки провести ещё одну прямую. Получается?

Запомните! Через любые две точки проходит одна единственная прямая.

Это свойство позволяет обозначать прямую, называя две любые её точки. Так, например, прямую, которую мы с вами сейчас построили, обозначают одним из двух способов: АВ или ВА. Читают: «прямая АВ» или «прямая ВА». Точки А и В лежат на прямой.

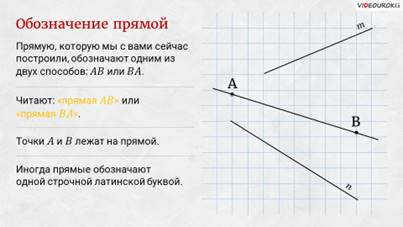
Но иногда прямые обозначают одной строчной латинской буквой. Посмотрите, на доске я построю две прямые: прямую m и прямую n.

4) Любая прямая делит плоскость на две части, на две полуплоскости.

5) А теперь вспомним загадку о фигуре, которая называется лучом.

Давайте построим прямую АВ и отметим на ней точку О. Посмотрите, эта точка разделила нашу прямую на две части. Каждую их этих частей называют лучом с началом в точке О. Конца у луча нет. Какой вывод можно сделать?

Вывод: Геометрический луч очень похож на световой, поэтому его так и назвали. Чтобы лучше представить себе луч, вспомним лазерную указку. Вспомнили? Луч света начинается в лазерной указке и уходит в бесконечность по прямой.

В математике лучи обозначают так же, как и прямую. Луч обозначают двумя прописными буквами, только сначала записывают букву, которая обозначает начало луча, а потом букву, обозначающую какую-либо другую точку этого луча. Так, в нашем примере, точка О делит прямую АВ на два луча: луч ОА и луч ОВ. Переставлять буквы в названии луча нельзя. Первой буквой всегда обозначается начало луча. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.

Запомните! В отличие от прямой, луч бесконечен только в одну сторону.

Чертят фигуры по ходу объяснения, подписывают названия и отвечают на вопросы.

V. Первичное закрепление с проговариванием (7 мин.)

1) Итак, мы познакомились с двумя новыми фигурами.

Какие это фигуры? Чем они отличаются от отрезка?

(Отрезок, луч, прямая являются прямыми линиями. А различаются они наличием концов)

2) Задание 1 на доске:

3) Задание 2 на доске:

Отвечают на вопросы, выполняют задания №1 и №2 в тетрадях.

VI. Работа по учебнику (10 мин)

Работа с учебником: с. 21-23,

1) №75

Отметьте в тетради точки С и D и проведите прямую CD. Отметьте на отрезке CD точку M. Лежит ли эта точка на прямой CD? Отметьте точку Р на прямой CD, не лежащую на отрезке CD.

2) №76

Начертите прямую и отметьте на ней точки А, Р и С. Запишите 6 различных обозначений прямой.

3) №77 (устно)

4) №90

Начертите отрезки МР, РК, КС, такие что:

МР = 3 см, РК = 2 см 5 мм и КС = 4 см 8 мм.

№ 91

Начертите пятиугольник АВСDE. Отметьте точку М на стороне АВ и точку N на стороне CD. Соедините точки M и N отрезком. Какие получились многоугольники? Назовите их.

Выполняют задания из учебника на доске и в тетрадях.

VII. Самостоятельная работа (5-7 мин)

1) стр. 22, №89

Сложите:

а) 3 м 45 см и 1 м 20 см; в) 2 м 80 см и 4 м 60 см;

б) 7 дм 8 см и 19 см; г) 1 км 250 м и 800 м.

2) стр 23, №92

Выразите:

а) в дециметрах: 50 см; 230 см; 67 м; 800 м;

б) в метрах: 600 см; 30 дм; 2 км; 6 км 50 м; 12000 мм.

3) Проверка выполненных заданий (выборочно, устно).

Выполняют в тетрадях самостоятельно.

VIII. Рефлексия учебной деятельности на уроке (3 мин.)

Цели:

— зафиксировать новое содержание урока;

-организовать рефлексию и самооценку учениками собственной учебной деятельности

Подведем итог работы на уроке.

1. Задать вопросы устно:

— Назвать тему урока.

— Рассказать, чему вы научились на уроке.

2. Раздать небольшие листочки, на которых ученики анонимно ответят на следующие вопросы:

1) Оцени собственное участие, активность на уроке по 10-бальной шкале (напиши на листочке соответствующее число от 1 до 10)

2) Напиши — с какими трудностями ты встретился во время урока.

3) Удалось ли тебе преодолеть эти трудности?

Собрать листочки.

Отвечают на вопросы учителя. Осуществляют самооценку.

Домашнее задание (1 мин.)

Учебник: стр. 20-21, п. 3 «Плоскость. Прямая. Луч» (выучить определения),

№99 (устно), №100, №101

Записывают домашнее задание

Резерв

стр. 23, №96 (решение комбинаторной задачи)

Заключение: мною проведены уроки по данному конспекту в двух 5-х классах. Хочу отметить, что при самостоятельном выполнении чертежей и обозначений на них на доске и в тетрадях ученикам легко было понять различия между прямой, лучом, отрезком. На последующих уроках мы продолжили решать задачи, учащиеся правильно называли определения данных геометрических фигур, умели выполнять задания по исходным условиям. Считаю поставленную задачу выполненной.

Использованная литература:

План-конспект урока по геометрии (5 класс) на тему: Плоскость. Прямая. Луч.

Тема: Плоскость. Прямая. Луч. ( Дата 19.09 Класс 5а )

Тип урока: изучение нового материала

Цели:

Предметные

— познакомить учащихся с геометрическими фигурами : плоскость. прямая. луч ;

— научить распознавать на рисунках эти фигуры, а в окружающем мире — объекты, для которых плоскость. прямая. луч являются моделями.

Личностные

— проявлять интерес к изучению темы и желание применять приобретённые знания и умения.

Метапредметные

— формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.

Планируемые результаты: учащиеся научаться распознавать на чертежах геометрические фигуры: плоскость. прямая. луч.

Основные понятия: плоскость. прямая. луч.

Организационная структура урока.

Организационный этап.

Ну-ка, проверь, дружок!

Готов ли ты начать урок?

Всё ль на месте? Всё ль в порядке?

Книжка, ручка и тетрадка…

Проверили? Вот здорово!

К уроку всё готово!

2 Активизация знаний обучающихся.

Верным помощником на уроке у нас будет самая маленькая геометрическая фигура

«Весёлая точка».

№1 Прочитайте числа: 180000509, 300001700, 608600005003(фронтально)

№2 Какое число нужно вписать в последнюю клетку?(индивидуально по цепочке)

№3 Выразите в дециметрах: 50 см, 230 см, 67 м, 800 м. (фронтально)

Выразите в метрах : 600 см, 30 дм, 2 км, 12000 мм.

3. Мотивация урока. Анаграммы. Просмотр презентации.

Расшифруйте слова: КОСТЬПЛОС, МАЯПРЯ, РЕЗООТК, КАТОЧ, ЧУЛ, ТКИНИ.

-Это слова»плоскость», «прямая», «отрезок», «точка», «луч», «нитки».

-Все ли расшифрованные слова вам знакомы?

-А где вы с ними встречались?

(На уроке математики, а нитки на уроке труда).

-Какое слово лишнее?

(Нитки. Они не относятся к уроку математики).

-Но все эти слова сегодня помогут нам сделать открытие.

Сообщение темы и цели урока.

-Рассмотрите фигуры на доске.

— Какую из этих фигур вы уже знаете?(отрезок)

— В какие группы фигуры можно объединить?

(В ходе рассуждения можно разбить на 3 группы: мы рассмотрим «отрезки» )

-Но возникает проблема: куда можно отнести фигуры 1, 3 и 4?

4. Изучение нового материала.

— понятие плоскости (с. 27-28 рассмотреть на окружающих примерах)

— Сравните фигуры с уже известными нам отрезком

-Что можно сказать?

-Можно ли эту фигуры назвать отрезком? Почему?

-Тогда давайте выполним одну операцию.

-В руках у меня 2 катушки тесьмы. Мы раздвигаем их в разные стороны.

-Что заметили?

(Это прямая линия, только в воздухе)

-Можно ли её продолжить в обоих направлениях?

-А эту прямую можно изобразить на доске?

(Чертим на доске, а дети в тетради).

Без начала и без края линия прямая,

Хоть 100 лет по ней идти,

Не найдёшь конца пути.

(Эта геометрическая фигура — прямая)

— У людей есть имена, у животных клички.

-А прямую линию можно обозначить одной или двумя буквами.

— Предложите имя прямой линии.

Вывод: У прямой линии нет ни начала, ни конца.

Мы можем изобразить только маленькую часть прямой линии. Её можно продолжить.

-Наша Весёлая Точка поможет нам ещё поработать с прямой линией.

-Поставьте точку, проведите через неё прямую линию.

-Можно ещё провести линию через эту точку?

-Сколько прямых линий можно провести через одну точку?

-Поставьте 2 точки. Через эти точки проведите прямую линию. Можно ли ещё провести?

А К

Вывод: Через одну точку можно провести сколько угодно линий, а через 2 точки – только одну.

-Теперь нашу прямую линию я разрежу.

(К месту разреза прикреплю Солнышко).

-Что получилось?

-На что похоже?

(Луч солнца)

О новой фигуре разносится весть

Конца пусть в ней нет,

Начало-то есть!

И солнце, тихонько взойдя из-за туч,

Сказало: «Друзья, назовём его луч!»

-Можно ли продолжить луч со стороны разреза?

(Нет, мешает круг и нечего продолжать)

-А с другой стороны?

(Можно продолжить до бесконечности)

СРАВНИТЕ: Луч и прямую линию.

(Прямую линию можно продолжить в обе стороны, а луч только в одну. Луч имеет начало)

-Начертите луч на доске и в тетради

-Луч обозначается двумя прописными буквами.

На первом месте всегда указывается начало луча.

-Поставьте точку, проведите луч, а ещё можно провести из этой точки, ещё…

-Какие лучи бывают?

(Солнечные лучи, лампа, фонарик и т.д.)

Вывод: Луч – это прямая линия, ограниченная с одной стороны. Из одной точки можно провести бесконечное множество лучей.

-У луча я отрезаю ту часть, которую можно продолжить…и прикреплю ещё одну точку.

-Что получилось?

(Отрезок)

-Линия, ограниченная с двух сторон.

СРАВНИТЕ: Луч и отрезок.

-У луча есть только начало, а отрезок имеет и начало и конец.

-Можно отрезок изобразить на доске и в тетради?

Точки две поставь в тетради,

Чтоб потом нарисовать между ними

Под линеечку – прямую,

И окажется, мой друг,

Что отрезок вышел вдруг,

Только точкам имена дать ты

Не забудь!

-Отрезок обозначается двумя буквами, но порядок при чтении и записи не имеет значения.

Вывод: Отрезок – это прямая, ограниченная с двух сторон.

-Что нового узнали об этих фигурах?

Вывод: Луч, прямая – это геометрические фигуры.

Работа с учебником $ 4 с.17-28.

5. Физкультминутка.

Раз, два, три, четыре, пять,-

Все умеем мы считать,

Отдыхать умеем тоже,

Руки за спину заложим,

Голову поднимем выше

И легко – легко подышим,

Раз – подняться, потянуться,

Два – согнуться, разогнуться,

Три – в ладоши три хлопка,

На четыре – руки шире,

Пять – руками помахать,

Шесть – за парту тихо сесть.

6. Первичное закрепление нового материала.

(На доске изображены геометрические фигуры)

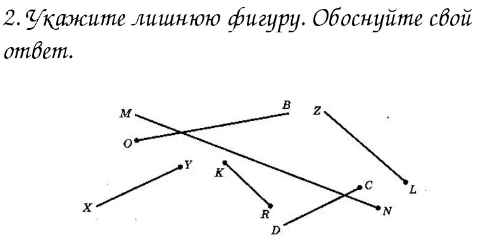
-Найдите отрезок, луч, прямую.

-Обоснуйте свой ответ.

-Можно ли сказать, что они пересекающиеся?

-А могут ли они пересечься?

Учебник: №85, 87(устно), 88(устно), 90, 91 — фронтально

Рабочая тетрадь: № 32, 34, 35, 36 — индивидуально(обучающая самостоятельная работа)

№ 33- работа в парах

Повторение: № 105

7. Обучающая самостоятельная работа.

8. Домашнее задание.

На дом вам будет дано следующее задание: $ 4, № 86, 89, 106, доп. № 111.

9. Подведение итогов урока. Рефлексия.

Вопросы : 1-7 с. 29.

— Соедините названия фигуры с фигурой.

Подберите правильное название.

ОТРЕЗОК ЛУЧ ПРЯМАЯ линия ПЛОСКОСТЬ

ПРЯМАЯ линия – не имеет начала и конца; можно обозначать одной или двумя буквами; через одну точку можно провести сколько угодно линий, через две – только одну.

ЛУЧ- прямая, ограниченная с одной стороны; продолжать можно только в одну сторону; из одной точки можно провести сколько угодно лучей; лучи бывают разные.

ОТРЕЗОК – прямая линия, ограниченная с двух сторон; на одной прямой может быть несколько отрезков; любую прямую можно превратить в отрезок.

ПЛОСКОСТЬ — воображаемая геометрическая модель; модели части плоскости: тетрадь, крышка стола, пол, стены, поле, море и т.д. Плоскость бесконечна, её нельзя изобразить.

Нарисовать свое настроение в виде солнышка в конце урока. «Лестница успеха».

-Вы сегодня дружно и творчески работали (Оценивается работа обучающихся).

-Спасибо всем! Урок окончен.

План-конспект урока математики в 5 классе по теме «Плоскость.Прямая.Луч»

ООО «Столичный учебный центр».

План-конспект урока

по математике

в 5 классе в муниципального автономного общеобразовательного учреждения « Акбашевская основная общеобразовательная школа имени кавалера ордена Мужества Ильдуса Зиннатовича Кучукбаева»

на тему «Плоскость .Прямая .Луч»

Разработал: Тагирова Лилия Мухаматзакировна

ФИО

слушатель курсов профессиональной переподготовки «Математика:теория и методика преподавания в образовательной организации»

Проверил: _Мурзыева Альфина Назимовна

ФИО руководителя практики

Акбаш ,20018

Тема урока. Плоскость. Прямая. Луч

Дата проведения.12.09.2018

Тип урока. Открытие новых знаний

Технология урока. Технология критического мышления

Цель урока

.Создать условия для вывода определений геометрических фигур: плоскость, прямая, луч; для формирования умений находить прямую и луч на чертеже, читать и чертить их.

Задачи.

— продолжить работу по формированию у учащихся пространственного воображения; научить различать простые геометрические фигуры.

— вести работу по развитию математической речи, логического мышления, умения анализировать, делать выводы;

-содействовать формированию положительного отношения к урокам, понимания необходимости знаний; показать практическую значимость математики при решении задач из повседневной жизни; воспитывать культуру поведения учащихся во время работы.

Планируемые образовательные результаты.

Обучающиеся научатся распознавать на чертежах геометрические фигуры: плоскость, прямая, луч; научатся читать и чертить .

УДД:

Личностные: формирование устойчивой мотивации к изучению и закреплению нового и способности обучающихся к саморазвитию и самообразованию.

Метапредметные:

Познавательные: анализировать , сравнивать , классифицировать и обобщать факты, строить логически обоснованное рассуждение, использовать доказательную математическую речь

Регулятивные : умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач , проверка по визуальному чертежу, умение корректировать свои действия, основы самоконтроля.

Коммуникативные: самостоятельно организовывать взаимодействие в группе , отстаивать свою точку зрения, приводить аргументы, подтверждая их фактами.

Основные термины, понятия: плоскость, прямая, луч.

Оборудование : учебник , классная доска, компьютер, мультимедийный проектор.

План урока:

Организационный момент(5мин)

— мотивация;

— целепологание.

Актуализация опорных знаний, подготовка к изучению нового материала(5 мин).
Изучение нового материала(10мин).

— первичная проверка усвоения нового материала

-физкультминутка (1 мин).

Решение учебных задач

-выполнение упражнений(12 мин)

— контроль знаний(7 мин)

Рефлексия(3 мин).
Итог урока.(2 мин)
Список использованной литературы:

Н.Я.Виленкин, В .И.Жохов, А.С.Чесноков, С.И.Швардцвурд Математика , 5 класс ; Мнемозина, М.2015
Ю.А.Глазков, В.И.Ахременкова, М.Я.Гаишвили КИМ математика, 5 класс; «Экзамен», М.2015.
Л.П.Попова, поурочные разработки по математике, 5 класс, «ВАКО», М, 2011

Ход урока:

Этап урока

Деятельность учителя

Деятельность

обучающихся

время

Результат выполнения

(предпологаемый)

I.Организационный момент.

Добрый день, ребята! Я рада приветствовать вас на нашем уроке, где вы узнаете много нового и интересного. Сегодня у нас в гостях учителя нашей школы.

Девиз нашего урока:

Слушать и слышать,

Смотреть и видеть,

Думать и рассуждать

Приветствуют учителя.

Концентрация внимания, воли, положительный настрой на работу.

Мотивация к учебной деятельности:

Организует работу учащихся, помогает с формулировкой темы и цели урока.

Вопрос : почему исключили пример №

Устная работа с выходом на тему урока.

Совместно с учителем формулируют тему урока и записывают в тетрадях

Вывод : сегодня на уроке изучаем геометрические фигуры — плоскость

-прямая

-луч

II. Актуализация опорных знаний.

Подготовка к изучению нового материала (Стадия «Вызов»)

Прием верные –неверные утверждения

Задает вопросы

Верите ли вы что:

1.Луч имеет и начало и конец?

2.Прямая не имеет концов?

3.Через любые две точки проходит единственная прямая?

4. Точка лежащая на прямой делит прямую на две части?

5.Плоскость имеет края?

6. Если две прямые имеют одну общую точку , то они пересекаются?

Отвечают на вопросы

Да или Нет

1-да

2-да

3-нет

4-нет

5-да

III.Изучение нового материала (Стадия «Осмысление»)

прием INSERT, напоминает инструктаж по заполнению таблицы.

Слушает выводы обучающихся, отвечает на вопросы

Первичная проверка усвоения новых знаний (слайд 8,9)

«v» — известная информация.

«+» — новая информация.

«?» — непонятная информация.

« -» — информация, идущая в разрез с имеющимися представлениями и знаниями.

2.Обсуждение текста в парах и заполнение таблицы.(стр16-17 учебника)

«галочка»

Знак «минус»

Знак «плюс»

«вопр.

Знак»

Обучающиеся заполняют таблицу ,

в парах знакомят друг- друга с итогом своей работы

физкульминутка

Раз – подняться на носки и улыбнуться.

Два – согнуться, разогнуться.

Три – в ладоши три хлопка,

Головою три кивка.

На четыре – руки шире.

Пять – руками помахать.

Шесть – за парту тихо сесть.

Решение учебных задач (закрепление пройденного материала,

.Организует пары и работу в них. Индивидуально работает с той парой у которого возникли затруднения.

Первая пара,№75, стр 17

Вторая пара, №77

Третья пара, №76

Четвертая пара, № 79, стр 18

Один обучающийся из пары выполняет работу у доски.

Контроль знаний, обратная связь.

По желанию можно выполнить часть 1 или часть 2, выполняем на листах и сдаем учителю.

Выполняют задания КИМ , тест №2, по вариантам

Рефлексия.

1. Оцените свою работу.

Оценивают работу в баллах.

10б. – все понял(«5»).

8б. – все понял, но затрудняюсь в решении задач(«4»).

6б. – понял не все(«3»).

4б. – ничего не понял(нужна помощь)

Ответьте на вопрос: мне было трудно ,,,,,,

Итог урока и домашнее

задание.

Комментирует домашнее задание

Записывают домашнее задание

№100, №101 стр 20

Творческое задание: составить синквейн к понятиям.

Самоанализ урока.

Урок « Плоскость.Прямая.Луч.» является 8 уроком в теме «Натуральные числа и шкалы», урок проходит после темы «Отрезок.Длина отрезка.Треугольник».

Тип урока – урок изучения нового материала . Урок проводится в классе со средними математическими способностями.

В основе нового стандарта лежит системно-деятельностный подход, который обеспечивает активную учебно-познавательную деятельность учащихся. Для включения учащихся в активную познавательную деятельность как нельзя лучше подходит технология развития критического мышления через чтение и письмо.

Урок направлен на развитие личностных, познавательных, коммуникативных и регулятивных УУД.

На первом этапе урока идет концентрация внимания, происходит положительный настрой на урок.. Дети сами формулируют тему урока, при этом проверяется умения устного счета, происходит развитие регулятивных и коммуникативных учебных действий

На стадии вызова используется методический прием «Верно — не верно», дети работают самостоятельно, учащиеся выдвигают версии, формулируют собственные мысли, учатся слушать товарищей, высказывать свою точку зрения. Развивается интерес к предмету, возникают желания к приобретению новых знаний.

На стадии осмысления используется прием INSERT. Этот прием учит работать с информацией, развивает умение выделять главное, умения сравнивать. Развиваются умения представлять информацию в виде таблиц. Учитель выступает в роли координатора, он направляет работу учащихся, помогает слабым учащимся в выполнении заданий.

Обсуждение в парах помогает развивать умения делового сотрудничества, сравнивать различные точки зрения, считаться с мнением других.

Первичная проверка усвоения новых знаний (слайд 8,9)происходит на этапе изучения нового материала, это позволяет увидеть проблемные моменты усвоения нового матриала.

При решении практических задач обучающиеся работают в парах, один из которых объясняет решение задания у доски . Дети учатся перерабатывать полученную информацию, делать самостоятельно выводы о проделанной работе. Идет развитие личностных УУД, в частности творческое отношение к процессу выбора и выполнению заданий. Формируются умения выполнять учебные действия в соответствии с планом работы.

На уроке выполняются задания по КИМ, но работу оценивает учитель. Учитель организует индивидуальную работу при решении учебных задачю.

На стадии рефлексии продолжается развитие познавательных умений, умений давать оценку действий, оценивать результат. 30% учащихся все поняли, 40% все поняли, но затрудняются в решении, Остальные материал поняли, но не все.

При подведении итогов урока и сообщении домашнего задания идет развитие таких познавательных умений, как находить ответы на поставленные вопросы, используя свой жизненный опыт и информацию, полученную на уроке. На последующих уроках пройдет закрепление материала с использованием технологии критического мышления.

Урок по математике «Луч, отрезок, прямая» 5 класс

Урок математики в 5 классе

Тема:

Луч, отрезок, прямая

Тип урока:

Урок усвоения новых знаний, умений и навыков

Место урока в разделе:

Первый урок в теме «Измерение величин»

Оборудование:

Мультимедийный комплекс

Формы работы на уроке

Индивидуальная, групповая, фронтальная,

Цели:

обучающие

Ввести понятия «плоскость», «луч», «прямая», «отрезок»; научить распознавать и строить данные фигуры.

развивающие

Развивать образное мышление;

формировать коммуникативность;

воспитательные

участвовать в коллективном обсуждении проблем;

УУД:

познавательные

Поиск и выделение необходимой информации;

регулятивные

Прогнозирование своей деятельности; планирование своей деятельности для решения поставленной задачи.

коммуникативные

Умение слушать и вступать в диалог; умение выражать свои мысли.

личностные

Проявление внимания и терпения; проявление доброжелательности в дискуссии, доверия к собеседнику.

Ход урока

I.Организационный момент

Приветствие учителя, проверка готовности учащихся к уроку.

II. Мотивация учебной деятельности

1. Сообщение темы (устный счет).

Решите примеры, расположите ответы в порядке возрастания, вы узнаете тему урока (прямая, луч, отрезок).

15х0= (П)

44+150= (Р)

120:2= (Л)

32:32= (Р)

16-14= (Я)

25х4= (Ч)

160-80= (У)

90:10= (М)

11х10= (О)

920-800= (Т)

12+18= (А)

1000х15= (К)

1000:2= (О)

90-35= (Я)

50х4= (Е)

450-150= (З)

2. Формулирование цели урока.

Что вы хотите узнать по данной теме?

3. Актуализация опорных знаний, полученных в начальной школе.

(Вспомнить понятия точки, прямой, отрезка)

III. Восприятие и первичное осознание нового материала

1. Определение плоскости.

2. Определение и обозначение прямой.

3. Определение луча.

4. Определение отрезка.

IV. Первичное применение новых знаний

Соотнесите

Предположим, что кто-то из ваших знакомых знает, что такое точка и что такое прямая, но не знает, что такое отрезок и что такое луч. Как бы вы ему это объяснили?

Какие из следующих утверждений вы выбрали бы для того,

чтобы объяснить, что такое отрезок и что такое луч:

— отрезок – это часть прямой;

— отрезок – часть прямой, ограниченная

двумя точками этой прямой;

— отрезок – все точки прямой,

расположенные между какими-либо двумя

точками этой прямой, и сами эти две точки.

— луч – это часть прямой;

— луч – часть прямой, ограниченная с

одной стороны какой-либо точкой этой

прямой;

— луч – все точки прямой, расположенные

по одну сторону от какой-либо точки этой

прямой и сама эта точка

Решение упражнений №342, 354, 355, 356, 359.

V. Физминутка

Луч, отрезок и прямая,

Угол, нолик и кривая.

Вправо! Влево! Вверх и вниз!

«Будь здоровым!» — наш девиз

VI. Применение знаний в стандартных условиях с целью усвоения навыков

1. Фронтальный опрос

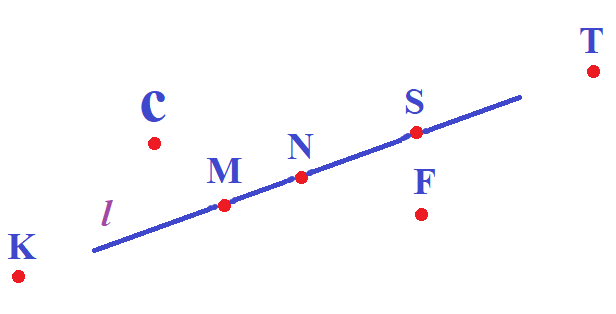
— Какие точки лежат на прямой l ?

— Какие точки не лежат на прямой l ?

— Назовите все лучи с вершиной в точках M, N, S?

— Какие точки не лежат на луче MS?

— Перечислите все отрезки, изображенные на рисунке.

Начало формы

Конец формы

VII. Итог урока.

Сообщение домашнего задания:

Прочитать п.2.1. стр. 77-79, выполнить №353,357 – 1 группа;

№358,360 – 2 группа.

Нарисуй фигуры, состоящие из отрезков, прямых и лучей.
Рефлексия:

— Сегодня на уроке я научился…

— Мне было интересно…

— Мне было трудно…

— Я понял, что…

— Больше всего мне понравилось…

— Своей работой на уроке я доволен (не совсем, не доволен), потому что…

Введение в точку, луч, линию и отрезок — MathsTips.com

Point

Точка является основным строительным блоком геометрии. Каждая форма сделана путем объединения точек.

Маленькая точка, отмеченная карандашом, является точкой. Точка не имеет длины или ширины. У него нет толщины. Точка — это знак позиции. Точка указывает точное местоположение. Точка обозначена точкой (.) И названа алфавитом.

На приведенном выше рисунке O — это точка, поскольку она имеет определенную отметку.Здесь это указывает, что эта точка O находится в центре плоскости. На рисунке ниже есть еще одна точка А. Она расположена в правом нижнем углу плана.

Луч

Давайте подумаем о факеле. Лучи света выходят из него и уходят. Давайте возьмем пример солнца. Лучи исходят от солнца и идут во всех направлениях и доходят до нас.

В геометрии луч также начинается с точки и может уходить в бесконечность. Он имеет начальную точку, но не имеет конечной точки. Мы говорим, что луч имеет одну конечную точку и идет без конца в одном направлении.

На рисунке выше, начинается с A, и стрелка указывает, что он может идти в бесконечность.

Его длина не может быть измерена. Неограниченное количество лучей может быть проведено в разных направлениях от данной точки

Лучи, исходящие от факела или солнца, являются примерами лучей.

Это луч, потому что луч имеет одну конечную точку и идет без конца в одном направлении.

Линия

Посмотрите на рисунок выше. Есть стрелки на обеих сторонах.Это указывает на то, что он может идти дальше с обеих сторон без конца. Это называется линия.

Линия идет без конца в обоих направлениях. Оба конца линии могут уходить в бесконечность. Линия не имеет конечных точек. Длина линии не может быть измерена. Линия не имеет определенной длины.

Линия именуется любыми двумя точками на ней и записывается как линия AB или строка PQ. Можно провести одну и только одну линию, проходящую через две заданные точки A и B. Эта линия называется AB. Его также можно назвать БА. Линия BA такая же, как линия AB.Оба проходят через те же две точки A и B.

Можно провести неограниченное количество линий, проходящих через данную точку A.

Горизонтальная линия идет прямо влево или вправо. Вертикальная линия идет прямо вверх или вниз.

Диагональная линия может находиться в любом направлении между горизонтальной и вертикальной линиями.

линейный сегмент

Теперь посмотрите на рисунок выше. Там нет стрелки на любом конце. Он начинается с одной точки и заканчивается в другой точке.Это называется отрезком. Раздел линии — это отрезок.

Сегмент линии имеет две конечные точки. Сегмент прямой — это прямая линия, соединяющая две точки. Это кратчайший путь между двумя точками. Линейный отрезок имеет определенную длину. Его длина может быть измерена.

Отметим карандашом две маленькие точки (.) Как точки A и B. Давайте соединим их, нарисовав прямую линию. Это формирует отрезок. Линейный сегмент именуется двумя конечными точками и записывается как линейный сегмент AB или линейный сегмент PQ.

На приведенном выше рисунке отрезок линии AB имеет две конечные точки A и B. Он начинается в точке A и заканчивается в точке B. Один и только один отрезок может находиться между двумя указанными точками A и B. Этот отрезок линии называется AB. Его также можно назвать БА. Линия BA такая же, как линия AB. Оба проходят через те же две точки A и B.

Сегмент линии также может быть частью линии, как показано на рисунке ниже.

Линейный сегмент также может быть частью луча.На рисунке ниже отрезок AB имеет две конечные точки A и B. Он является частью луча, начинающегося с A.

Параллельные линии

Две линии в одной плоскости либо встречаются, либо не встречаются. Если две линии на плоскости встречаются, мы говорим, что две линии пересекаются, и точка, где они встречаются, называется точкой пересечения. Если две линии не могут встретиться в любой точке, они называются параллельными линиями. Никакие две точки не могут быть общими для двух параллельных линий.

На рисунке выше две линии не пересекаются друг с другом.Даже если мы продолжим эти строки дальше, они не будут касаться или встречаться друг с другом. Это параллельные линии.

Пересекающиеся линии

Давайте посмотрим на две строки AB и CD на рисунке выше. Они пересекаются в точке О. Следовательно, они не параллельные линии. Точка O является точкой их пересечения.

Параллельные линии

Три или более прямых, проходящих через одну и ту же точку на плоскости, называются параллельными линиями. На рисунке ниже три линии AB, CD и EF пересекаются друг с другом в точке O.

Коллинеарные точки

Три или более точек на плоскости * называются коллинеарными, если они все лежат на одной прямой.

На рисунке выше точки A, B и C находятся на одной линии. Следовательно, эти три точки A, B и C коллинеарны.

* Плоская поверхность называется геометрией в плоскости. Мы можем сказать, что лист бумаги из нашей тетради — это самолет.

Измерение отрезка линии

Линейка — это инструмент, используемый в геометрии.Мы используем линейку для рисования отрезка. Мы используем это также для измерения длины отрезка.

Линейка, как правило, 1 фут (30 см) в длину и называется Линейка. Иногда это просто называется масштабом. Некоторые линейки имеют шесть дюймов (15 см) в длину и называются полфутовыми линейками. Один край линейки имеет шкалы, отмеченные в дюймах, а другой край имеет шкалы, отмеченные в сантиметрах.

Поместим линейку с ее ребром вдоль отрезка AB с нулевой отметкой линейки в начальной точке A отрезка.Мы читаем отметку на линейке в другой конечной точке B отрезка.

очков, которые нужно запомнить

Маленькая отмеченная точка — это точка.
Точка не имеет длины, ширины или толщины.
Точка указывает точное местоположение.
Луч начинается с точки и уходит в бесконечность.
Линия не имеет конечных точек.
Линейный сегмент имеет две конечные точки.
Сегмент линии соединяет обе конечные точки.
Если две линии не могут встретиться в любой точке, они называются параллельными линиями.
Три или более точек на одной прямой называются коллинеарными точками
Линейка используется для рисования отрезка и измерения его длины.

Вопросы и ответы

Вопрос 1 : Нарисуйте две точки A и B на бумаге и нарисуйте отрезок.

Ответ : Мы отмечаем точку A на странице для записи, а затем отмечаем другую точку B на той же странице. Мы соединяем эти две точки, используя линию. Это отрезок.

Вопрос 2: Нарисуйте две пересекающиеся линии.

Ответ: Берём линейку и рисуем линию АВ. Затем мы слегка поворачиваем линейку и рисуем еще одну линию CD таким образом, чтобы она проходила через любую точку линии AB.

Вопрос 3: Напишите два основных различия между отрезком и отрезком.

Ответ:

Линейный сегмент имеет две конечные точки. Линия не имеет конечной точки.
Линейный сегмент имеет определенную длину. Но линия не имеет определенной длины.

Вопрос 4: Напишите два ключевых различия между линией и лучом.

Ответ:

Линия проходит без конца в обоих направлениях, но луч имеет одну конечную точку и проходит без конца в одном направлении.
Линия AB такая же, как линия BA. Но луч AB отличается от луча BA.

Вопрос 5: Что означают коллинеарные точки?

Ответ: Коллинеарные точки — это точки на одной линии.Три или более точек на плоскости называются коллинеарными, если они все лежат на одной прямой.

Упражнение

1. Определите рисунок ниже?

Луч
Линия
Сегмент линии

2. Определите рисунок ниже?

Луч
Линия
Сегмент линии

3. Определите рисунок ниже?

Луч
Линия
Сегмент линии

4.Что из следующего имеет определенную длину?

Луч
Линия
Сегмент линии

Верно или Неверно

5. Две линии на рисунке ниже — это параллельные линии

True
Ложь

6. Две линии на рисунке ниже — это параллельные линии

True
Ложь

Заполните пробелы

7. ………………… имеет определенную длину

Луч
Линия
Сегмент линии

8.………………… не имеет конечных точек

Луч
Линия
Сегмент линии

9. Что из следующего является только одной конечной точкой?

Луч
Линия
Сегмент линии

10. Какое из следующих утверждений НЕ является правильным?

Можно провести неограниченное количество линий, проходящих через точку.
Две линии всегда встречаются в какой-то момент.
Линия длиннее отрезка.

3d — Проверьте, находится ли точка внутри отрезка плоскости Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру

Пересекающиеся линии. (Координатная геометрия) — Math Open Reference Пересекающиеся линии. (Координатная геометрия) — Math Open Reference Точка пересечение из двух непараллельный линии можно найти от
уравнения двух прямых.

Попробуй это Перетащите любую из 4 точек ниже, чтобы переместить линии. Обратите внимание, где они пересекаются.

Чтобы найти пересечение двух прямых:

Сначала нам нужны уравнения двух прямых.Если у вас нет уравнений, см. Уравнение линии — наклон / форма пересечения и Уравнение прямой — точка / наклон (Если одна из линий вертикальная, см. Раздел ниже).
Тогда, поскольку в точке пересечения, два Уравнения будут иметь одинаковые значения x и y, мы устанавливаем два уравнения равными друг другу. Это дает уравнение, которое мы можем решить для х
Мы подставляем это значение x в одно из линейных уравнений (неважно, какое) и решаем его для y.

Это дает нам координаты x и y пересечения.

Пример

Так, например, если у нас есть две строки, которые имеют следующие уравнения (в форме пересечения по уклону):

у = 3х-3

у = 2,3х + 4

В точке пересечения они оба будут иметь одинаковое значение y-координаты, поэтому мы устанавливаем уравнения равными друг другу:

3x-3 = 2,3x + 4

Это дает нам уравнение в одном неизвестном ( x ), которое мы можем решить: Переупорядочить, чтобы получить x терминов слева

3x — 2.3x = 4 + 3

Сочетание одинаковых терминов

0,7х = 7

дающий

х = 10

Чтобы найти y, просто установите x равным 10 в уравнении любой строки и решите для y: Уравнение для линии (любая линия будет делать)

у = 3х — 3

Установите х равным 10

у = 30 — 3

дающий

у = 27

Теперь у нас есть и x, и y, поэтому точка пересечения (10, 27)

Какую форму уравнения использовать?

Напомним, что строки могут быть описаны наклон / форма перехвата и форма точки / склона уравнения.Поиск пересечения работает одинаково для обоих. Просто установите уравнения, как указано выше. Например, если у вас было два уравнения в форме точка-наклон:

у = 3 (х-3) + 9

у = 2,1 (х + 2) — 4

просто установите их равными:

3 (х-3) + 9 = 2,1 (х + 2) — 4

и продолжайте, как описано выше, решая для х, затем подставляя это значение в любое уравнение, чтобы найти у.

Два уравнения не обязательно должны быть в одинаковой форме. Просто установите их равными друг другу и действуйте в обычном порядке.

Когда одна линия вертикальна

Когда одна из линий является вертикальной, она не имеет определенного наклона, поэтому ее уравнение будет выглядеть примерно как x = 12. См. Вертикальные линии (Координатная геометрия). Мы находим пересечение немного по-другому. Предположим, у нас есть линии, уравнения которых

у = 3х-3	Линия, наклоняющаяся вверх и вправо
х = 12	Вертикальная линия

На вертикальной линии все точки на ней имеют X-координату 12 (определение вертикальной линии), поэтому мы просто устанавливаем x равным 12 в первом уравнении и решаем его для y.
Уравнение для линии:

у = 3х — 3

Установите x равным 12, используя уравнение второй (вертикальной) линии

у = 36 — 3

дающий

у = 33

Таким образом, точка пересечения находится в (12,33).

Если обе линии являются вертикальными, они параллельны и не имеют пересечений (см. Ниже).

Когда они параллельны

Когда две линии параллельны, они нигде не пересекаются. Если вы попытаетесь найти пересечение, уравнения будут абсурдом.Например, линии у = 3х + 4 и у = 3х + 8 параллельны, потому что их наклоны (3) равны. Смотрите Параллельные Линии (Координатная Геометрия). Если вы попробуете описанный выше процесс, вы напишите 3х + 4 = 3х + 8. Очевидная невозможность.

Сегменты и лучи могут вообще не пересекаться
Рис. 1. Сегменты не пересекаются
В случае двух непараллельных линий пересечение всегда будет где-то на линиях. Но в случае отрезки или лучи которые имеют ограниченную длину, они могут не пересекаться.
На рисунке 1 мы видим два отрезка линии, которые не перекрываются и поэтому не имеют точки пересечения. Тем не менее, если вы примените метод выше, к ним, Вы найдете точку, в которой они пересеклись бы, если бы были достаточно вытянуты.
Что попробовать
На приведенной выше диаграмме нажмите «сброс».
Перетащите любую из точек A, B, C, D вокруг и отметьте местоположение пересечения линий.
Перетащите точку, чтобы получить две параллельные линии и обратите внимание, что они не имеют пересечения.
Нажмите «Скрыть детали» и «Показать координаты». Переместите точки в любое новое место, где пересечение еще видимо. Рассчитайте наклоны линий и точки пересечения. Нажмите «показать детали», чтобы подтвердить свой результат.
Ограничения
В целях ясности в апплете выше координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Это может привести к тому, что расчеты будут немного отклонены.
Для более см. Учебные заметки
Другие темы координатной геометрии
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
,
языковая независимость — самое короткое расстояние между двумя отрезками линии

Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру