Математика 4 класс сложение и вычитание многозначных чисел: карточки по матем 4 кл сложение многозначных чисел | Тренажёр по математике (4 класс):
карточки по матем 4 кл сложение многозначных чисел | Тренажёр по математике (4 класс):
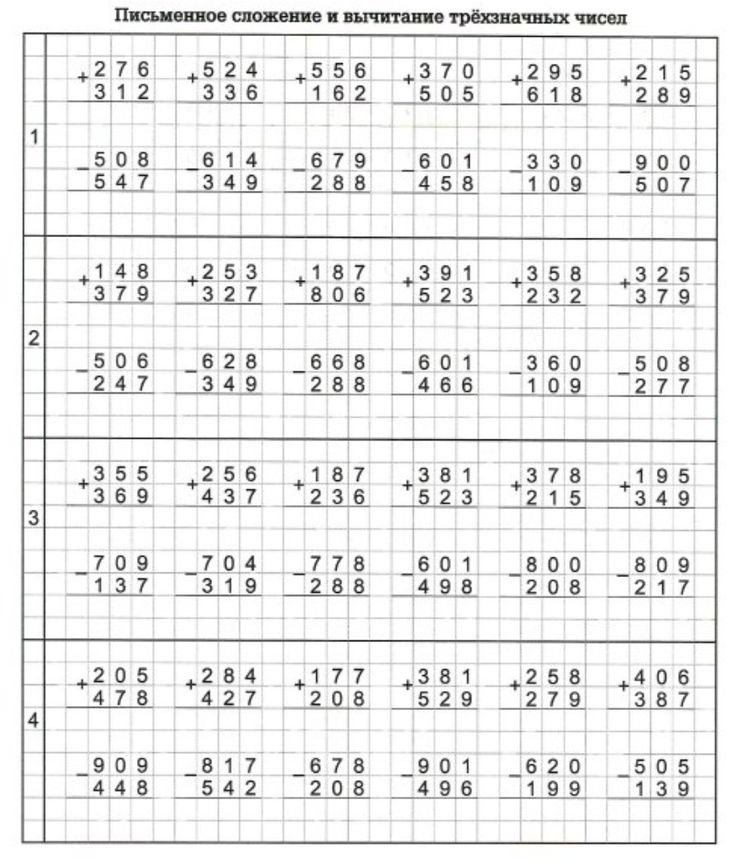
Реши примеры столбиком.
737246 + 54337 = 28238 + 5468 = 392476 + 1346 =
600010 – 25086 = 9652311 – 329864 = 500000 – 453644 =
Реши примеры столбиком.
358219 + 12275 = 516739 + 175152 = 485754 + 334674 =
877223 – 412667 = 700100 – 4345 = 500010 – 14075 =
Реши примеры столбиком.
175216 + 419335 = 427753 + 16824 = 238624 + 316376 =
958432 – 431764 = 500000 – 13777 = 801300 – 239005 =
Реши примеры столбиком.
737246 + 54337 = 28238 + 5468 = 392476 + 1346 =
600010 – 25086 = 9652311 – 329864 = 500000 – 453644 =
Реши примеры столбиком.
358219 + 12275 = 516739 + 175152 = 485754 + 334674 =
877223 – 412667 = 700100 – 4345 = 500010 – 14075 =
Реши примеры столбиком.
175216 + 419335 = 427753 + 16824 = 238624 + 316376 =
958432 – 431764 = 500000 – 13777 = 801300 – 239005 =
Реши примеры столбиком.
737246 + 54337 = 28238 + 5468 = 392476 + 1346 =
600010 – 25086 = 9652311 – 329864 = 500000 – 453644 =
Реши примеры столбиком.
358219 + 12275 = 516739 + 175152 = 485754 + 334674 =
877223 – 412667 = 700100 – 4345 = 500010 – 14075 =
Реши примеры столбиком.
175216 + 419335 = 427753 + 16824 = 238624 + 316376 =
958432 – 431764 = 500000 – 13777 = 801300 – 239005 =
Реши примеры столбиком.
737246 + 54337 = 28238 + 5468 = 392476 + 1346 =
600010 – 25086 = 9652311 – 329864 = 500000 – 453644 =
Реши примеры столбиком.
358219 + 12275 = 516739 + 175152 = 485754 + 334674 =
877223 – 412667 = 700100 – 4345 = 500010 – 14075 =
Реши примеры столбиком.
175216 + 419335 = 427753 + 16824 = 238624 + 316376 =
958432 – 431764 = 500000 – 13777 = 801300 – 239005 =
Реши примеры столбиком.
737246 + 54337 = 28238 + 5468 = 392476 + 1346 =
600010 – 25086 = 9652311 – 329864 = 500000 – 453644 =
Реши примеры столбиком.
358219 + 12275 = 516739 + 175152 = 485754 + 334674 =
877223 – 412667 = 700100 – 4345 = 500010 – 14075 =
Реши примеры столбиком.
175216 + 419335 = 427753 + 16824 = 238624 + 316376 =
958432 – 431764 = 500000 – 13777 = 801300 – 239005 =
Реши примеры столбиком.
737246 + 54337 = 28238 + 5468 = 392476 + 1346 =
600010 – 25086 = 9652311 – 329864 = 500000 – 453644 =
Реши примеры столбиком.
358219 + 12275 = 516739 + 175152 = 485754 + 334674 =
877223 – 412667 = 700100 – 4345 = 500010 – 14075 =
Реши примеры столбиком.
175216 + 419335 = 427753 + 16824 = 238624 + 316376 =
958432 – 431764 = 500000 – 13777 = 801300 – 239005 =
Урок.
 «Сложение и вычитание многозначных чисел» 4 класс. Школа России
«Сложение и вычитание многозначных чисел» 4 класс. Школа РоссииМБОУ Новоселковская СШ
Подготовила и провела: Чернышова Н.В.,
учитель начальных классов
высшей квалификационной категории
15 ноября, 2017 г.
Тема урока: Сложение и вычитание многозначных чисел.
УМК:
Школа России.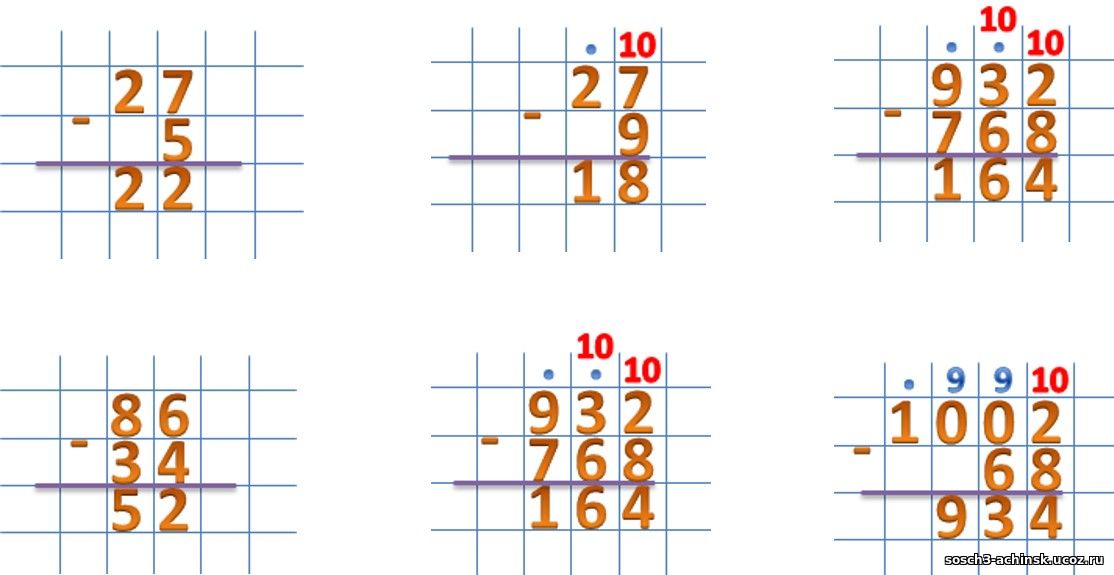
Тип урока: урок комплексного применения знаний и умений (урок изучения новой темы).
Цель урока: Отработка вычислительных навыков с многозначными числами.
Планируемый результат обучения, в том числе и формирование УУД:
— учащиеся научатся складывать и вычитать многозначные числа, систематизируют и закрепят знания, полученные на уроках математики.
Формируемые УУД:
Познавательные:
— формировать умения самостоятельно выделять и формулировать познавательную цель всего урока и отдельного задания;
— совершенствовать умение детей выполнять действия с многозначными числами;
— отрабатывать навыки решения задач изученных видов;
— строить логическое рассуждение.
Коммуникативные:
— развивать умение грамотно, логично, полно давать ответы, уметь доказать, аргументировать свое мнение;
— формировать умение работать в паре, группе, находить общее решение, умение аргументировать своё предложение;
— развивать способность сохранять доброжелательное отношение друг к другу, взаимоконтроль и взаимопомощь по ходу выполнения задания;
— Регулятивные:
— создать благоприятный психологический климат для возможного раскрытия потенциала каждого ребенка;
— проявлять
познавательную инициативу в учебном сотрудничестве.
Личностные:
— развивать умение применять свои знания в ситуации, близкой к жизненной;
— формировать способности к самооценке на основе критериев успешности учебной деятельности.
Оборудование и материалы: учебник для 4-го класса «Математика» // Моро М.И., Бантова М.А., Бельтюкова Г.В. и др. – М.: Просвещение, 2015; компьютер, проектор; карточки математического лото, карточки быстрого счета, карточки с задачами, «Лист оценки работоспособности на уроке», конверты с домашним заданием.
Ход урока
1.Организационный момент. Самоопределение к деятельности.
— Добрый день!
— Ребята, сегодня на уроке мы продолжим постигать тайны царицы всех наук – Математики. Нашими помощниками будут: знания, умения, старание.
2. Актуализация
знаний и фиксация затруднения в деятельности
Актуализация
знаний и фиксация затруднения в деятельности
1. -Проверим вашу готовность к предстоящей работе.
I. Что это такое?
o как называются числа при сложении?
o как называются числа при вычитании?
o как узнать на сколько одно число больше или меньше другого?
o на какие группы можно разделить числа?
o как узнать во сколько раз одно число больше или меньше другого?
o что такое периметр?
o как найти площадь?
o что такое квадрат?
o как найти неизвестное слагаемое?
o Как проверить вычитание?
o Как проверить сложение?
o если к числу прибавить 0, то…(то число не изменится)?
o если из числа вычесть 0, то…(число не изменится)?
o разность двух одинаковых чисел равна…(0)
o какое число получится при делении на 0?
o сколько дней в году?
o сколько кг в 1 т.?
o сколько ушей в классе у присутствующих детей? (шутка)
II. Вычисли
наиболее лёгким способом.
Вычисли
наиболее лёгким способом.
96+98+904 =
61+58+39=
24+65+76=
2. Индивидуальная работа (карточки).
a — b : c + o
(a + o — c) : b . k
a + o – c : b
(100 . 9 :30) +120 :2 + 140
– Откройте свои тетради. Запишем
15 ноября.
Классная работа.
3. Игра «Математическое лото».
У вас карточки с числами, я задаю вам выражение, вы находите ответ и зачёркиваете:
1. Найдите число, в котором 3 тысячи, 2 сотни, 5 десятков, 4 единицы. (3254)
2. Найдите одну пятую числа 600. (120)
3. Увеличь в
4 раза число 250 . (1000)
(1000)
4. Уменьшаемое 320 вычитаемое 30.Найдите частное. (290)
5. На стадионе 5000 мест. Половина из них, заняты зрителями. Сколько мест свободных? (2500)
6. 9 сотен умножить на 7. (6300)
7. 7 часов — сколько это минут. (420)
8. На сколько надо увеличить 25, чтобы получить 170? (145)
9. Найдите площадь прямоугольника со сторонами 700 м и 4 м (2800)
10.41 увеличить в 100 раз. (4100)
11.32 центнера – сколько кг?(3200)
|
145 | 3200 | 2500 | |||
290 | 32496 | 3254 | 854671 | 420 | |
6300 | 4100 | 2800 | 1000 |
Взаимопрверка
(меняются тетрадями)
Оцените
работу товарища.
— На какие две группы можно разделить эти числа (чётные и нечётные), (трёхзначные и четырёхзначные).
— Какие числа вы не зачеркнули?
4. Запишите числа из таблицы, которые вы не зачеркнули, в порядке возрастания. (один на доске)
Проверка! 32496, 854671
-Дайте характеристику любому из этих числу ОЦЕНКА!
—Какие арифметические действия, вы можете выполнить с этими числами? (сложение и вычитание)
5.Постановка учебной задачи.
— Как вы, думаете, над какой темой будем работать сегодня?
- Итак,
тема урока: Сложение и вычитание многозначных чисел.
- Какую задачу перед собой поставим?
Научиться письменному сложению и вычитанию многозначных чисел.
6.Построение проекта выхода из затруднения, открытие нового знания
— Чтобы правильно решать такие примеры, нужно вспомнить алгоритм
решения.
— Что такое алгоритм? (План)
— Сейчас вы самостоятельно вспомните алгоритм сложения и вычитания 3-х значных чисел и попробуете его восстановить.
У вас на партах карточки, на которых напечатаны разные действия алгоритма. Работая и обсуждая в парах, расставьте порядок алгоритма для сложения и вычитания многозначных чисел.
I вариант
Алгоритм письменного сложения многозначных чисел
Для того чтобы выполнить сложение многозначных чисел, надо:
1. Пишу единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч.
2. Складываю единицы …….
3. Складываю десятки …….
4. Складываю сотни ……
5. Складываю единицы тысяч
6. Складываю десятки тысяч
7. Складываю сотни тысяч
8. Читаю ответ …….
II вариант
Алгоритм письменного вычитания многозначных чисел
Для того чтобы выполнить вычитание многозначных чисел,
надо:
- Пишу единицы
под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под
единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под
сотнями тысяч.

- Вычитаю единицы …….
- Вычитаю десятки …….
- Вычитаю сотни ……
- Вычитаю единицы тысяч
- Вычитаю десятки тысяч
- Вычитаю сотни тысяч
- Читаю ответ …….
ПРОВЕРКА (дети зачитывают алгоритм сложения и вычитания) ОЦЕНКА!
—Что самое главное при решении?
(правильно записывать числа, чтобы единицы разрядов совпадали, вычислять начинать с единиц)
+ ESAKHP + ESAKHP + ESAKHP
LVFA LVFA LVFA
ФИЗКУЛЬТМИНУТКА
1.)- Составьте из чисел, которые вы выписали, все возможные варианты примеров (дети называют устно)
Решим у доски, применяя алгоритм сложения и вычитания многозначных чисел.
Решение примеров на доске. «Поспешишь – людей насмешишь»
854671+32496 =
854671-32496 =
2. ) Первичное
закрепление.
) Первичное
закрепление.
«Все тайное становится явным»
(решение примеров по вариантам с взаимопроверкой)
У вас на партах лежат листы с заданием. Каждый из вас сам выбирает тот вариант заданий, с которым он справится.
Вариант 1
98765+2232 =100.997 189456-23124=166.332
Вариант 2
3806578+344612=4.151.190 7689438-828129=6.861.309
Вариант 3
3274560198+64789321= 3339349519 6472318059-708913724=3339349519
Самостоятельно решаем и выполняем проверку по слайду.
3.) Творческое применение и добывание знаний в новой ситуации.
«Без труда нет добра» (решение задач, самостоятельная работа)
Откроем учебник с. 60 Задача 264.
Выдано -327 к.
Осталось -? на 246 r <
1) _327
246
81 (к. )
–осталось
)
–осталось
2) _З27
81
408 (к.) – всего книг
Ответ: 408 книг.
Дополнительно : № 265
1.Укажи верно решённый пример:
518.304 518.304 518.304
+ 420.296 + 420.296 +420.296
939.600 938.600 939.590
2. Укажи верно решённый пример:
_ 54.762 _ 54.762 _54.762
49.826 49.826 49.826
4.934 5.946 4.936
1.Запиши вычисления в столбик:
26 637 + 176 12 765 – 2937
34 600 + 2548 63 243 — 62 754
428 095 + 74 340 176850 – 94768
120 470 + 639 842 535 200 – 484940
Подведение итогов
6. Домашнее задание: с.60 № 262, 263.
Домашнее задание: с.60 № 262, 263.
7. Рефлексия.
Тихо все на месте сядем
И закроем глазки.
Вспомним, всё, что повторяли,
Без моей подсказки.
— В чём вы упражнялись на уроке?
— Ребята, оцените свою работоспособность на уроке.
Работал (ла) на уроке:
а) отлично (смайлик с улыбкой),
б) хорошо (смайлик с удивлением),
в) мог (ла) бы работать лучше (смайлик грустный).
Спасибо за урок!
a — b : c + o (a + o — c) : b . k a + o – c : b (100 . 9 :30) +120 :2 + 140
| a — b : c + o (a + o — c) : b . a + o – c : b (100 . 9 :30) +120 :2 + 140
|
a — b : c + o (a + o — c) : b . k a + o – c : b (100 . 9 :30) +120 :2 + 140
| a — b : c + o (a + o — c) : b . k a + o – c : b (100 . 9 :30) +120 :2 + 140
|
a — b : c + o (a + o — c) : b . k a + o – c : b (100 . 9 :30) +120 :2 + 140
| a — b : c + o (a + o — c) : b . k a + o – c : b (100 . 9 :30) +120 :2 + 140
|
Вариант 1
98765+2232 = 189456-23124=
Вариант 2
3806578+344612= 7689438-828129=
Вариант 3
3274560198+64789321= 6472318059-708913724=
Вариант 1
98765+2232 = 189456-23124=
Вариант 2
3806578+344612= 7689438-828129=
Вариант 3
3274560198+64789321= 6472318059-708913724=
Вариант 1
98765+2232 = 189456-23124=
Вариант 2
3806578+344612= 7689438-828129=
Вариант 3
3274560198+64789321= 6472318059-708913724=
Вариант 1
98765+2232 = 189456-23124=
Вариант 2
3806578+344612= 7689438-828129=
Вариант 3
3274560198+64789321= 6472318059-708913724=
Алгоритм письменного сложения многозначных чисел
- Складываю
единицы …….

- Складываю единицы тысяч
- Пишу единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч……
- Складываю сотни тысяч
- Читаю ответ …….
- Складываю десятки …….
- Складываю сотни ……
- Складываю десятки тысяч
Алгоритм письменного вычитания многозначных чисел
- Вычитаю единицы …….
- Читаю ответ …….
- Вычитаю сотни ……
- Вычитаю десятки тысяч
- Пишу единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч.
- Вычитаю десятки …….
- Вычитаю единицы тысяч
- Вычитаю сотни тысяч
|
120 | 145 | 3200 | 2500 | ||
290 | 32496 | 3254 | 854671 | 420 | |
6300 | 4100 | 2800 | 1000 |
|
120 | 145 | 3200 | 2500 | ||
290 | 32496 | 3254 | 854671 | 420 | |
6300 | 4100 | 2800 | 1000 |
|
120 | 145 | 3200 | 2500 |
| |||
290 | 32496 | 3254 | 854671 | 420 |
| ||
6300 | 4100 | 2800 | 1000 |
| |||
1.
518.304 518.304 518.304 + 420.296 + 420.296 +420.296 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.934 5.946 4.936
| 1.Укажи верно решённые примеры:
518.304 518.304 518.304 + 420.296 + 420.296 +420.296 939.600
938.
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.934 5.946 4.936 | ||||||
1.Укажи верно решённые примеры:
518.304 518.304 518.304 + 420.296 + 420.296 +420.296 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.
| 1.Укажи верно решённые примеры:
518.304 518.304 518.304 + 420.296 + 420.296 +420.296 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.934 5.946 4.936 | ||||||
1.Укажи верно решённые примеры:
518.304 518.304 518.304 + 420. 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.934 5.946 4.936
| 1.Укажи верно решённые примеры:
518.304 518.304 518.304 + 420.296 + 420.296 +420.296 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49. 4.934 5.946 4.936 | ||||||
1.Укажи верно решённые примеры:
518.304 518.304 518.304 + 420.296 + 420.296 +420.296 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.934 5.946 4.936
| 1.Укажи верно решённые примеры:
518. + 420.296 + 420.296 +420.296 939.600 938.600 939.590
_ 54.762 _ 54.762 _54.762 49.826 49.826 49.826 4.934 5.946 4.936 | ||||||
1.Запиши вычисления в столбик:
26 637 + 176 12 765 – 2937
34 600 + 2548 63 243 — 62 754
428 095 + 74 340 176850 – 94768
120 470 + 639 842 535 200 – 484940
1. Запиши вычисления в столбик:
Запиши вычисления в столбик:
26 637 + 176 12 765 – 2937
34 600 + 2548 63 243 — 62 754
428 095 + 74 340 176850 – 94768
120 470 + 639 842 535 200 – 484940
1.Запиши вычисления в столбик:
26 637 + 176 12 765 – 2937
34 600 + 2548 63 243 — 62 754
428 095 + 74 340 176850 – 94768
120 470 + 639 842 535 200 – 484940
1.Запиши вычисления в столбик:
26 637 + 176 12 765 – 2937
34 600 + 2548 63 243 — 62 754
428 095 + 74 340 176850 – 94768
120 470 + 639 842 535 200 – 484940
Сложение и вычитание многозначных чисел (стратегии и примеры)
Содержание
- Стратегии сложения и вычитания многозначных чисел
- Стратегии операции сложения многозначных чисел Стратегии для Операция вычитания многозначных чисел
- Решаемые примеры
- Часто задаваемые вопросы
Стратегии сложения и вычитания многозначных чисел
Существует множество способов или стратегий, применяемых для сложения и вычитания многозначных чисел. Некоторые используются для меньших или простых чисел, а другие используются для больших или сложных чисел.
Некоторые используются для меньших или простых чисел, а другие используются для больших или сложных чисел.
Это базовый навык, который ученики младших классов должны развить, чтобы решать многие сложные вопросы по сложению и вычитанию в младших классах.
Эти стратегии, которые мы вскоре рассмотрим, дают учащимся различные способы решения задач на сложение и вычитание.
Стратегии сложения многозначных чисел
Сложение многозначных чисел — очень простая операция, которую дети должны освоить в младших классах.
В операции сложения добавляемые числа называются слагаемыми, а результат называется суммой.
Существует множество способов сложения многозначных чисел, например:
- Использование частичной суммы
Метод частичной суммы представляет собой двухэтапный процесс и использует концепцию разряда в числах.
В этом методе соответствующие цифры в столбце разряда добавляются, начиная слева направо, для получения частичных сумм.
Затем эти частичные суммы складываются, чтобы получить требуемую сумму.
Например, 123 + 242,
123 можно разбить как 100 + 20 + 3
Аналогично, число 242 можно разбить как 200 + 40 + 2
Теперь сложите цифры обоих чисел в разряде сотен, то есть 1 + 2 = 3, следовательно сотни. Точно так же сложите цифры обоих чисел в разряде десятков и разряде единиц соответственно, то есть 2 + 4 = 6, что дает 6 десятков и 3 + 2 = 5, или 5 единиц.
Как упоминалось выше, метод частичной суммы представляет собой двухэтапный процесс.
На первом этапе цифры в столбце разряда складываются, чтобы получить частичную сумму двух чисел.
На приведенном выше рисунке 300, 60 и 5 представляют собой частичные суммы, полученные после сложения цифр в соответствующих столбцах разряда.
На втором этапе эти частичные суммы складываются, чтобы получить окончательную сумму 365. увеличить или уменьшить на очень небольшое число, чтобы сделать число проще и упростить процесс сложения.
увеличить или уменьшить на очень небольшое число, чтобы сделать число проще и упростить процесс сложения.
Позже это добавление или вычитание очень небольшого числа компенсируется в сумме, чтобы получить окончательную сумму.
Например: 520 + 229
При добавлении 1 к 229 получается 230, что упрощает сложение данных чисел.
520 + 229
⇒ 520 + 230
⇒ 750 → 750 – 1 = 749 добавлено [для первоначальной компенсации].
- Использование подсчета:
Сложение чисел является основной ментальной стратегией. Обычно мы берем большее число и считаем оттуда.
Например: 45 + 6
Сначала мы берем большее число из двух, которое здесь равно 45.
Затем прибавляем оттуда 6 раз, то есть 46, 47,…51, получаем 51.
Отсюда получается сумма 51.0051
Это метод сложения, при котором десять единиц перегруппировываются в один десяток, или десять десятков объединяются в одну сотню, или десять сотен объединяются в одну тысячу и так далее.
Обычно используется, когда сумма цифр в разряде превышает 9.
Например: 145 + 236
чем 9, то есть 5 + 6 = 11, следовательно, +1 переносится, сдвигается в разряд десятков, 4. Он добавляется к цифре 4, чтобы получить 5. Затем применяется обычный процесс сложения.
Стратегии операции вычитания для многозначных чисел
Вычитание — одна из четырех основных арифметических операций, с помощью которых вычисляется разница между двумя числами. В уравнении вычитания большее число, из которого вычитается меньшее число, называется уменьшаемым, а меньшее вычитаемое число называется вычитаемым.
Результат вычитания называется разностью.
Подобно сложению, для вычитания чисел можно использовать несколько стратегий.
- Использование частичной разницы:
Это двухэтапный процесс, аналогичный используемому дополнительно методу частичной суммы. Единственная разница между ними заключается в том, что здесь частичные различия получаются путем вычитания соответствующих цифр из столбца разряда двух чисел. Затем эти частичные разности складываются, чтобы получить результат вычитания.
Единственная разница между ними заключается в том, что здесь частичные различия получаются путем вычитания соответствующих цифр из столбца разряда двух чисел. Затем эти частичные разности складываются, чтобы получить результат вычитания.
- Использование компенсации:
Вычитание по компенсации — это стратегия, аналогичная сложению по компенсации.
В этом методе уменьшаемое или вычитаемое либо увеличивается, либо уменьшается на очень небольшое число, которое впоследствии компенсируется в конечном результате.
Например: 249 – 120
Если прибавить 1, чтобы получить число 249→ 250, вычитание будет проще.
249-120
⇒ 250-120 (1 добавляется к 249)
= 130 → 130-1 = 129 [-1 используется для компенсации]
Рассмотрите другой пример, 129 [-1. 321 – 50
Если из 1 вычесть число 321 → 320, вычитание будет проще.
321 – 50
320 – 50 (1 вычитается из 321)
= 270 → 270 + 1 = 271 [+1 используется для компенсации]
- Использование подсчета:
число, из которого вычитается другое число.
Кроме того, другое вычитаемое число должно быть меньшим числом.
Например, 42 – 5
Здесь мы считаем 5 раз в меньшую сторону от 42.
41,40….,37, следовательно, мы получаем 37 как разницу.
- Использование перегруппировки:
Это противоположность метода перегруппировки, используемого дополнительно.
В этом методе один десяток преобразуется в десять единиц, или одна сотая преобразуется в десять десятков и так далее.
Например: 245 – 126
Поскольку цифра в разряде единиц вычитаемого равна 5, что меньше цифры 6 в уменьшаемом, мы заимствуем 1 десяток из разряда десятков , то есть 4, что делает его 15, а цифра 4 становится 3, поскольку она потеряла один десяток в одном разряде.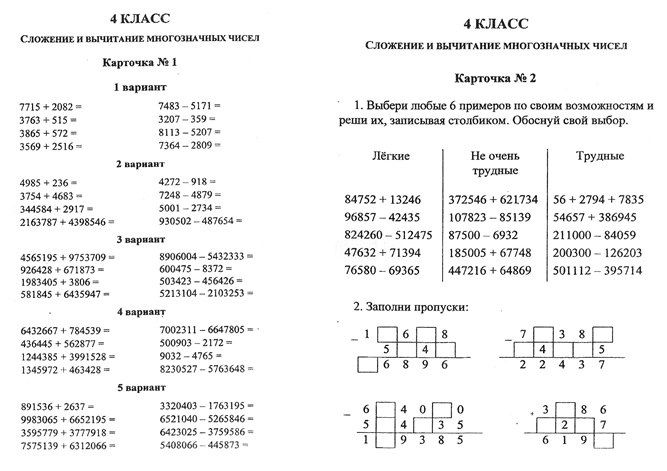
5 → 5 + 10 = 15
4 – 1 → 3
Теперь вычитание можно сделать как обычно.
Решено Сложение и вычитание многозначных чисел Примеры
Пример 1: Если у Ноя 134 конфеты, а у Дейзи всего 247 конфет?
Решение:
Ной → 134 конфеты
Daisy → 247 Candies
Использование метода перегруппировки,
Общее количество конфет, как Noah, так и Daisy IS,
= 134 + 247
= 381.
Следовательно, у Ноя и Дейзи всего 381 конфета.
Пример 2:
Ньютон покупает упаковку зубной пасты стоимостью 2 доллара. Если он даст кассиру купюру в 5 долларов, сколько денег Ньютон получит от кассира?
Решение:
У Ньютона есть 5 долларов наличными.
Он тратит 2 доллара на зубную пасту.
Используя метод подсчета, мы считаем от 5 дважды,
5, 4 и 3 доллара
= 3
= 3
.
Пример 3:
Роберт покупает дом стоимостью 240 000 долларов. Он тратит 20 000 долларов на мебель для дома. Сколько всего он тратит?
Решение:
Использование метода частичной суммы,
$ 240 000 + 20 000 долл. США (ADD)
= $ 260 000
баллов, ROBERT APNDS APDEND AS APEND AS APDEND AS APDEND AS AS AS APDEND AS AS AS AS AS APDEND.
Пример 4:
Элайджа покупает пачку блестящих ручек за 21 доллар. Если он даст кассиру купюру в 9 долларов, сколько еще ему придется ему заплатить?
Решение:
Используя компенсирующую стратегию,
21–9
Если прибавить 1, чтобы получить число 9 → 10, вычитание будет проще.
$21 – $10 [вычесть]
= $11 → $11 + $1 = $12 [Чтобы компенсировать -$1]
Следовательно, Элайджа должен заплатить кассиру еще 12 долларов.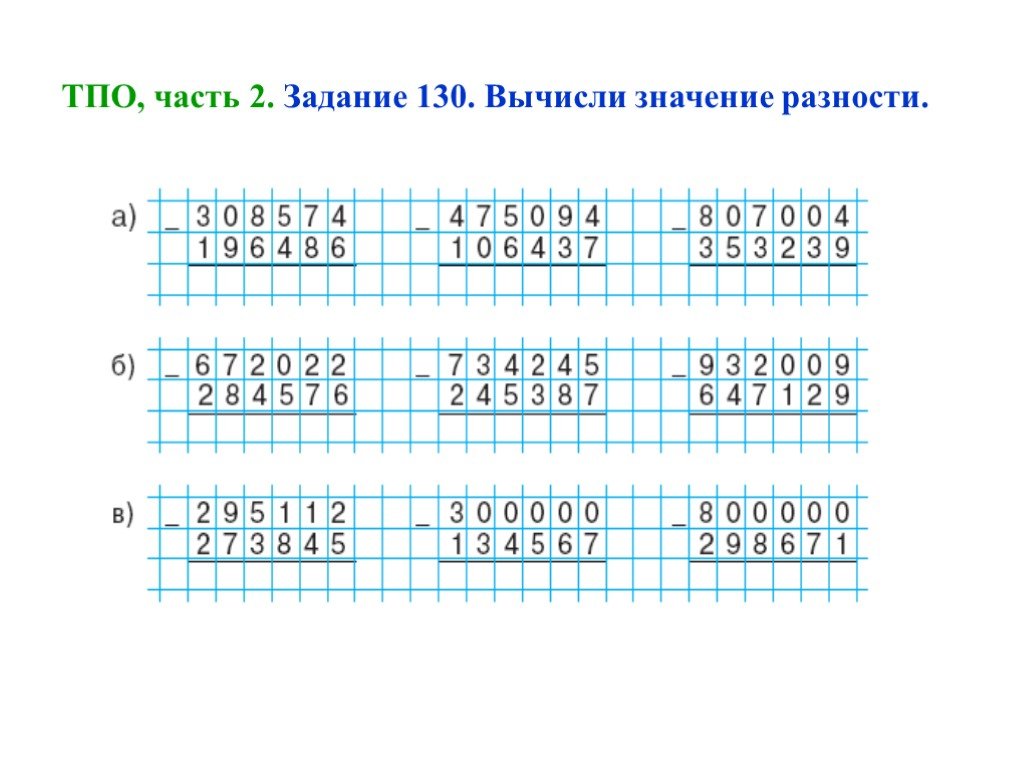
Часто задаваемые вопросы
Какие существуют типы стратегий сложения?
Ниже приведены несколько дополнительных стратегий.
- Добавление путем перегруппировки
- Дополнение к компенсации
- Дополнение по частичной сумме
- Дополнение на
9501
- . стратегии вычитания?
Ниже приведены некоторые из стратегий, используемых для вычитания.
- Вычитание путем компенсации
- Вычитание с помощью перегруппировки
- Вычитание по частичной сумме
- Субтрокция по подсчете
- . Считается подсчет
- . важно в повседневной жизни?
Сложение и вычитание очень важны для определенных действий в повседневной жизни, таких как изменение количества продуктов в супермаркете, игра в определенные игры, которые включают вычитание или сложение набранных очков, ведение финансового учета и т.
 д. на.
д. на.Ознакомьтесь с другими нашими курсами
Сложение и вычитание многозначных чисел 4 класс
6,50 $
Сложение и вычитание многозначных чисел — Математика 4-го класса — Печать и цифра 4.NBT.B.4 количество
Добавить в мой список желаний
Категории: 4-й класс, Сложение и вычитание, Уроки цифровой математики, Магазин по навыкам Теги: 4th, Сложение и вычитание, Сложение, Дистанционное обучение, Google Apps, Математика, Умственная арифметика, Числа, Печатные формы, Вычитание, Проблемы со словами, Рабочие листы
- Описание
- Отзывы (0)
⭐ Этот математический блок Google Slides для 4-го класса, предназначенный для печати и цифровой печати, предназначен для обучения учащихся тому, как складывать и вычитать многозначные числа. Этот модуль включает в себя якорные диаграммы, практику, страницы, манипуляции, обзор тестов и оценку, чтобы научиться и попрактиковаться в том, как свободно складывать и вычитать многозначные целые числа с использованием стандартного алгоритма.
 Студенты будут практиковать эти навыки с различными стратегиями, включая визуальные эффекты, массивы, манипуляции, модели и многое другое в различных версиях и уровнях задач и игр.
Студенты будут практиковать эти навыки с различными стратегиями, включая визуальные эффекты, массивы, манипуляции, модели и многое другое в различных версиях и уровнях задач и игр.Основные характеристики:
✏️ Форматы классного и дистанционного обучения — Печатные PDF-файлы и форматы Google Slides включены!
✏️ Леса – Рабочие листы разработаны для развития навыков работы с визуальными средствами.
✏️ Интерактивный – Действия по вырезанию и вставке и цифровые подвижные элементы.
Что включено:
1. Анкерные диаграммы (2 страницы)
2. Рабочие листы и задания на сложение (5 страниц)
3. Рабочие листы и упражнения на вычитание (5 страниц)
4. Рабочие листы и задания на смешанные операции (11 страниц)
5. Словесные задачи на сложение и вычитание (6 страниц)
6.Тестовый обзор (4 страницы)
7.
 Тестовый обзор (4 страницы)
Тестовый обзор (4 страницы)Посмотрите, как выглядит этот ресурс, в этом видео-превью.
Авторские права и условия использования
Информацию об авторских правах и краткую информацию о том, как этот ресурс можно и нельзя использовать, см. на странице Условий использования.
******************************************************* ***************************
Сопутствующие товары:
Значение места – 4.NBT.A.1
Блок мультипликативных сравнений – Дистанционное обучение Google Slides 4.OA.A.1
Словесные задачи мультипликативного сравнения Google Slides Дистанционное обучение 4.OA.A.2
Многоступенчатые словесные задачи – Дистанционное обучение Google Slides 4.OA.A.3
Факторы, кратные, простые и составные – Дистанционное обучение Google Slides 4.OA.B.4
Образцы чисел – Google Slides Distance Learning 4.




 k
k
 Укажи верно решённые примеры:
Укажи верно решённые примеры: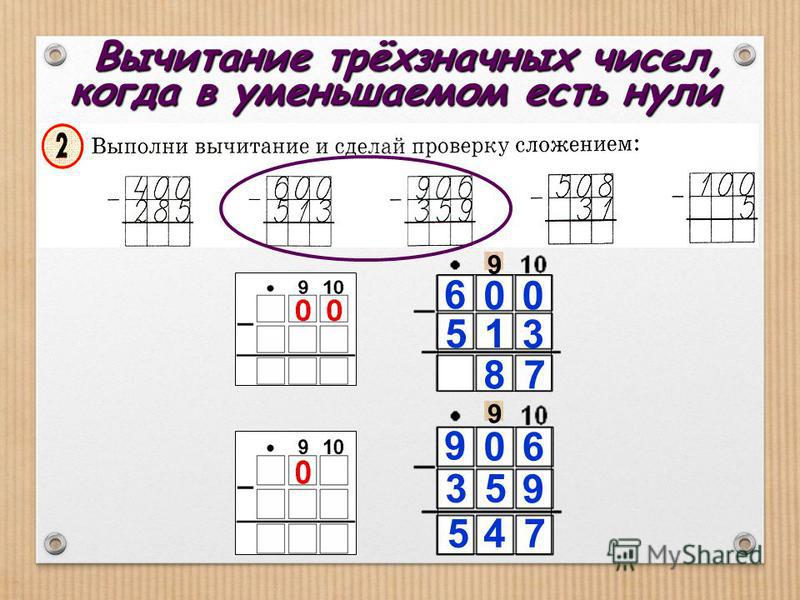 600 939.590
600 939.590 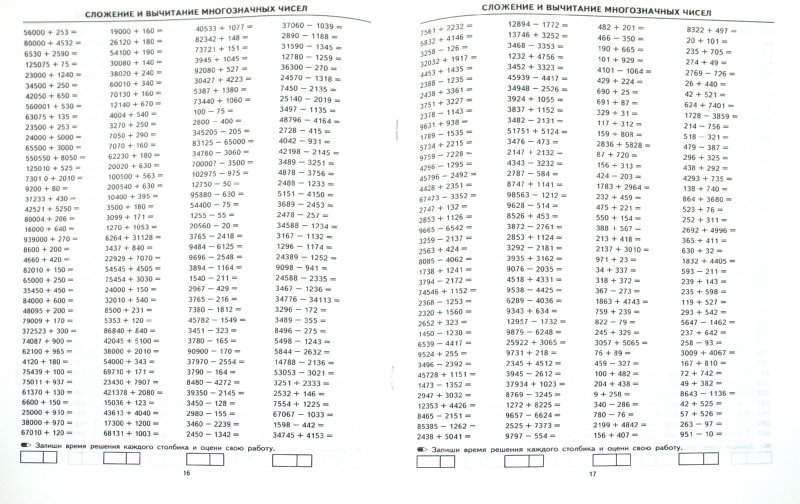 934
5.946 4.936
934
5.946 4.936  296 + 420.296 +420.296
296 + 420.296 +420.296  826 49.826 49.826
826 49.826 49.826  304
518.304 518.304
304
518.304 518.304  д. на.
д. на. Студенты будут практиковать эти навыки с различными стратегиями, включая визуальные эффекты, массивы, манипуляции, модели и многое другое в различных версиях и уровнях задач и игр.
Студенты будут практиковать эти навыки с различными стратегиями, включая визуальные эффекты, массивы, манипуляции, модели и многое другое в различных версиях и уровнях задач и игр. Тестовый обзор (4 страницы)
Тестовый обзор (4 страницы)