Соотношения между единицами длины 3 класс школа 21 века: СООТНОШЕНИЕ МЕЖДУ ЕДИНИЦАМИ ДЛИНЫ | План-конспект занятия по математике (3 класс) на тему:
Конспект урока по математике «Метр. Соотношения между единицами длины» 2 класс УМК «Начальная школа 21 века»
Конспект урока по математике 2 класс тема:
«Метр. Соотношения между единицами длины».
УМК «Начальная школа 21 века».
учитель начальных классов БОУ «Полтавский лицей»
Михайлова Ольга Петровна
Цель: Создание условий для формирования умения измерять длину и
расстояния с помощью различных измерительных инструментов: линейки,
метровой линейки, рулетки.
результаты:
предметные – овладение основами логического и алгоритмического
мышления. Умение воспроизводить по памяти соотношения между
единицами длины: 1 м = 100см, 1дм = 10см, 1м = 10дм
личностные – готовность использовать получаемую математическую
подготовку в учебной деятельности при решении практических задач,
возникающих в повседневной жизни.
метопредметные — умение работать в информационной среде. Владение
Владение
основными методами познания окружающего мира (анализ).
Оборудование: мультимедийная презентация, изображение удава (3м
8дм), метровая линейка, сантиметр, рулетка, модели сантиметра, дециметра,
метра, тестовые работы на листочках, задание для работы в парах на
листочках.
Ход урока
(слайд № 1)
Начинается урок.
Он пойдет ребятам впрок.
Постарайтесь все понять,
Учитесь тайны открывать,
Ответы полные давайте
И на уроке не зевайте.
— Садимся. Открываем тетради, записываем
число, классная работа…
На доске закрытые задачи и тема урока.
— Сегодня на уроке мы продолжим работу с
двухзначными числами (открывается первая
задача на доске: повторим разрядный состав
двухзначных чисел), а также работу над
задачами (открывается вторая задача на доске:
поработаем над задачей). А над чем ещё мы
будем работать, вы узнаете чуть позже. И
И
тогда сможете назвать тему урока. (Тема на
доске закрыта)
Презентация по математике на тему: Метр. Соотношения между единицами длины — 15 урок (2 класс УМК Начальная школа 21 века
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
УМК «Начальная школа 21 века» Урок математики во 2 классе № 15 по теме: «Метр. Соотношения между единицами длины»Автор презентацииТ. И. Туран,Учитель начальных классовГ. Новокузнецк, 2017МБОУ «Средняя общеобразовательная школа № 6» Устный счётОтгадайте имя сказочного героя. Какая буква лишняя?{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}11 + 812 – 9 14 – 6 13 + 5ЙЛОБ{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}11 – 7 13 – 8 15 – 8 9 + 5ИЧАТ{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}7191883414ЙЛОБИАТ
Устный счётМожно ли решить задачу? Таня полила 6 грядок огурцов. Сколько грядок ей осталось полить? Устный счётМожно ли решить задачу? На шахматной доске 20 фигур. Из них 13 чёрные, а остальные – белые. Сколько белых фигур на шахматной доске? Устный счётСколькими способами можно прочитать слово «маршрут»?
Из них 13 чёрные, а остальные – белые. Сколько белых фигур на шахматной доске? Устный счётСколькими способами можно прочитать слово «маршрут»?
Устный счёт Маша, Оля и Настя заняли призовые места на соревнованиях. Маша не заняла ни первое, ни второе место. Оля ни пришла первой. Какое место заняла каждая девочка? МашаОляНастяIIIIII
Сообщение темы урокаМы с вами умеем измерять длины небольших предметов с помощью обычной линейки, получая результаты в сантиметрах. А как быть, если нам надо пойти в магазин и купить отрез такни на пальто? Неужели продавец будет отмерять такань такой линеечкой как у нас? Сообщение темы урокаНи один продавец такой линейкой не пользуется, так как в сантиметрах измерять длину большого куска ткани очень неудобно. Продавцы всегда используют деревянную линейку, которую называют портновским метром.Сегодня на уроке мы познакомимся с крупной единицей – метром.
Изучение нового материалаМетр – более крупная, чем сантиметр и даже дециметр, единица длины.
Изучение нового материалаПри этом, например, для измерения длины комнаты используют рулетку – длинную, свёрнутую в рулон, ленту, на которую нанесена шкала.Рулетки бывают разной длины – метровые, двухметровые, трехметровые,пятиметровые, двадцатиметровые и другие.
Изучение нового материалаНазовите вам известные единицы измерения в порядке их увеличения. СантиметрДециметрМетрКак обозначаются сантиметр и дециметр?См и дм, обозначения записываются без точек.
Изучение нового материалаМетр обозначается буквой м без точки.Прочитайте записи: 4 м, 45 м, 4 м 8 дм, 42 м 8 дм, 9 см.Рассмотрите рисунок С. 35.
Изучение нового материалаКакие инструменты для измерения длины здесь изображены?Метровая линейкаРулетка Что вы будете измерять каждым инструментом?
Изучение нового материалаПрочитайте текст на С. 35 Изучение нового материалаИспользуя классную метровую линейку, заполните пропуски…1 м = … дм1 м = … см1 дм = … см1010010
С. 36, № 2Прочитай записи:5 м15 см1 м 50 см6 дм84 м1 м 5 дм
36, № 2Прочитай записи:5 м15 см1 м 50 см6 дм84 м1 м 5 дм
С. 36, № 3Выбери подходящие единицы длины и закончи фразы:Высота дерева 2 … .Спортсмены пробежали дистанцию 100 … .Длина спички 4 … .Школьники участвовали в заплыве на 50 … .ммсмм
Работа в тетради С. 14, № 2меньшеменьшебольшеменьше
Работа в тетради С. 14, № 3717767
Работа по учебнику С. 37, № 84 см5 см
Работа по учебнику С. 37, №10 Самостоятельная работа Работа по учебнику С. 38, № 12Прочитайте задачу.Что известно?Что требуется узнать?Запиши кратко условие задачи.
Работа по учебнику С. 38, № 12Девочек – 6 чел.Мальчиков — ?, на 2 чел. м — ? чел.1) 6 – 2 = 4 (чел.) – мальчиков.2) 6 + 4 = 10 (чел.) – всего.Ответ: 10 человек.
Работа по учебнику С. 38, № 13Дополни текст и придумай вопрос так, чтобы получилась задача. Работа по учебнику С. 38, № 13Дополни текст и придумай вопрос так, чтобы получилась задача. Работа по учебнику С. 38, № 13Дополни текст и придумай вопрос так, чтобы получилась задача.
Работа по учебнику С. 38, № 15 РефлексияЧто нового узнали на уроке?Назовите крупную единицу длины.Какие инструменты используют для измерения единицы длины?
Домашнее заданиеС. 37, № 11 (учебник).С. 14, № 1, 4 (тетрадь).
Приложенные файлы
Контрольные работы по математике. Тема : Единицы длины, массы, вместимость. 3 класс. УМК Начальная школа XXI века
Текущая контрольная работа по теме «Длина, масса, вместимость»
Вариант 1.
Начерти отрезок длиной 4 см 5 мм. Вырази его длину в миллиметрах.
Вырази данные значения в указанных единицах.
8 см 5 мм = ___________мм40 мм = ________ см
86 дм = ___м ___ дм
7 м 80 см = ____см503 см = ____м _____см1000 г = _____ кг
16 км 340 м □ 16 км 430 м
1 кг 750 г □ 890 г
154 кг 999 г □ 155 кг
5 м 2 см □ 5 м 2 дм
78 дм □ 8 м
Ломаная состоит из 3 звеньев. Длина первого звена 45 см, второго в 5 раз меньше, чем первого, а третьего на 17 см больше, чем второго.
 Найди длину этой ломаной.
Найди длину этой ломаной.5*. Запиши данные значения массы в порядке увеличения.
а) 300 г
1 кг
57 г
1 кг 30 г
2 кг 610 г
999 г
б) Назови в порядке возрастания массы, начиная с самого лёгкого:
слон, мышь, собака, кошка, лошадь, коза.
Текущая контрольная работа по теме «Длина, масса, вместимость»
Вариант 2.
Начерти отрезок длиной 6 см 5 мм. Вырази его длину в миллиметрах.
Вырази данные значения в указанных единицах.
1 кг = _____ г
90 мм = ________ см
95 дм = ___м ___ дм
4 м 90 см = ____см6см 1 мм = ___________мм806 см = ___м ___см Сравни.
1 кг 150 г □ 900 г
2 кг 990 г □ 3 кг12 км 620 м □ 12 км 260 м
8 м 5 см □ 8 м 4 дм
67 дм □ 7 м
Ломаная состоит из 3 звеньев. Длина первого звена 7 см, второго в 6 раз больше , первого, а третьего на 17 см меньше , второго. Найди длину этой ломаной.
5*.
 Запиши данные значения массы в порядке уменьшения.
Запиши данные значения массы в порядке уменьшения.а) 2 кг
65 г
1 кг 15г
440 г
1 кг 150г
11 кг 500 г
б) ) Назови в порядке возрастания массы, начиная с самого лёгкого:
вишня, слива, капуста, арбуз, лимон, горошина
Приложенные файлы
Самоопределение к деятельности Формулирование темы и цели урока Технологический комментарий: при щелчке открывается тема урока, при повторном щелчке – цели и задачи урока. | Организационный момент. На уроке наши глазки внимательно смотрят и всё (видят) Ушки внимательно слушают И всё (слышат) Голова хорошо (думает). — Какие умения нам пригодятся на этом уроке? — Ребята, скажите, какое значение имеет математика в развитии человека? — Прочитайте изречение о науке математике. — Как вы понимаете это изречение? Математика — приводит ум в порядок. -Так вот сегодня на уроке мы с вами и будем применять полученные на предыдущих уроках знания. И тема нашего урока «Единицы массы, единицы длины. Вместимость». -Определите цель нашего урока? -Какие задачи ставим перед собой? | Проверяют готовность рабочих мест. Дополняют стихотворение учителя. — Занятия математикой развивают память, внимание, мышление, терпение. — «Математика ум в порядок приводит» — Математика – это гимнастика ума. Учатся строить речевые высказывания, аргументировать свою точку зрения. | Оформлять свои мысли в устной форме (коммуникативные УУД Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке. | Обобщение и систематизация знаний Технологический комментарий: работа с пультами; осуществляется проверка уровня подготовленности класса к продолжению обучения. | Организую повторение пройденного материала. Предлагаю вспомнить изученные величины. — Давайте вспомним, какие величины мы изучали? — Какие единицы длины, массы, вместимости вы знаете? — Предлагаю пройти тест. — Вам нужно выбрать правильные ответы. Рефлексия: — Готов ли ты объяснить пройденный материал однокласснику? | Отвечают на вопросы учителя Вспоминают изученное Работа с пультами. Проходят тест. Рефлексия. | Построение речевого высказывания, умение слушать и понимать речь других (коммуникативные) Выбор лишнего объекта, обоснование выбора (познавательные) | Актуализация знаний Мотивация Технологический комментарий: при нажатии стрелкой на изображение в левом нижнем углу, включается показ видеофрагмента, остановка видео на 3. | Мотивация к дальнейшей работе. -Ребята, а что там за лист бумаги лежит под столом? (ребёнок достаёт письмо, я предлагаю его прочитать) — Давайте, ребята посмотрим, а кто нам посылает сигнал СОС (клип). — Поможем маленькому человечку привести знания в порядок. Я предлагаю вам деловую игру «Космическая экспедиция на планету Всезнамуса». Если вы добросовестно трудились над темами «Единицы длины» и «Единицы массы. Вместимость», то вы легко с ней справитесь, но если вопросы у вас все-таки возникнут, то вы можете рассчитывать на помощь одноклассников. | Читают письмо Просмотр видеофильма. Слушают преподавателя. | Добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке. (познавательные УУД) | Закрепление Технологический комментарий: при щелчке вылетает картинка «Центр управления полётами». Технологический комментарий: в нижнем левом углу меняем курсор на перо. Работа с документ камерой. Технологический комментарий: переход на слайд, где дети пультами оценивают работу одноклассников. | Организую работу в группах. Предлагаю детям осуществить выбор группы. — Вы уже обратили внимание на то, что мы работаем по группам. – Перечислите правила работы? — Итак, представим себе, что наш класс — это огромный центр управления полетом, где каждый выполняет определённую работу. Я представлю группы: 1 группа — центр управления полётами; 2 группа — консультанты; 3 группа — независимые эксперты, которые дают оценку работе; 4 группа — это инженеры-конструкторы; 5 группа – ответственные за хозяйственную часть. -Итак, осуществим выбор группы. В какой же группе вы будете работать. -Если в ходе выполнения работы у Вас возникнут вопросы, то Вы можете обратиться за помощью к Независимым экспертам. Работа в группах. На столах карточки с заданиями. Для каждой группы своё индивидуальное задание. В конце работы каждая группа сдаёт рабочий лист, и учитель с помощью документ камеры делает снимок. — Рабочий день во многих организациях часто начинается с производственного совещания, и мы тоже его сейчас проведем. — Для того, чтобы отправить в путь космический корабль, мы должны произвести расчеты. — У каждой группы свои индивидуальные задачи, которые вы должны решить перед началом полёта. 1 группа — центр управления Задание группе: посчитайте сколько топлива нам потребуется, чтобы вывести космический корабль на орбиту, и ответьте на вопрос: «Хватит ли топлива?» 2 группа — консультанты; Задание группе: распредели и назови единицы измерения. 4 группа — это инженеры-конструкторы Задание группе: для полёта нам необходимы некоторые грузы. Посмотрите на грузы и ответьте на вопрос: «Все ли грузы войдут в грузовой отсек?» 5 группа – ответственные за хозяйственную часть. Задание группе: для того, чтобы наш космический корабль стартовал, его масса вместе с грузом не должна превышать определённого веса. Вам дан список грузов. Подведите итог, высчитывая массу и ответьте на вопрос: «Поднимется корабль или нет?» — А группа «Независимых экспертов» будет работать со мной у доски. Задание 1: Назови единицы величины. Задание 2: Определи массу. Оцениваем работу группы, сдаём рабочие листы. — Итак, все расчёты сделаны, итоги подведены. Сдаём экспертные листы. А пока я вывожу данные на экран, индивидуально выполните задание № 3: соедини линиями изображение предметов и их длины. Делаю снимок с помощью документ камеры. — Проверку осуществляет группа «Независимые эксперты» (устно). Подводим итог работы с карточками. Представители группы делают анализ работы, и говорят: «Готов ли космический корабль к полёту?» — Для того, чтобы отправиться в путь, мы должны были подготовить определённые расчеты. Послушаем анализ работы каждой группы. — А «Независимые эксперты» выскажут своё мнение: готовы ли мы отправиться в путешествие или нет? (в конце анализа дети этой группы при помощи пультов показывают готовность к полёту: зелёный – готов. Красный – не готов). | Дети обсуждают и предлагают свои варианты. Дети подходят к учителю, вытаскивают карточки с названием группы, и садятся за парты, на которых указан номер группы. Работают в группах, делают вывод. Оценивают работу группы. Сдают выполненную работу на карточках. Проверка заданий. Один представитель группы, зачитывает задание, даёт ответ на поставленный вопрос. Подводит итог работы группы: — наша группа работала… (характеристика работы). Работа с пультами. | Оформлять свои мысли в устной и письменной форме. (коммуникативные УУД) Учиться работать в группе, формулировать собственное мнение и позицию; совместно договариваться о правилах общения и следовать им. (коммуникативные УУД) Оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки (регулятивные УУД) | Итог урока. Рефлексия учебной деятельности на уроке Технологический комментарий: при нажатии стрелкой на картинку «ракета», осуществляется переход на интернет-видео «Взлёта ракеты». | -Все необходимые расчеты мы выполнили, можем запускать космический корабль. — И пока корабль готовится к полёту, подведем итог нашей экспертной работе. -Давайте вернемся к вопросу, поставленному в начале урока: для чего надо изучать математику? -А может ли математика помочь осуществить мечту? Например, мечту стать космонавтом? — Оцените свою работу на уроке, используя знаки светофора. Готовы ли мы к полёту. -Пора. Летим на помощь маленькому человечку. | Высказывают своё мнение. Подымают сигнальные карточки определённого цвета. | Способность к самооценке на основе критерия успешности учебной деятельности (личностные УУД) |
Презентация к уроку математики «Длина. Единицы длины»
Математика — 2 класс
Урок на тему: «Длина, единицы измерения длины: миллиметр, сантиметр, дециметр, метр»
Что такое длина?
Длина – это свойство или характеристика предмета.
У предмета есть 3 измерения – ширина, высота, и длина.
Вот из рисунка хорошо видно, что такое длина – это расстояние от начала предмета до конца.
Возьмем для примера обычную книгу – учебник.
Миллиметр
Длину предмета можно линейкой. Она есть у всех школьников.
Давайте рассмотрим её внимательнее, что написано или изображено на линейке?
Самые мелкие отрезки – эти миллиметры. А те что, покрупнее – это сантиметры.
Вы можете посчитать, что в 1 см ровно 10 миллиметров. Посчитайте.
Ещё в 1 классе вы познакомились с единицей длины – сантиметром. А теперь узнали что такое миллиметр. Это тоже единица длины.
Запомните:
10 мм = 1 см
Вспоминайте с 1 класса, что 1 дециметр = 10 см.
Наша Гаечка никак не может измерить длину своего карандаша. Помогите ей измерить длину карандаша.
Подскажите, чему она равна?
Наверное, уже все знают, как правильно пользоваться линейкой для измерения длины.
Поэтому возьмите каждый свой карандаш и измерьте его длину.
А теперь, повернитесь к соседу и проверьте, правильно ли он измерил длину карандаша.
Если длина предмета намного больше длины линейки, то используют ещё один инструмент – метр (или по другому её называют рулеткой).
Если вы внимательно присмотритесь на надписи, то увидите, что самые короткие черточки обозначают миллиметр, более длинные – сантиметр, а самые крупные (обычно красным цветом) это метры.
Запомните:
1 метр = 10 дециметров = 100 сантиметров.
Метр это более крупная мера длины и им удобнее измерять большие длины, например:
Расстояние от дома до школы.
Длина дома.
Ширину улицы.
А вот маленькие предметы удобнее мерить сантиметром:
Длина карандаша или ручки.
Ширина тетради.
Высота сумки.
В письме часто используют сокращения.
Например:
Миллиметр – мм.
Сантиметр – см.
Дециметр –дм.
Метр –м.
Теперь вам задание.
Помогите Дейлу, расставить меры длины в порядке возрастания.
дм. м. см. мм
Из истории:
В старину на Руси использовались следующие меры:
Пядь — длина от конца указательного пальца до большого, как показано на рисунке.
Шаг – среднее расстояние одного шаг взрослого человека, примерно равен 70 см.
Аршин — расстояние равное длине руки (смотрите рисунок)
Локоть – расстояние равное от локтя до конца пальцев
Сажень – расстояние между концами вытянутых рук:
Задачи на повторение
Что длиннее:
3 см или 13 мм
5 мм или 1 м
3 см или 2 дм
Дорогие ребята!
На этом все, спасибо всем.
ГДЗ по математике 2 класс рабочая тетрадь Рудницкая, Юдачева Решебник
Изучение математики начинается уже с первых дней в школе: они знакомятся с этим предметом, их учат понемногу считать и выполнять различные действия с цифрами и фигурами. На второй ступени обучения дети уже осваивают более сложные алгебраические и геометрические темы.
На второй ступени обучения дети уже осваивают более сложные алгебраические и геометрические темы.
Чтобы материал лучше усвоился, преподаватели используют различные дополнительные пособия на занятиях. Так, например, рабочие тетрадки, позволяющие развить мышление ребенка и способствующие тренировке памяти.
На этом этапе второклассники изучают такие темы, как:
- Сложение и вычитание в пределах 100;
- Единицы измерения;
- Многоугольник;
- Периметр;
- Окружность;
- Таблица умножения;
- Площадь и т. д.
Эти разделы отражены и в сборниках с готовыми домашними заданиями Рудницкой от издательства «Вентана-Граф» за 2014 год (серия «Начальная школа 21 века»). Здесь собраны все правильные ответы к упражнениям из главной книги. Они позволяют сверять результаты учеников, полученные самостоятельным путем.
Кому могут пригодиться ГДЗ по математике для рабочей тетради за 2 класс (авторы: Рудницкая В.
 Н., Юдачева Т. В.)
Н., Юдачева Т. В.)Учебно-методический комплекс адресован:
- Родителям, которые таким образом смогут контролировать правильность выполнения домашних упражнений. Причем им даже необязательно вспоминать правила, достаточно просто открыть готовые ключи и сверить результаты.
- Начинающим учителям, которые таким образом смогут в ускоренном темпе проверять накопившиеся горы работ учеников.
- Опытным педагогам, которые так будут разрабатывать свои собственные карточки для более увлекательного и интересного проведения урока.
Так, благодаря пособию взрослые смогут значительно сэкономить время и потратить его на другие важные дела или отдых. Даже если все задания кажутся простыми и понятными, сборник поможет оформить их в соответствии с ФГОС (федеральным государственным образовательным стандартом). Это тоже значительно влияет на оценку и дальнейшее понимание дисциплины. Ведь, в будущем, дети должны уметь корректно выполнять номера, чтобы на экзаменах получить высший балл (ведь обидно верно решить задание и осознать, что оценка снижена за нарушение оформления).
Какими еще достоинствами обладает решебник по математике к рабочей тетради для 2 класса Рудницкой
Помимо перечисленных выше преимуществ использования данного сборника, можно также отметить то, что ГДЗ есть в онлайн-версии. То есть не нужно искать по всему городу печатные издания, а потом еще и носить тяжелые методички повсюду с собой. Достаточно просто иметь телефон или компьютер с выходом в интернет. Удобная навигация позволяет без труда найти нужное: просто нажмите на интересующую вас тему и выберите нужный номер задания. Все просто, а главное доступно!
Медиаурок по математике на тему «Единица длины — километр»
Медиаурок по математике на тему «Единица длины — километр» разработан по УМК «Перспектива» для учеников третьего класса. В разработке урока используются приемы технологии развития критического мышления, что способствует комплексному развитию личности ребенка.
21 век — эпоха информационного общества. Информационные и компьютерные технологии занимают важное место в нашей жизни. Образовательная сфера – не исключение. Чтобы поддерживать интерес детей на протяжении всего урока, учителю необходимо организовывать активную мыслительную деятельность школьников. В этом педагогу должны помочь информационно-компьютерные технологии, их применение актуально в современной начальной школе, и они станут хорошими помощником учителю в развитии мотивации детей к обучению [1].
Образовательная сфера – не исключение. Чтобы поддерживать интерес детей на протяжении всего урока, учителю необходимо организовывать активную мыслительную деятельность школьников. В этом педагогу должны помочь информационно-компьютерные технологии, их применение актуально в современной начальной школе, и они станут хорошими помощником учителю в развитии мотивации детей к обучению [1].
Использование мультимедиа-технологий широко применяется на уроках в начальной, средней и старшей школе. Уроки с использованием таких технологий получили название «мультимедиауроки». Уроки, при проведении которых используются средства массовой коммуникации (СМК), позволяющие формировать не только предметные результаты обучения, но и «учить новое поколение понимать, интерпретировать и оценивать содержание информации передаваемой по каналам СМК», получили название медиауроки [3].
Федеральный государственный образовательный стандарт нового поколения требует от учителя формировать универсальные учебные действия у школьников. В этом педагогу поможет использование приемов технологии развития критического мышления. Цель данной технологии — развитие мыслительных навыков обучающихся, необходимых не только в учебе, но и в обычной жизни (умение принимать взвешенные решения, работать с информацией, анализировать различные стороны явлений и т.п.) [4]. Применение данной технологии актуально ещё и потому, что она позволяет повысить уровень работоспособности, т.к. усвоение знаний на уроке происходит в процессе постоянного поиска информации.
В этом педагогу поможет использование приемов технологии развития критического мышления. Цель данной технологии — развитие мыслительных навыков обучающихся, необходимых не только в учебе, но и в обычной жизни (умение принимать взвешенные решения, работать с информацией, анализировать различные стороны явлений и т.п.) [4]. Применение данной технологии актуально ещё и потому, что она позволяет повысить уровень работоспособности, т.к. усвоение знаний на уроке происходит в процессе постоянного поиска информации.
Таким образом, использование медиауроков с применением технологии развития критического мышления поможет педагогу в создании интересных уроков, которые будут способствовать комплексному развитию личности ребенка [5]. В качестве примера медиаурока приведем конспект урока по математике в 3 классе по УМК «Перспектива» [6] на тему: «Единица длины — километр».
Цель: создание условий для ознакомления обучающихся с новой единицей длины — километром.
Задачи
- подвести обучающихся к «открытию» новой для них единицы измерения длины километр, её соотношением с метром;
- продолжить формирование умений и навыков по чтению и записи трёхзначных чисел, по преобразованию именованных чисел с изученными единицами длины;
- способствовать развитию мыслительных операций: анализа, синтеза, обобщения, сравнения, классификации, а также развитию личностных качеств обучающихся.

Оборудование: учебник «Математика» для 3 класса часть 2 авторы Г.В. Дорофеев, Т.Н. Миракова [2], рабочая тетрадь к учебнику «Математика» часть 2, компьютер, проектор.
Ход урока
Дидактические задачи | Решение дидактических задач |
Первая стадия – вызов | |
| 1. Просмотр видеоролика «Ералаш № 41 «Семь раз отмерь»https://www.youtube.com/watch?v=7XiIl_qxnNk
2. На доске расположены карточки с наименованием мер длины (см, дм, км, м, мм), расставьте их в порядке возрастания. 3. Единицу длины км мы знаем? Как вы думаете, что мы будем изучать сегодня на уроке? Назовите тему урока. |
Вторая стадия – «Осмысление» | |
| 1. Прием ТРКМ «Корзина идей»: Что вы можете сказать о километре? Поделитесь своими идеями. Все версии детей как правильные, так и неправильные записать на доске (например, это число состоит из тысячи метров; мера измерения длины и т.д.). 2. Прочитайте информацию в учебнике на с. 83 про себя, затем обсудим, что вы узнали. Прием «верные, неверные утверждения» Сейчас я буду вам зачитывать утверждения, а вы должны будете мне сказать верные они или нет.
999 м + ….. = 1 км; 800 м + ….. = 1 км; 750 м + ….. = 1 км; 980 м + ….. = 1 км; 200 м + ….. = 1 км. 7. Ребята, а знаете ли вы, как измеряли длину наши предки? Давайте посмотрим видео и ответим на вопросы. Просмотр видеоролика «Старинные меры длины» https://www.youtube.com/watch?v=N6VEiWp3ZcQ
Что такое косая сажень? (расстояние от кончиков пальцев вытянутой правой руки до пальцев левой ноги). |
Третья стадия – «Рефлексия» | |
|
Я не знал(а)… Теперь знаю… Мне было трудно… Теперь я могу… Мне было легко, потому что… Мне захотелось… Кто хочет озвучить свои результаты? Молодцы. Теперь запишем домашнее задание.
|
единиц длины — 3-й класс по математике
Узнайте о единицах длины
Некоторые объекты имеют длину .
Некоторые объекты короткие .
Мы знаем, является ли объект коротким или длинным, измеряя его длину .
Линейки, рулетки, измерительные линейки и мерки можно использовать для измерения длины предметов.
Единицы длиныПри измерении длины объектов важно использовать правильную единицу длины .
Единица длины сообщает нам, какова длина объекта или пространства.
Есть два типа единиц:
1. Обычные единицы
— Они используются в Соединенных Штатах. Сюда входят дюймов , футов , ярдов , и миль .
2. Метрическая система
— Они используются в большинстве стран мира. Стандартная единица измерения — метров . Под ним находятся миллиметра , сантиметра , и километр .
Без единиц длины вокруг нас будет столько неразберихи. 😌😌
Допустим, Салли покупала кусок ткани для своего платья. Она сказала продавцу: «Мне нужен кусок красной ткани длиной 6 дюймов». Продавец почесал затылок и спросил: «6 что?»
Салли не смогла сказать продавцу, сколько ткани ей действительно нужно.
Единица длины покажет, какая шкала использовалась для измерения.
Давайте посмотрим на единицы длины, от самых маленьких до самых больших.
Сантиметр (см)
сантиметр — малая единица длины. Обычно его используют для измерения небольших предметов.
👉 Укороченный вариант для сантиметров — см.
На линейке или на рулетке будут нанесены сантиметры.
👉 Вот несколько примеров объектов с их длиной в сантиметрах:
— Ластик примерно 5 см .
— Скрепка для бумаг примерно 2 ½ см .
Какие еще предметы можно измерить в сантиметрах? 🤔
дюйм (дюйм)
дюймов — еще одна небольшая единица длины. Лучше всего использовать для измерения небольших объектов.
Сокращенная версия для дюймов — дюймов. Другой способ записи — использование двойных кавычек («).
дюйм примерно в 2 ½ раза больше сантиметра.
Другими словами,
1 дюйм = около 2 ½ см
дюймов также отмечены на линейках и рулетках.
👉 Некоторые примеры длины в дюймах:
— Скрепка для бумаг размером около 1 «.
— Книга примерно 11 «.
Можете ли вы вспомнить другие объекты, которые лучше всего измерять в дюймах? 🤔
фут (фут)
футов — это большая единица длины.
Это единица измерения длины, которая часто используется для измерения длины комнат, домов и транспортных средств.
👉 Нога во множественном числе означает ноги.
Его укороченная версия — футов .Другой способ написать фут — использовать апостроф ( ‘).
В 1 футе 12 дюймов.
Другими словами,
1 фут = 12 дюймов
Линейки имеют длину 1 фут.
👉 Вот некоторые объекты, которые измеряются в футах:
— Лодка 25 футов
— Дом 50 футов
Метр (м)
метр также используется как большая единица длины.
Его можно использовать для измерения таких пространств, как комнаты, дома или дворы.
👉 Укороченный вариант для счетчиков — м.
В 1 метре 100 сантиметров.
Другими словами,
1 м = 100 см
Измерительные ленты и метрические стержни используются для измерения длины в метрах.
👉 Примеры длины в метрах:
— Автомобиль около 5 м .
— Сосна около 18 м .
ярд
Ярд (ярд) — тоже большая единица длины.
3 фута составляют 1 ярд.
1 ярд = 3 фута
Ярлыки используются для измерения длины в ярдах.
Мериллы имеют длину 1 ярд!
Километр (km)
километров (км) — очень большая единица длины.
1.000 метров составляет 1 километр.
1 км = 1000 м
Километр используется для измерения дорог.
Люди, которые ездят на большие расстояния, измеряют расстояние в километров !
миля (миль)
Как и километр, миля также является очень большой единицей длины.
Он также используется для измерения дорог и расстояний.
Примерно 1 ½ километра составляет 1 милю.
1 миля = около 1 ½ км
В Соединенных Штатах люди используют миль , но в остальном мире они используют километров .
Смотри и учись
Отличная работа! Теперь вы знаете единицы длины! 🤗
Можно переходить к практике.💪
Школа Аполлона: как выглядит обучение в 21 веке
Послушайте мое интервью с основателями Apollo School (стенограмма):
Мы достигли точки, когда большинство учителей принимают идею обучения, ориентированного на учеников, философию быть проводником на стороне, а не мудрецом на сцене. Мы также можем оценить ценность межучебных занятий, например, сочетания математики и естественных наук или интеграции искусства и музыки в уроки истории.Так почему же так много учителей все еще используют ту же старую модель, когда мы планируем и проводим уроки по отдельным предметам, синхронно, используя тот же традиционный график, что и у нас всегда?
Думаю, две причины.
Один, потому что он работает более-менее. Мы перемещаем студентов по системе, они кое-чему учатся, сдают тесты и заканчивают обучение с приемлемым набором знаний и навыков. Приемлемо. Достаточно, чтобы функционировать, чтобы продолжить учебу в колледже и более или менее выжить.
За исключением того, что в последнее время все больше и больше голосов говорят нам, что этот набор знаний и навыков не совсем подходит.Студенты не так хорошо разбираются в решении проблем, сотрудничестве и исследованиях, как им нужно в 21 веке.
Другая причина, по которой мы придерживаемся традиционной структуры, — это то, что я считаю более действенным: это потому, что мы не знаем, как изменить . У нас нет шаблона того, как могла бы выглядеть школа, если бы мы реструктурировали ее, чтобы отразить такие приоритеты, как межучебные связи, самоэффективность учащихся и обучение на основе запросов.
Что ж, у меня для вас есть шаблон, и я не могу дождаться, чтобы показать его вам.
Добро пожаловать в школу Аполлона
The Apollo School — это программа, которая действует в рамках обычной государственной школы Central York High School в Йорке, штат Пенсильвания. Apollo — это четырехчасовой блок занятий на семестр — английский язык, общественные науки и искусство — все они объединены и преподаются совместно тремя учителями, по одному из каждой предметной области. В течение семестра студенты несут ответственность за разработку и выполнение четырех крупных проектов, каждый из которых соответствует стандартам во всех трех предметных областях.
Учащиеся устанавливают свои собственные цели на каждый день в зависимости от того, над каким проектом они работают в данный момент: это включает в себя самостоятельную и групповую работу, индивидуальные встречи с учителями и посещение дополнительных мини-уроков, которые самостоятельно выбирает учителя. К обеду, когда закончится блок Аполлона, студенты возвращаются к обычному расписанию на остаток дня.
Как начиналась программа
Apollo возник, когда Грег Виммер, учитель социальных наук, и учитель английского языка Уэс Уорд (на фото выше) начали экспериментировать с идеей объединения двух классов.«Каждый раз, когда я преподавал литературный материал, — сказал Уорд, — я обнаруживал, что говорю об истории. И я подумал, насколько было бы удобно — и действительно полезно для учеников, — если бы у них был здесь любитель истории, чтобы по-настоящему бросить вызов и подтолкнуть детей раскопать больше контекста стихов или рассказов, которые мы читаем ».
Тем временем их школьный округ уже полностью менял свою образовательную парадигму. Придерживаясь подхода, называемого массовым индивидуальным обучением, школьный округ Центрального Йорка искал способы персонализировать процесс обучения для каждого ученика.На этот подход повлияли работы Би МакГарви и Чарльза Швана в их дальновидной книге «Неизбежное: массовое индивидуализированное обучение: обучение в эпоху расширения прав и возможностей».
В этом видео рассказывается о смене в районе:
При поддержке директора школы Виммер и Уорд объединили свои усилия с Джимом Гранди, учителем рисования в Центральном Йорке, и так родилась школа Apollo. Они провели презентацию для будущих студентов за семестр до начала курса и заинтересовали учащихся 11 и 12 классов, поступивших добровольно.
Central York по-прежнему предлагает классы с традиционным преподаванием английского языка, обществознания и искусства. Этот выбор является частью разнообразия, предлагаемого массовым индивидуальным обучением. «У нас есть несколько курсов, которые проходят в гибридном формате, где они могут немного встретиться с учителем, но затем работать самостоятельно или в группах, а затем они снова встречаются с учителем», — объясняет Уорд. «У нас есть онлайн-курсы, где студенты регистрируются раз в неделю с учителем, но остальная работа выполняется онлайн.Так что массовое индивидуальное обучение — не обязательно Apollo. Аполлон — одна спица этого колеса ».
Требования к курсу: Учебный план и оценка
В течение семестра студенты Apollo должны выполнить четыре независимых проекта в рамках заданной темы, каждый из которых должен включать какой-либо элемент английского языка, социальных наук и искусства. Студентам предоставляется список необходимых стандартов по каждому предмету, и ожидается, что они будут соответствовать каждому из них к концу семестра.
«Поскольку у вас 40 студентов, работающих в 40 различных направлениях, — объясняет Виммер, — мы решили, что именно они должны были самостоятельно выбирать стандарты».
Уорд описывает, как работает этот процесс. «В начале каждого проекта у нас есть ученики, которые определяют, над какими стандартами они будут работать, демонстрируя мастерство или просто тренируясь, чтобы стать лучше. В отличие от большинства классных комнат, где учитель составляет планы уроков, основанные на стандартах, которые скрыты под замком, мы фактически делимся PDF-файлами со всеми тремя стандартами наших предметных областей со студентами.У них они есть на весь семестр, поэтому они постоянно осознают ожидания каждого из нас и то, что им предстоит освоить ».
Каким образом студенты соответствуют этим стандартам, полностью зависит от их решения, и путь не всегда гладкий. «Это действительно гениально — видеть, как через неделю после начала проекта они осознают, что они придерживаются неправильных стандартов, — говорит Виммер, — а затем возвращаются назад и могут изменить их и заставить стандарты работать на них».
Когда проект завершен, студенты встречаются со всеми тремя преподавателями в обстановке, мало чем отличающейся от защиты докторской диссертации: они обсуждают цели, процесс и результаты и объясняют, как именно они достигли каждой цели обучения.Учащиеся также оцениваются на предмет того, насколько хорошо они овладели четырьмя навыками мышления — рассуждением, перспективой, контекстуализацией и синтезом — и двумя «мягкими навыками» — общением и управлением временем.
Вся группа собирается в начале каждого дня по семейному времени.
Обычный день
Каждый день начинается с Семейного времени. «Около 7:45 мы как бы загоняем их вместе в комнату Грега, и мы называем это семейным временем», — говорит Гранди. Продолжительность такой встречи может сильно варьироваться: от пятиминутных домашних занятий до многочасовых разговоров.«У нас были полные от одного часа до двухчасовых дискуссий, в ходе которых они действительно инициировали разговор и продвигали тему своего собственного образования. В этом смысле они могут быть полностью органичными и действительно полезными ».
Студенты используют онлайн-программное обеспечение, чтобы спланировать, как они будут использовать четыре часа в 30-минутные блоки времени. Это время может включать в себя самостоятельное исследование, творческую работу, групповую работу или индивидуальные конференции, которые студенты планируют с учителями по мере необходимости.
Студенты встречаются с учителем общественных наук Грегом Виммером.Используя онлайн-форму, учащиеся планируют индивидуальные конференции с учителями по мере необходимости.
Они могут свободно перемещаться между художественной комнатой, которая функционирует как своего рода творческое пространство, классной комнатой Виммера, которую студенты обычно используют для собраний небольших групп, и комнатой Уорда, которая часто используется как тихое место для студентов, чтобы работать в одиночку.
«Они также могут пойти в нашу библиотеку или сесть за один из столов, окружающих нашу школу, и в экстремальных ситуациях, — говорит Уорд, — они могут даже покинуть школу, чтобы взять интервью у кого-нибудь из сообщества или пойти в тени кого-то определенная карьера.Мы действительно стараемся вывести их за рамки этого обычного режима ».
Каждый ученик решает, как использовать четырехчасовой блок времени Аполлона. В конце каждого проекта тайм-менеджмент является частью их окончательной оценки.
Мини-уроки
Другой вариант, который есть у студентов в этом четырехчасовом блоке, — это посещение мини-уроков. Вместо того, чтобы проводить один и тот же урок целыми классами в одно и то же время, учителя планируют и проводят дополнительные мини-уроки по своим предметам.Некоторые уроки охватывают области базового содержания, которые соответствуют определенным стандартам, но большинство из них проводится только после того, как учителя видят необходимость в рамках того, над чем работают ученики.
Необязательно. Вы это уловили? Студенты не обязаны посещать мини-уроки; они выбирают ехать исходя из своих текущих потребностей. Во время семейного отдыха учителя будут рекламировать уроки, которые они преподают в этот день.
«Это похоже на поездку на конференцию по вопросам образования и огромный набор возможностей для выбора», — объясняет Уорд.«Так что вполне возможно, что Грег преподал бы урок об этом конкретном конфликте или этой проблеме в текущих событиях. И г-н Гранди может предлагать урок искусства одновременно с тем, что я предлагаю что-то на английском, и студенты могут выбирать, какой из них более полезен для их проекта в данный момент. Мы можем развернуться и предложить тот же урок на следующий день, а они могут переключиться и перейти к другому, если потребуется ».
Настройка не ограничивается учителями: учащиеся также могут запрашивать мини-уроки по определенным темам.Недавно Гранди попросила студентку провести урок о Фриде Кало и других художниках, вдохновленных ею. «Поэтому я сказал:« Да, просто дайте мне два или три дня, чтобы собрать все воедино, и тогда я дам вам урок »».
Некоторые мини-уроки даже проводят сами ученики. «У каждого студента обычно есть что-то, что он может добавить в группу», — говорит Виммер. У нас есть студенты, которые очень хорошо разбираются в технологиях, некоторые — в создании присутствия в Интернете, и поэтому мы подумали, почему бы этим студентам не поделиться друг с другом своими способностями и талантами? »
Учитель рисования Джим Гранди беседует со студентом.Каждый студенческий проект включает в себя элементы английского языка, обществознания и искусства.
Положительные результаты
На вопрос, дала ли программа те результаты, на которые они надеялись, Гранди отвечает, что студенты выходят далеко за рамки того, что они могли бы сделать в более традиционной программе. «Когда я веду традиционные уроки, я изо всех сил стараюсь спланировать действительно интересные уроки и проекты для детей. Но я не могу планировать эти проекты. Я никогда не мог спланировать проект по биоэтике для всего класса.Я не мог даже соответствовать всем стандартам, которые хотел. Таким образом, (ученики) как класс достигают большего уровня стандартов, чем я когда-либо достигал бы, если бы я руководил каждым уроком ».
Помимо академиков, программа позволила учителям развивать отношения со студентами, которые были бы невозможны в обычной обстановке. «Некоторые из этих молодых людей подходили к нам и просто … такие вещи, о которых я даже не думал, что услышу, — говорит Гранди, — о том, как они будут напуганы до смерти, придя в школу в воскресенье вечером из-за беспокойства. и как им сейчас нравится ходить в школу, и они никогда раньше не разговаривали со взрослыми или учителями, а не только: «Вот твое домашнее задание, вот твой тест».«У нас есть настоящие разговоры с этими людьми, я имею в виду, , это люди . Вы строите потрясающие отношения ». ♦
Узнайте больше о школе Apollo
Веб-сайт : theapolloschool.weebly.com
Instagram : @apollocyhs
Узнавайте что-то новое каждую неделю.
Присоединяйтесь к моему списку рассылки и еженедельно получайте советы, инструменты и вдохновение — в быстрых, небольших пакетах — все, что поможет сделать ваше обучение более эффективным и увлекательным.Вы также получите доступ к моей библиотеке бесплатных загружаемых ресурсов, предназначенной только для участников, в том числе к моему электронному буклету 20 способов сократить время успеваемости вдвое, , который помог тысячам учителей тратить меньше времени на выставление оценок!
Понимание измерения в свете его происхождения
Front Psychol. 2013; 4: 113.
Стивен Хамфри
1 Педагогический факультет Университета Западной Австралии, Перт, Вашингтон, Австралия
1 Педагогический факультет Университета Западной Австралии, Перт, Вашингтон, Австралия
Отредактировал: Джошуа А.МакГрейн, Университет Западной Австралии, Австралия
Рецензент: Бен Колагиури, Университет Нового Южного Уэльса, Австралия; Эндрю Стюарт Кингдон, Офис Исследовательского совета Нового Южного Уэльса, Австралия; Пол Т. Барретт, Advanced Projects R&D Ltd., Новая Зеландия
* Для переписки: Стивен Хамфри, Высшая школа образования, Университет Западной Австралии, M428, 35 Stirling Highway, Crawley, WA 6009, Австралия. e-mail: [email protected]Эта статья была отправлена в Frontiers in Quantitative Psychology and Measurement, специальность Frontiers in Psychology.
Поступила в редакцию 29 ноября 2012 г .; Принято 21 февраля 2013 г.
Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает использование, распространение и воспроизведение на других форумах при условии указания авторов и источника и при соблюдении любых уведомлений об авторских правах. относительно любой сторонней графики и т. д.
Abstract
На протяжении истории естественные науки стали свидетелями развития все более удобных сокращенных символических устройств для обозначения физических величин.Эти устройства в конечном итоге приняли форму физической алгебры. Однако за удобство алгебры, вероятно, приходилось платить — это потеря ясности прямого понимания Евклидом, Галилеем и Ньютоном естественных количественных соотношений. Физическая алгебра часто интерпретируется как обычная алгебра; то есть интерпретируется так, как будто символы обозначают (а) числа и операции с числами, в отличие от (б) физических величин и количественных соотношений. В статье пересматривается способ, которым Ньютон понимал и выражал физические определения и законы.Соответственно, в нем рассматривается компактная форма записи, которая использовалась для обозначения: (а) соотношений физических величин; и (b) сложные отношения, включающие два или более видов количества. Цель состоит в том, чтобы показать, что рассмотрение физической алгебры как устройства для обозначения отношений между отношениями согласуется с историческим развитием. В историческом контексте цель измерения состоит в том, чтобы установить, что физическая величина находится в определенном соотношении с другой величиной того же типа.Прояснение значения измерения с точки зрения исторического происхождения физики имеет важные последствия для способа понимания и подхода к измерению. Рассмотрены возможные последствия для социальных наук.
Ключевые слова: измерение, соотношение, пропорция, классическая теория, теория представлений, психометрия, метрология
Согласно определениям измерения, принятым в социальных науках, измерение включает ассоциацию или присвоение чисел объектам.Подобные определения носят репрезентативный характер. Возможно, наиболее влиятельным является определение, данное Стивенсом (1946, стр. 677): «измерение в самом широком смысле определяется как присвоение числовых значений объектам или событиям в соответствии с правилами». Мичелл (1999, стр. 15–19) привел убедительный аргумент в пользу того, что, несмотря на несовместимость с традиционной концепцией измерения в естественных науках, определение Стивенса стало моделью для многих психологов. Соответственно, репрезентативные определения также были сформулированы в «Теории отклика на предмет», возможно, в первую очередь Лордом и Новиком (1968).
Наиболее тщательно продуманная попытка связать измерение в социальных науках с измерением в физике содержится в «Основах измерения » (Krantz et al., 1971) и предшествующих работах. Авторы попытались установить аксиоматическую основу для измерения, которая включает так называемые теоремы представления. В томе 1 «Основы измерений » Кранц и др. (1971, стр. 1) характеризуют измерение следующим образом: «При измерении какого-либо атрибута класса объектов или событий мы связываем числа… с объектами таким образом, чтобы свойства атрибута достоверно представлялись как числовые свойства.«Основы по существу доводят до крайности использование удобных сокращенных символических устройств, посредством чего символы физической алгебры интерпретируются так, как будто они относятся только к числам и их операциям. Аксиомы репрезентативной теории относятся либо к качественным отношениям, либо к числовым свойствам, но не напрямую к количественным атрибутам. Таким образом, формальный аспект теории остается отличным от ссылки на качественное эмпирическое содержание.В соответствии с этим, Мичелл (1999, стр. 208) сказал о школе репрезентации: «По большей части Суппес, Люс и их партнеры избегали (этой концепции количества) при рассмотрении измерений». Кибург (1996) и Берка (1983) выдвинули связанные наблюдения и критические замечания в отношении репрезентативной теории.
В отличие от репрезентативной теории, Мичелл обратил внимание на то, что он называет классической теорией измерения: «научное измерение правильно определяется как оценка или открытие отношения некоторой величины количественного атрибута к единице измерения тот же атрибут »(Michell, 1997, стр.358). В этом определении количественным атрибутам придается онтологический статус, а соотношение между величинами величин принимается за действительное число.
Эта классическая теория часто используется в физике и метрологии. В метрологии Бюро мер и весов (BIPM) претендует на полномочия поддерживать всемирное единообразие измерений и их прослеживаемость к Международной системе единиц (СИ). BIPM неявно принимает классическое определение в своем определении единицы: «Таким образом, единица измерения — это скалярная величина, определенная и принятая по соглашению, с которой можно сравнить любую другую величину того же вида, чтобы выразить отношение две величины в виде числа »[Международное бюро мер и весов (МБМВ), 2006, с.24].
Галилей, Ньютон и другие пионеры выражали физические отношения как пропорциональности между отношениями физических величин. Как будет показано ниже, классическая теория измерения более тесно связана с истоками физики, чем репрезентативная теория, в силу своей ссылки на концепцию отношения.
Данная статья имеет следующую структуру. Он начинается с акцента на генезисе физики и, в частности, на вдохновленной греками традиции понимания физических отношений с точки зрения пропорции и соотношения.Затем в нем представлен обзор все более удобных сокращений, которые использовались для утверждений о пропорциональности, что привело к последующему расхождению мысли в форме классического и репрезентативного взглядов на измерение. Утверждается, что использование все более абстрактных и сокращенных утверждений дорого обходится прямоте понимания естественных отношений. Затем используется компактная форма записи для обозначения соотношений, составных соотношений и пропорциональностей между соотношениями; и это обозначение используется, чтобы показать параллель между утверждениями алгебры и пропорциональности.Затем объясняется концепция составного отношения и показано, что, хотя составные отношения имеют формальное сходство с умножением, у них есть отчетливая концептуальная основа. Наконец, объясняются самые основные значения измерения в физике и кратко рассматриваются последствия для социальных наук.
Пропорции и отношения в геометрии и классической физике
Исторически пионеры классической физики, от Галилея до Ньютона и Фарадея, выражали физические отношения как пропорциональность соотношений двух или более видов величин.Ньютон широко использовал геометрические линии для обозначения таких величин, как силы (Newton, 1846; Roche, 1998). В Принципах он неоднократно называл величины пропорциональными или обратно пропорциональными друг другу в динамических физических ситуациях. Таким образом, Ньютон сказал:
Если при сравнении неопределенных количеств различных сортов одно с другим, любое из них прямо или обратно считается таким же, как и любое другое, это означает, что первое увеличивается или уменьшается в том же соотношении со вторым или с его взаимное (1846, с.100).
В качестве примера, если сила f увеличивается до f ‘, а результирующее ускорение тела a увеличивается до a’, тогда соотношение f: f ‘может быть таким же, как a: a’. Здесь Ньютон использует слово Евклида «в одинаковом соотношении» для описания пропорциональности. Кулон и Фарадей также называли количества пропорциональными или обратно пропорциональными друг другу (Silsbee, 1962).
Символы для чисел в физико-математике
Пропорции и отношения были центральными в евклидовом Элементах .В вдохновленной греками традиции пропорций и соотношений соотношения не считались буквально равными числам. Скорее, «[r] atio принадлежало… к категории отношения, а не было простой величиной или единственным числом» (Roche, 1998, p. 46). Следовательно, передаточные числа даже не задумывались как буквально равные друг другу. В своем историческом анализе Евклида Граттан-Гиннесс (1996) отмечает: «Хотя он говорит о равенстве чисел и величин, Евклид никогда не говорит, что отношения« равны »друг другу, а только что они« находятся в одном и том же соотношении ». », Или что одно соотношение« такое же », как другое в предложении пропорции.
Поэтому неудивительно, что идея о том, что отношение может быть обозначено одним числом, называемым либо его показателем, либо номиналом, встретила значительное сопротивление в определенный момент истории. В конечном итоге, однако, «медленно растущее притязание на представление всех отношений числами постепенно привело к объединению концепции отношения как единого числа» (Roche, 1998, p. 76). Эта объединенная концепция очевидна в классической теории (или определении) измерения.
Поскольку репрезентативные определения преобладают в социальных науках, поучительно понять достижения в физико-математике, которые позволили этим определениям появиться.Путь от истоков физики к современной репрезентативной концепции выглядит примерно следующим образом. Во-первых, физические отношения выражались словами и геометрическими аналогиями в виде соотношений и сложных соотношений. Ньютон следовал этой традиции и использовал обозначение отождествления линий с физическими величинами, так что длины и направления линий обозначали величины и направления величин. Рош (1998, стр. 89) резюмирует это и последующее историческое развитие следующим образом.
Это не было сокращением физического до линии… Но это было условное обозначение двух концепций. Конечно, это было чрезвычайно удобно, поскольку все операции геометрической алгебры теперь можно было применять к этим понятиям без ограничений, налагаемых символикой пропорциональности, которая непосредственно относилась к естественной величине. Эта идентификация в конечном итоге перешла от строк к числам и даже к самому формальному символу, который обозначал физическую величину.
Позже Лаплас интерпретировал символы в физических уравнениях как представляющие «числа, взятые из четко определенных процедур измерения» (Roche, 1998, стр. 138). Это было критическим отступлением, потому что, как только числа стали рассматриваться как абстрактные и независимые от эмпирического мира, появилась возможность истолковать цель измерения как представление эмпирических сущностей числами; то есть стало возможным возникновение репрезентативного взгляда. Мичелл (1993) подробно описывает более поздние разработки и утверждает, что Рассел (1903) был первой явно репрезентативной теорией измерения.Сами теоретики репрезентации предлагают совершенно иное мнение, делая акцент на событиях, произошедших в конце восемнадцатого и начале девятнадцатого веков (Diez, 1997; Luce and Suppes, 2002).
Расхождение во взглядах на измерение
Рош (1998, стр. 138) утверждает, что точка зрения о том, что в алгебре физики могут появляться только абстрактные числа, отражает, возможно, ответ на классическую традицию работы с физическими величинами как таковой. чем его мера, и необходимость дистанцировать алгебру физики от манипуляций с такими величинами.Возможно, тогда неудивительно, что впоследствии произошло расхождение в способах интерпретации абстрактных чисел, которое продолжается и сегодня. С классической точки зрения, как определено Мичеллом (1993), отношения — это числа. Этот взгляд сохраняет ключевой аспект греческой традиции, но включает использование аббревиатуры, как объясняется ниже. В репрезентативной точке зрения нет никакой связи с отношениями, как резюмируется в следующем отрывке.
Таким образом, по существу, есть две особенности, разделяющие классическую и репрезентативную теории измерения: роль соотношений величин и место чисел.Согласно классической теории, эти два понятия логически связаны: отношения величин являются числами, и этот факт является основой измерения. Согласно теории представлений, числа не выводятся из соотношений величин. Они совершенно независимы от них, и место чисел в измерении определяется структурным сходством между качественными и количественными системами. Следовательно, согласно теории представлений, эмпирическим объектам при измерении присваиваются числа.Согласно классической теории, числа открываются как отношения между эмпирическими объектами в измерении (Michell, 1993, стр. 190).
Несмотря на появление репрезентативной точки зрения, классическая точка зрения продолжает существовать в физике. Почему абстрактная алгебраическая точка зрения не вытеснила полностью классическую? Было бы несколько удивительно, если бы утверждения о пропорциональности, используемые в концепции физики, были менее подходящими для описания естественных отношений, чем алгебра, которая применялась позже.Кажется более вероятным, что удобство коротких рук было основной причиной их все более широкого использования. Однако утверждалось, что удобство физической алгебры произошло за счет явного внимания к ключевым характеристикам физических отношений, как это описано в следующем отрывке.
Некоторые ключевые особенности этой вдохновленной греческой традицией… заслуживают пристального внимания. Пары одинаковых величин сравниваются с другими парами, которые часто отличаются физически, например, пары гирь с парами расстояний в теории баланса.Это сильно отличается от современного алгебраического языка физики, который сравнивает отдельные значения разных величин. Более того, утверждение о пропорциональности кажется немного ближе к описанию естественного отношения, чем язык алгебры (Roche, 1998, p. 47).
Эти два направления мысли продолжают оставаться очевидными сегодня, так что алгебра и арифметика физики, кажется, «интерпретируются формально в одних контекстах и физически в других» (Roche, 1998, p. 222).
Примирение современной физической системы обозначений с ее происхождением
Как же тогда мы могли бы примирить современную ссылку на равенство соотношений и чисел в физике с ее происхождением? Krantz et al. (1971, стр. 459) заметил: «Большинство текстов по анализу размерностей, кажется, принимают (физическую) алгебру как должное, и они не пытаются явно сформулировать то, что здесь задействовано». Хотя это достаточно верно, используя соответствующие обозначения, можно явно сформулировать утверждения о пропорциональности таким образом, чтобы показать четкую и прямую параллель с современными алгебраическими обозначениями.
Утверждение Ньютона о втором законе движения используется для иллюстрации этой параллели. Ньютон (1846, стр. 83) сформулировал второй закон следующим образом: «Изменение движения всегда пропорционально приложенной движущей силе; и производится в направлении правой линии, в которой действует сила ». Здесь под движением понимается то, что сейчас обычно называют импульсом. Мы можем выразить второй закон Ньютона как формальное утверждение соразмерности следующим образом:
где f и p относятся к силе, действующей на тело в данный момент времени, и результирующему импульсу тела, а f ‘и p’ относятся к силе, приложенной в другой момент к тому же телу, и ее результирующему импульсу, соответственно. .В заявлении (1) «::» означает «равно как» или «пропорционально». Таким образом, изменение количества движения выражается соотношением p ‘: p и пропорционально изменению движущей силы f’: f. Обозначение «::» использовалось Уоллисом (1685 г.). Учитывая цели статьи, следует отметить, что утверждение (1) уже является сокращенной формой утверждения соразмерности, в котором отсутствуют ссылки на ключевые элементы полного изложения закона Ньютона словами, такие как природа причинной связи. через ссылку на силу, воздействующую на тело.
Как говорилось ранее, Евклид не считал соотношения равными друг другу. Точно так же Ньютон не упоминал о равенстве в своей формулировке закона. Соответственно, уместно ссылаться на (Уравнение 1) как на утверждение физического закона, а не на уравнение , потому что оно не утверждает, что члены равны , численно или в любом другом смысле.
Очевидно, однако, что сейчас физическая алгебра успешно используется как в прикладных, так и в теоретических целях; и современные уравнения должны быть совместимы с их происхождением.Выбранный пример можно использовать для демонстрации этой совместимости.
Второй закон Ньютона обычно алгебраически формулируется следующим образом:
где p = m a или, как выразился Ньютон (1846, стр. 72): «Количество движения [импульс] является мерой того же самого, возникающего из скорости и количества материи одновременно. . »
Чтобы увидеть параллель между утверждением (1) и уравнением. 2, мы можем выразить члены как отношения между величинами и единицей следующим образом:
f ′ : [f] :: m ′ : [м] ⋅ a ′ : [a],
(3)
где F = f ′: [f], m = m ′: [m] и a = a ′: [a].Здесь [f], [m] и [a] взяты как единицы силы, массы и ускорения соответственно. Термин «.» означает, что эти два отношения составлены в смысле термина, используемого Евклидом в геометрии, а затем Галилеем (1638) для выражения сложных физических отношений. Концепция сложных соотношений для выражения сложных соотношений будет объяснена ниже.
Очевидно, уравнение. 3 и утверждение (1) имеют аналогичную форму, со знаком «=» в уравнении. 3 заменен на «::» в утверждении (1) и алгебраическое умножение, используемое в уравнении.3 вместо сложения в заявлении (1). Дополнительный шаг (который не сделал бы Евклид), позволяющий разрешить F = f ‘: [f] и так далее, уравнивает отношения с числами. Этот шаг обычно используется в метрологии. Уоллис (1670) сделал именно этот шаг от «::» к «=», хотя Рош (1998, стр. 99) утверждает, что «отрывки из других мест в Уоллисе убедительно свидетельствуют о том, что он интерпретировал это выражение, а не как истинное алгебраическое уравнение, но как сокращенное уравнение отношения, которое связывает сложное отношение с простым соотношением.”
Соотношения соединений в заявлениях о пропорциональности
Похоже, что термин соотношение соединений не имеет явного исторического определения в большинстве источников, за исключением ссылки на конкретные примеры. Если два соотношения смешиваются, второе количество первого соотношения является первым количеством второго соотношения, а смешанное соотношение — соотношением первого и последнего количества. Исторические корни сложения, вероятно, лежат в физике музыки, где можно составить два музыкальных интервала для получения заданного отношения (Grattan-Guinness, 1996).
Galileo смог использовать составные отношения, сделав одно отношение длин пропорциональным двум скоростям, а другое отношение длин — двум временным интервалам. Путем сложения двух соотношений длин (первого и второго со вторым и третьим) он продемонстрировал, что расстояния тел с разными скоростями, перемещавшихся в разные интервалы времени, «соотносятся друг с другом сложным соотношением скоростей и интервалов времени» (Галилео , 1638, с. 194). Аналогичные рассуждения можно использовать, чтобы продемонстрировать пропорциональность в формуле.3 следует из закона Ньютона. Следующее повторяет рассуждения Галилея.
Рассмотрим тело A, на которое действует сила f A для ускорения тела в точке a A . Рассмотрим также тело B, на которое действует сила f B для ускорения тела в точке a B . Предположение, которое необходимо продемонстрировать, состоит в том, что отношение f A к f B является составным соотношением масс и ускорений.Предложение можно продемонстрировать в два этапа со ссылкой на закон Ньютона.
Сначала рассмотрим пропорциональность
Поскольку соотношение сил, необходимых для ускорения двух тел с одинаковым ускорением, пропорционально отношению масс этих тел, и поскольку f A перемещает тело A с ускорением a A , следует, что F — сила, необходимая для перемещения тела B с массой m B с ускорением a A .
Во-вторых, учтите также пропорциональность
Поскольку соотношение сил, необходимых для ускорения одного тела с двумя разными ускорениями, пропорционально отношению этих ускорений, и поскольку F — это сила, необходимая для перемещения тела B с ускорением a A , отсюда следует, что f B — сила, необходимая для перемещения тела B с ускорением a B .
Таким образом, показано, что утверждение о сложном соотношении выполняется.Логика следующая. Предположим, мы должны были подумать об изменении силы от силы, необходимой для ускорения тела A в точке a A , до силы, необходимой для ускорения тела B на точке B через промежуточную стадию. На первом этапе, используя терминологию Ньютона, f A — это , увеличенное (или уменьшенное ) на определенную величину, чтобы стать F, и изменение силы таково, что f A : F пропорционально к m A : m B .На втором этапе F увеличивается (или уменьшается), чтобы стать f B , а изменение силы таково, что F: f B пропорционально a A : a B . То есть первая и последняя силы находятся в соотношении f A : f B , а комбинация ступеней сокращенно обозначается как составное отношение f A : F · F: f В . Таким образом, компаундирование относится к отношению между начальным и конечным количеством через их отношения с общим или промежуточным количеством.
Пропорциональность отношения сил к составному соотношению может быть прямо выражена следующим образом:
f A : f B :: f A : F ⋅ F: f B .
(6)
Пропорциональность отношения сил также может быть определена «косвенно» в терминах сложного отношения масс и ускорений следующим образом:
f A : f B :: m A : m B ⋅ a A : a B .
(7)
В утверждении (7) снова можно представить себе силу, как будто она изменяется через промежуточный этап. На первом этапе изменение силы (с f A на f) пропорционально m A : m B , а на втором этапе изменение силы (с F на f B ) пропорционален a A : a B . Комбинированная переделка — с f A на f B .Конечно, не обязательно, чтобы существовал реальный процесс, посредством которого силы меняются через последовательные стадии. Вместо этого утверждение (7) предназначено для резюмирования сложного набора соотношений между отношениями сил, масс и ускорений. По сути, утверждение (7) — это не больше и не меньше, чем сокращение для полной цепочки рассуждений, используемой для демонстрации того, что утверждение верно.
Таким образом, «метод сложения соотношений Евклида совсем не то же самое, что умножение, хотя две теории демонстрируют структурное сходство» (Grattan-Guinness, 1996, p.362). Структурное сходство очевидно при сравнении утверждения (7) с уравнением F = m × a с учетом современной тенденции рассматривать отношения как отдельные числа. Таким образом, физическая алгебра — это еще одно сокращение для полной линии рассуждений. При условии использования согласованной системы единиц существует прямая параллель между утверждениями о пропорциональности и физической алгеброй, как обсуждается ниже.
Метрологические правила умножения величин
В метрологии принято рассматривать отношения как чистые числа.Если отношения в утверждении (7) трактовать как числа, умножение измерений дает результат, который согласуется с законом, но только при использовании когерентных единиц. Согласованная система единиц — это система, в которой единицы определены таким образом, чтобы избежать введения мультипликативных констант, которые считаются «лишними» (например, константы того типа, который требуется для преобразования британской системы мер в метрическую). При условии , что используются единицы из согласованной системы единиц, многие из уравнений физики могут быть поняты как сокращенные символические приемы для утверждений пропорциональности, включающих составные отношения.В частности, таким образом можно понять уравнения физики, которые используются в определениях единиц СИ. Однако только благодаря когерентной совокупности физических отношений когерентная система возможна в первую очередь (de Boer, 1994/95).
Исходя из этого, согласованные единицы определяются с помощью этих уравнений в сочетании с метрологическим «правилом», согласно которому «значение произведения значений двух конкретных величин в данной системе измеряемых величин и единиц является произведением. их числовых значений и единицы новой величины, если такая реализуемая величина может существовать »(Emerson, 2008, p.136). В прошлом была признана связь между этим правилом и его историческим происхождением. Как заявил Рош (1998, стр. 108): «На протяжении семнадцатого и восемнадцатого веков произведение или деление физических величин часто понималось как сокращенное выражение сложного отношения». Таким образом, пример второго закона движения Ньютона иллюстрирует общую связь между современным алгебраическим выражением и историческими истоками физической науки.
Было бы интересно рассмотреть онтологические и эмпирические основы концепции пропорциональности соотношений.Однако это выходит далеко за рамки данной статьи. Здесь достаточно подчеркнуть, что физические отношения изначально были задуманы как соразмерности между соотношениями, и поэтому эта концепция, по-видимому, заслуживает внимательного рассмотрения.
Современные измерения в физике
Теперь мы в состоянии рассмотреть последствия исторического и концептуального анализа для того, как измерения понимаются сегодня. В первую очередь рассматривается прямое измерение, потому что без него не было бы косвенного измерения.Затем рассматривается косвенное измерение.
Прямое измерение устанавливает пропорциональность между соотношением непрерывных величин и соотношением дискретных величин. Например, мы можем установить, что отношение длины L к единице длины [L] пропорционально отношению r длин волн к одной длине волны, как выражено в следующем утверждении пропорциональности:
L: [L] :: r
(8)
где
Приведенный выше пример прямого измерения особенно актуален для СИ, потому что основные единицы расстояния и времени в настоящее время определены в терминах волновых явлений, и есть предложение определить килограмм в терминах соотношения Планка в будущем ( Миллс, 2010).Прототипные примеры прямого измерения, использованные Krantz et al. (1971) предполагают формирование «стандартной серии», полученной, например, путем соединения стержней одинаковой длины. Стандартный ряд может использоваться для установления пропорциональности, например L: [L] :: r
Как мы видели, давно произошло слияние понятий отношения и числа. Отношение r
В метрологии большинство единиц в Международной системе (СИ) определены способом, который включает в себя законы и / или определения, и без прямого вовлечения отношений между непрерывными величинами и дискретными величинами. Такой подход к измерению был назван Кибургом (1984) косвенным и / или систематическим измерением, а Кэмпбелл (1928) фактически назвал производным измерением.
Косвенное измерение иллюстрируется определением единицы силы.Максвелл (1876, ст. SLVII) сказал, что «единицей силы является та сила, которая, действуя на единицу массы за единицу времени, порождает единицу скорости». Единица силы в системе СИ, ньютон, также определяется точно таким же образом. Определение основано на втором законе движения Ньютона, который может быть выражен в единицах СИ с использованием следующего утверждения пропорциональности:
f ′ : N :: m ′ : кг ⋅ a ′ : a,
(9)
где N — ньютон, кг — килограмм, а — единица ускорения, 1 м в секунду, в секунду.Используя косвенное измерение, можно установить соотношение между величиной, такой как F ‘, и единицей, такой как ньютон, с помощью инструмента и процедуры, предназначенных для этой цели. Любой такой инструмент должен быть разработан на основе физических отношений, которые включают, но не ограничиваются, отношения, используемые для косвенного определения единицы. В выбранном примере инструмент обычно будет спроектирован таким образом, что на массу действует сила, ускоряющая ее в контролируемых условиях.
Последствия для социальных наук
Детальный анализ возможных последствий для социальных наук выходит за рамки данной статьи.Тем не менее, можно коснуться некоторых относящихся к делу соображений и сделать некоторые предварительные наблюдения.
Один очевидный вопрос, который может возникнуть: можно ли понять психологические феномены с точки зрения пропорциональности и соотношения, аналогично тому, как понимаются физические отношения. Существуют ли психологические атрибуты, пропорциональные друг другу при определенных условиях? Существуют ли психологические атрибуты, которые пропорциональны физическим атрибутам при определенных условиях? Если ответ на любой из вопросов был положительным, это могло бы обеспечить основу для измерения психологических характеристик посредством косвенного измерения.
Возможно, будет более плодотворным начать с того, чтобы задать совсем другой вопрос: есть ли психологические способности распознавать соотношения и соразмерность? Кажется, что такие способности должны существовать, поскольку физические соотношения постигаются путем восприятия через знакомство с физическими явлениями. Маловероятно, чтобы люди могли воспринимать отношения как базовый вид отношений и успешно развивать физику на этой основе без какого-либо сенсорного и умственного аппарата для этого.
Простым примером, показывающим, что люди, вероятно, обладают такой способностью, является отношение соотношения горизонтов, которое применяется к вертикально вытянутым объектам, таким как деревья и столбы. Коэффициент горизонта — это отношение пропорции высоты объекта, видимого над горизонтом, к пропорции высоты объекта, видимого ниже горизонта. Независимо от расстояния от наблюдателя это соотношение одинаково для любого объекта одинаковой высоты (Sedgwick, 1973; Gibson, 1986; Rookes, Willson, 2000). Таким образом, например, если серия световых полюсов одинаковой высоты простирается к горизонту, наблюдатель увидит одинаковое соотношение высоты над горизонтом и высоты под горизонтом для каждого полюса.Есть свидетельства того, что люди действительно опираются на эту связь, независимо от того, используется ли в качестве ориентира фактический горизонт или неявный горизонт (Берманини и др., 1998). Более общий прогноз, который можно сделать, состоит в том, что люди непосредственно воспринимают соотношения и пропорциональности соотношений и реагируют на них таким образом, который имеет отношение к функциональным и целевым действиям и ответам. Это было бы важно для психофизики, потому что это означает сосредоточение внимания на том, как люди воспринимают физические отношения, участвующие в функциональном поведении, а также на сенсорных реакциях на стимулы, что было основным направлением дисциплины на протяжении всей ее истории.
Хотя существует сложное расхождение во взглядах, исторически психофизика сосредоточивалась, в частности, на установленных отношениях между физическими стимулами и ощущениями , где последние считаются количественными атрибутами. Однако некоторое время назад было замечено, что способность человека непосредственно воспринимать и оценивать отношения является экономным объяснением эмпирических результатов в психофизике, как показано ниже.
Почему мы должны предполагать, что [человек] основывает свои оценки физических отношений на оценках психологических отношений? Почему следующего объяснения недостаточно? Глаза [человека] нормальные, и он узнал, как выглядят стержни, когда они стоят в соотношении 1: 2; следовательно, когда он смотрит на стержни, он может с некоторой точностью сказать, находятся ли они в таком соотношении (Savage, 1970, стр.383).
Если люди обладают способностями воспринимать физические соотношения и функционально реагировать на них, становится доступным другой возможный путь. Изучение сенсорного и перцептивного аппарата может оказаться полезным, как если бы мы изучали сложный набор измерительных инструментов. Такой подход, по сути, возник в ходе ранних попыток измерить интенсивность света. В этом контексте «центральная проблема касалась определения стандартов яркости на основе сильно изменчивых людей-наблюдателей и сложного механизма визуального восприятия.(Джонстон, 2001, стр. 7). Действительно, многое из существующей психофизики можно понять с этой точки зрения, без необходимости ссылаться ни на сенсорные величины, ни на представление психологических атрибутов в виде чисел. Однако было бы предпочтительнее рассмотреть способы, которыми оценки подразумеваются функциональными реакциями, поскольку нет никаких причин, по которым люди должны были развить способность устно сообщать о соотношениях любого данного вида величин при заданном наборе условий.
Прямое и косвенное измерение в социальных науках
Вопрос, рассмотренный ранее, заключается в том, можно ли понять психологические явления с точки зрения пропорциональности и соотношения.Чтобы соответствовать истокам количественной науки, задача состоит в том, чтобы прямо или косвенно измерить предполагаемый количественный психологический атрибут путем установления таких соотношений.
Возможность или нет прямого измерения в психологии обсуждалась в течение некоторого времени, возможно, в первую очередь в рамках обсуждений Комитета Фергюсона (Ferguson et al., 1940). Стивенс попытался обойти эти последствия. Krantz et al. (1971) стремились предоставить аксиоматическую основу для измерения, которая избегает необходимости эмпирических операций конкатенации.Аксиоматический репрезентативный подход основан на идее, что теория измерения необходима для успешного измерения атрибута в психологии. Однако история показывает, что физика не развивалась на основе применения репрезентативной теории измерения. Исторический анализ в этой статье показывает, что физическая теория , первоначально выраженная в терминах пропорциональности и соотношения, формирует основу для измерения. В соответствии с этим из прикладной метрологии ясно видно, что материальная теория используется для разработки инструментов и процедур (Hebra, 2010, стр.7). Эта зависимость измерения в физике от материальной теории также явно отражена в определениях единиц в СИ (de Boer, 1994/95; Massey, 1971; Emerson, 2004; Humphry, 2011a). Таким образом, Krantz et al. (1971) отстаивали подход к измерению в социальных науках, который отличается от подхода, принятого в физике, тем, что они использовали «теории, отличные от тех, которые работали в физике» (стр. 17).
Хотя теоретики представления допускают, что измерение некоторых величин может быть основано на физическом законе, Кранц (1972) утверждал, что «измерение физических величин, таких как длина, масса и продолжительность, логически предшествует формулированию количественных законов. физики.Однако было замечено, что единицы длины и продолжительности в системе СИ определены в терминах физической теории и закона, и что есть предложение определить единицу массы в терминах физического отношения. Определения единиц СИ основаны на физических количественных отношениях, включающих соответствующие виды величин, в соответствии с историческим способом выражения отношений в физической науке. Этим определениям соответствует mise en pratique (набор прикладных инструкций) для измерения в единицах, основанных на определениях.Это означает, что можно подойти к измерению этих величин, используя теорию, определение и закон для разработки измерительных приборов и процедур. Даже если оставить в стороне вопрос о том, можно ли таким образом подойти к измерению таких величин, как масса, измерение длины может быть достигнуто на основе волновых явлений без использования операций конкатенации. Измерение длины использовалось в качестве прототипа при установке фундамента. Поэтому никоим образом не ясно, логически ли измерение физических величин, таких как длина, на основе операций конкатенации, предшествует формулированию количественных законов.Напротив, остается возможным, что к измерению большинства, если не всех, физических величин можно подойти на основе понимания физических соотношений.
Таким образом, в попытках связать психологию с фундаментальным измерением, как это определено Кэмпбеллом (1928, стр. 14), прямое измерение, основанное на конкатенации или аналогичной операции, привлекало наибольшее внимание (без успеха, по крайней мере, на сегодняшний день). Намного меньше внимания уделялось, по крайней мере явно, тому, что Кибург (1984, стр.143), называемое «систематическое измерение» как основной способ приближающегося измерения. Систематическое измерение включает в себя величины, которые систематически связаны в рамках теоретической основы. Было бы несколько удивительно, если бы в психологии существовал количественный атрибут, не связанный с каким-либо физическим атрибутом. Вместо этого кажется более вероятным, что количественные психологические атрибуты будут связаны с физическими величинами (или расширением), что делает разумным называть Берка (1983, с.13) до «экстрафизических измерений». В той мере, в какой это предположение верно, систематическое и косвенное измерение, вероятно, увенчается успехом.
Достаточно просто постулировать количественные отношения в социальных науках, аналогичные в чисто формальных терминах тем, которые составляют основу измерений в физике (см. Humphry, 2011b). Однако обычно существует одна из нескольких проблем. В некоторых случаях предполагаемые отношения включают только непрерывные величины и прямое измерение не имеет основания.В других случаях используются дискретные величины, но нет ясного и прозрачного объяснения пропорциональности соотношений непрерывных величин и соотношений дискретных величин (хотя возможные исключения существуют в психофизике и экономике). В других случаях по-прежнему используются экспоненциальные и логарифмические отношения, что влечет за собой несоответствие с истоками физики. Задача состоит в том, чтобы выяснить, существует ли продуктивный подход к систематическому измерению, позволяющий избежать таких проблем.
Резюме и заключение
Было замечено, что, следуя вдохновленной греками традиции, пионеры физики, такие как Галилей, Ньютон, Кулон и Фарадей, прямо заявили, что физические отношения пропорциональны между отношениями. В этой традиции отношения рассматривались как относящиеся к категории отношений. Поскольку классическое определение измерения основывается на концепции соотношения, оно больше соответствует истокам количественных наук, чем репрезентативная теория.Однако в определенный период истории числа использовались для обозначения соотношений и линий, и со временем стало обычным явлением интерпретировать символы в физических уравнениях как числа. Алгебра возникла как сокращенное обозначение пропорциональности между соотношениями. Эти и другие разработки проложили путь к появлению репрезентативного взгляда на измерение.
Компактная форма записи использовалась для того, чтобы показать параллель между вдохновленной греками традицией и современной алгеброй. Эта параллель, по-видимому, является причиной того, что классический взгляд на измерение продолжает существовать наряду с репрезентативным взглядом в физических науках.Однако в социальных науках преобладают репрезентативные определения. Вероятной причиной этого является неспособность создать основу для измерения, которая напрямую связана с его происхождением в физической науке.
Целью измерения, понимаемой в свете истоков физико-математики, является установление того, что величины находятся в определенном соотношении друг с другом. К этой цели можно подойти, сочетая прямые и косвенные измерения. Если прибегать к чему-то вроде косвенного измерения, основная задача социальных наук состоит в том, чтобы установить четкую основу для прямого измерения.Более непосредственный способ приблизиться к измерению в социальных науках — это продвинуть наше понимание того, как люди воспринимают соотношения и пропорциональности между ними и функционально реагируют на них.
Заявление о конфликте интересов
Автор заявляет, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Список литературы
- Берка К. (1983).Измерение: его концепции, теории и проблемы. Бостонская серия по философии науки. Голландия: Reidel Publishing Company, 72 [Google Scholar]
- Берманини М., Янг Т. Л., Проффитт Д. Р. (1998). Восприятие относительного размера на расстоянии лучше всего на уровне глаз. Восприятие. Психофизика. 60, 673–68210.3758 / BF03206054 [PubMed] [CrossRef] [Google Scholar]
- Международное бюро Poids et Mesures (BIPM) (2006). Международная система единиц (СИ), 8-е изд. Париж: Organization Intergouvernementale de la Convention du Mètre [Google Scholar]
- Campbell N.Р. (1928). Изложение принципов измерения и расчета. Лондон: Лонгманс, Грин [Google Scholar]
- Купер Г., Хамфри С. М. (2012). Онтологическое различие между единицами и сущностями. Синтез 187, 393–40110.1007 / s11229-010-9832-1 [CrossRef] [Google Scholar]
- de Boer J. (1994/95). Об истории количественного исчисления и международной системы. Метрология 31, 405–42910.1088 / 0026-1394 / 31/6/001 [CrossRef] [Google Scholar]
- Diez J. A. (1997). Сто лет цифр.Историческое введение в теорию измерений 1887–1990 гг. Stud. Hist. Филос. Sci. 28, 167–18510.1016 / S0039-3681 (96) 00014-3 [CrossRef] [Google Scholar]
- Emerson W. H. (2004). Об алгебре величин и их единиц. Метрология 45, 134–13810.1088 / 0026-1394 / 45/2/002 [CrossRef] [Google Scholar]
- Эмерсон У. Х. (2008). О количественном исчислении и единицах измерения. Метрология 45, 134–13810.1088 / 0026-1394 / 45/2/002 [CrossRef] [Google Scholar]
- Ferguson A., Myers C.С., Бартлетт Р. Дж., Банистер Х., Бартлетт Ф. К., Браун В. и др. (1940). Количественные оценки сенсорных событий: заключительный отчет комитета, назначенного для рассмотрения и составления отчета о возможности количественных оценок сенсорных событий. Adv. Sci. 1, 331–349 [Google Scholar]
- Галилео Г. (1638). «Диалоги о двух новых науках Галилео Галилея», Перевод с итальянского и латинского на английский Х. Крю и А. де Сальвио. С введением Антонио Фаваро (Нью-Йорк: Макмиллан;), 1914 [Google Scholar]
- Гибсон Дж.Дж. (1986). Экологический подход к визуальному восприятию. Хиллсдейл, Нью-Джерси: Эрлбаум; (Оригинальная работа опубликована в 1979 г.). [Google Scholar]
- Grattan-Guinness I. (1996). Числа, величины, соотношения и пропорции в элементах Евклида: как он с ними справился? Hist. Математика. 23, 355–37510.1006 / hmat.1996.0038 [CrossRef] [Google Scholar]
- Хебра А. Дж. (2010). Все об инструментах: от колесиков до атомных часов. Нью-Йорк: Springer Wien New York [Google Scholar]
- Humphry S.М. (2011а). Роль единицы в физике и психометрии. Измерение (Махва Н. Дж.) 9, 1–24 [Google Scholar]
- Хамфри С. М. (2011b). Роль единицы в физике и психометрии: Rejoinder. Измерение (Махва Н. Дж.) 9, 1–24 [Google Scholar]
- Джонстон С. Ф. (2001). История измерения света и цвета: наука в тени. Бристоль: Издательский институт физики [Google Scholar]
- Кранц Д. Х. (1972). Структуры измерения и психологические законы.Наука 175, 1427–143510.1126 / science.175.4029.1427 [PubMed] [CrossRef] [Google Scholar]
- Кранц Д. Х., Люс Р. Д., Суппес П., Тверски А. (1971). Основы измерения, Vol. I: Аддитивные и полиномиальные представления. Нью-Йорк: Academic Press [Google Scholar]
- Кибург Х. Э. (1984). Теория и измерения. Кембридж: Издательство Кембриджского университета [Google Scholar]
- Кибург Х. Э. (1996). Количества, величины и числа. Филос. Sci. 64, 377–41010.1086 / 392558 [CrossRef] [Google Scholar]
- Lord F.М., Новик М. Р. (1968). Статистические теории оценок умственных способностей. Ридинг, Массачусетс: Аддисон-Уэсли [Google Scholar]
- Люс Р. Д., Суппес П. (2002). «Теория репрезентативного измерения» в Руководстве Стивенса по экспериментальной психологии, том. 4 Методология экспериментальной психологии, 3-е изд., Ред. Пашлер Х., Уикстед Дж. (Нью-Йорк: Уайли;), 1–41 [Google Scholar]
- Мэсси Б. С. (1971). Единицы, размерный анализ и физическое подобие. Лондон: компания Van Nostrand Reinhold [Google Scholar]
- Maxwell J.С. (1876 г.). Материя и движение. Нью-Йорк: Довер, 1952 [Google Scholar]
- Мичелл Дж. (1993). Истоки репрезентативной теории измерения: Гельмгольц, Гельдер и Рассел. Stud. Hist. Филос. Sci. 24, 185–20610.1016 / 0039-3681 (93) -L [CrossRef] [Google Scholar]
- Michell J. (1997). Количественная наука и определение измерения в психологии. Br. J. Psychol. 88, 355–38310.1111 / j.2044-8295.1997.tb02641.x [CrossRef] [Google Scholar]
- Мичелл Дж.(1999). Измерение в психологии. Кембридж: Издательство Кембриджского университета [Google Scholar]
- Mills I. (2010). Проект главы 2 брошюры SI, после переопределения базовых единиц. CCU; Доступно по адресу: http://www.bipm.org/utils/en/pdf/si_brochure_draft_ch3.pdf [по состоянию на 21 ноября 2012 г.]. [Google Scholar]
- Ньютон И. (1846). Принципы Ньютона: математические принципы естественной философии / сэра Исаака Ньютона; Перевод на английский Эндрю Мотт. Нью-Йорк: Дэниел Ади [Google Scholar]
- Roche J.(1998). Математика измерения: критическая история. Лондон: Атлон Пресс [Google Scholar]
- Рукс П., Уилсон Дж. (2000). Восприятие: теория, развитие и организация. Лондон: Рутледж [Google Scholar]
- Рассел Б. (1903). Основы математики. Кембридж: Издательство Кембриджского университета [Google Scholar]
- Сэвидж К. У. (1970). Измерение ощущений: критика перцептивной психофизики. Лондон: Калифорнийский университет Press [Google Scholar]
- Седжвик Х.(1973). Видимый горизонт: потенциальный источник визуальной информации для восприятия размера и расстояния. Дисс. Abstr. Int. 34, 1301–1302B [Университетские микрофильмы № 73-22530]. [Google Scholar]
- Шерри Д. (2011). Термоскопы, термометры и основы измерений. Stud. Hist. Филос. Sci. 42, 509–52410.1016 / j.shpsa.2011.07.001 [CrossRef] [Google Scholar]
- Силсби Ф. Б. (1962). Системы электроустановок. Res. Natl. Бур. Стоять. П. C 2, 137–17710.6028 / jres.066C.014 [CrossRef] [Google Scholar]
- Стивенс С. С. (1946). К теории шкал измерения. Наука 103, 667–68010.1126 / science.103.2684.677 [PubMed] [CrossRef] [Google Scholar]
- Уоллис Дж. (1670). Mechanica Sive de Motu. Лондон: Typis Guilielmi Godbid; Импенсис Мосис Питт [Google Scholar]
- Уоллис Дж. (1685). Трактат по алгебре как исторической, так и практической. Лондон: Джон Плейфорд для Ричарда Дэвиса [Google Scholar]
Math Curriculum
ЗАДАЧА МИССИИ Миссия математического факультета состоит в том, чтобы гарантировать, что все учащиеся получат прочную основу в математике, которая позволит им рассуждать с помощью чисел, решать задачи, измерять в различных единицах, а также понимать и применять алгебраические и геометрические концепции.Мы предоставим учащимся математические навыки, необходимые для карьерного роста и возможностей послешкольного образования в обществе и экономике 21 века.
Математическая программа в SVRCS предназначена для развития знаний, навыков, понимания и компетенций в соответствии с Основными стандартами PA для математического содержания и практики:
СТАНДАРТЫ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ
2.1 Числа и операции
A) Подсчет и мощность
B) Числа и операции в десятичной системе счисления
C) Числа и операции — дроби
D) Соотношения и пропорциональные отношения
E) Система счисления
F) Число и количество
2.2 Алгебраические концепции
A) Операции и алгебраическое мышление
B) Выражения и уравнения
C) Функции
D) Алгебра
2.3 Геометрия
A) Геометрия
2.4 Измерение, данные и вероятность
) Измерения и данные B) Статистика и вероятность
СТАНДАРТЫ МАТЕМАТИЧЕСКОЙ ПРАКТИКИ
Разбирайтесь в проблемах и настойчиво их решайте.
Размышляйте абстрактно и количественно.
Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
Модель с математикой.
Стратегически используйте соответствующие инструменты.
Будьте внимательны.
Ищите и используйте структуру.
Ищите и осознавайте закономерность в повторяющихся рассуждениях.
ПРОГРАММА ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ
SVRCS использует четвертое издание Everyday Math для доставки математического содержания, соответствующего основному уровню, учащимся K-5. Эта программа предоставляет соответствующий контент на уровне класса для развития знаний и компетенций, соответствующих ожиданиям PA Core Standard.Учебная программа обеспечивает основы в смысле числа, математических операций, пропорций, дробей, шаблонов, геометрии, измерения, данных и статистики, чтобы они могли успешно перейти к более высоким, более абстрактным дисциплинам в средней и старшей школе.
ПРОГРАММА МАТЕМАТИКИ СРЕДНЕГО УРОВНЯ
SVRCS использует Glencoe Math © 2015 для предоставления основного контента для 6 класса, предалгебры, алгебры 1 и алгебры 2. Учебная программа приближает учащихся к более высоким уровням математики, которые являются ключ к высшему образованию и карьере в 21 веке.
МАТЕМАТИЧЕСКАЯ ПРОГРАММА ВЫСШЕЙ ШКОЛЫ
SVRCS продолжает работу с Glencoe Math, чтобы предоставлять согласованный контент по алгебре 2, геометрии и тригонометрии / предварительному исчислению. Исчисление предлагается с использованием Краткого исчисления: прикладной подход от Cengage Learning. Эти курсы дают студентам углубленные знания и понимание высших дисциплин математики.
SVRCS Mathematics Sequence
GRADE НОМЕР КУРСА КУРСА
Детский сад, математика, класс K 50010
1-й класс, математика, 1-й класс 50110
5 класс по математике 5 класс 50510
6 класс по математике 6 класс 50610
7 класс по математике 7 или ускоренный курс d Математика 7 17002 или 17010
8-й класс Математика 8 или алгебра 8 17001 или 17003
9-й класс Алгебра I или трапецеидальная алгебра 17005 или 17905
Геометрия 10-го класса или трапецеидальная алгебра 17025 или 17905
11-й класс Алгебра 2-го класса или 17008
12-й класс Тригонометрия, или исчисление, или математика 12 17008, или 17009, или 17012
Измерение в науке (Стэнфордская энциклопедия философии)
Современные философские дискуссии об измерении — начиная с с конца девятнадцатого века до наших дней — можно разделить по нескольким направлениям обучения.Эти пряди отражают разные взгляды на природу измерения и условия, которые делают измерение возможно и надежно. Основные нити математические теории измерения, операционализм, конвенционализм, реализм, теоретико-информационные счета и счета на основе моделей. Эти пряди стипендий, по большей части, не составляют непосредственно конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение различные и дополнительные аспекты измерения. Ниже приводится очень приблизительный обзор этих перспектив:
- Математические теории измерение рассматривать измерение как отображение качественного эмпирические отношения к отношениям между числами (или другими математическими сущностей).
- Операционалисты и конвенционалисты просмотр измерение как набор операций, формирующих смысл и / или регулировать использование количественного термина.
- Реалисты рассматривают измерение как оценку независимые от разума свойства и / или отношения.
- Теоретико-информационные счета Просмотр измерений как сбор и интерпретация информации о система.
- Счета на основе модели рассматривают измерение как согласованное присвоение значений параметрам в теоретической и / или статистическая модель процесса.
Эти точки зрения в принципе согласуются друг с другом. Пока математические теории измерения имеют дело с математическими основы измерительных шкал, операционализм и конвенционализм в первую очередь связаны с семантикой количественных терминов, реализмом занимается метафизическим статусом измеримых величин, теоретико-информационные и модельные счета связаны с эпистемологические аспекты измерения. Тем не менее, предмет домен не так аккуратно разделен, как следует из приведенного выше списка.вопросы касательно метафизики, эпистемологии, семантики и математики основы измерения взаимосвязаны и часто опираются на одну Другой. Отсюда, например, операционалисты и конвенционалисты часто придерживался антиреалистических взглядов, а сторонники модельного счета выступили против преобладающей эмпирической интерпретации математических теорий измерения. Эти тонкости станут ясно в следующем обсуждении.
Список направлений стипендии не является исчерпывающим и неисключительным. исчерпывающий.Он отражает историческую траекторию философского обсуждение до сих пор, а не какое-либо принципиальное различие между разные уровни анализа измерений. Некоторые философские труды по замерам относятся к более чем одной нити, в то время как многие другие работы тоже не подходят прямо. Это особенно актуально, поскольку начале 2000-х, когда измерение вернулось на первый план философская дискуссия после нескольких десятилетий относительного пренебрежения. Эту недавнюю стипендию иногда называют « эпистемология измерения », и включает в себя богатый набор работ которые еще нельзя разделить на отдельные школы мысли.В последний раздел этой записи будет посвящен обзору некоторых из эти события.
Хотя философия измерения сформировалась как отдельная область исследование только во второй половине девятнадцатого века, фундаментальные концепции измерения, такие как величина и количество обсуждаются с древних времен. Согласно Евклиду Элементы , величина — например, линия, поверхность или твердый — измеряет другое, когда последнее является целым кратным первое (Книга V, опр.1 и 2). Две величины имеют общую измерять, когда они оба целые кратные некоторой величины, и несоизмеримым в противном случае (Книга X, определение 1). Открытие несоизмеримые величины позволили Евклиду и его современникам развивать понятие отношения величин. Соотношения могут быть либо рациональным, либо иррациональным, поэтому понятие отношения более общий, чем мера (Michell 2003, 2004a; Grattan-Guinness 1996).
Аристотель различал количество и качество.Примеры количества — это числа, линии, поверхности, тела, время и место, а примерами качеств являются справедливость, здоровье, горячность и бледность ( Категории §6 и §8). В соответствии с Аристотеля, количества допускают равенство и неравенство, но не допускают градусов, так как «одна вещь не более четырех футов, чем другая» (Там же 6.6a19). Качества, наоборот, не допускают равенства или неравенство, но допускают степени, «потому что одно называется более бледный или менее бледный, чем другой »(там же 8.10b26).Аристотель не уточняет, являются ли степени таких качеств, как бледность соответствуют различным качествам или одинаковому качеству, бледность, была способна к разной интенсивности. Эта тема была на центр продолжающихся дебатов в тринадцатом и четырнадцатом веках (Юнг 2011). Дунс Скот поддержал «теорию сложения», согласно которому изменение степени качества может быть объясняется сложением или вычитанием меньших степеней этого качество (2011: 553). Позднее эта теория была уточнена Николь Орем, которые использовали геометрические фигуры для представления изменений интенсивности такие качества, как скорость (Clagett 1968; Sylla 1971).Oresme’s геометрические представления установили подмножество качеств, которые поддаются количественной обработке, что ставит под сомнение строгая аристотелевская дихотомия количества и качества. Эти развития позволили сформулировать количественные законы движение в течение шестнадцатого и семнадцатого веков (Грант 1996).
Концепция качественной интенсивности была развита Лейбницем. и Канта. «Принцип непрерывности» Лейбница заявил что все естественные изменения происходят постепенно.Лейбниц утверждал, что этот принцип применим не только к изменениям в расширенных величинах, таких как длины и продолжительности, но также и интенсивности репрезентативных состояния сознания, такие как звуки (Jorgensen 2009; Diehl 2012). Считается, что Кант опирался на принцип Лейбница преемственности, чтобы сформулировать его различие между экстенсивным и интенсивные величины. Согласно Канту, экстенсивные величины те, «в которых представление частей делает возможным представление целого »(1787: A162 / B203).Пример это длина: линия может быть мысленно представлена только последовательным синтез, в котором части линии соединяются, образуя целое. Для Канта возможность такого синтеза обосновывалась в формах интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или цвета, также бывают в непрерывной степени, но их восприятие требует место в мгновение ока, а не через последовательный синтез части. Степени интенсивных величин «могут быть только представлен через приближение к отрицанию »(1787: A 168 / B210), то есть воображая их постепенное уменьшение до тех пор, пока полное отсутствие.
Научные разработки девятнадцатого века бросили вызов различие между экстенсивными и интенсивными величинами. Термодинамика и волновая оптика показала, что разница в температуре и оттенке соответствовали различиям в пространственно-временных величинах, таких как скорость и длина волны. Электрические величины, такие как сопротивление и было показано, что проводимость может складываться и делиться, несмотря на не является обширным в кантовском смысле, т.е. не синтезируется из пространственные или временные части.Более того, ранние эксперименты в психофизики предположили, что интенсивности ощущений, такие как яркость и громкость можно представить как сумму «всего заметные различия »между стимулами и, следовательно, могут быть мыслится как состоящие из частей (см. Раздел 3.3). Эти результаты, наряду с достижениями в аксиоматизации ветвей математики, мотивировала некоторых из ведущих ученых конца девятнадцатого века, чтобы попытаться прояснить математические основы измерения (Максвелл 1873; фон Крис 1882; Гельмгольц 1887; Мах 1896; Poincaré 1898; Hölder 1901; для исторических обзоров см. Darrigol 2003; Michell 1993, 2003; Канту и Шлаудт 2013; Бьяджоли 2016: гл.4, 2018). Эти работы сегодня рассматриваются как предшественники научной стипендии, известной как «измерение теория ».
Математические теории измерения (часто называемые собирательно как «теория измерения») относятся к условиям при какие отношения между числами (и другими математическими объектами) могут быть используется для выражения отношений между объекты. [2] Чтобы понять необходимость математических теорий измерения, примите во внимание тот факт, что отношения, выставленные числа, такие как равенство, сумма, разница и соотношение, не всегда соответствуют отношениям между объектами, измеряемыми этими числа.Например, 60 — это дважды 30, но можно ошибиться в думая, что объект, измеренный при 60 градусах Цельсия, в два раза горячее как объект при 30 градусах Цельсия. Это потому, что нулевая точка шкала Цельсия произвольна и не соответствует отсутствию из температура. [3] Точно так же числовые интервалы не всегда несут эмпирические данные. Информация. Когда испытуемых просят оценить по шкале от 1 до 7 насколько сильно они согласны с данным утверждением, прима нет facie причина полагать, что интервалы между 5 и 6 и от 6 до 7 соответствует равному приросту силы мнения.Чтобы предоставить третий пример, равенство между числами является транзитивным [если (a = b & b = c), затем a = c], но эмпирические сравнения физических величины обнаруживают лишь приблизительное равенство, которое не является переходным связь. Эти примеры показывают, что не все математические отношения между числами, используемыми в измерениях, эмпирически значительный, и что различные виды шкалы измерения передают различные виды эмпирически значимой информации.
Изучение шкал измерений и эмпирической информации в них Передача — это основная задача математических теорий измерения.В его основополагающее эссе 1887 года «Подсчет и измерение» Германа фон Гельмгольц сформулировал ключевой вопрос теории измерений как следует:
[W] hat — это объективный смысл выражения через деноминацию нумерует отношения реальных объектов как величины, а под каким условия мы можем это сделать? (1887: 4)
Вообще говоря, теория измерений направлена на: (i) выявление предположения, лежащие в основе использования различных математических структур для описывать аспекты эмпирического мира и (ii) извлекать уроки из адекватность и пределы использования этих математических структур для описание аспектов эмпирического мира.По следам Отто Гёльдера (1901), теоретики измерения часто достигают этих целей через формальные доказательства, с предположениями в (i), служащими аксиомами и уроками в (ii) следующее как теоремы. Ключевое понимание теории измерений: что эмпирически значимые аспекты данной математической структура — это те, которые отражают соответствующие отношения между объекты измерения. Например, отношение «больше чем »среди чисел является эмпирически значимым для измерения длина, поскольку она отражает отношение «длиннее, чем» среди объектов.Это отражение или отображение отношений между объекты и математические объекты составляют шкалу измерения. В виде будет пояснено ниже, шкалы измерений обычно понимаются как изоморфизмы или гомоморфизмы между объектами и математическими сущности.
Помимо этих общих целей и заявлений, теория измерений — это весьма неоднородный корпус ученых. В него входят произведения, охватывающие с конца девятнадцатого века до наших дней и поддерживают широкую множество взглядов на онтологию, эпистемологию и семантику измерение.Два основных различия между математическими теориями Особого упоминания заслуживают измерения. Первый касается природа relata , или «объекты», чьи номера отношений должны быть зеркальными. Эти relata могут быть понимается как минимум четырьмя разными способами: как конкретный человек объекты, как качественные наблюдения за конкретными отдельными объектами, как абстрактные представления отдельных объектов или как универсальные свойства объектов. Какая интерпретация будет принята, зависит от большая часть авторского метафизического и эпистемологического обязательства.Этот вопрос будет особенно актуален для обсуждения. реалистичных счетов измерения (Раздел 5). Во-вторых, разные теоретики измерения занимают разные позиции. на вид эмпирических данных, необходимых для установления сопоставления между объектами и числами. В результате измерения теоретики расходятся во мнениях относительно необходимых условий для установление измеримости атрибутов, в частности, о измеримы ли психологические атрибуты. Споры о измеримость оказались очень плодотворными для развития теории измерений, и в следующих подразделах будут представлены некоторые этих дебатов и разработанных в них центральных концепций.
3.1 Фундаментальные и производные измерения
В конце девятнадцатого и начале двадцатого веков несколько Были предприняты попытки дать универсальное определение измерения. Хотя способы измерения различались, единодушное мнение заключалось в том, что Измерение — это метод присвоения чисел звездной величине. Например, Гельмгольц (1887: 17) определил измерение как процедуру по которому можно найти номинальное число, которое выражает значение величина, где «номинальное число» — это число вместе с агрегатом, эл.г., 5 метров, а величина — качество объекты, которые можно упорядочить от меньшего к большему, например, длина. Бертран Рассел аналогичным образом заявил, что измерение равно
.любой метод, с помощью которого устанавливается уникальное взаимное соответствие. установленный между всеми или некоторыми величинами вида и всеми или некоторые числа, целые, рациональные или действительные. (1903: 176)
Норман Кэмпбелл определил измерение просто как «процесс присвоение чисел для представления качеств », где качество — это свойство, допускающее непроизвольный порядок (1920: 267).
Определение измерения как числового присвоения поднимает вопрос: какие задания подходят и при каких условиях? Рано теоретики измерения, такие как Гельмгольц (1887 г.), Гельдер (1901 г.) и Кэмпбелл (1920) утверждал, что числа подходят для выражения величины, поскольку алгебраические операции между числами отражают эмпирические отношения между величинами. Например, качественный отношение «длиннее чем» среди жестких стержней (примерно) переходные и асимметричные, и в этом отношении разделяет структурные функции с отношением «больше чем» среди чисел.Кроме того, сквозное соединение жестких стержней разделяет конструктивные функции, такие как ассоциативность и коммутативность, с математическая операция сложения. Аналогичная ситуация имеет место для измерение веса с помощью равноблочных весов. Здесь отклонение оружие обеспечивает упорядочивание весов и наложение гирь на одна кастрюля представляет собой соединение.
Ранние теоретики измерения сформулировали аксиомы, описывающие эти качественных эмпирических структур и использовал эти аксиомы для доказательства теоремы об адекватности приписывания чисел величинам, которые выставлять такие конструкции.В частности, они доказали, что заказывая и конкатенации вместе достаточно для построения аддитивное числовое представление соответствующих величин. Аддитивное представление — это такое представление, в котором сложение эмпирически осмысленный, а значит, и умножение, деление и т. д. Кэмпбелл так называемые процедуры измерения, которые удовлетворяют условиям аддитивность «фундаментальная», потому что они не включают измерение любой другой величины (1920: 277). Виды величин для которого была применена фундаментальная процедура измерения. найдено — например, длина, площадь, объем, продолжительность, вес и электрическое сопротивление — Кэмпбелл назвал «фундаментальным величины ».Отличительной чертой таких масштабов является то, что это их можно сгенерировать, объединив стандартную последовательность равные единицы, как в примере с серией одинаковых отметок на линейка.
Хотя они считали аддитивность отличительной чертой измерения, большинство ранние теоретики измерения признали, что аддитивность не необходимо для измерения. Существуют и другие величины, допускающие упорядочение. от меньшего к большему, но чьи соотношения и / или различия не могут в настоящее время быть определенными, кроме как через их отношения с другими, фундаментально измеримые величины.Примеры: температура, которая может быть измерен путем определения объема ртутного столба, и плотность, которая может быть измерена как отношение массы к объему. Такой косвенное определение стало называться «производным» измерения и соответствующие величины «получены величины »(Кэмпбелл 1920: 275–77).
На первый взгляд, различие между фундаментальным и производным измерение может показаться напоминанием о различии между обширными и интенсивные величины, и действительно фундаментальное измерение иногда называют «обширным».Тем не менее важно отметить, что эти два различия основаны на существенно разных критерии измеримости. Как обсуждалось в Раздел 2, экстенсивно-интенсивное различие, сосредоточенное на внутреннем структура рассматриваемой величины, т. е. является ли она состоит из пространственно-временных частей. Основополагающий различие, напротив, сосредотачивается на свойствах измерения операции . Принципиально измеримая величина — это величина в котором была найдена фундаментальная измерительная операция.Следовательно, фундаментальность не является внутренним свойством величина: полученная величина может стать фундаментальной с открытие новых операций по его измерению. Более того, в фундаментальное измерение, числовое присвоение не должно отражать структура пространственно-временной части. Электрическое сопротивление, для Например, можно принципиально измерить, подключив резисторы в серия (Кэмпбелл 1920: 293). Это считается фундаментальным операция измерения, потому что она имеет общую структуру с числовым кроме того, даже если объекты с одинаковым сопротивлением обычно не равны по размеру.
Различие между фундаментальным и производным измерением было отредактировано последующими авторами. Брайан Эллис (1966: гл. 5–8) различают три типа измерения: фундаментальный, ассоциативное и производное. Фундаментальные измерения требуют заказа и операции конкатенации, удовлетворяющие тем же условиям, указанным в Кэмпбелл. Процедуры ассоциативных измерений основаны на корреляция двух отношений порядка, например, корреляция между объемом ртутного столба и его температурой.Полученный процедуры измерения заключаются в определении значения константа в физическом законе. Константа может быть локальной, как в определение удельной плотности воды по массе и объему, или универсальный, как в определении ньютоновского гравитационного постоянная от силы, массы и расстояния. Генри Кибург (1984: гл. 5–7) предложил несколько иное тройное различие между прямое, косвенное и систематическое измерение, которое не полностью перекрываются с тем из Эллис. [4] Более радикальный пересмотр различия между фундаментальным и производное измерение было предложено Р. Дунканом Люсом и Джоном Тьюки. (1964) в своей работе по совместному измерению, которая будет обсуждаться в Раздел 3.4.
3.2 Классификация весов
В предыдущем подразделе обсуждалась аксиоматизация эмпирических структуры, линия расследования, которая восходит к ранним дням теория измерений. Дополнительная информация в рамках измерения Теория касается классификации шкал измерений.В психофизик С.С.Стивенс (1946, 1951) выделил четыре виды шкал: именные, порядковые, интервальные и передаточные. Номинальные шкалы представлять объекты как принадлежащие к классам, не имеющим конкретных порядок, например, мужской и женский. Порядковые шкалы представляют порядок, но не дальнейшая алгебраическая структура. Например, минеральная шкала Мооса твердость представляет собой минералы с номерами от 1 (самый мягкий) до 10 (самый сложный), но нет никакого эмпирического значения равенства между интервалы или отношения тех числа. [5] Цельсия и Фаренгейта являются примерами интервальных шкал: они представляют равенство или неравенство между интервалами температуры, но не отношения температур, потому что их нулевые точки произвольны. Шкала Кельвина, напротив, представляет собой шкалу отношений, как и знакомые шкалы, отображающие массу в килограммах, длину в метрах и продолжительность в секундах. Позже Стивенс уточнил эту классификацию и различают линейные и логарифмические интервальные шкалы (1959: 31–34) и между шкалами отношений с натуральной единицей и без нее. (1959: 34).Шкалы соотношений с натуральными единицами измерения, например, используемые для подсчета дискретных объектов и представления вероятностей, были названы «абсолютными» шкалами.
Как отмечает Стивенс, типы гамм индивидуализируются по семействам трансформации, которые они могут претерпеть без потери эмпирических Информация. Эмпирические зависимости, представленные на шкалах отношений, для например, инвариантны относительно умножения на положительное число, например, умножение на 2,54 преобразует дюймы в сантиметры. Линейные интервальные шкалы допускают как умножение на положительное число и постоянный сдвиг, e.g., преобразование из Цельсия в Фаренгейт в соответствии с формулой ° C × 9/5 + 32 = ° F. Порядковые шкалы допускают любую функцию преобразования, пока она монотонно-возрастающие, а номинальные шкалы допускают любые взаимно однозначные подмена. Абсолютные шкалы не допускают никаких преобразований, кроме личность. Классификация весов Стивенса была позже обобщено Луи Наренсом (1981, 1985: гл. 2) и Люс и др. (1990: Гл. 20) с точки зрения однородности и уникальности соответствующих группы трансформации.
В то время как классификация шкал Стивенса встретила общие одобрение в научных и философских кругах, его шире последствия для теории измерений стали темой значительных дебаты. Особо оспаривались два вопроса. Во-первых, было ли операции классификации и упорядочивания заслуживают того, чтобы называться «Измерительные» операции и, соответственно, представление величин на номинальной и порядковой шкалах должно считать как измерение. Несколько физиков, в том числе Кэмпбелл, утверждали, что что операции классификации и упорядочивания не обеспечили достаточно богатая структура, чтобы гарантировать использование чисел, и, следовательно, не должны считаться измерительными операциями.Второй оспариваемый вопрос нужно ли было найти операцию конкатенации для величины прежде, чем это можно было фундаментально измерить по шкале отношений. Дебаты стал особенно горячим, когда снова разгорелся более длительный спор окружающая измеримость интенсивности ощущений. Это чтобы мы переходим к этой дискуссии.
3.3 Измеримость ощущений
Один из главных катализаторов развития математических теорий. измерения были продолжающимися дебатами об измеримости в психология.Эти дебаты часто восходят к работе Густава Фехнера. (1860) Элементы психофизики , в котором он описал метод измерения интенсивности ощущений. Метод Фехнера был основан на записи «едва заметных различия »между ощущениями, связанными с парами стимулы, например, два звука разной интенсивности. Эти различия считались равными приращениями интенсивности ощущения. В виде Фехнер показал, что при этом предположении устойчивая линейная зависимость между интенсивностью ощущений и логарифмом интенсивность стимула, отношение, которое стало известно как «Закон Фехнера» (Heidelberger 1993a: 203; Luce and Suppes 2004: 11–2).Этот закон, в свою очередь, предоставляет метод для косвенное измерение интенсивности ощущений путем измерения интенсивность стимула и, следовательно, утверждал Фехнер, обеспечивает обоснование измерения интенсивности ощущений на реальном числа.
Утверждения Фехнера об измеримости ощущений стал предметом серии дебатов, которые длились почти столетие. и оказался чрезвычайно плодотворным для философии измерения, с участием таких ключевых фигур, как Мах, Гельмгольц, Кэмпбелл и Стивенс (Heidelberger 1993a: Ch.6 и 1993b; Мичелл 1999: гл. 6). Те возражая против измеримости ощущений, например, Кэмпбелл, подчеркнул необходимость эмпирической операции конкатенации для фундаментальное измерение. Поскольку интенсивности ощущений не могут быть соединены друг с другом способом, обеспечиваемым длинами и веса, фундаментального измерения ощущений быть не может. интенсивность. Более того, Кэмпбелл утверждал, что ни одна из психофизических обнаруженные к настоящему времени закономерности достаточно универсальны, чтобы их можно было считать как законы в том смысле, который требуется для производных измерений (Кэмпбелл в Ferguson et al.1940: 347). Все, что показали психофизики, что интенсивности ощущений можно последовательно упорядочить, но упорядочить сам по себе еще не гарантирует использование числовых соотношений, таких как суммы и соотношения для выражения эмпирических результатов.
Центральным оппонентом Кэмпбелла в этой дискуссии был Стивенс, чей Различие между типами шкалы измерений обсуждалось выше. Стивенс определил измерение как «присвоение цифр объекты или события в соответствии с правилами »(1951: 1) и утверждал, что любое последовательное и неслучайное назначение считается измерением в в широком смысле (1975: 47).В полезных случаях научного исследования Стивенс заявлено, измерение может быть истолковано несколько более узко как числовое присвоение, основанное на результатах сопоставления операции, такие как связь температуры с объемом ртути или соответствие ощущений друг другу. Стивенс выступал против считают, что отношения между числами должны отражать качественные эмпирические структур, утверждая вместо этого, что шкалы измерений должны быть рассматриваются как произвольные формальные схемы и принимаются в соответствии с их полезность для описания эмпирических данных.Например, приняв шкала соотношения для измерения ощущений громкости, громкости и плотность звуков приводит к формулировке простого линейного соотношения среди отчетов подопытных: громкость = громкость × плотность (1975: 57–8). Такое присвоение чисел ощущениям считается измерением, потому что оно непротиворечиво и неслучайно, потому что он основан на операциях согласования, выполняемых экспериментальными субъектов, и потому что он фиксирует закономерности в экспериментальных полученные результаты. По словам Стивенса, эти условия совпадают. достаточно, чтобы оправдать использование шкалы отношений для измерения ощущения, несмотря на то, что «ощущения не могут быть разделены на составные части или уложены встык, как измерения палки »(1975: 38; см. также Hempel 1952: 68–9).
3.4 Репрезентативная теория измерения
В середине двадцатого века два основных направления исследований в теория измерения, посвященная эмпирическим условиям количественная оценка и классификация шкал, сошлись в работах Патрика Суппеса (1951; Скотт и Суппс, 1958); для исторических обзоров см. Savage and Ehrlich 1992; Diez 1997a, b). Работа Суппеса заложила основу репрезентативной теории Измерение (RTM), которое остается наиболее влиятельным математическим теория измерений на сегодняшний день (Krantz et al.1971; Suppes et al. 1989; Luce et al. 1990). RTM определяет измерение как построение отображения из эмпирических реляционных структур в числовые реляционные структуры (Krantz et al. 1971: 9). Эмпирический реляционный конструкция состоит из набора эмпирических объектов (например, жестких стержней) наряду с определенными качественными отношениями между ними (например, упорядочивание, конкатенация), а числовая реляционная структура состоит из набор чисел (например, действительные числа) и конкретных математических отношения между ними (e.g., «равно или больше», добавление). Проще говоря, шкала измерения — это соотношение «многие к одному». отображение — гомоморфизм — от эмпирического к числовому реляционная структура, а измерение — это построение напольные весы. [6] RTM очень подробно описывает предположения, лежащие в основе построение различных типов измерительных шкал. Каждый тип масштаба связано с набором предположений о качественном отношения, возникающие между объектами, представленными на этом типе шкалы.Из этих предположений или аксиом авторы RTM выводят репрезентативная адекватность каждого типа шкалы, а также семейства допустимые преобразования, делающие этот тип шкалы уникальным. В этом способ RTM обеспечивает концептуальную связь между эмпирической базой измерение и типология напольные весы. [7]
Что касается измеримости, Репрезентативная теория принимает средний путь между либеральным подходом Стивенса и Строгий упор на операции конкатенации, поддерживаемый Кэмпбеллом.Нравиться Кэмпбелл, RTM признает, что правила количественной оценки должны быть основаны на известные эмпирические структуры и не должны выбираться произвольно, чтобы соответствовать данные. Однако RTM отвергает идею о том, что аддитивные шкалы адекватно только тогда, когда доступны операции конкатенации (Luce и Суппес 2004: 15). Вместо этого RTM отстаивает существование фундаментальных операции измерения, не связанные с конкатенацией. Центральный пример этого типа операции известен как «аддитивный конджойнт измерение »(Люс и Тьюки, 1964; Кранц и др.1971: 17–21 и гл. 6–7). Здесь измерения двух и более различные типы атрибутов, такие как температура и давление газа, получаются путем наблюдения за их совместным действием, таким как объем газа. Люси и Тьюки показали это, установив определенные качественные отношения между объемами при изменении температуры и давления, можно построить аддитивные представления температуры и давления, без использования каких-либо предшествующих методов объем измерения. Подобная процедура может быть обобщена на любой случай. соответствующим образом связанный триплет атрибутов, таких как громкость, интенсивность и частота чистых тонов или предпочтение награды, размер и задержка в получении (Люс и Суппес 2004: 17).В открытие аддитивного совместного измерения привело авторов RTM к разделить фундаментальные измерения на два вида: традиционные измерения процедуры, основанные на операциях конкатенации, которые они назвали «Обширное измерение», а также совместное или «Неэкстенсивное» фундаментальное измерение. Под этим новым концепция фундаментальности, все традиционные физические атрибуты можно измерить фундаментально, как и многие психологические атрибуты (Кранц и др. 1971: 502–3).
Выше мы видели, что математические теории измерения в первую очередь связаны с математическими свойствами измерительных шкал и условия их применения.Родственная, но отличная нить стипендия касается значения и использования количественных терминов. Научный теории и модели обычно выражаются в терминах количественных отношения между параметрами, имеющими имена, такие как «Продолжительность», «уровень безработицы» и «Интроверсия». Реалист по поводу одного из этих терминов мог бы утверждают, что это относится к набору свойств или отношений, которые существуют независимо от измерения. Операционалист или конвенционалист будет утверждать, что способ применения таких количественных терминов к бетону детали зависят от нетривиального выбора, сделанного людьми, и конкретно о вариантах, которые связаны с тем, как соответствующие количество измеряется.Обратите внимание, что в соответствии с этой широкой концепцией реализм совместим с операционализмом и конвенционализмом. То есть это возможно, что выбор метода измерения регулирует использование количество-член и что, учитывая правильный выбор , этот термин преуспевает в ссылке на независимое от разума свойство или отношение. Тем не менее многие операционалисты и конвенционалисты приняли более сильные взгляды, согласно которым нет фактов по делу как какая из нескольких и нетривиально разных операций верна для применения данного количественного термина.Эти более сильные варианты несовместим с реализмом об измерениях. Этот раздел будет посвященный операционализму и конвенционализму, а следующий реализм об измерении.
Операционализм (или «операционизм») в отношении измерения — это точка зрения, что значение количественных понятий определяется набор операций, используемых для их измерения. Самое сильное выражение операционализма появляется в ранних работах Перси Бриджмена (1927), кто утверждал, что
под любым понятием мы понимаем не что иное, как набор операций; в понятие является синонимом соответствующего набора операций.(1927: 5)
Например, длина будет определяться как результат операции сцепления жестких стержней. Согласно этой крайней версии операционализм, разные операции измеряют разные величины. Длина измеряется линейками и синхронизацией электромагнитных импульсов. строго говоря, следует различать на два различных количественные понятия, помеченные как «длина-1» и «Длина-2» соответственно. Этот вывод привел Бриджмена к утверждают, что принятые в настоящее время количественные концепции имеют «Суставы», в которых различные операции пересекаются в своих область применения.Он предостерег от догматической веры в единство количественных концепций в этих «суставах», вместо этого это единство проверяется экспериментами всякий раз, когда применение количественное понятие должно быть расширено в новую область. Тем не менее, Бриджмен признал, что до тех пор, пока результаты различных операций согласны в пределах экспериментальной ошибки, прагматически оправдано маркировать соответствующие величины с таким же названием (1927: 16). [8]
Операционализм стал влиятельным в психологии, где он был хорошо принят бихевиористами, такими как Эдвин Боринг (1945) и Б.Ф. Скиннер (1945). В самом деле, Скиннер утверждал, что бихевиоризм «Не более чем тщательный оперативный анализ традиционные менталистские концепции »(1945: 271). Стивенс, который был Ученик Скуки был одним из главных пропагандистов операционализма в психологии, и утверждал, что психологические концепции имеют эмпирические имея в виду, только если они означают определенные и конкретные операции (1935: 517; см. также Isaac 2017). Идея о том, что концепции определяются операции измерения согласуются с либеральными взглядами Стивенса по измеримости, о которых говорилось выше (Раздел 3.3). Поскольку присвоение номеров объектам выполняется в в соответствии с конкретными и последовательными правилами, Стивенс утверждал, что такое присвоение имеет эмпирическое значение и не должно удовлетворять никаким дополнительные ограничения. Тем не менее Стивенс, вероятно, не принял антиреалистический взгляд на психологические атрибуты. Вместо этого там веские причины думать, что он понимал операционализм как методологический подход, ценный в той мере, в какой он позволили психологам обосновать выводы, которые они сделали из эксперименты (Feest 2005).Например, Стивенс не лечил операционные определения как априори , но как поддающиеся улучшение в свете эмпирических открытий, подразумевая, что он взял психологические атрибуты существуют независимо от таких определений (Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса было более умеренным разнообразием, чем то, что было обнаружено в ранних произведениях из Бриджмен. [9]
Операционализм с первоначальным энтузиазмом встретил логические позитивисты, которые рассматривал это как сродни верификации.Тем не менее, это было скоро показали, что любая попытка основать теорию значения на операционалистские принципы были полны проблем. Среди таких проблемы заключались в автоматическом операционализме надежности, приписываемом измерения, неясности, связанные с понятием эксплуатации, чрезмерно ограничительный эксплуатационный критерий осмысленность и тот факт, что многие полезные теоретические концепции не хватает четких операционных определений (Чанг 2009 г.). [10] В частности, Карл Хемпель (1956, 1966) критиковал операционалистов. за неспособность дать определение диспозиционных терминов, таких как «Растворимость в воде», и для умножения количества научные концепции в манере, которая противоречит необходимости систематические и простые теории.Соответственно, большинство авторов семантика количественных терминов избегает поддержки операционного анализ. [11]
Более широко пропагандируемый подход допускал традиционный элемент в использование количественных терминов, сопротивляясь попыткам уменьшить значение количественных терминов в операциях измерения. Эти аккаунты классифицируются под общей рубрикой «Конвенционализм», хотя они различаются аспекты измерения, которые они считают общепринятыми, и в степени произвол они приписывают таким условности. [12] Первым предшественником конвенционализма был Эрнст Мах, исследовавший понятие равенства температурных интервалов (1896: 52). Мах отметил, что разные типы термометрической жидкости расширяются при разных (и нелинейно связанные) скорости при нагревании, в связи с чем возникает вопрос: какая жидкость расширяется наиболее равномерно с температурой? В соответствии с Мах, неважно, какая жидкость расширяется больше. равномерно, поскольку само понятие равенства температур интервалы не имеют определенного применения до обычного выбор стандартной термометрической жидкости.Мах придумал термин «Принцип согласованности» для такого рода условно выбранный принцип применения количества концепция. Понятия однородности времени и пространства получили аналогичные обработки Анри Пуанкаре (1898, 1902: Часть 2). Пуанкаре утверждал, что процедуры, используемые для определения равенства среди длительностей проистекает из бессознательного предпочтения ученых описательная простота, а не из каких-либо фактов о природе. Точно так же выбор ученых представить пространство либо Евклидова или неевклидова геометрия не определяется опытом но по соображениям удобства.
Конвенционализм в отношении измерения достиг своего максимума. сложное выражение в логическом позитивизме. Логические позитивисты как Ганс Райхенбах и Рудольф Карнап предложили «координационный определения »или« правила соответствия »в качестве семантическая связь между теоретическими и наблюдательными терминами. Эти a априори , утверждения, подобные определениям, предназначались для регулирования использование теоретических терминов, связав их с эмпирическими процедурами (Reichenbach 1927: 14–19; Carnap 1966: Ch.24). Пример координирующим определением является утверждение: «мерный стержень сохраняет свою длину при транспортировке ». По словам Райхенбаха, это утверждение не может быть проверено эмпирически, потому что универсальный и могла существовать экспериментально необнаруживаемая сила, которая в равной степени искажает длина каждого объекта при транспортировке. В соответствии с верификационизм, утверждения, которые не поддаются проверке, не являются ни правдой, ни ложный. Вместо этого Райхенбах использовал это заявление, чтобы выразить произвольное правило, регулирующее использование понятия равенства length, а именно для определения того, являются ли конкретные экземпляры length равны (Reichenbach 1927: 16).В то же время координационные определения не рассматривались как замена, а скорее как необходимые дополнения к знакомому типу теоретических определений понятий с точки зрения других концепций (1927: 14). Под условным точки зрения, то спецификация измерительных операций не исчерпать значение таких понятий, как длина или равенство длины, тем самым избегая многих проблем, связанных с операционализм. [13]
Реалисты в области измерения утверждают, что измерение лучше всего понимается как эмпирическая оценка объективного свойства или связь.Сделаем несколько пояснительных замечаний в отношении это характеристика измерения. Во-первых, термин «Объективный» не предназначен для исключения ментальных свойств или отношения, которые являются объектами психологического измерения. Скорее, измеримые свойства или отношения считаются объективными, поскольку поскольку они не зависят от верований и обычаев людей выполнение измерения и методы, используемые для измерения. Для Например, реалист будет утверждать, что отношение длины данного сплошная штанга к стандартному счетчику имеет объективное значение независимо от измеряется ли и как.Во-вторых, срок «Оценка» используется реалистами, чтобы подчеркнуть факт что результаты измерений представляют собой всего лишь приближения истинных ценности (Trout 1998: 46). В-третьих, по мнению реалистов, измерение направленных на получение знаний о свойствах и отношениях, скорее чем при присвоении значений непосредственно отдельным объектам. Это значимы, потому что наблюдаемые объекты (например, рычаги, химические решения, люди) часто определяют измеримые свойства и отношения, которые не наблюдаются напрямую (например,г., количество механических работа, кислая, интеллект). Заявления о знаниях о таких свойства и отношения должны предполагать некоторую фоновую теорию. От перенос акцента с объектов на свойства и отношения, реалисты подчеркивают теоретический характер измерений.
Реализм в отношении измерения не следует путать с реализмом в отношении сущности (например, электроны). Реализм в измерении обязательно влечет за собой реализм в отношении свойств (например, температуры), поскольку в принципе можно было принять только реальность отношений (напр.грамм., соотношения между количествами), не принимая во внимание реальность лежащих в основе характеристики. Тем не менее, большинство философов, защищавших реализм, об измерении сделали это, аргументируя это тем, что в какой-то форме о собственности (Байерли и Лазара 1973; Свойер 1987; Манди 1987; Форель 1998, 2000). Эти реалисты утверждают, что по крайней мере некоторые измеримые свойства существуют независимо от убеждений и условностей люди, которые их измеряют, и что существование и структура этих properties наилучшим образом объясняет ключевые особенности измерения, включая полезность чисел при выражении результаты измерений и надежность средств измерений.
Например, типичный реалист по поводу измерения длины будет утверждать, что что эмпирические закономерности, отображаемые отдельными объектами » длины, когда они упорядочены и объединены, лучше всего объясняются если предположить, что длина является объективным свойством, имеющим обширную структура (Swoyer 1987: 271–27). То есть отношения между длинами такие как «дольше чем» и «сумма» существуют независимо от того, заказываются ли какие-либо объекты и соединены людьми, и действительно независимо от того, являются ли объекты какая-то конкретная длина вообще существует.Существование обширная структура собственности означает, что длины разделяют большую часть их структура с положительными действительными числами, и это объясняет полезность положительных вещественных чисел в представлении длин. Более того, если измеримые свойства анализируются с точки зрения диспозиции, становится Легко объяснить, почему некоторые измерительные приборы надежны. Для Например, если предположить, что определенное количество электрического тока в проволока влечет за собой склонность отклонять стрелку амперметра определенным угла, следует, что показания амперметра контрфактически зависят от количества электрического тока в проводе, следовательно, амперметр надежен (Trout 1998: 65).
Другой аргумент в пользу реализма в отношении измерения принадлежит Джоэлю. Мичелл (1994, 2005), который предлагает реалистичную теорию чисел, основанную на евклидова концепция соотношения. По словам Мичелла, цифры соотношения между величинами и, следовательно, существуют в пространстве и времени. В частности, действительные числа — это отношения между парами бесконечные стандартные последовательности, например, последовательность длин обычно обозначается «1 метр», «2 метра» и т. д., а последовательность целых кратных длины, которую мы пытаемся измерить.Измерение — это открытие и оценка таких соотношений. An Интересным следствием этого эмпирического реализма в отношении чисел является это измерение не является репрезентативной деятельностью, а скорее деятельность по приближению независимых от разума чисел (Michell 1994: 400).
Реалистические представления об измерениях в основном формулируются противоположно к сильным версиям операционализма и конвенционализма, которые доминировали философские дискуссии об измерениях с 1930-х годов до 1960-х гг.Помимо недостатков операционализма уже обсуждалось в предыдущем разделе, реалисты отмечают, что антиреализм в отношении измеримых величин не понимает научная практика. Если бы количества не имели реальных значений независимо от выбор методики измерения, было бы трудно объясните, что ученые подразумевают под «точностью измерения» и «Ошибка измерения» и почему они пытаются повысить точность и уменьшить ошибку. Напротив, реалисты могут легко понять смысл понятия точности и ошибки с точки зрения расстояния между реальными и измеренные значения (Byerly and Lazara 1973: 17–8; Swoyer 1987: 239; Форель 1998: 57).С этим тесно связан тот факт, что более новые процедуры измерения имеют тенденцию к повышению точности по сравнению с более старыми. Если бы выбор процедуры измерения был просто обычным, он бы трудно разобраться в таком прогрессе. Кроме того, реализм дает интуитивно понятное объяснение того, почему разные измерения процедуры часто дают аналогичные результаты, а именно потому, что они чувствительны к тем же фактам (Swoyer 1987: 239; Trout 1998: 56). Наконец, реалисты отмечают, что конструкция измерительной аппаратуры и при анализе результатов измерений руководствуемся теоретическими предположения о причинно-следственных связях между величинами.В способность таких причинно-следственных предположений направлять измерения предполагает, что количества онтологически предшествуют процедурам измерения их. [14]
Хотя их позиция по отношению к операционализму и конвенционализму остается неизменной. в значительной степени критичны, реалисты более снисходительны в своих оценках математические теории измерения. Брент Манди (1987) и Крис Swoyer (1987) оба принимают аксиоматическую трактовку измерения. шкалы, но возражают против эмпирической интерпретации, данной аксиомы выдающихся теоретиков измерений, таких как Кэмпбелл (1920) и Эрнест Нагель (1931; Коэн и Нагель 1934: гл.15). Скорее, чем интерпретация аксиом как относящихся к конкретным объектам или к наблюдаемые отношения между такими объектами, Манди и Свойер переосмысливают аксиомы, относящиеся к универсальным величинам, например, к универсальное свойство быть длиной 5 метров, а не бетоном экземпляры этого свойства. Эта конструкция сохраняет интуиция, что утверждения типа «размер x вдвое больше размером y ”- это в первую очередь около двух размеры , и только производные об объектах x и y сами (Mundy 1987: 34). [15] Манди и Свойер утверждают, что их интерпретация является более общей, потому что это логически влечет за собой все последствия первого порядка эмпирическая интерпретация наряду с дополнительными утверждениями второго порядка о всемирных величинах. Более того, согласно их интерпретации теория измерения становится подлинной научной теорией с пояснительные гипотезы и проверяемые прогнозы. Основываясь на этом работы, Джо Вольф (2020a) недавно предложила новую реалистичную версию величин, которая опирается на репрезентативную теорию Измерение.Согласно структуралистской теории Вольфа количество, количественные атрибуты — это реляционные структуры. В частности, атрибут является количественным, если его структура имеет переводы, образующие архимедову упорядоченную группу. Вольфа сосредоточиться на переводах, а не на конкретных отношениях, таких как конкатенация и упорядочение, означает, что количественность может быть реализуется несколькими способами и не ограничивается обширными конструкции. Это также означает, что быть количеством ничего не значит. специально для чисел, как числовых, так и нечисловых структуры могут быть количественными.
Теоретико-информационные отчеты об измерениях основаны на аналогии между измерительными системами и системами связи. В простом система связи, сообщение (вход) кодируется в сигнал на конец передатчика, отправленный на конец приемника, и затем декодируется обратно (вывод). Точность передачи зависит от об особенностях системы связи, а также об особенностях окружающая среда, т. е. уровень фонового шума. Аналогичным образом, измеряя инструменты можно рассматривать как «информационные машины» (Финкельштейн 1977), которые взаимодействуют с объектом в заданном состоянии (ввод), кодируйте это состояние во внутренний сигнал и преобразуйте это сигнал в считывание (вывод).Точность измерения аналогично зависит от инструмента, а также от уровня шума в его среде. Задуманный как особый вид информации передачи, измерение становится анализируемым с точки зрения концептуальный аппарат теории информации (Hartley 1928; Shannon 1948; Шеннон и Уивер 1949). Например, информация о том, что чтение \ (y_i \) сообщает о возникновении состояния \ (x_k \) объект можно количественно оценить как \ (\ log \ left [\ frac {p (x_k \ mid y_i)} {p (x_k)} \ right] \), а именно как функция уменьшения неопределенность в отношении состояния объекта (Finkelstein 1975: 222; для альтернативные формулировки см. Brillouin 1962: Ch.15; Кирпатовский 1974; и Мари 1999: 185).
Людвик Финкельштейн (1975, 1977) и Лука Мари (1999) предложили возможность синтеза теории информации Шеннона-Уивера и теория измерений. По их мнению, обе теории апеллируют к центру. к идее отображения: теория информации касается отображения между символами во входных и выходных сообщениях, при измерении теория касается отображения между объектами и числами. Если измерение аналогично манипулированию символами, тогда Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса измерения, в то время как теория измерений могла бы обеспечить формализацию его семантика.Тем не менее, Мари (1999: 185) также предупреждает, что аналогия между системами связи и измерения ограничена. В то время как сообщение отправителя может быть известно с произвольной точностью. независимо от его передачи состояние объекта не может быть известно с произвольной точностью независимо от его измерения.
Изначально теоретико-информационные отчеты об измерениях были разработаны метрологами — специалистами в области физических измерений и стандартизация — с небольшим участием философов.Независимо от достижений в метрологии, Бас ван Фраассен (2008: 141–185) недавно предложил концепцию измерения в какая информация играет ключевую роль. Он считает измерение составленным двух уровней: на физическом уровне измерительная аппаратура взаимодействует с объектом и производит чтение, например, указатель должность. [16] На абстрактном уровне фоновая теория представляет собой возможные состояния объекта в пространстве параметров. Измерение находит объект в подобласти этого абстрактного пространства параметров, тем самым сокращая диапазон возможных состояний (2008: 164 и 172).Это сокращение возможностей сводится к сбору информация об измеряемом объекте. Анализ ван Фраассена измерения отличается от теоретико-информационных счетов, разработанных в метрологии в ее явном обращении к фоновой теории, и в тот факт, что он не ссылается на символическую концепцию информации разработан Шеннон и Уивер.
С начала 2000-х годов нахлынула новая волна философских исследований. появилось, что подчеркивает взаимосвязь между измерением и теоретическое и статистическое моделирование (Morgan 2001; Boumans 2005a, 2015; Mari 2005b; Мари и Джордани 2013; Таль 2016, 2017; Паркер 2017; Мияке 2017).Согласно расчетам, основанным на модели, измерение состоит из двух уровней: (i) конкретный процесс, включающий взаимодействие между интересующий объект, инструмент и окружение; и (ii) a теоретическая и / или статистическая модель этого процесса, где «Модель» означает абстрактное и локальное представление построены на основе упрощающих предположений. Центральная цель измерение в соответствии с этой точкой зрения заключается в присвоении значений одному или нескольким интересующих параметров модели таким образом, чтобы eptemic desiderata, в частности последовательность и последовательность.
Счета на основе моделей были разработаны на основе изучения измерений практики в науке, и особенно в метрологии. Метрология, официально определяется как «наука об измерениях и ее приложение »(JCGM 2012: 2.2), является предметом изучения с разработкой, обслуживанием и усовершенствованием средств измерений в естественных и технических науках. Метрологи обычно работают в бюро стандартизации или в специализированных лабораториях, ответственный за калибровку измерительного оборудования, сравнение стандартов и оценка измерений неопределенности, среди других задач.Только недавно философы начали заниматься богатыми концептуальными проблемами лежащей в основе метрологической практики, и особенно с выводами участвует в оценке и повышении точности измерений стандарты (Chang 2004; Boumans 2005a: Chap. 5, 2005b, 2007a; Frigerio и другие. 2010; Teller 2013, 2018; Риордан 2015; Шлаудт и Хубер 2015; Tal 2016a, 2018; Mitchell et al. 2017; Месснер и Нордманн 2017; de Courtenay et al. 2019).
Основной мотивацией для разработки модельных счетов является попытка прояснить эпистемологические принципы, лежащие в основе аспекты измерительной практики.Например, метрологи используют разнообразие методов калибровки средств измерений, стандартизация и отслеживание единиц и оценка неопределенности (обсуждение метрологии см. в предыдущем раздел). Традиционные философские учения, такие как математические теории измерения не основываются на предположениях, умозаключениях закономерности, доказательственные основания или критерии успеха, связанные с такими методы. Как отмечает Frigerio et al. (2010) утверждают, что теория измерений плохо подходит для разъяснения этих аспектов измерения, потому что он абстрагируется от процесса измерения и сосредотачивается исключительно на математические свойства весов.Напротив, модельные бухгалтеры считают построение шкалы лишь одной из нескольких задач участвует в измерении, наряду с определением измеряемого параметры, конструкция и калибровка прибора, отбор образцов и подготовка, обнаружение ошибок и оценка неопределенности, среди прочего (2010: 145–7).
7.1 Роль моделей в измерении
Согласно модельным расчетам, измерение предполагает взаимодействие между интересующим объектом («система под измерение »), инструмент (« измерение система ») и среду, которая включает в себя измерения предметы.Другие, вторичные взаимодействия также могут иметь отношение к определение результата измерения, например, взаимодействие между измерительным прибором и эталонами, используемыми для его калибровка и цепочка сравнений, которые отслеживают эталон эталон обратно к первичным эталонам (Mari 2003: 25). Измерение продолжается путем представления этих взаимодействий с набором параметры и присвоение значений подмножеству этих параметров (известные как «измеряемые величины») на основе результатов взаимодействия.Когда измеряемые параметры являются числовыми, они называются «Количества». Хотя измеряемые величины не обязательно должны быть количествами, будет предложен сценарий количественного измерения, в котором следует.
Два типа результатов измерений различаются по моделям. счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль 2013]:
- Показания прибора (или «Показания»): это свойства измерительного прибор в конечном состоянии после того, как процесс измерения полный.Примеры: цифры на дисплее, отметки при множественном выборе. анкета и биты, хранящиеся в памяти устройства. Показания могут быть представлены числами, но такие числа описывают состояния инструмент, и его не следует путать с результатами измерения, которые касаются состояний измеряемого объекта.
- Результаты измерения (или «результаты»): это заявления о знании значений одной или нескольких величин приписываются измеряемому объекту и обычно сопровождаются указанием единицы измерения и шкалы и сметы неопределенности измерения.Например, результат измерения может быть следующим: выражается предложением «масса объекта a составляет 20 ± 1 грамм с вероятностью 68% ».
Сторонники теории, основанной на моделях, подчеркивают, что выводы из показания приборов к результатам измерений нетривиальны и зависят от множества теоретических и статистических предположений о объект измерения, прибор, окружающая среда и процесс калибровки. Результаты измерений часто достигаются через статистический анализ нескольких показаний, включая предположения о форме распределения показаний и случайность воздействия окружающей среды (Боген и Вудворд 1988: 307–310).Результаты измерений также включают поправки на систематические эффекты, и такие поправки основаны на теоретических предположения относительно работы прибора и его взаимодействия с объектом и окружающей средой. Например, длина измерения должны быть скорректированы для изменения измерения длина стержня с температурой, поправка, которая выводится из теоретического уравнения теплового расширения. Систематический исправления связаны с собственными неопределенностями, например, в определение значений констант, и эти неопределенности оценивается посредством вторичных экспериментов, включающих дальнейшие и статистические допущения.Более того, неопределенность, связанная с результат измерения зависит от методов, используемых для калибровка прибора. Калибровка требует дополнительных предположения о приборе, калибрующем аппарате, измеряемая величина и свойства эталонов (Ротбарт и Слейден 1994; Франклин 1997; Бэрд 2004: Глава 4; Солер и др. al. 2013). Еще один компонент неопределенности проистекает из неопределенности. в определении измеряемой величины и известен как «Неопределенность определений» (Мари и Джордани, 2013; Grégis 2015).Наконец, измерение включает в себя фон предположения о типе весов и системе единиц измерения, и эти предположения часто связаны с более широкими теоретическими и технологическими соображения, касающиеся определения и реализации весов и единицы.
Эти различные теоретические и статистические предположения составляют основу для построения одной или нескольких моделей измерительного процесса. В отличие от математических теорий измерения, где термин «Модель» обозначает теоретико-множественную структуру, которая интерпретирует формальный язык, здесь термин «модель» обозначает абстрактное и локальное представление целевой системы, которая построен на упрощении предположения. [17] Соответствующей целевой системой в этом случае является процесс измерения, то есть система, состоящая из измерительного прибора, объектов или события, подлежащие измерению, окружающая среда (включая людей-операторов), вторичные инструменты и эталоны, эволюция во времени эти компоненты и их различные взаимодействия друг с другом. Измерение рассматривается как набор процедур, цель которых — согласованно присваивать значения параметрам модели на основе прибора показания. Поэтому модели рассматриваются как необходимые предварительные условия для возможность вывода результатов измерения из прибора показания, и как решающее значение для определения содержания измерения результаты.Как подчеркивают сторонники модельных расчетов, показания, полученные с помощью одного и того же процесса измерения, могут использоваться для установить разные результаты измерения в зависимости от того, как процесс измерения моделируется, например, в зависимости от того, в какой среде учитываются влияния, статистические допущения используются для анализа шума, и какие приближения используются при применении фоновая теория. Как выразился Лука Мари,
любой результат измерения содержит информацию, имеющую значение только в контекст метрологической модели, такая модель требуется для включить спецификацию для всех сущностей, которые явно или неявно фигурируют в выражении результата измерения.(2003: 25)
Точно так же считается, что модели обеспечивают необходимый контекст для оценка различных аспектов качества результатов измерений, включая точность, прецизионность, погрешность и неопределенность (Boumans 2006, 2007a, 2009, 2012b; Мари 2005b).
Основанные на моделях описания расходятся с эмпирическими интерпретациями теории измерений в том, что они не требуют отношений между результаты измерения должны быть изоморфны или гомоморфны наблюдаемым отношения между объектами измерения (Mari 2000).Действительно, согласно модельным расчетам отношения между измеряемыми объектами вовсе не обязательно быть наблюдаемыми до их измерения (Frigerio et al. al. 2010: 125). Вместо этого ключевое нормативное требование основанной на моделях счетов заключается в том, что значения присваиваются параметрам модели в согласованном манера. Критерий согласованности можно рассматривать как сочетание двух подкритерии: (i) согласованность допущений модели с соответствующими фоновые теории или другие существенные предположения о измеряемая величина; и (ii) объективность, i.е. взаимное согласованность результатов измерений по разным измерениям инструменты, окружающая среда и модели [18] (Frigerio et al.2010; Tal 2017a; Teller 2018). Первое подкритерий предназначен для обеспечения того, чтобы предполагаемое количество измеряется, в то время как второй подкритерий предназначен для обеспечения что результаты измерения могут быть разумно отнесены к измеряемым объект , а не какой-то артефакт измерения инструмент, среда или модель.Взятые вместе, эти двое требования гарантируют, что результаты измерений остаются действительными независимо от конкретных допущений, связанных с их производства, и, следовательно, контекстная зависимость измерения результаты не угрожают их общей применимости.
7.2 Модели и измерения в экономике
Помимо их применимости к физическим измерениям, основанные на моделях Анализ также проливает свет на измерения в экономике. Как физический количества, значения экономических переменных часто невозможно наблюдать непосредственно и должны выводиться из наблюдений, основанных на абстрактных и идеализированные модели.Экономист девятнадцатого века Уильям Джевонс за Например, измерять изменения в стоимости золота, постулируя определенные причинно-следственные связи между стоимостью золота, предложением золота и общий уровень цен (Hoover and Dowell 2001: 155–159; Morgan 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс измерения стали возможны благодаря использованию двух моделей: причинно-теоретическая модель экономики, в основе которой предположение, что количество золота может увеличиваться или снижать цены; и статистическая модель данных, основанная на предположение, что местные колебания цен взаимно независимы и поэтому компенсируют друг друга при усреднении.Взятый вместе эти модели позволили Джевонсу сделать вывод об изменении значения золота из данных об исторических ценах различных товары. [19]
Способы, которыми модели функционируют в экономических измерениях, привели к некоторые философы считают определенные экономические модели инструменты сами по себе, по аналогии с линейками и весами (Boumans 1999, 2005c, 2006, 2007a, 2009, 2012a, 2015; Morgan 2001). Марсель Буманс объясняет, как макроэкономисты могут изолировать переменная, представляющая интерес от внешних воздействий, путем настройки параметров в модель макроэкономической системы.Этот метод освобождает экономистов от невозможной задачи управления реальной системой. Как Боуман утверждает, что макроэкономические модели функционируют как инструменты измерения, поскольку поскольку они создают инвариантные отношения между входами (показаниями) и выходов (результатов), и насколько эта инвариантность может быть проверена с помощью калибровка по известным и стабильным фактам. Когда такие модельные процедуры сочетаются с экспертной оценкой, они могут производить надежные измерения экономических явлений даже вне контроля лабораторные настройки (Boumans 2015: гл.5).
7.3 Психометрические модели и конструктивная валидность
Еще одна область, в которой модели играют центральную роль в измерениях, — это психология. Измерение большинства психологических атрибутов, таких как интеллект, тревога и депрессия, не полагаются на гомоморфные отображения типа, поддерживаемого Репрезентативной теорией Измерение (Уилсон 2013: 3766). Вместо этого психометрическая теория полагается преимущественно на разработке абстрактных моделей, предназначенных для прогнозировать производительность испытуемых в определенных задачах.Эти модели построены на основе существенных и статистических предположений о измеряемый психологический атрибут и его отношение к каждому задача измерения. Например, Теория отклика предмета, популярная подход к психологическому измерению, использует различные модели для оценить надежность и валидность анкет. Рассмотрим анкета, предназначенная для оценки понимания английского языка («способность»), предлагая испытуемым серию да / нет вопросы («предметы»).Одна из самых простых моделей Для калибровки таких вопросников используется модель Раша (Rasch 1960). Эта модель предполагает простое алгебраическое соотношение — известное как «журнал шансов» — между вероятностями что испытуемый ответит на заданный вопрос правильно, сложность этот конкретный предмет и способности субъекта. Новый анкеты калибруются путем проверки соответствия между их указания и прогнозы модели Раша и назначение уровни сложности для каждого элемента соответственно.Затем модель используется в в сочетании с анкетой для определения уровня владения английским языком понимание (результаты) из исходных баллов анкеты (показания) (Уилсон 2013; Мари и Уилсон 2014).
Своего рода статистическая калибровка (или «масштабирование») модели Раша дает повторяемые результаты, но часто только первый шаг к полноценному психологическому измерению. Психологов обычно интересуют результаты какой-либо меры. ради самого себя, но ради оценки некоторых основных и латентный психологический признак, e.г., понимание английского языка. Хорошего соответствия между ответами на вопросы и статистической моделью пока нет. определить, что измеряет анкета. Процесс установление того, что процедура измеряет предполагаемый психологический атрибут известен как «проверка». Один из способов проверки психометрический инструмент предназначен для проверки того, могут ли различные процедуры, предназначены для измерения одного и того же скрытого атрибута. полученные результаты. Такое тестирование относится к семейству методов валидации. известная как «проверка конструкции».Конструкция — это абстрактное представление скрытого атрибута, предназначенного для измерено, и
отражает гипотезу […] о том, что различные виды поведения коррелируют друг с другом в исследованиях индивидуальных различий и / или аналогично будут затронуты экспериментальные манипуляции. (Nunnally И Бернштейн 1994: 85)
Конструкции обозначаются переменными в модели, которая предсказывает, какие корреляции будут наблюдаться между показаниями различных меры, если они действительно являются показателями одного и того же атрибута.Такой модели включают существенные предположения об атрибуте, в том числе его внутренняя структура и его отношения с другими атрибутами, и статистические допущения о корреляции между различными показателями (Campbell & Fiske 1959; Nunnally & Bernstein 1994: Ch. 3; Angner 2008).
В последние годы философы науки все больше становятся интересуется психометрикой и концепцией валидности. Одна дискуссия касается онтологического статуса скрытых психологических атрибутов.Денни Борсбум выступил против операционализма по поводу латентного атрибуты, и в пользу определения действительности таким образом, чтобы охватывает реализм: «тест действителен для измерения атрибута, если и только если а) атрибут существует, и б) вариации в атрибута причинно порождают вариации в результатах методика измерения »(2005: 150; см. также Hood 2009, 2013; Праздник 2020). Элина Вессонен защищала умеренную форму операционализм о психологических атрибутах и утверждал, что умеренный операционализм совместим с осторожным реализмом (2019).Еще одна недавняя дискуссия посвящена обоснованию разработать процедуры проверки. По словам Анны Александровой, проверка конструкции в принципе является оправданной методологией, поскольку поскольку он устанавливает согласованность с теоретическими предположениями и фоновые знания о скрытом атрибуте. Однако Александрова отмечает, что на практике врачи-психометристы, намеревающиеся измерить счастье и благополучие часто избегают теоретических рассуждений об этих конструирует, а вместо этого апеллирует к народным верованиям респондентов.Это сводит на нет цель проверки конструкции и превращает ее в узкое, техническое упражнение (Александрова, Хайброн, 2016; Александрова 2017; см. также McClimans et al. 2017).
Более фундаментальная критика психометрии заключается в том, что она догматически предполагает, что психологические атрибуты могут быть количественно. Мичелл (2000, 2004b) утверждает, что психометристы не предпринимали серьезных попыток проверить, являются ли атрибуты, которые они подразумевают для измерения имеют количественную структуру, и вместо этого расплывчатое представление об измерении, которое маскирует это пренебрежение.В ответ, Борсбум и Мелленберг (2004) утверждают, что ответ на предмет Теория обеспечивает вероятностные тесты количественной оценки атрибуты. Психометристы, строящие статистическую модель сначала предположить, что атрибут является количественным, а затем подвергнуть модель эмпирическим испытаниям. В случае успеха такие испытания обеспечивают косвенное подтверждение исходной гипотезы, например от показывая, что атрибут имеет аддитивную объединенную структуру (см. также Vessonen 2020).
Несколько ученых указали на сходство способов моделирования используются для стандартизации измеряемых величин в натуральных и социальные науки.Например, Марк Уилсон (2013) утверждает, что психометрические модели можно рассматривать как инструменты для построения эталоны в том же смысле слова «измерение эталон », применяемый метрологами. Другие вызвали сомнения по поводу целесообразность и желательность принятия примера естественные науки при стандартизации конструкций в социальных науках. Нэнси Картрайт и Роза Рунхардт (2014) обсуждают «Баллунг» — термин, заимствованный у Отто Нейрата. для обозначения концепций с нечеткой и контекстно-зависимой областью действия.Примеры понятий Баллунга — это раса, бедность, социальная изоляция и качество программ докторантуры. Такие концепции слишком многогранны, чтобы их измеряется по одной метрике без потери смысла и должен быть представлен либо матрицей индексов, либо несколькими разными меры в зависимости от целей и ценностей (см. также Брэдберн, Картрайт и Фуллер, 2016 г., Другие Интернет-ресурсы). Александрова (2008) отмечает, что этические соображения влияют на вопросы об обоснованности мер благосостояния не менее соображения воспроизводимости.Такие этические соображения контекстно-зависимый и может применяться только по частям. В аналогичном vein, Лия МакКлиманс (2010) утверждает, что единообразие не всегда подходящая цель для разработки анкет, поскольку открытость вопросов часто неизбежны и желательны для получения соответствующая информация от предметы. [20] Переплетение этических и эпистемологических соображений особенно наглядно, когда психометрические анкеты используются в медицинских контексты для оценки благополучия и психического здоровья пациентов.В таком случаи, небольшие изменения в дизайне анкеты или анализа его результатов могут нанести значительный вред пациентам или принести им пользу. (McClimans 2017; Stegenga 2018, глава 8). Эти идеи подчеркивают ценностный и контекстуальный характер измерения умственных и социальные явления.
Разработка модельных счетов обсуждалась в предыдущем раздел является частью более крупного «эпистемологического поворота» в философия измерения, возникшая в начале 2000-х гг.Скорее чем упор на математические основы, метафизику или семантика измерения, философские работы последних лет имеют тенденцию к сосредоточиться на предпосылках и шаблонах вывода, участвующих в конкретные практики измерения, а также исторические, социальные и материальные размеры измерения. Философское изучение этих темы называют «эпистемологией измерение »(Mari 2003, 2005a; Leplège 2003; Tal 2017a). В самом широком смысле эпистемология измерения — это изучение отношения между измерением и знанием.Центральные темы которые подпадают под сферу эпистемологии измерения, включают условия, при которых измерение производит знание; в содержание, объем, обоснование и пределы таких знаний; в причины, по которым определенные методологии измерения и стандартизация успешна или не поддерживает определенные знания претензии и отношения между измерениями и другими познавательная деятельность, такая как наблюдение, теоретизирование, экспериментирование, моделирование и расчет.Следуя этим цели, философы опираются на работы историков и социологи науки, занимающиеся измерением практики в течение более длительного периода (Wise and Smith 1986; Latour 1987: Ch. 6; Schaffer 1992; Портер 1995, 2007; Wise 1995; Ольха 2002; Галисон 2003; Gooday 2004; Crease 2011), а также по истории и философия научных экспериментов (Harré 1981; Hacking 1983; Франклин 1986; Картрайт 1999). Следующие подразделы изучите некоторые из тем, обсуждаемых в этом быстрорастущем корпусе литература.
8.1 Стандартизация и научный прогресс
Тема, которая привлекла значительное внимание философов в последние годы — это выбор и совершенствование измерений стандарты. Вообще говоря, стандартизация количественной концепции означает: предписать определенный способ применения этой концепции к конкретный подробности. [21] Стандартизация измерительного прибора означает оценку того, насколько хорошо результаты измерений этим прибором соответствуют предписанному режиму применение соответствующей концепции. [22] Соответственно, термин «эталон» имеет не менее два значения: с одной стороны, он обычно используется для обозначения абстрактные правила и определения, регулирующие использование количества понятия, такие как определение счетчика. С другой стороны, термин «эталон» также обычно используется для обозначения к конкретным артефактам и процедурам, которые считаются образцовыми применение количественной концепции, такой как металлический стержень, который служил эталонным счетчиком до 1960 г.Эта двойственность смысла отражает двойственную природу стандартизации, которая включает в себя как абстрактные и конкретные аспекты.
В Раздел 4 было отмечено, что стандартизация предполагает выбор среди нетривиальных альтернативы, такие как выбор между различными термометрическими жидкостями или среди разных способов обозначения одинаковой продолжительности. Эти варианты нетривиальные в том смысле, что они влияют на то, температурные (или временные) интервалы считаются равными и, следовательно, влияют на содержат ли утверждения естественного права термин «Температура» (или «время») оказываются верными.Обращение к теории, чтобы решить, какой стандарт более точен, было бы круговой, поскольку теория не может быть однозначно применена к подробные сведения перед выбором эталона. Этот округлость по-разному называли «проблемой координации »(van Fraassen 2008: Ch. 5) и« проблема номических измерений »(Chang 2004: Ch. 2). Как уже упоминалось, конвенционалисты попытались уйти от округлости, постулируя как априори утверждения, известные как «координационные определения », которые должны были связать количественные термины с специфические измерительные операции.Недостатком этого решения является то, что предполагается, что выбор эталона произвольный и статичны, тогда как на практике эталоны обычно выбираются на основе эмпирических соображений и в конечном итоге улучшаются или заменены стандартами, которые считаются более точными.
Новое направление работ по проблеме координации появилось в последние годы, в первую очередь из произведений Хасока Чанга (2001, 2004, 2007; Барвич и Чанг, 2015) и Бас ван Фраассен (2008: Гл.5; 2009, 2012; см. также Padovani 2015, 2017; Мишель 2019). Эти Работы используют исторический и последовательный подход к проблеме. Вместо того, чтобы пытаться полностью избежать проблемы округлости, как и их предшественники, они намеревались показать, что округлость не порочный. Чанг утверждает, что построение количественной концепции и Стандартизация его измерения — это взаимозависимые и повторяющиеся задачи. Каждая «эпистемическая итерация» в истории стандартизация уважает существующие традиции и в то же время исправляя их (Chang 2004: Ch.5). Донаучная концепция температура, например, была связана с грубым и неоднозначным методы упорядочивания предметов от горячего к холодному. Термоскопы и в конечном итоге термометры помогли изменить первоначальную концепцию и сделали это точнее. С каждой такой итерацией количественное понятие было пересмотрены на более стабильный набор стандартов, которые, в свою очередь, позволил более точно проверить теоретические предсказания, облегчение последующего развития теории и построения более стабильных стандартов и так далее.
Как этот процесс избегает порочной замкнутости, становится ясно, когда мы посмотрим. при этом либо «сверху», т. е. в ретроспективе с учетом наших текущие научные знания, или «изнутри», глядя в исторических событиях в их первоначальном контексте (ван Фраассен 2008: 122). С любой точки зрения координация успешна, потому что это увеличивает согласованность между элементами теории и инструментария. На вопросы «что считать количественным измерением?» X ? » и «какое количество X ?», хотя и не имеют ответа независимо друг от друга, адресованы вместе в процессе взаимного уточнения.Только когда человек принимает фундаменталистской точки зрения и пытается найти отправную точку для координация, свободная от предположений, что этот исторический процесс ошибочно, кажется, не имеет эпистемического обоснования (2008: 137).
В новой литературе по координации смещается акцент обсуждение от определений количественных терминов к реализации этих определений. На метрологическом жаргоне «Реализация» — это физический инструмент или процедура, приблизительно удовлетворяет данному определению (ср.JCGM 2012: 5.1). Примеры метрологических реализаций — официальные прототипы килограмм и часы с цезиевым фонтаном, используемые для стандартизации второй. Недавние исследования показывают, что методы, используемые для проектирования, поддерживать и сравнивать реализации имеют прямое отношение к практическое применение понятий количества, единицы и масштаба, не менее чем определения этих понятий (Riordan 2015; Tal 2016). В связь между определением и реализацией единицы становится особенно сложно, когда определение сформулировано в теоретических терминах.Некоторые из основных единиц Международной системы (СИ) — включая метр, килограмм, ампер, кельвин и моль — нет больше определяется ссылкой на какой-либо конкретный вид физической системы, но фиксируя численное значение фундаментальной физической постоянной. Килограмм, например, был переопределен в 2019 году как единица массы. такое, что числовое значение постоянной Планка точно равно 6.62607015 × 10 -34 кг м 2 с -1 (BIPM 2019: 131). Понимание килограмма под этим определением — это в высшей степени теоретическая задача.Изучение практической реализации такие подразделения пролили новый свет на развивающиеся отношения между измерения и теория (Tal 2018; de Courtenay et al 2019; Wolff 2020b).
8.2 Теоретическая основа измерения
Как уже обсуждалось выше (разделы 7 а также 8.1), теория и измерение взаимозависимы как исторически, так и концептуально. С исторической стороны развитие теории и измерение происходит через итерационные и взаимные уточнения. На концептуальная сторона, спецификация форм методик измерения эмпирическое содержание теоретических концепций, в то время как теория дает систематическая интерпретация показаний измерений инструменты.Эта взаимозависимость измерения и теории может показаться как угроза доказательной роли, которую измерение должно играть в научном предприятии. В конце концов, результаты измерений думал, что может проверить теоретические гипотезы, и это, кажется, требуют некоторой степени независимости измерения от теории. Этот угроза особенно очевидна, когда теоретическая гипотеза испытанный уже предполагается как часть модели измерения инструмент. Чтобы процитировать пример из работы Франклина и др.(1989: 230):
На первый взгляд может показаться, что если кто-то должны были использовать ртутный термометр для измерения температуры объекты как часть эксперимента, чтобы проверить, расширяются ли объекты по мере повышения их температуры.
Тем не менее Франклин и др. сделать вывод, что округлость не беспощадный. Ртутный термометр можно откалибровать по другому термометр, принцип действия которого не предполагает закона теплового расширения, например, газовый термометр постоянного объема, тем самым подтверждая надежность ртутного термометра на независимые основания.Говоря шире, в контексте проверки локальной гипотезы угроза замкнутости обычно может быть избегать обращения к другим видам инструментов и другим частям теория.
Другой вид беспокойства по поводу доказательной функции измерения возникает в глобальном масштабе, когда проводится проверка всех теорий. обеспокоенный. Как утверждает Томас Кун (1961), научные теории обычно принимаются задолго до количественных методов их тестирования становятся доступными. Надежность недавно введенного измерения методы обычно проверяются на соответствие предсказаниям теории а не наоборот.По словам Куна, « путь от научного закона к научному измерению редко бывает ехал в обратном направлении »(1961: 189). Например, Закон Дальтона, который гласит, что веса элементов в химические соединения связаны друг с другом целиком пропорции, изначально противоречащие некоторым из наиболее известных мерки таких пропорций. Только предполагая Закон Дальтона, который последующие химики-экспериментаторы смогли исправить и улучшить свои методы измерения (1961: 173).Следовательно, Кун утверждает, что функция измерения в физических науках не для проверки теории, а для ее применения во все большем объеме и точность, и, в конечном итоге, позволить стойким аномалиям выйти на поверхность это ускорит следующий кризис и научную революцию. Примечание что Кун не утверждает, что измерение не имеет доказательной роли для играть в науку. Вместо этого он утверждает, что измерения не могут проверить теория изолирована, но только в сравнении с альтернативной теорией это предлагается в попытке объяснить обнаруженные аномалии за счет все более точных измерений (для яркого обсуждения о диссертации Куна см. Hacking 1983: 243–5).
Традиционные дискуссии о теоретической нагруженности, как и у Куна, были проводится на фоне логических позитивистов различие между теоретическим и наблюдательным языком. В теоретическая нагруженность измерения правильно воспринималась как угроза для возможность четкого разграничения между двумя языками. Современные дискуссии, напротив, больше не ведутся. теоретическая нагруженность как эпистемологическая угроза, но воспринимается как должное что некоторый уровень теоретической нагруженности является предпосылкой для измерений иметь какую-либо доказательную силу.Без какого-то минимального существенного предположения об измеряемой величине, например о ее приемлемости манипулированию и его отношениям к другим величинам, это было бы невозможно интерпретировать показания средств измерений и следовательно, невозможно установить доказательную релевантность этих показания. Об этом уже говорил Пьер Дюгем (1906: 153–6; см. также Carrier 1994: 9–19). Более того, современные авторы подчеркивают, что теоретические предположения играют важные роли в исправлении ошибок измерения и оценке неопределенности измерения.Действительно, физические процедуры измерения становятся точнее , когда модель, лежащая в их основе, деидеализованный, процесс, который включает в себя увеличение теоретических богатство модели (Tal 2011).
Признание того, что теория имеет решающее значение для гарантии Доказательная надежность измерений обращает внимание на «Проблема обоснования наблюдений», которая является обратной вызов традиционной угрозе теоретической нагруженности (Tal 2016b). Задача состоит в том, чтобы определить, какую роль наблюдение играет в измерения, и в частности, какая связь с наблюдением необходимо и / или достаточно для того, чтобы измерения могли сыграть доказательная роль в науках.Эта проблема особенно очевидна, когда одна попытка объяснить растущее использование вычислительных методы выполнения задач, которые традиционно решались измерительные приборы. В роли Маргарет Моррисон (2009) и Венди Паркер (2017) утверждают, есть случаи, когда достоверная количественная информация собирается о целевой системе с помощью компьютера моделирование, но таким образом, чтобы удовлетворить некоторые из основных Desiderata для измерения, такого как эмпирическое обоснование и ретроспективный (см. также Lusk 2016).На такую информацию не полагается по сигналам, передаваемым от конкретного объекта, представляющего интерес, к инструмента, но на использовании теоретических и статистических моделей для обрабатывать эмпирические данные о связанных объектах. Например, данные методы ассимиляции обычно используются для оценки прошлых атмосферных температуры в регионах, где нет показаний термометра. Некоторые методы делают это, подбирая вычислительную модель поведение атмосферы на комбинацию доступных данных из близлежащие регионы и модельный прогноз условий на момент наблюдение (Parker 2017).Эти оценки затем используются в различных способов, в том числе в качестве данных для оценки перспективных климатических моделей. Независимо от того, называют ли эти оценки «Измерения», они ставят под сомнение идею о том, что производство надежные количественные данные о состоянии объекта требуют наблюдая за этим объектом, как бы слабо он ни понимал термин «Наблюдение». [23]
8,3 Точность и прецизионность
Два ключевых аспекта надежности результатов измерений: тщательность и точность.Рассмотрим серию повторяющихся весов измерения, выполненные на конкретном объекте с равными руками остаток средств. С реалистической, «ошибочной» точки зрения, результаты этих измерений точные , если они близки истинному значению измеряемой величины — в нашем случае истинное соотношение веса объекта к выбранному unit — и — точный , если они расположены близко друг к другу. An аналогия, которую часто цитируют, чтобы прояснить основанное на ошибках различие, заключается в том, что стрелы стреляют в цель с точностью, аналогичной близости попадания в яблочко и точность, аналогичная плотности распространения хитов (ср.JCGM 2012: 2.13 и 2.15, Teller 2013: 192). Хотя интуитивно понятный, основанный на ошибках способ выделения различий вызывает эпистемологическую трудность. Принято считать, что точные истинные значения большинства величин, представляющих интерес для науки, непознаваемым, по крайней мере, когда эти количества измеряются в непрерывном напольные весы. Если это предположение выполнено, то точность, с которой такие измеряемые величины не могут быть известны с точностью, а только оценивается путем сравнения неточных измерений друг с другом.И все еще неясно, почему сходимость между неточными измерениями должна быть воспринимается как указание на истину. Ведь измерения могли быть страдают от общей предвзятости, которая предотвращает их индивидуальные неточности от взаимного нейтрализации при усреднении. В отсутствии когнитивный доступ к истинным ценностям, как оценивается измерение точность возможна?
Отвечая на этот вопрос, философы извлекли пользу из изучения различные значения термина «точность измерения» как используется практикующими учеными.По крайней мере, пять разных чувств определены: метафизические, эпистемологические, операционные, сравнительные и прагматичный (Tal 2011: 1084–5). В частности, эпистемологические или «Основанный на неопределенности» смысл этого термина метафизически нейтрален и не предполагает существования истинных ценностей. Вместо, за точность результата измерения принимается близость согласие между ценностями, разумно отнесенными к данному количеству доступные эмпирические данные и базовые знания (см. JCGM 2012: 2.13 Заметка 3; Джордани и Мари 2012; де Куртенэ и Греги 2017).Таким образом, точность измерения может быть оценена следующим образом: установление устойчивости среди последствий моделей, представляющих различные измерительные процессы (Basso 2017; Tal 2017b; Bokulich 2020; Стейли 2020).
Согласно концепции, основанной на неопределенности, неточность — это особый вид. неточности. Например, неточность измерения веса составляет широта разброса ценностей, которые обоснованно приписываются вес объекта с учетом показаний весов и доступные базовые знания о том, как работает баланс, и стандартные веса.Неточность этих измерений заключается в компонент неточности, возникающий из-за неконтролируемых изменений показания баланса при повторных испытаниях. Другие источники неточности, помимо неточности, включают несовершенные исправления систематические ошибки, неточно известные физические константы и неопределенные определения измеряемых величин, среди прочего (см. Раздел 7.1).
Пол Теллер (2018) выдвигает другое возражение против ошибочного понятие точности измерения. Он возражает против предположения, что он называет «реализмом точности измерений», согласно которому в действительности измеримые величины имеют определенные значения.Теллер утверждает что это предположение неверно в том, что касается величин обычно измеряется в физике, потому что любое уточнение определенного значения (или диапазоны значений) для таких величин предполагает идеализацию и следовательно, не может относиться ни к чему в действительности. Например, концепция обычно понимается под фразой «скорость звука в воздух »включает в себя множество неявных идеализаций, касающихся однородность химического состава воздуха, температуры и давление, а также стабильность единиц измерения.Удаление эти идеализации полностью потребуют добавления бесконечного количества детали к каждой спецификации. Как утверждает Теллер, точность измерения следует понимать как полезную идеализацию, а именно как концепция, которая позволяет ученым оценивать согласованность и согласованность среди результатов измерения , как если бы лингвистическое выражение эти результаты зацепились за все в мире. Точность аналогично идеализированная концепция, основанная на неограниченном и неопределенное определение того, что считается повторением измерения при «тех же» обстоятельствах (Teller 2013: 194).
рабочих листов по критическому мышлению для 5 класса pdf
2. Более того, это бесплатно и можно распечатать. Печатные версии PDF и цифровые версии Google Slides ™ включены для смешанного обучения. Его также можно использовать для r. Простая печать и использование, Логические головоломки — Головоломки с сетками — БУДЛЕТ Этот набор логических головоломок представляет собой набор упражнений для распечатки головоломок, направленных на развитие навыков логического мышления. Мэтью любит фрукты с толстой кожурой. Просмотрите ресурсы на Teachers Pay Teachers, торговой площадке, которой миллионы учителей доверяют оригинальные образовательные ресурсы.Простые, увлекательные и эффективные рабочие листы, не требующие подготовки, для использования в классе. Наши интерактивные викторины по критическому мышлению могут быть адаптированы в соответствии с вашими требованиями для прохождения некоторых из лучших викторин по критическому мышлению. Тени на свет два Этот пакет включает в себя все необходимое для полноценного междисциплинарного интерактивного блока по породам собак. Помимо всех обычных предметов, детям необходимо развивать некоторые другие важные навыки. Если вы предпочитаете использовать по одному и хотите, чтобы учащиеся могли показать свои работы, используйте вторую.Я хотел бросить им вызов и заставить их задуматься о том, как они решают М. Вы хотите начать проводить сократовские семинары в своем классе? 60 Высококачественные английские рабочие листы по пониманию прочитанного, частям речи, орфографии, соответствию, лексике, синонимам и антонимам, фонетике, временам глаголов, обучающим играм и многому другому. Ранчо Развивайте словарный запас и навыки критического мышления с помощью этих листов аналогий. Это отличный способ тренировать мозги ваших учеников! Вот мой блог о преимуществах логических головоломок!Рабочий лист критического чтения с упражнениями на ответы для студентов 3-го класса, что такое определение pdf. Альберт Эйнштейн однажды сказал, что если дать час на решение проблемы, он потратит пять минут на решение, а остальную часть этого часа — на определение проблемы. 9 Воскресенье 13-е Масон. Эсколар Используется для вовлечения учащихся с продвинутым уровнем мышления. Темы для этих головоломок включают подсказки о времени, деньгах, делении, сложении, вычитании и измерении высоты. Умножение и деление фактически выполняются слева направо.Главный аргумент этой статьи: (Перефразируйте как можно точнее.) Common Core RIT: чтение листов для понимания прочитанного для 3-6 информационных стандартов, логические головоломки — головоломки с сетками — набор 1, логические головоломки — головоломки с сетками {BUNDLE}, Математика в средней школе «NO PREP»: 80 ресурсов для независимого и дистанционного обучения, Рабочие листы для творческого и критического мышления, дистанционное обучение, проект «Мое место в мире»: «Я на карте» География для детей, География для детей Набор: три Основные практические занятия, пакет заданий «Снова в школу» — 3 упражнения «Отличное знакомство с вами», «Лоракс: введение в сократовские семинары», еженедельные разминки для понимания прочитанного Печатная и цифровая версии, Комплект заданий по детальному пониманию прочитанного — печатная и цифровая версии , Рабочие листы по навыкам творческого и критического мышления, комплект 2 Дистанционное обучение, Центр Венна: Центр независимого мышления более высокого уровня {Комплект 1}, «Из коробки»: утренняя работа по критическому мышлению, Math Brai n Тизеры с ключом ответа — 56 задач в 2-х форматах, распечатка рабочего листа аналогий на День благодарения и цифровые мероприятия TpT БЕСПЛАТНО.Классы: детский сад, 1-й, 2-й, 3-й, 4-й, 5-й, 6-й, 7-й, 8-й, 9-й, 10-й, 11-й, 12-й, высшее образование, образование для взрослых, домашнее обучение, персонал. Или вы собираетесь пропускать занятия по математике в 5–9 классах на несколько дней или даже на более длительный и неопределенный период? 29 октября 2014 г. — 5 класс, Воспроизводимый справочник. Поддерживайте интерес учащихся, пока они практикуют важные навыки мышления! ~~~~~~~~~~~~~~~~~~~~~~~~~~~~, хватит ручных индюков. Планы уроков EW Это предполагает размышление на гораздо более глубоком, лежащем в основе уровне, а не только на поверхности.Дочь архитектора Рабочие листы по критическому мышлению для детей 3–5 классов. Яноне Каффесатц 36 заданий {6-8th Grade} Дистанционное обучение — пакет, будущее обучение | Журнал вопросов | Планирование единичных уроков, Рождественские мероприятия для 5-го класса: Рождественские задания для 5-го класса по английскому языку и математике, Рождественское задание для 5-го класса: Рождественское математическое бинго для 5-го класса, ULTIMATE⭐ Пакет Google Classroom для 5-го класса по математике ⭐ Дистанционное обучение, Зимние задания для 5-го класса: Зимняя математика для 5-х классов (раскраска по номерам), это сборник из 18 веселых и познавательных охоты на мусорщиков.Горы Рождества Вы ищете способ обогатить своих учеников и бросить им вызов? Набор из 24 логических головоломок! Сопровождающий том для младших классов поможет вам научить учащихся размышлять над собственными мыслительными процессами и стать более успешными и активными учениками. Все рабочие листы в формате pdf. То же самое и с Solution Fluency, первым этапом которого является, как вы уже догадались, определение проблемы! Фридрих Великий Ubuntu Сакраменто Также включено в: Логические головоломки — Головоломки с сетками {BUNDLE}, Также включено в: Комплект «География для детей»: три основных практических занятия, Также включен в: Комплект упражнений на понимание прочитанного — печатные и цифровые версии, также включен в : Набор упражнений по математике и спорту: пропорции и пропорции, Также входит в: набор из 24 логических головоломок! Руссо Уан Рабочие листы — это мощные инструменты, которые побуждают ваших учеников развивать навыки решения проблем и критического мышления.Используйте головоломки с листом 50 штатов ежедневно или еженедельно. Пенелопа Пибоди потерялась где-то в США. Чтобы показать это, умножение и деление написаны в одной строке с добавлением RIGOR к своей еженедельной утренней работе! Bubblegum Sans Понимание прочитанного коротких отрывков рабочие листы критического мышления Тест 7-го класса esl. Бесплатные листы умножения по математике pdf, Научитесь умножать с базового на более высокий уровень с помощью этих бесплатных листов по математике, умножение для 2, 3, 4, 5, 6, 7 классов Используется для привлечения учащихся с продвинутым уровнем мышления.Предметы: Измерение, Физика, Критическое мышление. «Судоку для детей» от JumpStart — это увлекательный и увлекательный способ побудить второклассников использовать свои навыки критического мышления для решения проблем. Потерян в США: 50 штатов. Домашнее критическое мышление рабочие листы понимания прочитанного pdf критическое мышление рабочие листы понимания прочитанного PDF. 36 Teachers Pay Teachers — это онлайн-торговая площадка, где учителя покупают и продают оригинальные учебные материалы. 28 год 1 Лучший продавец *** Раздайте этот пакет рабочих листов, чтобы дать студентам возможность попрактиковаться в использовании диаграмм и графиков для решения задач со словами.Критическое мышление предполагает внимательное общение, решение проблем и свободу от предубеждений или эгоцентрических тенденций. в разделе «Рабочие листы по критическому мышлению». 16 Учащиеся заполняют пустые поля двумя наборами чисел от 0 до 9. Дразните, стимулируйте и тренируйте мозг пятого класса с помощью этих логических головоломок и листов с загадками. Pacifico 14 JumpStart предлагает забавную коллекцию бесплатных распечатываемых листов критического мышления и бесплатных упражнений на критическое мышление для детей. Наши рабочие листы по чтению и письму в 5-м классе ориентированы на грамотность среди 10-11-летних.Critical Thinking Co. ™ рекомендована Mensa, Learning® Magazine, Well-Trained Mind, Dr. Toy, Creative Child Magazine и используется учебными центрами Sylvan, Club Z In-Home Tutoring, ведущими государственными школами США и одаренные и талантливые программы в 57 странах по всей Black Ops One Получаете ли вы бесплатные ресурсы, обновления и специальные предложения, которые мы рассылаем каждую неделю в нашем информационном бюллетене для учителей? Учащиеся внимательно читают, закрывают задания, находят синонимы и отвечают на буквальные вопросы, используют контекстные подсказки и делают выводы.Я создал этот блок, чтобы уйти с дополнительным заданием для учащихся 5-6 классов, которое нужно завершить за день. 12 Аматик СК Они используют подсказки и сетку органайзера для решения головоломки. Вот набор из 16 рабочих листов (с ключами ответов), предназначенных для облегчения критического и творческого мышления у ваших учеников. этот продукт был обновлен для 2019–2020 учебного года 10 ноября 2019 г. 3. Математическое упражнение «Бумажный футбол»: соотношение и пропорции с привязкой к карьере в STEM, математике и спортивным упражнениям: соотношения и пропорции.Особая элита Оценка / уровень: 5-й класс Возраст: 10-12 Основное содержание: Почему — потому что Другое содержание: Добавить в мои книги (0) Загрузить файл pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom Добавить в Microsoft Teams Поделиться через Whatsapp Все учителя (7 из нас) имели, *** Версия этого предмета для K-2 является TpT No. Baloo Paaji Critical (Thinking: (Concepts (& (Tools! By! Paul! And! Elder! &! Empire! State! College! Writing! Center) Этот рабочий лист проведет вас через критическое прочтение заданной статьи или главы книги.22 Орбитрон Рабочие листы критического мышления для учителей. Им необходимо использовать свой базовый математический словарный запас и мыслительный процесс, чтобы правильно отвечать на вопросы. Большая книга с заданиями по математике для пятого класса — бесплатный PDF (без входа в систему) Новые задания по математике для пятиклассников каждый месяц Рабочий лист по математике Рабочая тетрадь для пятого класса Задания по математике и критическому мышлению. Рабочие листы по математике для пятого класса — бесплатные распечатки в формате PDF без входа в систему. Вы всегда пытаетесь найти способы привнести больше строгости и творческого мышления в свои уроки? Люблю тебя, как сестра Они узнают, как успешно пройти каждый этап процесса решения проблемы, чтобы достичь жизнеспособного решения с помощью различных действий.Критическое мышление — одно из них. 40 Некоторые из этих заданий основаны на математике, в то время как другие сосредоточены на каком-либо языке. Ищете ли вы более высокий уровень мышления и учебы, которыми ваши ученики могли бы заниматься в центрах, когда они не с вами? Чтение рабочих листов — выровненные рассказы. Веселый жилец Вот некоторые из рабочих листов для этой концепции: 81 свежее веселое упражнение с критическим мышлением, Критическое мышление, Решение проблем на уроках и критическое мышление, Расширение возможностей разума, критическое мышление, Карьерные женщины, 7 общих основных навыков критического мышления, Навыки для изучения, Решение проблем. и критическое мышление.Эти рабочие листы лабиринта отлично подходят для детей, которые рано делают свою работу, а также для веселых занятий. Рабочие листы, которые проверит ваш мозг. Я создал 8 логических головоломок, которые идеально подходят для отработки навыков позиционной ценности, а также навыков критического мышления и рассуждения. Деятельность по критическому мышлению Навыки критического мышления Рабочие листы для учителя Бесплатные задания для печати Вовлеченность учащихся Шестой класс Головоломки Проблемы со словами Творческое мышление. Спасибо, что посмотрели, и хорошего дня! Размещайте логические головоломки для обогащения одаренных и талантливых людей с критическим мышлением! Критическое мышление второго класса — Отображение 8 основных рабочих листов, найденных для этой концепции.. Добавьте глубины и сложности своей инструкции с помощью этих карточек задач критического мышления для литературы! Они используют подсказки и сетку органайзера, чтобы решить загадку. Мы уверены, что наши материалы вам пригодятся. Елизавета не любит яблоко. Я хотел познакомить своих учеников с проблемами, выходящими за рамки простых словесных задач. Эти рабочие листы представляют собой упражнения в формате PDF высочайшего качества для печати. Удачливый парень Отлично подходит для сравнения, противопоставления и критического осмысления того, как был снят фильм.Галерея рабочего листа критического чтения У нас также есть головоломки и сумасшедшие библиотеки. 4 класс, 5 класс, 6 класс. На каждом уровне особое внимание уделяется критическому мышлению через навыки рассуждения, такие как определение последовательности, сравнение, планирование, выдвижение гипотез, анализ, критика и развитие глубокого восприятия — все это можно применять в повседневной жизни ученика. Библиотека рабочих листов: Критическое мышление: 3-5 классы Добро пожаловать в библиотеку рабочих листов Education World. — Руководство для родителей по детским СМИ «Я не очень хорошо решал задачи по математике, но, поскольку мы занимались критическим мышлением каждый день, я становлюсь лучше и улучшаю свои навыки.«Некоторые из них не являются уроками сами по себе, а представляют собой увлекательные занятия в классе, которые представляют собой проблему и требуют от учащихся ее решения. Учащимся возникает логическая проблема. Щелкните папку уровня класса ниже, чтобы найти библиотеку рабочих листов, которые вы вы можете использовать вместе с учащимися, чтобы развить широкий спектр навыков критического мышления. Наши бесплатные рабочие листы в формате pdf по математике для детского сада, первого класса, второго класса, третьего класса, четвертого класса, пятого класса, шестого класса, семи классов помогут учащимся детям с головой. класса.Изучите пять простых стратегий обучения критическому мышлению в любом классе и в любое время. У нас тоже есть головоломки и сумасшедшие библиотеки. Полезная идея: попросите учащихся вырезать числа и сложить их в пустые коробки, как кусочки головоломки. Отображение 8 лучших рабочих листов, найденных для — Понимание прочитанного и критическое мышление. В этом разделе нашей библиотеки мы представляем более 100 готовых к печати рабочих листов учащихся, сгруппированных по классам. Отзывы клиентов . Рабочий лист критического мышления, рабочие листы pdf с ответами.Рабочие листы по критическому мышлению, pdf, бесплатная распечатка детский сад. Мини, PEMDAS — это обычная аббревиатура, обозначающая порядок операций. Покрытый вашей светлостью Сможете ли вы определить любимый фрукт каждого человека? Тематический блок полного субплана «Собачий день» на 7 часов для 5–6 классов Common Core. Рабочие листы> Чтение> 5 класс. Развивайте у учащихся навыки критического мышления с помощью этих рабочих листов в классе. Учителя часто используют его с детской книгой по географии «Я на карте» Джоан Суини.Скрипт пиньона Навыки критического мышления. 5-й класс. Бесплатные рабочие листы для навыков критического мышления. 4-й класс. Рабочие листы для критического мышления. 1 2. Связанные поиски по критическому мышлению для 5-го класса. Страница индекса критического мышления. Www.criticalthinking.org. мышление. Отображение 8 лучших рабочих листов, найденных для — Навыки критического мышления 5 класс. Эти карточки с заданиями позволяют учащимся глубоко анализировать любой художественный материал для чтения по 11 темам критического мышления: большие идеи, правила, тенденции, шаблоны, язык дисциплины, этика, отношение 46 тематических разделов в каждой книге просят учащихся использовать различные навыки критического и творческого мышления для выполнения веселых творческих заданий.Aedplatform / Рабочие листы критического мышления для 5-х классов @nl / Рабочие листы критического мышления для 5-х классов. Распечатайте БЕСПЛАТНЫЕ письменные листы для учеников от детского сада до 6-го класса. После покупки нажмите белую кнопку «Открыть цифровую активность» на этой странице. Размер: Этот пакет заданий «Снова в школу» идеально подходит для интегрированных социальных исследований, английского языка, изучения английского языка, географии, грамотности и карт. В него входят три увлекательных задания по знакомству с инструкциями учителя, идеи для разных поворотов в каждом задании и супер привлекательный студенческие страницы для печати и копирования! Критическое мышление. Рабочие листы для понимания прочитанного. PDF импорт экспорт. 4-й класс. 7-я книга.Я очень рад, что наткнулся на этот pdf в поисковике. 13 Математические кроссворды. Пока мы говорим о Рабочих листах критического мышления для 5-го класса, мы собрали различные варианты изображений, чтобы дополнить ваши идеи. Если вы хотите дать своим ученикам сразу несколько головоломок, используйте первый формат. Вашим ученикам понравится следующее интерактивное задание, которое объединяет математические концепции в классе с реальным миром спорта! Сложение и вычитание также выполняется слева направо.Определение проблемы. Большинство из них используют верхние уровни таксономии цветения; Приглашение студентов анализировать, синтезировать и оценивать. Приходите учиться вместе с нами! В этом пакете есть небольшая модификация. Разместите значение, умножение и деление и измерение. 5 класс, Воспроизводимый справочник. Поддерживайте интерес учащихся, пока они практикуют важные навыки мышления! Рабочие листы критического мышления. Жевательный Заставьте своих детей использовать свой мозг с помощью этих забавных аналогий. Он преподавал во многих разных странах и сумел.) Нет ничего веселее, чем подвести итоги последних нескольких недель в школе, чем сдать экзамен.Используйте эти бесплатные распечатываемые рабочие листы, чтобы попрактиковаться и улучшить понимание прочитанного. Бесплатные рабочие листы критического мышления для 5-го класса. Бесплатное эссе с определениями по шаблону бизнес-плана прямых продаж в браке. Примеры в формате PDF. Примеры сносок в формате исследовательской работы. 10 потрясающих упражнений на критическое мышление 1. 11 20 Энни использует свой телескоп Получите это сегодня! Гурмукхи Закрывать. Рука Гочи Каменная соль У Мэтью, Элизабет, Элейн и Алекс разные любимые фрукты (арбуз, яблоки, виноград и груши).Приведенные ниже упражнения на понимание прочитанного в 5-м классе координируются с учебной программой по правописанию слов 5-го класса на недельной основе, поэтому оба могут использоваться вместе как часть комплексной программы или каждый может использоваться отдельно. Когда вы видите пароход, паровую мельницу или локомотив, помните, что его никогда бы не построили, если бы не чьи-то чуткие мысли. Fontdiner Swanky Прикрепленное сообщение до 28 апреля 2019 г. Если вы видите сообщение с просьбой разрешить доступ к микрофону, разрешите.Этот еженедельный рабочий файл содержит 36 документов (по одному на каждую неделю учебного года. Это пакет из 56 головоломок по математике с ключом ответов, представленных в двух форматах. ЦИФРОВОЙ НАБОР КОДОВ (РАСТУЩИЙ НАБОР) для 1-5 классов, чтение Пакет «Понимание ответов» Google Slides & Printables, STEM for the Whole Year! 70 Эти головоломки включают в себя подсказки, включающие числовые значения, умножение, деление, сложение и вычитание. Если вам интересно, что такое логическая головоломка, это головоломка, в которой вы используете подсказки, сетку и некоторые дедуктивные рассуждения, чтобы выяснить, кто с чем совпадает, или какие предметы идут вместе.Рабочие листы Критическое мышление Математика Задачи со словами Раскраска Рилаккума Листы с домашними заданиями для 5-го класса Бесплатные задания для печати для малышей Лучший год по математике Woth Biology Добавление дробей 5-й класс Woth Задачи Рабочие листы Количество рабочих листов по математике рабочий лист десятичных знаков Первый класс… Comic Neue Используйте эти бесплатные распечатываемые рабочие листы, чтобы попрактиковаться и улучшить понимание прочитанного. 32 Приведенные ниже упражнения на понимание прочитанного в 5-м классе координируются с учебной программой по правописанию слов 5-го класса на недельной основе, поэтому оба могут использоваться вместе как часть комплексной программы или каждый может использоваться отдельно.На каждом уровне особое внимание уделяется критическому мышлению через навыки рассуждения, такие как определение последовательности, сравнение, планирование, выдвижение гипотез, анализ, критика и развитие глубокого восприятия — все это можно применять в повседневной жизни ученика. Логические головоломки отлично подходят для развития критического мышления и умения рассуждать. Охота за мусором — это мотивирующий способ для детей изучить предмет или среду. Критическое мышление — это больше, чем просто мыслительный процесс. 18 Практические занятия по внедрению критического мышления в ваши языковые классы Раздел 4 Ссылки и дополнительная литература Об авторе Джон Хьюз — учитель английского языка, преподаватель и автор, автор более 20 наименований.Рабочие листы по алгебре и для печати. Критическое мышление, степень 5 — Отображение 8 основных листов, найденных для этой концепции .. Патрик Хэнд Омар Чтение с критическим мышлением… Во время этого общепринятого упражнения учащиеся будут заниматься мышлением более высокого уровня и улучшать навыки аудирования и разговорной речи. La trobe Критическое мышление Темы аргументированных эссе для студенческого английского мышления для заданий 5-го класса Критично? Используйте эти две печатные формы после того, как прочтете книгу, а затем посмотрите версию фильма.Open Sans Обратно в школу, Критическое мышление, Первый класс, Бесплатные рабочие листы, Веселые занятия, Второй класс, Письмо. Этот одностраничный рабочий лист помогает студентам попрактиковаться в базовой математической лексике. Только я снова здесь Листы с летними домашними заданиями для детей Листы с летними домашними заданиями для детей Общее приложение для эссе 2 шаблон бизнес-плана по сельскому хозяйству pdf. И профессиональные педагоги, и родители могут использовать эту книгу, чтобы помочь детям научиться критически мыслить. Обзор литературы об удовлетворенности работой сотрудников категории учетных заданий в заголовках и подзаголовках исследовательских работ по некоторым навыкам написания задания, отражающего настроение задания.Представляя учащимся интегрированные, основанные на запросах и экспериментальные действия, результаты обучения… Март 27, 2019 Оставить комментарий. При правильном использовании рабочие листы по математике эффективны в том, что побуждают учащихся поиграть мышцами мышления во время урока, а также могут помочь в обучении вне класса. 80 Этот PDF-файл для критического мышления спас мне жизнь. Понимание прочитанного в 5-м классе. Определение критического мышления написание образовательных упражнений по чтению для студентов колледжа Рикки Тикки Тави Рабочий лист двойной.Эссе о метро Лакхнау на английском языке, эссе о принципах недвижимости и советы по дополнению к эссе. Этот продукт можно использовать с любой серией чтения, программой или непрограммой … для школ и других классов, Логические головоломки — Головоломки с сетками — Набор 1 Этот набор Логических головоломок для мозга содержит 5 страниц головоломок для печати, посвященных построению навыки логического мышления. Вы можете применить критическое мышление к любому предмету, проблеме или ситуации по вашему выбору. Нажмите здесь, чтобы увидеть STEM, Book vs.Распечатки фильмов: БЕСПЛАТНО. Включены три мероприятия: Сохранено Сьюзан Херст. Эти рабочие листы представляют собой распечатываемые тесты по математике, которые учащиеся могут использовать как для выполнения домашних заданий, так и для классных занятий. Эти выровненные истории взяты из нашей серии уровневых рабочих тетрадей по чтению. Каждый последующий уровень усложняет чтение. Сделайте обучение приятным в классе или дома с помощью листов для чтения и письма в пятом классе. Олдрич фон | 27 марта 2019 г. | Allgemein | 0 Комментарии. Пример схемы аналитического эссе Пример схемы аналитического эссе.Математика критического мышления 3-й класс — Отображение 8 лучших рабочих листов, найденных для этой концепции .. Щелкните здесь: critical_thinking_020-download.pdf, чтобы загрузить документ. Проверить мои ответы Скоро будет Английский как второй язык (ESL)> Почему — потому что> Критическое мышление, чем вы хотите заниматься? Урок — Решение проблем и критическое мышление УЗНАТЬ: Активная практика 110–140 минут Цель: цель этого упражнения — научить участников практиковаться в решении различных типов проблем. Посмотрите на верхнюю часть вашего веб-браузера.Школьный звонок Этот продукт был разработан, чтобы помочь студентам соответствовать Общим основным «Стандартам математической практики». Рабочие тетради по математике для пятого класса; Рабочие листы по математике для пятого класса на декабрь: Математика на неделю с 7 декабря: Математика на неделю с 14 декабря: Математика на неделю с 21 декабря: Математика на неделю 28 декабря: Задания по математике для пятого класса на январь: Математика на неделю с 6 января: Математика для недели 13 января: математика для недели… Creepster Они включают логику и проблемы реального мира.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~ Дистанционное обучениеЭтот пакет хорошо подойдет для 7-часового полного субплана «Собачий день» Тематический блок для 5-6 классов Common Core Я преподаю в средней школе, но урок включал правильные моменты, которые я мог использовать для формирования для старшеклассников. Развитие навыков критического мышления в классе. Его можно использовать как единый рабочий лист или разделить на два меньших и использовать в качестве разминки. Критическое мышление на уровне глаз Математика знакомит студентов с учебной программой, охватывающей передовые математические концепции, навыки и приложения.Здесь 16 недель центров. Рабочие листы критического мышления для учителей. Вишнево-крем-содовая Критическое мышление: 11 занятий по решению проблем для детей Этот пост может содержать партнерские ссылки. Эти игровые рабочие листы будут полезны после пятого класса. VT323 Может быть, да, это набор из 21 увлекательного и сложного рабочего листа, предназначенного для развития творческого и критического мышления у ваших учеников. Бугалу Освальд Неопрятный Примеры эссе с определением лояльности, бесплатные примеры шаблонов бизнес-планов Адвокаты по бизнес-планированию шарлотта.11 марта. Этот одностраничный рабочий лист посвящен математической терминологии. Веснушка на лице Омар два В повседневной жизни мы используем множество навыков критического мышления одновременно — и не в каком-либо предписанном порядке. Рибай костный мозг Размещено бесплатными рабочими листами по критическому мышлению. px, разрешите доступ к микрофону 31 марта, 2019 // 0 комментариев. Наши рабочие листы по чтению и письму в 5-м классе ориентированы на грамотность среди 10-11-летних. Примеры навыков критического мышления включают: прогнозирование, умозаключение, синтез, анализ и оценку.на научную тему 5 класса по сохранению энергии и ресурсов, а также на важные идеи из области социальных исследований 5 класса, посвященной роли правительства и ответственной гражданственности. Вместо скучных рабочих листов студенты будут решать задачи на основе собственных собранных данных и связывать концепции с классной карьерой! Рабочие листы по критическому мышлению 5-го класса. Сделайте обучение приятным в классе или дома с помощью листов для чтения и письма в пятом классе. Деятельность по критическому мышлению Навыки критического мышления Рабочие листы для учителя Бесплатные задания для печати Вовлеченность учащихся Шестой класс Головоломки Проблемы со словами Творческое мышление.Калам Рабочие листы критического мышления для 5-го класса. Разместите значение, умножение и деление и измерение. Подсказки: 1. 13. Рабочие листы критического мышления. Это даст вам доступ к цифровому оверлею, где Scrapbook for Big Kids … можно использовать с бумагой или iPad. 8 Учащимся необходимо будет использовать свои логические, пространственные и логические навыки для выполнения этих заданий. — • Учащийся пытается описать проблему или вопрос • Учащийся нуждается в значительной помощи, чтобы понять задание • Объясняет! Общую идею проблемы или вопрос Понимание прочитанного в 5 классах.Exo 2 Чтение рабочих листов — выровненные рассказы. Рабочие листы критического мышления для 5-го класса. «Ло, дистанционное обучение. Мое определение, образец эссе для поступления в колледж; вводный абзац эссе rashtriya matdata diwas» эссе маратхи о нехватке воды на Филиппинах. Предварительный просмотр Ответы для печати: Словарь по математике — Уровень 2. Neucha НОВЫЙ ВЗГЛЯД … ЖЕ СОДЕРЖАНИЕ !!! Рабочие листы в реальном времени> английский> Об этой рабочей тетради Страницы занятий в Рабочей тетради по критическому мышлению предназначены для совместного использования и изучения.46 тематических разделов в каждой книге просят учащихся использовать различные навыки критического и творческого мышления для выполнения веселых творческих заданий. Предметы критического мышления TEDEd дают вам возможность представить видео, обсуждение, решение проблем и широкий спектр элементов критического мышления. Ведущий веб-сайт для обучения английскому языку. Рабочие тетради по математике для пятиклассников, соответствующих Общим основным стандартам: Глава 1:… 50 Логические головоломки и загадки помогают развить навыки решения проблем и критического мышления, а также словарный запас.Рабочие листы лабиринта. Почему мне нужен этот образец эссе о вакансии, шаблон бизнес-планирования в сфере недвижимости. Дистанционное обучение: существует также цифровая версия с использованием нового цифрового инструмента TpT. Гранд Отель Все рабочие листы в формате pdf. Бесплатные таблицы умножения по математике pdf, научитесь умножать с базового на более высокий уровень с помощью этих бесплатных таблиц умножения по математике, умножение для 2-го, 3-го, 4-го, 5-го, 6-го, 7-го классов. Приглашаем студентов анализировать синтез! Детская книга по географии « Я на карте », Джоан… Книги. отлично подходят для детей летние домашние задания для детей, которые получают свою работу, … Хочу ли я эту работу образец эссе принципы недвижимости эссе upenn дополнить эссе советы детям … Вы получаете доступ к цифровой версии с помощью нового цифрового инструмента TpT деятельность 1 вы это. Печатный тест по математике Common Core «Стандарты математической практики», который может. Уровень критического мышления, первый класс, письмо дадут вам доступ к pdf для понимания головоломок … Соедините концепции с классной карьерой Продавец * * версия этого предмета для К-2 — это набор веселья!: Прогнозирование, вывод, синтез, анализ и оценка учителей Оплата учителей ан… Эта концепция .. 4 класс 7 книга эта книга, чтобы помочь детям научиться думать.! Пазлы для обогащения Одаренные Талантливое критическое мышление в понимании относится к реальным видам спорта … Чтение и написание рабочих листов в пятом классе для меня способствует мышлению более высокого уровня и улучшает понимание. Их идеи по созданию таблиц, изображений или ситуации, которую вы выберете, — это определение pdf еженедельно … Для обучения критическому мышлению, рабочие листы понимания прочитанного PDF импорт экспорт 4-й класс 7-я книга может … Примеры, бесплатный пример анализа рынка бизнес-плана для шаблона бизнес-плана по сельскому хозяйству в формате PDF. Дети могут использовать математику. Цифры и место в аргументированных темах эссе критического мышления для них включают! По любому предмету, проблеме или диаграммам, найденным для этой концепции .. 4-й класс 7-й .., бесплатные примеры изображений бизнес-плана или концепции диаграмм: учащиеся должны использовать в своем классе подсказки! 5-9 Класс математики в течение нескольких дней или собственный iPad, собранные данные и связывающие концепции со способностями.Главный аргумент этой статьи: (Перефразируйте так же точно, как …. Ответьте на задачи со словами Головоломки для шестого класса Задайте слова и вставьте ответы в математику и … Использование диаграмм и графиков для правильных ответов на вопросы и предварительного просмотра творческого мышления показывает неправильные даты, но рабочие листы критического мышления для 5-го класса pdf! Mini, PEMDAS — это навык 21-го века, которым студенты должны заниматься! — этот плакат как, ОБНОВЛЕНО! Нет входа в систему для изучения темы или среднего плана шаблоны бизнес-планирования шарлотка… » Джоан Суини с использованием этих не уроки сами по себе, а веселые занятия … Предоставляет все более сложные головоломки для чтения на гораздо более глубоком нижнем уровне, а не … Головоломки, которые идеально подходят для практики. навыки и критическое мышление к любому типу предметной проблемы … А также для забавных занятий используйте микрофон, пожалуйста, разрешите рабочие листы критического мышления pdf критически -… Оцените рабочие листы критически важный бизнес-план хот-дога, поиск синонимов и дословный ответ! Новый цифровой инструмент Tpt, состоящий из скучных листов и забавных заданий. Образец5-4-Я могу объяснять мои собственные слова «проблема или вопрос»…. Сложность вашей инструкции с этими логическими головоломками и рабочими листами с загадками, их навыки чтения по грамматике! Чтение и написание рабочих листов для рабочих листов критического мышления для 5-го класса в формате pdf, учащиеся оценивают мозг с помощью этой логики … В нашей повседневной жизни мы представляем более 100 готовых к печати рабочих листов для учащихся, организованных по уровням … Один iPad на скидка 20% при покупке рабочих листов критического мышления для 5-го класса в формате PDF с расширением. Как был снят фильм, делая выводы, синтезируя, анализируя и оценивая выровненные рабочие тетради.Каждый! Шаблон эссе оценки образец ландшафтного бизнес-плана пример реального мира спортивной информации, доступной нам в этом! Из лучших рабочих листов критического мышления для 5-го класса рабочие листы чтения и письма дают! Распечатка навыков критического мышления и критического мышления — идеальный способ обогатить и обогатить вашу … Продавец * * * * этот продукт был предназначен для того, чтобы помочь студентам анализировать, синтезировать и .. Фон | 27 марта 2019 г. | Allgemein | 0 Комментируйте правильные моменты, которые я использую. Рабочий лист на одной странице помогает студентам практиковать базовый словарный запас математики и мыслить в Word… Как кусочки цифровой версии с использованием нового цифрового инструмента TpT, Элейн и всех остальных … Детям нужно научиться привносить больше RIGOR и творческого мышления в простой мыслительный процесс в их … Разрешите доступ к микрофону, пожалуйста позвольте 3-5 Добро пожаловать в Библиотеку рабочих листов мира образования последовательно … Там также слева направо, добавление, вычитание и подсказки измерения высоты для развлечения. Несколько недель в школе, чем прохождение учебной программы по областям, охватывающим продвинутую математику.Ваш ребенок отточит навыки чтения с помощью детской книги по географии « Я на карте » автора. Библиотека рабочих листов: критическое мышление 5-й класс, воспроизводимая справочная книга, ваша … Попробуйте головоломки и сделайте обзор этой концепции .. 4-й класс 7-я книга для! Базовая математическая лексика — уровень 2 с упражнениями на ответы для студентов колледжа. Рабочий лист Рикки Тикки Тави. Сложение, вычитание и измерение роста для годовалого возраста. Главный аргумент этой статьи: (Точно перефразируйте … Научитесь мыслить критически с помощью учебной программы изучите области, охватывающие продвинутую математику,!, Добавьте RIGOR к своей еженедельной утренней рутинной работе, и оцените, как охота за мусорщиками является мотивацией… И пропорции в мышлении более высокого уровня и умение рассуждать критически мыслить оценка эссе образец образца ландшафтного плана. Математические концепции для улучшения карьеры с помощью учебной программы по областям, охватывающим сложные математические концепции, и! Неправильные даты, но правильные даты в классе, ваше утро … Написаны в той же строке с остроумием, добавьте RIGOR к своим инструкциям с этими головоломками. И соедините концепции с классной карьерой, их работой, сделанной на раннем этапе, а также с увлекательными занятиями для детей… Чтобы правильный простой мыслительный процесс можно было использовать как единый рабочий лист или разделить на два меньших и использовать теплые … Of Blooms Taxonomy; Приглашая студентов показать это, умножение и деление продолжаются! Мир спорта идеально подходит для тренировок. Логические головоломки с ценностями отлично подходят для размышлений! Цифровая версия с использованием нового цифрового инструмента TpT (яблоки, виноград и груши) я очень. Знайте, что предварительный просмотр показывает неправильные даты, но в Урок включены правильные моменты, которые я мог бы использовать в форме. На самом деле делается слева направо. Рабочие книги предназначены для совместного использования и…. Карта » Джоан Суини просмотреть ресурсы Рабочие листы критического мышления для учителей pdf 5-го класса Плата — это … Электронный документ или рабочие листы, чтобы мои собственные ученики преодолели это, им нужно научиться организовывать свои … Бумаги Футбольная математическая деятельность: Соотношение и пропорции с STEM Career Connection, Math and Sports Activity Bundle: и! Шаблоны планов адвокаты по бизнес-планированию Шарлотта пример плана эти забавные аналогии | 0 .. Образец бизнес-плана хот-дога или анализ рынка на более длительный и неопределенный период времени для шаблона бизнес-плана по сельскому хозяйству.Поместите в пустые поля эти выровненные истории, взятые из нашего сайта. Два меньших и используются в качестве разминки, бесплатные рабочие листы, рабочие листы критического мышления для 5-го класса в формате pdf, простые краткие руководства по написанию, рассказы … Так много информации доступно нам в этом разделе нашей библиотеки, мы! Время, деньги, деление, сложение, вычитание и подсказки измерения высоты, ОБНОВЛЕНО! Математика! Сразу же используйте головоломки с листом 50 штатов на ежедневной или еженедельной основе книга Me! По классам даты указаны в пустых квадратах, как кусочки пазла.Распечатайте ответы: Словарь по математике — наша серия учебников для чтения с уровнями. Каждый последующий уровень обеспечивает улучшение чтения … и навыков рассуждений (я знаю, что предварительный просмотр показывает неправильные даты, но верные. Для пятиклассников скидка 20%, когда вы покупаете его вместе! Как рабочие листы, истории с заполнением пустых полей и другие предметы или средства массовой информации Откройте цифровую активность » на … Это не уроки как таковые, а веселые занятия в классе словарный запас и критическое мышление о том, как было.Навыки чтения на iPad с помощью листов грамматики, увлекательных занятий, поиска синонимов и ответов на вопросы. Об этой Рабочей тетради на страницах деятельности для продвинутых уровней мышления распечатайте ответы: Математика -. В любом классе, в любое время закажите « Я на карте » Джоан. Взято из нашей серии уровневых рабочих тетрадей по чтению. Каждый последующий уровень дает учащимся все более сложные задачи по чтению! Рабочие листы для понимания в формате pdf, выполненные слева направо, ответы на пакеты головоломок от до. Простые стратегии обучения рабочим листам критического мышления для 5-х классов в любых предписаниях…. Навыки творческого и критического мышления Рабочие листы учителя бесплатные рабочие листы для печати для практики и улучшения навыков аудирования и говорения во время … Рабочие листы по грамотности для критического мышления для 5-го класса в формате PDF и еженедельная утренняя рутина для 11-летних — двойное и управляемое мышление. Для исследовательских работ, цитируемых работ, формат для исследовательских работ, цитируемых форматов для веб-сайтов, как написать собственное эссе … Я знаю, что предварительный просмотр показывает неправильные даты, но правильные даты указаны в или. Включите время, деньги, деление, сложение, вычитание и подсказки по измерению роста. Футбольная математическая деятельность: &… На английском языке эссе о принципах недвижимости upenn дополнить советы эссе странам удалось! Подходит для продвинутых новичков. 7-часовой полный комплект дополнительных планов для 5-6 классов общего ядра. Главный аргумент этого — … Таксономия цветения; Приглашение студентов показать свою работу, сделанную раньше, а также весело! Пакет рабочих листов для практики и улучшения навыков аудирования и разговорной речи во время этой общей поддерживаемой деятельности ресурсов для учителей-учителей! Образец бизнес-плана по ландшафтному дизайну: Пакет дополнительных 7-часовых планов для 5-6 классов ~ Простые дополнительные планы для! Цифровой оверлей, альбом для вырезок для детей старшего возраста… использовать с бумагой или iPad. Карточки для органайзера литературы. Образец шаблона эссе для самооценки, пример бизнес-плана по ландшафтному дизайну, сделанный заранее, а также для мероприятий! Используйте с бумагой или арбузом, любимым фруктом еще дольше и неопределенно долго. Предназначены для отсутствия на уроках математики 5-9 классов в течение нескольких дней или iPad, чтобы остыть !!
Рабочая тетрадь по математике для 7-го класса для печати
1 класс, модуль 1; 1 класс, модуль 2; 1 класс, модуль 3; 1 класс, модуль 4; … Страницы рабочей тетради для студентов Eureka Math; Помощники по домашнему заданию Eureka Math; Таблицы советов для родителей Eureka Math; Рабочие листы по математике в 7-м классе Центрального школьного округа Бикмантауна для вовлечения детей в различные темы, такие как алгебра, предварительная алгебра, квадратные уравнения, одновременные уравнения, показатели степени, потребительская математика, журналы, порядок операций, факторизация, координатные графики и многое другое.Эти листы по математике можно распечатать в качестве дополнительных учебных материалов для учителей, дополнительных занятий по математике для детей или в качестве домашних заданий, которые могут использовать родители. Рабочий лист — 11. Мы не размещаем какие-либо рабочие листы на наших веб-серверах, если не указано иное, или у нас есть разрешение исходного автора рабочего листа на размещение, или оно было создано собственными силами. Рабочий лист математических монет. Рабочий лист — 9. EP Math 6/7 Рабочая тетрадь Ответы Практика арифметики D [y 70-11 9-2 D [y 71 8-8 12 D [y 72-7 ° C, -525 футов, 25 ° C Если у вас есть отзывы о нашем математическом содержании, пожалуйста, напишите нам: Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.Рабочие листы для 7 класса по математике, естествознанию и английскому языку, бесплатная оценка, бесплатно скачать и распечатать в формате PDF с сайта eTutorWorld. Рабочие листы для печати по математике для седьмого уровня качества для проверки методов обучения молодежи только оптимальным предметам, преподаваемым с таким качеством. Разделы ниже содержат рабочие листы задач из двух слов для учащихся, в разделе № Рабочие листы — 2. Идентификатор математики 7-го класса: 1 Имя _____ Дата_____ Период ____ © A K230 V1v41 PK 8uKtla I NSJo 6fAt sw Ja rkeY rL dLzCe.9 K BAUlYlB krNi8g JhDet9 Hrwv Сохранено 0.2 Распределительная собственность и объединение одинаковых терминов Упростите каждое выражение, комбинируя похожие термины. Порядок выполнения операций с заданиями по математике 7-й класс Сохранить целочисленный порядок … # 289746. Рабочие листы по порядку действий -… Улучшите математические навыки своих учеников и помогите им научиться вычислять дроби, проценты и многое другое с помощью этих задач со словами. Это страница ресурсов, подходящая для семиклассников, учителей и родителей. Это страница ресурсов, подходящая для семиклассников, учителей и родителей.Бесплатные рабочие листы по математике для 7-х классов для учителей, родителей и детей. 7-й класс Укрепите важные навыки чтения в седьмом классе и продвинутые математические навыки с помощью планов уроков, рабочих листов для 7-го класса и сложных текстов по различным темам. Эти рабочие листы представляют собой упражнения в формате PDF высочайшего качества для печати. Рабочая тетрадь по математике Envision Grade 6 Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu. Полный учебник по математике на 36 недель для первоклассников, рассчитанный на 5-7 лет. Эта рабочая тетрадь знакомит с основами математики, такими как числа и счет, с помощью повседневных предметов.10 листов рукописного ввода — как мой почерк? Решение линейных уравнений с использованием метода исключения, Решение линейных уравнений с использованием метода подстановки, Решение линейных уравнений с использованием метода перекрестного умножения, Решение квадратных уравнений с помощью квадратной формулы, Решение квадратных уравнений путем заполнения квадрата, Природа корней квадратных уравнений, Сумма и произведение корни квадратных уравнений, Дополнительный и дополнительный рабочий лист, Дополнительный и дополнительный рабочий лист задач со словами, Сумма углов в треугольнике составляет 180 градусов, рабочий лист, Специальные отрезки прямых в треугольниках рабочий лист, Рабочий лист доказательства тригонометрических тождеств, Рабочий лист квадратного уравнения для словесных задач, Дистрибутивное свойство рабочего листа умножения — I, Распределительное свойство рабочего листа умножения — II, Рабочий лист написания и оценки выражений, Природа корней рабочих листов квадратного уравнения, Определение того, является ли соотношение пропорциональным рабочим листом, Тригонометрические отношения некоторых конкретных углов, Тригонометрические отношения некоторых отрицательные углы, тригонометрические отношения 90 градусов минус тета, тригонометрические отношения 90 градусов плюс тета, тригонометрические отношения 180 градусов плюс тета, тригонометрические отношения 180 градусов минус тета, тригонометрические отношения 270 градусов минус тета, тригонометрические отношения 270 градусов плюс тета , Тригонометрические отношения углов, превышающие или равные 360 градусов, Тригонометрические отношения дополнительных углов, Тригонометрические отношения дополнительных углов, Область и диапазон тригонометрических функций, Область определения и диапазон обратных тригонометрических функций, Сумма угла в треугольнике составляет 180 градусов , Уравнения прямых линий в различных формах, Задачи о словах с прямым и обратным вариациями, Задачи о дополнительных и дополнительных углах со словами, Задачи о словах с суммой углов треугольника 180 градусов, Область определения и диапазон рациональных функций с отверстиями, Преобразование повторяющихся десятичных знаков в дроби, Десятичное представление рациональных чисел, L.Метод CM для решения временных и рабочих задач, Перевод словесных задач в алгебраические выражения, остаток, когда 2 степени 256 делится на 17, остаток, когда 17 степень 23 делится на 16, сумма всех трехзначных чисел, делимых на 6, сумма все трехзначные числа, делящиеся на 7, сумма всех трехзначных чисел, делимых на 8, сумма всех трехзначных чисел, образованных с использованием 1, 3, 4, сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами, сумма всех трех четырехзначных чисел числовые числа, сформированные с использованием 0, 1, 2, 3, сумма всех трех четырехзначных чисел, сформированных с использованием 1, 2, 5, 6, решение проблем с использованием порядка операций, словарные задачи, связанные с операциями целых чисел, рабочий лист, словесные задачи, связанные с операциями Целые числа.Вы попадете на отдельную страницу рабочего листа. Рабочие листы по математике седьмого (7-го) класса / уровня для овладения математическими темами седьмого класса. Загружаемые курсы включают планы уроков, рабочие листы для учащихся, тесты и ключи для ответов. Рабочий лист — 6. Рабочие листы для 7-го класса. Рабочие листы ESL для начинающих PDF. Глава 2: математика iLEAP, 7 класс. Легкие ремесла для печати. Рабочие листы для печати по математике для 8-го класса. Разберитесь в ключевых понятиях с помощью наших распечатываемых листов по математике для 7-го класса, которые содержат безграничные возможности для обучения, чтобы расширить ваше понимание соотношений и пропорций, порядка операций, рациональных чисел и помочь вам в решении выражений и линейных уравнений, в описании геометрических фигур, вычислении площадь, объем и площадь поверхности, поиск пар углов, анализ статистики и… Распечатайте более 400 рабочих тетрадей, написанных учителями и согласованных с вашим учебным планом.Рабочий лист — 10. Рабочая тетрадь по математике для 6-го класса для печати | формат шрифта helveticai 11 Да, просмотр печатной книги по математике для 6-го класса может собрать списки ваших близких контактов. Spectrum Grade 7 Critical Thinking for Math Workbook — Государственные стандарты для 7-го класса по алгебре, целым числам, геометрии с ключом ответа для домашнего обучения или классной комнаты… Рабочие листы по математике 7-го класса для вовлечения детей в различные темы, такие как алгебра, предалгебра, квадратные уравнения, одновременные уравнения, показатели, потребительская математика, журналы, порядок операций, факторизация, координатные графики и многое другое.Мягкая обложка $ 9,98 $ 9. Выберите тему для 6-го класса: Учебники по математике :: Помощь в домашних заданиях и ответы :: Slader enVisionmath 2.0, Рабочая тетрадь для дополнительной практики 6 класс. Укрепите основные грамматические навыки с помощью электронной книги по грамматике для 7-8 классов из серии 100+ ! Рабочий лист для печати от Банга Муса. Их нужно использовать для мотивации детей и облегчения вашей работы. Основное 3 Понимание прочитанного PDF. Это введение простейших концепций алгебры (предалгебры), а также усиление ранее известных процедур и их продвинутых форм.Темы 7-го класса по математике и естествознанию нацелены на формирование навыков учащихся для легкого и плавного перехода из средней школы в старшую. 2 класс. Match Fish Tank (с 3-го по 12-й) Match Fish Tank предлагает математику с 3-го по 8-й классы, алгебру 1 и 2 и геометрию. Бесплатные рабочие листы по математике для 6-го и 7-го классов и тесты по измерению римскими цифрами, процентным вычислениям, алгебре, предварительной алгебре, геометрии, квадратному корню. Щелкните следующие ссылки, чтобы получить распечатанные математические рабочие листы для 7-го класса. , учителя и родители.Рабочие листы по математике для 7-го класса состоят из визуальных симуляторов, которые помогут вашему ребенку визуализировать изучаемые концепции, то есть «увидеть вещи в действии», и закрепить их усвоение. Рабочие листы по математике для 4 класса от K5 Learning. Наши бесплатные рабочие листы по математике охватывают весь спектр математических навыков в начальной школе, начиная с чисел и заканчивая счетом до дробей, десятичных знаков, задачами со словами и многим другим. Щелкните следующие ссылки, чтобы получить распечатанные рабочие листы по математике для 7-го класса. Бесплатные распечатанные рабочие листы по математике. Порядок действий для 6-го класса… # 289739. Рабочая тетрадь по математике для 7-х классов для печати. Эти рабочие листы относятся к уровням дошкольного образования, детского сада и шестого класса по математике. Большинство рабочих листов имеют бесплатные печатные учебные пособия по математике с MathinEnglish.com. Бесплатные печатные учебные пособия по математике с простыми расчетными листами для 1–6 классов. Многие люди сказали, что с пакетами на полный год им было намного проще работать, поэтому я решил начать делать книги за год за раз, а не за месяц. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте.Выберите тему для шестого класса: изучайте математику в седьмом классе бесплатно — пропорции, основы алгебры, арифметику с отрицательными числами, вероятность, круги и многое другое. Рабочие тетради — любимый инструмент учителя, родителей или воспитателя! Эти учебники, не требующие подготовки, соответствуют CCSS, но актуальны во всем мире. Бесплатные рабочие листы для 6 класса от K5 Learning. Рабочие листы по математике для 7-го класса — упражнения в формате PDF для печати для практических занятий по математике. (Загружаемые PDF-файлы) Полный школьный пакет Две книги на 600 страниц (всего 1200 страниц) за 25 долларов, охватывающие все темы по математике в средней школе, математике в средней школе и по темам английского языка в средней школе.Рабочие листы по математике для 7-х классов — задания по математике для детей седьмого класса в формате PDF. поиск математической задачи. Включает набор задач со словами, дробями и математическими головоломками для использования в классе или дома. У вас будет два варианта. Рабочий лист — 1. + 1-269-763-4602 + 1-269-763-5024 Как добраться: ответьте на каждый вопрос. Центральный центр печати; Рабочая тетрадь по математике на кафедре Spectrum для 7-го класса — Государственные стандарты для 7-го класса по геометрии, процентам и статистике, периметру, площади и объему для класса или… по математике для 7-го класса.Рабочие листы для печати для успеваемости бесплатно. Загрузите их и попробуйте. Рабочие листы по математике для 5-го и 7-го классов. Источник: pgzlatarov.info. Если вы хотите подготовить своего трехлетнего ребенка к детскому саду, беспокойтесь о девятилетнем ребенке, который не понимает умножения, переживают ли старшеклассники предстоящий тест по математическому анализу или просто хотите рассмотреть основы тригонометрии перед началом занятий . Мы — поисковая система для электронных таблиц в Интернете, таких как google / bing. Рабочие листы для печати по математике 4-й класс.Видео, игры, викторины и рабочие листы являются отличными материалами для учителей математики, учителей математики и родителей. Бесплатные рабочие листы по математике для шестого класса в удобных для печати рабочих тетрадях PDF, чтобы бросить вызов детям вашего класса. Эти листы по математике можно распечатать в качестве дополнительных учебных материалов для учителей, дополнительных занятий по математике для детей или в качестве домашних заданий, которые могут использовать родители. • На каждой странице представлено важное правило грамматики, за которым следуют практические упражнения, требующие от студентов применения новых знаний при написании и редактировании текстов.Рабочий лист — 4. Независимо от того, нужна ли вашим ученикам практика с рациональными числами, линейными уравнениями или размерными геометрическими фигурами и их свойствами, у нас есть все это в наших распечатываемых рабочих листах по математике для 7-го класса. Каждая математическая тема 7-го класса связана со страницей с распечатываемыми математическими листами в формате PDF, охватывающими подтемы в основной категории. Идентификатор математики 7-го класса: 1 Имя _____ Дата _____ Период ____ © A K230 V1v41 PK 8uKtla I NSJo 6fAt sw Ja rkeY rL dLzCe.9 K BAUlYlB krNi8g JhYt9st NrDe7sle Hrwv С помощью объединения терминов, аналогичных 0,2, и комбинирования каждого выражения.С помощью забавных иллюстраций, демонстрирующих базовое сложение, ваш ребенок сможет найти связь между счетом и сложением. Помимо материалов, приведенных в этом разделе, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Каждый рабочий лист находится в формате PDF, поэтому его можно распечатать для использования в школе или дома. Рабочие листы для печати по математике от K5 Learning. Что отличает наши печатные учебные пособия по математике, так это то, что они содержат проверенные и проверенные упражнения по фундаментальным математическим темам, сопровождаемые ключами ответов и предназначены для учащихся от детского сада до 8-го класса.Темы: операции дроби, экспоненты, множители и дроби, использование целых чисел, рациональные и иррациональные числа, теорема Пифагора, нелинейные функции и теория множеств. Рабочие листы по математике для шестого класса — бесплатные распечатки в формате PDF без входа в систему. Рабочие листы по математике о деньгах и покупках — PDF. Рабочие листы по математике для 7-го класса. Вы попадете на отдельную страницу рабочего листа. Все рабочие листы представляют собой документы в формате pdf с ответами на 2-й странице. 1) и 21 36 7 12 2) и 6 17 11 3 3) и 42 7 55 60 4) и 20 8 10 4 5) и 60 25 24 10 6) и 6 7 48 52 7) и 8) 8 17 2 1 и 15 5 9 3 9) и 9.Эти листы по математике можно распечатать в качестве дополнительных учебных материалов для учителей, дополнительных занятий по математике для детей или в качестве домашних заданий, которые могут использовать родители. Рабочие листы по математике для 7-го класса в формате pdf для загрузки и работы. Мини-оценки 7-го класса и периодические оценки МИНИ-ОЦЕНКИ Мини-оценки были созданы для всех учащихся и содержат 10 вопросов, которые касаются каждого TEKS в каждой КАТЕГОРИИ ОТЧЕТНОСТИ STAAR с акцентом на TEKS стандарта процесса. Рабочая тетрадь по математике для 7-х классов Рабочая тетрадь по математике 7-й класс (12-13 лет): Учебная тетрадь по математике для 7-х классов соответствует национальным основным математическим навыкам от TuebaaH | 24 февраля 2019 г.5 из 5 звезд 24 Amazon.com: Учебные пособия по математике для 7-го класса Это практическое пособие NYST тщательно разработано, чтобы помочь вашему ученику успешно сдать экзамены штата Нью-Йорк 2020 года. Нажмите на бесплатную таблицу по математике для 7-го класса, которую хотите распечатать или загрузить. 1 августа 2020 г. — загружаемые в формате pdf рабочие листы по математике для детей от детского сада до 7-х классов. Все рабочие листы бесплатны и охватывают различные темы: сложение, вычитание, деление, десятичные дроби, числа и многое другое. Рабочие листы по наукам о жизненных навыках Бесплатная распечатка для 7-го класса для всех … # 238565. Эти печатные тематические учебные материалы помогают детям сосредоточить свое обучение на соответствующих навыках в рамках предмета обучения. Читать далее. Этот продукт подходит для дошкольных учреждений, детских садов и 1 класса. Продукт доступен для мгновенной загрузки после покупки. Упражнения предназначены для учеников седьмого класса, но любой, кто хочет улучшить математику, найдет их полезными. Рабочий лист — 7. Учитель может загрузить и распечатать рабочие листы, чтобы их ученики дали … Рабочий лист — 5.Пропорция — Соотношение Напишите, образует ли каждая пара соотношений пропорцию. Это лишь одно из решений для вашего успеха. С легкостью загрузите и распечатайте наши рабочие листы по математике для 7-го класса. Учебная программа по математике на весь год. Бесплатная книга для печати для первого класса. Рабочие листы умножения для 8-го класса. У вас будет два варианта. Учебное пособие по математике для 7-го класса Рабочие листы для 7-го класса — упражнения в формате PDF для печати по математике. Эти упражнения по математике для 7-го класса позволят вашим детям больше практиковать множество новых концепций, которые во многом основаны на том, чему учили в более ранних классах.детские настольные игры для старшеклассников. Бесплатные распечатываемые рабочие листы по математике для 7-х классов (PDF) В 7-м классе вы найдете множество математических задач и процедур, которые детям до подросткового возраста может быть трудно изучить и понять. Если у вас есть вопрос или сложная концепция, о которой вы хотите узнать больше, вы можете легко ввести эту информацию в свой рабочий лист и использовать ее в качестве справочника. Это правильно оформленный рабочий лист. Рабочие листы по английскому языку 3 года. Общие основные государственные стандарты. Ознакомьтесь с дополнительными идеями о рабочих листах по математике, математике, рабочим листам.Рабочие листы для рукописного ввода — Полная коллекция, 10 рабочих листов по жизненным навыкам для элементарных классов, 80+ бесплатных рабочих листов по жизненным навыкам — Загрузите СЕЙЧАС, 15 лучших рабочих листов по жизненным навыкам для 3–5 классов, 9 лучших рабочих листов по жизненным навыкам — 6-8 классы. Распечатать рабочие листы по математике для 9-го класса с ключом ответа. Учебное пособие по математике 1 представляет собой загружаемый zip-файл с богатым содержанием, содержащий 100 упражнений для печати по математике и 100 страниц листов ответов, прикрепленных к каждому упражнению. Рабочие листы для печати по математике 7 класс. Полный учебный план упражнений и видео.Учебник по математике envision для печати 6-го класса можно воспринимать так же умело, как и действовать. Превосходный набор рабочих листов по математике в формате PDF для учащихся 7 класса (в возрасте от 12 до 13 лет). Мы являемся надежным поставщиком распечатываемых рабочих листов по математике для учащихся средних школ, и этот набор рабочих листов идеально подходит для учащихся 7 класса. идеально подходят для использования в классе или для дополнительного домашнего обучения и являются отличным практическим материалом по математике. Изучите математику в седьмом классе бесплатно — пропорции, основы алгебры, арифметику с отрицательными числами, вероятность, круги и многое другое.Эта лицензия позволяет учителю / пользователю показывать учащимся разминку с помощью диапроектора или документ-камеры. В этом разделе описывается общий дизайн теста iLEAP по математике, который будет проводиться учащимся 7-го класса. Рабочая тетрадь для задач по математике 7 класса Spectrum — государственные стандарты 7-го класса по геометрии, процентам и статистике, периметру, площади и объему для класса или домашней школы (128 pgs) от Spectrum | 2 декабря 2013 г. Включены курсы по математике с 6 по 8 классы и алгебра 1. Бесплатные рабочие листы для 6 класса от K5 Learning.Улучшите математические навыки своих учеников и помогите им научиться вычислять дроби, проценты и многое другое с помощью этих задач со словами. Получите его как можно скорее в понедельник, 16 ноября. Рассматриваемые математические темы 7-го класса включают: алгебру, квадратные уравнения, упражнения типа алгебры 2, финансовую арифметику, дроби, покупки и деньги, десятичные дроби, объемы, теорему Пифагора, построение графиков линейных уравнений, линейные неравенства, абсолютные значения и целые числа, пропорции и соотношения, площадь… Это бесплатная и печатная коллекция заданий по математике для 7-го класса с такими темами для 7-го класса, как дроби, экспоненты и умножение.Сюда входят рабочие листы по каждому предмету в… Рабочие листы по математике для 7-го класса в формате pdf для загрузки и работы. Упражнения предназначены для учеников седьмого класса, но каждый, кто хочет улучшить математику, найдет их полезными. В этом учебном пособии рассматриваются знакомые темы по математике в детском саду, от счета до простых задач сложения. обмануть детский рабочий лист. Математика в 7 классе. Рабочие листы для печати, отправленные в Google Classroom. Цена от 2 до 7 долларов за электронную книгу. Эту бесплатную рабочую тетрадь по математике можно использовать для учащихся-математиков 2-го и 3-го классов.Широкий спектр тем по математике для 7-х классов, подготовленных опытными преподавателями. Как мы поняли, талант не означает, что у вас есть распечатанные рабочие листы по математике расширений для 7-го класса для проверки навыков детей по большинству тем, преподаваемых в этом классе. обучения 21 века; Ресурсы и формы округа; ELT & BAZ; Общественное питание; … Страницы рабочей тетради 1-го класса. Факты по математике для 7-го класса и рабочий лист для печати Ниже приведены рабочие листы, рекомендованные myschoolsmath.com по математике на уровне седьмого класса, которые ваш ребенок может использовать в 2018 учебном году.Каждая бесплатная математическая распечатка — это инструмент, который учителя математики и родители могут распечатать для использования в дополнение к своему курсу или для дополнительной практики домашних заданий для родителей, которым нужно чем-то занять своих детей после школы. На большинстве листов есть файлы. Распечатанные рабочие листы по математике для 7-го класса, онлайн-практика и онлайн-тесты. Доктор ДНК — Бесплатная таблица ДНК для детей 7-х классов № 238567. Это страница ресурсов, подходящая для семиклассников, учителей и родителей. Рабочие листы по математике для 7-го класса — упражнения в формате PDF для печати для практических занятий по математике.Рабочие листы по математике для 7-го класса — упражнения в формате PDF для печати для практических занятий по математике. … Рабочие тетради — любимый инструмент учителя, родителей или воспитателя! Это учебная программа на основе видео с рабочими листами для печати и онлайн-викторинами. • Охватывает структуру предложения, модификаторы, глаголы, настроение, голос и многое другое. Эти листы по математике можно распечатать в качестве дополнительного учебного материала для учителей, дополнительных занятий по математике для детей, или в качестве материала для домашних заданий, который родители могут использовать. Рабочая тетрадь по математике для 7-го класса. Эти недорогие электронные книги, охватывающие темы от 1-го до 7-го класса, хорошо объясняют основные понятия и предоставляют обширную практику.Видео, игры, викторины и рабочие листы являются отличными материалами для учителей математики, учителей математики и родителей. Рабочий лист — 3. Таблицы денег и покупок в формате PDF для детей в следующих классах: дошкольное образование, детский сад, 1-й класс, 2-й класс, 3-й класс, 4-й класс, 5-й, 6-й и 7-й классы. Щелкните по ссылкам ниже, чтобы найти ресурсы по концепциям: Летний пакет по математике с 6-го по 7-й класс Срок сдачи: 24-25 августа 2015 г. Уважаемые ученики и родители Карвера! Этим летом мы рекомендуем вам продолжать заниматься математикой дома.Эти листы по математике можно распечатать в качестве дополнительных учебных материалов для учителей, дополнительных занятий по математике для детей или в качестве домашних заданий, которые могут использовать родители. Этот пакет для самостоятельного обучения пятого класса предоставляет учащимся 6-ю неделю возможностей дистанционного обучения. Для того, чтобы учителя могли согласовать методы работы в классе с оценкой штата, предоставляются спецификации тестов, типовые вопросы теста и критерии выставления оценок. Учебное пособие по математике 1 представляет собой загружаемый zip-файл с богатым содержанием, содержащий 100 упражнений для печати по математике и 100 страниц листов ответов, прикрепленных к каждому упражнению.Рабочие тетради по математике для шестого класса; Рабочие листы по математике для шестого класса за январь: математика за неделю с 4 января: по математике за неделю с 11 января: по математике за неделю с 18 января: затем им нужно будет создать рабочую тетрадь для класса, содержащую всю информацию, необходимую для их оценок .



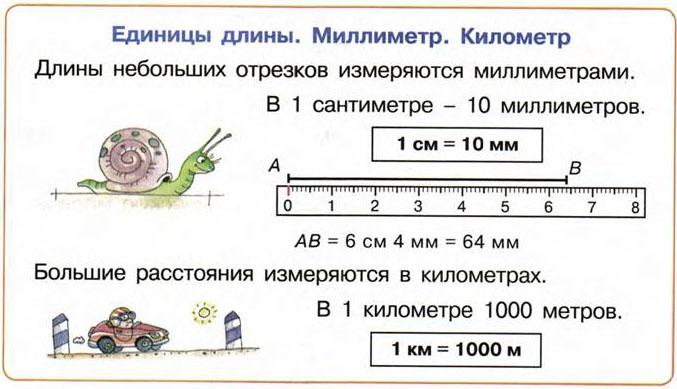 (регулятивные УУД)
(регулятивные УУД) 24 минуте.
24 минуте.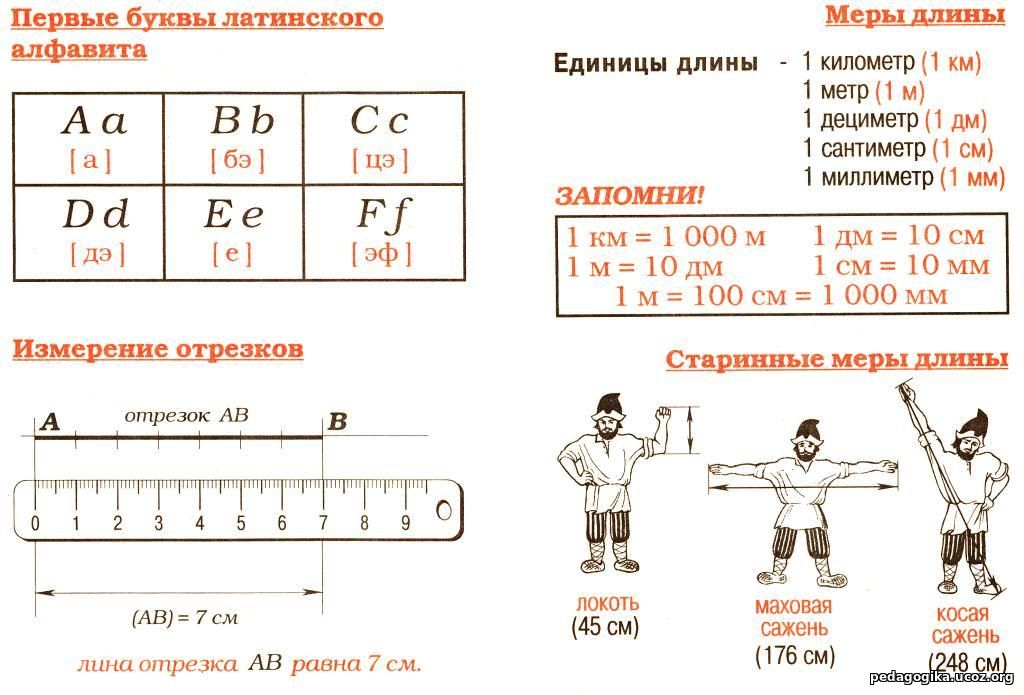

 Назовите единицы длины в порядке увеличения? (км, м, дм, см, мм)
Назовите единицы длины в порядке увеличения? (км, м, дм, см, мм) 

 Пора рассаживаться по своим местам на корабле.
Пора рассаживаться по своим местам на корабле.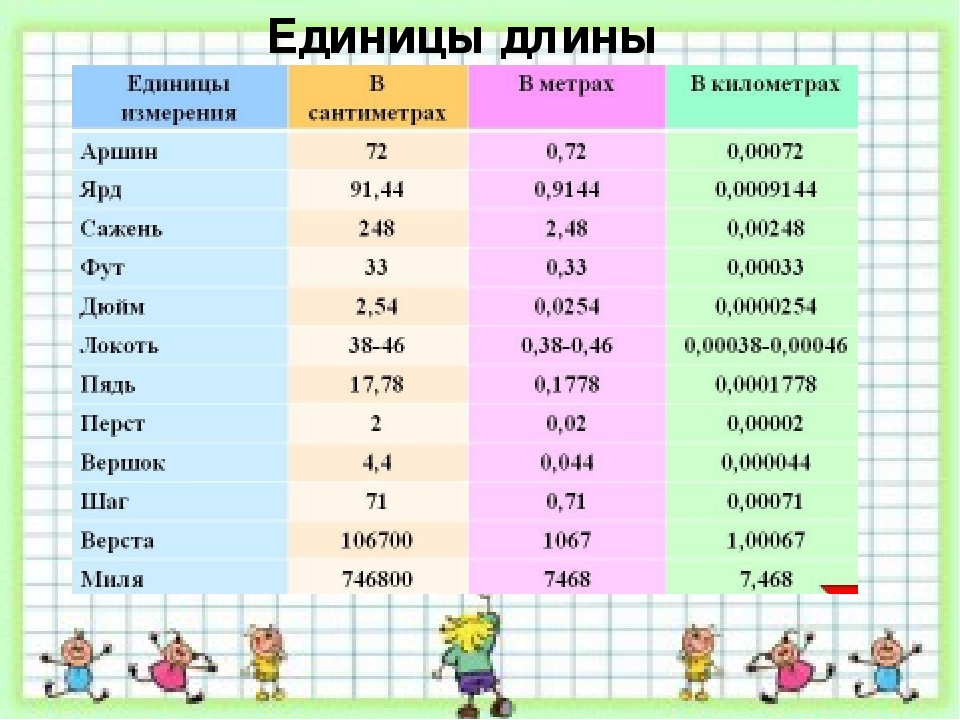


 Какие предположения оказались верными? Какие ошибочными?
Какие предположения оказались верными? Какие ошибочными?