Обратная задача это 3 класс: Обратные задачи / Задачи / Справочник по математике для начальной школы

Содержание

Обратные задачи / Задачи / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Задачи
Обратные задачи

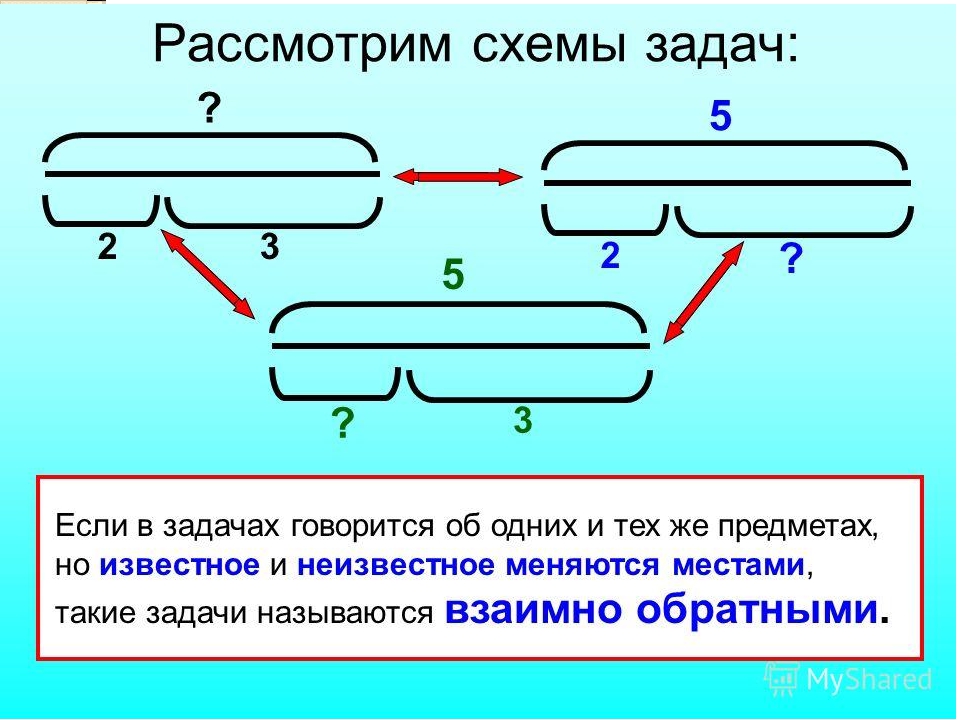
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.

Прямая задача:

У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?

Первая обратная задача:

У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?

Ты видишь, что известная величина — красные шарики — стала неизвестной.

А неизвестная величина — общее количество шариков — стало известной.

Вторая обратная задача:

У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные.

Сколько зелёных шариков было у Тани?

Ты видишь, что известная величина — зелёные шарики — стала неизвестной.

А неизвестная величина — общее количество шариков — стало известной.

ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Образцы оформления задачи

Цена. Количество. Стоимость

Скорость, время, расстояние

Задачи

Правило встречается в следующих упражнениях:

1 класс

Страница 48. Урок 25, Петерсон, Учебник, часть 2

Страница 50. Урок 26, Петерсон, Учебник, часть 2

Страница 53. Урок 27, Петерсон, Учебник, часть 2

Страница 60. Урок 31, Петерсон, Учебник, часть 2

Страница 63. Урок 32, Петерсон, Учебник, часть 2

Страница 8. Урок 5, Петерсон, Учебник, часть 3

Страница 25. Урок 13, Петерсон, Учебник, часть 3

Страница 33. Урок 17, Петерсон, Учебник, часть 3

Страница 65. Урок 33, Петерсон, Учебник, часть 3

Страница 91. Повторение, Петерсон, Учебник, часть 3

2 класс

Страница 54, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 88, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Задание 50, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 9.

Вариант 2. № 3, Моро, Волкова, Проверочные работы

Страница 17. Вариант 2. № 1, Моро, Волкова, Проверочные работы

Страница 44, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

3 класс

Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 36, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 64, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 21, Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 49, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 68, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 44, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29, Моро, Волкова, Рабочая тетрадь, часть 2

com, 2021

Пользовательское соглашение

План-конспект «Обратные задачи» — математика, уроки

Тема: Обратные задачи

Цели:

1)Способствовать формированию умения составлять и решать обратные задачи;

2)Содействовать развития сообразительности, логического мышления, внимания;

3)Способствовать воспитанию аккуратности письма.

Оборудование: учебное пособие «Математика» 2 класс Г.Л.Муравьёва, М.А.Урбан, парашюты, карточки с примерами, иллюстрация ёжика, схемы задач

План урока:

1.Организация начала урока

1 Приветствие

1.2 Создание учебной мотивации

2. Проверка домашнего задания

2.1 Фронтальная проверка №1,2 , с.89

3.Устный счёт

3.1 Сравнение чисел

3.2 Парашюты с примерами

3.3 Решение задач

4. Минутка чистописания

5.Объявление темы и постановка цели

6. Изучение нового материала

7.Закрепление нового материала

7.1 Решение задачи №1, с.90 (письменно, составление обратной)

Физкультминутка

7.2 Решение задачи №4, с.90 (письменно)

7.3 Решение задачи № 7, с.91 (устно)

7.5 Решение задачи с вопросом с.91 (письменно, составление обратной)

8. Подведение итогов урока

9. Рефлексия

10. Инструктаж по домашнему заданию

Ход урока:

1.Организация начала урока

1.1 Приветствие

-Здравствуйте, ребята! Садитесь.

Дружно будем задачи решать,

Мы хотим математику знать.

Что б водить корабли,

Чтобы лётчиком стать,

Надо многое уметь,

Надо многое знать.

Не беда, что идти далеко,

Не боимся, что путь будет труден,

Никогда не давались легко

Достижения людям.

1.2 Создание учебной мотивации

-Сегодня мы с вами отправимся в далёкое путешествие, а совершать это путешествие мы будем в страну Математики. И раз мы путешественники в стране Математики, то нам нужно быть очень внимательными, чтобы там не заблудиться.

2.Проверка домашнего задания

-Наша первая остановка «Проверяйкино».

2.1 Фронтальная проверка

Ребята, посмотрите на доску, дома вы решали похожие примеры, вам необходимо решить по аналогии:

72-2+9
66-60+9

-Прочитайте ответ первого примера

-Прочитайте ответ второго примера

-А сейчас мы проверим домашнюю задачу.

-Каким действием мы решали задачу?

+сложением

-Как мы нашли сколько кубиков было в коробке?

+к 20 прибавили 6

-Молодцы! Все справились с домашним заданием

3.Устный счёт

-Движемся дальше. И наша остановка «Считалкино».

3.1. Сравнение чисел

-Ребята, вам необходимо будет сравнить числа и величины. Но перед этим давайте с вами повторим:

-Сколько в одном десятке единиц?

+10 единиц

— Откройте учебники на с.90 №2

71 < 72 5 дес. 8 ед. > 5 дес. 4 ед.

89 > 69 2 дес.5ед. < 3 дес. 5 ед.

11<28 4 дес.1 ед. > 2 дес. 4 ед.

-Молодцы, ребята, мы с вами повторили сравнение чисел, а теперь, двигаемся дальше!

3.2 Парашюты с примерами

Обратите внимание на доску. Для того, чтобы продолжить наше путешествие необходимо решить примеры, которые прикреплены к парашютикам. (Решаем вместе)

-Но, перед этим давайте повторим названия компонентов при вычитании

+Уменьшаемое, вычитаемое, разность

-Как найти неизвестное уменьшаемое?

+Нужно к разности прибавить вычитаемое

-Как найти неизвестное вычитаемое?

+Нужно из уменьшаемого вычесть разность

-Как найти разность?

+Нужно из уменьшаемого вычесть вычитаемое

70-20= ? (2)

?-10= 40 (50)

50-?=0 (50)

16-8=? (8)

?-4=8 (4)

50-1=? (49)

-Молодцы, мы с вами повторили компоненты при действии вычитании, повторили как они находятся. Движемся дальше!

3.3 Решение задач

-А сейчас нам нужно решить задачки, но давайте повторим

-Как называются компоненты при действии сложения?

+1 слагаемое, 2 слагаемое, сумма

-Как найти неизвестное первое слагаемое?

+из суммы вычесть второе слагаемое

-Как найти неизвестное второе слагаемое?

+из суммы вычесть первое слагаемое

-Как найти сумму чисел?

+К первому слагаемому прибавить второе слагаемое

1) В вазе лежало 17 яблок. Когда несколько съели, осталось 8.Сколько яблок съели?

+ 9.

-Как узнали?

+17 – 8= 9

2) В автобусе ехало несколько человек. Когда 8 вышло, там оставалось 15. Сколько человек было в автобусе?

+23.

-Как узнали?

+8+ 15=23

3)Васе 10 лет. Он на 3 года младше Стёпы. Сколько лет Стёпе?

+13 лет

-Как узнали?

+10+3=13

-Молодцы! Мы повторили с вами названия компонентов при действии сложения, повторили как находятся компоненты при сложении. Едем дальше!

4.Минутка чистописания

—Мои друзья, следующая наша станция «Чистописалкино». Откройте учебники на с. 90 №3

-Назовите числа в порядке возрастания

+34,43,68,86

-Назовите эти числа в порядке убывания

+86,68,34,43

-Посмотрите на первые два числа, что изменилось?

+цифры поменялись местами

-Посмотрите на вторые два числа, а в этих числах, что изменилось?

+цифры тоже поменялись местами

-Отступите от написанного 4 клеточки и запишите дату 27 декабря классная работа, от классной работы отступите 2 клеточки вниз, и запишите эти числа в виде суммы разрядных слагаемых, красиво и аккуратно

-Вы очень аккуратно написали эти числа, вспомнили как записываются числа в виду суммы разрядных слагаемых.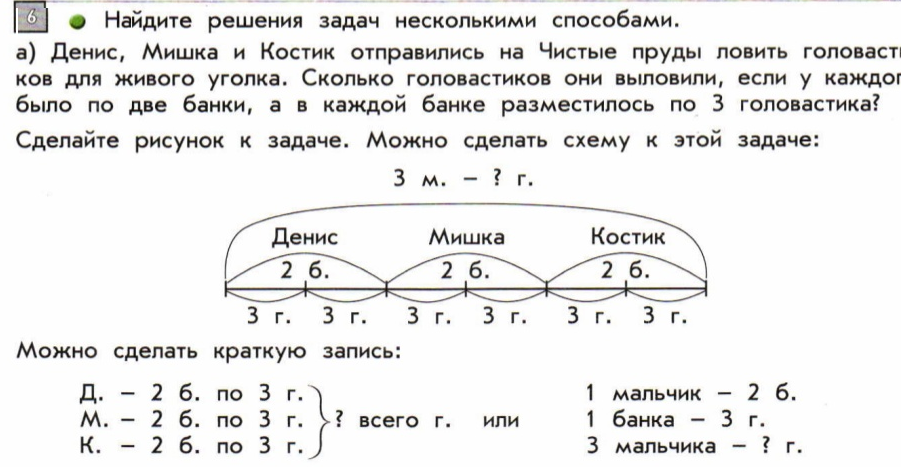

5. Объявление темы и постановка цели

— На предыдущих уроках вы работали с новыми видами задач. Осваивали способ их решения. А сегодня мы познакомимся с обратными задачами, научимся их решать.

6.Изучение нового материала

-Следующая остановка «Изучалкино». Нас встречает ёжик, который просит у нас помощи, ему нужно помочь составить и решить задачи на стр. 90. давайте ему поможем.

+В саду ёжик собрал 3 кг слив и 5 кг груш. Сколько всего килограммов слив и груш собрал ёжик в саду?

-Ребята, как мы можем одним словом назвать груши и сливы?

+фрукты

-Посмотрите на схему. Что означает цифра 3?

+Количество слив

-Что означает цифра 5?

+Количество груш

-Можем мы найти сколько было фруктов?

-Каким действием?

+Сложением

-Как?

+3+5 =8

-Так, какие числа были при решении?

+ 3,5,8

-А теперь, составим обратную задачу. Посмотрите на схему под №2

-Сколько было всего фруктов?

— Из них 3 сливы

+Можем мы найти сколько было груш?

-Каким действием?

+Вычитанием

-Как?

+8-3=5

-Так ,какие числа были при решении?

+3,5,8

-Хорошо, давайте составим ещё одну обратную задачу данной

-Сколько всего было фруктов?

-Из них 5 груш

-Можем мы найти сколько было слив?

-Каким действием?

+Вычитанием

-как?

+ 8-5 =3

-Так какие числа были при решении?

+3,5,8

-Ребята, обратная задача- это задача, в которой известное становится неизвестным, а неизвестное – известным.

7.Закрепление нового материала

7.1 Решение задачи № 1,с.90

-Наша следующая станция «Закреплялкино»

-А сейчас мы закрепим наши знания решая задачу под № 1 на стр. 90.

— (Читает задачу вслух). Ребята, а как одним словом можно назвать кошек и собак?

+Животные

Обратите внимание на доску, здесь написана краткая запись задачи

-Сколько кошек участвовало в цирковом номере?

+ 6 кошек участвовало в номере.

-Сколько собачек?

+7 собачек.

-Можем ли мы узнать сколько всего животных участвовало в номере?

-Каким действием?

+Сложением

-Как?

+К 6+7=13 животных участвовало в номере

-Отступите от написанного 2 клеточки вниз, запишите слово задача и напишите её решение

Запись решения и ответа задачи

+6+7=13 (ж. )

-Что являлось неизвестным в данной задаче?

+Общее количество кошек и собачек

-Чтобы составить обратные задачи, что должно стать неизвестным?

+Количество кошек (меняю числа)

-Сколько всего животных участвовало в цирковом номере?

+13

-Сколько участвовало собачек?

-Можем мы найти сколько участвовало кошек?

-Каким действием?

+Вычитанием

-Как?

+13-7 = 6

-Какие числа были в задаче?

+6,7,13

Запись решения и ответа задачи

+13-7= 6 (к.)

-Хорошо давайте составим вторую обратную задачу данной

-Сколько всего животных участвовало в цирковом номере?

+13

-Из них 6 кошек

-Можем узнать сколько участвовала в цирком номере собачек?

-Каким действием?

+Вычитанием

-Как?

+13-6=7

-Какие числа были в этой задаче?

+6,7,13

— Запись решения и ответа задачи

+13-6= 7 (с. )

-Прочитайте какие у вас получились обратные задачи

+ 1) В цирковом номере участвовали несколько кошек и 7 собачек. Всего участвовало 13 животных. Сколько кошек участвовало в цирковом номере?

+ 2) В цирковом номере участвовали 7 кошек и несколько собачек. Всего участвовало 13 животных. Сколько собачек участвовало в цирковом номере?

-Молодцы! Мы решили задачу и научились составлять ей обратные задачи.

Физкультминутка

7.2 Решение задачи №4, с.90 (письменно)

-Выполним сейчас здание №4. Прочитайте условия этой задачи

-Сколько человек было на палубе?

+47 человек

-Сколько человек ушло в каюты?

+Неизвестно

-Сколько человек осталось?

+40

-Как узнать, сколько человек ушло в каюты?

+Чтобы узнать, сколько человек ушло в каюты, надо от того, что было, отнять то, что осталось

-Каким действием будем решать задачи?

+вычитанием

-Как?

+47-40=7

-Запишите решение этой задачи в тетрадь

-Мы закрепили с вами вычислительные навыки. Продолжаем работу.

7.3 Решение задачи №7, с.91 (устно)

-Ребята, посмотрите задачу под № 7. Но, будьте внимательны, эта задача на внимание

Прочитайте её условие

-Все ли данные в задаче нам необходимы для её решения?

+Нет

-Что здесь лишнее?

+2 бульвара

-Сколько на плане города туристы увидели улиц?

+7 улиц

-Сколько переулков

+15

-Напомните мне правило, которое нам поможет ответить на вопрос задачи

+Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа отнять меньшее

-Какое будет решение этой задачи?

+15-7=8

-Молодцы, вы хорошо умеете вычислять и решать задачи.

7.4 Решение задачи, с.91 (письменно, составление обратной)

—Ребята, а теперь давайте решим задачу под знаком вопроса на с.91

Прочитайте условия этой задачи.

-А чтобы вам было легче, на доске для вас подсказка

-Посмотрите, что это такое?

+Огурцы и помидоры

-Как можно назвать их одним словом?

+овощи

-Давайте с вами составим задачу

+В корзине лежало 12 огурцов и 8 помидор. Сколько всего овощей лежало в корзине?

-Сколько огурцов лежало в корзине?

+12

-Сколько помидор лежало в корзине?

-Можем мы найти сколько всего было овощей в корзине?

-Каким действием?

+Сложением

-Как?

+12+8 = 20 (ов. )

-Так, какие числа были в этой задаче?

+12,8, 20

-Отступите от написанного 2 клеточки вниз, запишите слово задача и напишите её решение

-А теперь, составьте обратные задачи данной.

— Что являлось неизвестным в данной задаче?

+Общее количество овощей в корзине

-Чтобы составить обратные задачи, что должно стать неизвестным?

+Количество огурцов (меняю числа)

-Составьте задачу

+ В корзине лежало всего 20 овощей. Из них 8 помидор. Сколько лежало в корзине огурцов?

-Сколько всего овощей лежало в корзине?

+20

-Из них 8 помидор

-Можем мы найти сколько лежало огурцов в корзине?

-Каким действием?

+Вычитанием

-Как?

+ 20-8 = 12 (ог. )

Запишите решение в тетрадь

-Какие числа были в этой задаче?

+12,8,20

-Хорошо, давайте составим вторую обратную задачу данной

+ В корзине лежало всего 20 овощей. Из них 12 огурцов. Сколько лежало в корзине помидор?

-Сколько всего лежало овощей в корзине?

+20

-Из них 12 огурцов

-Можем мы найти сколько лежало помидор в корзине?

-Каким действием?

+Вычитанием

-Как?

+20-12 = 8 (п.)

-Какие числа были в этой задаче?

+8, 12, 20

Ребята, обратная задача- это задача, в которой известное становится неизвестным, а неизвестное – известным.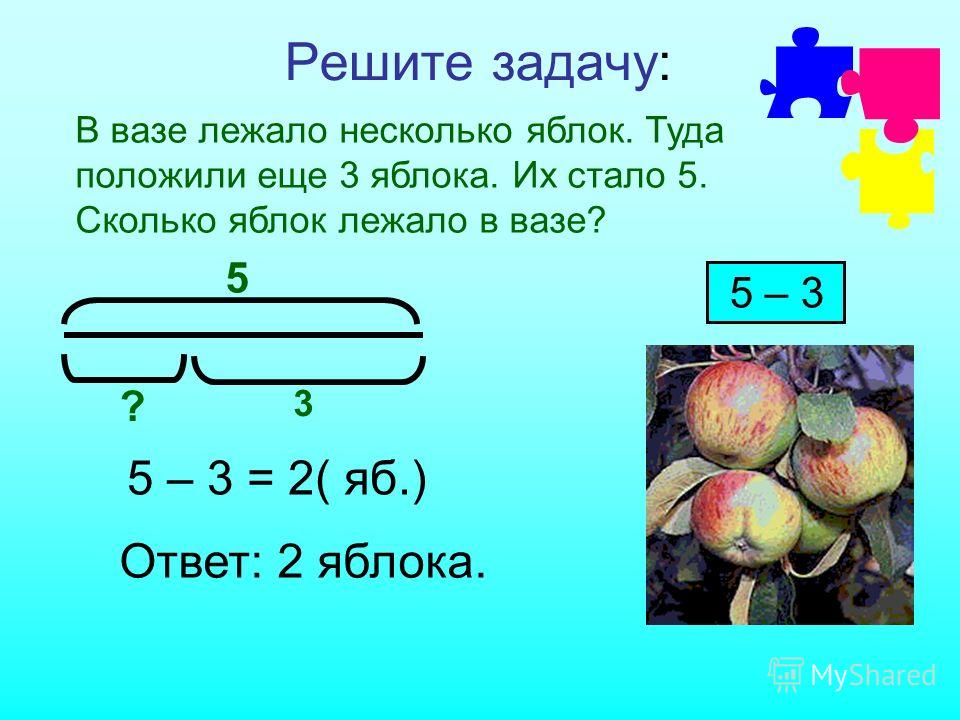

8.Подведение итогов урока

-Вот и закончилось наше путешествие в страну Математики.

-Что мы делали на уроке?

+учились составлять и решать обратные задачи

9.Рефлексия

-Кто понял, как составлять и решать обратные задачи, прикрепляет магнитик к нашему Ёжику, а кому ничего не понятно, то к Незнайке.

Урок по математике «Обратная задача»

КСП по математике в 1 классе

3 четверть 31 урок

*В контексте тем:

«Путешествие», «Традиции и фольклор»

Школа:

Дата: «____»____________20___г.

ФИО учителя:

Класс: 1 «____» класс.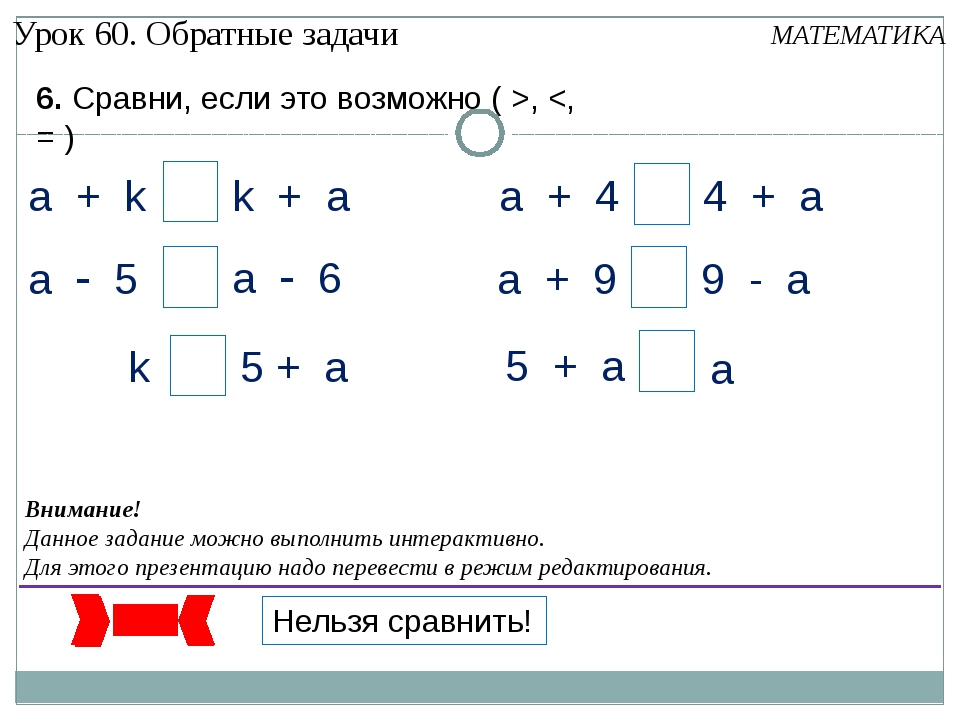

Количество присутствующих:

отсутствующих:

Тема урока:

Обратная задача

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):

анализировать и решать задачи на нахождение суммы и остатка; составлять и решать обратные задачи;
моделировать задачу в виде схемы, краткой записи; подбирать опорную схему для решения задачи.

Цели урока:

Познакомить первоклассников с понятием «обратная задача»; определить взаимосвязь между прямой и обратными задачами, сформировать умение составлять к задачам на сложение пары обратных задач на вычитание.

Критерии успеха

Учащиеся к концу урока научатся:

строить графические модели к задачам.

Привитие

ценностей

Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.

Межпредметные

связи

Межпредметные связи содержат перечень ссылок на другие предметы, которые имеют отношение к уроку. Разнообразные виды заданий выполняются на уроке с целью осуществления интеграции с другими предметами. Например, задачи обучения в рамках конкретного урока по предмету «Математика» можно рассмотреть через такие предметы, как «Естествознание» и «Художественный труд».

Навыки

использования

ИКТ

На данном уроке учащиеся не используют ИКТ. Возможный уровень:

организованная деятельность, включающая презентации и ИKT;
самостоятельное изучение информации, обсуждение в группе; представление классу полученных выводов;

Предварительные

знания

Умение решать задачи на нахождение остатка от целого. Анализируя взаимосвязь компонентов при вычитании, учащиеся знают о том, что найти неизвестную часть (остаток) можно путем вычитания из целого известной части.

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

Вводное задание. Организуйте работу в группах. Для этого раздайте каждой группе карточки с текстами трех задач. Предложите подобрать к каждой задаче схему и решить ее. Примерный текст задачи:

В кошельке лежат 2 монеты: 10 тенге и 20 тенге. Сколько всего денег лежит в кошельке?
В кошельке лежат 2 монеты. В сумме они составляют 30 тенге. Одна монета — 20 тенге. Узнай, какая еще монета лежит в кошельке.
В кошельке лежат 2 монеты. В сумме они составляют 30 тенге. Одна монета — 10 тенге. Назови вторую монету.

Наблюдайте за тем, как учащиеся решают задачи. Используйте результаты данного наблюдения при оценивании. В ходе работы дети определяют, что тексты всех трех задач похожи и в них используются одни и те же числовые значения. Эти выводы ребята смогут озвучить при обсуждении проделанной работы. Похвалите их за наблюдательность и помогите им сформулировать определение для подобного вида задач. Для этого задайте следующие вопросы:

На что направлена первая задача? (На нахождение неизвестного целого.)
Каким действием она решается? (Действием сложения.)
На что направлена вторая задача? (На нахождение неизвестной части.)
Каким действием она решается? (Действием вычитания.)
Чем похожи эти 2 задачи? (Темой и числовыми значениями.)

Будет хорошо, если учащиеся почувствуют тесную взаимосвязь между задачами: то, что известно в первой задаче, становится неизвестным во второй, и наоборот. Сообщите, что задачи бывают прямыми и обратными. К каждой прямой задаче на сложение можно составить пару обратных задач на вычитание. (Имеются в виду задачи, рассматриваемые на данном уроке. Бывают задачи, к которым можно составить больше двух обратных. )

Предложите школьникам еще раз перечитать текст задач и решить, какая из них прямая, а какие две — обратные. Учащиеся смогут сделать вывод о том, что первая задача на сложение является прямой, а вторая и третья — обратными. Проверить, правильно ли решена прямая задача, можно с помощью составления и решения обратной задачи.

Критерии успеха

Середина урока

Сравни задачи. Предложите первоклассникам поработать в парах. Учащиеся читают тексты задач и определяют, что эти задачи взаимосвязаны. Они объединены одной темой, содержат одинаковые числовые значения, Опираясь на схемы и содержание задач, дети смогут сделать вывод о том, что задача под буквой «А» является прямой, а задачи под буквами «Б» и «В» являются обратными. Выслушайте предположения учащихся. Попросите составить по выбранной схеме обратную задачу. Таким образом школьники закрепят вывод о том, что к задаче на сложение можно составить пару обратных задач на вычитание.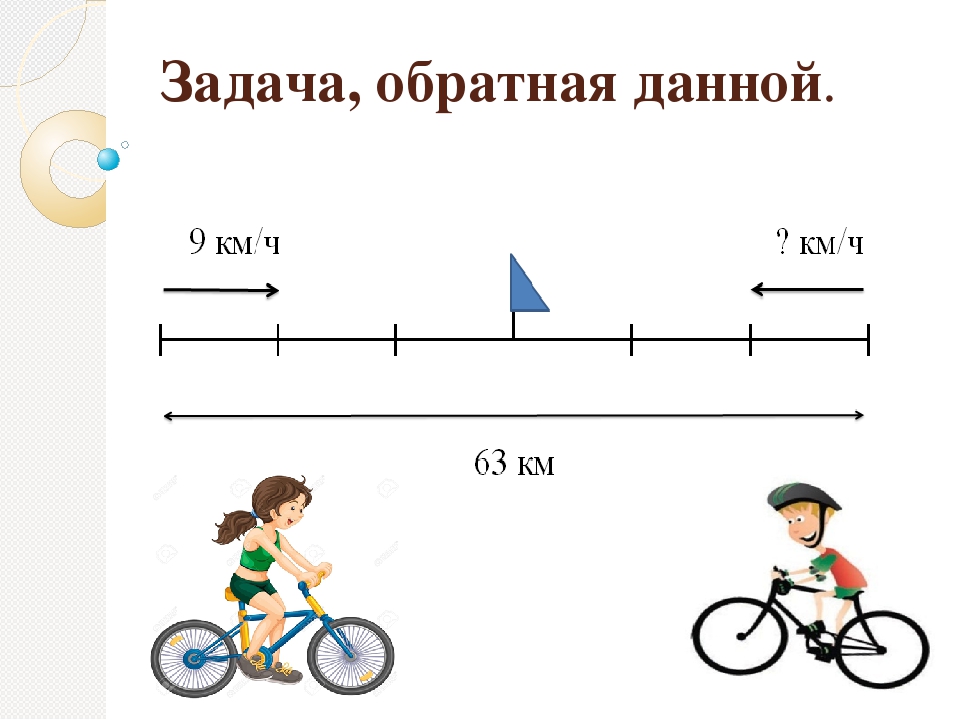

Реши. Предложите учащимся поработать самостоятельно и определить, какая из предложенных схем подходит для решения задачи. Попроситe детей аргументировать свой выбор. Для проверки правильности сделанного выбора предложите составить и решить обратную задачу. В ходе обсуждения и проведения взаимопроверки первоклассники смогут сделать вывод о том, что к задаче на сложение можно составить 2 обратные задачи на вычитание. Таким образом, они смогут не только выполнить проверку решения задачи, но и увидеть взаимосвязь между компонентами задачи.

Ответ

б) 12 + 7 = 19 (д.) Ответ: 19 детей.

Обратные задачи:

1.19-7=12 (д.)

Ответ: 12 детей ходят в танцевальный кружок.

2.19-12 = 7 (д.)

Ответ: 7 человек занимаются музыкой.

Попробуй. Учащиеся составляют текст прямой задачи на сложение из предложенных слов, опираясь на схему. После этого они составляют пару обратных задач, используя слова с противоположным значением. Затем нужно решить задачи.

Ответ

Пример составления прямой задачи:

У Арины в копилке было 70 монет, родители

добавили еще 10 монет. Сколько монет стало

в копилке у Арины?

Обратные задачи:

У Арины в копилке было 80 монет. Она взяла из копилки 70 монет. Сколько монет осталось в копилке?
У Арины в копилке было 80 монет. Она потратила из них 10 монет. Сколько монет осталось в копилке?

Учебник:

Обратная задача, с. 66—67. Рабочая тетрадь:

Рабочий лист 61 «Обратные задачи», с. 63. Рабочий лист 62 «Составь задачи», с. 64.

Ресурсы:

листы ламинированной бумаги.

Критерии успеха

Конец урока

Подумай. Организуйте работу в группах. Учащиеся читают тексты двух задач, сравнивают их и определяют, что вторая задача не является обратной первой.

Критерии успеха

Критерии определения:

тематика задачи;
числовые значения;
взаимосвязь между частями и целым.

Таким образом, дети определят, что по теме задачи одинаковые, в них используются одни и те же числовые значения. Однако в первой задаче число 15 является частью, а во второй задаче — целым, поэтому вторая задача не может являться обратной для первой задачи.

Дифференциация

Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание

Как Вы планируете проверить уровень усвоения материала учащимися?

Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.

Здоровье и соблюдение техники безопасности

Здоровьесберегающие технологии.

Используемые физминутки и активные виды деятельности.

Дополнительные задания

Весенний сад. Ученик должен прочитать текст задачи и подобрать к ней обратные задачи, соединив линией основную задачу с обратными.

Ответ

а) и г).

Перелетные птицы. Учащийся должен прочитать текст задачи, построить к ней схему, оформить решение и ответ. Затем он должен составить 2 обратные задачи и оформить к ним краткие записи, схемы, решения и ответы.

Ответ

20 + 30 = 50 (п.) Ответ: 50 перелетных птиц вернулось с юга.
Всего прилетело 50 птиц. Из них 30 скворцов, а остальные грачи. Сколько грачей прилетело?
Всего прилетело 50 птиц. Из них 20 грачей, а остальные скворцы, Сколько скворцов прилетело?

Задайте вопросы с целью проверки знаний:
Что такое обратная задача?
На чю нужно обращать внимание при составлении обратной задачи?
Сколько обратных задач можно составить к задаче на сложение?

Проведите работу с учащимися по самооцениванию с помощью «Лестницы успеха» в рабочей тетради.

Динамическая пауза.

На луне жил звездочет — («смотрят» в телескоп)

Он планетам вел учет: (показывать в небо рукой)

Меркурий — раз, (описать круг руками)

Венера — два, (хлопок)

Три — Земля, четыре — Марс, (присесть)

Пять — Юпитер, шесть — Сатурн, (наклон вправо-влево)

Семь — Уран, восемь — Нептун, (наклон вперед, прогнуться назад)

Девять — дальше всех — Плутон, (прыжок)

Кто не видит — выйди вон! (развести руки в стороны)

СТАВРОПОЛЬЕ И КОМПАНИЯ «ИННОПРАКТИКА» ЗАКЛЮЧИЛИ СОГЛАШЕНИЕ О РАЗВИТИИ ИННОВАЦИЙ В АПК РЕГИОНА ← Официальный комментарий Портал органов государственной власти Ставрополького края

13 июля 2021 10:16

Заключено соглашение о сотрудничестве между Правительством Ставропольского края и Фондом поддержки научно-проектной деятельности студентов, аспирантов и молодых ученых «Национальное интеллектуальное развитие» (бренд «Иннопрактика»).

В соответствии с документом на Ставрополье будет реализован ряд передовых научных проектов в сфере использования биологических средств защиты растений, кормовых пробиотиков и биоконсервантов для развития органического растениеводства.

Направлением сотрудничества станет также улучшение племенных качеств крупного рогатого скота молочных пород. Партнерами выступят Сколковский институт науки и технологий (Сколтех), компания «Мираторг Генетика» и Ставропольский государственный аграрный университет.

Также соглашением предусмотрено участие региональных вузов и научных центров в разработке программ развития аграрного образования.

Губернатор Владимир Владимиров подчеркнул важность партнерства с компанией «Иннопрактика» с учетом производственного потенциала Ставрополья и регионального опыта научно-исследовательской и внедренческой работы в сельском хозяйстве.

— В крае действуют крупные исследовательские институты аграрного профиля: есть собственные разработки в выведении новых сортов растений, пород сельхозживотных. Эти результаты сегодня помогают нам решать задачи продовольственной безопасности, расширения экспорта. А приоритетом является дальнейшее развитие аграрного комплекса с опорой на науку и инновации. В том числе, это относится к молочному животноводству, где только за последние 3 года реализовано более 20 инвестиционных проектов. Рассчитываю, что работа в рамках соглашения поможет этот итог умножить и дать дополнительный импульс роста для всего регионального АПК, — прокомментировал соглашение Владимир Владимиров.

— Ставропольский край является признанным лидером агропромышленного комплекса Российской Федерации. Именно здесь, на Ставрополье, как и еще в 20 российских регионах, мы будем внедрять инновационные биологические практики и агротехнологии в сельское хозяйство, что позволит создать дополнительные конкурентные преимущества для агробизнеса. Это становится особенно важным при выходе отечественной продукции на мировой рынок, где спрос на органическую продукцию и продукцию с улучшенными характеристиками опережает предложение. Также использование новых биотехнологий способствует снижению нагрузки на окружающую среду и восстановлению почв, — отметил директор дирекции развития агро – и биотехнологий компании «Иннопрактика» Владимир Авдеенко.

Справочно: «Иннопрактика» — негосударственный институт развития, с 2012 года реализующий инфраструктурные проекты в сельском хозяйстве и в сфере аграрного образования. В структуру компании входят Центр национального интеллектуального резерва МГУ имени М.В. Ломоносова и Фонд поддержки научно-проектной деятельности студентов, аспирантов и молодых ученых «Национальное интеллектуальное развитие».

автомобили для выездной вакцинации и скорой медпомощи от ГАЗа / Общество / Независимая газета

Мобильный медицинский комплекс. Фото пресс-службы «Группы ГАЗ»

Горьковский автозавод и ГК «Современные транспортные технологии», эксклюзивный дистрибьютор марки ГАЗ, представили линейку автомобилей, предназначенных для организации выездного медицинского обслуживания в соответствии с современными задачами здравоохранения. Автомобили демонстрируются на Всероссийском форуме «Здоровье нации – основа процветания России», который проходит с 13 по 15 июля в ЦВЗ «Манеж» в Москве.

ГАЗ – крупнейший в России производитель медицинского и социального транспорта. Представленные медицинские машины открывают новые возможности для повышения эффективности работы парков автомобилей скорой медицинской помощи (АСМП), организации выездной вакцинации, диагностики и лечения пациентов, а также повышения комфорта работы медиков.

Опираясь на компетенцию собственных инженерных кадров, ГАЗ производит современные и востребованные автомобили, в том числе для решения широких социальных задач. Этот стало возможным благодаря инвестициям промышленника Олега Дерипаски в масштабную модернизацию автопредприятия еще в начале 2000-х годов.

Медицинские автомобили ГАЗ.
Фото пресс-службы «Группы ГАЗ»

Мобильный медицинский комплекс на базе каркасного автобуса «ГАЗель NEXT Ситилайн» с возможностью присоединения дополнительного модуля предназначен для оказания квалифицированной помощи жителям удаленных населенных пунктов, в том числе – для выездной вакцинации. Автомобиль и прицеп становятся двумя самостоятельными кабинетами, которые также могут быть оборудованы под передвижной диагностический центр, фельдшерско-акушерский пункт, кабинет маммологии, стоматологии, кардиологии, флюорографии, рентген-кабинет, центр детского здоровья, мобильную лабораторию. Помимо медицинского оборудования и мебели машина оснащена автономными системами жизнеобеспечения, генератором и санузлом.

Модульный АСМП открывает возможности для гибкой планировки и размещения оборудования в зависимости от стоящих перед медицинской бригадой задач. При необходимости автомобиль быстро перепрофилируется путем замены медицинского модуля. Большой объем свободного пространства и строго прямоугольная, без сужения в верхней части, форма салона, повышают комфорт работы медиков при сохранении общих компактных габаритов автомобиля. В салоне возможно разместить сразу двух пациентов.

Модульный подход к изготовлению АСМП позволяет легко сокращать или увеличивать парк медицинских автомобилей в зависимости от эпидемиологической ситуации (например, во время пандемии). При износе базового шасси в результате интенсивной эксплуатации модуль с дорогостоящим оборудованием можно целиком перенести на новое шасси, что позволит существенно снизить расходы на обновление парка станций скорой помощи.

АСМП класса B «ГАЗель NEXT» выполнен на основе цельнометаллического фургона с низкой крышей, что обеспечивает возможность доступа автомобиля в ограниченные по высоте места. Медицинский отсек оснащен необходимым для оказания неотложной помощи оборудованием. Обивка салона выполнена из водонепроницаемых, антистатических материалов, что облегчает обслуживание автомобиля.

АСМП «ГАЗель NEXT» с телекоммуникационным комплексом раскрывает возможности применения современных мультимедийных коммуникационных систем для оказания помощи пациентам на выезде. Автомобиль оборудован набором камер, мониторов и систем высокоскоростной связи для проведения сеансов телемедицины и удаленного консультирования медицинской бригады профильными специалистами во время обследования пациента или проведения медицинских манипуляций. Это открывает возможности для лечения больных в самых удаленных точках страны под наблюдением опытных врачей. Функциональность и надежность классической модели АСМП «ГАЗель NEXT» дополняют инновационные технические средства обеспечения транспортной безопасности: система видеонаблюдения и система контроля усталости водителя.

Центральная тема форума – «Укрепление общественного здоровья – сфера взаимной ответственности государства и граждан». На пленарном заседании Валентина Цывова, главный врач частного лечебно-профилактического учреждения «Центр медицинской профилактики ГАЗ», расскажет о лучших практиках «Группы ГАЗ» в сфере сбережения здоровья сотрудников компании и общества. Речь пойдет о внедренных противоэпидемических мерах, расширении спектра медицинских услуг, оказываемых сотрудникам компании и жителям Нижегородской области, инвестициях компании в создание высокотехнологичных диагностических медицинских отделений и инфекционных лабораторий. Кроме того, спикер представит концепцию мобильных госпиталей быстрого реагирования.

Футболисты «Амкар-Пермь» провели свой первый официальный матч

Сегодня, 14 июля, состоялся первый официальный матч футбольного клуба «Амкар-Пермь» в его новейшей истории. В рамках 1/256 Бетсити Кубка России пермяки принимали «Тюмень».

В связи с принятием мер против распространения коронавирусной инфекции на трибуны стадиона «Звезда» были допущены только 500 зрителей, предъявившие отрицательные результаты ПЦР-тестов на COVID-19 или QR-коды о пройденной вакцинации или недавно перенесенной болезни.

Поддержать футболистов пришел губернатор Пермского края Дмитрий Махонин. Он обратился к болельщикам с просьбой с пониманием отнестись к ситуации. «Для нас всех сейчас главным является здоровье жителей. Я благодарю тех, кто пришел сегодня на стадион «Звезда» и тех, кто смотрит матч по онлайн-трансляциям. Эта поддержка нашей команде очень нужна. Как и нашим врачам, которые сейчас тоже ведут борьбу с коронавирусом», — подчеркнул глава региона Дмитрий Махонин.

Но и в таком ограниченном составе болельщики гнали свою команду вперед, вспомнив исторические кричалки про красно-черных. Поддержка зрителей помогла игрокам открыть счет уже на 4 минуте встречи – автором первого гола «Амкар-Пермь» стал полузащитник Александр Голубцов. Однако, удержать преимущество хозяевам не удалось: достаточно быстро «Тюмень» восстановила равенство. Всю игру соперники искали бреши в обороне друг друга. Капитан красно-черных справился с этой задачей – Евгений Тюкалов, на последних минутах матча забил «гол в раздевалку».

Во втором игровом отрезке команды показали зрелищный футбол с большим количеством голевых моментов, один из которых принес успех гостям. За 3 минуты до конца основного времени матча тюменцы вновь восстановили равенство 2:2. По регламенту в таких случаях победителя выявляет серия пенальти. И в этой лотерее удача оказалась на стороне гостей – 3:2.

«Амкар-Пермь» выбыл из борьбы за Кубок России и теперь сконцентрируется на чемпионате ФНЛ-2, который стартует 20 июля. Первые матчи красно-черные проведут на выезде. На родном стадионе команда Рустема Хузина сыграет 1 августа вновь против «Тюмени».

Отметим, только на странице клуба в соцсети «ВКонтакте» игру посмотрели более 24 тыс. зрителей. По ходу матча и по окончании они оставляли комментарии в поддержку футболистов. «Достойная игра против крепкой команды нашего дивизиона. Все еще будет, разыграются парни!», «Молодцы! Сыгранности не хватает, а так очень нормально! За такой-то короткий период!», «Отличная игра, спасибо за эмоции! Обидно что проиграли, но без поражений не бывает побед. Все впереди! Вперед Амкар!» — писали болельщики.

В ответ футболисты поблагодарили зрителей: «Всем спасибо за поддержку! Мы бились достойно! Следующая игра — 20 июля в Барнауле. Верим в команду!», — написали представители клуба после игры на своей странице в соцсети.

Напомним, футбольный клуб «Амкар» был возрожден по инициативе губернатора Пермского края Дмитрия Махонина. Бренд приобретен в краевую собственность летом 2020 года. Название было передано региональной Академии игровых видов спорта. На базе нее была сформирована молодежная команда, выступавшая в прошлом году в Первенстве России среди любительских клубов.

По словам президента ФК «Амкар-Пермь» Валерия Чупракова, перед клубом стоит задача за ближайшие два года пройти путь до второго по значимости футбольного дивизиона – Футбольной национальной лиги.

Что такое обратные операции? — Определение, факты и примеры

Обратные операции

Операция — это математический процесс, включающий сложение, вычитание, умножение, деление, возведение в квадрат, квадратные корни и т. Д.

Все указанные символы (+, -, ×, ÷) в математике известны как операторы.

Обратная операция отменяет действие первой операции.

Например, если мы сложили два числа, скажем, 5 + 3 = 8

Обратной операцией будет вычитание этих двух чисел: 5-3 = 2.

Обратные операторы

Основными математическими операциями являются сложение, вычитание, умножение и деление. Обратные операции приведены в таблице ниже:

Обратные операции

Операции	Обратные операции
Дополнение	Вычитание
Вычитание	Дополнение
Умножение	Дивизион
Дивизион	Умножение

Обратные операторы

Еще примеры обратных операций

Оператор

Обратный оператор

Пример

5 + 4 = 9

5-4 = 1

6-3 = 3

6 + 3 = 9

2 × 3 = 6

6 ÷ 3 = 2

8 ÷ 2 = 4

2 × 4 = 8

Свойства обратных операций

Свойство обратной аддитивности: Обратная операция сложения двух одинаковых чисел приведет к нулю.

2 + (-2) = 0

или

Когда мы прибавляем число к противоположному, результат всегда 0.

Свойство обратного умножения: Когда мы умножаем число на его (мультипликативное) обратное, результат всегда 1.

Множитель, обратный 10, равен ¹ ⁄ ₁₀

Итак, 10 × ¹ ⁄ ₁₀ = 1

Свойство добавки: Рассмотрим операцию, 5 + 0 = 5

Обратная операция: 5-0 = 5

Таким образом, когда мы прибавляем любое число к нулю, и операция, и обратная операция дадут одно и то же число.

Мультипликативное свойство: Рассмотрим операцию, 5 × 1 = 5

Обратная операция: 5 ÷ 1 = 5

Таким образом, когда мы умножаем любое число на 1, и операция, и обратная операция дадут одно и то же число.

Формулировка обратной задачи для оценки параметров реакционно-диффузионной модели глиом низкой степени злокачественности

. 2016 Янв; 72 (1-2): 409-33. DOI: 10.1007 / s00285-015-0888-х. Epub 2015 12 мая.

Принадлежности Расширять

Принадлежности

¹ Институт вычислительной техники и наук Техасского университета в Остине, Остин, Техас, 78712, США[email protected].
² Институт вычислительной техники и наук Техасского университета в Остине, Остин, Техас, 78712, США. [email protected].
³ Институт вычислительной техники и наук Техасского университета в Остине, Остин, Техас, 78712, США. [email protected].

Бесплатная статья PMC

Элемент в буфере обмена

Амир Голами и др.J Math Biol. 2016 Янв.

Бесплатная статья PMC Показать детали Показать варианты

Показать варианты

Формат АннотацияPubMedPMID

.2016 Янв; 72 (1-2): 409-33. DOI: 10.1007 / s00285-015-0888-х. Epub 2015 12 мая.

Принадлежности

¹ Институт вычислительной техники и наук Техасского университета в Остине, Остин, Техас, 78712, США[email protected].
² Институт вычислительной техники и наук Техасского университета в Остине, Остин, Техас, 78712, США. [email protected].
³ Институт вычислительной техники и наук Техасского университета в Остине, Остин, Техас, 78712, США. [email protected].

Элемент в буфере обмена

Полнотекстовые ссылки Опции CiteDisplay

Показать варианты

Формат АннотацияPubMedPMID

Абстрактный

Мы представляем численную схему решения задачи оценки параметров для модели роста низкосортной глиомы.Наша цель — оценить пространственное распределение концентрации опухоли, а также величину анизотропной диффузии опухоли. Мы используем формулировку оптимизации с ограничениями с моделью реакции-диффузии, которая приводит к системе нелинейных уравнений в частных производных. В нашей формулировке мы оцениваем параметры, используя частично наблюдаемые зашумленные данные о концентрации опухоли в двух разных временных точках, а также направления волокон белого вещества, полученные из визуализации тензора диффузии. Задача оптимизации решается с помощью алгоритма сокращенного пространства Гаусса-Ньютона.Приведем формулировку и опишем численные алгоритмы решения полученных уравнений. Мы тестируем метод с использованием синтетического набора данных и вычисляем ошибку реконструкции для различных уровней шума и порогов обнаружения для монофокальных и мультифокальных тестовых случаев.

Ключевые слова: Мультиформная глиобластома; Глиома; Обратные задачи; Оценка параметров; Рост опухоли.

Цифры

Фиг.1

Прямое моделирование роста опухоли…

Фиг.1

Прямое моделирование роста опухоли с использованием модели реакции-диффузии по формуле.1. От…

рисунок 1

Прямое моделирование роста опухоли с использованием модели реакции-диффузии по формуле. 1. Сверху вниз в строках показано распределение опухолей при t = 0,1 и 2, что в размерной форме соответствует 0, 14 и 28 месяцам соответственно.

Фиг.2

L-кривая для выбора регуляризации…

Фиг.2

L-кривая для выбора параметра регуляризации. Угол L-кривой дает β…

Рис. 2

L-кривая для выбора параметра регуляризации. Угол L-кривой дает β _p = 0,01 в качестве оптимального параметра регуляризации для c _d = 0,2 и η = 5%.

Фиг.3

Результаты реконструкции для тестового примера…

Фиг.3

Результаты реконструкции для теста 2. В верхнем ряду показана целевая опухоль…

Рис. 3

Результаты реконструкции для контрольного примера 2. В верхнем ряду показано целевое распределение опухолей в разные моменты времени.Три столбца показывают распределение опухолей при t = 0 1 и 2, что в размерной форме соответствует 0 14 и 28 месяцам соответственно. Синий контур показывает наблюдаемую концентрацию опухоли c _d = 0,2. Реконструкция основана на зашумленных наблюдениях ( η = 5%) плотности клеток внутри этого контура (при t = 0 и t = 1). Во второй строке показаны результаты реконструкции в соответствующие моменты времени.Относительные ошибки реконструкции составляют 6,6%, 4,5% и 5,3% соответственно. Последняя строка показывает ту же разницу, но с измененной цветовой картой (k) исходной цветовой карты (j).

Фиг.4

Результаты реконструкции для мультифокального теста…

Фиг.4

Результаты реконструкции для многоочагового теста 3. В верхней строке отображается цель…

Рис. 4

Результаты реконструкции для многоочагового теста 3. В верхнем ряду показано целевое распределение опухолей в разное время. Три столбца показывают распределение опухолей при t = 0, 1 и 2, что в размерной форме соответствует 0, 5 и 10 месяцам соответственно. Белый контур показывает наблюдаемую концентрацию опухоли c _d = 0.2. В нижнем ряду показаны результаты реконструкции при t = 0, 1 и 2 для η = 5%. Ошибки реконструкции составляют 10,3%, 6,97% и 6,56% соответственно.

Процитировано

8 статей

ГДЕ НАЧИНАЛАСЬ ОПУХОЛЬ? ОБРАТНЫЙ РЕШАЮЩИЙ РЕШАЮЩИЙ РЕШАЮЩИЙ РЕШЕНИЕ С РЕЗЬБНОЙ ЛОКАЛИЗАЦИЕЙ ДЛЯ МОДЕЛЕЙ РОСТА ОПУХОЛЕЙ.
Субраманиан С., Шойфеле К., Мель М., Бирос Г. Subramanian S, et al. Обратная Пробл. 2020 Апрель; 36 (4): 045006. DOI: 10.1088 / 1361-6420 / ab649c. Epub 2020 26 февраля. Обратная Пробл. 2020. PMID: 33746330 Бесплатная статья PMC.
КАЛИБРОВКА МОДЕЛИ БИОФИЗИЧЕСКОГО РОСТА ОПУХОЛЕЙ ПО ИЗОБРАЖЕНИЮ.
Scheufele K, Subramanian S, Mang A, Biros G, Mehl M. Scheufele K, et al. SIAM J Sci Comput. 2020; 42 (3): B549-B580. DOI: 10.1137 / 19M1275280. Epub 2020 6 мая. SIAM J Sci Comput. 2020. PMID: 33071533 Бесплатная статья PMC.
Интегрированное биофизическое моделирование и анализ изображений: применение в нейроонкологии.
Манг А., Бакас С., Субраманиан С., Давацикос К., Бирос Г. Mang A, et al. Annu Rev Biomed Eng. 2020 4 июня; 22: 309-341. DOI: 10.1146 / annurev-bioeng-062117-121105. Annu Rev Biomed Eng. 2020. PMID: 32501772 Бесплатная статья PMC.
Сопряжение биофизических моделей головного мозга и опухоли и регистрация диффеоморфных изображений.
Scheufele K, Mang A, Gholami A, Davatzikos C, Biros G, Mehl M. Scheufele K, et al. Вычислительные методы Appl Mech Eng. 2019 15 апреля; 347: 533-567. DOI: 10.1016 / j.cma.2018.12.008. Epub 2019 7 января. Вычислительные методы Appl Mech Eng. 2019. PMID: 31857736 Бесплатная статья PMC.
Моделирование роста глиобластомы на трехмерной модели многовидовой опухоли с масс-эффектом.
Субраманиан С., Голами А., Бирос Г. Subramanian S, et al. J Math Biol. 2019 август; 79 (3): 941-967. DOI: 10.1007 / s00285-019-01383-у. Epub 2019 24 мая. J Math Biol. 2019. PMID: 31127329 Бесплатная статья PMC.

Условия MeSH

Новообразования / патологии головного мозга *
Визуализация, трехмерная
Инвазивность / патология новообразования

LinkOut — дополнительные ресурсы

Источники полных текстов
Другие источники литературы
Медицинские

Формулировка обратной задачи для оценки параметров модели реакции-диффузии глиом низкой степени злокачественности

Андерсон А., Се Дж., Пиццония Дж., Бронен Р., Спенсер Д., Гор Дж. (2000) Влияние изменений объемной доли клеток на кажущуюся диффузию в клетках человека.Магнитно-резонансная томография 18 (6): 689–695

Статья Google Scholar

Atuegwu NC, Arlinghaus LR, Li X, Chakravarthy AB, Abramson VG, Sanders ME, Yankeelov TE (2013) Параметризация логистической модели роста опухоли с помощью данных DW-MRI и DCE-MRI для прогнозирования ответа на лечение и изменений в клеточность рака груди во время неоадъювантной химиотерапии. Transl Oncol 6 (3): 256–264

Статья Google Scholar

Bangerth W, Joshi A (2008) Адаптивные методы конечных элементов для решения обратных задач в оптической томографии.Обратная задача 24 (3): 034,011

MathSciNet Статья Google Scholar

Белломо Н., Ли Н., Майни П.К. (2008) Об основах моделирования рака: избранные темы, предположения и перспективы. Математические модели, методы, прикладные науки, 18 (04): 593–646

MathSciNet Статья МАТЕМАТИКА Google Scholar

Бирос Г., Гаттас О. (2005a) Параллельные методы Лагранжа – Ньютона – Крылова – Шура для оптимизации с ограничениями в частных производных.Часть I. Решатель Крылова – Шура. SIAM J Sci Comput 27 (2): 687–713

MathSciNet Статья МАТЕМАТИКА Google Scholar

Бирос Г., Гаттас О. (2005b) Параллельные методы Лагранжа – Ньютона – Крылова – Шура для оптимизации с ограничениями в частных производных. Часть II: решатель Лагранжа – Ньютона и его применение для оптимального управления установившимися вязкими потоками. SIAM J Sci Comput 27 (2): 714–739

MathSciNet Статья МАТЕМАТИКА Google Scholar

Bondiau P-Y, Clatz O, Sermesant M, Marcy P-Y, Delingette H, Frenay M, Ayache N (2008) Биокомпьютеры: численное моделирование роста глиобластомы с использованием визуализации тензора диффузии.Phys Med Biol 53 (4): 879

Статья Google Scholar

Clatz O, Sermesant M, Bondiau P-Y, Delingette H, Warfield SK, Malandain G, Ayache N (2005) Реалистичное моделирование трехмерного роста опухолей головного мозга на МР-изображениях, сочетающих диффузию с биомеханической деформацией. Med Imaging IEEE Trans 24 (10): 1334–1346

Статья Google Scholar

Cobzas D, Mosayebi P, Murtha A, Jagersand M (2009) Граница инвазии опухоли в римановом пространстве мозговых волокон.В: Вычисление медицинских изображений и вмешательство с помощью компьютера — MICCAI 2009. Springer, pp 531–539

Cocosco CA, Kollokian V, Kwan RK-S, Pike GB, Evans AC (1997) Brainweb: онлайн-интерфейс для 3D МРТ смоделировала базу данных мозга. В: NeuroImage, Citeseer

Del Pino S, Pironneau O (2003) Общий решатель PDE на основе фиктивных доменов. В: Численные методы для научных вычислений вариационных задач и приложений, Барселона

Долечек Т.А., Пропп Дж. М., Строуп Н. Е., Кручко С. (2012) Статистический отчет CBTRUS: первичные опухоли головного мозга и центральной нервной системы, диагностированные в США в 2005– 2009 г.Нейроонкология 14 (приложение 5): v1 – v49

Статья Google Scholar

Engwer C, Hillen T, Knappitsch M, Surulescu C (2014) Глиома соответствует трактам белого вещества: многомасштабная модель на основе DTI. J Math Biol 1–32. DOI: 10.1007 / s00285-014-0822-7

Fathi A, Kallivokas L, Poursartip B (2015) Полная инверсия формы волны в трехмерной упругой среде, усеченной PML. Вычислительные методы Appl Mech Eng.arXiv: 1408.6221

Giese A, Kluwe L, Laube B, Meissner H, Berens ME, Westphal M (1996) Миграция клеток глиомы человека на миелин. Нейрохирургия 38 (4): 755–764

Статья Google Scholar

Хабиб С., Молина-Парис С., Дейсбок Т.С. (2003) Сложная динамика опухолей: моделирование возникающей системы опухоли головного мозга с помощью связанных уравнений реакции-диффузии. Phys A: Stati Mech Appl 327 (3): 501–524

Статья МАТЕМАТИКА Google Scholar

Hansen PC (1992) Анализ дискретных некорректных задач с помощью L-кривой.SIAM Ред. 34 (4): 561–580

MathSciNet Статья МАТЕМАТИКА Google Scholar

Hansen PC (1999) L-кривая и ее использование при численной обработке обратных задач. IMM, Департамент математического моделирования, Технический университет Дании

Hawkins-Daarud A, Rockne RC, Anderson AR, Swanson KR (2013) Моделирование опухолевого отека в глиомах во время антиангиогенной терапии и ее влияние на визуализируемую опухоль.Front Oncol 3:66

Артикул Google Scholar

Hillen T (2006) Мезоскопические и макроскопические модели M5 для движения мезенхимы. J Math Biol 53 (4): 585–616

MathSciNet Статья МАТЕМАТИКА Google Scholar

Hochberg FH, Pruitt A (1980) Предположения в лучевой терапии глиобластомы. Неврология 30 (9): 907–907

Статья. Google Scholar

Hogea C, Davatzikos C, Biros G (2007) Моделирование роста глиомы и массового эффекта на трехмерных МРТ-изображениях головного мозга.В: Вычисление медицинских изображений и вмешательство с помощью компьютера — MICCAI 2007. Springer, pp 642–650

Hogea C, Davatzikos C, Biros G (2008a) Биофизические модели взаимодействия мозга и опухоли для регистрации медицинских изображений. SIAM J Sci Comput 30 (6): 3050–3072

MathSciNet Статья МАТЕМАТИКА Google Scholar

Hogea C, Davatzikos C, Biros G (2008b) Задача оценки параметров на основе изображений для модели роста реакционно-диффузионной глиомы с массовыми эффектами.J Math Biol 56 (6): 793–825

MathSciNet Статья МАТЕМАТИКА Google Scholar

Холланд Б.А., Брант-Завадски М., Норман Д., Ханс Ньютон Т. (1985) Магнитно-резонансная томография первичных внутричерепных опухолей: обзор. Int J Radiat Oncol Biol Phys 11 (2): 315–321

Статья Google Scholar

Хорсфилд М.А., Джонс Д.К. (2002) Применение диффузионно-взвешенной и диффузно-тензорной МРТ к заболеваниям белого вещества — обзор.ЯМР Биомед 15 (7–8): 570–577

Статья Google Scholar

Jbabdi S, Mandonnet E, Duffau H, Capelle L, Swanson KR, Pélégrini-Issac M, Guillevin R, Benali H (2005) Моделирование анизотропного роста глиом низкой степени злокачественности с использованием диффузионного тензора. Magn Reson Med 54 (3): 616–624

Артикул Google Scholar

Калливокас Л., Фатхи А., Кучуккобан С., Стокое К. II, Билак Дж., Гаттас О. (2013) Характеристика участка с использованием полной инверсии формы волны.Soil Dyn Earthq Eng 47: 62–82

Статья Google Scholar

Konukoglu E, Clatz O, Bondiau P-Y, Delingette H, Ayache N (2010a) Экстраполяция границы инвазии глиомы на магнитно-резонансных изображениях головного мозга: предлагая новые границы облучения. Med Image Anal 14 (2): 111–125

Статья Google Scholar

Konukoglu E, Clatz O, Menze BH, Stieltjes B, Weber M-A, Mandonnet E, Delingette H, Ayache N (2010b) Персонализация моделей роста опухолей реакционно-диффузионного типа с использованием модифицированных анизотропных уравнений эйконала под контролем изображения.Med Imaging IEEE Trans 29 (1): 77–95

Статья Google Scholar

Лоуренс YR, Ли XA, Эль-Нака I, Hahn CA, Marks LB, Merchant TE, Dicker AP (2010) Эффекты объема дозы излучения в головном мозге. Int J Radiat Oncol Biol Phys 76 (3): S20 – S27

Статья Google Scholar

Ле Бихан Д., Мангин Дж.Ф., Пупон С., Кларк К.А., Паппата С., Молко Н., Чабриат Х. (2001) Визуализация тензора диффузии: концепции и приложения.J Magn Reson Imaging 13 (4): 534–546

Статья Google Scholar

Лима Э., Оден Дж., Алмейда Р. (2014) Гибридная десятивидовая модель фазового поля роста опухоли. Математические модели Методы Appl Sci 24 (13): 2569–2599

MathSciNet Статья МАТЕМАТИКА Google Scholar

Mang A, Toma A, Schuetz TA, Becker S, Eckey T., Mohr C, Petersen D, Buzug TM (2012) Биофизическое моделирование прогрессирования опухоли головного мозга: от безусловно стабильной явной интеграции по времени к обратной задаче с параболической PDE ограничения для калибровки модели.Med Phys 39 (7): 4444–4459

Статья Google Scholar

Mohamed A, Davatzikos C (2005) Конечно-элементное моделирование масс-эффекта опухоли головного мозга по трехмерным медицинским изображениям. В: Вычисление медицинских изображений и вмешательство с помощью компьютера — MICCAI 2005. Springer, pp 400–408

Mori S, Oishi K, Jiang H, Jiang L, Li X, Akhter K, Hua K, Faria AV, Mahmood A. , Woods R et al (2008) Стереотаксический атлас белого вещества, основанный на визуализации тензора диффузии в шаблоне межконтинентальной баллистической ракеты.Neuroimage 40 (2): 570–582

Статья Google Scholar

Mosayebi P, Cobzas D, Murtha A, Jagersand M (2012) Граница инвазии опухоли в римановом пространстве мозговых волокон. Med Image Anal 16 (2): 361–373

Статья Google Scholar

Мюррей Дж. Д. (1989) Математическая биология. Спрингер, Нью-Йорк

Бронировать МАТЕМАТИКА Google Scholar

Nazzaro JM, Neuwelt EA (1990) Роль хирургии в лечении супратенториальных астроцитом средней и высокой степени злокачественности у взрослых.J Neurosurg 73 (3): 331–344

Статья Google Scholar

Newton H (1994) Первичные опухоли головного мозга: обзор этиологии, диагностики и лечения. Am Fam Physician 49 (4): 787–797

Google Scholar

Painter K, Hillen T (2013) Математическое моделирование роста глиомы: использование данных визуализации тензора диффузии (DTI) для прогнозирования анизотропных путей инвазии рака.J Theor Biol 323: 25–39

MathSciNet Статья Google Scholar

Powathil G, Kohandel M, Sivaloganathan S, Oza A, Milosevic M (2007) Математическое моделирование опухолей головного мозга: эффекты лучевой терапии и химиотерапии. Phys Med Biol 52 (11): 3291

Статья Google Scholar

Rekik I, Allassonnière S, Clatz O, Geremia E, Stretton E, Delingette H, Ayache N (2013) Оценка параметров роста опухоли и локализация источника с уникальной временной точки: применение к глиомам низкой степени злокачественности.Comput Vis Image Underst 117 (3): 238–249

Статья Google Scholar

Rockne R, Alvord E Jr, Rockhill J, Swanson K (2009) Математическая модель ответа опухоли головного мозга на лучевую терапию. J Math Biol 58 (4–5): 561–578

MathSciNet Статья МАТЕМАТИКА Google Scholar

Rockne R, Rockhill J, Mrugala M, Spence A, Kalet I, Hendrickson K, Lai A, Cloughesy T., Alvord E Jr, Swanson K (2010) Прогнозирование эффективности лучевой терапии у отдельных пациентов с глиобластомой in vivo: подход к математическому моделированию.Phys Med Biol 55 (12): 3271

Статья Google Scholar

Ропп Д.Л., Шадид Дж. Н. (2009) Устойчивость методов расщепления операторов для систем с неопределенными операторами: системы адвекции-диффузии-реакции. J Comput Phys 228 (9): 3508–3516

MathSciNet Статья Google Scholar

Salcman M (1980) Выживание при глиобластоме: историческая перспектива. Нейрохирургия 7 (5): 435–439

Статья Google Scholar

Seither R, Jose B, Paris K, Lindberg R, Spanos W. (1995) Результаты облучения пациентов с глиомами высокой степени злокачественности, оцененные с помощью магнитно-резонансной томографии.Am J Clin Oncol 18 (4): 297–299

Статья Google Scholar

Silbergeld DL, Chicoine MR (1997) Выделение и характеристика клеток злокачественной глиомы человека из гистологически нормального мозга. J Neurosurg 86 (3): 525–531

Статья Google Scholar

Sodt R, Rockne R, Neal M, Kalet I, Swanson KR (2014) Количественная оценка роли анизотропной инвазии в глиобластоме человека.В кн .: Вычислительная хирургия и дуальное обучение. Springer, pp 315–329

Stadlbauer A, Pölking E, Prante O, Nimsky C, Buchfelder M, Kuwert T, Linke R, Doelken M, Ganslandt O (2009) Выявление инвазии опухоли в пирамидный тракт у пациентов с глиомой с сенсомоторным дефицитом путем корреляции 18f-фторэтил-1-тирозина ПЭТ и магнитно-резонансной диффузной тензорной визуализации. Acta Neurochir 151 (9): 1061–1069

Статья Google Scholar

Stein AM, Demuth T, Mobley D, Berens M, Sander LM (2007) Математическая модель инвазии сфероида опухоли глиобластомы в трехмерном эксперименте in vitro.Biophys J 92 (1): 356–365

Статья Google Scholar

Странг Г. (1968) О построении и сравнении разностных схем. SIAM J Numer Anal 5 (3): 506–517

MathSciNet Статья МАТЕМАТИКА Google Scholar

Swanson K, Alvord E, Murray J (2000) Количественная модель дифференциальной подвижности глиом в сером и белом веществе. Cell Prolif 33 (5): 317–330

Статья Google Scholar

Swanson K, Rostomily R, Alvord E (2008) Инструмент математического моделирования для прогнозирования выживаемости отдельных пациентов после резекции глиобластомы: доказательство принципа.Br J Cancer 98 (1): 113–119

Статья Google Scholar

Swanson KR, Alvord E, Murray J (2002) Виртуальные опухоли головного мозга (глиомы) усиливают реальность медицинской визуализации и подчеркивают недостатки современной терапии. Br J Cancer 86 (1): 14–18

Статья Google Scholar

Тихонов А. (1963) Решение некорректно сформулированных задач и метод регуляризации.Sov Math Dokl 5: 1035–1038

MATH Google Scholar

Tracqui P, Cruywagen G, Woodward D, Bartoo G, Murray J, Alvord E (1995) Математическая модель роста глиомы: влияние химиотерапии на пространственно-временной рост. Cell Prolif 28 (1): 17–31

Статья Google Scholar

Weis JA, Miga MI, Arlinghaus LR, Li X, Chakravarthy AB, Abramson V, Farley J, Yankeelov TE (2013) Механически связанная реакционно-диффузионная модель для прогнозирования ответа опухолей молочной железы на неоадъювантную химиотерапию.Phys Med Biol 58 (17): 5851

Статья Google Scholar

Wrensch M, Minn Y, Chew T., Bondy M, Berger MS (2002) Эпидемиология первичных опухолей головного мозга: современные концепции и обзор литературы. Нейроонкология 4 (4): 278–299

Google Scholar

ECE598ID — Обратные задачи и обучение

Описание курса

Обратные задачи занимают центральное место в технике и науке.Наиболее интересные обратные задачи некорректно поставлены и нуждаются в регуляризации. Этот курс будет охватывать основы теории обратных задач, включая элементы функционального анализа, теория регуляризации и оптимизация. После изучения основ обратных задач будут рассмотрены теория и приложения машинного обучения для решения обратных задач.

Значительная часть курса будет посвящена основным методам машинного обучения и управления данными. В частности, изучение словаря, преобразование обучения и приложений глубоких нейронных сетей и генеративных состязательные сети будут охвачены.

Вторник и четверг, 12: 30–13: 50, 2013 ECEB

Инструктор: Иван Докманич, dokmanic at illinois dot edu (Часы работы: вторник с 16:30 до 17:30, CSL 313)
Ассистент учителя: Сидхарт Гупта, gupta67 at illinois dot edu (Часы работы: четверг с 14:30 до 15:30, CSL 469B)

Объявления

15 января 2019: Курс начинается!
12 февраля 2019: доступно домашнее задание 1.Он состоится 27 февраля 2019 года в 23:59.
27 февраля 2019: доступно домашнее задание 2. Он состоится 12 марта 2019 года в 23:59.
9 марта 2019 г .: Предложение по проекту должно быть принято 17 марта 2019 г. в 23:59.
27 марта 2019: доступно домашнее задание 3. Он состоится 7 апреля 2019 года в 23:59.

Подача заявки

Подача будет через Box. Пожалуйста, свяжитесь с ассистентом преподавателя, если вы не получили приглашение Box или у вас возникли проблемы с отправкой своей работы.
Дополнительный балл будет отдан набранным материалам LaTeX.

Программа

Неделя 1 (1 / 14–1 / 18)

Неделя 2 (21–1.25)

Лекция 1: Примеры обратных задач
Лекция 2: Классическая регуляризация
Блокнот Python: удаление размытия и CT

Неделя 3 (1 / 28–2 / 1)

Лекция 1: Регуляризация
Лекция 2: Основы оптимизации

Неделя 4 (2 / 4–2 / 8)

Неделя 5 (2 / 11–2 / 15)

6-я неделя (18.02-22)

Лекция 1: Редкость способствует регуляризации
Лекция 2: Проксимальные методы

7 неделя (2 / 25–3 / 1)

8-я неделя (3/4–3 / 8)

Лекция 1: Сжатое зондирование
Лекция 2: Сжатое зондирование

Неделя 9 (3 / 11–3 / 15)

10 неделя (18.03–222)

11-я неделя (25-33-29)

Лекция 1: Матричные обратные задачи
Лекция 2: Спектральная инициализация для матричных обратных задач

Неделя 12 (4 / 1–4 / 5)

13 неделя (4 / 8–4 / 12)

14 неделя (15.04.19)

15-я неделя (22.04–4.26)

Оценка

40% домашних заданий
30% один среднесрочный
30% класс

Чтение

Шерцер, Отмар, Маркус Грасмайр, Харальд Гроссауэр, Маркус Хальтмайер и Франк Ленцен. Вариационные методы визуализации . Springer Science + Business Media LLC, 2009.

обратных задач, весна 2017 — mathstat

Вопрос: О чем эта картина?

Ответ: Это образец рентгеновской томографии! Смотрите это видео. И эта страница.

Класс 2017 г. (стендовая сессия):

Учитель: Самули Силтанен

Объем: 15 кр (лекционная часть и проектная работа вместе)

Тип: Углубленное изучение

Преподавание:

Темы: Обратные задачи связаны с измерением и пытаюсь восстановить это что-то из данных.Например, врач может сделать несколько рентгеновских снимков пациента с разных сторон и пожелать понять трехмерную структуру внутренних органов пациента. Но каждое из двухмерных изображений показывает только проекцию внутренних органов; фактически необходимо рассчитать трехмерную структуру, используя алгоритм реконструкции. Этот курс учит, как

смоделировать (линейный) процесс измерения как матричное уравнение m = Ax + шум,
определить, приводит ли матрица A к некорректно поставленной обратной задаче,
спроектировать и реализовать метод регуляризованной реконструкции для восстановления x из m.Мы изучаем декомпозицию усеченного сингулярного числа, регуляризацию Тихонова, регуляризацию полной вариации и разреженность на основе вейвлетов,
измеряем томографические данные в рентгеновской лаборатории,
сообщаем о своих выводах в виде научного плаката.

См. Эту страницу для получения дополнительной информации об обратных задачах.

Вот старые домашние страницы этого курса: 2015, 2014, 2013. В этом году курс примерно такой же, как и в прошлые годы.

Пререквизиты: Линейная алгебра, базовые навыки программирования на Matlab, интерес к практическим приложениям и любознательный ум.Курс подходит (и очень полезен) для студентов, изучающих математику, статистику, физику или информатику.

Рассмотрим вышеупомянутую фотографическую ситуацию. Вы хотели бы получить левое изображение: резкое и красивое. Однако из-за неправильной фокусировки и высоких значений ISO в камере вы получили размытое и зашумленное изображение справа. Есть ли шанс спасти положение? Что ж, можно применить удаление размытости, это одна из тем этого курса. Ниже вы видите три различных метода удаления заусенцев с переменным успехом.Слева направо: основная регуляризация, полная вариация и полная обобщенная вариация. (Спасибо профессору Кристиану Бреди за его удивительный алгоритм TGV!)

Новости

Результаты промежуточного опроса (15 февраля). В общем, вроде все идет хорошо. Давайте обсудим в лекции, как упростить поиск материала.

Плейлист видео с новой лекцией

000 000 000 000 000 000 000 000 000 16 (000) Информация о работе над проектом.Цели этого занятия:

Разделение студентов на проектные группы по два человека в каждой,
Выбор темы (данные томографии или деконволюции, какова цель проекта, какие методы попробовать),
Понимание целей Фаза 1 и Фаза 2 проекта,
Согласование времени встреч для обзора Фазы 1 проектов.

Лекция 15 ( 22 марта) 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 Рентгеновская томография в реальном времени.Как перейти от проекционных изображений к линейным интегральным данным? Каковы важнейшие свойства вариантов томографии, таких как томография с ограниченным углом, область интереса, разреженная и внешняя томография?

Лекция, часть 1/2 (снимок экрана)
Лекция, часть 2/2 (снимок экрана)

Лекция 14 ( 17 марта)

Выбор параметра регуляризации.Существует несколько методов, применимых к более или менее различным подходам к регуляризации.

Метод L-кривой (в основном для Тихонова)
Принцип несоответствия Морозова (Тихонов, был распространен на телевидение в недавнем исследовании из Гонконга)
Метод S-кривой (для регуляризации, способствующей разреженности)
метод консистенции (для телевизора, см. этот файл)

Мы рассмотрим эти методы и протестируем некоторые из них.

Лекция, часть 1/2 (снимок экрана)
Лекция, часть 2/2 (снимок экрана)

Лекция 13 ( 15 марта) 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 преобразовать в размерности 1 и 2.Крупномасштабная реконструкция, способствующая разрежению, с помощью итеративного алгоритма мягкого порогового определения (ISTA).

Ресурсы Matlab:

recon_DB_comp.m
recon_Haar_comp.m
scale01.m
Smu_wavelet_oper.m
Smu.m
thresholding_demo.m
wavetrans2D_inv.m
wavetransce0009

Лекция, часть 1/2 (снимок экрана)
Лекция, часть 2/2 (снимок экрана) 0003

Лекция 12 (пятница, марта 3) 9000 Мы использовали метод мозгового штурма «двойная команда» и в итоге получили следующий набор предложений:

Результаты планирования представлены в темах лекций 13, 14 и 15 выше.

Среда, сезон 1 марта. Преподаватель заболел!

Вместо лекции прочтите Раздел 3.2 этой заметки о вейвлет-преобразовании Хаара: FourierSeries_Wavelets_v3.pdf

Изучите эти процедуры Matlab и выясните себе, как связаны коды и текст.

Ресурсы Matlab:

Wavelet_tr_test.m

Wavelet_tr_onestep.m

Wavelet_tr_inv_onestep.m

000

Краткое содержание построения томографического фантома «прямоугольник».Моделирование томографических данных без обратного преступления с использованием моделирования и интерполяции с более высоким разрешением. Применение

усеченного SVD (TSVD),
регуляризации Тихонова и
регуляризации полной вариации

для томографической задачи с разреженными углами. Обратите внимание, что приведенный выше код регуляризации Тихонова написан без использования матриц с использованием метода сопряженного градиента (CG). Позже мы поговорим о компьютерной графике и других итеративных решателях.Вычисление общей вариации представляет собой двумерную адаптацию формулировки квадратичного программирования, включая ограничения неравенства и равенства.

Файлы MyDS2.m и MyDScol.m представляют собой простые процедуры для уменьшения разрешения изображения в два раза.

См. Разделы 2.3, 4.4, 5.5, 6.2 и 5.2 в книге Mueller-Siltanen (2012).

Ресурсы Matlab:

SqPhantom.m
SqPhantom_plot.m
tomo01_RadonMatrix_comp.m
tomo02_firstTSVD_comp.м

tomo02_firstTSVD_plot.m tomo03_NoCrimeData_comp.m

tomo03_NoCrimeData_plot.m tomo04_Tikhonov_comp.m

tomo04_Tikhonov_plot.m tomo07_TV_comp.m

tomo07_TV_plot.m MyDS2.m
MyDScol.m

Лекция, часть 1/2 (снимок экрана)
Лекция, часть 2/2

В среду, 22 февраля, ЛЕКЦИИ НЕТ.Лектор едет.

Вместо лекции, пожалуйста, запустите все файлы Matlab, приведенные ниже, относящиеся к лекции 10, используя целевой сигнал этого года И с фотографическими данными, собранными в лекции 9.

Лекция 10 (17 февраля)

Обсуждались три формы вариационной регуляризации: Тихоновская, обобщенная Тихоновская и Тотальная вариационная регуляризация.Мы сосредоточились на одномерной модели свертки и использовали простую конечно-разностную матрицу L в терминах регуляризации.

Демонстрации Matlab были основаны на процедурах, разработанных в курсе обратных задач 2015 года. Они приведены ниже. Я рекомендую вам выполнить их с целью на этот год и с фотографическими данными, собранными в лекции 9.

Обратите внимание, что всякий раз, когда вы меняете размер n неизвестного, вам нужно запускать deconv2_discretedata_comp.m, deconv3_naive_comp.m, deconv4_SVD_comp.m и deconv5_truncSVD_comp.m перед запуском любой из подпрограмм Тихонова или TV.

Matlab ресурсы:

DC_convmtx.m deconv1_cont_comp.m
deconv1_cont_plot.m
deconv2_discretedata_comp.m
deconv2_discretedata_plot.m
deconv3_naive_comp.m
deconv3_naive_plot.m
deconv4_SVD_comp.m
deconv4_SVD_plot.m
deconv5_truncSVD_comp.m
deconv5_truncSVD_plot.m
deconv6_Tikhonov_comp.m
deconv6_Tikhonov_plot.м
deconv7_genTikhonov_comp.m
deconv7_genTikhonov_plot.m
deconv8_L1reg_comp.m
deconv8_L1reg_plot.m
deconv9_TVreg_comp.m
deconv9_TVreg_plot.m

000

часть 3/3 (снимок экрана)

Лекция 9 (15 февраля)

Фотографические данные с различными уровнями размытия (от расфокусировки объектива) и шума (от увеличения ISO) как измерения.

Мы сфотографировали распечатки этих двух изображений, прикрепленных к стене:

Далее мы выделили строки из краевого изображения и проанализировали значения пикселей в Matlab.

Вот два изображения краев, которые мы сняли и обработали:
edge_blur3.tif
edge_blur3_noisy.tif

Ресурсы Matlab:

deco03_data_meas.m
deco03_data_plot.m
deco_p0003_ 9TSVD_plot.m
deco_p0003_ 9TSVD_deco
Лекция, часть 1/4
Лекция, часть 2/4
Лекция, часть 3/4 (снимок экрана)
Лекция, часть 4/4 (снимок экрана)

Лекция 8 ( 10 февраля)

Наивная инверсия для неквадратных матриц.Т м.

См. Разделы 4.1 и 5.2 в книге Mueller-Siltanen (2012).

Ресурсы Matlab:

QuadraticTest.m

Вот «видео-доказательство» минимального требования
Лекция, часть 1/4
Лекция, часть 2/4 (снимок экрана)
Лекция, часть 3/4
Лекция, часть 4/4

Лекция 7 (8 февраля)

Построение вычислительной модели Af = m для задачи 2D томографии.То есть
— проектирование фантома для тестовых случаев (мы выбрали три прямоугольника на пустом фоне в единичном квадрате), называемое SqPhantom.m,
— построение и сохранение матрицы A для выбора размеров f и коллекций X -направления проекции лучей,
-расчет и сохранение разложения по сингулярным значениям для матрицы A.

Кроме того, мы опробовали усеченное разложение по сингулярным значениям (TSVD) для надежной реконструкции.

Ресурсы по Matlab:
SqPhantom.m
SqPhantom_plot.m
tomodata_test.m
tomo01_RadonMatrix_comp.m
tomo02_firstTSVD_comp.m
tomo02_firstTSVD_plot.m

, часть экрана, часть
, лекция 1/5 )
Лекция, часть 4/5 (снимок экрана)
Лекция, часть 5/5 (снимок экрана)

Лекция 6 (3 февраля)

Резюме троицы

(1) вектор данных измерений дается устройством,
(2) континуальная модель физического процесса измерения и
(3) вычислительная модель, используемая в практической инверсии.
Цель состоит в том, чтобы построить две разные модели-примеры, а именно 1D деконволюцию и 2D томографию. Эти два случая будут использоваться на протяжении всего курса.

Построение матричной модели m = Af с использованием программы Matlab radon.m. Матрица строится столбец за столбцом путем последовательного применения radon.m к единичным векторам. Хотя этот подход неэффективен с точки зрения вычислений, он обеспечивает простой способ построения системных матриц для томографических задач. Затем матрица A может быть изучена, например, с помощью разложения по сингулярным числам.

Ресурсы Matlab:

RadonMatrix.m

Видео с экрана

Лекция 5 (1 февраля)

Лектор потерял голос! Так что лекция отменяется.

Вместо лекции откройте следующую страницу:

Прочтите эти предметы:

Предпосылки и приложения
Математическая модель ослабления рентгеновского излучения
Томографическая визуализация с полными данными
Томографическая визуализация с разреженными данными

Самым важным является «Томографическая визуализация с разреженными данными.

Также прочтите раздел 2.3 учебника (Mueller & Siltanen 2012).

Построение модели моделирования континуума для одномерной свертки в Matlab. См. Раздел 2.1.1 в книге Mueller-Siltanen (2012).

Ресурсы по Matlab:

Краткий обзор первого метода шумоустойчивой реконструкции курса: усеченное разложение по сингулярным числам (TSVD).

Мы тестируем TSVD на примере простой свертки из лекции 2. Главы книги: 2.1, 4.2 и 4.1.1.

Первое замечание о TSVD: реконструкция всегда представляет собой линейную комбинацию сингулярных векторов.Сингулярные векторы — это столбцы матрицы V, появляющиеся при разложении по сингулярным числам.

Второе наблюдение относительно TSVD: , если мы используем очень мало сингулярных значений, реконструкция будет не очень точной, но чрезвычайно устойчивой к шуму. Это означает, что реконструкция не сильно меняет форму измерения на измерение, даже если к данным добавлен большой случайный шум.

Третье наблюдение по поводу ЦВД: не понятно, как вообще выбрать индекс усечения r_ \ alpha.Это действительно сложная проблема, и мы увидим некоторые подходы к ней позже в ходе курса.

Кроме того, мы начали обсуждать разницу между континуальной моделью для свертки (глава 2.1.1 книги) и дискретной моделью свертки (глава 2.1.2 книги).

Ресурсы Matlab:

SimpleDeconvolutionTSVD.m

Видео захвата экрана 1/2, видео захвата экрана 2/2

Лекция 2 (20 января)

двух векторы.Как усиливается шум в наивных попытках инверсии. Главы книги: 2.1.

Лекционный материал: Convolution.pdf, 1D_convolution.pdf

Ресурсы Matlab:

SimpleConvolution.m

Видео с экрана

Лекция 1 (18 января)

Введение в обратные задачи

9000. Практические занятия по курсу.
Лекционные материалы: слайды в формате PDF
000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 Стартовая сессия 24 марта (обычное время и место лекции): быть там, чтобы получить информацию о работе над конкретным проектом.

Фаза 1 обзорных интервью состоится в период с 5 по 7 апреля. Обязательно договоритесь о временном интервале с лектором!

Фаза 2 Конечная цель — стендовая сессия в пятницу, 5 мая, с 10 до 12 в коридоре на 1-м этаже Exactum.

Ассистенты проектной работы: Александр Мини, Зенит Пуриша и Маркус Ювонен.

Идея состоит в том, чтобы теоретически и вычислительно изучить обратную задачу в командах по два студента .Конечным продуктом является научный плакат, который команда представит на стендовой сессии 5 мая (подробности выше).

Плакат можно распечатать на широкоформатном принтере лаборатории. Пожалуйста, отправьте свой плакат Маркусу Ювонену по электронной почте в виде вложения в формате pdf до среды, 3 мая, 12 часов дня. Тогда ваш плакат будет напечатан как раз к стендовой сессии.

Идея работы над проектом — теоретически и вычислительно изучить обратную задачу. Для структурирования отчета первой фазы и плаката рекомендуется классическое оглавление:

1 Введение
2 Материалы и методы
3 Результаты
4 Обсуждение

Раздел 1 должен кратко объяснить тему в доступной для неспециалистов форме. .
Раздел 2 предназначен для описания данных и используемых методов инверсии.
В разделе 3 методы раздела 2 применяются к данным, описанным в разделе 2, и результаты сообщаются без какой-либо интерпретации; описаны только факты и результаты вычислений.
Раздел 4 — место для обсуждения результатов и выводов.

Проект либо рентгеновской томографии или цифровой обработки изображений . Вы можете самостоятельно измерить набор данных в лаборатории промышленной математики.

Рентгеновская тема: вы можете выбрать свой собственный объект для изображения в рентгеновской лаборатории. Мы можем предложить ряд проверенных на практике предметов и инструментов, чтобы адаптировать их по своему вкусу. Также вы можете составить собственное представление об измеряемом объекте. Размер объекта не должен намного превышать размер яйца, а химический состав важен, поскольку контраст ослабления рентгеновских лучей возникает из-за электронной плотности в материалах. Свяжитесь с Александром Мини, чтобы узнать, подходит ли ваш объект для визуализации.

Тема фотографии: Делайте размытые или зашумленные фотографии подходящих целей.

В проекте предполагается применить некоторые методы регуляризации, обсуждаемые в курсе. В оптимальном случае у вас должен быть автоматический метод выбора параметра регуляризации и критерии автоматической остановки итерации. Оба эти требования являются сложными, поэтому используйте простой подход, такой как план Б, если более сложный подход не работает. Кроме того, при выборе объектов измерения хорошо подумать о математических моделях априорной информации (кусочно-постоянной, гладкой, кусочно-гладкой), поскольку это влияет на выбор регуляризатора.

Первая цель: два первых раздела ( Введение, и Материалы и методы) должны быть предварительно написаны в LaTeX, но не обязательно в формате плаката. Наиболее важные вещи, которые необходимо объяснить:

, какие данные следует измерять,
, какой метод инверсии применить для реконструкции, и
, как реализовать вычисления.

Оценка первой цели составляет 30% итоговой оценки работы по проекту.Пожалуйста, договоритесь о времени встречи (в период 5-7 апреля) с лектором для рассмотрения и оценки первой цели.

Вторая и конечная цель: стендовая сессия . Плакат будет напечатан в формате А1. Вы можете создать свой собственный плакат (с нуля) или использовать, например, этот шаблон в качестве отправной точки и редактируйте его макет, цвета, шрифты и т. д. по своему усмотрению.

На этой странице вы можете посмотреть старые плакаты.

Расписание занятий

Недели 3–9 и 11–18, среда 10–12 и пятница 10–12 в зале C123.

Пасхальный праздник 13.-19.4.

Экзамен

Срок сдачи экзаменов — 17-27 марта. Крайний срок для отправки по электронной почте — 12 часов дня в понедельник, 27 марта.

Примечание: Ожидается, что каждый студент решит задачи и напишет ответы индивидуально с без сотрудничества . Несколько студентов будут случайным образом выбраны для собеседования, чтобы обсудить детали их ответов.

2017_home_exam.pdf

2017_home_exam.tex

Примечание: Если у вас есть вопросы по экзамену, отправьте лектору электронное письмо. Здесь будут показаны вопросы и ответы.

Вопрос: Можно ли ответить на экзамене по финскому языку? (Саако тенттиин вастата суомекси?)
Ответ: Да. (Kyllä)

Вопрос: Рассматривается ли функция F (s) для действительных или комплексных значений s в задаче 2b? (Käsitelläänkö F (s) -funktiota tehtävän 2 b-kohdassa kompleksi- vai reaalimuuttujan funktiona?)
Ответ: Считается для реальных значений s.(Reaalimuuttujan.)

Вопрос: Можно ли использовать меньшее разрешение в Задаче 3, если вычислительной мощности недостаточно для 128×128? (Voiko tehtävässä 3 käyttää pienempää resoluutiota, jos laskentateho ei riitä tuohon 128×128?)
Ответ: Да. (Voi.)

Вопрос: В пунктах 1 (a) и 1 (b) следует понимать буквально требование брать как можно меньшие k и n? Другими словами, является ли проблема оптимизации поиском математически наименьших возможных значений, дающих желаемые примеры?
Ответ: Нет.Используйте свой здравый смысл и выберите небольшие значения для k и n таким образом, чтобы дать хорошее объяснение.

Материалы курса

Курс соответствует этому учебнику:

Дженнифер Л. Мюллер и Самули Силтанен: Линейные и нелинейные обратные задачи с практическим применением (SIAM 2012)

? Что делать?

Упражнения

Здесь будут отображаться еженедельные упражнения.

Exercise6.pdf

Exercise5.pdf (ссылка в M3 исправлена)

Exercise4.pdf

Exercise3.pdf

Второе упражнение (PDF, упражнение T1 (b) исправлено ДВАЖДЫ 2 февраля 2017 г.)

deco02_data_comp.m
deco02_data_plot.m
Пример решения Ex2 M2: Ex2_M2.m PSF.m targetf.m
Первое упражнение (PDF)
Классы упражнений
Помощники преподавателей:
Сантери Каупинмяки (имя[email protected])
Группа День Время Комната Инструктор
1. Среда 12:15 — 14 00
C128
2. Четверг 8:15 — 10:00 C128
Еженедельные наборы задач будут оцениваться на упражнениях, таким образом, посещаемость на одной из еженедельных тренировок требуется для того, чтобы ваша работа была оценена.В случае противоречий в расписании, пожалуйста, свяжитесь с одним из ассистентов преподавателя; мы можем принять специальные меры для тех, кто не может присутствовать ни на одной из тренировок.
Теоретические упражнения выполняют студенты. На каждом занятии ученики отмечают выполненные ими упражнения, и в соответствии с этим списком для каждого упражнения будет выбран один ученик, который представит свою работу.
Упражнения Matlab будут проверяться индивидуально в классе упражнений.
Очки за все выполненные упражнения будут накапливаться и являются частью итоговой оценки.
Отзывы о курсе
Отзывы о курсе могут быть предоставлены в любой момент в течение курса. Кликните сюда.
обратных операций в математике: определение и примеры — видео и стенограмма урока
Свойства инверсий
Есть четыре математических свойства, которые имеют дело с инверсиями.
Аддитивное обратное свойство
Аддитивное обратное свойство утверждает, что когда вы добавляете число к противоположному, результат всегда равен 0.
2 + (-2) = 0
369 + (-369) = 0
Мультипликативное обратное свойство
Мультипликативное обратное свойство утверждает, что когда вы умножаете любое число на его противоположное, результат всегда равен 1.
6 * 1/6 = 1
213 * 1/213 = 1
Аддитивное свойство
Аддитивное свойство утверждает, что когда вы прибавляете любое число к нулю, результатом будет то же самое число.
7 + 0 = 7
Мультипликативное свойство
Мультипликативное свойство утверждает, что каждый раз, когда вы умножаете число на 1, оно не меняется.
13 * 1 = 13
Как использовать обратные операции
Обратные операции можно использовать для решения алгебраических задач. Давайте решим для x :
2 x + 3 = 17
Чтобы решить эту проблему, мы должны изолировать x на одной стороне уравнения. Первый шаг — помнить, что обратные операции сложения и умножения — это вычитание и деление. Следующий шаг — «переместить» 3 в правую часть уравнения, вычтя его из обеих частей уравнения.Это дает 2 x = 14. Следующий шаг — разделить обе стороны на 2, поскольку деление противоположно умножению. 2 x /2 = 14 / 2. Это дает x = 7.
Ответ на эту проблему: x = 7. Если вы не уверены, вы всегда можете вернуться и проверить свой ответ. Для этого замените 7 на x в исходной задаче.
2 (7) + 3 = 17
Затем решите 14 + 3 = 17
17 = 17
Таким образом решаются все алгебраические задачи.0,845 = 7
Тригонометрические функции, такие как синус, косинус и тангенс, также имеют обратные значения. Их называют арксинусом, арккосинусом и арктангенсом. Обратные тригонометрические функции можно использовать для определения угла прямоугольного треугольника, если вам известны длины как минимум двух сторон.
Например, вам нужно добраться до окна второго этажа вашего дома, которое находится в 10 футах от земли. Ваша лестница 18 футов высотой. Под каким углом ( x ) вам нужно разместить лестницу, чтобы добраться до окна?
Поскольку вы знаете гипотенузу и сторону, противоположную углу, вам необходимо использовать уравнение sin: sin ( x ) = противоположная / гипотенуза.(-1) * (10/18)
x = 34 градуса.
Резюме урока
Математически обратные операции — противоположные операции. Сложение противоположно вычитанию; деление противоположно умножению и так далее. Обратные операции используются для решения простых алгебраических уравнений в более сложные уравнения, которые включают показатели степени, логарифмы и тригонометрию.
Результаты обучения
Когда вы закончите, вы сможете:
Определить обратные операции
Указать свойства обратных операций
Решить алгебраическую задачу с помощью обратных операций
Распределительное свойство 3-го класса при умножении на сложение
26 декабря 2014 г. · SPI 0306.3.1 Ссылки проверены 26.12.2014. Модель площади распределительного свойства — видео на TeacherTube [2:18] Модели площади для умножения и деления — план урока Анненберга из их серии Learning Math; Основные свойства чисел: ассоциативный, коммутативный и распределительный — объяснение от Purple Math
Зарегистрируйтесь или войдите в систему, чтобы просмотреть дополнительные материалы. Вы получите доступ к вмешательствам, расширениям, руководствам по реализации задач и многому другому. Например, примените свойство распределения к выражению 3 (2 + 𝘹), чтобы получить эквивалентное выражение 6 + 3𝘹; применить распределительное свойство к…
Представьте дистрибутивное свойство умножения. — Определите арифметические шаблоны (включая шаблоны в таблице сложения или таблице умножения) и объясните их, используя свойства операций.
80 40 8 ярдов 5 ярдов 10 ярдов Теперь суммируйте две области. + 80 40 8 ярдов 5 ярдов 10 ярдов 40 + 80 = 120 квадратных ярдов Напишите выражение, которое показывает, как найти площадь прямоугольника и использует свойство распределения. 9 ярдов 5 ярдов 20 ярдов Найдите площади для каждого отдельного прямоугольника.9 ярдов 5 ярдов 20 ярдов Найдите площади для каждого отдельного прямоугольника …
Свойство распределения — одно из наиболее часто используемых свойств в математике. В общем, этот термин относится к распределительному свойству умножения, которое гласит, что. Определение: свойство распределения позволяет вам умножать сумму, умножая каждое слагаемое отдельно, а затем складывать …
Давайте посмотрим. 3 + 5 = 8. 5 + 3 = 8 Легкие вещи, не так ли? То же самое верно, когда ваш ребенок начинает складывать больше чисел: 5 + 6 + 4 = 15.4 + 6 + 5 = 15. 6 + 5 + 4 = 15. Приведенный выше пример более подробно рассматривается в моем уроке о свойстве ассоциативности. Теперь применим это на практике. Коммутативность рабочих листов сложения
26 сентября 2013 г. · В третьем классе учащихся просят применять эти знания, чтобы исследовать и распознавать закономерности и отношения между сложением, умножением и делением. Исследование и обучение, ориентированное на учащихся. Целью данного стандарта является понимание и применение учащимися распределительных, ассоциативных и коммутативных свойств умножения.
Чтение в 3-м классе. Курсивное письмо. Некоторые из рабочих листов для этой концепции: Умножение распределительных свойств, Применение распределительного свойства умножения по, Дополнение для 4-го класса, Пакет алгебраических выражений, Разделение алгебраических выражений, распределительное свойство .

Группа	День	Время	Комната	Инструктор
1.	Среда	12:15 — 14 00	C128
2.	Четверг	8:15 — 10:00	C128