Что такое множество в математике 3 класс петерсон: Множество.Элементы множества. Подмножество. Пересечение и объединение множеств. Л.Г.Петерсон — 3 класс | Методическая разработка по математике (3 класс) по теме:
ГДЗ по математике 3 класс Петерсон решебник
Авторы: Петерсон Л.Г.
2015-2014
Решебник по математике за 3 класс автора Петерсона Л.Г. 2015 года издания. Данное пособие включает готовые решения на разнообразные задания, упражнения, задачи и тесты. Сборник делится на 3 основные части, каждая из которых содержит определенное количество уроков. Первая и вторая части охватывает 33 урока, третья – 21.
После изучения всех тем прилагаются дополнительные занятия, направленные на повторение и закрепление третьеклассниками целого комплекса изученного материала. Все готовые ответы расписаны детально и доступны каждому школьнику.
В предлагаемом издании рассматриваются следующие темы: «Множество и его элементы», «Способы задания множеств», «Равные множества. Пустое множество», «Диаграмма Эйлера-Венна», «Решение задач», «Пересечение множеств» и прочее. Сюда вошел также дополнительный раздел, рассчитанный для проверки знаний учащихся за весь учебный год. Сюда же отнесены и точные, лаконичные ответы на все контрольные вопросы, рассчитанные для текущего и итогового контроля знаний школьников.
Быстрый поиск
Часть 1
Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12 13 14Урок 2: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 3: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 4: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 5: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 6: 1 2 3 4 5 6 7 8 9 10 11
Урок 7: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 8: 1 2 3 4 5 6 7 8 9
Урок 9: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 10: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 11: 1 2 3 4 5 6 7 8 9 10 11
Урок 12: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 13: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 14: 1 2 3 4 5 6 7 8 9 10 11 12 13
Урок 15: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Урок 16: 1
Урок 17: 1
Урок 18: 1 2 3 4 5 6 7 8 9 10
Урок 20: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 21: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 22: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 23: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 24: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 25: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 26: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 27: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 28: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 29: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 30: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 31: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Урок 32: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 33: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Часть 2
Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12Урок 2: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 3: 1 2 3 4 5 6 7 8 9 10
Урок 4: 1 2 3 4 5 6 7 8 9 10
Урок 5: 1 2 3 4 5 6 7 8 9 10
Урок 6: 1 2 3 4 5 6 7 8 9 10 11
Урок 7: 1 2 3 4 5 6 7 8 9 10
Урок 8: 1 2 3 4 5 6 7 8 9 10 11
Урок 9: 1 2 3 4 5 6 7 8 9 10
Урок 10: 1 2 3 4 5 6 7 8 9 10 11
Урок 11: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 12: 1 2 3 4 5 6 7 8 9 10 11 12 13
Урок 13: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 14: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 15: 1 2 3 4 5 6 7 8 9 10
Урок 16: 1 2 3 4 5 6 7 8 9 10 11 12 13
Урок 17: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 18: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 19:
Урок 20: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 21: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 22: 1 2 3 4 5 6 7 8 9 10 11 12 13
Урок 23: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Урок 24: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 25: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 26: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 27: 1 2 3 4 5 6 7 8 9
Урок 28: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 29: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 30: 1 2 3 4 5 6 7 8 9 10
Урок 21: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 32: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 33: 1 2 3 4 5 6 7 8 9 10 11
Часть 3
Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12Урок 2: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 3: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 4: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 5: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 6: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 7: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Урок 8: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 9: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 11: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок 12: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Урок 13: 1 2 3 4 5 6 7 8 9 10 11
Урок 14: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 15: 1 2 3 4 5 6 7 8 9 10 11 12
Урок 16: 1 2 3 4 5 6 7 8 9 10 11 12 13
Урок 17: 1 2 3 4 5 6 7 8 9 10 11
Урок 18: 1 2 3 4 5 6 7 8 9 10
Урок 19: 1 2 3 4 5 6 7 8 9 10
Урок 21: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Повторение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90ГДЗ: Математика 3 класс Петерсон
Стр.
1-3. Часть 1. Урок №1. Множество и его элементы1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 4-6. Часть 1. Урок №2. Задание множества перечислением и свойством
1 2 3 4 5 6 7 8 9 10 11 12Стр. 7-9. Часть 1. Урок №3. Равные множества. Пустое множество
1 2 3 4 5 6 7 8 9 10 11 12Стр. 10-12. Часть 1. Урок №4. Диаграмма Венна. Знаки G и £
1 2 3 4 5 6 7 8 9 10 11 12Стр. 13-15. Часть 1. Урок №5. Диаграмма Венна. Знаки G и £
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 16-18. Часть 1. Урок №6. Подмножество
1 2 3 4 5 6 7 8 9 10 11Стр. 19-21. Часть 1. Урок №7. Решение задач
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 22-23. Часть 1. Урок №8. Разбиение множества на части
1 2 3 4 5 6 7 8 9Стр. 24-26. Часть 1. Урок №9. Пересечение множеств. Знак
1 2 3 4 5 6 7 8 9 10 11 12Стр. 27-29. Часть 1. Урок №10. Свойства пересечения множеств
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 30-32. Часть 1. Урок №11. Решение задач
1 2 3 4 5 6 7 8 9 10 11Стр.
33-35. Часть 1. Урок №12. Объединение множеств. Знак U1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 36-38. Часть 1. Урок №13. Объединение множеств. Знак U
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 39-41. Часть 1. Урок №14. Свойства объединения множеств
1 2 3 4 5 6 7 8 9 10 11 12 13Стр. 42-45. Часть 1. Урок №15. Сложение и вычитание множеств
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Стр. 59-61. Часть 1. Урок №18. Многозначные числа
1 2 3 4 5 6 7 8 9 10Стр. 62-64. Часть 1. Урок №19. Многозначные числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 65-67. Часть 1. Урок №20. Многозначные числа
1 2 3 4 5 6 7 8 9 10 11 12Стр. 68-70. Часть 1. Урок №21. Многозначные числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 71-73. Часть 1. Урок №22. Многозначные числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 74-76. Часть 1. Урок №23. Многозначные числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 77-79. Часть 1. Урок №24. Многозначные числа
1 2 3 4 5 6 7 8 9 10 11 12Стр.
80-82. Часть 1. Урок №25. Многозначные числа1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 83-85. Часть 1. Урок №26. Умножение на 10, 100, 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 86-88. Часть 1. Урок №27. Умножение круглых чисел
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 89-91. Часть 1. Урок №28. Деление на 10, 100, 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 92-94. Часть 1. Урок №29. Деление круглых чисел
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 95-97. Часть 1. Урок №30. Единицы длины
1 2 3 4 5 6 7 8 9 10 11 12 13Стр. 98-100. Часть 1. Урок №31. Единицы длины
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Стр. 101-103. Часть 1. Урок №32. Единицы массы. Грамм
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 104-106. Часть 1. Урок №33. Единицы массы. Тонна. Центнер
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 107-112. Часть 1. Урок №34. Игра-путешествие «ИКС-педиция к Математическому полюсу»
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр.
1-2. Часть 2. Урок №1. Умножение на однозначное число1 2 3 4 5 6 7 8 9 10 11 12Стр. 3-5. Часть 2. Урок №2. Умножение на однозначное число
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 6-7. Часть 2. Урок №3. Умножение на однозначное число
1 2 3 4 5 6 7 8 9 10Стр. 8-9. Часть 2. Урок №4. Умножение на однозначное число
1 2 3 4 5 6 7 8 9 10Стр. 10-12. Часть 2. Урок №5. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10Стр. 13-15. Часть 2. Урок №6. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10 11Стр. 16-18. Часть 2. Урок №7. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10Стр. 19-21. Часть 2. Урок №8. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10 11Стр. 22-24. Часть 2. Урок №9. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10Стр. 25-27. Часть 2. Урок №10. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10 11Стр. 28-30. Часть 2. Урок №11. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр.
31-33. Часть 2. Урок №12. Деление на однозначное число1 2 3 4 5 6 7 8 9 10 11 12Стр. 34-36. Часть 2. Урок №13. Деление на однозначное число
1 2 3 4 5 6 7 8 9 10 11 12Стр. 37-39. Часть 2. Урок №14. Преобразование фигур
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 40-42. Часть 2. Урок №15. Симметрия
1 2 3 4 5 6 7 8 9 10Стр. 43-45. Часть 2. Урок №16. Симметрия
1 2 3 4 5 6 7 8 9 10 11 12 13Стр. 46-48. Часть 2. Урок №17. Симметричные фигуры
1 2 3 4 5 6 7 8 9 10 11 12Стр. 49-52. Часть 2. Урок №18. Меры времени. Календарь
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 53-55. Часть 2. Урок №19. Меры времени. Календарь
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18Стр. 56-58. Часть 2. Урок №20. Таблица мер времени
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 59-61. Часть 2. Урок №21. Часы
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 62-64. Часть 2. Урок №22. Сравнение, сложение и вычитание единиц времени
1 2 3 4 5 6 7 8 9 10 11 12 13Стр.
65-67. Часть 2. Урок №23. Переменная1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Стр. 68-70. Часть 2. Урок №24. Выражение с переменной
1 2 3 4 5 6 7 8 9 10 11 12Стр. 71-73. Часть 2. Урок №25. Верно и неверно. Всегда и иногда
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 74-76. Часть 2. Урок №26. Равенство и неравенство
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 77-79. Часть 2. Урок №27. Уравнения
1 2 3 4 5 6 7 8 9Стр. 80-82. Часть 2. Урок №28. Уравнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 83-85. Часть 2. Урок №29. Уравнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 86-88. Часть 2. Урок №30. Формулы
1 2 3 4 5 6 7 8 9 10Стр. 89-91. Часть 2. Урок №31. Формула объёма прямоугольного параллелепипеда
1 2 3 4 5 6 7 8 9 10 11 12Стр. 92-94. Часть 2. Урок №32. Формула деления с остатком
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 95-96. Часть 2. Урок №33. Решение задач с помощью формул
1 2 3 4 5 6 7 8 9 10 11Стр.
1-3. Часть 3. Урок №1. Скорость. Время. Расстояние1 2 3 4 5 6 7 8 9 10 11 12Стр. 4-6. Часть 3. Урок №2. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 7-9. Часть 3. Урок №3. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 10-12. Часть 3. Урок №4. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12Стр. 13-15. Часть 3. Урок №5. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12Стр. 16-18. Часть 3. Урок №6. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12Стр. 19-21. Часть 3. Урок №7. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Стр. 22-24. Часть 3. Урок №8. Формула пути
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 25-27. Часть 3. Урок №9. Умножение на двузначное число
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 28-30. Часть 3. Урок №10. Формула стоимости
1 2 3 4 5 6 7 8 9 10 11 12Стр. 31-33. Часть 3. Урок №11. Формула стоимости
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 34-36. Часть 3. Урок №12. Формула стоимости
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр.
37-39. Часть 3. Урок №13. Умножение на трёхзначное число1 2 3 4 5 6 7 8 9 10 11Стр. 40-42. Часть 3. Урок №14. Умножение на трёхзначное число
1 2 3 4 5 6 7 8 9 10 11 12Стр. 43-45. Часть 3. Урок №15. Формула работы
1 2 3 4 5 6 7 8 9 10 11 12Стр. 46-48. Часть 3. Урок №16. Формула работы
1 2 3 4 5 6 7 8 9 10 11 12 13 14Стр. 49-51. Часть 3. Урок №17. Формула работы
1 2 3 4 5 6 7 8 9 10 11Стр. 52-55. Часть 3. Урок №18. Формула произведения
1 2 3 4 5 6 7 8 9 10Стр. 56-59. Часть 3. Урок №19. Решение задач
1 2 3 4 5 6 7 8 9 10Стр. 60-62. Часть 3. Урок №20. Решение задач
1 2 3 4 5 6 7 8 9 10 11 12 13Стр. 63-65. Часть 3. Урок №21. Умножение многозначных чисел
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Стр. 66-80. Задания на повторение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90Множества — типы, символы, свойства, примеры
Множества в математике — это просто набор отдельных объектов, образующих группу.
В наборе может быть любая группа предметов, будь то набор чисел, дней недели, видов транспорта и так далее. Каждый элемент множества называется элементом множества. Фигурные скобки используются при написании множества. Очень простой пример набора будет таким. Установите А = {1,2,3,4,5}. Существуют различные обозначения для представления элементов множества. Наборы обычно представляются с помощью формы списка или формы построителя наборов. Остановимся подробно на каждом из этих терминов.
| 1. | Наборы Определение |
| 2. | Комплекты Представительства |
| 3. | Наборы символов |
| 4. | Типы наборов |
| 5. | Наборы формул |
| 7. | Задает свойства |
| 8. | Операции с множествами |
| 9. | Часто задаваемые вопросы о наборах |
Наборы определения
В математике множество — это четко определенный набор объектов.
Множества в математике Примеры
определено менее 10, тогда как совокупность умных учеников в классе не определена. Таким образом, набор четных натуральных чисел меньше 10 можно представить в виде множества A = {2, 4, 6, 8}. Давайте используем этот пример, чтобы понять основную терминологию, связанную с множествами в математике.
Элементы набора
Элементы, присутствующие в наборе, называются либо элементами, либо членами набора. Элементы множества заключены в фигурные скобки, разделенные запятыми. Для обозначения того, что элемент содержится в множестве, используется символ «∈». В приведенном выше примере 2 ∈ A. Если элемент не является членом множества, то он обозначается символом «∉». Здесь 3 ∉ A.
Кардинальное число набора
Кардинальное число, мощность или порядок набора обозначает общее количество элементов в наборе.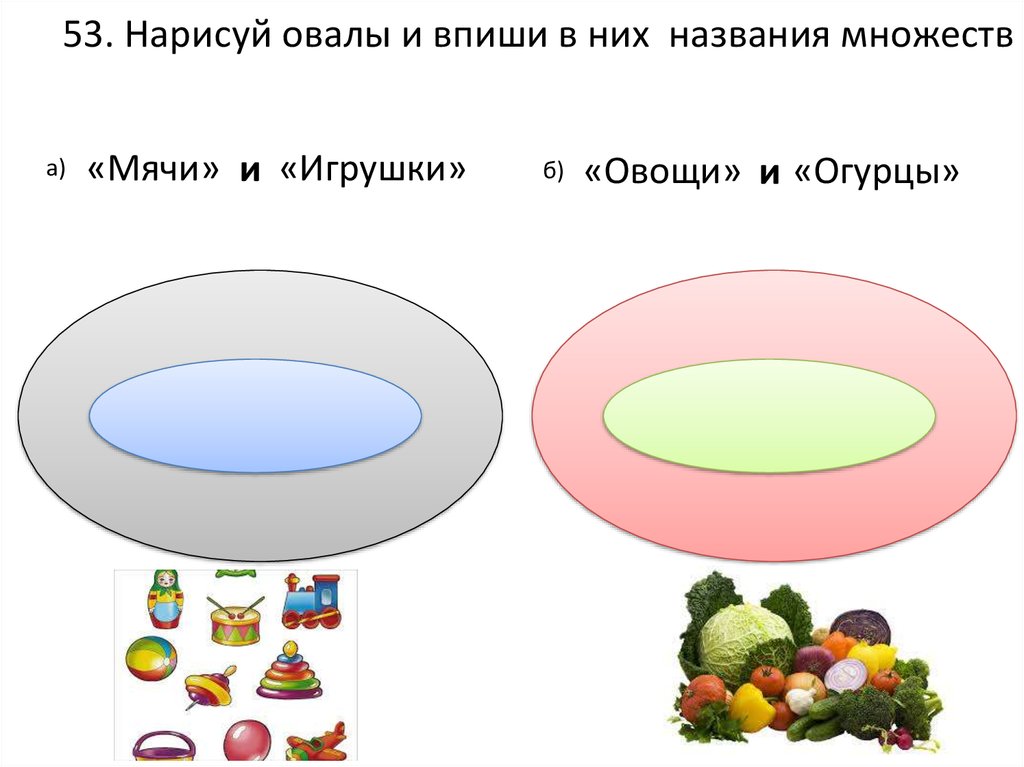
Для натуральных четных чисел меньше 10 n(A) = 4. Наборы определяются как набор уникальных элементов. Одним из важных условий определения множества является то, что все элементы множества должны быть связаны друг с другом и иметь общее свойство. Например, если мы определим множество с элементами как названия месяцев в году, то мы можем сказать, что все элементы множества являются месяцами года.
Представление наборов
Для представления множеств используются различные нотации множеств. Они отличаются способом перечисления элементов. Для представления множеств используются три обозначения множеств:
- Семантическая форма
- Форма реестра
- Набор конструктора форма
Семантическая форма
Семантическая нотация описывает оператор, показывающий, что является элементами множества. Например, набор А — это список первых пяти нечетных чисел.
Форма реестра
Наиболее распространенной формой, используемой для представления наборов, является запись реестра, в которой элементы наборов заключены в фигурные скобки, разделенные запятыми.
Например, Set B = {2,4,6,8,10}, который представляет собой набор первых пяти четных чисел. В ростерной форме порядок элементов множества не имеет значения, например, множество первых пяти четных чисел также можно определить как {2,6,8,10,4}. Кроме того, если в наборе имеется бесконечный список элементов, то они определяются с помощью набора точек в конце последнего элемента. Например, бесконечные множества представлены как X = {1, 2, 3, 4, 5…}, где X — множество натуральных чисел. Чтобы подытожить нотацию формы реестра, пожалуйста, взгляните на примеры ниже.
Обозначение множеств с конечным списком: множество A = {1, 2, 3, 4, 5} (первые пять натуральных чисел)
Обозначение наборов с бесконечным реестром: набор B = {5, 10, 15, 20 ….} (кратное 5)
Форма построителя набора
Нотация построителя набора имеет определенное правило или утверждение, которое конкретно описывает общее свойство всех элементов множества. Форма построителя набора использует в своем представлении вертикальную черту с текстом, описывающим характер элементов набора.
Например, А = {к | k — четное число, k ≤ 20}. В заявлении говорится, что все элементы множества A являются четными числами, меньшими или равными 20. Иногда вместо «|» используется «:».
Визуальное представление множеств с помощью диаграммы Венна
Диаграмма Венна — это графическое представление множеств, где каждое множество представлено в виде круга. Элементы множества находятся внутри кругов. Иногда прямоугольник окружает круги, что представляет универсальный набор. Диаграмма Венна показывает, как данные наборы связаны друг с другом.
Наборы символов
Набор символов используется для определения элементов данного набора. В следующей таблице показаны некоторые из этих символов и их значение.
| Символы | Значение |
|---|---|
| У | Универсальный набор |
| н(Х) | Кардинальный номер набора X |
| б е А | ‘b’ является элементом множества A |
| а ∉ Б | ‘a’ не является элементом множества B |
| {} | Обозначает набор |
| ∅ | Нулевой или пустой набор |
| А У Б | Набор соединительных элементов A Набор B |
| А ∩ В | Набор пересечений A Набор B |
| А ⊆ В | Набор А является подмножеством набора В |
| Б ⊇ А | Набор B является надмножеством набора A |
Типы наборов
Наборы подразделяются на разные типы.
Некоторые из них являются одноэлементными, конечными, бесконечными, пустыми и т. д.
Одноэлементные наборы
Набор, состоящий только из одного элемента, называется одноэлементным набором или также называется единичным набором. Пример. Установите A = { k | k — целое число от 3 до 5}, то есть A = {4}.
Конечные множества
Как следует из названия, множество с конечным или счетным числом элементов называется конечным множеством. Пример. Установите B = {k | k — простое число меньше 20}, то есть B = {2,3,5,7,11,13,17,19}
Бесконечные множества
Множество с бесконечным числом элементов называется бесконечным множеством. Пример: Установите C = {кратное 3}.
Пустые или нулевые наборы
Набор, который не содержит ни одного элемента, называется пустым набором или нулевым набором. Пустое множество обозначается символом «∅». Читается как « фи ». Пример: Установите X = {}.
Равные множества
Если два множества содержат одни и те же элементы, то они называются равными множествами.
Пример: А = {1,2,3} и В = {1,2,3}. Здесь множество A и множество B являются равными множествами. Это можно представить как A = B.
Неравные множества
Если два множества имеют хотя бы один отличающийся элемент, то они являются неравными множествами. Пример: A = {1,2,3} и B = {2,3,4}. Здесь множество A и множество B являются неравными множествами. Это можно представить как A ≠ B.
Эквивалентные множества
Два множества называются эквивалентными множествами, если они имеют одинаковое количество элементов, хотя элементы разные. Пример: A = {1,2,3,4} и B = {a,b,c,d}. Здесь множество A и множество B являются эквивалентными множествами, поскольку n(A) = n(B)
Перекрывающиеся множества
Два множества называются перекрывающимися, если хотя бы один элемент из множества A присутствует в множестве B. Пример: A = {2,4,6} B = {4,8,10}. Здесь элемент 4 присутствует как в множестве A, так и в множестве B. Следовательно, множества A и B перекрываются.
Непересекающиеся множества
Два множества являются непересекающимися множествами, если в обоих множествах нет общих элементов. Пример: А = {1,2,3,4} В = {5,6,7,8}. Здесь множество A и множество B — непересекающиеся множества.
Подмножество и надмножество
Для двух множеств A и B, если каждый элемент множества A присутствует в множестве B, то множество A является подмножеством множества B(A ⊆ B), а B является надмножеством множества A(B ⊇ А).
A ⊆ B, так как все элементы множества A присутствуют в множестве B.
B ⊇ A означает, что множество B является надмножеством множества A.
Универсальный набор
Универсальный набор — это совокупность всех элементов, относящихся к конкретному предмету. Универсальный набор обозначается буквой «У». Пример: Пусть U = {Список всех автотранспортных средств}. Здесь множество автомобилей является подмножеством этого универсального множества, множество велосипедов, поездов — все подмножества этого универсального множества.
Наборы мощности
Набор мощности — это набор всех подмножеств, которые может содержать набор. Пример: Установите A = {1,2,3}. Набор мощностей A = {{∅}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
Наборы формул
Множества находят свое применение в области алгебры, статистики и вероятностей. Ниже перечислены некоторые важные формулы набора.
Для любых двух перекрывающихся множеств A и B
- n(A U B) = n(A) + n(B) — n(A ∩ B)
- n (A ∩ B) = n(A) + n(B) — n(A U B)
- n(A) = n(A U B) + n(A ∩ B) — n(B)
- n(B) = n(A U B) + n(A ∩ B) — n(A)
- n(A — B) = n(A U B) — n(B)
- n(A — B) = n(A) — n(A ∩ B)
Для любых двух непересекающихся множеств A и B
- n(A U B) = n(A) + n(B)
- А ∩ В = ∅
- n(A — B) = n(A)
Свойства наборов
Подобно числам, множества обладают такими свойствами, как ассоциативность, коммутативность и т.
д. Существует шесть важных свойств множеств. Имея три множества A, B и C, свойства этих множеств следующие.
| Собственность | Пример |
|---|---|
| Коммутативное имущество | А У Б = Б У А А ∩ В = В ∩ А |
| Ассоциативная собственность | (А ∩ В) ∩ С = А ∩ (В ∩ С) (А У Б) У С = А У (Б У С) |
| Распределительная собственность | A U (B ∩ C) = (A U B) ∩ (A U C) А ∩ (B U C) = (A ∩ B) U (A ∩ C) |
| Идентификационное свойство | А U ∅ = А А ∩ U = А |
| Дополнение Свойство | А U А’ = U |
| Идемпотентное свойство | А ∩ А = А АУ А = А |
Операции с множествами
Некоторые важные операции над множествами включают объединение, пересечение, разность, дополнение множества и декартово произведение множества.
Краткое объяснение операций над множествами состоит в следующем.
Объединение множеств
Объединение множеств, которое обозначается как A U B, перечисляет элементы множества A и множества B или элементы как множества A, так и множества B. Например, {1, 3} ∪ {1, 4 } = {1, 3, 4}
Пересечение множеств
Пересечение множеств, обозначаемое A ∩ B, перечисляет элементы, общие как для множества A, так и для множества B. Например, {1, 2} ∩ {2, 4} = {2}
Разность наборов
Разность наборов , которая обозначается A — B, перечисляет элементы набора A, которые не присутствуют в наборе B. Например, A = {2, 3, 4} и B = {4, 5, 6}. А — В = {2, 3}.
Дополнение к множеству
Дополнение к множеству, которое обозначается A’, представляет собой множество всех элементов универсального множества, которые не присутствуют в множестве A. Другими словами, A’ обозначается как U — A, что является разностью в элементах универсального множества и множества А.
Декартово произведение множеств
Декартово произведение двух множеств, обозначаемое A × B, является произведением двух непустых множеств, в котором получаются упорядоченные пары элементов. Например, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.
☛ Темы, связанные с наборами:
Ознакомьтесь с некоторыми интересными темами, связанными с наборами.
- Операции с множествами
- Диаграммы Венна
- Подмножество
- Обозначение реестра
- Универсальный набор
- Пересечение множеств
- Набор нотаций конструктора
Часто задаваемые вопросы о наборах
Что такое множества в математике и примерах?
Наборы представляют собой набор отдельных элементов, заключенных в фигурные скобки и разделенных запятыми. Список элементов множества называется элементами множества. Примеры: коллекция фруктов, коллекция картинок.
По-другому множества представляются следующим образом. Установите A = {a,b,c,d}. Здесь a,b,c,d — элементы множества A.
Какие существуют различные обозначения множеств для представления множеств?
Наборы могут быть представлены тремя способами. Представление множеств означает способ перечисления элементов множества. Они следующие.
- Семантическая запись: Элементы набора представлены одним оператором. Например, Set A — это количество дней в неделе.
- Нотация реестра: в этой форме представления наборов используются фигурные скобки для перечисления элементов набора. Например, установите A = {2,4,6,8,10}
- Обозначение построителя набора: Форма построителя набора представляет элементы набора по общему правилу или свойству. Например, {х | x — простое число меньше 20}
Какие существуют типы наборов?
Наборы отличаются друг от друга в зависимости от присутствующих в них элементов. Исходя из этого, мы имеем следующие виды наборов.
Это одноэлементные множества, конечные и бесконечные множества, пустые или нулевые множества, равные множества, неравные множества, эквивалентные множества, перекрывающиеся множества, непересекающиеся множества, подмножества, надмножества, степенные множества и универсальные множества.
Каковы свойства множеств в теории множеств?
Различные свойства, связанные с множествами в математике:
- Коммутативное свойство: A U B = B U A и A ∩ B = B ∩ A
- Ассоциативное свойство: (A ∩ B) ∩ C = A ∩ (B ∩ C) и (A U B) U C = A U (B U C)
- Распределительное свойство: A U (B ∩ C) = (A U B) ∩ (AU C) и A ∩ (B U C) = (A ∩ B) U (A ∩ C)
- Свойство идентичности: A U ∅ = A и A ∩ U = A
- Свойство дополнения: A U A’ = U
- Свойство идемпотента: A ∩ A = A и A U A = A
Что такое Союз множеств?
Объединение двух наборов A и B представляет собой элементы из обоих наборов A и B или оба вместе. Обозначается символом «U».
Например, если установить A = {1,2,3} и установить B = {4,5,6}, то AUB = {1,2,3,4,5,6}. A U B читается как «союз B».
Что такое пересечение множеств?
Пересечение двух множеств A и B – это элементы, общие для множества A и B. Оно обозначается символом ‘∩’. Например, если установить A = {1,2,3} и установить B = {3,4,5}, то A ∩ B = {3}. A ∩ B читается как «пересечение A B».
Что такое подмножества и надмножества?
Если каждый элемент множества A присутствует в множестве B, то множество B является надмножеством множества A, а множество A является подмножеством множества B.
Пример: А = {1,4,5} В = {1,2,3,4,5,6}
Поскольку все элементы множества A присутствуют в множестве B. ⇒ A ⊆ B и B ⊇ A.
Что такое универсальные множества?
Универсальный набор, обозначаемый буквой «U», представляет собой совокупность всех элементов, относящихся к определенному предмету.
Пример: Пусть U = {Список всех автотранспортных средств}. Здесь множество циклов является подмножеством этого универсального множества.
Что такое дополнение в наборах?
Дополнением множества, обозначаемого А’, является множество всех элементов универсального множества, не присутствующих в множестве А. Другими словами, А’ обозначается как U — А, что является разностью элементы универсального множества и множество А.
Что такое Декартово произведение в множествах?
Декартово произведение двух множеств, обозначаемое A×B, есть произведение двух непустых множеств, при котором получаются упорядоченные пары элементов. Например, если A = {1,2} и B = {3,4}, то A×B = {(1,3), (1,4), (2,3), (2,4)} .
Какая польза от диаграммы Венна в множествах?
Диаграмма Венна — это графическое представление отношений между двумя или более множествами. Круги используются для представления наборов. Каждый круг представляет набор. Прямоугольник, окружающий круги, представляет универсальное множество.
системные задачи по системам уравнений в формате pdf0003
cdn.kutasoftware.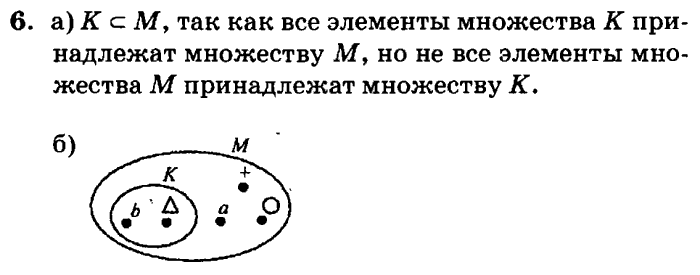
com › Рабочие листы › Alg1 › Системы уравнений …
Рабочий лист от Kuta Software LLC. Программное обеспечение Kuta — Бесконечная алгебра 1 … Системы уравнений Словесные задачи. 1) Найдите значение двух чисел, если их сумма равна …
[PDF] System of Equations Word Problems — Kuta Software
cdn.kutasoftware.com › Worksheets › Alg2 › Systems of Equations …
Рабочий лист от Kuta Software LLC. Программное обеспечение Kuta — Бесконечная алгебра 2 … Системы уравнений Словесные задачи. 1) Школа, в которую ходит Лиза, продает …
[PDF] Решение текстовых задач по системам уравнений Для
www.hoodriver.k12.or.us › cms › lib06 › Centricity › Domain ›
Решение текстовых задач по системам уравнений. Для всех задач определите переменные, напишите систему уравнений и решите для всех переменных.
[PDF] Системы уравнений Словесные задачи | Effortless Math
cdn.effortlessmath.com › wp-content › uploads › 2019/09 › Systems-.
..
Рабочие листы по математике. Имя: ______. Дата: ______ … Многое другое онлайн! Пожалуйста, посетите: EffortlessMath.com. Системы уравнений Словесные задачи. ✍ Решите каждое слово …
[PDF] Системы линейных уравнений — Задачи Word
cpb-us-e1.wpmucdn.com › cobbleearning.net › dist › файлы › 2015/09
Системы линейных уравнений — Word Проблемы … Напишите систему уравнений, чтобы представить ситуацию. … 2.9 — Постановка задач Домашнее задание.
[PDF] Раздел 6.6: Системы уравнений Word Проблемы Название
www.napls.us › lib › Centricity › Domain › 6.6 Практический рабочий лист.pdf
Раздел 6.6: Системы уравнений Словесные задачи. Название: Практический рабочий лист … Помните: определите свои переменные, напишите систему уравнений для представления.
[DOC] 3-4 Системы уравнений Словесные задачи — Mayfield City Schools
www.mayfieldschools.org › Загрузки › 3-4 Системы уравнений …
уравнения и/или неравенства, которые лучше всего моделируют реальную проблему.
Для каждой проблемы укажите свои переменные ( …
[PDF] Решение текстовых задач с использованием систем уравнений (часть 2). Определите …
cavitt.eurekausd.org › документы › Задания на замену
Рабочий лист: Решение текстовых задач с использованием систем уравнений (часть 2). Определите свои переменные, создайте систему уравнений и найдите свои переменные.
[PDF] Linear Systems Word Problems 1. Тест состоит из двадцати вопросов на сумму …
www.prosper-isd.net › cms › lib5 › Centricity › Domain
Сколько вопросов с несколькими вариантами ответов в тесте? Уравнение 1: Уравнение 2: Решение: 2. Разница двух чисел равна 3. Их …
[PDF] Системы уравнений Word Problems
ny01000947.schoolwires.net › сайт › обработчики › загрузка файла › FileNa. ..
Рабочий лист от Kuta Software LLC … Системы уравнений Словесные задачи … 6) Все 231 ученик Математического клуба отправились на экскурсию.