Порядок выполнения действий в числовых выражениях 2 класс: Числовые и Буквенные выражения
Конспект урока математики «Порядок выполнения действий. Скобки» (2 класс)
Урок математики 2 класс
Тема: Порядок выполнения действий. Скобки.
Тип урока: урок изучения и первичного закрепления новых знаний
Цели: создать условия для знакомства с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.
Формирование УУД:
Регулятивные УУД:
— определять цель деятельности на уроке с помощью учителя;
— находить и формулировать проблему совместно с учителем;
— планировать учебную деятельность на уроке;
-оценивать полученный результат.
Познавательные УУД:
-добывать новые знания в учебнике;
-перерабатывать полученную информацию, наблюдать и делать выводы.
Коммуникативные УУД:
-слушать и понимать речь других;
—
участвовать в беседе на уроке.
Предметные результаты:
— использовать в своей речи название компонентов действий сложения и вычитания;
-осознанно следовать алгоритму выполнения действий в выражениях со скобками;
-находить значение выражений в двух действиях;
-уметь читать числовые выражения.
Оборудование: учебник «Математика» 2 класс, М.И. Моро, М.А.Бантова, проектор, экран, презентация.
Ход урока:
1. Мотивация (самоопределение) к учебной деятельности.
— Пусть хорошее настроение поможет вам преодолеть трудности на уроке. Пусть урок пролетит, как одно мгновение, но оставит полезный след в ваших головках.
— Сейчас у нас урок математики. Зачем нам нужно изучать математику?
— Откройте тетради, запишите число и слова «Классная работа»
-Какое число записали? (18)
— Что можете о нем сказать? (двузначное, четное, состоит из 1 десятка и 8 единиц, соседи числа 18 – это 17 и 19)
— Как можно получить число 18? (9+9, 10 +8, 17+1, 19-1)
2.
Актуализации знаний.
Устный счёт. Математический диктант
1. Уменьшаемое 12, вычитаемое 3, найдите разность. (9)
2. Первое слагаемое 16, второе слагаемое 4, найдите сумму. (20)
3. Чему равна сумма чисел 8 и 5.(13)
4.Найдите разность чисел 19 и 8.(11)
5.На столе 4 яблока, а груш на 2 больше. Сколько на столе груш? (6)
6.На сколько 15 больше 6 (9)
7.Из 48 вычтите число 20. (28)
8.20 уменьшите на 5 (25)
Взаимопроверка по образцу на доске. (оцените работу товарища – зеленый и красный)
-Давайте еще раз вспомним названия компонентов при сложении (слагаемое, слагаемое, сумма)
— Названия компонентов при вычитании (уменьшаемое, вычитаемое, разность)
3. Актуализация и фиксирование индивидуального затруднения.
(На доске записаны примеры.)
12-2+8=18
12-2+8=2
-Давайте рассмотрим примеры и
сравним их. Чем они похожи? (числами и действиями).
— Чем отличаются? (ответами)
— Почему у одинаковых примеров получились разные ответы?
-Какой из этих примеров решен верно? (Первый)
— Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)
-А кто уже знает, в каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 2 и 8, а затем из 12 вычесть их сумму.)
4. Выявление места и причины затруднения.
— Мы поняли, как нужно решать эти примеры.
— Чего мы не знаем? (Как показать, в каком порядке нужно выполнять действия во втором примере.)
5. Построение проекта выхода из затруднения (тема, цель, задачи).
— О чём сейчас говорили? (О порядке выполнения действий.)
— Какая тема урока? (Порядок выполнения действий.)
—
Чему нам надо научиться? Что нам надо узнать? (В
каком порядке нужно выполнять действия при вычислениях).
6. Поиск решения проблемы.
(Учитель выставляет карточку с примером)
10 – 5 + 2
— Прочитайте. Какое действие надо выполнить первым? (Сложение)
— Почему? (Оно выделено)
— Как называется то, что выделено? (Сумма)
— Из 10 вычесть сумму чисел пяти и двух. Для того, чтобы показать, что первым действием будет сложение, в математике используют скобки. По-другому наш пример можно записать так: 10 – (5 + 2)
— Что показывают скобки? (Что данное действие надо выполнять первым).
Давайте вычислим: 10 – (5 + 2) = 3 (надписываем результат, полученный в скобках)
— Какие действия выполняют первыми, если в выражении есть скобки?
( Действия в скобках)
— Посмотрите, чем отличаются столбики примеров? (записаны на доске)
8-3+4=9 8-(3+4)=1
18-8+9=19 18- (8+9)=1
(В первом столбике нет скобок, а во втором есть.
)
-Как выполняли действия в первом столбике? (По порядку.)
-Как будем выполнять действия во втором столбике, чтобы получить эти значения выражений? (Сначала выполним действие в скобках.)
-Сравните порядок выполнения действий в первом и во втором столбиках. Что вы можете сказать? ( В первом столбике мы выполняли действия по порядку, а во втором сначала в скобках.)
-Что нам поможет указать на порядок выполнения действий? (Скобки.)
-Сформулируйте правило, как правильно выполнять действия в выражениях со скобками. (Сначала выполняются действия в скобках, а потом по порядку)
7. Первичное закрепление новых знаний.
— Мы получили новое знание. Проверим, правильно ли мы сделали вывод.
— Сравним наше новое знание с научным в учебнике.
Прочитайте на с.38 выделенное в рамочку правило. (Прочитал каждый, потом проговариваем хором).
— Кто уже сможет рассказать правило?
—
Давайте вернемся к нашему выражению.
— Кто может показать, что 1 действие нужно выполнить сложение?
Физминутка
И.п. — стоя руки на поясе. 1 — махом левую руку занести через правое плечо, голову повернуть налево. 2 — и.п., 3 — 4 — то же правой рукой. Повторить 4 — 6 раз. Темп медленный. | И.п. — стойка ноги врозь, руки за голову. 1 — резко повернуть таз направо. 2 — резко повернуть таз налево. Во время поворотов плечевой пояс оставить неподвижным. Повторить 6 — 8 раз. Темп средний. Опустить руки потрясти Поморгать глазами |
— Попробуем применить наше новое знание на практике.
Работа по учебнику. Решение примеров.
С.
38 № 1
(Коллективное выполнение с комментированием. Выходят к доске.)
— Нашли №1 на стр.38. Прочитайте задание.
— Что вас просят сделать?
(Ученик у доски, остальные в тетрадях решают примеры №1.)
-Давайте прочитаем запись. / Дети правильно читают числовые выражения/
Памятка:
1) посмотри на знак в скобках и назови действие (сумма, разность)
2) назови второе действие в выражении
3) правильно употребляй предлоги в речи (к числу … прибавить , из числа … вычесть)
(В скобках стоит сумма, а перед скобкой действие сложение. Нам нужно к числу 6 прибавить сумму чисел 3 и 1.)
— А теперь нам нужно выполнить действия.
– Какое действие следует выполнить первым? (Действие в скобках.)
– Найдите значение выражения:
сумма чисел трех и одного равна четырем (надписываем результат, полученный в скобках)
к шести прибавить четыре – получится десять;
значение выражения равно десяти.
Аналогично разбираются остальные равенства. (последний столбик самостоятельно – один на откидной доске)
Оцените свою работу светофором, проверка на доске.
-Молодцы! Справились с заданием.
8. Повторение пройденного материала.
Решение задачи.
С. 39 № 5
— Обратимся к задаче на стр.39 №5.
— Прочитайте. ( Дети читают задачу сначала про себя, а затем один ученик читает её вслух).
— О ком говорится в задаче?
— Чем занимался Коля?
— Какую пользу приносит людям посещение бассейна? ( Укрепляет здоровье человека.)
— Вы тоже должны укреплять своё здоровье, заниматься спортом.
— Что известно в задаче?
— Что нужно найти в задаче?
— Давайте обратимся к чертежу задачи.
— Что обозначают числа 100? 60?
— Как ответить на вопрос задачи?
— Запишите решение и ответ. (Один ученик работает у доски).
— Молодцы, справились с заданием.
9. Рефлексия.
— Вот видите, как хорошо мы потрудились! Это потому, что все вместе работали. Спасибо всем, особенно ………. хорошо потрудились (перечисляю).
— Итак, что нового мы узнали? (Действия, записанные в скобках, выполняются первыми)
— Для чего нам нужны полученные сегодня на уроке знания?
— А сейчас проверим как вы усвоили сегодняшний материал. Выполните самостоятельно рубрику «Проверь себя» на стр.39. (Самопроверка по образцу)
— А теперь, пусть каждый из вас оценит свою работу на уроке. Перед вами светофоры. Если вы довольны своей работой поднимите — зеленый, если у вас не всё сегодня получалось, были трудности — желтый, а если вы совсем собой не довольны, считаете, что у вас вообще ничего не получилось — красный.
— Даже если у вас не все получилось, не волнуйтесь, тема сложная, и скоро вы во всём разберётесь. Нужно просто еще потренироваться.
10. Домашнее задание
№3, 6 стр 38-39, выучить правило
Урок математики 2 класс Порядок выполнения действий.
Скобки | План-конспект урока по математике (2 класс) по теме:Муниципальное казённое общеобразовательное учреждение
Бутурлиновская основная общеобразовательная школа № 9
Урок математики
2 класс
Тема: Порядок выполнения действий. Скобки.
УМК «Школа России»
Автор : учитель начальных классов
Акиншина Н.А.
2012г.
Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.
УУД:
Познавательные :учащиеся научатся соблюдать порядок действий при вычислениях; находить значения выражений, содержащих скобки;
Регулятивные: использовать графические модели при решении задач;
Коммуникативные: слушать собеседника и вести диалог;
Личностные: оценивать себя и товарищей.
Ход урока:
- Мотивация (самоопределение) к учебной деятельности.
Прозвенел звонок и смолк-
Начинается урок.
Вы за парты тихо сели,
На меня все посмотрели.
Пожелайте успехов глазами
И вперёд за новыми знаниями!
— Работать сегодня мы будем коллективно и в парах. Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу)
В конце урока каждый из вас оценит свою работу.
- Актуализация и фиксирование индивидуального затруднения в пробном действии.
(На доске записаны примеры.)
20-9+8=19
20-9+8=3
-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?
-Какое равенство верно? (Первое.)
— Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)
— В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 9 и 3, а затем из 20 вычесть их сумму.
)
3. Выявление места и причины затруднения.
— Мы поняли, как нужно решать эти примеры. А как показать это другим?
— Чего мы не знаем? (Как показать, в каком порядке нужно выполнять действия в некоторых примерах.)
- Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)
— О чём сейчас говорили? (О порядке выполнения действий.)
— Какая тема урока? (Порядок выполнения действий.)
-Какова цель нашего урока? (Научиться обозначать в записи порядок действий.)
5.Поиск решения проблемы.
-Посмотрите, чем отличаются столбики примеров?
8-3+4=9 8-(3+4)=1
18-8+9=19 18-(8+9)=1
20-5+3=18 20-(5+3)=12
(В первом столбике нет скобок, а во втором есть.)
— Зачем же они нужны?
-Как выполняли действия в первом столбике? (По порядку.)
-Как будем выполнять действия во втором столбике, чтобы получить эти значения выражений? (Сначала выполним действие в скобках.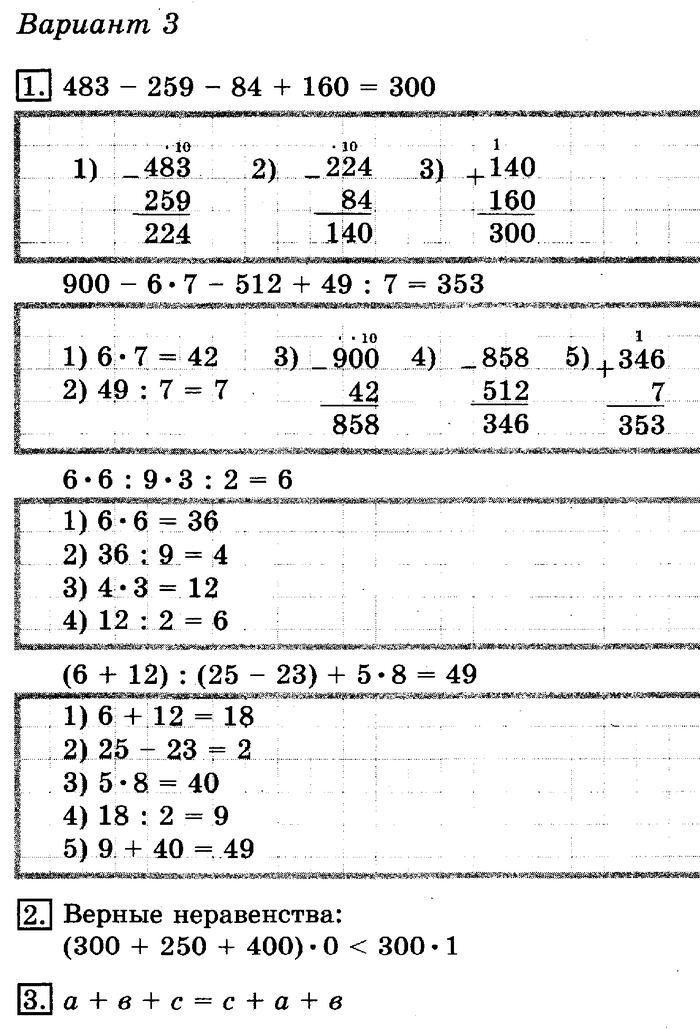
)
-Сравните порядок выполнения действий в первом и во втором столбиках. Что вы можете сказать? ( В первом столбике мы выполняли действия по порядку, а во втором сначала в скобках.)
-Что нам поможет указать на порядок выполнения действий? (Скобки.)
-Сформулируйте правило, как правильно выполнять действия в выражениях со скобками. (Сначала выполняются действия в скобках, а потом по порядку)
- Первичное закрепление с проговариванием во внешней речи
— Мы получили новое знание. Проверим, правильно ли мы сделали выводы.
Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.
-Попробуем применить наше новое знание на практике.
№ 1 (с. 38).
(Коллективное выполнение с комментированием.)
Физкультминутка
Ветер тихо клен качает,
Вправо, влево наклоняет.
Раз наклон и два наклон,
Зашумел листвою клен.
(Ноги на ширине плеч, руки за голову.
Наклоны туловища вправо и влево.
)
Видишь бабочка летает,
(Взмахи руками.)
На лугу цветы считает:
(Считать пальчиком.)
Раз, два, три, четыре, пять —
(Хлопки в ладоши.)
Ох, считать не сосчитать!
(Прыжки на месте.)
Шесть, семь, восемь, девять, десять —
(Хлопки в ладоши.)
Даже мудрая пчела (Взмахи руками.)
Сосчитать бы не смогла!
(Считать пальчиком.)
- Самостоятельная работа в парах с самопроверкой по эталону.
№2 (с. 38).
-Решите первый пример. Проверьте, получим ли мы нужный результат, если вычисления будем выполнять по порядку. (Не получим.)
-Измените порядок действий. Какое действие выполним первым? (Сложение.)
-Вычислите. Получился ли у вас нужный результат? (Да.)
-Поставьте скобки.
(Остальные примеры разбираются аналогично. Следует обратить внимание учащихся на то, что, если скобки не меняют порядок действий, их можно не ставить.)
- Включение в систему знаний повторение.
№3 (с. 38).
(Один ученик выполняет на доске с комментированием, остальные— в тетрадях.)
№4 (с. 38).
-Рассмотрите рисунок.
( Составьте задачу по первому решению. (В лодке плыли 5 детей и 1 взрослый. Сколько всего человек плыло в лодке ?)
( Составьте задачу по второму решению. (В лодке было 6 человек. На берег вышли 2 человека. Сколько человек осталось и лодке?)
Можно ли задачи назвать обратными? (Нет.)
-Решите задачи.
(Ученик, решивший задачу первым, записывает решение и ответ на доске. Проверка. Тем, кто справится с заданием быстрее других, дополнительно можно предложить составить ко второй задаче обратные задачи.)
№5 (с. 39).
(Самостоятельное выполнение. Проверка по образцу на ли сточке, который находится у учителя.)
8. Рефлексия.
— Итак, над какой темой мы работали? Удалось ли решить поставленную задачу?
— В чём испытывали трудности?
(«Проверь себя» (учебник, с. 39). Самостоятельное выполнение.
Коллективная проверка.
— Я поздравляю Вас, вы поднялись ещё на одну ступеньку знаний вверх Молодцы. Спасибо за урок.
9.Домашнее задание (по выбору).
- Учебник: № 6 (с. 39).
- Тетрадь с печатной основой: № 27 (с. 37).
Порядок операций — ChiliMath
ПоискФундаментальная концепция порядка операций заключается в выполнении арифметических операций в «правильном» порядке или последовательности. Давайте посмотрим, как Роб и Пэтти пытались упростить заданное числовое выражение, применяя порядок или правило операций.
В чем ошибка Роба?
- Он небрежно упростил числовые выражения, применяя арифметические операции слева направо.
Пэтти получила правильный ответ, потому что правильно применила правила порядка действий.
- Сначала она выполнила умножение и деление, а затем сложение и вычитание.
Порядок операций — это просто набор правил, которые определяют приоритет последовательности операций , начиная с наиболее важных и заканчивая наименее важными.
Это правило правильного упрощения числовых выражений также известно как PEMDAS 9.Правило 0006 (аббревиатура от P лизинга E xcuse M y D ear A unt S ally).
Шаг 1: Сделайте все возможное, чтобы упростить все внутри круглых скобок или символа группировки.
Шаг 2: По возможности упрощайте экспоненциальные числа в числовом выражении.
Шаг 3: Умножить и разделить слева направо
Шаг 4: Сложите и вычтите то, что наступит раньше, слева направо
Примеры применения порядка операций для упрощения числовых выражений
Пример 1: Упростите приведенное ниже выражение, используя порядок операций.
- Изучая числовые выражения с несколькими операциями слева направо, мы видим, что сначала мы должны выполнить деление, то есть 5 \div 5 = 1.
- На данный момент у меня есть три (3) возможных операции . В порядке операций умножение имеет приоритет перед сложением и вычитанием. Следовательно, мы должны умножить дальше. Имеем 6 х 2 = 12,9.0010
- Что нам делать дальше, прибавлять или вычитать? Основываясь на порядке операций, сложение и вычитание имеют одинаковое значение. Чтобы определить, какую операцию выполнять первой, мы прибавляем или вычитаем то, что идет первым слева направо, что в данной ситуации означает прибавление, 1 + 3 = 4.
- Теперь у нас осталась одна операция — вычитание. Казалось бы сложное числовое выражение сводится к окончательному ответу — 8.
Пример 2: Упростите приведенное ниже выражение, используя порядок операций.
- Умножить
- Разделить
- Вычесть
- Сложить
Пример 3: Упростите приведенное ниже выражение, используя порядок операций.
- Взгляните на выражения в скобках. Правило говорит нам сначала делить, прежде чем вычитать.
- Мы можем избавиться от скобок, вычитая 7 на 2.
- Умножение гораздо «сильнее» операции, чем вычитание, поэтому мы должны сначала умножить 5 и 4. на 20.
Пример 4: Упростите приведенное ниже выражение, используя порядок операций.
- Сначала упростите выражения в скобках. Умножьте на первую скобку и разделите на вторую.
- Сложите числа внутри первой скобки, затем вычтите числа внутри второй скобки.
- Здесь есть умножение и деление. Поскольку умножение предшествует делению, мы собираемся сначала умножить.
- Между вычитанием и делением деление имеет приоритет, поэтому мы делим 5 на 5, чтобы получить 1.
- Последняя оставшаяся операция — это вычитание, поэтому это то, что мы собираемся сделать.
В последних примерах будут задействованы экспоненты, поэтому будьте осторожны с каждым шагом, потому что происходит так много вещей. Пока вы сосредоточены на соблюдении правил, регулирующих порядок операций, это не должно быть так сложно! Вот так…
Пример 5: Упростите приведенное ниже числовое выражение, используя правила порядка операций.
- Упростите выражения в скобках. А если точнее, упростите числа с помощью показателей.
- Две скобки для упрощения. Мы упростим второй, \left( {30 — 27} \right), потому что он намного проще. Здесь разница между 30 и 27 равна 3.
- Теперь обратим внимание на другую скобку. Порядок операций говорит нам делить, прежде чем мы вычтем.
- Наконец, мы можем избавиться от круглых скобок, выполнив вычитание, так как больше ничего делать не нужно.
- Глядя на то, что у нас осталось, упрощение экспоненциальных чисел имеет приоритет над операциями умножения, сложения и вычитания.
- Просматривая слева направо, очевидно, что мы должны умножить перед сложением и/или вычитанием.
- В соответствии с порядком операций сложение и вычитание одинаково важны. Мы должны сначала вычесть, потому что операция вычитания предшествует сложению, если смотреть слева направо.
- Последний шаг — добавить, потому что других операций не осталось.
Пример 6: Упростите приведенное ниже выражение, используя порядок операций. 93} первый.
- Глядя внутрь скобок, мы должны сначала разделить перед умножением и вычитанием.
- Удерживая наше внимание внутри скобок, порядок операций говорит нам умножать, прежде чем мы вычтем.
- Последней операцией, оставленной в скобках, является вычитание. Давайте исполним это!
- Давайте сделаем здесь паузу. На данный момент ясно, что мы можем выполнить три (3) упрощения одновременно. Очевидно, что у нас есть три экспоненциальных выражения: {2^5}, {4^2} и {3^2}.
- Казалось бы, сложная проблема теперь сводится к тому, что очень легко упростить. Если смотреть слева направо, деление имеет приоритет над вычитанием и сложением.
- Потому что вычитание и умножение находятся на одном уровне в иерархии операций. Способ, которым мы разрываем ничью, как вы уже должны знать, заключается в том, чтобы выполнить тот, который идет первым, если смотреть слева направо. В этой ситуации мы будем вычитать, а затем добавлять. Вот и все!
Пройти тест
Тест на порядок действий
Вам также может быть интересно: «В математике нам часто приходится переписывать слова и фразы, используя числа и символы. Сегодня мы будем практиковаться в написании и интерпретации математических выражений, чаще называемых математическими выражениями». Представьте следующие ситуации: Теперь помогите учащимся научиться писать выражения для представления этих ситуаций. Многие студенты, вероятно, захотят найти ответы, и это нормально. Однако важно помочь им написать числовое выражение, которое представляет ситуацию. Способность учащегося переводить слова в математические символы и цифры очень важна при решении задач. Спросите учащихся, есть ли у них идеи о том, как написать выражение для числа двоюродных братьев и сестер Амелии. Если идей несколько, запишите их на доске. Работайте всем классом, чтобы определить, какое из выражений верное. Это потребует от студентов использования их практических знаний о порядке операций из предыдущего урока. Спросите учащихся, «Какие подсказки вы нашли в ситуации, чтобы помочь написать выражение? Какие конкретные слова были для вас подсказками?» Учащиеся, скорее всего, скажут, что «в разы больше» означает умножение. Студенты также, вероятно, скажут «меньше чем» указанное вычитание. Математические выражения похожи на фразы на уроках английского языка — в них нет «пунктуации» (например, знака равенства в математике). Математические уравнения похожи на предложения на уроках английского языка — они имеют «пунктуацию» (например, знак равенства в математике). Итак, 4 × 5 — это выражение, а 4 × 5 = 20 — это уравнение. Снова попросите придумать, как написать выражение для количества карандашей, купленных учителем во второй ситуации. Работайте всем классом, чтобы определить, какие выражения, созданные учащимися, являются правильными. (Как 3 × (6 + 12), так и (6 + 12) × 3 являются правильными выражениями. Спросите учащихся, «Какие подсказки вы нашли в ситуации, чтобы помочь написать выражение? Какие конкретные слова были для вас подсказками?» Учащиеся, скорее всего, скажут, что «умножить» означает умножение, а «вместе» — сложение. Помогите учащимся просмотреть некоторые ключевые термины, прежде чем продолжить. «Есть четыре основных действия: сложение, вычитание, умножение и деление. Результат каждой операции имеет свой срок. Результатом сложения двух чисел является сумма. Результат вычитания – разность. Результатом умножения двух чисел является произведение. Результат деления двух чисел есть частное». Напишите на доске следующую таблицу и предложите учащимся записать ее в свои математические тетради. Эксплуатация Результат Другие ключевые слова или фразы Дополнение Сумма Вычитание Разница Умножение Продукт Отдел Коэффициент Теперь раздайте лист практики написания числовых выражений (M-5-6-3_Практический лист написания числовых выражений и KEY. Обеспечьте необходимое вмешательство и поддержку по мере необходимости. Изучающим английский язык и другим учащимся, испытывающим трудности с грамотностью, может потребоваться дополнительная помощь при переводе слов и символов. Сосредоточьтесь на ключевых словах и фразах, собранных в таблице выше. Вы также можете поместить эти слова и фразы на стену слов в своем классе. Попросите шестерых учащихся написать на доске выражения для каждой из ситуаций. Попросите других учащихся проверить, совпадают ли у них выражения. Если у них есть другое выражение, попросите их написать и это на доске. Обратите внимание, что для каждой ситуации можно написать два или три выражения (КЛЮЧ также приведен в рабочей таблице M-5-6-3_Writing Numerical Expressions Practice Worksheet и KEY.docx). Попросите класс использовать порядок операций, чтобы убедиться, что разные выражения, написанные учащимися для конкретной ситуации, имеют одинаковое значение. После того, как учащиеся заполнили Практикум по написанию числовых выражений, попросите их назвать любые другие ключевые слова или фразы, чтобы заполнить последний столбец таблицы. «Просмотреть ситуации. Определили ли вы какие-либо другие ключевые слова или фразы в этих ситуациях, которые указывают на конкретную операцию?» Учащиеся, скорее всего, узнают некоторые слова и фразы, перечисленные ниже в третьем столбце. Если нет, предложите их и помогите им определить ситуацию из Практического листа написания числовых выражений, в которой использовалось это слово или фраза. Эксплуатация Результат Другие ключевые слова или фразы Дополнение Сумма Всего, всего, более Вычитание Разница Менее Умножение Продукт В разы больше, В разы больше Отдел Коэффициент Разделить на Чтобы попрактиковаться в интерпретации числовых выражений, познакомьтесь с играми на сопоставление выражений 1, 2 и 3 (M-5-6-3_Игры на сопоставление выражений 1, 2 и 3. Каждой паре учеников потребуется по одной копии каждой из трех версий игры. Важно подготовить их заранее, так как 10 карт в каждом игровом наборе необходимо вырезать перед игрой. Если возможно, скопируйте каждый игровой набор на бумагу другого цвета. Это поможет отделить разные версии игры друг от друга. Попросите учащихся работать в парах. Раздайте игру «Сопоставление выражений 1» и представьте игру 1 следующим образом. «Теперь мы будем использовать игру на соответствие, чтобы попрактиковаться в интерпретации числовых выражений. Игра на соответствие состоит из 10 карт. На пяти карточках есть словесная фраза, а на пяти — математическая фраза или выражение. Цель состоит в том, чтобы сопоставить каждую словосочетание с соответствующим математическим выражением. Для начала положите все 10 карточек на стол так, чтобы надписи были видны. Работайте вместе, чтобы найти все совпадающие наборы карт». Когда все группы закончат игру «Сопоставление выражений 1», спросите учащихся, какие выражения было труднее всего подобрать к их фразам. Теперь раздайте игры «Собери выражения 2 и 3» каждой паре учащихся. Для игры 2 вы можете предложить учащимся разложить 10 карточек так, чтобы надпись не была видна. Затем учащиеся могут по очереди переворачивать две карточки. Если две карты, которые они раскрывают, совпадают, они сохраняют эту пару карт. Ученик, набравший наибольшее количество совпадений по окончании игры, считается победителем. Также предусмотрена третья игра на сопоставление выражений. Сложность немного возрастает от игры 2 к игре 3. За 5-8 минут до конца урока раздайте каждому учащемуся каталожную карточку. Соберите все эти «выходные листы» до того, как ученики покинут класс. Перед началом следующего урока просмотрите бланки на выход, чтобы определить распространенные ошибки, которые допускают учащиеся, и конкретных учащихся, которым требуется дополнительная поддержка. (7 + 8 × 3 можно описать как на 7 больше, чем произведение 8 и 3. Выражение 9 × 2 – 4 или (9 × 2) – 4 может представлять «на 4 меньше, чем произведение 9 и 2».) Расширение : Используйте следующие стратегии и мероприятия, чтобы удовлетворить потребности ваших учеников во время урока и в течение всего года. Написание и интерпретация числовых выражений
У Амелии на три двоюродных сестры меньше, чем в пять раз больше, чем у Лии. Сколько кузенов у Амелии? 
(Как 4 × 5–3, так и 5 × 4–3 являются правильными выражениями.)
) Важно, чтобы учащиеся использовали круглые скобки в этой ситуации, чтобы указать, что сначала должна быть найдена сумма 6 и 12, а затем сумма должна быть умножить на 3. По этой причине понимание учащимися порядка операций очень важно для этого урока.
Последний столбец таблицы будет заполнен после того, как учащиеся закончат практику написания числовых выражений.
docx). Попросите учащихся работать в парах и написать выражения для каждой из шести ситуаций. Отслеживайте прогресс учеников во время работы.
docx).
Если учащиеся не считают это сложным, обязательно обсудите фразу «на четыре меньше, чем сумма 7 и 3», поскольку она часто является самой сложной для учащихся. Студенты часто думают, что это должно быть записано как 4 – (7 + 3). Напомните учащимся, что порядок решения задачи на вычитание важен. Например, нахождение «на четыре меньше» 20 на самом деле означает, что вы вычитаете 4 из 20, записанного как 20 — 4.
Представьте выражение 7 + 8 × 3 и попросите учащихся написать словосочетание, описывающее это выражение. Также представьте словесную фразу «на 4 меньше, чем произведение 9 и 2». Попросите учащихся написать математическое выражение для представления этой фразы.