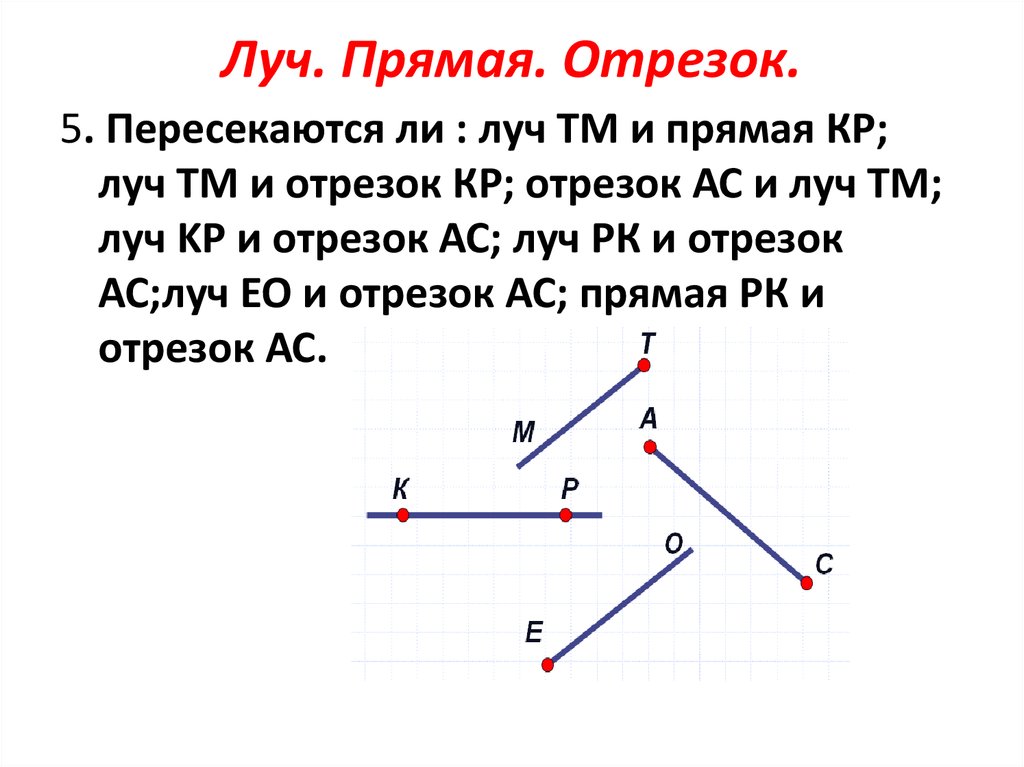
Математика что такое луч 2 класс: Луч — урок. Математика, 2 класс.

Содержание

Прямая. Луч. Отрезок. Задачи по математике 2 класс

Математика 2 класс

Нестандартные задачи
Математические диктанты
Примеры
Логические примеры
Тесты
Диагностические работы

Задачи для 2 класса

Операции
Обратные операции
Прямая, луч, отрезок
Сложение и вычитание двузначных чисел
Сотня. Счет сотнями.
Метр

Контрольные работы

Контрольная работа 1

Контрольная работа 2

Итоговая контрольная работа

Итоговая контрольная работа

Контрольная работа 1

Контрольная работа 2

Итоговая контрольная работа

Задача 1

Точка О разбивает прямую AB на две части. Что напоминает каждая из частей? Чем каждая часть отличается от прямой и отрезка?

Решение
1) Каждая из частей напоминает луч.

2) Луч имеет начальную точку, но не имеет конечной точки. Отрезок имеет начальную и конечную точки. Прямая не имеет ни начальной ни конечной точек.

Задача 2

Отметь цветным карандашом начало каждого луча. Как обозначен первый луч? Можно ли поменять местами буквы? Почему? Обозначь остальные лучи.

Решение

Луч обозначен: первая буква — начальная точка луча, вторая конец.

Буквы нельзя менять мстами, потому что первая буква обозначает начало луча.

Задача 3

а) Подбери правильные названия для чертежей и проведи линии:
б) Начерти в тетради прямую, луч и отрезок и обозначь их.

Решение
а)

Задача 4

Обведи с помощью линейки на чертеже прямые линии красным карандашом, лучи — синим, а отрезки — зелёным:

Решение

Задача 5

«Машенька испекла вчера 32 пирожка, а сегодня — на 4 пирожка больше».
Какие вопросы можно поставить к этому условию, чтобы получилась задача:

1) Сколько пирожков испекла Машенька вчера?
2) Сколько пирожков испекла она сегодня?
3) С какой начинкой были пирожки?
4) Сколько пирожков испекла Машенька за 2 дня?
Подбери к полученным задачам подходящие схемы и реши их:

Решение
2) Сколько пирожков испекла она сегодня?

4) Сколько пирожков испекла Машенька за 2 дня?

Задача 6

В одном вагоне поезда едут 46 человек, а в другом — на 18 человек меньше. Сколько человек едут в двух вагонах?

Решение
46 — 18 = 28

46 + 28 = 74

Ответ:74 человека.

Задача 7

Решение
а) Заменить букву о на букву и. Заменить букву и на букву о.

б) 1м 5см выразить в сантиметрах. 105см выразить в метрах и сантиметрах.

Задача 8

Реши задачу, а затем составь и реши обратную задачу:
«В ларёк привезли 180 кг винограда и продали его за 3 дня. В первый день продали 56 кг, а во второй — на 8 кг больше. Сколько килограммов винограда продали в третий день?»

Решение
1) 56 + 8 = 64

2) 64 + 56 = 120

3) 180 — 120 = 60

60кг продали в 3 день.

Задача 9

Найди закономерность и вставь пропущенные числа. Кто быстрее назовёт все числа этого ряда?

Решение Каждое последующее число больше предыдущего на 3.
3 6 9 12 15 18 21 24 27 30

На странице использован материал из книги Л. Г. Петерсон «Математика второй класс. Часть2».
Ссылка на сайт автора: www.sch3000.ru

Составные задачи

Задачи на нахождение слагаемого и вычитаемого

Задачи на нахождение третьего слагаемого

Задачи на нахождение суммы

Задачи на нахождение уменьшаемого

Задачи на разностное сравнение

Задачи на нахождение суммы

Простые задачи

Простые задачи на умножение

Задачи на деление по содержанию и на равные части

2 класс — точка, отрезок, луч, прямая, ломанная

Дата публикации: 13 апреля 2017.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Скачать:Геометрические фигуры: точка, прямая, отрезок, ломаная (PDF)

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 2 класса

Тренажер к учебнику Л.Г. Петерсон Тренажер к учебнику М.И. Моро

Точка и прямая

1. Посмотри внимательно на рисунок. Сколько прямых пересекает точку А?

2. Нарисуй точку В. Начерти три прямые, пересекающих точку В. Сколько еще прямых, пересекающих точку В, можно начертить?

3. Нарисуй точки А и B, расстояние, между которыми равно 5 см. Соедини эти точки прямой.

4. Продолжи две прямые на рисунке так, чтобы они пресеклись в точке О.

5. Начерти три параллельные прямые. Определи точку, в которой они пересекаются.

Отрезок

1. Начерти отрезок AB, длина которого равна 5 см.

2. Начерти отрезок CD, длина которого равна 7 см.

3. Начерти отрезок EF, длина которого равна 10 см.

4. Начерти 2 отрезка. Длина первого отрезка равна 4 см, а второго – 7 см. Какой отрезок длинее?

5. Сколько отрезков на рисунке? Покажи самый короткий отрезок. Покажи самый длинный отрезок.

6. Начерти отрезок, длина которого равна 12 см. Поставь на нем точку так, чтобы получился отрезок, равный 3 см. Чему будет равна длина второго, получившегося отрезка?

7. Начерти прямую и отметь на ней два отрезка, длины которых равны 4 см и 6 см.

8. Определи на глаз длину каждого отрезка, а затем проверь себя, измерив длину линейкой.

Ломаная

1. Определи, какая из линий является ломаной?

2. Нарисуй ломаную, составленную из звеньев, равных 4 и 6 см. Сколько звеньев в этой ломаной? Какова общая длина ломаной?

3. Нарисуй ломаную, составленную из звеньев, равных 2, 3 и 6 см. Сколько звеньев в этой ломаной? Какова общая длина ломаной? Какое звено самое длинное?

4. Нарисуй ломаную. Определи ее длину в сантиметрах и в миллиметрах.

Линии, отрезки. Задачи на измерения.

1. Начертите в тетрадях 6 отрезков прямых линий: первый отрезок длиной 4 см, под ним второй — длиной 6 см и т. д. (каждый следующий отрезок на 2 см длиннее предыдущего). Справа против каждого запишите длину отрезка.

Когда все отрезки будут начерчены, ответьте на следующие вопросы: 1) Какой из этих отрезков вдвое длиннее другого (и какого)?
2) Какой из отрезков вдвое короче другого (и какого)?
3) На сколько сантиметров первый отрезок короче последнего (самого длинного)?
4) На сколько сантиметров шестой отрезок длиннее первого?
5) Какие из этих отрезков при сложении их по два дадут одинаковую общую (и какую именно) длину?
Начертите сами другие 4 отрезка, один больше другого на одно и то же число, и ответьте на такие же вопросы.

2. По дороге в школу Сережа проходит по одной улице 44 м., а по другой — на 12 м больше, чем по первой. Подсчитайте, сколько метров от дома Сережи до школы.

3. Начертите по клеткам прямоугольник длиной 5 см и шириной 3 см и рядом или внизу квадрат, каждая сторона которого 3 см. Подсчитайте, какая из этих фигур занимает больше клеток и на сколько больше.

4. Проведите по линейке небольшой отрезок на неграфленой бумаге и затем ниже его проведите отрезок на глаз, вдвое больший, и еще ниже — втрое больший. Затем проверьте длины отрезков по линейке.

5. Поучитесь измерять отрезки на глаз, а для этого сделайте в тетради запись для учета работы примерно в таком виде. Учет работы по глазомерному измерению Наименование отрезка Измерено на глаз рулеткой или веревкой ошибка
АБ 10 дм 9 дм 1 дм
ВГ 65 см 72 см 7 см
Расстояния от края доски до стены 2 м 50 см 2 м 80 см 30 см
Указание. Эту работу лучше проводить так: учитель предлагает учащимся оценить на глаз длину на-черченного на доске, или отбитого шнуром на полу, или указанного учителем на каком либо предмете отрезка и записать в графу «на глаз», а затем двое учеников (каждый раз разные) измеряют этот отрезок линейкой или рулеткой.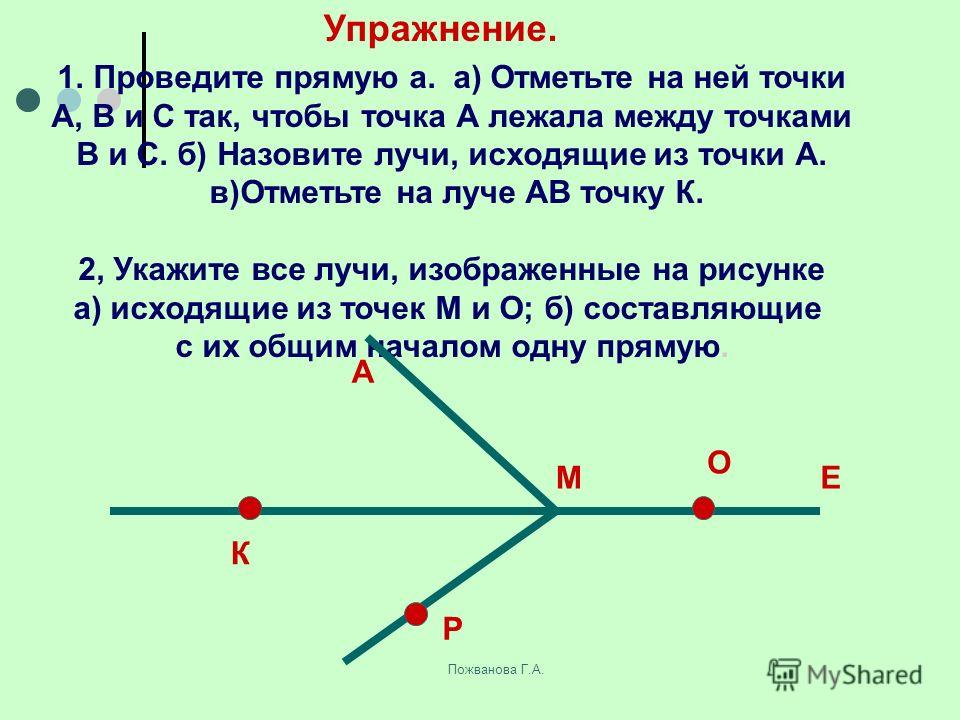

Результат измерения записывается на доске, а дети вписывают его в следующую графу и вычисляют ошибку.

6. Поучитесь проводить отрезки прямых линий от руки. Например, проведите на глаз отрезки в 5 см, 8 см и 11 см. Проверку отрезков делайте по линейке.

7. а) Начертите на бумаге три разных треугольника, определите на глаз сумму длин всех сторон (периметр) каждой фигуры и затем проверьте по линейке.
Результаты измерений запишите.
б) Сложите из одинаковых палочек модель ломаной линии. Определите длину этой ломаной линии на глаз и затем проверьте линейкой.
Указание. Палочек можно взять сначала штук 5—6, а затем больше. Хорошо, если дети догадаются, что подсчет общей длины здесь можно делать умножением.

8. Поучитесь делить отрезок на 2, 4, 8 равных частей на глаз. Отрезки чертите на бумаге.
Указание. Сначала надо показать деление отрез¬ка на равные части на доске: начертить произвольной длины отрезок, вызвать ученика и предложить ему поставить посередине отрезка черточку, а затем проверить деление полоской бумаги или линейкой, другому ученику можно предложить разделить тот же (или другой), отрезок на 4 равные части и т. д. После освоения методики деления отрезка на доске надо предложить учащимся то же самое проделать в тетрадях и дать такую же работу на дом.
9. Поучитесь делить отрезок на 3 равные части.

10. Построить прямоугольник, у которого одна сторона 6 см, а другая 4 см. Как можно построить прямоугольник при помощи линейки и угольника?

Указание. Надо объяснить и показать учащимся, что этот прямоугольник можно построить, взяв за основание 6 см, а за высоту 4 см, и наоборот, взяв за основание 4 см, а за высоту 6 см.
Объяснение ученикам можно провести примерно в следующем плане.
Проведем прямую МН и отложим на ней отрезок АБ длиной 6 см. Затем к концам этого отрезка (к точкам А и Б) приложим угольник и проведем прямые, на которых отложим отрезки АС и БД, равные 4 см. Точки С и Д соединим.
Таким же. образом строится прямоугольник, за основание которого принимается 4 см, а за высоту 6 см.

11. Поучитесь строить квадрат на бумаге. Постройте, например, квадраты: 1) со стороной 3 см, 2) 5 см.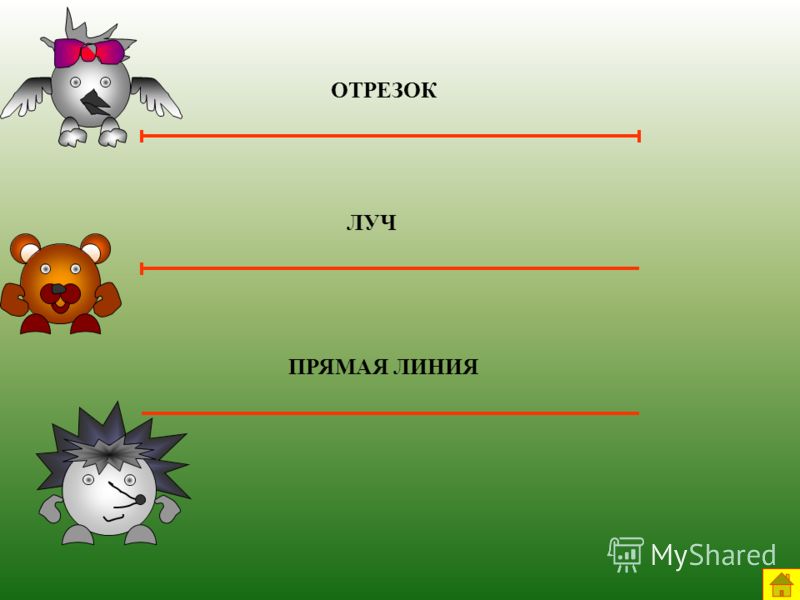
Указание. Построение такое же, как указано в предыдущей задаче, только отрезки откладываются равные.

12. Толя сделал рисунок из шести прямоугольников, прилегающих друг к другу. Нижние стороны каждого из этих прямоугольников имели длину 1 см и лежали на одной прямой. Высота первого прямоугольника была равна 5 мм, а высота каждого следующего была больше предыдущего на 5 мм.
Сделайте чертеж фигуры, которую нарисовал Толя. Раскрасьте ее разноцветными карандашами, а квадрат, имеющийся в фигуре, затушуйте черным карандашом. Какой высоты будет крайний справа прямоугольник?

13. Гена сделал рисунок из прямоугольников, но у него самый длинный прямоугольник, длиной 30 мм, был внизу, а каждый из выше лежащих был на 5 мм короче соседнего нижнего. По высоте эти прямоугольники были одинаковые — в 1 см, и левые их края лежали на одной прямой, проведенной сверху вниз. Сделайте чертеж фигуры, которую нарисовал Гена. Раскрасьте ее разноцветными карандашами, а квадрат, который имеется в фигуре, затушуйте черным карандашом.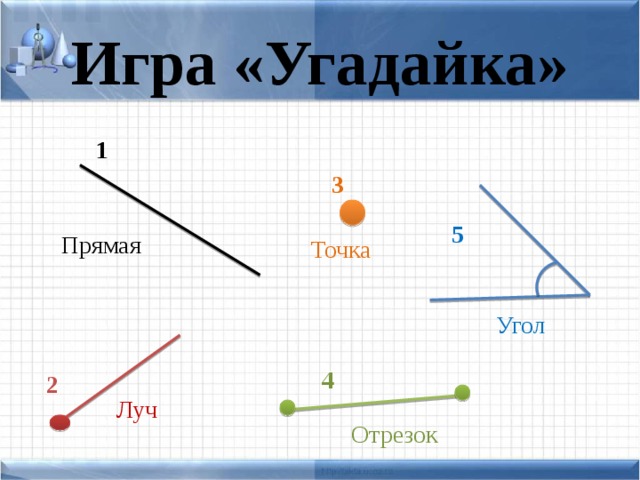

14. а) Коля сделал из картона для детского сада 3 игрушечные коробки с квадратными основаниями, причем основания этих коробок были окантованы красным шнуром. Сколько потребовалось шнура для окантовки основания этих коробок, если сторона квадратного основания большой коробки составила 16 см, средней — вдвое меньше, а меньшей — еще вдвое меньше? Сделайте чертеж оснований этих коробок.
Решение: 1) Найдем стороны среднего и меньшего квадратов: 16 см : 2 = 8 см; 8 см ; 2=4 см.
2) Найдем периметры квадратов 16 см х 4 = 64 см; 8 см х 4 = 32 см; 4 см х 4 = 16 см.
3) Найдем общую длину шнура:
64 см+ 32 см+ 16 см = 112 см.
б) Сиденье табуретки имеет вид квадрата со стороной 38 см. Во время перерыва в работе на пришкольном участке дети поставили рядом 3 такие табуретки и накрыли их сиденья газетами. Получился «походный» стол для завтрака. Какую фигуру представляет собой крышка полученного стола? Какова длина и ширина этой крышки? Какова сумма длин всех сторон крышки стола?
Ответ: Прямоугольник; длина 114 см, ширина 38 см; периметр 304 см.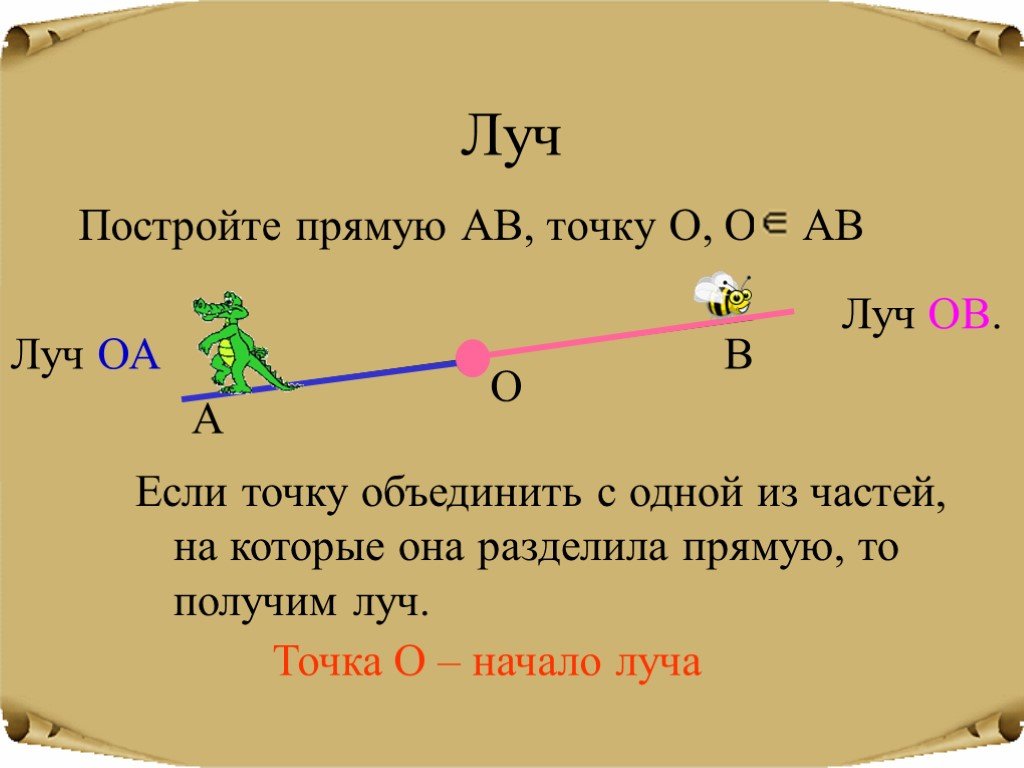

15. У Гали было несколько кусочков ленты шириной 2 см и длиной по 6 см. Она приложила их друг к другу и получился квадрат. 1) Покажите на Галя. 2) Сколько кусочков длины сторона полученного квадрата? Какова сумма длин сторон квадрата? Указание. 1) См. чертеж полученного квадрата;
2) у Гали было 3 куска ленты; 3) сторона полученного квадрата 6 см; 4) длина всех сторон этого квадрата равна 6 см х 4 = 24 см.

16. Скорняку (специалисту по подборке мехов) нужно было на меховом воротнике заменить поношенное место, имеющее форму квадрата, новым мехом. Для этого он подобрал и соединил швами (с тыловой стороны) три кусочка меха: 1) квадратный со стороной 3 см; 2) прямоугольный со сторонами 2 см и 3 см. 3) прямоугольный со сторонами 2 см и 5 см. Покажите на чертеже, как соединил скорняк свои кусочки меха. Какова сторона и сумма длин всех сторон полученного квадратного куска заплатки?
Указание. Вырезать из клетчатой бумаги указан¬ные лоскутки и сложить из них квадрат. Полученный квадрат имеет сторону длиной 5 см; длина всех сторон его 5 см х 4 = 20 см; кусочки чеха скорняк сложил следующим образом (см.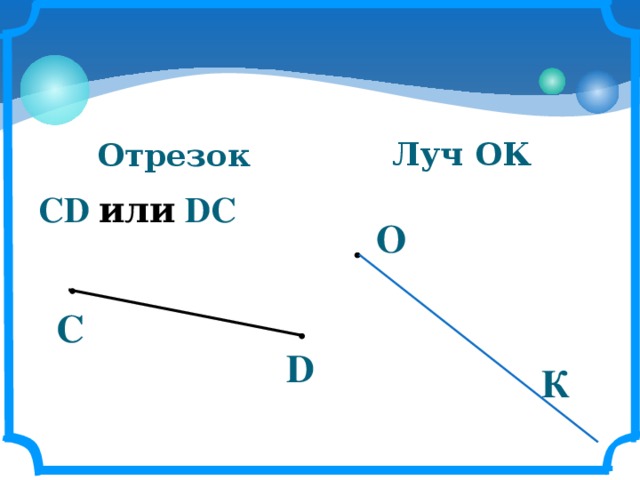 черт, слева).

17. Вырежьте из бумаги три квадрата со сторонами 4 см, 2 см и 2 см. Составьте из этих грех квадратов один прямоугольник. Покажите на чертеже и определите периметр этого прямоугольника. Указание. См. чертеж полученного прямоугольника. Длина полученного прямоугольника 6 см, ширина 4 см, периметр его 20 см.

18. Измерьте в миллиметрах длину и ширину почтового конверта обычного формата и запишите полученные данные в свои тетради. Форму какой геометрической фигуры представляет собой конверт?

Балансир | НСТА

Тесты для формирующего оценивания

Определение математического правила

Балансир

Пейдж Кили

В начальных классах дети исследуют с помощью бревна, чтобы развивать представления о силе, движении и весе, подвешивая различные комбинации объектов, чтобы выяснить, как они балансируют.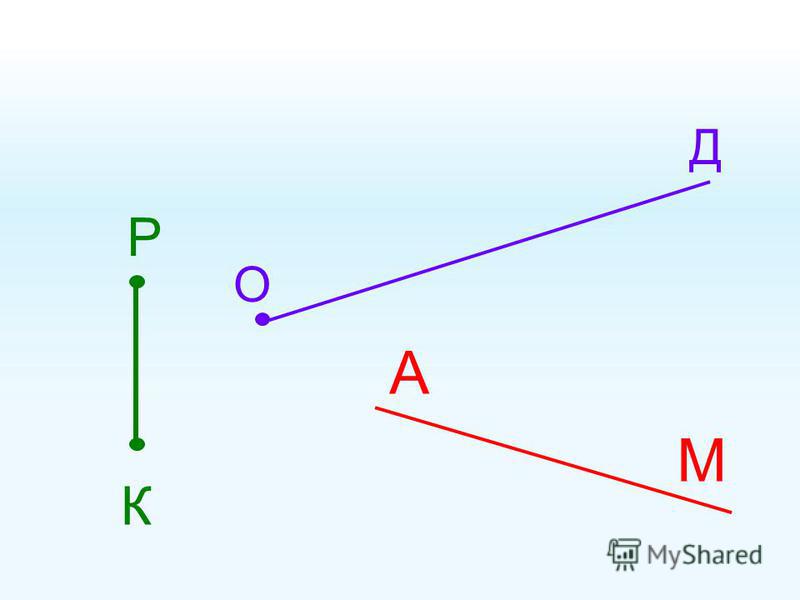 Балансир имеет длинное плечо, которое опирается на одну точку опоры (точку опоры). Когда учащиеся переносят больший вес на одну сторону руки, они наблюдают, как гравитация тянет руку вниз. Поместив такой же вес в то же место на противоположной руке, они наблюдают, как эта рука опускается и балансирует балка. Путем исследования они обнаружили, что размещение гирь ближе к точке поворота оказывает меньшее влияние на опускание руки, чем размещение гирь на конце руки. Когда они взаимодействуют с бревном, у них начинает формироваться интуитивное понимание уравновешенных сил. Тем не менее, бревна дают представление не только о ранних идеях о сбалансированных силах — они также открывают окно в математическое мышление учащихся.

Тест формирующего оценивания «Бревно» (рис. 1) выявляет у учащихся идеи о балансировании (Keeley and Harrington 2010). Он также используется, чтобы выяснить, признают ли учащиеся, что разное количество веса можно сбалансировать с помощью математического правила. Это исследование сочетает в себе три измерения: основную дисциплинарную идею Сил и Движения, научную практику Использование Математики и Вычислительного Мышления и сквозную концепцию Паттернов.

РИСУНОК 1

Начиная с самого раннего возраста, дети имеют интуитивное представление о моментах (

).0019 момент относится к мере сопротивления объекта изменениям его вращательного движения). Пиаже и Инхельдер (1969) провели ранние исследования детей, манипулирующих весами с бревном. Из своего повседневного опыта с качелями некоторые дети знали, что «вес», расположенный дальше от середины качелей, оказывает большее влияние, чем такой же вес ближе к середине. Они также, казалось, знали, как интуитивно достичь баланса с разным весом на качелях. Зиглер (1982) провел аналогичные исследования балансировки с использованием «подхода к оценке правил» и обнаружил, что дети проходят четыре стадии развития, пытаясь понять, как балансировать на бревне. Маленькие дети (в возрасте 4 и 5 лет) принимают во внимание только вес, когда решают, будет ли балансировать балка. В возрасте около 6 лет дети учитывают как вес, так и расстояние, когда веса одинаковы. Примерно в возрасте 7–9 лет дети начинают учитывать как вес, так и расстояние, но с трудом предсказывают, что произойдет, если одна сторона будет иметь больший вес, а другая — большее расстояние. На последнем этапе (в возрасте 10 лет и во взрослом возрасте) дети используют математическое правило, чтобы умножить расстояние на вес и сравнить продукты, чтобы определить, будет ли балка сбалансирована. При использовании этого теста ищите признаки любой из этих четырех стадий развития, помня о том, что дети могут быть не готовы описать математическое правило до промежуточных классов.

Лучший ответ на вопрос — шесть кубиков. Это связано с тем, что грузы, висящие ближе к точке поворота, оказывают меньшее влияние на балансировку, чем грузы, которые висят дальше от точки поворота. Чтобы сбалансировать балку, вы должны положить больший вес в чашку слева. Некоторые учащиеся могут признать, что требуется больший вес, но не могут использовать математическую зависимость между весами и количеством интервалов между лучами (расстоянием).

Чтобы найти числовой ответ, учащиеся должны понимать, что расстояние между висящими кубиками (гирьками) и точкой вращения так же важно, как и количество кубиков. Произведение 3 (количество единиц, удаленных от точки вращения), умноженное на 2 (количество кубов), равно 6. Это число должно быть равно такому же произведению на левой стороне, чтобы рука балансировала. Поскольку чашка висит на расстоянии 1 единицы от точки вращения, количество кубиков должно быть 6 (6 × 1 = 6).

Внимательно слушайте, как дети делают свои прогнозы и объясняют их причины. Прислушивайтесь к доказательствам того, учитывают ли они только вес или вес и расстояние. Учащимся, которые учитывают как вес, так и расстояние, предложите им придумать математическое правило, подтверждающее их прогноз. После того, как учащиеся поделятся своими мыслями, дайте им весы с бревном, чтобы они могли проверить свои идеи. Если весы балансира недоступны, баланс и точка опоры могут быть такими же простыми, как плоская доска и клиновидный блок.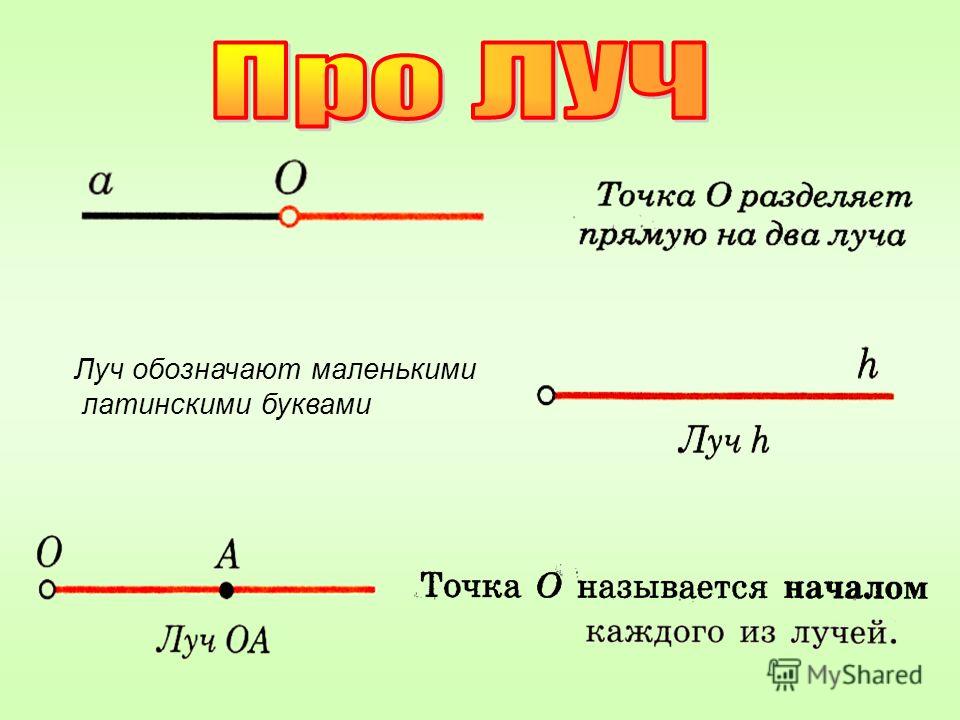 Кубики Unifix можно заменить гирями. Предложите учащимся дополнительно изучить различные комбинации весов и расстояний и открыть математическое правило, применимое ко всем их различным комбинациям. Для детей младшего возраста используйте сквозную идею количества. Прислушайтесь к свидетельствам их растущего понимания математики, когда они используют количественные слова для описания объектов на каждой стороне весов, например, большой , маленький , тяжелый , легкий , слишком много и недостаточно .

Этот зонд в сочетании с возможностью изучить, как работает бревно, дает учащимся ранний опыт понимания алгебраических уравнений задолго до того, как они начнут изучать алгебру. Балансир представляет собой физическую модель алгебраического уравнения. Обе стороны должны равняться одинаковой сумме, а точка опоры является знаком равенства. Математическая цель учащихся начальных классов состоит в том, чтобы заставить их понять, что все, что они кладут на одну сторону, должно быть пропорционально равно тому, что они кладут на другую сторону.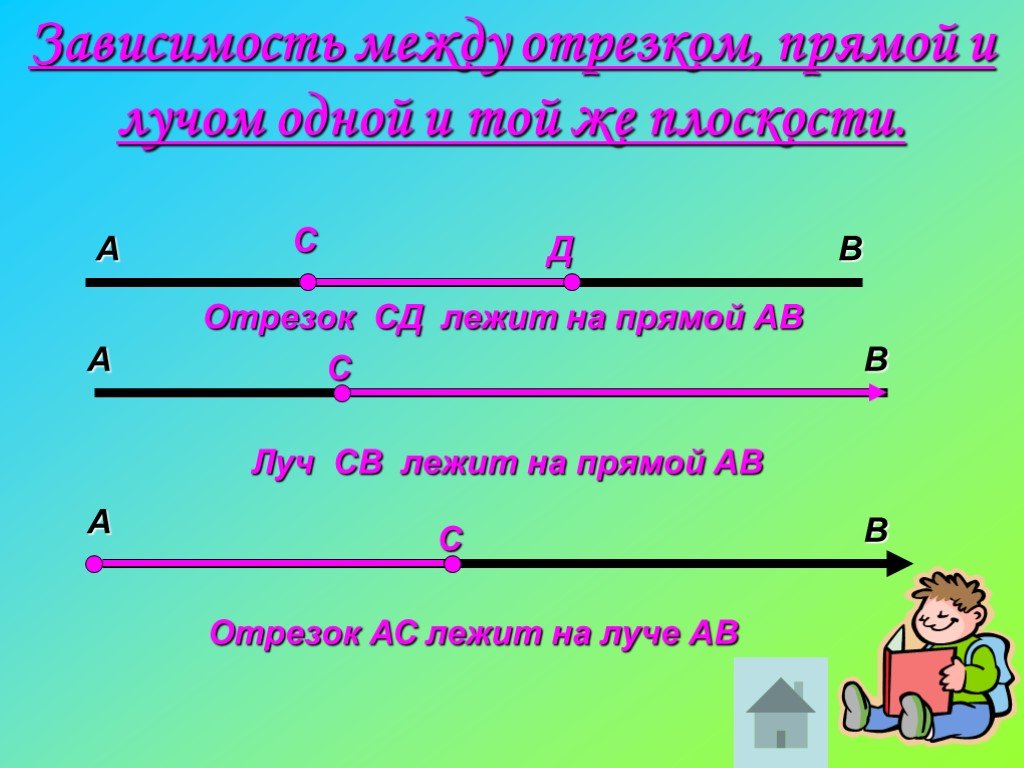 Это можно сделать в разных конфигурациях с разным количеством объектов, разным весом и разным расстоянием от точки опоры, в конечном итоге поняв, что разные атрибуты могут вносить вклад в объекты, а также числа, равные друг другу. Например, 1 × 12 = 1 × 12 или 2 × 6 = 1 × 12 или 3 × 4 = 2 × 6. «Вычисляя» это математически, учащиеся узнают о важности математики, помогающей им делать прогнозы в науке.

Ссылки

Кили, П. и Р. Харрингтон. 2010. Раскрытие студенческих идей в физике: 45 новых датчиков для оценки силы и движения. Арлингтон, Вирджиния: NSTA Press

Пиаже, Дж. и Б. Инхелдер. 1969. Психология ребенка. Нью-Йорк: Основные книги.

Зиглер, Р. 1982. Подход к оценке правил и образование. Современная педагогическая психология 7 (3): 272–288.

Вам также может понравиться

Журнальная статья

Делать все это

Журнальная статья

Не забудьте демо!

Журнальная статья

Когда мы сможем увидеть Макалии?

Журнальная статья

Наблюдение за ненаблюдаемым

класс — Что нового в BEAM? — Мост к углубленной математике

Линн Картрайт-Паннетт

20 июля 2019 г.

BEAM Discovery 2019

Линн Картрайт-Паннетт

20 июля 2019 г.

BEAM Discovery 2019

Так что же именно происходит в BEAM Discovery? Вот взгляд на типичный день с фотографиями из кампуса BEAM Discovery в центре Нью-Йорка!

Утро начинается с завтрака, затем утренние занятия. BEAM верит в возможность выбора, поэтому ученики выбирают предметы, которые могут быть «Победа над Шерлоком» или «Дроби, головоломки и игры».

После уроков у учащихся есть час Открытого математического времени, время, когда они могут работать над любой математикой по своему выбору, индивидуально или в группах. Они обязательно выполняют необходимые PSets (наборы задач) из класса, а затем могут изучать задачи (задача недели или задача из 100 задач), книги по математике, веб-сайты по программированию, искусство решения задач и многое другое.

После уроков пора на занятия! Учащиеся BEAM могут выбрать спорт, настольные игры, декоративно-прикладное искусство и другие творческие занятия. Недавние хиты включали в себя сборку кубика Рубика, оригами, аниме-клуб и эстафету в крестики-нолики.

После занятий пора обедать. BEAM ежедневно оплачивает обеды в местных ресторанах. Эти фотографии из empanada в четверг!

В большинстве дней послеобеденный блок полностью повторяет утренний: занятия, открытая математика, занятия. Но один раз в неделю у нас есть специальные послеобеденные занятия, на которых проводятся эстафеты, командные математические соревнования, в ходе которых учащиеся решают математические задачи с примесью некоторой глупости. Недавняя задача требовала от учащихся напевать мелодию, которую их судья узнает, прежде чем они сдали свою математику. отвечать!

Когда день подходит к концу, студенты присоединяются к своим туристическим группам, чтобы поехать домой на метро, расслабиться и перезарядиться, чтобы их мозги были свежими для следующего дня в BEAM!

Tagged: класс, открытое время математики, эстафеты, мероприятия, BEAM Discovery, Нью-Йорк, 6-й класс

Линн Картрайт-Паннетт

15 августа 2018 г.

BEAM 6 NYC 2018

Линн Картрайт-Паннетт

15 августа 2018 г.

BEAM 6 NYC 2018

В этом месяце мы приветствуем трех новых штатных сотрудников BEAM! Одна из них, Алисса Лавинг Юнг, является новым координатором по развитию и коммуникациям BEAM. Она провела свою первую неделю в BEAM, посетив BEAM 6, и написала этот пост в блоге о своем опыте. Добро пожаловать в команду, Алиса!

—-

Моя цель — посетить четыре математических занятия BEAM 6 Uptown за один час. Хотя у меня может быть ученая степень по математике (точнее, степень магистра), это амбициозный план. Мне не терпится увидеть, какую математику будут решать ученики BEAM 6 сегодня. 922?

Ничего не могу поделать. Я сразу же начинаю строчить в блокноте работу, пытаясь решить вопрос. Но по мере того, как вокруг меня кружится дискуссия, я отвлекаюсь от своих попыток решить проблему, мне любопытно, что придумывают студенты. Студенты вслух задаются вопросом, как решить подобную задачу, не прибегая к головокружительной степени умножения. Преподаватель Хуан дружески предупреждает, что такой подход займет гораздо больше времени, чем у них есть в классе. Возвращаясь к моей странице заметок, я понял из своей собственной работы, что ключ к проблеме заключается в том, чтобы обнаружить закономерность и не потеряться в громоздких вычислениях.

Эмили работает во время урока.

Вокруг меня я слышу, как ученики приближаются к шаблону, и это так весело, что я должен заставить себя помнить, что у меня есть максимум 15 минут с ними, прежде чем я должен идти на следующий урок.

Еще до того, как мое время истекло, один из студентов встает у доски и представляет идею.

Коллективная математика, смелость представить перспективное решение, еще не оформившуюся идею всему классу сверстников — это важнейший элемент изучения продвинутой математики. Я рад, что студенты BEAM так взаимодействуют друг с другом и со своими преподавателями. Но, взглянув на часы, я должен оторваться и отправиться на следующий урок.

—-

Здесь на доске совсем другая картинка.

Нарисованы пересекающиеся круги и разбросаны числа. Ученик у доски аккуратно расставляет числа. Хотя поначалу числа кажутся беспорядочно распределенными, вдумчивость учащегося является первым признаком того, что происходит нечто большее. Затем я замечаю метки: делители 6, кратные 6, простые числа.

Они изучают логику. Странную картинку на доске я узнаю как диаграмму Венна, способ визуализировать наложение и взаимодействие между различными наборами.

Они переходят от диаграммы Венна на доске к работе над листом задач. Студент замечает неоднозначность в одной из задач. Задача просит их изучить утверждение «не А и не Б». Он задается вопросом, имеет ли инструктор, Сиан, в виду «(не А) или Б» или, скорее, «не (А или Б)».

Весь класс изучает эту тонкость. Этот процесс напоминает мне написание математических доказательств в аспирантуре. Часто самый крошечный оборот фразы, самая мельчайшая недостающая деталь могут создать или разрушить сложный математический аргумент. Я рад видеть, что студенты так внимательно относятся к чтению и письму по математике. Но мне пора переходить в третий класс.

Т. А. Амайя работает со студенткой Карен над решением задачи во время Open Math Time.

Йорлан работает над сложной задачей геометрии.

Этот класс говорит «Геометрия и логика» в углу классной доски впереди. По-видимому, это еще один класс по логике, но теперь в смесь добавлена геометрия. Я заинтригован.

Преподаватель, Ксавье, очень энергичен и называет каждого ученика по имени, засыпая комнату вопросами. 92=8. Ученик кричит, что c — это квадратный корень из 8.

Ксавьер с улыбкой смотрит, не угадал ли Эдуардо, но нет:

«Нет, я не догадывался. ..» Эдуардо отвечает: » Это потому, что извлечение квадратного корня противоположно возведению чего-то в квадрат».

Меня впечатлило, что в одном предложении Эдуардо дошел до сути того, что математики подразумевают под обратными уравнениями. Это понятие может сбить с толку даже студентов колледжа. Но я не могу остаться, чтобы узнать больше сегодня. 92. Немедленно начинается усердное царапанье карандашом, головы склонены, брови сосредоточенно нахмурены.

Это то, что я называю «грязной работой» математики. Сложные вычисления не охватывают того, что делают математики. В конце концов, математики — это гораздо больше, чем просто люди-калькуляторы. Но такие расчеты составляют важный аспект работы многих математиков и ученых. Студенты BEAM в этом классе развивают терпение и выносливость, чтобы справиться даже с очень сложными формулами, и в то же время изучают ошеломляющую астрономию.

Таро, ТА, наблюдает, как Джамал размышляет над большими числами.

Между тем, я установил новый личный рекорд по количеству занятий, которые я посетил за один час, и, что еще лучше, у меня была возможность подумать о действительно классной математике. Я не могу дождаться того, что готовит следующий час BEAM 6!

—-

Хотите знать, какие классы посещала Алисса? Все учащиеся BEAM 6 посещают занятия по четырем темам: основы математики, логика, командные стратегии математики и прикладная математика. В рамках каждой темы учащиеся могут выбирать из меню классов, поэтому каждый из них выбирает класс, который вызывает у них любопытство. По утрам, когда Алисса посещала занятия, учащиеся были либо на уроке основ математики, который исследует, зачем нужна элементарная математика, либо на уроке логики, который фокусируется на том, как обосновать свои рассуждения. Хуан и Сьюзен преподавали курсы по основам математики, а Сиан и Ксавье преподавали курсы по логике.

Вот полные описания четырех классов, которые она посетила!

Экспоненты: сверхспособности чисел! (Хуан)

Используя силу умножения, мы составим несколько очень-очень больших чисел и сравним их, чтобы увидеть, какие из них окажутся самыми большими. Мы также исследуем странную планету, на которой всего 11 чисел!

Криптарифмы и другие арифметические задачи (Сиан)

Если А + В = АС, то что такое А + В + С? Криптарифмы — это математические головоломки, в которых арифметика проста, но «мыслительная часть» головоломки сложна. Мы начнем с простых задач и создадим набор логических стратегий для решения этих задач и всех математических задач.

Геометрия и логика (Ксавье)

Вы когда-нибудь рассматривали задачу и не знали, с чего начать? Этот класс разовьет вашу способность решать сложные задачи. Мы узнаем, как, казалось бы, неполная информация может быть объединена для формирования полных решений.

Большие числа, Маленькие числа и Промежуточные числа (Сьюзен)

Представьте, что у вас есть очень длинная числовая строка, где все числа, которые вы обсуждали в этом году в школе, находятся на числовой прямой. Вводится новый номер. Куда это идет? Ты уверен? В этом классе мы будем использовать различные инструменты (сила мозга, линейки, логика и т. д.), чтобы идентифицировать большие числа, маленькие числа и промежуточные числа.

Tagged: BEAM NYC, BEAM 6, BEAM 6 2018, BEAM 2018, классы, класс, математика

Линн Картрайт-Паннетт

22 июня 2018 г.

BEAM 6 Лос-Анджелес 2018 г.

Линн Картрайт-Паннетт

22 июня 2018 г.

BEAM 6 Лос-Анджелес 2018 г.

Сегодня пятница, а это значит, что мы прошли почти 20% пути с BEAM 6 Los Angeles 2018. Куда ушло время??

Итак, как проходит неделя в BEAM 6? Особенности на каждый день:

Завтрак
Утренний урок
Открытый урок математики
Занятия
Обед
Дневной урок
Открытый урок математики
Занятия

Давайте углубимся в каждый из этих блоков!

День начинается со сбалансированного завтрака, который подается по меню в столовой.

Академики

Тогда на занятия! Учащиеся BEAM проходят четыре занятия, по одному из следующих направлений: логическое мышление, основы математики, командные стратегии математики и прикладная математика. В начале лета студенты выбирали, какую версию каждого занятия они хотели пройти. Их варианты были:

Логическое мышление:
- Головоломки KenKen и многое другое
- Лучшие головоломки!
- Элементарно, дорогой мой!
- Лжецы, истины и более
Математические основы:
- Фракции и пищи
- Экспоненты: Super-Powers of Числа
- Паттерны, линии и номеры. Криптография
- Голосование: как управлять страной
- Компьютерное программирование
Math Team Strategies:
- Using Patterns to Solve Problems
- Counting Without Counting and Fantastic (Number) Beasts
- Words, Meet Numbers: An Algebra Story
Don’t those sound fun? Как студенты выбирали?? Каждый инструктор дал описание курса и образец задачи! Вот один набор для рассмотрения!
Элементарно, дорогой мой!
Описание курса:
Вы когда-нибудь задумывались, как такие детективы, как Шерлок Холмс, разгадывают запутанные тайны? Все дело в деталях. На этом занятии мы изучим различные методы, используемые для решения сложных загадок, и способы их применения в сложных математических задачах.
Пример задачи:
Мистер Красный, Мистер Синий и Мистер Белый встречаются в ресторане за обедом. Под пальто они носят красную, синюю или белую рубашку. Мистер Блю говорит: «Эй, вы заметили, что мы все носим рубашки разного цвета из-за наших имен?» Мужчина в белой рубашке говорит: «Вау, мистер Блю, верно». Можете ли вы сказать, кто носит рубашку какого цвета?
Open Math Time
Одной из основных целей BEAM является то, что учащиеся проводят время, занимаясь математикой, которая им нравится! Таким образом, во время Open Math Time учащиеся получают меню вариантов, которые они могут использовать. Мы рекомендуем учащимся продолжать возвращаться к этому меню опций в 7-м классе всякий раз, когда они ищут вызов! Во время Open Math Time учащиеся могут:
- Повысьте эффективность своих занятий с помощью наборов задач
- Попробуйте решить еженедельную задачу
- Работайте над задачей из 100 задач (подробнее об этом позже!)
  Студенты могут работать самостоятельно или в группах! Это действительно до того, что делает каждого студента наиболее продуктивным.
  Мероприятия
  Утренние занятия длятся всю неделю! Это время, чтобы освоить новые навыки или потратить целую неделю на увлечение. Варианты на этой неделе:
  - Настольные игры: старая классика и новинка!
  - Украсьте свою папку
  - Смотрите чемпионат мира: смотрите живые и старые футбольные матчи!
  - Научитесь собирать кубик Рубика
  - Веселье на крыше: украсть бекон и акулу Sharky
  - Научитесь играть в Settlers: торговая и строительная настольная игра, действие которой происходит в мифическом мире Катана!
  - Learn Dominion: стратегическая карточная игра, в которой каждый раз вы играете по-новому!
  Вторая половина дня
  Затем наступает обед (шведский стол из местных ресторанов), следующий урок, следующий блок Open Math Time и дневные мероприятия, которые меняются каждый день.
  В общем, сегодня насыщенный и захватывающий день, и в ближайшие недели у нас будет чем поделиться!
  Tagged: Лос-Анджелес, ЛУЧ 6, ЛУЧ 6 2018, ЛУЧ 6 Лос-Анджелес 2018, ЛУЧ 6 Лос-Анджелес, луч Лос-Анджелес, 6-й класс, математика, открытое время математики, мероприятия, класс, занятия, день из жизни
  Даниил Захарополь
  28. 07.2016
  Бард 2016
  Даниил Захарополь
  28.07.2016
  Бард 2016
  Теги: лагерь, лето, математика, Бард 2016, класс
  Даниил Захарополь
  22 июля 2016 г.
  Вассар 2016
  Даниил Захарополь
  22 июля 2016 г.
  Вассар 2016
  Как упоминалось ранее, все студенты BEAM изучают решение задач на протяжении всей программы. Помимо математических командных стратегий, есть еще один вариант — «Решение больших проблем»: работа над одной и той же проблемой в течение 2 с лишним часов и работа над ее пониманием.
  На сегодняшнем занятии учащиеся решили следующую задачу:
  Какие положительные целые числа можно представить в виде суммы последовательных целых чисел?
  У студентов было несколько первых предположений, в том числе:
  - Все нечетные целые числа обладают этим свойством.