Обратная функция. Видеоурок. Алгебра 10 Класс

Пусть задана функция , множество  и множество . Функция из  в :  Каждому элементу из первого множества  соответствует единственный элемент второго множества . С этой функцией связано две основные задачи:

1 задача – прямая. Вычислить значение функции по заданному значению аргумента.

задано, необходимо вычислить .

2 задача – обратная. Найти те значения аргумента, при которых функция принимает заданное значение . Задаем , далее необходимо решить уравнение , которое может иметь одно решение, второе решение и т. д. …

Пример обратной задачи: требуется найти время  для достижения ракетой заданной высоты, самолетом скорости звука, автомобилем заданной скорости 100 км/ч. Нас будет интересовать такая обратная задача, которая имеет единственное решение.

Пусть  – множество слов. Слово – конечная последовательность букв, смысл здесь не важен.  – множество слов из тех же букв, но записанных в обратном порядке.

Например: .

Итак, задана функция, два множества и соответствие между ними. Обратная задача для этой функции имеет единственное решение. Слову «ток» из множества  соответствует единственное слово «кот» из множества .

Пусть задано множество , состоящее из двух элементов  и множество , состоящее также из двух элементов . Для этих множество возможно четыре функции :

а) 1→3 б)1→4

 2→4 2→3

Нас интересует количество решений в обратной задаче. Рассмотрим первую функцию. Мы видим, что 3 соответствует только один элемент и 4 соответствует только один элемент, аналогично и во второй функции. Таким образом, обратная задача для этих двух функций имеет единственное решение. Запишем еще две функции:

в)1→3 г)1→4

 2→3 2→4

Каждому элементу из первого множества соответствует единственный элемент из второго множества. Обратная задача имеет здесь не единственное решение. 3 соответствует пара элементов 1 и 2, также 4 соответствует пара элементов 1 и 2.

Итак, мы рассмотрели второй пример и выяснили, что обратная задача может иметь единственное решение или нет. Здесь довольно простой случай, так как возможен перебор. Давайте рассмотрим случаи, когда перебор невозможен.

Числовая функция . Область определения функции – множество всеx положительных чисел: . Мы знаем график этой функции. Нарисуем его схематически (рис. 1).

Рис. 1. График функции

Нас интересует обратная задача, то есть сколько решений имеет она при заданном . Перебор здесь невозможен, однако можно просто решить уравнение , если  задан, то . При любом ,  единственный.

. Область определения . Нарисуем схематичный график этой функции (рис. 2).

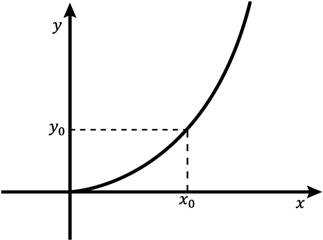
Рис. 2. График функции , область определения .

Вот ветвь параболы – график данной функции. Нас интересует обратная задача. Сколько решений она имеет. Здесь также можно решить уравнение.

. При любом допустимом ,  – единственное число.

, область определения – все действительные числа, . График этой функции нам известен – парабола (рис. 3).

Рис. 3. График функции , область определения – все действительные числа

Итак, нам необходимо узнать, сколько решений имеет обратная задача. Если , то легко видеть, что 16 достигается и при -4, и при +4. Таким образом, уравнение  имеет не единственное решение.

Следует отметить, что единственное решение обратная задача имеет для монотонных функций. В примере 3 функция монотонно убывает, каждый  достигается при одном значении . В примере 4 функция монотонно возрастает, то есть каждый y достигается только при одном значении x.

Числовую функцию  называют возрастающей или убывающей на множестве  ∈ , если для любых чисел  , таких, что , имеем , то есть большему значению аргумента соответствует большее значение функции. Чем больше аргумент, тем больше функция, эта функция монотонно возрастает.

Если большему значению аргумента соответствует меньшее значение функции, то есть , то такую функцию называют убывающей.

Пусть  – монотонная функция. Тогда уравнение  имеет единственное решение  для любого  из множества значений функции.

Предположим, что функция монотонно возрастает на отрезке  принимает значение из отрезка  (рис. 4). Необходимо доказать, что любое значение  эта монотонная функция принимает при единственном значении аргумента .

Рис. 4. График функции

Доказательство

Докажем методом от противного. Предположим, что существует такое значение  из множества значений функции, что уравнение  имеет не единственное решение. Например, два решения

interneturok.ru

Примеры обратных функций | Математика

Обратная функция — функция y=g(x), которая получается из данной функции y=f(x), если из отношения x=f(y) выразить y через x.

Чтобы для данной функции y=f(x) найти обратную, надо:

1.В соотношении y=f(x) заменить x на y, а y — на x: x=f(y) .

2.В полученном выражении x=f(y) выразить y через x.

Функции f(x) и g(x) — взаимно обратны.

Примеры нахождения обратных функций:

1) y=3x-8

1. x=3y-8

2. 3y=x+8

y=(x+8)/3.

2) y=11-5x

1. x=11-5y

2. 5y=11-x

y=(11-x)/5.

Область определения и область значений функций f и g меняются местами: область определения f является областью значений g, а область значений f — областью определения g.

Не для всякой функции можно указать обратную. Условие обратимости функции —  ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.

Пример обратных функций, заданных на промежутке.

y=x².

Это — квадратичная функция. Она убывает на промежутке (-∞;0), и

возрастает на промежутке (0;∞). Возьмем промежуток [0;∞). На этом промежутке функция монотонна, поэтому обратима. Ищем обратную функцию.

1. x=y²

2. y=√x.

y=x² и y=√x на [0;∞) — взаимно обратные функции.

Графики взаимно-обратных функций симметричны относительно прямой y=x.

 

www.matematika.uznateshe.ru

Обратная функция. Урок алгебры в 10-м классе (профильный уровень)

Разделы: Математика

---

Цели урока:

Образовательная:

• формировать знания по новой теме в соответствии с программным материалом;
• изучить свойство обратимости функции и научить находить функцию, обратную данной;

Развивающая:

• развивать навыки самоконтроля, предметную речь;
• овладеть понятием обратная функция и усвоить методы нахождения обратной функции;

Воспитательная:  формировать коммуникативную компетентность.

Оборудование: компьютер, проектор, экран, интерактивная доска SMART Board, раздаточный материал (самостоятельная работа) для работы в группе.

Ход урока.

1. Организационный момент.

Цель – подготовка учащихся к работе на уроке:

-определение отсутствующих,

— настрой учащихся на работу, организация внимания;

— сообщение темы и цели урока.

2. Актуализация опорных знаний учащихся. Фронтальный опрос.

Цель — установить правильность и осознанность изученного теоретического материала, повторение пройденного материала.<Приложение 1>

Для учащихся на интерактивной доске демонстрируется график функции. Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования. Учитель справа от графика функции маркером на интерактивной доске записывает названные свойства.

Свойства функции:

1. D(f) = [-4;),E(y) = [0;), 
2. ни четная, ни нечетная, непериодическая, непрерывная, ограничена снизу;
3. y=0, при х=0
4. y>0 при на [-4;0) и на [0;)
5. возрастает на [-2;-1] и на [0;)
   убывает на [-4;-2] и на [-1;0]
6. y_наиб— не существует
   y_наим=0 при х=0
7. x_max= -1 ,y_max = 2
   x_min = -2, y_min = 1
   x_min = 0, y_min = 0
8. Выпукла вниз на [4;-1], выпукла вверх на [1;), невыпуклая на [-1;1].

По окончании исследования учитель сообщает, что сегодня на уроке они познакомятся еще с одним свойством функции – обратимостью. Для осмысленного изучения нового материала учитель предлагает ребятам познакомиться с основными вопросами, на которые учащиеся должны дать ответ по окончании урока. Вопросы записаны на обыкновенной доске и в виде раздаточного материала есть у каждого ученика (раздается до урока)

Вопросы:

1. Какая функция называется обратимой?
2. Любая ли функция обратима?
3. Какая функция называется обратной данной?
4. Как связаны область определения и множество значений функции и обратной ей функции?
5. Если функция задана аналитически, как задать формулой обратную функцию?
6. Если функция задана графически, как построить график обратной ей функции?

3. Объяснение нового материала.

Цель — формировать знания по новой теме в соответствии с программным материалом; изучить свойство обратимости функции и научить находить функцию, обратную данной; развивать предметную речь.

Учитель проводит изложение материала в соответствии с материалом параграфа. На интерактивной доске учитель проводит сравнение графиков двух функций, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет, тем самым подводит учащихся под понятия обратимой функции.

Затем учитель формулирует определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.

Определение 1: Функцию y=f(x), x X называют обратимой, если любое свое значение она принимает только в одной точке множества X.

Теорема: Если функция y=f(x) монотонна на множестве X , то она обратима.

Доказательство:

1. Пусть функция y=f(x) возрастает на Х и пусть х₁≠х₂— две точки множества Х.
2. Для определенности пусть х₁< х₂.
   Тогда из того, что х₁ < х₂ следует, что f(х₁) < f(х₂).
3. Таким образом, разным значениям аргумента соответствуют разные значения функции, т.е. функция обратима.

(По ходу доказательства теоремы учитель маркером делает все необходимые пояснения на чертеже)

Перед тем как сформулировать определение обратной функции учитель просит учащихся определить, какая из предложенных функций обратима? На интерактивной доске показаны графики функций и записаны несколько аналитически заданных функций:

 А)

 Б)

Г) y = 2x + 5 

Д) y = -x₂ + 7

Учитель вводит определение обратной функции.

Определение 2: Пусть обратимая функция y=f(x) определена на множестве Х и Е(f)=Y. Поставим в соответствие каждому y из Y то единственное значение х, при котором f(x)=y. Тогда получим функцию, которая определена на Y, а Х – область значений функции

Эту функцию обозначают x=f ^-1(y) и называют обратной по отношению к функции y=f(x).

Учащимся предлагается сделать вывод о связи между областью определения и множеством значений обратных функций.

Для рассмотрения вопроса о способах нахождения функции обратной данной, учитель привлек двух учащихся. Ребята накануне получили задание у учителя самостоятельно разобрать аналитический и графический способы нахождения функции обратной данной. Учитель выступил в роли консультанта при подготовке учащихся к уроку.

Сообщение первого ученика.

Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.

Учащийся привел примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима

Затем ученик знакомит учащихся со способом нахождения обратной функции, заданной аналитически.

Алгоритм нахождения

1. Убедиться, что функция монотонна.
2. Выразить переменную х через у.
3. Переобозначить переменные. Вместо х=f ^-1(y) пишут y=f ^-1(x)

Затем решает два примера на нахождение функции обратной данной.

Пример 1: Показать, что для функции y=5x-3 существует обратная функция, и найти ее аналитическое выражение.

Решение. Линейная функция y=5x-3 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим Это и есть искомая обратная функция. Она определена и возрастает на R.

Пример 2: Показать, что для функции y=x², х≤0 существует обратная функция, и найти ее аналитическое выражение.

Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции.

Ответ:

Второй ученик выступает с сообщением о графическом способе нахождения обратной функции. В ходе своего объяснения ученик использует возможности интерактивной доски .

Чтобы получить график функции y=f ^-1(x), обратной по отношению к функции y=f(x), надо график функции y=f(x)преобразовать симметрично относительно прямой y=x.

Во время объяснения на интерактивной доске выполняется следующее задание:

Построить в одной системе координат график функции и график обратной ей функции. Запишите аналитическое выражение обратной функции.

4. Первичное закрепление нового материала.

Цель – установить правильность и осознанность понимания изученного материала, выявить пробелы первичного осмысления материала, провести их коррекцию.

Учащиеся делятся на пары. Им раздаются листы с заданиями, в которых они и выполняют работу в парах. Время на выполнение работы ограничено (5-7 мин). Одна пара учащихся работает на компьютере, проектор на это время выключается и остальным ребятам не видно, как работают учащиеся на компьютере.

По окончании времени (предполагается, что с работой справилось большинство учащихся) на интерактивной доске (вновь включается проектор) показывается работа учащихся, где и выясняется в ходе проверки правильность выполнения задания в паре. При необходимости учителем проводится коррекционная, разъясняющая работа.

Самостоятельная работа в парах <Приложение 2 >

5. Итог урока. По вопросам, которые были заданы перед началом лекции. Объявление оценок за урок.

Домашнее задание §10. №№ 10.6(а,в) 10.8-10.9(б) 10.12 (б)

Алгебра и начала анализа. 10 класс В 2-х частях для общеобразовательных учреждений (профильный уровень) /А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова и др.; под ред. А.Г.Мордковича, М: Мнемозина, 2007 год

31.03.2010

xn--i1abbnckbmcl9fb.xn--p1ai

Обратная функция

Вопросы занятия:

·     познакомиться с понятиями прямой и обратной функции;

·     познакомиться с понятием обратимой функции;

·     научиться находить обратные функции;

·     рассмотреть свойство обратных функций.

Материал урока

Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.

Определение.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

Область определения обозначается D(f).

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Рассмотрим задачу.

Задача.

Рассмотрим ещё одну задачу.

Задача.

Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.

Давайте рассмотрим с вами ещё одну задачу.

Задача.

 

Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.

Определение.

Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.

Приведём примеры обратимых функций:

 

Рассмотрим функцию y=x².

Определение.

Пусть y = f(x) – обратимая функция. Тогда каждому y из множества значений функции соответствует одно определённое число x из области определения, такое, что f(x) = y. Это соответствие определяет функцию x от y, которую обозначим x = g(y). Поменяем местами x и y: y = g(x). Функцию y = g(x) называют обратной к функции y = f(x). Обозначают f^-1(x).

Давайте разберём это определение на примере.

Пример.

Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.

Сформулируем основные свойства обратных функций.

Решим несколько примеров.

Пример.

Пример.

videouroki.net

Обратная функция. Алгебра, 10 класс: уроки, тесты, задания.

1.	Обратные функции Сложность: лёгкое	1
2.	Функция, обратная линейной функции Сложность: лёгкое	1
3.	Линейная функция Сложность: лёгкое	3
4.	Функция, обратная квадратичной функции Сложность: среднее	2
5.	Вычисление сложной функции Сложность: среднее	2
6.	Нахождение обратной функции Сложность: среднее	1
7.	Показательная функция Сложность: сложное	3
8.	Логарифмическая функция Сложность: сложное	3
9.	Обратная функция к показательной функции Сложность: сложное	3

www.yaklass.ru

Обратная функция | Алгебра

Что такое обратная функция? Как найти функцию, обратную данной?

Определение.

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо:

1) В формулу функции вместо y подставить x, вместо x — y:

x=f(y).

2) Из полученного равенства выразить y через x:

y=g(x).

Пример.

Найти функцию, обратную функции y=2x-6.

1) x=2y-6

2) -2y=-x-6

y=0,5x+3.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая.  Для построения прямой берём две точки.

   

   

Однозначно выразить y через x можно в том случае, когда уравнение  x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).

Теорема (необходимое и достаточное  условие обратимости функции)

Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.

Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.

Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.

Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.

Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).

1) x=y².

2)

   

Так как y≥0, то

   

то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:

В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.

www.algebraclass.ru

Взаимно обратные функции. — Алгебра

• МБУ «Нижнедевицкая гимназия»
• учитель математики
• Быканова Людмила Ивановна

• Обратная функция

Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определенному правилу f число у , то, говорят, что на этом множестве задана функция .

D(f) – область определения функции;

х – независимая переменная или аргумент;

у – зависимая переменная;

множество всех значений y=f(x), xϵХ называют областью значений функции и обозначают E(f).

Задача

Пусть дана функция y=f(x)

Найти значение функции в точке х=х 0

Например:

Найти значение функции у=5х+7 в точке х=7.

у(7)=5∙7+7

Ответ: у(7)=42

Прямая

Задача

Пусть дана функция y=f(x)

Найти значение аргумента в точке у=у 0

Например:

Дана функция у=5х+7. Найти значе-

ние аргумента при котором у=22.

22=5х+7

5х=22-7

5x=15

х=15:5

x=3

Ответ: у(3)=22

Обратная

=35+7=42

Пусть дан закон изменения скорости движения от времени

Найти закон изменения времени от скорости.

Решение:

0 – gt=

gt= – 0

t=

 

 

Обратимая функция

Обратная функция к

 

 

 

Если функция принимает каждое свое значение у только при одном значении x , то эту функцию называют обратимой .

Пусть обратимая функция. Тогда каждому из множества значений функции соответствует одно определенное число из области определения, такое, что Это соответствие определяет функцию от , которую обозначим . Поменяем местами и : Функцию называют обратной к функции . Обозначают .

 

 

 

Найти функцию, обратную функции

 

Решение:

Ответ:

 

y

y

5

0

x

x

5

0

 

 

• Область определения обратной функции совпадает с множеством значений исходной функции , а множество значений обратной функции совпадает с областью определения исходной функции

• Монотонная функция является обратимой:

а) если функция возрастает, то обратная к ней функция также возрастает;

б) если функция убывает, то обратная к ней функция также убывает.

 

• Свойства обратных функций:

Показать, что для функции существует обратная функция, и найти ее аналитическое выражение.

 

Решение:

Функция возрастает на R.

Значит, обратная функция существует на R.

Решим уравнение относительно . Получим,

Поменяв местами и получим:

Это и есть искомая обратная функция.

Дана функция

 

Доказать, что для нее существует обратная функция, записать аналитическое выражение обратной функции в виде и построить график обратной функции.

Решение:

 

Функция возрастает на промежутке значит, она имеет обратную функцию.

Из уравнения находим: или . Промежутку принадлежат лишь значения функции .

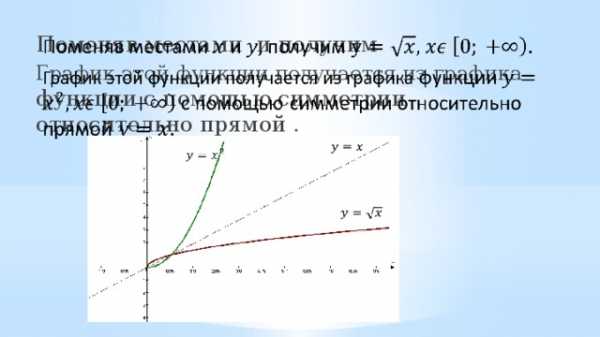
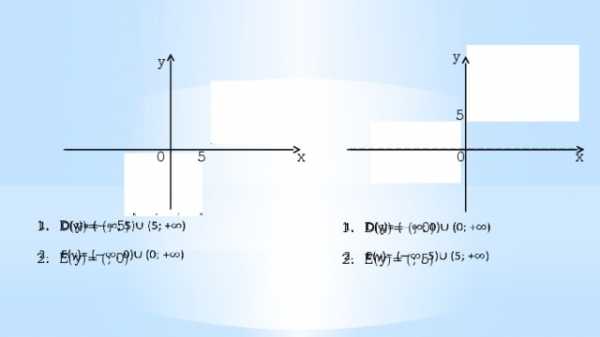
Поменяв местами и получим

 

График этой функции получается из графика функции с помощью симметрии относительно прямой .

 

 

 

multiurok.ru